Mostrando artículos por etiqueta: descartesjs
Primera sesión (25 de marzo de 2022)
|
1A.
1B.
|
La tercera edición del curso "Edición de libros interactivos" de la RED Descartes (segundo semestre de 2022, marzo a julio de 2022) se está desarrollando según la siguiente planificación:
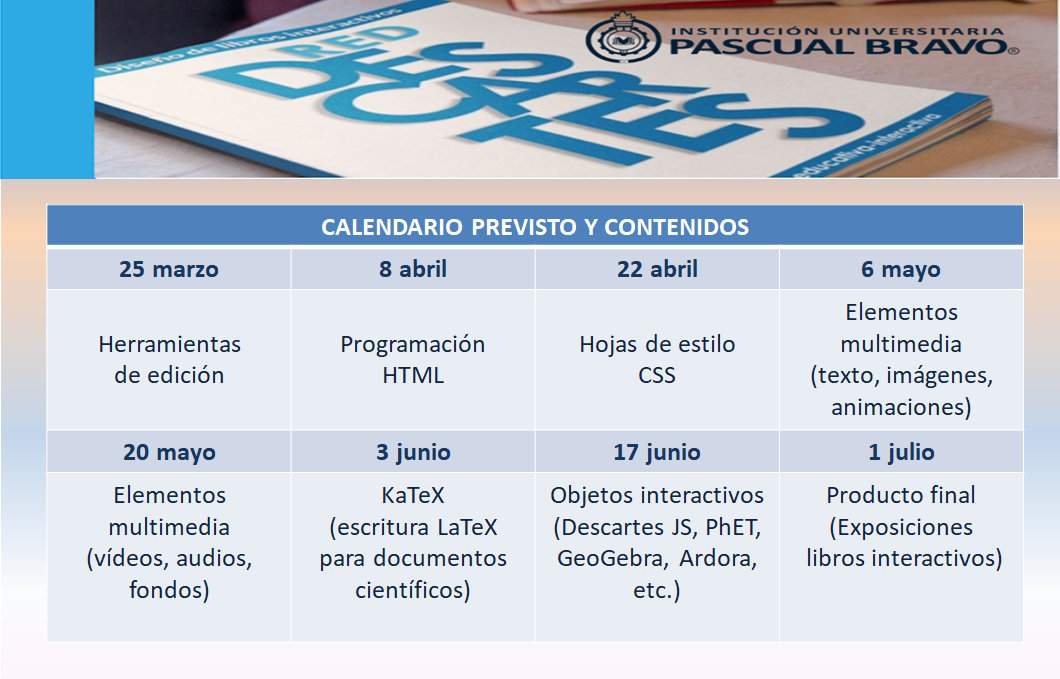
- Primera sesión (25 de marzo de 2022).
- Segunda sesión (8 de abril de 2022).
- Tercera sesión (22 de abril de 2022).
- Cuarta sesión (6 de mayo de 2022).
- Quinta sesión (20 de mayo de 2022).
- Sexta sesión (3 de junio de 2022).
- Séptima sesión (17 de junio de 2022).
- Octava sesión (1 de julio de 2022).
Página inicial del curso "Edición de libros interactivos" III edición
|
Diseño de libros interactivos |
- La plantilla o plantillas del libro interactivo. Acceda, mire, observe y descargue la plantilla que vaya a usar.
En el curso se comienza con una plantilla básica (Mi_libro) que puede ver aquí y también descargarla desde acá. - Necesita un editor de texto plano para poder editar ficheros en código html, puede ser el bloc de notas de Windows o TextEdit de iOS, pero le recomendamos Notepad++ o Sublime text porque estos colorean las etiquetas y faclitan la edición. Por favor, descargue el que vaya a usar.
Comience su auto-formación
Lea e interactúe con el libro "Curso de libros interactivos", antes enlazado. También puede descargarlo.
¿Alguna ayuda adicional?
- Puede escribirnos a Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo..
- Puede inscribirse a los cursos de formación en línea cuando se convoquen (ver convocatoria de la tercera edición).
- Puede consultar los vídeos grabados en las sesiones de la tercera edición del curso en línea que ha sido promovido por la Institución Universitaria Pascual Bravo de Medellín (Colombia), por RED Descartes de Colombia y RED Descartes España y que está dirigido e impartido por el Dr. Rivera, vicerrector de dicha institución y presidente de la RED Descartes de Colombia.
Vídeos de la tercera edición en línea del curso "Edición de libros interactivos"
Título: Diseño de libros interactivos
Sección: iCartesiLibri
Bloque: Formación
Unidad: Formación en Descartes JS
Nivel/Edad: Bachillerato y Universidad (16 años o más)
Idioma: Castellano
Autores: Juan Guillermo Rivera Berrío y Joel Espinosa Longi
ISBN: 978-84-18834-27-1
![]() Haz clic aquí para ver una versión en pdf
Haz clic aquí para ver una versión en pdf
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
La Semana de la Educación Abierta (Open Education Week) es una oportunidad para compartir activamente y aprender sobre los últimos logros en Educación Abierta en todo el mundo. OE Week brinda a los profesionales, educadores y estudiantes la oportunidad de obtener una mayor comprensión de las prácticas educativas abiertas y de inspirarse en el maravilloso trabajo que está desarrollando la comunidad en todo el mundo. Unos objetivos que encajan perfectamente con el lema de Red Descartes: "trabajando altruistamente por la comunidad educativa de la aldea global". Por ello, en esta nueva edición, que se desarrolla durante los días comprendidos entre el 7 y el 11 de marzo de 2022, desde Proyecto Descartes hemos decidido colaborar, compartir y aportar algunos de nuestros proyectos en la línea de la OE Week, centrándonos en los más recientes y abarcando las diferentes líneas de la Educación Abierta.
Pero antes, para nuestros seguidores, docentes, comunidad educativa y ciudadanía, en general, conviene recordar el origen oficial y concepto de Recurso Educativo Abierto, que aparece en París en junio de 2012, durante el Congreso Mundial sobre los Recursos Educativos Abiertos (REA), y que "designa a materiales de enseñanza, aprendizaje e investigación en cualquier soporte, digital o de otro tipo, que sean de dominio público o que hayan sido publicados con una licencia abierta que permita el acceso gratuito a esos materiales, así como su uso, adaptación y redistribución por otros sin ninguna restricción o con restricciones limitadas". Una definición cuyos requisitos cumplen escrupulosamente los recursos interactivos generados con la herramienta de autor Descartes JS y compartidos con la aldea global en el portal de la ong RED Descartes.

| RECURSOS EDUCATIVOS ABIERTOS EN LENGUA PORTUGUESA | ||
 |
 |
 |
 |
 |
 |
 |
 |
 |
| FORMACIÓN ABIERTA | |
 |
 |
Además de los recursos educativos abiertos en lengua portuguesa y de los cursos para formación, a los que puede accederse desde cada imagen al espacio de la Open Education Week, desde RED Descartes hemos presentado nuestra revista digital y la herramienta de autor de software libre Descartes JS, el pilar sobre el que se sostiene nuestra RED.
| REVISTA DIGITAL RED DESCARTES |
 |
¿Por qué es importante la Educación Abierta?
La gente quiere aprender. Al proporcionar acceso gratuito y abierto a la educación y al conocimiento, la educación abierta ayuda a crear un mundo para apoyar el aprendizaje. Los estudiantes pueden obtener información adicional, puntos de vista y materiales para ayudarlos a tener éxito. Los trabajadores pueden aprender cosas que los ayudarán en el trabajo. La facultad puede recurrir a recursos de todo el mundo. Los investigadores pueden compartir datos y desarrollar nuevas redes. Los maestros pueden encontrar nuevas formas de ayudar a los estudiantes a aprender.
Las personas pueden conectarse con otras personas que de otra manera no se encontrarían para compartir ideas e información. Los materiales se pueden traducir, mezclar, dividir y compartir abiertamente de nuevo, lo que aumenta el acceso e invita a nuevos enfoques. Cualquiera puede acceder a materiales educativos, artículos académicos y comunidades de aprendizaje de apoyo en cualquier momento que lo deseen. La educación está disponible, accesible, modificable y gratuita".
(El párrafo anterior ha sido extraído literalmente de la web de la Open Education Week)
| HERRAMIENTA DE AUTOR DE SOFTWARE LIBRE DESCARTES JS |
 |
Octava sesión (4 de febrero de 2022)
|
1A.
|
Séptima sesión (28 de enero de 2022)
|
1A.
|
Sexta sesión (21 de enero de 2022)
|
1A.
|
Quinta sesión (14 de enero de 2022)
|
1A.
|
Título: Comunicación DescartesJS-GeoGebra
Sección: iCartesiLibri
Bloque: Formación
Unidad: Formación en Descartes JS
Nivel/Edad: Bachillerato y Universidad (16 años o más)
Idioma: Castellano
Autores: Juan Guillermo Rivera Berrío
ISBN: 978-84-18834-23-3
![]() Haz clic aquí para ver una versión en pdf
Haz clic aquí para ver una versión en pdf
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)






 CONTACTO
CONTACTO
