Primera tarea
Descargar en instalar el editor de DescartesJS. Haz clic en la imagen de la siguiente página y, según tu sistema operativo, procede a cumplir con esta tarea inicial
Juan Guillermo Rivera Berrío
Red Educativa Digital Descartes
Institución Universitaria Pascual bravo
Córdoba (España)
2022
Título de la obra:
Comunicación DescartesJS - GeoGebra
Autor:
Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS y GeoGebra
Fuentes: Amaranth y UbuntuMono
Imágenes decorativas: https://placeit.net/
Fórmulas matemáticas: $\KaTeX$
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-23-3

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Este libro se ha desarrollado para explicar cómo se pueden diseñar objetos interactivos que incluyan dos herramientas de autor. La primera herramienta es Descartes en su versión JavaScript, la cual permite incluir diferentes elementos multimedia (imágenes, gráficas 2D y 3D, videos, audios, animaciones, textos y expresiones matemáticas en formato $\LaTeX$). La segunda herramienta es GeoGebra, que complementa la primera al permitir dasarrollar escenas interactivas con la incorporación del cálculo simbólico (CAS), una gran variedad de funciones (matemáticas, estadísticas, lógicas, financieras, entre otras) y, obviamente, la Geometría y Algebra que dieron origen a su nombre.
En 2016, nuestra colega Elena Álvarez Saiz de la Red Educativa Digital Descartes, presentó un modelo que permitía comunicar escenas Descartes con los comandos de GeoGebra e, incluso, construcciones completas que podían ser manipuladas desde la propia escenaVéase el artículo en el blog del Proyecto Descartes.. A partir de la propuesta de Elena, se abrió un abanico de posibilidades entre las que se incluyen: videos interactivos, tutoriales para la enseñanza de GeoGebra con Descartes como tutor y el diseño de objetos interactivos que aprovechen los recursos de ambas herramientas de autor.
Las escenas interactivas incluidas en el libro y los intérpretes de DescartesJs y de GeoGebra se encuentran en una carpeta, de tal forma que se puedan abrir sin necesidad de estar conectados al portal del Proyecto Descartes o de la web GeoGebra.
¡Se requieren conocimientos de DescartesJS y GeoGebra!
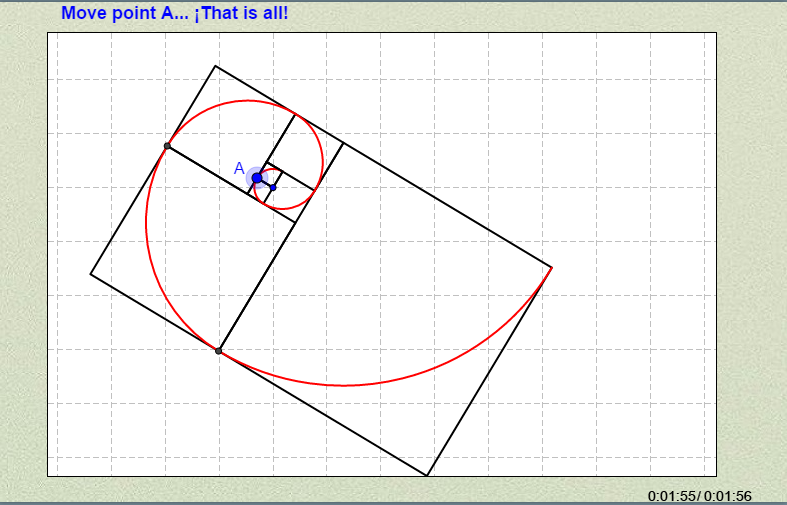
Descartes es una herramienta de autor que permite elaborar recursos didácticos interactivos que se embeben en páginas html y, por tanto, puede interactuarse con ellos en todos los dispositivos donde una página web sea accesible. La primera impresión al ver un recurso de Descartes puede inducir a interpretar que es una imagen animada o una animación, pero basta aproximar el ratón o el dedo a un recurso de Descartes para comprobar la esencia del mismo que se centra en la interactividad.
Esto es una animación, pero generada con Descartes. Si paras la animación podrás interactuar modificando el valor de N o posicionándote en el punto rojo y desplazándolo. Esto es una pequeña muestra de lo que diferencia un recurso de Descartes.
Al recurso básico generado con Descartes se le denomina escena. Al emplear este término teatral y cinematográfico para denominar a las actividades realizadas con Descartes, lo que se persigue es trasladar su significado, sus acepciones, al contexto educativo poniendo especial énfasis en que es algo muy diferente de una animación, si bien con una escena también pueden construirse animaciones. No es lo mismo ser un espectador viendo una película (animación) que ser actor en una obra de teatro. Descartes aporta el escenario, el decorado, la infraestructura técnica, y es el usuario, nuestro alumnado y nosotros mismos, los que en cada escena han de abordar su papel de actor protagonista. Y en el desarrollo de esa obra teatral habrá escenas en las que se verá guiado por el director, en algunas tendrá que descubrir el guión y en otras aportar su destreza e iniciativa para construir su propio guión, pero todo lo hará gracias a la interacción con Descartes. El escenario se adapta al actor y éste construye la obra. De esta analogía teatral surge la denominación de escena. Y en el esbozo anterior ya se está marcando la posibilidad de una utilización metodológica diversa.
Las escenas pueden adaptarse desde metodologías expositivas en las que se pueden usar como apoyo gráfico en una explicación, hasta metodologías constructivistas en las que las escenas promueven la investigación y a partir de ella la construcción del conocimiento logrando un aprendizaje significativo. El director de escena (el profesorado) es el que marca la puesta en escena a su alumnado. El profesor es el arquitecto del aprendizaje y sus alumnos los protagonistas del mismo. A veces puede verse condicionado por el autor del libreto (autor de la escena), pero él es quien organiza el aprendizaje y si lo desea (y quiere formarse para ello) puede también modificar ese guión o adaptarlo a sus necesidades y gustos particulares.
Descartes nace a fines del siglo XX como una herramienta de creación de interactivos que aprovecha el lenguaje de programación Java. Entonces consistió en un programa en Java que permitía generar archivos .html para ser visualizados como páginas web.
Los archivos html generados por Descartes suelen contener interactivos y son principalmente usados en la docencia de matemáticas y física en diversos niveles.
A pesar de que existe una gran variedad de programas interactivos con fines de docencia tales como GeoGebra, Cabri y otros, Descartes permite una gran versatilidad de interacciones. Adicionalmente, con Descartes es posible generar interacciones específicas diseñadas por el profesor, ejercicios aleatorios con restricciones particulares, además de presentar muchas otras ventajas.
En sus inicios, Descartes funcionaba directamente en Java para ser usados en computadora. No obstante, el advenimiento de dos tecnologías nuevas forzaron un cambio en Descartes, a saber:
Se volvió entonces necesario que los interactivos corrieran en dispositivos móviles (en JavaScript). Descartes 5 nace de esta necesidad. Un nuevo editor fue creado con esto en mente. Aunque no hubo cambios muy drásticos en el editor, fue necesario incluir una biblioteca nueva.
La versión 5 del editor de Descartes es la penúltima en la lista de versiones. También se encuentra programada en Java. No obstante, la versión JS de Descartes es la más actual.
Dicho editor se encuentra programado en JavaScript y su funcionalidad es básicamente muy similar al de la versión Descartes 5, aunque tiene muchas ventajas sobre él. También es importante mencionar que, a diferencia de Descartes 5, el nuevo editor DescartesJS tiene la virtud de que lo que se visualiza en el editor se representará idéntico en un navegador. Por ejemplo, en Descartes 5 existía el problema de los tamaños de fuente de texto mostrados en el editor, pues no necesariamente coincidían con los mostrados en un navegador. Esto ya no ocurre en la versión DescartesJS. Aunque la edición de escenas se efectúa en un entorno propio, ajeno al navegador que después elija el usuario para ver e interactuar con dichas escenas, la funcionalidad y el aspecto es exactamente el mismo al pasar de un contexto al otro pues en ambos casos se está utilizando el mismo intérprete de Descartes.
En sus inicios, Descartes se pensó como una herramienta de autor para el diseño y publicación de escenas interactivas para la enseñanza y aprendizaje de las matemáticas; sin embargo, por su versatilidad, ha sido posible diseñar escenas en varias áreas del conocimiento. Por ejemplo, la siguiente escena interactiva fue diseñada para Física:
Descargar en instalar el editor de DescartesJS. Haz clic en la imagen de la siguiente página y, según tu sistema operativo, procede a cumplir con esta tarea inicial

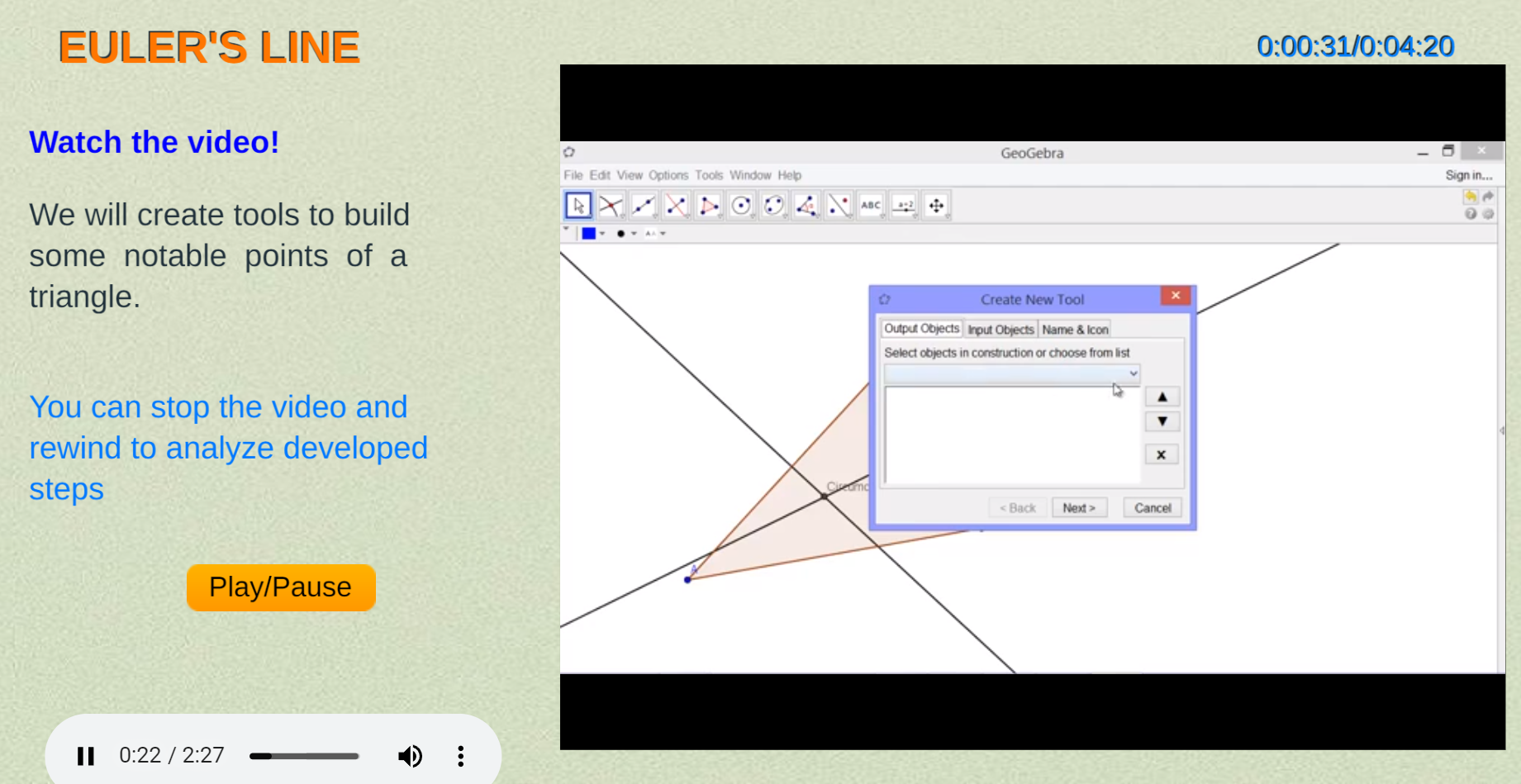
En los primeros dos minutos del siguiente video, puedes observar cómo se hizo para el sistema operativo Windows:
GeoGebra es un software matemático dinámico para todos los niveles de educación que reúne geometría, álgebra, hojas de cálculo, gráficos, estadísticas y cálculo en un paquete fácil de usar. GeoGebra es una comunidad en rápida expansión de millones de usuarios ubicados en casi todos los países
(https://www.geogebra.org/about).
El programa GeoGebra fue ideado por Markus Hohenwarter en el marco de su trabajo de tesis de Master, presentada en el año 2002 en la Universidad de Salzburgo, Austria. Se esperaba lograr un programa que reuniera las virtudes de los programas de geometría dinámica, con las de los sistemas de cálculo simbólico. El creador de GeoGebra valoraba todos estos recursos para la enseñanza de la matemática, pero notaba que para el común de los docentes, los programas de cálculo simbólico resultaban difíciles de aprender, dada la rigidez de su sintaxis, y que por esta razón evitaban su uso. Por otro lado, observaba que los docentes valoraban de mejor manera los programas de geometría dinámica, ya que su interfaz facilitaba su utilización. Así fue como surgió la idea de crear GeoGebra.
Rápidamente el programa fue ganando popularidad en todo el mundo y un gran número de voluntarios se fue sumando al proyecto desarrollando nuevas funcionalidades, materiales didácticos interactivos, traduciendo tanto el software como su documentación a decenas de idiomas, colaborando con nuevos usuarios a través del foro destinado para tal fin. En la actualidad, existe una comunidad de docentes, investigadores, desarrolladores de software, estudiantes y otras personas interesadas en la temática, que se nuclean en los distintos Institutos GeoGebra locales que articulan entre sí a través del Instituto GeoGebra Internacional (https://es.wikipedia.org/).
Las continuas actualizaciones de GeoGebra generan problemas de compatibilidad entre una y otra versión, en especial para el desarrollo de actividades interactivas como las que vamos a trabajar en este libro. Por ello, recomendamos tener decargada la versión 5 portable, la cual puedes hacerlo desde este enlace: versión 5; no obstante, todas nuestras actividades son compatibles con la versión 6 que, si lo deseas, puedes descargar su versión portable desde este enlace: versión 6.
Pero, para nuestros propósitos, la versión 5 es suficiente, pues ofrece las siguientes vistas que se vinculan dinámicamente:
En la siguiente escena interactiva, se muestran las vistas 2D y 3D, que permiten interactuar con una superficie paramétrica.
En este interactivo de GeoGebra, tienes dos opciones de ampliación de la ventana: haciendo clic en la esquina superior derecha o, mucho mejor, haciendo clic en el botón zoom de la esquina inferior derecha.
Nuestro propósito principal, en este libro, es diseñar escenas interactivas con DescartesJS y GeoGebra, en las que ambas herramientas se comunican. Para lograr este propósito es necesario crear una interfaz que comunique las dos herramientas.
Es una buena idea cargar las escenas de GeoGebra usando el intérprete en local, evitando posibles problemas con nuevas versiones pues, como lo dijimos antes, existen algunas incompatibilidades con las versiones anteriores de GeoGebra; por ello, adaptamos y simplificamos las versiones 4.4 y 5.0 con los archivos de GeoGebra, las cuales compartimos a continuación.
Descargar las carpetas de este enlace, descomprimirlas en una carpeta que llamarás interactivos.
Una ventaja del uso de estas carpetas en local, es que permiten presentar las escenas sin necesidad de enlazar a la web de GeoGebra; por ejemplo, la escena interactiva anterior es llamada desde la carpeta interactivos de este libro.
Veamos, ahora, cómo usar las carpetas anteriores; para ello, copia los códigos que presentamos en la siguiente página y, luego, lo pegas en un editor de textos planos, que puede ser el bloc de notas en Windows o el TextEdit de Mac (formato Texto Plano).
En el siguiente video, obervarás cómo creamos una escena en la versión 5 de GeoGebra, capturamos el código de la escena (base64) y, después, creamos el archivo HTML5 con el archivo anterior.
Debiste haber puesto mucho cuidado en cómo se captura el código base64, pues de igual forma lo puedes hacer desde una escena publicada en la red o en la web de GeoGebra. La escena obtenida es la siguiente:
Los códigos que aparecen en la etiqueta "article" son sencillos de entender:
Existen otros parámetros que se pueden incorporar; por ejemplo, data-param-customToolBar permite definir que herramientas aparecerán en la escena.
En la siguiente presentación, explicamos este parámetro, además de repasar cómo capturamos una escena que, para este caso, lo haremos desde la web de GeoGebra.
Para una mejor visualización, amplía la presentación con el botón de la esquina superior derecha. La presentación incluye audio y, si lo deseas, puedes avanzar o retroceder las diapositivas, conservando el audio correspondiente.
Los valores de las diferentes herramientas de GeoGebra, las puedes consultar a continuación:
Según las instrucciones anteriores, busca una escena de GeoGebra en el apartado recursos de https://www.geogebra.org/, captura el código base64 y lo copias en el archivo que debes tener en un editor de textos sin formato (bloc de notas o TextEdit)Los editores de textos "planos" se distinguen de los procesadores de texto en que se usan para escribir solo texto, sin formato y sin imágenes, es decir sin diagramación. Recomendamos algunos de estos editores: SublimeText: http://www.sublimetext.com/ (Mac, Windows y Linux) o Notepad++: http://notepad-plus-plus.org/ (Windows),, lo guardas con el nombre que quieras. Finalmente, lo abres en el navegador para verificar que la tarea ha quedado bien hecha.
Hasta aquí, tenemos los primeros insumos para iniciar la comunicación entre las dos herramientas; por ahora, pueden ir juntas pero sin comunicarse. Por ejemplo, en la siguiente escena interactiva, diseñada con DescartesJS, hemos usado un espacio 2D de Descartes y un espacio HTMLIframe con una escena de GeoGebra (amplía la escena):
Este ejemplo es un primer acercamiento al propósito de este libro pues, como veremos más adelante, es necesario el uso de espacios en DescartesJS para la comunicación de las dos herramientas.
Para los siguientes capítulos, recordamos la frase final del Prefacio:
¡Se requieren conocimientos de DescartesJS y GeoGebra!
Por ejemplo, para la escena anterior:
Como ya lo hemos advertido, GeoGebra ofrece varias herramientas que permiten diseñar escenas interactivas en el amplio campo de conocimiento de las matemáticas. El software presenta ventanas o "vistas" para construcciones geométricas en dos y tres dimensiones, representaciones algebraicas y numéricas, tratamiento matemático y estadístico de datos en hojas de cálculo y una vista especial para cálculo simbólico (CAS).
En este capítulo, presentamos la interfaz de GeoGebra que usaremos para recibir y ejecutar comandos desde DescartesJS, iniciando con el cálculo simbólico (véase la interfaz de DescartesJS en la página 53).
El Sistema de algebra computacional o CAS (por sus siglas en inglés: Computer Algebra System) de GeoGebra, incluye 160 comandos, de los cuales 19 son exclusivos.
La descripción de cada comando, se puede consultar en https://wiki.geogebra.org/es/; por ejemplo, para el comando Cauchy:
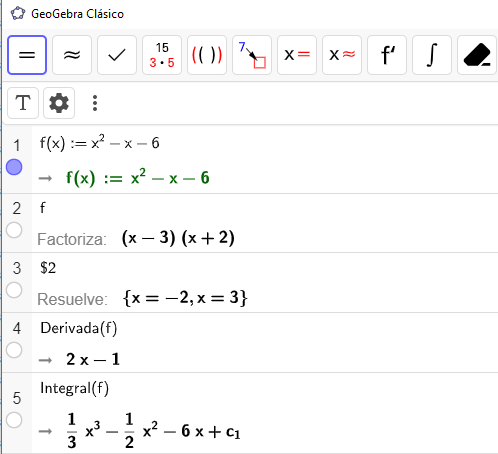
Si la vista CAS la abrimos en GeoGebra, nos aparece una barra de 11 herramientas; entre ellas: Cálculo simbólico, Cálculo numérico, Factoriza, Desarrolla, Resuelve, Derivada e Integral. Observa la Figura 3.1, en la que hemos usado la barra de herramientas para factorizar y hallar las raíces (Resuelve), pero para la derivada y la integral usamos los comandos correspondientes.
Pero, hasta este punto, solo hemos repasado algunos elementos de lo que ya sabes de la vista CAS de GeoGebra, lo que nos interesa es cómo comunicarnos con el CAS desde DescartesJs ¡Aquí viene la cuarta tarea!
En la carpeta interactivos creas una nueva carpeta con el nombre js. Copia el texto de la página siguiente (clic en el botón "copiar"), lo pegas en el editor de textos (plano) y, finalmente, lo guardas en la carpeta js que creaste. El nombre del archivo será comandos.js.
Son más de 450 comandos de GeoGebra en español e inglés (inlcuidos los del CAS), uno de los aportes significativos de Elena Álvarez... veamos porqué:
Como ya debes saber, GeoGebra está taducido en más de 40 idiomas, entre ellos el español, pero internamente sus comandos están en inglés; por ejemplo, cuando damos la orden Asíntota, GeoGebra la traduce a Asymptote, para poder ejecutar este comando.
Con esta cuarta tarea, tendrás uno de los insumos necesarios para todas la interfaces de GeoGebra que usaremos en este libroEn este video, se resumen las cuatro tareas a realizar hasta este apartado..
Ahora, vamos a conocer la primera interfaz que usaremos para comunicar DescartesJS con el Cálculo Simbólico (CAS) de GeoGebra:
En la carpeta interactivos creas una nueva carpeta con el nombre CAS1. Copia el texto anterior (clic en el botón "copiar"), lo pegas en el editor de textos (plano) y, finalmente, lo guardas en la carpeta CAS1 que creaste. El nombre del archivo será interface1.html.
En la siguiente imagen animada, se muestra el estado actual de nuestras tareas.
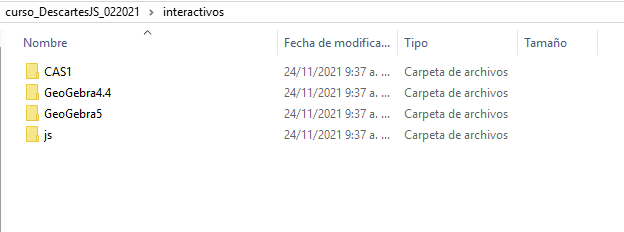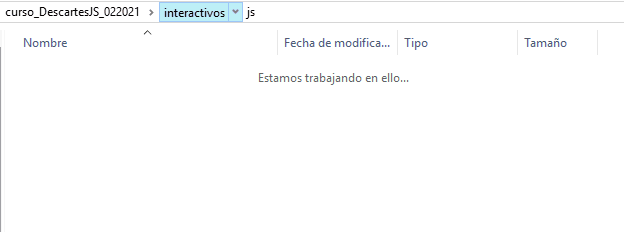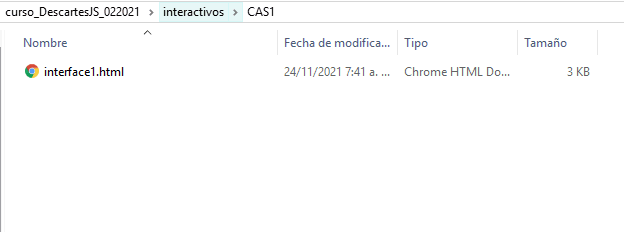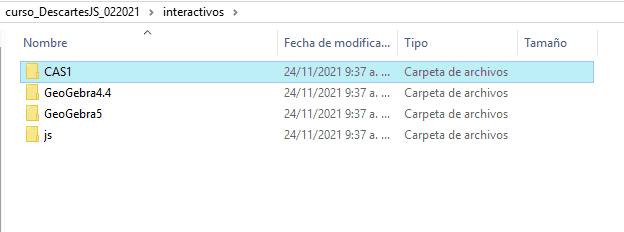
interactivos, hasta la tarea 5.Descripción del archivo
El cuerpo del archivo (body) se compone de dos partes principales, la primera tiene una $\lt script\gt$ y una $\lt article\gt$, que se encargan de ejecutar la herramienta de autor GeoGebra versión 5 para la web. Si se desea, se puede modificar para la versión 4.4.
La segunda parte del archivo la hemos dividido en cuatro bloques, así:
nombre=data.name; asigna el nombre de una variable enviada desde DescartesJS a la variable nombre, que para esta interfaz es evalua; esto significa que en la escena que diseñemos en DescartesJS (en el siguiente capítulo) se debe tener cuidado en la coincidencia de ambas variables.Este mismo nombre se asigna a la variable aux, si no hay coincidencia, aux será cero.
Por ejemplo, en DescartesJS ponemos evalua='Factoriza[x^2-1]' y enviamos ese mensaje a la interface1, entonces tanto nombre como aux se llamarán evalua.
A continuación, hay un condicional if que verifica el nombre data.name==="evalua" y que haya sido enviado a través de datos tipo set. Si lo anterior es cierto, captura el contenido de la variable evalua a través de la instrucción dComando=data.value;, para el ejemplo anterior el contenido sería el comando Factoriza[x^2-1].
Bueno, respiremos un poco antes de continuar, ¿qué tal este jueguito?
Continuemos pues. Si estás siguiendo la lógica de las instrucciones anteriores, ya habrás concluido que la variable dcomando tiene como contenido 'Factoriza[x^2-1]'.
El contenido de esta variable es enviado a una función del bloque 3, así calculosCAS(dComando), cuyo resultado se asigna a la variable rcomando.
Finalmente, en este bloque, sólo resta enviar el resultado a DescartesJS. eso se hace a través de la instrucción: window.parent.postMessage({ type: "set", name: "vCalculado", value: rComando }, '*'); ¿otro jueguito?, ¿no? sigamos pues.
Esta instrucción, en una forma sencilla, significa que se envía un mensaje a DescartesJS cuyo contenido es una variable de nombre vcalculado y cuyo contenido es el obtenido de la función calculosCAS(dComando); es decir, rComando.
calculosCAS(dComando). Lo que se realiza es una partición (split) en dos del comando enviado, separando la palabra que está antes del corchete de apertura (str[0]) de la expresión que está después de él (str[1]); por ejemplo, la orden 'Factoriza[x^2-1]', se divide en str[0]='Factoriza' y str[1]='x^2-1]'. Con la primera palabra, cadena o string, se busca en la matriz de comandos en español el índice del elemento que contiene esta palabra vComandosD.indexOf(com), donde com es la primera cadena (Factoriza), que para el ejemplo es $167$ (según la tabla de comandos anterior). Recuerda que esto es necesario, pues el comando a ejecutar en GeoGebra debe estar en español.Finalmente, se realiza la ejecución del comando con las siguientes expresiones:
cEjecuta=vComandosG[pos]; (Factor para nuestro ejemplo)
comando='f:'+cEjecuta+'['+str2; (Factor[x^2-1], para el ejemplo)
calculo=document.ggbApplet.evalCommandCAS(comando); el resultado se asigna a la variable calculo cuyo valor es retornado al bloque que invocó la función y se asigna a la variable vCalculado.
¿Quedaste exhausto con la explicación?, pues no te imaginas como quedé yo explicándola. Pero, si te sirve de algo, vamos a hacer una trazabilidad del algoritmo con un ejemplo, esto es lo que los programadores llaman "prueba de escritorio"En este video, se describe y explica la interface1.html..
nombre la expresión 'evalua'.dComando=data.value; o dComando='Derivada[x^2-9x]',rComando=calculoCAS(dComando), es decir, debemos ir al tercer bloque.com=str1=str[0]='Derivada'str2=str[1]='x^2-9x]'pos=95 (ver tabla de comandos )cEjecuta='Derivative' (ver tabla de comandos)comando='f:'+cEjecuta+'['+str2;='f:Derivative[x^2-9x]' (orden en inglés)
calculo=document.ggbApplet.evalCommandCAS(comando); (GeoGebra ejecuta la orden y el resultado se asigna a calculo)return calculo (se envía el resultado al bloque 2).rComando.window.parent.postMessage({ type: "set", name: "vCalculado", value: rComando }, '*'); (Se envía este resultado (rComando) a DescartesJS guardado en la variable vCalculado).El cuarto bloque garantiza la existencia de una escena de GeoGebra (ggbOninit), sin ésta no sería posible la comunicación. En el siguiente capítulo veremos la interfaz en DescartesJS, pero para que te animes, observa un ejemplo de aplicaciónEn la página 53 puedes obtener el archivo index.html de DescartesJS, que permite la comunicación con interface1.html y la explicación de esta interface de comunicación. Recomendamos estudiar estas dos interfaces una después de la otra.:
Esta segunda interfaz la usaremos para comunicar DescartesJS con el Cálculo Simbólico (CAS) de GeoGebra y, además, para mostrar la gráfica de la función obtenida (siempre que exista función":
En la carpeta interactivos creas una nueva carpeta con el nombre CAS2. Copia el texto anterior (clic en el botón "copiar"), lo pegas en el editor de textos (plano) y, finalmente, lo guardas en la carpeta CAS2 que creaste. El nombre del archivo será interface2.html.
Descripción del archivo
Similar a la interfaz anterior, el cuerpo del archivo (body) se compone de dos partes principales, en la primera parte tenemos la primera novedad ¿Recuerdas la captura de escenas de GeoGebra del capítulo anterior? ¿sí?, pues en esta interfaz usaremos parámetros similares para la configuración de la parte gráfica de GeoGebra:
Oberva que incluimos dos parámetros nuevos (los últimos), para poner un color de borde a la escena y otro para habilitar la herramienta de ayuda.
En la segunda parte del archivo, solo se presenta un cambio en el bloque 2:
Inclusión de la siguiente instrucción:
document.ggbApplet.evalCommand(rComando);: Evalúa la orden enviada por DescartesJS en el entorno GeoGebra (no en el CAS)En la página 60, presentamos una versión modificada de la interface2.html y la explicación de la interfaz de comunicación DescartesJS.
Como puedes observar, los cambios fueron mínimos, incluso, puedes eliminar los parámetros que incluimos en la etiqueta article y la escena seguirá siendo funcional, su incorporación obedece más a un acercamiento a la siguiente interfaz. Un ejemplo con esta interfaz, es el siguiente:
Puedes probar los siguientes comandos: Raíces[3x³ + 3x² - x, -2, 1], Punto[{1,2}], FactoresPrimos[24], PolinomioTaylor[x^3 sin(y), x, 3, 2] y Covarianza[{1, 2, 3}, {1, 3, 7}]
En la interfaz anterior pudimos comunicarnos, desde DescartesJS, con la vista gráfica de GeoGebra. A continuación, aprovecharemos lo anterior pero recibiendo varias órdenes de DescartesJS y, a su vez, enviando respuestas desde GeoGebra a DescartesJS, situación que se constituye en la base conceptual y procedimental para aplicaciones útiles como los tutoriales de GeoGebra asistidos por DescartesJS y los vídeos interactivos.
En la carpeta interactivos creas una nueva carpeta... bueno, ya sabes el resto.
Para comprender mejor la descripción de esta tercera interfaz, te presentamos el ejemplo de aplicación:
Puedes observar que al ingresar una nueva función, la anterior no se borra en la vista gráfica de GeoGebra. Un elemento adicional es la incorporación de un control tipo barra, para "controlar" un punto en la vista gráficaVéase en la página 66 la interfaz de comunicación de DescartesJS.
Descripción del archivo
Igual a las otras interfaces, el cuerpo del archivo se compone de dos partes principales. En la primera parte recuerda que puedes cambiar el código ggbbase64, tal como lo vimos en la captura de escenas de GeoGebra del capítulo anterior. Los parámetros usados que puedes cambiar, además del código ggbbase64, son:
Con respecto al anterior, sólo desactivamos la barra de herramientas. En la segunda parte, de nuevo, el primer bloque no cambia. Para el segundo bloque, vas a prestar mucha atención, pues trae novedades interesantes, observa y analiza el contenido de la primera estructura de decisión o condicional if. Las cuatro primeras instrucciones son:
Iniciemos con la instrucción num=nombre.charAt(6);. La cadena “chartAt” devuelve el caracter 6 del contenido de la variable nombre que, para varios mensajes de DescartesJS, puede ser "evalua1", "evalua2", "evalua3", ...
Es importante entender que los caracteres de una cadena se indexan iniciando con cero (0); es decir, el caracter 1 de "evalua3" es "v" y el sexto es "3". Así las cosas, num=nombre.charAt(6); devuelve "1", "2", "3", ...
Las instrucciones dComando1 = data.value; y rComando1 = calculosCAS(dComando1); se encargan de realizar los cálculos simbólicos (CAS) que, para la escena anterior, es la "derivada de la función". El resultado obtenido se asigna a "variable" a través de la instrucción variable = "vCalculado"+num;; es decir, "vCalculado1", "vCalculado2", "vCalculado3",..., variable que luego se envía a DescartesJD con el valor calculado (value: rComando1).
Hay cuatro instrucciones, de este primer condicional, que tienen efectos en la vista gráfica de GeoGebra. Observa:
document.ggbApplet.evalCommand(rComando1); permite que el resultado obtenido (función derivada) sea graficado.document.ggbApplet.setColor('g',0,0,255);. A la función se le asigna el color azul.document.ggbApplet.setColor('h',255,0,0);. A la función derivada se le asigna el color rojo.Nota importante: Seguro te habrás preguntado ¿por qué g y h? ¡Muy buena pregunta!, pues la clave de nuestro trabajo posterior, es identificar las etiquetas (label) que GeoGebra asigna a los elementos gráficos diseñados desde la interfaz.
Haz el siguiente ejercicio: en la escena anterior ingresa una función, mínimo una cuadrática para que muestre la función derivada. Luego, haz clic derecho sobre cada función (en la gráfica obviamente) y observarás las etiquetas asignadas... "g" y "h" (ignora la recta verde, que explicaremos a continuación.
¿Abrumado?, ¿Sí?, lo entiendo, tanta maravilla ¡abruma! Creo que necesitas despejar la mente; por ello, te propongo una pausa activa con el siguiente juegoRush Hour (Hora pico) fue creado por Nob Yoshigahara en los años 70 del siglo pasado, Yoshigahara fue uno de los más grandes especialistas en puzzles de la historia. Las combinaciones, para el tablero original, pueden llegar a 287.000 millones.
Michael Fogleman nos ofrece una aplicación con la posiblidad de generar diferentes combinaciones, entre posibles e imposibles de solucionar.
document.ggbAppletAhora, mas relajado y retornando al primer condicional de la interfaz, podemos concluir que toda instrucción de la forma document.ggbApplet tiene como propósito enviar información al applet o, mejor, a la escena que muestra GeoGebra.
Nuestro primer condicional se ejecuta una vez ingresemos la función y presionemos la tecla intro; hecho esto, nos aparecen, en la vista gráfica, las funciones "f" y "g". Pero, además de esta funciones, se pueden enviar otro tipo de órdenes, como el cambio de color o el grosor de las funciones. Solo como ilustración, incluimos las tres últimas instrucciones así:
Seguro que te estarás preguntando ¿por qué Line y no "Recta"?, ello es porque no enviamos la instrucción al bloque 3, encargado de la traducción. Es una alerta para que sepamos ubicar algunas instrucciones, antes de ejecutarlas. Pero, volvamos a ellas: la primera se encarga de graficar un Recta que pasa por los puntos $(1,3)$ y $(2,-2)$; la segunda instrucción, le asigna color verde; la última, le pone un grosor de 5.
En conclusión, para el primer condicional, se dibujan dos funciones y una recta, una vez igresemos la función.
El segundo condicional se ejecuta si a la variable nombre le llega como mensaje punto. Las primeras cuatro instrucciones son:
Observa que la variable dComando es la suma de dos cadenas, la primera es la letra A, y la segunda es el dato enviado desde DescartesJS, a través del control tipo barra que viste en la escena ejemplo.
Incluimos un punto adicional document.ggbApplet.evalCommand("C = (-1,2)");, solo para ilustrar que éste aparece, una vez usemos el control tipo barra en la escena.
Bueno, terminamos aquí este apartado para dar paso a la interfaz
de comunicación que usa
DescartesJS. Sólo así podrás diseñar escenas como las de los
tres ejemplos anteriores.
Hay otras funciones propias de Descartes que se usan para comunicar información entre un espacio principal y un espacio HTMLIFrame contenido en el principal.
<identificador>.set('vr',var). Esta función requiere un identificador de un espacio (principal o subordinado) antes del sufijo .set, y como argumentos lleva una cadena de texto y una variable. Se usa cuando una escena tiene un espacio principal y uno subordinado (como HTMLIFrame) que requieren comunicarse información. El primer argumento (la cadena de texto 'vr') representa el nombre de una variable que el espacio receptor de información usaráPara los ejemplos de GeoGebra, en el capítulo anterior, hemos usado 'evalua'., y el segundo argumento (la variable var) es la variable del espacio emisor de información que contiene el valor que se desea comunicar al receptorPara el primer ejemplo de GeoGebra, en el capítulo anterior, la variables son comandos de GeoGebra; por ejemplo, Derivada[x^4].. El <identificador> corresponde al espacio receptor de la información. <identificador>.update(). Esta función sirve para forzar una actualización de la escena principal posterior a recibir la información de la escena subordinada, por lo que suele incluirse justo después del <identificador>.set para que el espacio receptor de información se actualice inmediatamente después de hacer cambios en sus variables. Esta función no involucra argumento alguno dentro de sus paréntesis.Existen otras funciones de espacios HTMLIframe que, para nuestros propósitos en este libro, no describimos en la relación anterior.
interface1.htmlEn el capítulo anterior (página 30), vimos como diseñar la interfaz de GeoGebra para escenas de cálculo simbólico. También vimos un primer ejemplo de comunicación entre DescartesJS y el archivo interface1.html (página 39), el cual volvemos a presentar:
Con la escena anterior, vamos a realizar otra tarea, que consiste en capturar una escena de DescartesJS; es decir, copiar la escena anterior:
Copia la escena anterior y la guardas, desde DescartesJS, en la carpeta CAS1, con la librería descartes-min.js como proyecto ¿cómo hacerlo?, observa el siguiente video:
Una vez realizada la tarea, presta atención a la descripción de cómo pusimos a conversar DescartesJS con GeoGebra.
¿Conversar?
¡Claro que sí!, según https://definicion.de/, los elementos en una conversación son:
Expliquemos, entonces, el diseño de la escena, advirtiendo que sólo será lo que respecta a la interfaz de comunicación, pues los demás elementos, como buen cartesiano, ya los conoces.
Espacios
La escena tiene dos espacios. El primero (E1) del mismo tamaño de la escena, sin rejilla y de color blanco. El segundo, es un espacio HTMLIframe que hemos llamado Cal, pero igual lo puedes llamar como quieras (Maradona, Shakira, Mi marciano favorito..., bueno, este último no, para evitar espacios en el nombre).
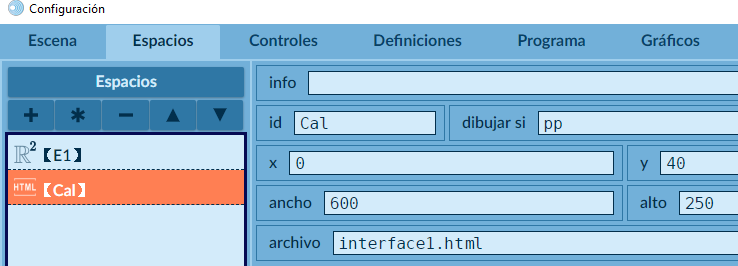
El archivo que invoca es nuestra primera interfaz (interface1.html). Las dimensiones no importan (puedes poner las que quieras), pues es un espacio que no se mostrará en la escena (ver la condición en dibujar-si).
Controles
La escena tiene tres controles. Explicamos el primero, que llamamos orden. Es un control tipo texto, cuyo contenido será enviado (comunicado) a interface1.html, a través de la función Cal.set('evalua',orden); es decir, al receptor interface1.html le llega un mensaje del emisor index.html con una variable de nombre evalua cuyo contenido es el que recibe el control orden del usuario.
¿Sencillo?, ¿No?, ¿Otro jueguito?, ¿Tampoco? Observa, mejor, la siguiente imagen animada:
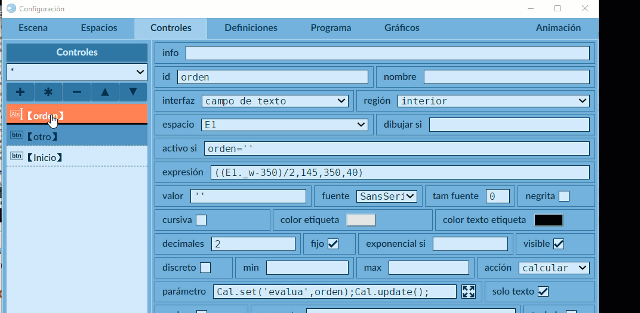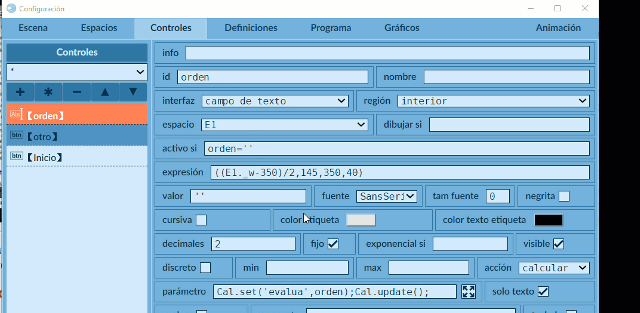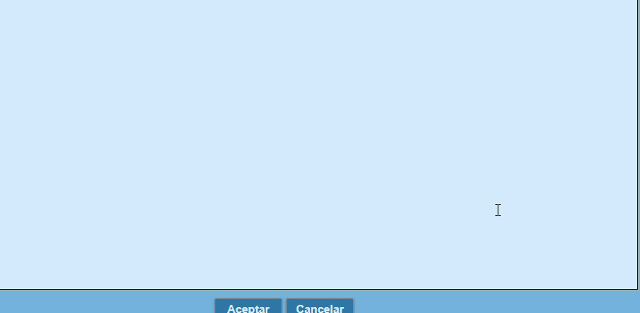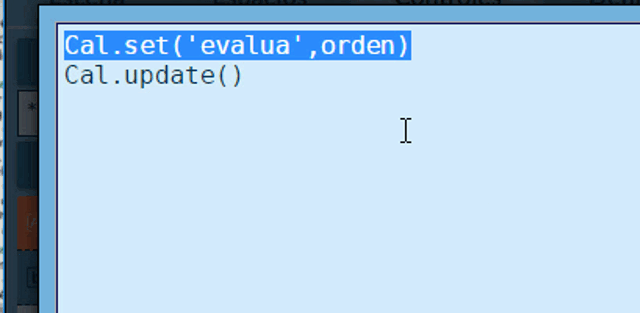
Observa que el Identificador del espacio es Var, que pudo haber sido Pelé, pero sin tilde, tal como hicimos con la variable evalua.
Supongamos que el usuario ingresa la orden 'Derivada[x^4]', entonces la comunicación se realiza como lo muestra la siguiente imagen:
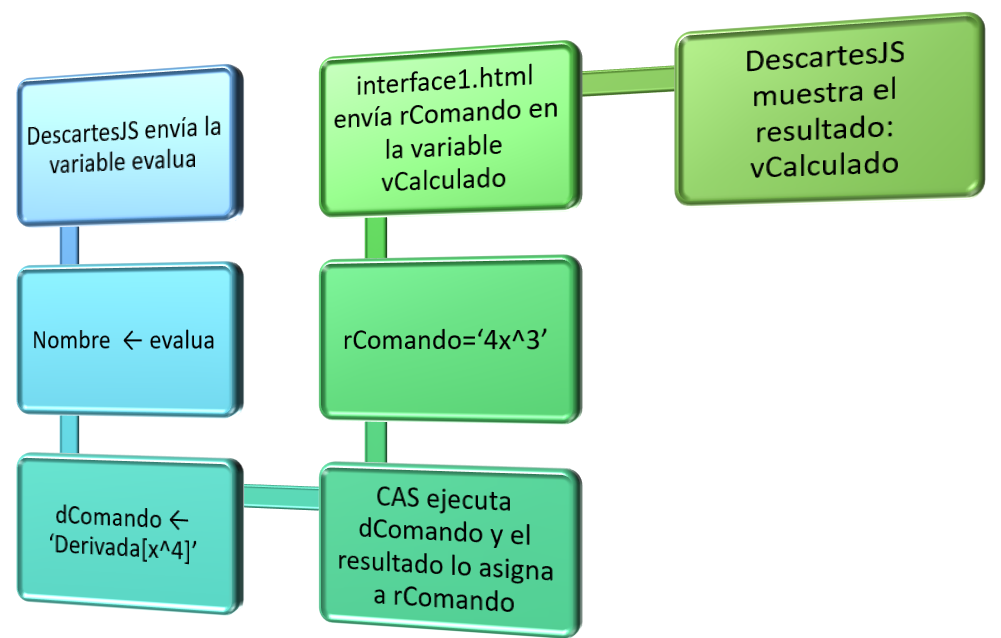
En la escena, una vez se reciba el mensaje con la variable vCalculado, muestra el resultado en un gráfico tipo texto:

Comprendido lo anterior, estás en capacidad de realizar la novena tarea propuesta en este libro. Como dicen mis amigos de España ¡Vamos a por ella!En este video, se describe y explica la interfaz de DescartesJS.
La siguiente escena interactiva fue diseñada usando la interfaz de comunicación interface1.html. Tu misión, si decides aceptarla, es capturar la escena en una carpeta que llamarás CAS4 y alojada en la carpeta interactivos ¡verifica que funcione!
Alguien podría afirmar que estos dos ejemplos no muestran la utilidad de esta comunicación, pues bastaría con usar sólo la herramienta GeoGebra para el cálculo simbólico, afirmación con la cual estamos de acuerdo. Pero, es necesario comprender que los ejemplos son solo para describir y explicar cómo se logra la comunicación, pues depende del diseñador cómo puede usarla. A continuación, mostramos una escena que pese a no haber comunicación entre las dos herramientas, nos da una idea de cómo usar esta primera interfaz.
La escena es una sección de la unidad interactiva "Derivada Direccional", diseñada por Elena Álvarez en el proyecto Proyecto Un_100.
Si haces clic en el botón "Herramienta de cálculo", se abre una escena de GeoGebra 4.4, que permite el cálculo de derivadas parciales. El resultado se demora algunos segundos en aparecer (sugerimos ampliar la escena).
¡Eso es todo!... para esta interfaz
interface2.htmlRecordemos que la interface2.html difiere de la interface1.html en la presentación del entorno GeoGebra. La interfaz de comunicación de DescartesJS básicamente es igual, pues usa el mismo espacio HTMLframe (Cal), el mismo control de texto (orden) y el mismo gráfico de texto (véase la página 41).
Para aprovechar mejor este apartado, hemos realizado algunos cambios a la interface2.html y a la interfaz de comunicación de DescartesJS, obteniendo la siguiente escena:
Este es el código de la nueva interface2b.html:
Captura la anterior escena interactiva (index.html) y la interfaz de comunicación de GeoGebra interface2b.html, que guardarás en la carpeta CAS5. Verifica que te funcione bien en local.
Vamos a explicar los cambios en la interface2b.html y la interfaz de comunicación de DescartesJS index.html; para ello, ten abiertos los editores de las dos herramientas.
Incicialmente, habrás observado que los fondos de los dos espacios tienen el mismo color ¿cómo se hizo?, veamos como:
Modificaciones interfaz de GeoGebra
Una primera intervención fue el color de fondo, según el siguiente procedimiento:
interface2.html que se encuentra en la carpeta CAS2RGB(164, 226, 198):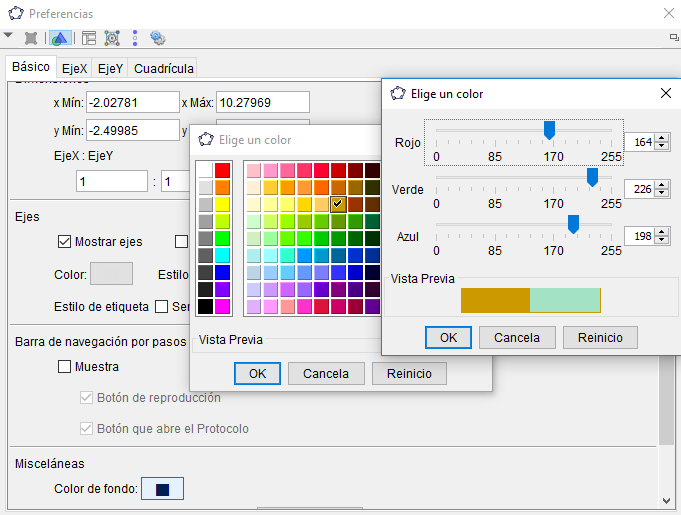
interface2b.htmlggbbase64 y lo reemplazamos en el archivo interface2.htmlCAS5 con el nombre interface2b.htmlUna última modificación es haber desactivado la barra de herramientas data-param-showToolBar
Modificaciones interfaz DescartesJS
Espacios
Los espacios son los mismos de la escena anterior CAS2, con los siguientes cambios:
E1, hemos cambiado el color del fondo, de tal forma que quede igual al de la interface2b.html de Geogebra: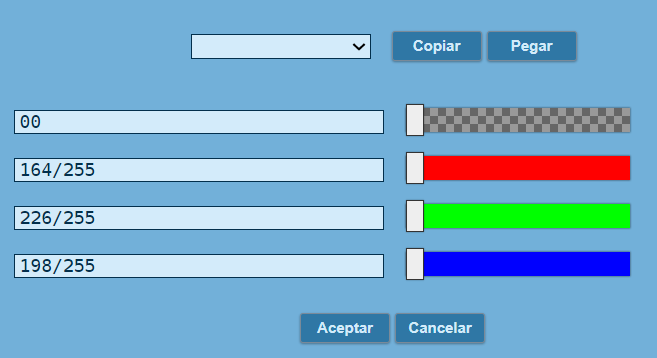
E1 de la escena CAS5En la imagen anterior, te habrás preguntado ¿por qué ese color?, ¿acaso no es en formato hexadecimal? La respuesta es que DescartesJS también admite el formato decimal, con un valor mínimo de 0 y un valor máximo del 1. Como GeoGebra usa valores decimales (Figura 4.5), el valor convertido al formato de DescartesJS se obtiene dividiendo entre 255 (el valor máximo admitido).
HTMLIframe cambiamos el archivo invocado a interface2b.html.Controles
Hemos modificado el primer control y agregado cuatro controles nuevos:
orden=''; es decir, desaparece una vez se ingrese el dato pedido. Pero, lo más importante es el cálculo que realiza:
orden2 tendrá como valor la cadena: 'Derivada[x^4,0]'. Ello significa que GeoGebra calcula la derivada de "cero" orden, lo cual se traduce en el retorno de la función ¡tal cual! Este truco es útil para que se dibuje la función ingresada.muestra es diferente de cero.Los otros tres controles nuevos tienen un funcionamiento análogo, con los comandos: Integral, Factoriza y Desarrolla. Observa que cuando se selecciona uno de estos controles, se asigna uno (1) a la variable muestra, lo que los inactiva y permite que aparezcan los controles Otro ejercicio e Inicio
Como en el apartado anterior, al final se muestra el resultado vCalculado, enviado por GeoGebra.
¿Exhausto? Es comprensible, tanto conocimiento abruma. Pero, descansemos un poco; para ello, presentamos el siguiente Puzle Giratorio, el cual incluye imágenes de Flickr de algunas regiones a las cuales pertenecen los cartesianos - geogebreros estudiosos de este libro ¿No está tu región?, sencillo, abre el index.html del puzle y, al final, incluye tu región.
¡Eso es todo!... para esta interfaz
interface3.htmlEn el capítulo anterior (página 43), vimos como diseñar la interfaz de GeoGebra para escenas de cálculo simbólico y numérico, que incluye un ejemplo de comunicación entre DescartesJS y el archivo interface3.html (página 44), el cual volvemos a presentar:
Para comprender lo que vamos a explicar...
Captura la anterior escena interactiva y la copias en el editor DescartesJS, luego la guardas en la carpeta CAS3 como (index.html).
En el editor de configuraciones, observarás:
Espacios
Igual que en los anteriores, son los espacio E1 y Cal, solo debes prestar atención en la posición y tamaño del espacio subordinado:
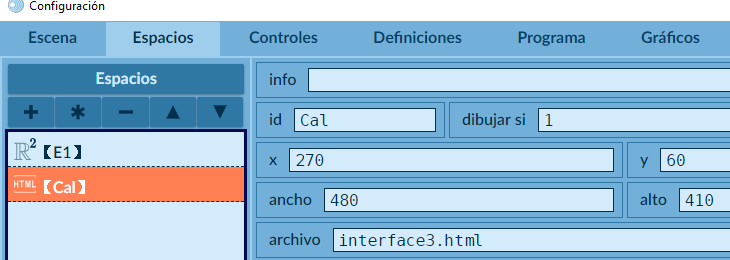
E1 y Cal.Controles
Son cuatro los controles utilizados:
calcula es igual a cero (0). Una vez el usuario ingresa la función pedida, el control calcula:
calcula, lo cual hace que desaparezca el control de la escena.A continuación, se envían dos mensajes a GeoGebra, los cuales explicamos:
Supongamos que ingresamos la función x^3, entonces fn=x^3 y la variable nombre sería nombre = 'Derivada[' + x^3 + ',0]'; es decir, nombre = 'Derivada[x^3,0]'. GeoGebra retorna como resultado la derivada de orden 0 de la función que no es otra cosa que la función misma. Te preguntarás porqué pedir algo que ya conocemos, pues el objetivo es obtener la función en formato simbólico: $x^3$.
Para la misma función x^3, GeoGebra retorna como resultado la derivada de orden 1 de la función, es decir: $3x^2$.
Aquí es importante recordar qué mensaje retorna interface3.html: vCalculado1 para evalua1, vCalculado2 para evalua2, vCalculado3 para evalua3, etc. Obviamente, vCalculado para evalua.
calcula = 1. Una vez movamos la barra, el control empieza a enviar mensajes a GeoGebra, según la posición de la barra, así:
Si el control tipo barra tiene valor de $-4$, entonces Punto = (-4,2) y GeoGebra grafica dicho punto. En el siguiente capítulo, haremos una análisis más profundo de la instrucción JavaScript document.ggbApplet.
Los otros dos controles, según lo visto anteriormente, son fáciles de entender.
Gráficos tipo texto
Al igual que en los ejemplos anteriores, los selectores Definiciones y Programa no fueron usados en este objeto interactivo. Los textos que aparecen los puedes analizar sin problemas, pues son similares a los explicados anteriormente.
¡Eso es todo!... para esta interfaz
y para este capítulo
En este capítulo diseñaremos objetos interactivos, trabajando con GeoGebra y DescartesJS simultáneamente. En la interfaz de la primera, recurriremos a la instrucción JavaScript document.ggbApplet descrita en el capítulo III, la cual nos permitirá intervenir objetos de la ventana gráfica de GeoGebra. Por otra parte, en la interfaz de DescartesJS usaremos los elementos de programación explicados en la sesión 4 del curso "Edición de objetos interactivos con DescartesJS".
Iniciemos con el siguiente objeto interactivo:
Nuevamente, es necesario aclarar que estos primeros ejercicios son para comprender cómo funcionan algunas instrucciones de comunicación, pues es claro que la escena anterior se puede diseñar independientemente en DescartesJs o en GeoGebra.
Veamos que está ocurriendo en cada interfaz.
Interfaz de GeoGebra. Esta es la interfaz usada para este primer ejemplo:
Un cambio en la interfaz es el uso de la variable dibuja enviada por DescartesJS, en lugar de la variable evalua que veníamos usando anteriormente. Este cambio tiene sentido, pues en los capítulos anteriores nos ocupamos de evaluar comandos CAS, ahora nos dedicaremos a dibujar en la vista gráfica de GeoGebra.
En el bloque 2, presta atención a las instrucciones :
Veamos que cada una de ellas:
dComando='A='+data.value;. Asigna a la variable dComando la cadena compuesta por 'A=' y el valor de la variable dibuja; por ejemplo, si dibuja es '(4,3)', entonces, A=(4,3) sería asignada a dComando.//document.ggbApplet.deleteObject('A');. Toda instrucción que tenga los caracteres // corresponden a un comentario; es decir, no se ejecuta, pero ¿por qué está puesta allí? Se puso provisional por si había que recurrir a ella, tal como ocurre en el próximo ejemplo, así que esperemos a él para explicarla.document.ggbApplet.evalCommand(dComando); ¡Es la instrucción que dibuja en la vista gráfica!, se encarga de enviar la orden a la vista gráfica que podrían ser puntos (A=(4,3), por ejemplo), polígonos, funciones o, para este primer ejemplo, circunferencias.document.ggbApplet.setColor('A',255,0,0);. Esta instrucción cambia el color del objeto a rojo.Existen otras intervenciones que podemos hacer sobre el objeto dibujado, además del cambio de color, como el cambio de grosor de la línea, el nombre, que iremos aplicando en los otros ejemplos.
Interfaz de DescartesJS. Bueno, para continuar con esta interfaz, es necesario que desarrolles la sigiente tarea:
En la carpeta interactivos crea una carpeta que llamarás tutor1. Copia la interfaz anterior de GeoGebra y la guardas en tutor1 con el nombre interfaz1.html. Finalmente, captura la escena DescartesJS de este ejemplo y lo guardas en tutor1 como ejemplo1.html
¿Complicada la cosa? Observa, entonces, este video:
¿Faltó la imagen de fondo?, la puedes descargar aquí y guardarla en una carpeta imagenes ubicada en tutor1 o, si lo deseas, puedes usar tu propio fondo.
Toma un respiro con el siguiente puzle, algo parecido al puzle Rush Hour:
Seguramente, te preguntarás ¿por qué estos puzles diseñados para niños de primaria? La respuesta es simple: es ese pensamiento complejo del niño el que necesitamos para comprender la lógica de las diferentes interfaces que vamos a analizar. En las próximas escenas interactivas, usaremos una lógica de programación simple, como la del niño, que "parece surgir originariamente de manera innata, como si la mente estuviera programada para realizar inferencias causales que adquieren formas de Modus Tollens o Modus Ponens, como casos formales específicos (Salgado, 2014, pág. 37).
Como lo afirma Salgado en su artículo, no son simples analogías como "pi papá" que se desprende de "mi mamá", sino de una "lógica simple" que no ha sido contaminada de la "lógica social" pero, si lo deseas, puedes leer el artículo a continuaciónConversión a HTML realizada con IDR Solutions.
Luego de esta breves reflexiones sobre la lógica infantil, continuemos con la interfaz de DescartesJS.
Con el editor de DescartesJS abres el ejemplo1.html, aunque creo que ya lo tienes abierto, pues debes haber realizado la tarea anterior.
Espacios
Usamos dos espacios, el principal y el subordinado. En el primero pusimos un fondo y en el segundo en lugar del nombre Cal, usado para los espacios subordinados en el capítulo III, hemos usado Geo, aunque pudo haber sido Covid o, mejor, Vacuna, pero el elegido se asocia más a "Geometría" o, si se prefiere, a "GeoGebra".
Controles
Usamos tres controles. En los dos primeros (como en la interfaz de GeoGebra) notarás algo que quizá te sorprenda: "sumamos textos" o, técnicamente, "concatenamos" textosConcatenar es una elegante palabra de la programación que significa: "unir". Para unir cadenas en JavaScript usamos el símbolo más (+), el mismo operador que usamos para sumar números, pero en este contexto hace algo diferente (https://developer.mozilla.org/es/).
inicia es igual a uno (1).A la variable C se le asigna la suma de las cadenas: 'Circle[(0,0),', el valor del radio y la cadena ']'. Por ejemplo, si el radio es 3, entonces C = Circle[(0,0),3]'. resultado que es comunicado a GeoGebra a través de la variable dibuja con la instrucción Geo.set('dibuja',C).
Te estarás preguntando ¿Por qué Circle y no Circunferencia?, la respuesta la encuentras en la interfaz de GeoGebra, pues en ella no pusimos la función function calculosCAS(dComando), la cual nos permitía la traducción, lo hicimos adrede, sólo como un ejercicio del uso de los comandos en inglés.
iniciaci en dibujar si es cero. Una vez se hace clic sobre el botón, se realizan los siguientes cálculos:Gráficos tipo texto
Son cuatro textos los que hemos usado, dos de ellos (el primero y el último) son fijos; es decir, permanecen durante toda la interacción. Los otros dos se presentan dependiendo del valor de la variable inicia; por ejemplo, el texto "Vamos a interactuar con GeoGebra enviándole mensajes desde DescartesJS. Hac clic en el botón 'Comenzar'" se presenta al inicio, cuando inicia es cero (0). Esta técnica la usaremos en todos los tutoriales del resto de este capítulo.
Estos dos ejemplos solo difieren en una instrucción de la interfaz de GeoGebra, que tiene efectos significativos en cómo se dibuja una función cuadrática en la vista gráfica. Observa los ejemplos, haciendo clic en las siguientes imágenes:
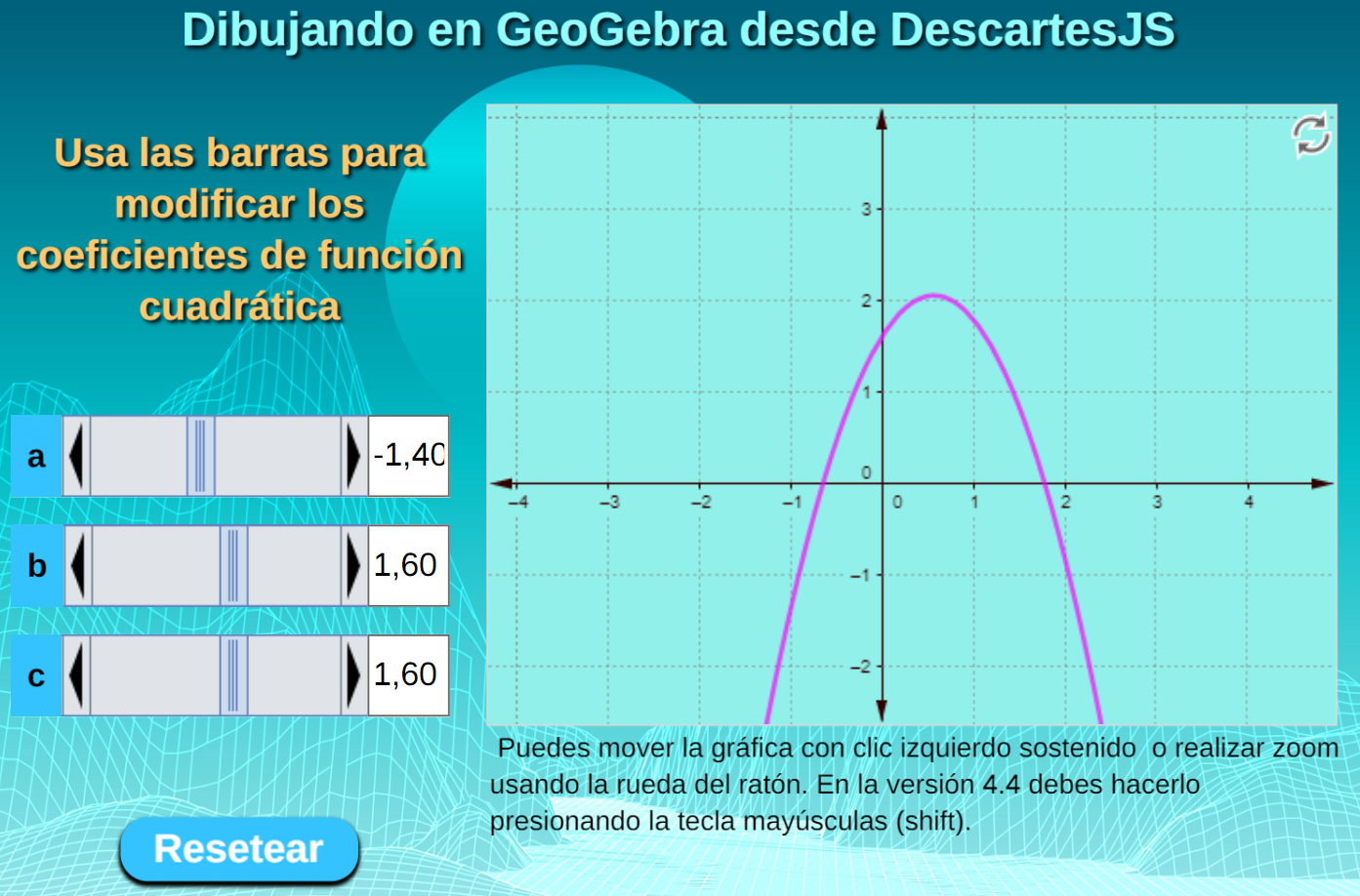
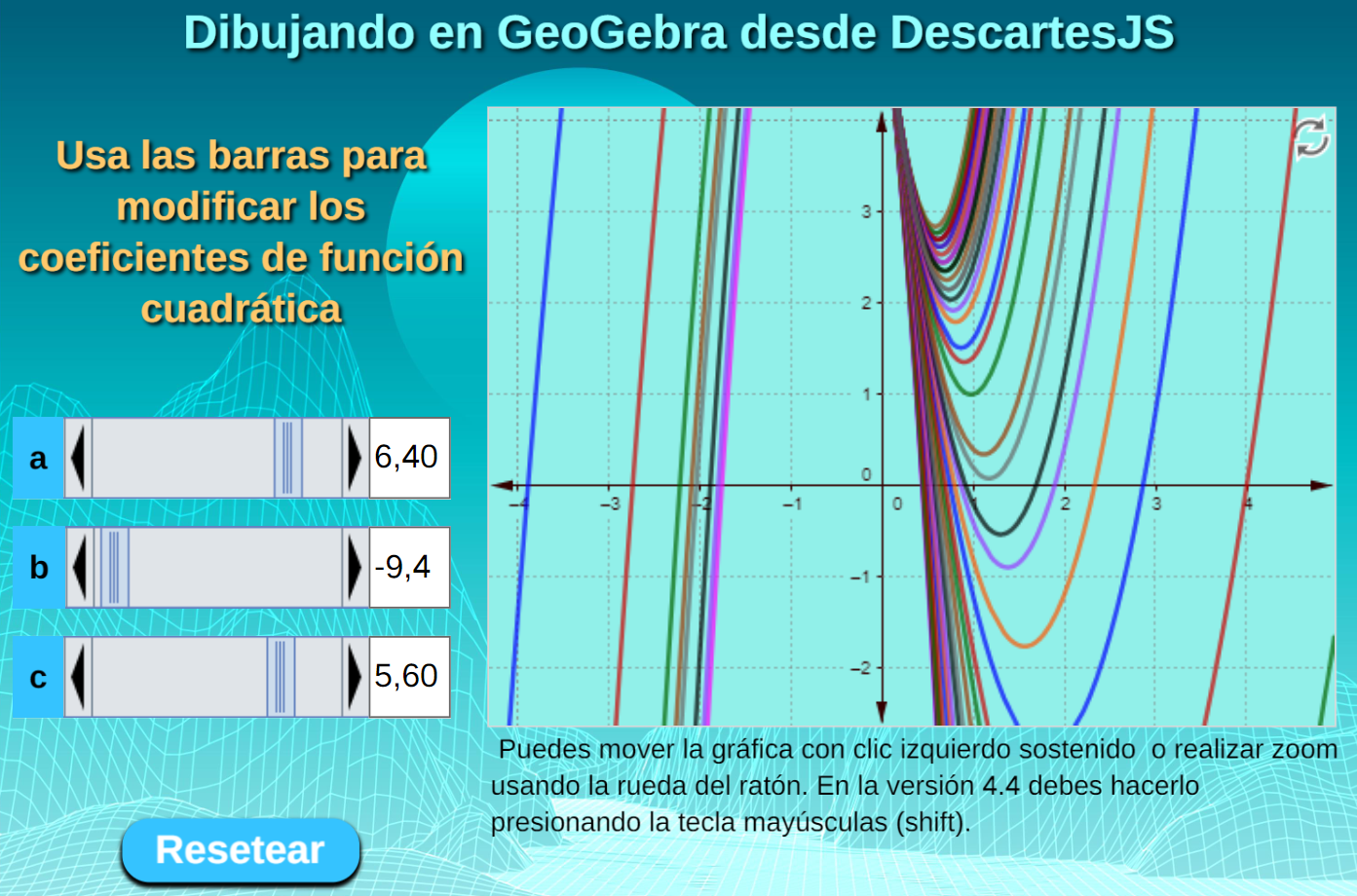
Interfaz de GeoGebra. Esta es la interfaz usada para el segundo ejemplo:
Solo nos detendremos en analizar las siguientes instrucciones del bloque 2:
document.ggbApplet.deleteObject('g');¿Por qué? Resulta que GeoGebra por cada cambio en los coeficientes de la función, genera una nueva función, así: 'g', 'h', 'p', 'q', 'r', 'p1', 'q1', 'r1', 'p2', ...
Pero hay otra diferencia entre los dos ejemplos. En el ejemplo 2 hemos usado la instrucción dComando="g="+data.value;, forzando a que la función siempre sea "g", mientras que en el ejemplo tres la instrucción es dComando=data.value;, permitiendo la generación de las funciones antes citadas.
Es importante que realices pruebas para que comprendas lo que ocurre al interior de GeoGebra; por ejemplo, identificar el nombre del objeto dibujado (clic derecho sobre el objeto):
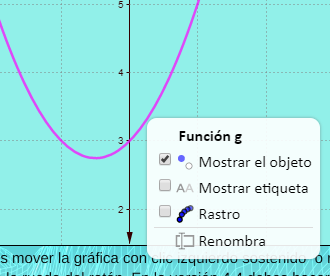
En conclusión, las dos diferencias del ejemplo 3 con respecto al 2, es la asignación a la variable dComando de la orden enviada por DescartesJS data.value; y, además, la no inclusión de la instrucción document.ggbApplet.deleteObject('g');. Para los dos ejemplos, hemos usado el color magenta para el objeto, a través de la instruccióndocument.ggbApplet.setColor('g',255,0,255);.
Interfaz de DescartesJS. Muy similar a la interfaz del ejemplo 1, pero en lugar de un control tipo "barra", se tienen tres que corresponden a los coeficientes de una función cuadrática. Explicaremos solo uno de ellos, pues los demás funcionan igual.
El control "a" (coeficiente de $x^2$) ejecuta las siguientes instrucciones, cada vez que desplacemos la barra o cambiemos el valor de "a":
Observa, nuevamente, la concatenación de textos que se asigna a la variable f, que luego se envía a GeoGebra, a través de la variable dibuja.
Lo de los asteriscos es por costumbre, pero se pueden omitir; por ejemplo, si a=2, b=-1 y c=3, entonces: f='2*x^2-1*x+3' que GeoGebra también acepta como f='2x^2-1x+3'.
El resto de los elementos del interactivo son similares a los del ejemplo 1.
En la carpeta tutor1. Copia la interfaz anterior de GeoGebra y la guardas con el nombre interfaz2.html, haces las dos modificaciones explicadas y la guardas como interfaz3.html. Finalmente, captura las escenas DescartesJS de los ejemplos 2 y 3 y los guardas en tutor1 como ejemplo2.html y ejemplo3.html
En el siguiente objeto interactivo DescartesJS envía un mensaje a GeoGebra con los datos del centro y radio de una circunferencia:
Ya es hora de demostrar lo que has aprendido, así que:
Diseña la interfaz de GeoGebra para la escena interactiva anterior, la guardas en la carpeta tutor1 con el nombre interfaz4.html. Finalmente, captura la escena DescartesJS y las guardas como ejemplo4.html.
En este apartado diseñaremos los tutoriales de GeoGebra, con DescartesJS como tutor. Es importante que el diseño contemple todas las posibles acciones del usuario, de tal forma que encuentre la respuesta adecuada y controle, además, los posibles errores que se cometa.
Un primer ejemplo, bastante simple, es el siguiente:
El usuario sólo tiene dos posibilidades, marcar puntos y/o dibujar triángulos. Interactúa con la escena de GeoGebra y observa si para cada interacción hay una respuesta adecuada.
Interfaz de GeoGebra. Esta es la interfaz usada para el tutorial 1
Analicemos las instrucciones del bloque 3:
A las variables valor1, valor2, valor3 y valor4 se les asignan los valores $(x_i, y_i)$ de los puntos $A$, $B$, $C$ y $D$, bajo el supuesto que dichos puntos hayan sido dibujados. Esta asignación se obtiene con el comando getValueString('nombre del punto').
Con estos cuatro valores es suficiente para determinar si el usuario dibujó uno, dos, tres o mas puntos e, incluso, si no dibujó ninguno. Las etiquetas $A$, $B$, $C$ y $D$ son las asignadas, en ese orden, por GeoGebra a los primeros puntos dibujados en la vista gráfica. Por otra parte, si el usuario opta por dibujar un polígono, GeoGebra asigna la etiqueta $polígono1$ al nombre de dicho polígono y su valor es asignado a la variable valor5.
El segundo grupo de instrucciones usa el comando postMessage({ type: "set", name: "puntoC", value: valor3 },'*');, el cual se encarga de enviar a DescartesJS los valores anteriores, almacenados en las variables puntoA, puntoB , puntoC, puntoD y poli.
setCon estos datos, analicemos cómo en DescartesJS son utilizados.
Interfaz de DescartesJS. Dada la cantidad de información enviada por GeoGebra, haremos uso de un mayor número de estructuras de decisión, para mostrar el mensaje adecuado a las acciones del usuario. Por ejemplo, hemos puesto un espacio adicional de color transparente, que se muestra si la variable verifica es igual a uno (1)... he ahí una estructura de decisión. El objetivo de este espacio es impedir que el usuario interactúe con la vista gráfica de GeoGebra, una vez haya hecho clic en el botón Verificar.
Selector programa
A partir de este tutor, el selector programa va a ser uno de nuestros aliados para garantizar una buena comunicación entre las dos herramientas de autor.
Habrás notado que en todas nuestras escenas interactivas diseñadas con DescartesJS, nos hemos limitado a usar los selectores Espacios, Controles y Gráficos pero, para este tipo de "conversación", vamos a necesitar más herramientas cartesianas, entre ellas los algoritmos INICIO y CALCULOS del selector ProgramaEl selector Programa incluye ya parte de la programación dura que se hace con Descartes. Consta básicamente de dos tipos de algoritmos presentes por defecto en cualquier escena (INICIO y CÁLCULOS), y de un elemento conocido como evento (Radillo et al., pág. 107).
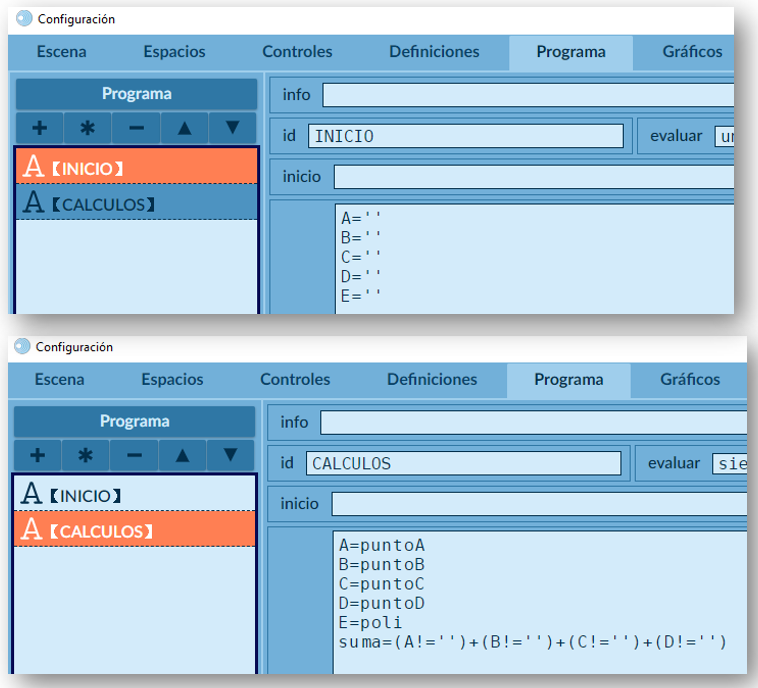
INICIO y CALCULOS.En el algoritmo INICIO (que se ejecuta una sola vez), hemos "inicializado" las variables de cadena A, B, C, D y E con contenido vacío.
En el algoritmo CALCULOS (que se ejecuta siempre), hemos puesto las siguientes instrucciones:
A y comunica a DescartesJS la variable puntoA = 'A = (2,3)', que luego se asigna a la variable A de DescartesJS.D? Se trata de un punto de control, pues si el usuario marca más de tres puntos, existirá, entonces, un punto D, el cual nos sirve para poner un mensaje de error.E se le asigna el contenido de la variable poli comunicada por GeoGebra, que corresponde a un polígono, siempre que el usuario lo dibuje en la vista gráfica de GeoGebra.A ya no tendrá un contenido vacío, por lo tanto A!='' será verdadero; es decir, tendrá un valor de uno(1) y suma tendrá un valor de uno(1) o más si se marcan más puntos.Selector Gráficos
Comprendidos los algoritmos anteriores, entenderás los mensajes puestos en el selector Gráficos. Por ejemplo, si el usuario marca un punto, dibuja un triángulo y hace clic en el botón "Verificar", el algoritmo CALCULOS identifica cuatro puntos y, entonces, se cumple la condición (verifica=1)&(suma>3).
Modifica la escena interactiva, de tal forma que se le pida al usuario dibujar un pentágono. El control se debe hacer por el número de puntos (vértices) del polígono dibujado. Recuerda inactivar la herramienta "Punto" en la vista gráfica de GeoGebra.
En este segundo ejemplo, hemos usado más herramientas de DescartesJS, tales como la variable general rnd que genera valores aleatorios, el selector Definiciones para incluir dos vectores, funciones de cadena y familias para mostrar los lados con los colores asignados en la interfaz de Geogebra. Pero, por ahora, interactúa con la escena:
El usuario debe dibujar un polígono seleccionado al azar (entre tres y ocho lados) y responder a una pregunta. A diferencia del ejemplo anterior, el reinicio es más rápido, pues se usa el comando document.ggbApplet.reset(); de GeoGebra, evitando la recarga de la herramienta.
Interfaz de GeoGebra. Esta es la interfaz usada para el tutorial 2
Como en el ejemplo anterior, solo nos interesa analizar el bloque 3 de instrucciones, el cual tiene tres propósitos. El primero, es identificar los elementos dibujados en GeoGebra, a través de instrucciones como:valor1 = document.ggbApplet.getValueString('a');
que, para este caso, identifica el segmento a del polígono.
Como lo hemos advertido antes, es importante la identificación previa en la ventana gráfica de GeoGebra (clic derecho sobre el elemento), es así como podrás observar que los segmentos de un octágono son a, b, c, d, e, f1, g y h.
¿$f_1$?, así es, por alguna razón GeoGebra ha dejado reservada la etiqueta f.
Observa, además, que hemos previsto la identificación de ochos segmentos y la del polígono, pese a que es posible que el polígono pedido, al azar, sea un triángulo. Cada una de estas identificaciones son asignadas a las variables: valor1, valor2, ..., valor9, siendo la última la del polígono.
El segundo propósito del bloque 3, es enviar a DescartesJS mensajes con los valores de los segmentos y del polígono (área), de tal forma que en DescartesJS podamos evaluar las acciones del usuario. Los mensajes son de la forma:
window.parent.postMessage({ type: "set", name: "ladoa", value: valor1 }, '*');
que, para este caso, envía el valor del segmento a (longitud) a través de la variable ladoa.
El último propósito es el cambio de dos propiedades de los elementos dibujados: la activación de la etiqueta del elemento y el cambio de color. Para la primera (en el segmento a) usamos:
document.ggbApplet.setLabelVisible('a',1)
y el cambio de color lo logramos con la instrucción:
document.ggbApplet.setColor('a',255,0,0);
que en este caso sería cambiar el color del segmento a a rojo.
Con estas instrucciones en mente, comprenderás cómo se ha diseñado la escena interactiva con la interfaz de DescartesJS.
Interfaz de DescartesJS. Recuerda que en el capítulo IV (página 54) puedes ver un vídeo de cómo capturar y copiar escenas de DescartesJS. Para continuar la explicación, es importante que hayas copiado la escena y la tengas abierta en el editor de DescartesJS.
Selector Espacios
Hemos usado cuatro espacios
E1. Es el espacio principal, su novedad está en el color de fondo, que hemos puesto del mismo color de la escena de GeoGebra, de tal forma que ambas herramientas parezcan una sola. Para ello, usamos los colores RGB con los que se diseñó el fondo de la interfaz de GeoGebra y lo convertimos a hexadecimal en DescartesJS, así:
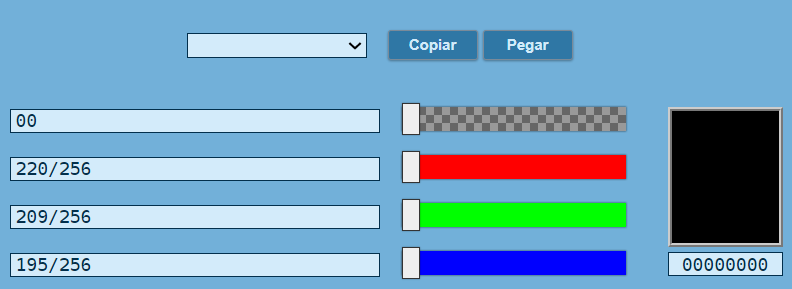
poligonos. Es el espacio HTMLIframe subordinado a E1, a través de interfaz.html.E4. Espacio con fondo transparente que se activa cuando se cumple la condición (verifica=1)&(suma!=N); es decir, cuando el usuario se equivoca en la respuesta. Su propósito es cubrir la vista gráfica de GeoGebra y evitar la corrección del usuario.pregunta. Espacio de dimensiones 150x180 pixeles, que se activa cuando se cumple la condicón (verifica=1)&(suma=N).Selector Controles
Son los siguientes controles:
verifica1. Control tipo botón que, una vez activado, envía a GeoGebra el mensaje poligonos.set('poligono',mensaje), con el propósito de ejecutar las instrucciones del bloque 3.inicio1. Control tipo botón que, una vez activado, reinicializa las variables y envía un mensaje a GeoGebra para que se "resetee". El mensaje enviado es poligonos.set('resetea',mensaje).inicio2. Control tipo botón que funciona similar al anterior.Selector Definiciones
En este Selector hemos definido dos vectores. El primero almacena los colores de los segmentos, definidos en el bloque 3 de la interfaz de GeoGebra. El segundo vector almacena los valores obtenidos para los segmentos del polígono.
Selector Programa
Como en el ejemplo anterior, hemos usado los algoritmos INICIO y CALCULOS. En el primero inicializamos las siguientes variables de cadena: A, B,... I, con un contenido vacío. En este mismo algoritmo hallamos un número N aleatorio entre 3 y 8 y asignamos el Nombre del polígono según el número N obtenido:
En el algoritmo CALCULOS, que se ejecuta permanentemente, hemos puesto las siguientes instrucciones:
Hemos usado dos funciones especiales de DescartesJS, que explicamos a continuación y con referencia a la siguiente figura:
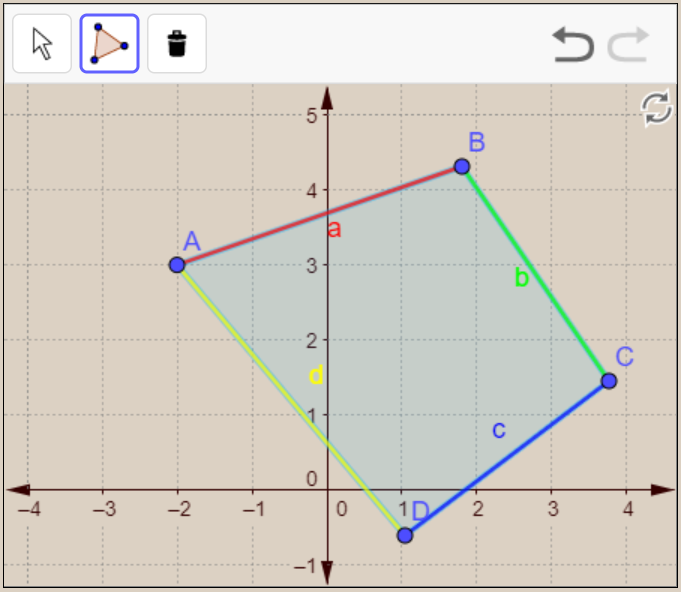
Area=substring(I,11,18). El mensaje enviado por GeoGebra, en la variable poli, es polígono1 = 14.76; es decir, una cadena de longitud 17, en la que el caracter 0 es 'p', el 1 es 'o',..., el 10 es '=' y el 11 es ' '. La función de cadena substring(I,11,18) captura los caracteres que hay entre el caracter 11 (espacio después del igual) y el 18; es decir, el valor del área. Hemos puesto hasta 18, pues es posible que el área sea mayor o igual a 100.
Termina=(_Eval_(Area)=10)&(N=3)|(_Eval_(Area)=36)&(N>3)?1:0. Como el valor del área es una cadena de caracteres (subcadena de la variablel I), es necesario convertirla a un valor numérico; para ello, se usa la función _Eval_(variable), ello permite que se ejecuten instrucciones numéricas como las indicadas en esta estructura de decisión.
Finalmente, en este algoritmo, calculamos las suma de todos los lados que tengan algún valor diferente (!=) de vacío, con el fin de determinar qué tipo de polígono dibujó el usuario.
Selector Gráficos
Hemos puesto 10 gráficos tipo texto y uno tipo rectángulo. La mayoría de los textos estás en capacidad de entender cómo se diseñaro, solo nos detendremos en el que usa la casilla familia:
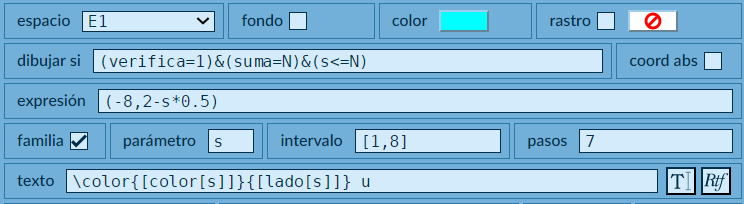
La familia está definida en el intervalo $[1,8]$, ello para incluir el polígono de mayor número de lados (octágono) pero, para nuestro ejemplo, sólo muestra los lados del cuadrilatero, en tanto que la estructura de decisión (verifica=1)&(suma=N)&(s<=N) controla que los miembros de la familia no superen el valor de N que es cuatro (s<=N).
La posición de los cuatro elementos de la familia (los lados del polígono), varían en función del parámetro s así: (-8,2-s*0.5), de tla forma que los lados aparezcan de esta forma:

Finalmente, para este texto, hemos puesto el texto de los elementos de la familia usando los dos vectores definidos en el Selector Definiciones, así: \color{[color[s]]}{[lado[s]] u}; por ejemplo, para s = 1, muestra el lado[1] que es el lado a y con el color[1] que es rojo.
Gráfico tipo rectángulo. Este gráfico es la otra novedad en este ejemplo. Se trata de un rectángulo cuya esquina inferior izquierda se encuentra en las coordenadas $(-8.1, -4.6)$ con un ancho de $6.3$ y una altura de $3.8$. En este rectángulo pondremos los mensajes de salida, como se muestra en la imagen anterior.
En este ejemplo hemos usado la misma estructura del ejemplo anterior, modificando la disposición de los espacios e incluyendo una función en Definiciones. Te queda como tarea explorarlo.
Captura la escena anterior y haz una exploración y análisis de su funcionamiento, en especial cómo se captura la primera coordenada de los puntos 3D.
La interfaz de GeoGebra usada, es la siguiente:
Observa que hemos usado
data-param-showFullscreenButton="true").
En este ejemplo usamos más funciones de cadena y una función de ratón (mouse) para el marcado de puntos.
Interfaz de GeoGebra. Esta es la interfaz usada para el tutorial 4
La mayoría de las instrucciones de esta interfaz las hemos trabajado anteriormente. Destacamos las siguientes novedades:
comandos.js, en su lugar, hemos puestos los dos únicos elementos que necesitamos de esta matriz:document.ggbApplet. setLineThickness('lado', 6);, modificamos el grosor de los lados del triángulo./web3d.nocache.js, no porque tengamos una escena 3D, sino porque solo así es posible habilitar el botón zoom de GeoGebra (data-param-showFullscreenButton).Interfaz de DescartesJS. Recuerda que en el capítulo IV (página 54) puedes ver un vídeo de cómo capturar y copiar escenas de DescartesJS. Para continuar la explicación, es importante que hayas copiado la escena y la tengas abierta en el editor de DescartesJS.
Selector Espacios
Similar al tutorial 2, hemos usado cuatro espacios de los que destacamos el espacio E3:
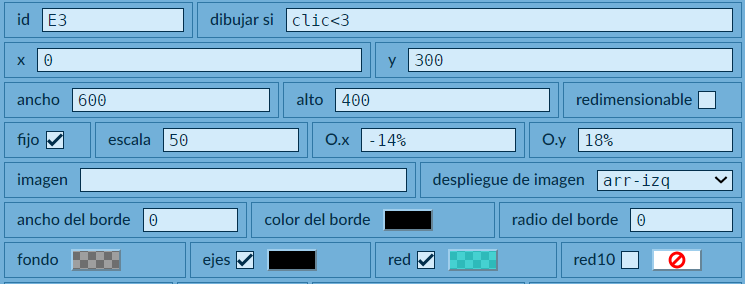
Se trata de una espacio de fondo transparente y red color turquesa, cuyas dimensiones, escala y posicionamiento coinciden con la vista gráfica de GeoGebra (espacio Ejemplo4). Esta técnica la usamos para dibujar los tres primeros puntos desde DescarteJS, aunque es posible hacerlo directemente en la ventana gráfica de GeoGebra, tal como lo hicimos en el Tutorial 1.
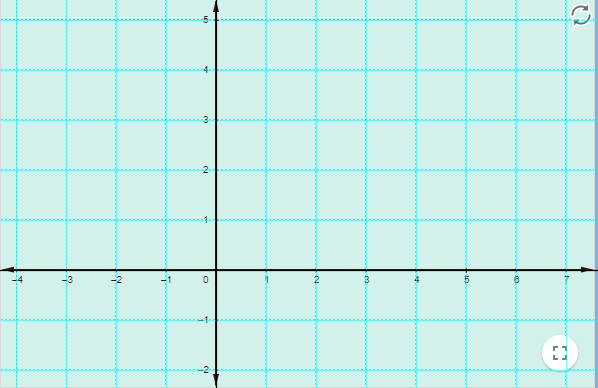
Este espacio está presente mientras la variable clic sea menor a tres. Esta variable se incrementa cada vez que hagamos "clic" con el ratón sobre el espacio E3, su funcionamiento lo esplicaremos en el Selector programa.
Selector Controles
Son cuatro controles tipo botón, que funcionan así:
triangulo. Este control aparece cuando (clic=3)&(tri=0); es decir, cuando se han marcado tres puntos y la variable tri es cero. Una vez el usuario hace clic sobre este botón, se ejecutan las siguientes instrucciones:Observa que la variable tri deja de ser cero, por lo que el botón desaparece. Pero, lo más importante es la comunicación con GeoGebra a través de los únicos dos comandos que necesitamos: Pólígono y Ángulo. Veamos un ejemplo:
Supongamos que hicimos clic en los puntos $(0,0)$, $(3,4)$ y $(5,0)$, los cuales serán los puntos $A$, $B$ y $C$ (que explicaremos en el selector Programa). Entonces, se envía un mensaje a la interfaz de GeoGebra así: 'Polígono[A, B, C, A]', perimitiendo que se dibuje el triángulo. A continuación se envían los mensajes 'Ángulo[ A, B, C ]', 'Ángulo[ B, C, A ]' y 'Ángulo[ C, A, B ]', dibujando los ángulos del polígono. La interfaz de GeoGebra retorna los valores de los ángulos $\alpha 1$, $\alpha 2$ y $\alpha 3$ (en la interfaz de GeoGebra puedes cambiar el nombre de estos ángulos).
Verificar. Este control aparece cuando las variables reto1 o reto2 valen uno y la variable verifica es cero. Su objetivo es verificar que la interacción del usuario con los ángulos del triángulo cumplen con el reto propuesto, al hacer clic en el botón, se ejecutan las siguientes instrucciones:Los otros dos controles son fáciles de comprender, por lo tanto no los describimos.
Selector Programa
Hemos usado el tercer tipo de programa que permite este selector: evento, en el cual recurrimos a variables de ratón, así:
E3.mouse_pressed. Esta variable es verdadera (1), si hacemos clic con el ratón. Cada vez que hacemos clic se ejecuta el evento calculando las siguientes instrucciones:E3.mouse_x y E3.mouse_y. Permiten obtener las coordenadas del punto en el cual hacemos clic. Por ejemplo, si hacemos clic en el punto $(0,0)$, significa que E3.mouse_x = 3 y E3.mouse_y = 4 y, por lo tanto, nombre = '('+3+','+41+')' = '(3,4)', que es comunicado a GeoGebra.Finalmente, la variable clic se incrementa en 1
En el algoritmo CALCULOS asignamos a diferentes variables los resultados enviados por GeoGebra, tales como el nombre y valor de los puntos y, en especial, el nombre y valor de los ángulos, que explicamos a continuación:
resultadon, donde n varía de 1 a 3:_length_(variable); por ejemplo, si resultado1 = 'α1 = 63.82°', su longitud será de 11 caracteres (recuerda que existe el caracter cero, que sería α). Estas longitudes se obtienen así:L-1 caracter ¿L-1?, claro que sí, pues la existencia del caracter en la posición cero nos obliga a restar 1. Los valores de los tres ángulos, los obtenemos así:Observa que usamos la función _Eval_(variable), para convertir a valor numérico la subcadena obtenida. Las demás instrucciones de este algoritmo (estructuras de decisión) son fáciles de comprender, al igual que todos los textos puestos en el selector Gráficos.
Modifica los retos de la escena anterior; por ejemplo, "cambia los ángulos de tal forma que el triángulo sea isósceles".
Este último tutorial consta de dos ejemplos. No haremos ninguna explicación, puesto que debes estar en capacidad de analizar y comprender las dos interfaces. Hemos dejado un enlace al archivo comprimido (zip) de cada ejemplo.
Circunferencia circunscrita a un triángulo
Este ejemplo lo puedes descargar en este enlace:  e interactuar con él haciendo clic en la siguiente imagen:
e interactuar con él haciendo clic en la siguiente imagen:
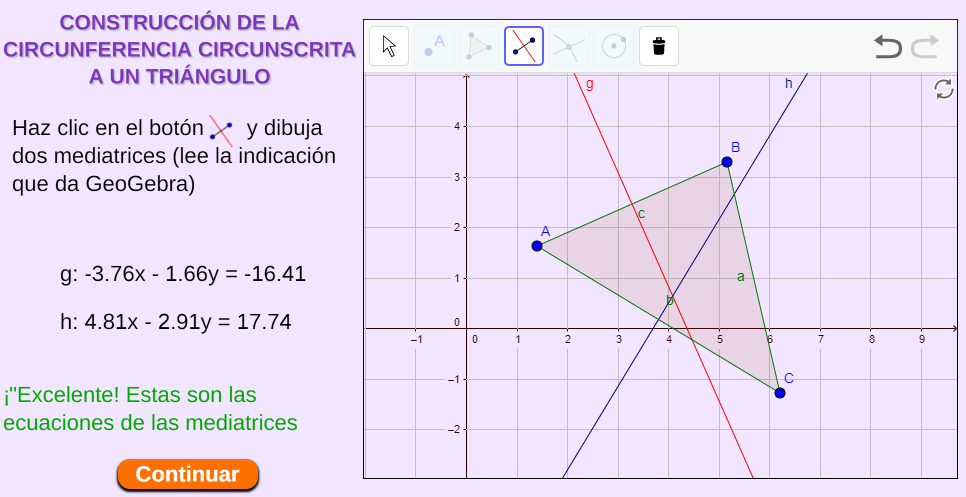
Una característica especial de este ejemplo, es el uso de varios espacios tipo "máscara", cuyo objetivo es evitar que se habiliten algunas herramientas de la vista gráfica de GeoGebra.
Construyendo una figura dada
Este ejemplo lo puedes descargar en este enlace:  e interactuar con él haciendo clic en la siguiente imagen:
e interactuar con él haciendo clic en la siguiente imagen:
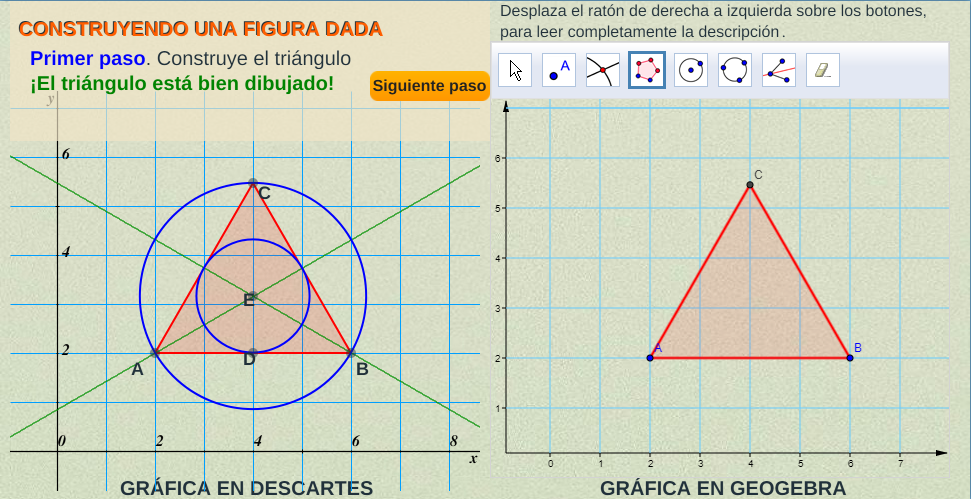
En este segundo ejemplo usamos una herramienta nueva de la vista gráfica de GeoGebra, la bisectriz. Algo a lo que debes prestarle atención es que los nombres de los elementos gráficos cambian de una versión a otra. La imagen anterior corresponde a la versión 4.4 de GeoGebra. Para que puedas evaluar estas diferencias, en el archivo zip hemos puesto el ejemplo en la versión 5 (index2.html e interfaz2.html).
En la siguiente imagen puedes abrir el ejemplo en la versión 5 de GeoGebra.
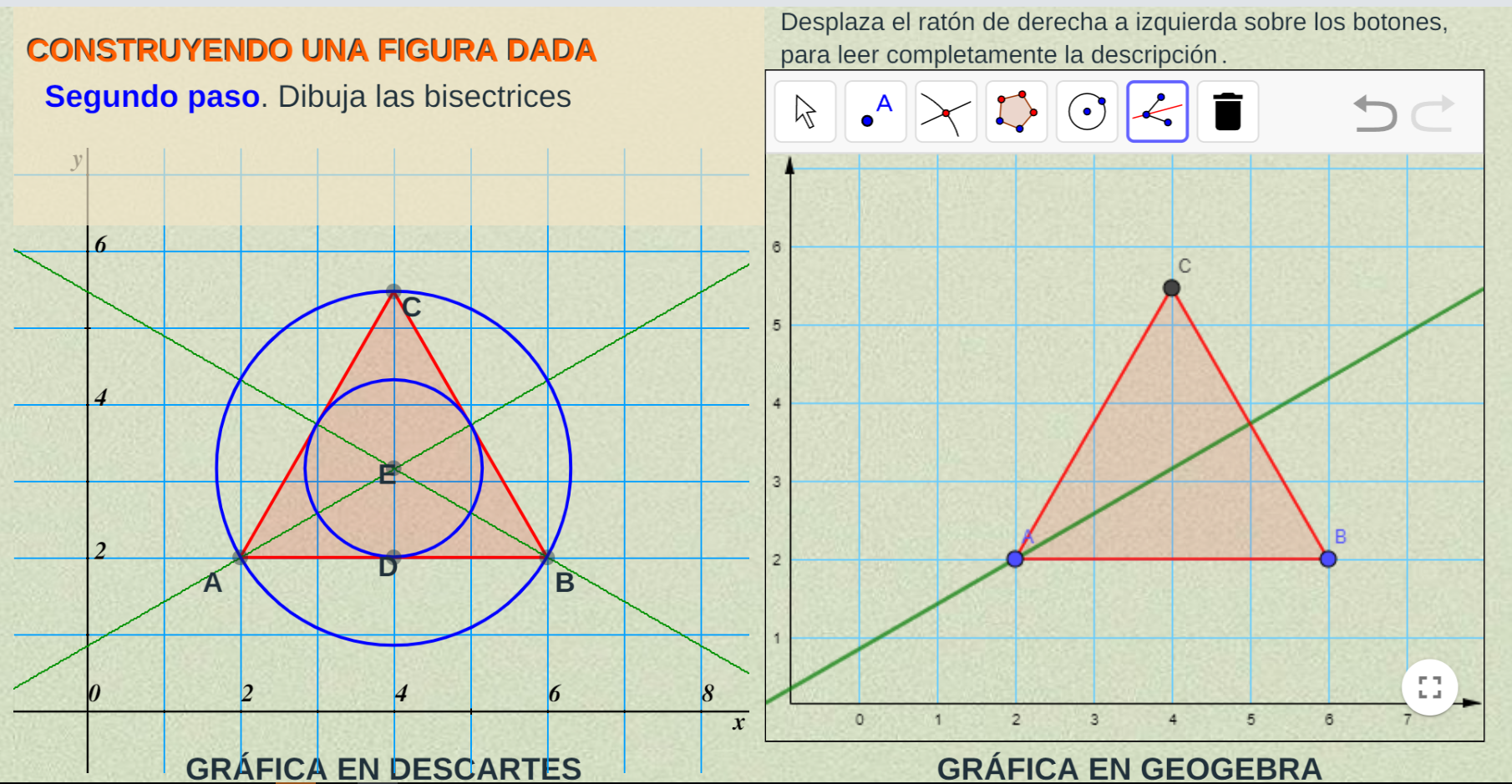
En el siguiente video, podrás observar algunas de las diferencias entre las versiones 4.4 y 5 de GeoGebra:
En varias publicaciones del proyecto iCartesiLibri, se explica cómo se diseñan los videos interactivos y algunas de sus características.
Los vídeos interactivos, normalmente, son vídeos a los que se le agregan capas transparentes, con el fin de sobreponer elementos externos como imágenes, textos, cuestionarios y actividades interactivas (Capacitación DescartesJS - Nivel I, pág. 168).
Es importante recordar que el objetivo del vídeo interactivo es permitir al usuario interactuar con la escena, en la cual el objeto principal es el vídeo. La interacción se realiza a través de preguntas o de la selección de opciones presentadas como botones o puntos gráficos dibujados sobre el vídeo (Capacitación DescartesJS - Nivel II, pág. 189).
Diseñar vídeos interactivos es "muy fácil", si usas una de las plantillas del libro Plantillas DescartesJS, en el que tenemos varios modelos para vídeos en local o de YouTube. Sin embargo, vamos a explicar cómo se intervienen dos vídeos (no incluidos en las plantillas) que, si prestas atención, estarás en capacidad de intervenir los demás modelos (Diseño de libros interactivos, pág. 120).
Como recurso digital, el vídeo es una excelente opción; no obstante, debe garantizar, al menos, las siguientes condiciones: i) perdurabilidad (en lo que hemos sido insistentes), ii) intencionalidad pedagógica (que permite un aprendizaje significativo), iii) motivador (de corta duración, buen diseño... atrapante) y, de ser posible, iv) interactivo (Ibid, pág. 126).
La perdurabilidad es una condición que debes considerar en el diseño de tus videos interactivos, pues si tienes tu video en un canal externo (YouTube, por ejemplo), corres el riesgo de generar un enlace roto, bien sea por cambio de políticas del canal o por eliminación debido, quizá, a una denuncia por derechos de autor.
También, en el diseño de contenidos digitales, solemos incluir enlaces a videos publicados en páginas web, blogs u otros canales como Vimeo o Dailymotion, costumbre que no recomendamos, pues sigue siendo un riesgo la eliminación de estos videos. El riesgo se minimiza si el video publicado en alguno de estos sitios es de tu propiedad o si el video tiene una licencia que te permita descargarlo y guardarlo, para corregir posibles enlaces rotos.
Actualmente existen nuevas herramientas, que permiten el diseño de videos interactivos de muy buena calidad; por ejemplo, en el siguiente video puedes apreciar porque el video del "libro de la selva" obtuvo el primer premio en 2017 en la categoría "Mejor uso del video interactivo" de los Webby Awards (The Jungle Book ).
Puedes interactuar con el video, mientras el enlace exista, en la página de Fandango.
En este capítulo veremos cómo realizar una comunicación con diferentes tipos de "parientes". Haremos escenas interactivas comunicando DescartesJS con GeoGebra, con YouTube, con un video en local y con el mismo DescartesJS. Observa un ejemplo inicial, en el que hay comunicación entre padre, hijo y nieto:
Como observaste en el ejemplo inicial, una de las actividades que pueden incluirse en un video interactivo es una escena de GeoGebra con una tarea específica. En este caso, se trata de una actividad evaluativa que solo permite la continuidad del video cuando se da respuesta acertada a la tarea propuesta.
En este apartado explicaremos cómo incluir otro tipo de actividad evaluativa. Se trata del uso de las actividades propuestas en el Proyecto Plantillas publicadas en la Red Educativa Digital Descartes. En este proyecto hemos publicado mas de 100 plantillas, de las cuales 53 son útiles para los propósitos de este apartado, en tanto que envían el resultado obtenido a la escena principal, tal como lo hizo la escena "nieta" en el ejemplo inicial.
Las plantillas que puedes usar, son las siguientes:
Uso de las plantillas
No vamos a describir cómo cambiar el contenido de una plantilla; para ello, puedes consultar el libro Plantillas DescartesJS. La edición de cada una de las plantillas es bastante sencilla, pues sólo se requiere de herramientas básicas como un editor de texto plano (Bloc de notas de Windows, TextEdit de Mac, Notepad++, etc.) y un editor de imágenes (Paint de Windows o Paintbrush de Mac).
Secuencias_temporales_1-JS/indexb.html. Con un mensaje tipo set se establece la comunicación padre e hijo, de tal forma que la escena principal pueda recibir y usar la variables $var1$.Una tarea, en la que podrías colaborar, es intervenir las plantillas que incluyen el archivo indexb, de tal forma que sólo quede el archivo index.html responsivo. Observa un ejemplo del uso de una plantilla en un video interactivo. Haz clic en la siguiente imagen:

En este ejemplo, hemos usado como espacio hijo una plantilla enlazada directamente al portal de Descartes, así: https://proyectodescartes.org/plantillas/ materiales_didacticos/Secuencias_temporales_1-JS/indexb.html. Observa que invocamos el archivo indexb.html, lo que nos obligó a usar una escena de 890x600px, situación que obliga, también, a ajustar el tamaño del video.
Esta plantilla la hemos descargado e intervenido con el editor DescartesJS, de tal forma que el espacio hijo sea: Secuencias_temporales_1-JS/index.html. Observa la diferencia, interactuando con la siguiente escena:
En este caso, la escena es de 700x500px.
Diseñando plantillas
Las plantillas anteriores se diseñaron para personas que no tienen formación en el diseño de objetos interactivos con DescartesJS o, teniéndola, sirvan para el diseño de un proyecto más ambicioso, como lo son los videos interactivos.
En la quinta sesión del curso Edición de objetos interactivos con DescartesJS explicamos cómo diseñar actividades de evaluación usando el control "casilla de verificación". En los siguientes videos puedes ver cómo diseñar evaluaciones de "Falso y Verdadero" y de "Selección Múltiple" que, al igual que las plantillas, incluyen las instrucciones parent.set('mensaje', var1) y parent.update(), para la comunicación con la escena padre.
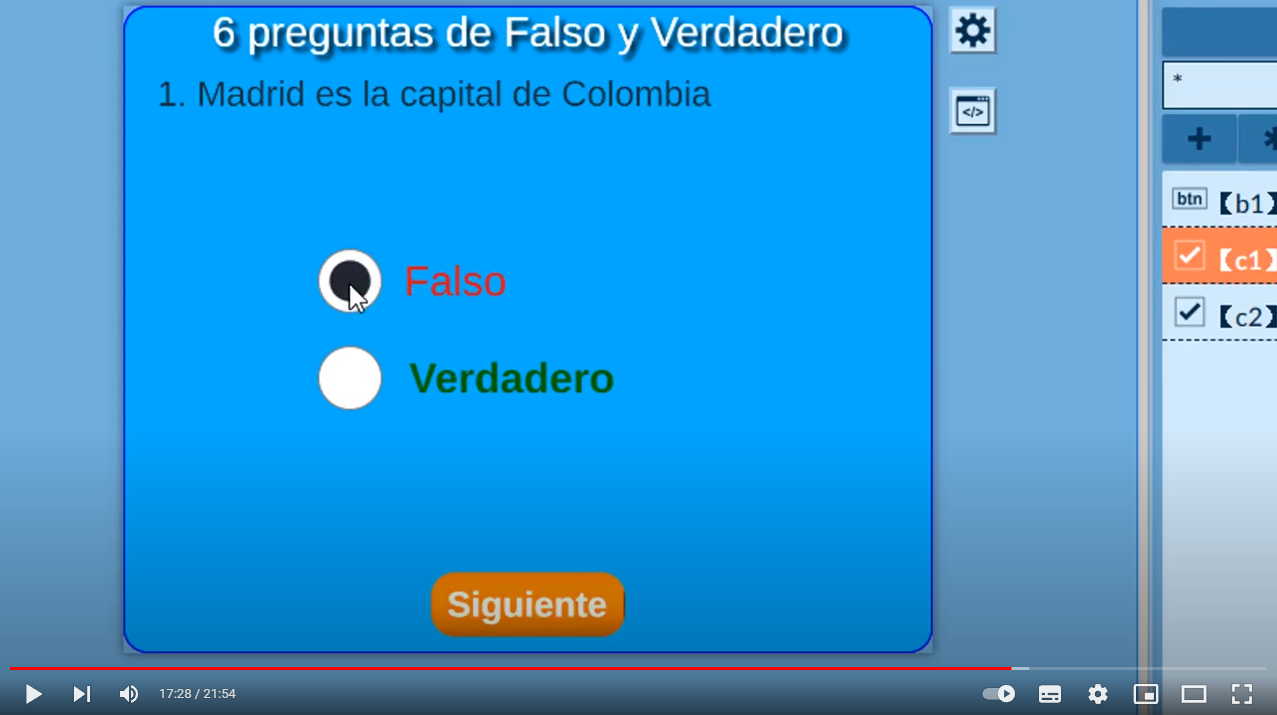
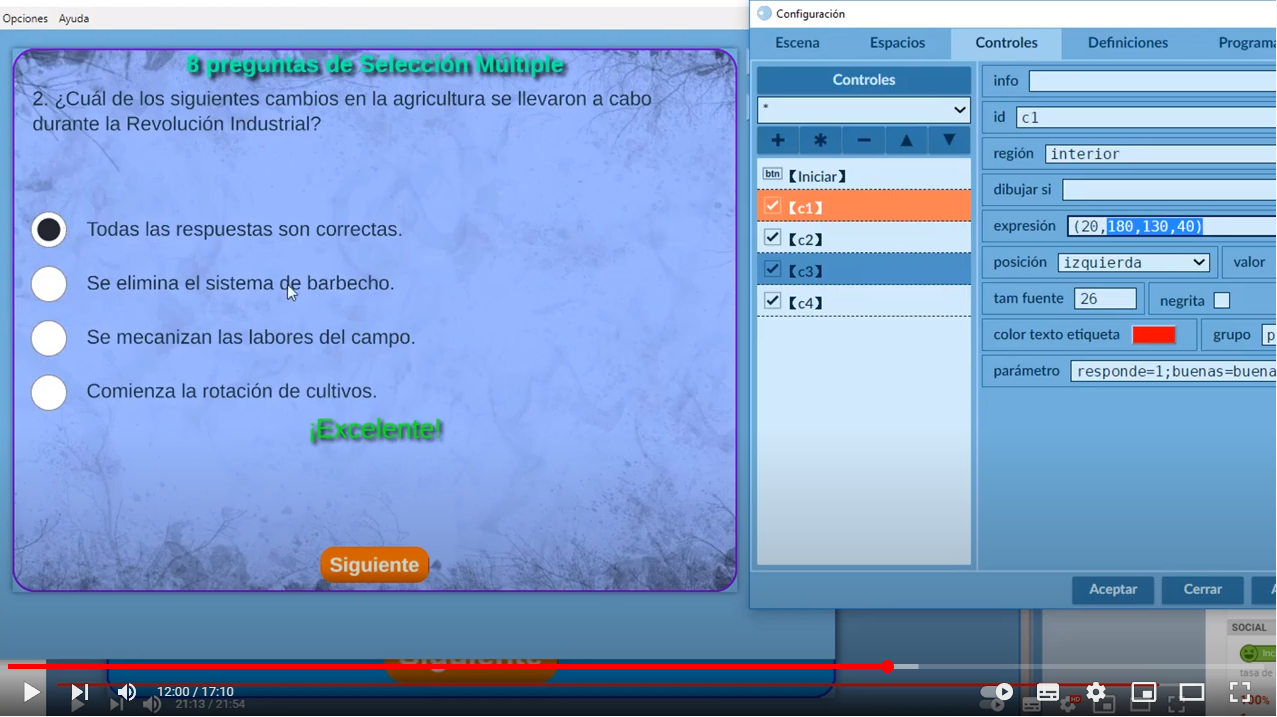
En este apartado vamos a diseñar nuestro primer modelo de video interactivo; para ello, debes preparar el material a usar en el video, tal como se pide en la siguiente tarea.
En la carpeta interactivos crea una carpeta que llamarás video_interactivo2. Selecciona y descarga, al menos, dos plantillas evaluativas. Selecciona y descarga una plantilla lúdica (un puzle, por ejemplo), selecciona o diseña una escena de GeoGebra. Todas esta escenas interactivas las guardarás en la carpeta video_interactivo2. Crea un video en formato mp4, de no más de dos minutos, si no tienes idea de cómo hacerlo, observa el siguiente video:
Selección de las actividades interactivas
 En nuestro caso, hemos seleccionado tres actividades evaluativas (Preguntas SI-NO, Selección Múltiple y una de Falso y Verdadero), una actividad lúdica (puzle animado) y una escena de GeoGebra (no evaluativa), todas ellas guardadas en la carpeta
En nuestro caso, hemos seleccionado tres actividades evaluativas (Preguntas SI-NO, Selección Múltiple y una de Falso y Verdadero), una actividad lúdica (puzle animado) y una escena de GeoGebra (no evaluativa), todas ellas guardadas en la carpeta video_interactivo2El nombre de la carpeta lleva el "2", porque ya habíamos ceado un videos interactivo en el apartado 6.3., tal como se observa en la imagen de la derecha.
Tamaño de la escena
Una de las actividades evaluativas (Preguntas SI-NO) incluye un archivo indexb.html de 790x500px; por ello, decidimos usar una escena de 850x600px.
Creación del video
Para nuestro primer modelo, hemos descargado un tráiler de la película "La bella y la bestia" de Disney. Sin embargo, nuestro interés es crear videos de DescartesJS o de GeoGebra o, quizá, de ambos, por lo que necesitaríamos alguna aplicación de "grabación de pantalla", tal como se explicó en el video anterior. Una buena opción es usar la grabación de nuestro video con PowerPoint, siempre que comprimamos el video obtenido, pues para un video de 2 minutos, PowerPoint te puede crear un video de más de 50MB (en mp4compress.com puedes comprimir tu video).
Con este video y las actividades interactivas seleccionadas, explicaremos cómo diseñar el siguiente video interactivo (espera unos 10 segundos a que cargue la escena de GeoGebra, antes de reproducir el video):
Espacios
Hemos creado ocho espacios. El primero, que llamamos E1, es el espacio principal, al cual le pusimos una imagen de fondo. Luego, creamos un espacio igual al principal llamado mascara, sin fondo y transparente, cuyo objetivo es evitar que el usuario manipule el video; sin embargo, si se desea, es posible eliminar este efecto cambiando el espacio del control tipo video como veremos más adelante.
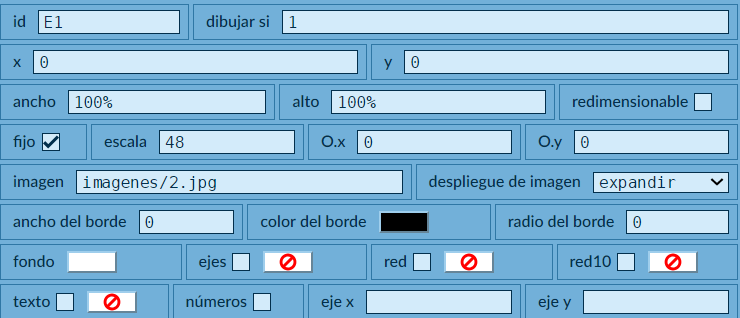
 A continuación, creamos cinco espacios con las actividades interactivas, tres de ellos subordinados (hijos) que hemos llamado
A continuación, creamos cinco espacios con las actividades interactivas, tres de ellos subordinados (hijos) que hemos llamado prueba1, prueba2 y prueba3, los cuales corresponden a FV.html, SM.html y Pregunta_SI-NO-JS/indexb.html, respectivamente. Los otros dos espacios son dos actividades no evaluativas, que corresponden al puzle animado y a una actividad de GeoGebra. Estos espacios tienen dimensiones de 790x500px
El último espacio, que llamamos final tiene una ligera transparencia y en él mostraremos los resultados obtenidos en las tres evaluaciones.
Antes de continuar, descarga el video interactivo en este enlace: 
Controles
Para nuestro primer video interactivo usamos cuatro controles:
id) de este control es v1, con dimensiones 790x500px y ubicado en el centro de la pantalla, lo cual se logra usando las variables de espacio: (E1._w-790)/2, (E1._h-500)/2. El archivo del video es disney.mp4 en la carpeta videos. El video se muestra si se cumple la condición (ver=0)&(inicia=1), que explicamos con los siguientes controles.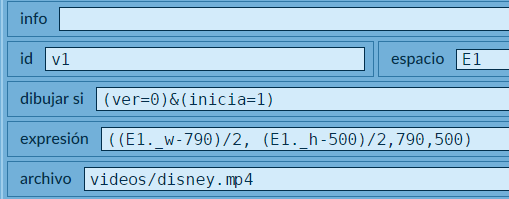
(ver=0) y (time+1)<L, de la cual explicamos la segunda: la variable $L$ corresponde a la duración del video que, para nuestro video de Disney, es de 41 segundos, la variable $time$ es el tiempo actual de reproducción. Dado que el tiempo se mide en fracciones de segundo, le hemos sumado un segundo para garantizar que el botón desaparezca antes de los 41 segundos.inicia=1 y v1.play(), esta última es una función de video que inicia la reproducción del video v1.v1.pause().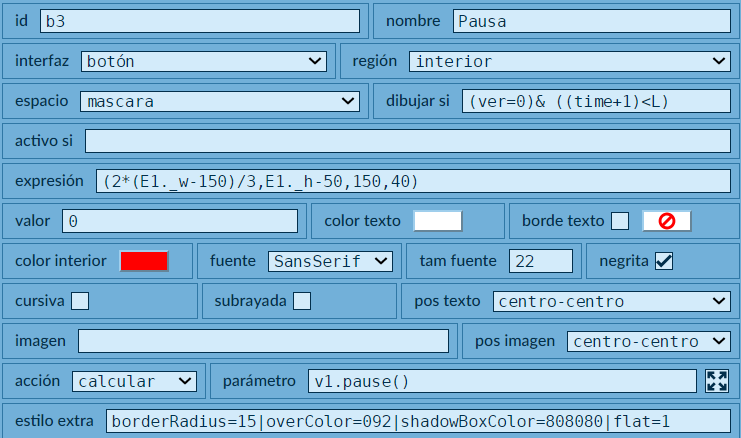
(ver!=0) y (var1!='') o cuando las variables para4 y para5 son iguales a uno (1).ver será diferente de cero cuando el tiempo de reproducción del video es igual a una de las paradas que definiremos en el selector Programa, la variable var1 será diferente de vacío cuando la actividad evaluativa correspondiente se ha realizado, y las variables para4 y para5 serán uno cuando el tiempo de reproducción del video es igual a una de las paradas definidas para las actividades no evaluativas; es decir, el botón aparece se interactúe o no con la actividad.En la variable prueba se suman en el número de actividades evaluativas, en el vector Nota[] se almacenan las notas y en la variable suma se suman las notas obtenidas. Para una próxima prueba, es necesario reinicializar la variable var1 con contenido vacío. Para cada parada, es necesario evitar que continúe la parada en el tiempo dado; por ello, recurrimos a asignar a cada parada lograda un tiempo de 2000 segundos (algo más de 33 minutos), garantizando que el video no se detendrá más en ese tiempo pues, como lo hemos reiterado, el video interactivo debe ser corto. Finalmente, se reanuda la reproducción del video con la función v1.play().
Definiciones
En este selector creamos los vectores Nota[] y frase[], el primero ya usado en el control anterior y el segundo que explicamos a continuación.
Selector Programa
INICIO. En este algoritmo se ejecutan las siguientes instrucciones:Se inicializan las variables de cadena var1, oye y listo con contenido vacío. Asignamos los tiempos de parada a las variables parada1, ..., parada5, los cuales lo hicimos cada cinco segundos, pues es solo un video ilustrativo. En el vector frase[] hemos almacenado el título de la actividad correspondiente. En la variable L asignamos la duración del video, que es 41 segundos.
CALCULOS. Se ejecutan las siguientes instrucciones:
Instrucción time=v1.currentTime. La variable de video v1.currentTime entrega el tiempo en segundos transcurrido del video, el cual se asigna a la variable time
Instrucciones parax=(ent(time)=paradax), donde $x=1,2,3,4,5$. Mediante la expresión $ent(time)=paradax$ se evalúa si el valor entero de la variable time es igual al valor de la variable paradax, si es cierto, se asigna uno (1) a la variable parax.
Instrucción parar=(para1=1)|(para2=1)|(para3=1)|(para4=1) |(para5=1)?v1.pause():parar. Si alguna de las variables parax es uno(1), se ejecuta la función de pausar el video (pause()).
Instrucción ver=para1+para2+para3+para4+para5. Si alguna de las variables parax es uno(1), la variable ver será también igual a uno.
Instrucción actividad2.set('oyeme',oye). Para este video, hemos establecido una comunicación con la escena de GeoGebra seleccionada, de tal forma que nos retorne un mensaje en la variable cargado con el contenido InputBox1Este contenido es aplicable solo para esta escena, en otras puede ser el valor de un punto, un segmento, etc., el cual se asigna a la variable listo. Cuando esto ocurre, significa que la escena fue cargada y desaparecerá el mensaje inicial de este videoEste control se puede elminar si se desea, se puso solo para advertir al usuario que la demora en activarse los botones es por la demora en cargar la o las escenas de GeoGebra.. La comunicación debe ir acompañade de la instrucción actividad2.update().
e3. Es un evento que activa una animación.Algunas escenas de DescartesJS, en especial las que incluyen el control tipo video, requieren de la ejecución de una animación para que las funciones y variables de video sena activadas.
Selector Gráficos
Consta de una imagen y ocho textos, de los cuales explicamos los siguientes:
[time]/[L]. Escribe en la esquina inferior derecha, la relación entre el tiempo transcurrido (time) y la duración del video (L).Nota [s]:. Es una familia de textos que, según el número de actividades evaluativas, escribirá el texto Nota 1:, Nota 2, ..., Nota x:, en las coordenadas (-7,3), (-7,2), ..., (-7,4-x).[Nota[s]]. Es una familia de textos que, según el número de actividades evaluativas, escribirá el valor de la Nota 1:, Nota 2, ..., Nota x:, en las coordenadas (-4,3), (-4,2), ..., (-4,4-x).Los mensajes sobre las notas se escribirán en el espacio final, los cuales fueron separados en dos columnas, pues el primero debe ir con cero decimales y el segundo (la nota) con un decimal.
¡Eso es todo!... para este primer modelo
Con el video y las actividades seleccionadas en la tarea anterior, diseña tu video interactivo.
Existen varios posibles modelos de videos interactivos, que incorporen escenas interactivas de diferentes herramientas de autor. En este apartado nos ocuparemos de los videos interactivos con escenas de GeoGebra, los cuales pueden incluir actividades formativas o no evaluativas, actividades evaluativas o la combinación de amas.
En el siguiente video interactivo se presenta una construcción geométrica y, al final del video, la escena interactiva obtenida.
La configuración de este segundo modelo es similar al anterior, con algunos cambios que explicamos a continuación.
videolocal.js, la cual es invocada por el archivo ivideo.html. Además de las funciones play() y pause(), usamos la función myVid.duration, donde myVid es el nombre del video (video1 en nuestro caso) y duration es la duración del video.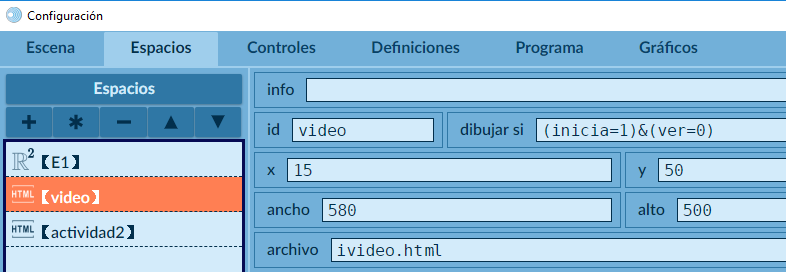
t), que la interfaz videolocal.js envía a DescartesJS a través de la instrucción window.parent. postMessage({type: "set", name: "t", value: contenido.value }, '*');. Esta variable la inicializamos con un valor vacío: t='', lo cual nos permite saber cuándo cambia de valor.Mientras t='' aparecerá el mensaje ¡Cargando GeoGebra!, aunque realmente sería ¡Cargando el video! Igualmente, el control tipo botón que permite la reproducción, sólo aparecerá cuando t!=''.
min:seg, el cual se obtiene con la función formato_tiempo():time=t y L=tf, donde tf es el tiempo de duración del video enviado por la interfaz videolocal.js.INICIO y CALCULOS son muy similares a los del video anterior, con diferencia en cómo se realiza la pausa del video en CALCULOS, pues ahora no es una función de DescartesJS, sino un mensaje enviado a ivideo.html:evento que ejecuta las siguientes instrucciones de parada del video, cuando para1=1:Esta es la interfaz videolocal.js:
Observa que cuando el mensaje es 'parar', se ejecuta la función myVid.pause();:
Una actividad evaluativa en un video interactivo puede configurarse de tal forma que impida la continuidad del video por realizar mal la actividad o, como en el tercer modelo que presentamos, presentar un mensaje de desaprobación.
Este video estás en capacidad, con lo explicado hasta ahora, de comprenderlo; sin embargo, explicaremos cómo se realiza la comunicación entre GeoGebra y DescartesJS.
actividad2.set( 'evalua',arco)) permite obtener de GeoGebra el arco pedido, mientras que el segundo (actividad2.set('arcos','')) permite obtener el arco (hecho o no) dibujado por el usuario.Dado que sólo usamos arcos de circunferencia, no hemos llamado la librería comandos.js, en su lugar hemos puesto el elemento requerido en la actividad tarea.html:
CALCULOS, hemos puesto las instrucciones:La variable A1 tiene como contenido el arco de circunferencia h dibujado por el usuario, y la variable A2 el arco k dibujado por GeoGebra.
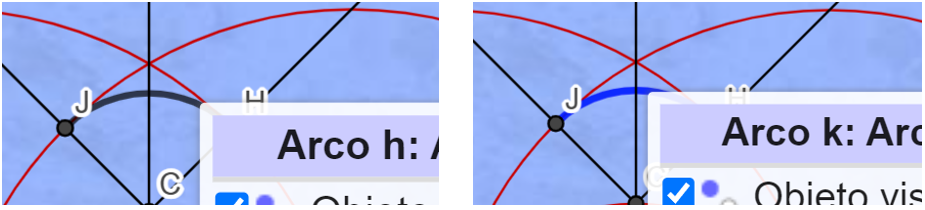
Las demás instrucciones ya las hemos explicado, así que puedes emprender la siguiente tarea:
Crea un video sobre una construcción de GeoGebra y, luego, usa uno de los dos modelos anteriores para diseñar un video interactivo (puedes cambiar imágenes de fondo y modificar la presentación a tu gusto).
Este último video interactivo incluye dos tipos de actividades. Para la primera, la evaluativa, hemos seleccionado dos actividades del proyecto plantillas de la Red Educativa Digital Descartes. Para la segunda, la formativa, incluimos cuatro actividades, dos de ellas corresponden a imágenes relacionadas con el video, otra actividad es de tipo lúdico, y la última es la escena de GeoGebra que se muestra en el video, para que el usuario interactúe con ella.
Muchas de las instrucciones y comandos usados en los videos anteriores, los hemos usado en este video. Las principales novedades son las siguientes: funciones adicionales de video, entre ellas las actualizaciones de tiempo de reproducción y sonido, y la incorporación de una barra de tiempo con marcas que indican cuándo el video se detendrá para abrir una actividad evaluativa o formativa.
La escena de DescartesJS la hemos configurado con un tamaño de $800\times 630px$, sobre la que hemos agregado 10 espacios, así:
E1, enviando el resultado de la evaluación en la variable var1,E2. Su propósito es evitar que el usuario manipule el video; sin embargo, se puede eliminar sin afectar los elementos de la escena.Controles
tiempo1<_Eval_(t2), donde t2 es el tiempo de duración del video, variable enviada por la interfaz videolocal.js del video. Cada vez que el usuario haga clic en este botón, se ejecutan esta instrucciones:g se le asigna el valor de $6$.g. Este control tiene una ordenada constante definida en la constricción como y = -E1._h/ ( 2*E1.escala ) + 1.1) que, para nuestro caso, sería igual a $-5.46$ y una abscisa que varía de $1$ a $6$, controlada en el algoritmo CALCULOS. Lo de la expresión para la ordenada, facilita el cambio de dimensiones y escala del espacio principal.
sonido. Este control tiene una ordenada constante definida en la constricción como (y = -E1._h/( 2*E1.escala ) + 0.25) que, para nuestro caso, sería igual a $-6.31$ y una abscisa que varía de $1$ a $6$, controlada en el algoritmo CALCULOS.
(accion='parar') & (tiempo1 = a_formativa[otro_f]); es decir, cuando la variable accion toma el valor de 'parar' y el tiempo de reproducción tiempo1 es igual al tiempo de una de las actividades formativas, que hemos almacenado en el vector a_formativa[otro_f].(accion='parar') & (tiempo1 = a_evaulativa[otro_e]) & (var1!=''); es decir, cuando la variable accion toma el valor de 'parar', el tiempo de reproducción tiempo1 es igual al tiempo de una de las actividades evaluativas, que hemos almacenado en el vector a_evaluativa[otro_e] y la variable var1 sea diferente de vacío. Este último elemento de la condición hace la diferencia con el control anterior, pues el botón no se mostrará hasta que la actividad se concluya y envíe la nota al espacio principal.Selector Definiciones
Para este video hemos puesto más definiciones que en los anteriores, con cinco vectores y dos funciones. La primera función (parada()) tiene instrucciones similares a las del botón "Play/Pause":
formato_tiempo()) descompone el tiempo de reproducción y de duración en horas, minutos y segundos, obviamente las horas no son necesarias, pues nuestros videos interactivos son de corta duración, pero las dejamos para alguien que no esté de acuerdo con ello.
Selector Programa
En el vector a_evaluativa[] se almacenan los tiempos de parada para las actividades evaluativas y en f_evaluativa[] los correspondientes a las actividades formativas.
tiempo1 y tiempo2 se asignan los tiempos de reproducción y duración, respectivamente, enviadas por el espacio subordinado E2. La variable barra es muda, solo nos sirve para enviar un mensaje a la interfaz de video, que permita actualizar el tiempo de reproducción del video; por ejemplo, si el video tiene una duración (tiempo2) de $60$ segundos y se ha detenido a los $20$ segundos (tiempo1 = avanzado) y, por otra parte, a la abscisa g.x en cada parada se le asigna el valor de $6$, entonces, el mensaje enviado es $'20\; segundos'$.avanzado en lugar de tiempo1.g y sonido, las cuales tienen valores entre $1$ y $6$.e3. Este evento se ejecuta cuando se cumple la condición (tiempo1 = a_evaluativa[otro_e]) | (tiempo1 = a_formativa[otro_f]); es decir, cuando el tiempo de reproducción del video es igual al tiempo de alguna de las actividades. La ejecución del evento se hace con las instrucciones g.x=6 y parada().Selector Gráficos
Hemos creado 22 objetos gráficos, de los cuales explicamos los siguientes:
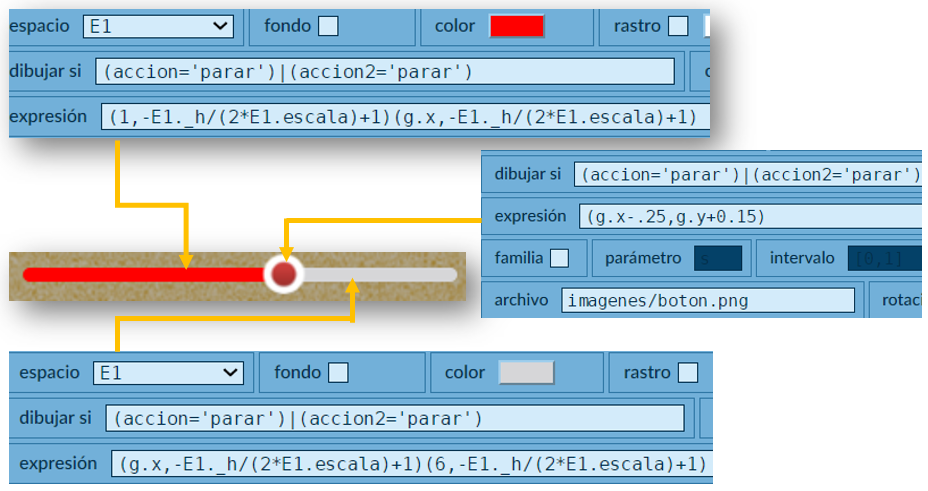
boton.png está vinculada al control gráfico g, por ello el usuario puede desplazarla modificando el valor de la abscisa $g.x$. El control se presenta cuando se cumple la condición (accion='parar') | (accion2='parar').[t1_minutos]:[t1_segundos] y para el segundo, en color narjanja, /\${\color{orange} {[t2_minutos]:[t2_segundos]}}.(a_evaluativa[s]>0)&(tiempo1>0)&(otro_e<=s) que cumpliéndose muestra un segmento de color naranja en la abscisa $(-6.8+a_evaluativa[s]*13.5/tiempo2,-5.2)$ y en la ordenada $(-6.8+a_evaluativa[s]*13.5/tiempo2,-4.8)$. Las marcas para las actividades formativas son similares y en color azul.
Google, en general, y YouTube, en particular, suministran rutinas JavaScript de programación, más conocidas como JavaScript API, las cuales permiten incrustar una aplicación Google (YouTube, Google Maps,...) en un sitio web y controlarla mediante JavaScript. Estas API, que hemos llamado interface o interfaz, anteriormente eran una especie de plug-in que hoy en día se han estandarizado en JavaScript, buscando una mayor compatibilidad con los sistemas operativos y navegadores.
En este último apartado del libro, veremos cómo aprovechar la API de YouTube para reproducir los vídeos, pausar o detener esos videos, ajustar el volumen, o recuperar información sobre el video como su duración.
No obstante, siempre recomendamos diseñar vídeos interactivos con los modelos en local, pues no tienen dependencia externa que puedan frustrar uno de los atributos que esperamos de nuestros objetos interactivos... la perdurabilidad. Esta frustración puede presentarse por dos razones; la primera es la eliminación del vídeo por el autor, incluso en nuestro propio canal (una demanda, por ejemplo); la segunda, porque Google cambie políticas o modificaciones en los atributos de sus aplicaciones que hagan inservible la interfaz (algo similar se ha presentado con la API de Google Maps, al modificar la llamada API key).
Inicialmente, interactúa con el siguiente video interactivo, en el que hemos enlazado a un video de YouTube.
Videos ocultos
Una costumbre de los youtuber es ocultar algunos videos, bien sea porque los crean como prueba o para compartir con un grupo de amigos, colegas, alumnos o familiares. En nuestro caso, solíamos crear videos en YouTube para incorporarlos en nuestros videos interactivos, como la interactividad no estaba en YouTube sino en la escena DescartesJS, apenas era obvio que el video se publicara como oculto. Pero, en 2021, YouTube toma una decisión que afectó varios de nuestros videos interactivos, entre ellos el video anterior (ahora corregido). La nueva política es la siguiente:

Así las cosas, una primera recomendación es publicar los videos con visibilidad para todo el mundo, así para "casi todo el mundo" el video no tenga sentido:

Videos relacionados
Habrás notado que en cada parada del video anterior aparecen los videos relacionados, en la parte inferior de la pantalla. Si revisas el archivo ivideo (puesto en el espacio subordinado), observarás que tenemos una etiqueta <iframe>, con el siguiente video de YouTube: https://www.youtube.com/embed/JT8DqP64yIE? enablejsapi=1 &html5=1 &rel=0 &autoplay=0&controls=0 &showinfo=0 &start=1 &disablekb=1
Las igualdades que están después del interrogante son parámetros de la API de YouTube, que funcionaban bien en el momento de crear el video, entre ellos rel=0 cuya función era evitar que aparecieran los molestos videos relacionados, pues "a partir del 25 de septiembre de 2018 dicho parámetro deja de funcionar". Sin embargo, como un "paño de agua tibia", YouTube acepta que los videos relacionados sean los de tu canal, siempre que el video esté en una "lista de reproducción.
Una segunda recomendación no es tener el video en la lista de reproducción, en lugar de ello podemos usar un espacio tipo "máscara" que oculte los videos relacionados; por ejemplo, en la imagen anterior podemos poner un espacio en la parte inferior, que oculte los videos relacionados y en dicho espacio realizar la actividad evaluativa mostrada en la imagen.
Autoplay en los videos YouTube.
Parece que 2018 fue un año de cambio radical en las políticas de YouTube, pues en el mes de abril de ese año, el parámetro autoplay=1 deja de funcionar, política a la que se adhieren la mayoría de navegadores con el argumento principal de "mejorar la experiencia del usuario". Si vuelves a revisar nuestro código, notarás que no nos afecta pues habíamos puesto autoplay=0; sin embargo, es posible que tengas la idea de un video interactivo en el cual la auto reproducción sea fundamental, YouTube te permite hacerlo siempre que silencies el video con el parámetro mute=0.
Nuestra recomendación:  o, mejor, eliminar el "autoplay" y dejar que el usuario tenga que hacer clic para iniciar el video interactivo, como en nuestro primer ejemplo.
o, mejor, eliminar el "autoplay" y dejar que el usuario tenga que hacer clic para iniciar el video interactivo, como en nuestro primer ejemplo.
Videos embebidos de YouTube embed.
Para nuestros videos interactivos, con YouTube, es "absolutamente necesario" que el video permita la inserción. En los tres últimos años, nos llevamos una sorpresa cuando en algunos de nuestros contenidos digitales que incorporaban (embebían) videos de YouTube nos aparecía el mensaje:
Se trata de una nueva política, la cual permite al dueño del video activar o no una casilla de inserción que, obviamente, los youtuber con propósitos de monetizar corrieron a desactivarla, obligando al usuario a ver el video directamente en el canal de YouTube.
Por supuesto, para nuestros propósitos (no monetizables) esta política nos afectó significativamente.

Recomendación: usa tu propio canal en YouTube.
¡Claro que sí!, si bien recomendamos usar nuestros videos en local, no por ello desconocemos la riqueza que tenemos en YouTube; por ejemplo, en el siguiente video interactivo no usamos un video de YouTube ¡Usamos nueve videos de YouTube! Observa el video para probar nuestra afirmación, cerca del final hay una actividad interactiva que incluye la mayoría de los videos.
El espacio principal, del video interactivo, se comunica con nueve videos de YouTube, enviando mensajes con el código del video y los tiempos de inicio y final de reproducción del video. No obstante, por las continuas políticas de YouTube, no podemos garantizar que este video sea perdurable en el tiempo. Una recomendación, para garantizar un mínimo de perdurabilidad, es usar canales educativos (universidades, por ejemplo), de organizaciones gubernamentales como la NASA o canales de divulgación como los usados en el video anterior; por ahora, después de dos años de creado, los nueve videos siguen funcionando.
Existen muchas posibilidades de diseño de un video interactivo, cuya configuración varía en el tamaño de la escena, posición y tamaño del video, cantidad de actividades, imágenes, colores, etcétera. Como parte final de este capítulo y del libro, presentamos y explicamos un modelo en el que el video ocupa un buen porcentaje de la escena (un poco mas del 80%), incluye tres tipos de actividades (evaluativas, formativas e informativas), botones independientes para las acciones de reproducir y pausar, nueve vectores, seis funciones, dos eventos (uno para las paradas del video y otro para el cálculo de notas).
Algo que es importante diferenciar tiene que ver con las "actividades informativas", que también usamos en el video del apartado 6.6.1. Nuestra postura es que un video no puede considerarse interactivo solo por el hecho de "hacer clic" en un botón, como ocurre con las actividades informativas que, en parte, están presentes en el video de la introducción de este capítulo (apartado 6.1). El video es interactivo porque tiene actividades interactivas (formativas o evaluativas).
El video
El video que hemos seleccionado es del Canal Encuentro de Argentina, publicado el 29 de mayo de 2015, con más de 38,000 visualizaciones.
El código del video es 8CUda-VITTY, el cual pusimos en el archivo de la interfaz del video: ivideo.html.
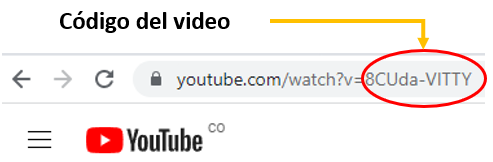

Los parámetros YouTube, pese a que algunos no funcionan, los hemos dejado sólo para describirlos, ellos son:
enablejsapi=1. Establecer este parámetro en 1 activa la API de JavaScript.html5=1. Obsoleto, era necesario cuando el video se reproducía en formato flash, con el parámetro en 1, el video se mostraba como HTML5 si estaba disponible, o como respaldo en Flash Player.rel=0. Su propósito era evitar que los videos relacionados no se mostraran. Ahora no funciona así.autoplay=0. El valor predeterminado es 0; es decir, no es necesario poner este parámetro. Define si el video inicial se reproduce automáticamente o no cuando se carga el reproductor. La nueva política exige que autoplay=1 vaya acompañado del parámetro mute=1.controls=0. El valor predeterminado es 1. Este parámetro indica si se muestran o no los controles del reproductor de video. Dado que le video interactivo usa sus propios controles, hemos puesto el parámetro en cero.showinfo=0. Obsoleto. Si se establecía el valor del parámetro en 0, el reproductor no mostraba información como el título del video o el usuario que lo subió antes de comenzar la reproducción.start=1. Este parámetro permite que el reproductor inicie la reproducción del video en el número exacto de segundos proporcionados desde el comienzo del video. Lo hemos puesto solo por ilustración.disablekb=1. El valor predeterminado es 0. Establecer el valor en 1 desactiva los controles de teclado del reproductor. Al no estar activados los controles, el usuario puede usar teclas como la Barra espaciadora para reproducir/pausar o las Flechas para controlar el avance/retroceso o el control de volumen.El video interactivo
Puedes, antes de continuar, ver el video interactivo diseñado:
El video lo puedes descargar en este enlace:  .
.
Selector Definiciones
Empezamos con este selector, pues la comprensión de los demás dependen de la descripción de los elemento de este selector. Hemos creado nueve vectores y seis funciones, así:
t_info[], t_pregunta[] y t_actividad[], que almacenan el tiempo en el que el video debe pausar para mostrar las actividades informativas, evaluativas y formativas, respectivamente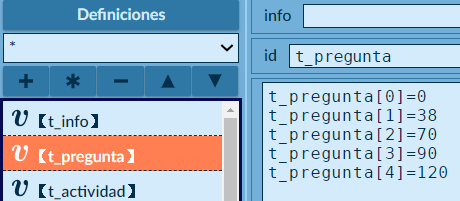
informacion con un tamaño cercano a los 600x440 pixeles.AC[] y PL[] que almacenan los nombres de las carpetas correspondientes a las actividades formativas y evaluativas, respectivamente.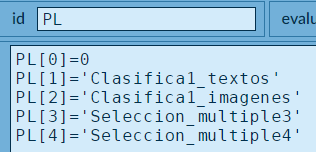
archivo[]. Almacena el archivo indexb.html de las plantillas usadas en este video interactivo. Si la plantilla tiene como archivo ejecutable index.html, se sugiere cambiarlo a indexb.html.escena[]. Almacena el archivo index.html de las actividades formativas.promedio[]. Aalmacena la nota obtenida en cada actividad evaulativa.calcula_preguntas(). Es un algoritmo que calcula cuántas preguntas están de finidas en el vector PR. En forma similar se calcula el número de actividades eveluativas e informativas. Se parte del supuesto que no serán mayores a 11.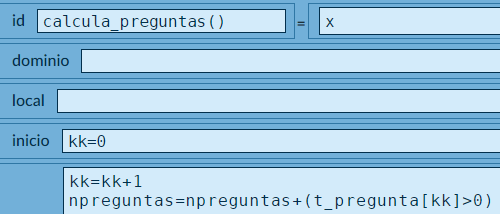
calcula_plantillas(). Realmente no calcula, lo que hace es asignar un archivo al vector archivo[]; por ejemplo, a archivo[1] se le asigna 'Clasifica1_textos/indexb.html'. En forma similar se crea la función calcula_escenas().calcula_mensajes(). Dependiendo del número de actividades, determina el mensaje a poner en el pantallazo inicial.formato_tiempo(). Explicado en el video anterior, solo hemos cambiado el nombre de las variables y usado un condicional para que el formato se ajuste al estándar; por ejemplo, en lugar de '3:25', escribirá '03:25'.Selector Espacios
De los seis espacios creados, solo describimos los espacios e1 y e2, pues los demás ya han sido explicados.
Espacio e1. Corresponde a las actividades evaluativas, cuyos archivos ejecutables están almacenados en el vector archivo[]. Dado que, en este ejmplo, estamos usando plantillas con archivos indexb.html (no escalables), las dimensiones de este espacio son 790x500 pixeles.
Espacio e2. Corresponde a las actividades formativas, cuyos archivos ejecutables están almacenados en el vector escena[].
Selector Controles
Son 12 controles, de los cuales explicamos los siguientes:
Inicio. Este botón aparece cuando la variable inicia es cero; es decir, al inicio del video. Lo describimos porque, una vez se haga clic, tendría que iniciar la reproducción del video; sin embargo, en navegadores como Chrome ello no ocurre, por lo que debe hacerse clic sobre el botón de YouTube. Esta anomalía la hemos tenido en cuenta para que el espacio mascara se active cuando tiempo1>3.silencio. Además de la barra de sonido, incluimos el botón volumen, que una vez se haga clic en este botón, da paso para que aparezca el botón silencio, inidicando que el audio ha sido inactivado, al hacer clic sobre este segundo botón, el audio se activa nuevamente.En el selector Programa no hay necesidad de mayores explicaciones a las ya dadas anteriormente, excepto por la instrucción utilizada para que las variables para1, para2 y para3 sean verdaderas.
Por ejemplo, para1 es verdadera cuando: ent(tiempo1) = t_actividad[act], o cuando ent(tiempo1)-1 = t_actividad[act], o cuando ent(tiempo1)+1 = t_actividad[act] es verdadero. Hemos recurrido a estas tres posibilidades, pues por las cifras decimales, es posible que la primera posibilidad no se cumpla.
Tampoco daremos explicaciones sobre el selector Gráficos, pues ya estás en capacidad de entender cada uno de los objetos gráficos empleados.
Con este último modelo, estarás en capacidad de incluir, también, actividades evaluativas y formativas de GeoGebra, como las que te proponemos en la siguiente tarea:
A continuación te presentamos dos videos interactivos que incluyen construcciones de GeoGebra. Los videos fueron diseñados algunos años atrás, por lo que presentan algunas deficiencias de diseño, además de presentar problemas si se intervienen con el editor actual de DescartesJS. Tu tarea es diseñar dos nuevo videos interactivos, incluyendo los datos que suministran los videos anteriores (tiempos de parada, escenas de GeoGebra, etc.). Puedes descargar los videos en estos enlaces:  y
y 
Haz clic en las siguientes imágenes, para que interactúes con los videos interactivos propuestos en la tarea.