Matemáticas de media:
Grado 11°
INTERACTIVO

Carlos Alberto Rojas Hincapié
Red Educativa Digital Descartes, Colombia
1ª edición – 2024
Córdoba (España)
2024
Título de la obra Autor Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Matemáticas de media:
Grado 11°
Carlos Alberto Rojas Hincapié
Primera edición: 2024
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm

ISBN: 978-84-10368-06-4
Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
 Puedes descargar el libro en formato pdf:
Puedes descargar el libro en formato pdf:
Tabla de contenido
Este libro digital interactivo se ha diseñado con fundamento en la filosofía del Proyecto DescartesJS: "Trabajando altruistamente por la comunidad educativa de la aldea global", que sólo busca desarrollar contenidos educativos para el provecho de la comunidad académica, esperando únicamente como retribución el uso y difusión de estos contenidos. El contenido del libro, al igual que los objetos interactivos se han diseñado de tal forma que se puedan leer en ordenadores y dispositivos móviles sin necesidad de instalar ningún programa o plugin. El libro se puede descargar para su uso en local sin dependencia con la red, a excepción de algunos vídeos incluidos en el texto. Todos los objetos interactivos se han diseñado con el Editor DescartesJS.
Véase https://proyectodescartes.org/iCartesiLibri/descripcion.htm.
El contenido de este libro se basa en un curso de capacitación del editor DescartesJS para docentes que, por la dificultad de concertar un horario presencial, permite una opción autodidacta acompañada de material interactivo para una mayor comprensión de los temas tratados.
Retomando la introducción a la documentación de DescartesJS de Radillo, Abreu y Espinosa, podríamos coincidir en que este libro está destinado tanto a personas que no han usado DescartesJS como a personas que tienen cierta experiencia y desean mejorarla. En cada apartado del libro se proponen ejercicios y se incluyen ejemplos para que el lector pueda comprender paso a paso la funcionalidad de DescartesJS y su enorme potencial para crear objetos interactivos de aprendizaje.
El Estado colombiano, decidido a elevar la calidad de la educación, introdujo el enfoque basado en el desarrollo de competencias en los estudiantes, lo cual supone el tránsito desde el aprendizaje que centra la atención en el dominio de contenidos, a una educación basada en competencias que no se agota en el sistema educativo, sino que se desarrolla de manera permanente en interacción con el mundo.
De esta manera, consolidar una política de calidad enmarcada en el desarrollo de competencias implica, entonces, una transformación de fondo de las prácticas pedagógicas, del funcionamiento de la institución educativa y del papel de los actores educativos, teniendo como protagonista al estudiante. Buscando desarrollar este modelo se han realizado esfuerzos por elevar la calidad de la educación en el país; en este sentido, el Ministerio de Educación Nacional (MEN) ha puesto a disposición de docentes, directivos docentes, padres de familia y público en general herramientas pedagógicas como:
Herramientas que constituyen el punto de partida y sustento de todas las estrategias de mejoramiento, además son un importante insumo para el diseño curricular
y el cambio en las prácticas pedagógicas
ESTRATEGIAS DE MEJORAMIENTO
Elementos que contribuyen a mejorar los procesos de evaluación por competencias y las prácticas en el aula de clase por parte de los docentes para alcanzar cada vez mejores resultados y hacer que la educación en Colombia mejore su calidad. Ampliar imagen
Componentes / Pensamientos
Específicos del área de matemáticas.
5 categorías conceptuales que conforman esta asignatura según los Lineamientos y los Estándares Básicos de Competencia diseñados por el Ministerio de Educación Nacional (M.E.N.), los cuales son:
1. Pensamiento numérico y sistemas numéricos.
Se asocia con "la organización de actividades centradas en la comprensión del uso y de los significados de los números y de la numeración; el desarrollo de diferentes técnicas de cálculo y estimación".
2. Pensamiento espacial y sistemas geométricos.
Contempla las actuaciones del sujeto en todas sus dimensiones y relaciones espaciales para interactuar de diversas maneras con los objetos situados en el espacio, hacer acercamientos conceptuales que favorezcan la creación y manipulación de nuevas representaciones mentales.
3. Pensamiento métrico y sistemas de medidas.
Hace referencia a la comprensión general que tiene una persona sobre las magnitudes y las cantidades, su medición y el uso flexible de los sistemas métricos o de medidas en diferentes situaciones.
4. El pensamiento variacional y sistemas algebraicos y analíticos.
Comprensión y uso de los conceptos y procedimientos de las funciones y sus sistemas analíticos, para el aprendizaje con sentido del cálculo numérico y algebraico.
5. Pensamiento aleatorio y sistemas de datos.
El pensamiento aleatorio se apoya directamente en conceptos y procesos de la teoría de probabilidades y de la estadística inferencial, e indirectamente, en la estadística descriptiva y en la combinatoria.
¿Qué son los Estándares Básicos de Competencias?
"Un estándar es un criterio claro y público que permite juzgar si un estudiante, una institución o el sistema educativo en su conjunto cumplen con unas expectativas comunes de calidad; expresa una situación deseada en cuanto a lo que se espera que todos los estudiantes aprendan en cada una de las áreas a lo largo de su paso por la Educación Básica y Media, especificando por grupos de grados (Ciclo I: 1° a 3°, Ciclo II: 4° a 5°, Ciclo III: 6° a 7°, Ciclo IV: 8° a 9°, y Ciclo V: 10° a 11°) el nivel de calidad que se aspira alcanzar.
(Ministerio de Educación Nacional, 2006, p. 11)".

El desarrollo de estos Estándares Básicos de Competencia permitirá fortalecer los procesos de formulación, modelación y resolución de problemas.
Competencias específicas del área de matemáticas.
Son las encargadas de desarrollar la capacidad de formular, resolver y modelar fenómenos de la realidad; comunicar, razonar, comparar y ejercitar procedimientos para fortalecer la adquisición de conocimientos, habilidades, actitudes y comprensiones del pensamiento matemático, relacionándolos entre si para facilitar el desempeño flexible, eficaz y con sentido. El área de matemáticas evalúa en la prueba Saber para el ciclo 10° y 11° lo siguiente:
1. Interpretación y representación.
Esta competencia consiste en la habilidad para comprender y transformar la información presentada en distintos formatos como tablas, gráficos, conjuntos de datos, diagramas, esquemas, etcétera, así como la capacidad de utilizar estos tipos de representación para extraer de ellos información relevante que permita, entre otras cosas, establecer relaciones matemáticas e identificar tendencias y patrones. Con el desarrollo de esta competencia, se espera que un estudiante manipule coherentemente registros, entre los cuales pueden incluirse el simbólico, el natural, el gráfico y todos aquellos que se dan en situaciones que involucran las matemáticas.
2. Formulación y ejecución.
Esta competencia se relaciona con la capacidad para plantear y diseñar estrategias que permitan solucionar problemas provenientes de diversos contextos, bien sean netamente matemáticos o del tipo de aquellos que pueden surgir en la vida cotidiana y son susceptibles de un tratamiento matemático.
Se relaciona también con la habilidad o destreza para seleccionar y verificar la pertinencia de soluciones propuestas a problemas determinados, y analizar desde diferentes ángulos estrategias de solución. Con el desarrollo de esta competencia, se espera que un estudiante diseñe estrategias apoyadas en herramientas matemáticas, proponga y decida entre rutas posibles para la solución de problemas, siga las estrategias para encontrar soluciones y finalmente resuelva las situaciones con que se enfrente.
3. Argumentación.
Esta se relaciona con la capacidad para validar o refutar conclusiones, estrategias, soluciones, interpretaciones y representaciones en situaciones problemáticas, dando razones del porqué, o del cómo se llegó a estas, utilizando ejemplos y contraejemplos, o bien señalando y reflexionando sobre inconsistencias presentes. Con el desarrollo de esta competencia se espera que un estudiante justifique la aceptación o el rechazo de afirmaciones, interpretaciones, y estrategias de solución basándose en propiedades, teoremas o resultados matemáticos, o verbalizando procedimientos matemáticos.
¿Qué son los Derechos Básicos de Aprendizajes (DBA)?
Los DBA, en su conjunto, explicitan los aprendizajes estructurantes para un grado y un área particular. Se entienden los aprendizajes como la conjunción de unos conocimientos, habilidades y actitudes que otorgan un contexto cultural e histórico a quien aprende.
Los DBA se organizan guardando coherencia con los Lineamientos Curriculares y los Estándares Básicos de Competencias (EBC)
Su importancia radica en que plantean elementos para construir rutas de enseñanza que promueven la consecución de aprendizajes año a año para que, como resultado de un proceso, los estudiantes alcancen los EBC propuestos por cada grupo de grados.
Estructura de los DBA.
La estructura para la enunciación de los DBA está compuesta por tres elementos centrales: El enunciado, las evidencias de aprendizaje y el ejemplo.
Grado 11°, DBA 2. "Justifica la validez de las propiedades de orden de los números reales y las utiliza para resolver problemas analíticos que se modelen con inecuaciones."
$\rightarrow$ "Utiliza propiedades del producto de números Reales para resolver ecuaciones e inecuaciones."
$\rightarrow$ "Interpreta las operaciones en diversos dominios numéricos para validar propiedades de ecuaciones e inecuaciones."
 “Ana una estudiante de undécimo decide resolver una inecuación como se muestra en la siguiente figura:
“Ana una estudiante de undécimo decide resolver una inecuación como se muestra en la siguiente figura:
Ana argumenta que para resolver la inecuación, todo lo que está sumando al lado izquierdo se pasa a restar al lado derecho y posteriormente, realiza las operaciones. Luego, termina su ejercicio de la siguiente manera: dice que para despejar la x pasa a multiplicar el 3 a ambos lados”.
Los Derechos Básicos de Aprendizajes.
"El número gobierna el universo.".
Pitágoras

DERECHOS BÁSICOS DE APRENDIZAJE (DBA)
DBA.1. Utiliza las propiedades de los números (naturales, enteros, racionales y reales) y sus relaciones y operaciones para construir y comparar los distintos sistemas numéricos.
DBA.2. Justifica la validez de las propiedades de orden de los números reales y las utiliza para resolver problemas analíticos que se modelen con inecuaciones.
Derechos Básicos de Aprendizaje - Grado 11°.
DESEMPEÑOS / ESTANDAR
Componente 1 - Pensamiento numérico.
1.5 M.V Establezco relaciones y diferencias entre diferentes notaciones de números reales para decidir sobre su uso en una situación dada. DBA 1.
1.12 M.V Reconozco la densidad e incompletitud de los números racionales a través de métodos numéricos, geométricos y algebraicos. DBA 2.
Componente 5 - Pensamiento Variacional.
5.1 M.V Utilizo las técnicas de aproximación en procesos infinitos numéricos. DBA 2.

El desarrollo de estos Estándares Básicos de Competencia permitirá fortalecer los procesos de formulación, modelación y resolución de problemas.
Capitulo I. Los números reales
 Uno de los problemas que más controversia generó entre los matemáticos de finales del siglo $XIX$ fue el de la aceptación de la existencia de los números irracionales.
Uno de los problemas que más controversia generó entre los matemáticos de finales del siglo $XIX$ fue el de la aceptación de la existencia de los números irracionales.
Karl Weierstrauss construyó los números reales a partir de sucesiones infinitas de números racionales pero contó con el rechazo de algunos de los más prestigiosos matemáticos de su época encabezados por Leopold Kronecker, quienes no consideraron válido el empleo de métodos finitistas en el tratamiento de problemas al infinito; es así como al conocer la demostración dada por Ferdinand Lindemann en la que probaba que $\pi$ no es raíz de alguna ecuación poligonal no nula con coeficientes enteros, Kronecker le dijo: “¿De qué sirve todo esto, si los números irracionales no existen?

Como consecuencia de lo anterior, uno de los más importantes matemáticos de este siglo David Hilbert, partiendo de la premisa de que una entidad existe en cuanto se ha demostrado que no implica ninguna contradicción, logró probar que el sistema de axiomas que definen los números reales es no contradictorio, introduciendo de esta manera el método axiomático como sustituto del método geométrico en el tratamiento de los números reales.
Por otra parte, usando la geometría también demostró que cualquier contradicción que la geometría analítica pudiera aparecer en la geometría euclidiana, debía también aparecer como una contradicción en la aritmética de los números reales; quedando de esta forma demostrando que la aritmética de los números reales es tan consistente como la geometría euclidiana.

La concepción filosófica, así como los métodos introducidos por Hilbert, para determinar lo que es válido en matemáticas, dieron origen a la denominada Escuela formalista, la cual representa una de las más importantes corrientes del pensamiento matemático moderno.
23 problemas de Hilbert, en 1900, Hilbert presentó una relación de 23 problemas sin resolver que, a su juicio, en caso de ser solucionados, representarían un avance considerable para las matemáticas. Él define sus famosos 23 problemas. Al hacerlo, tuvo un efecto mayor en matemáticas que forma en el siglo XX que cualquier otra persona. Hilbert contorneado 23 problemas o preguntas, que pensó, si contesta correctamente, sería llevar las matemáticas a un nuevo nivel. La lista, dijo, no fue significada para excluir otros problemas. Era simplemente una muestra de los problemas.
Capitulo I. Los números reales
Se entenderá por conjunto cualquier colección o agregado de objetos de naturaleza cualquiera. Los conjuntos se notan con letras mayúsculas; los objetos que lo componen con letras minúsculas.
Toda la matemática tiene mucho que ver con el estudio de conjuntos, así, por ejemplo, la geometría estudia conjuntos de puntos, el álgebra conjuntos de los números especialmente, entre otros.

¡Recordemos!
 Si un objeto $a$ es un elemento de un conjunto $B$ se escribirá:
$$a \in B$$
que se lee: “$a$ pertenece a $B$, o $a$ es un elemento de un conjunto $B$”, en cambio si $a$ no es un elemento de $B$ se escribirá:
$$a \notin B$$
que se lee: “$a$ no pertenece a $B$”.
Si un objeto $a$ es un elemento de un conjunto $B$ se escribirá:
$$a \in B$$
que se lee: “$a$ pertenece a $B$, o $a$ es un elemento de un conjunto $B$”, en cambio si $a$ no es un elemento de $B$ se escribirá:
$$a \notin B$$
que se lee: “$a$ no pertenece a $B$”.
Un conjunto se dice que está bien determinado si dado cualquier objeto podemos decir si él forma o no parte del conjunto.
Se acostumbra en el primer método separar los elementos con comas y encerrarlos entre paréntesis, por ejemplo,
$$A = \{2, 4, 6, 8\}$$ Es decir, $A$ es el conjunto formado por los números $2, 4, 6, 8$.

Existen unas operaciones básicas que se pueden realizar con los conjuntos. Estas operaciones son la unión, la intersección, la diferencia, la diferencia simétrica y el complemento.
Capitulo I. Los números reales
¿Qué es un diagrama de Venn?
Un diagrama de Venn usa círculos que se superponen u otras figuras para ilustrar las relaciones lógicas entre dos o más conjuntos de elementos, se usan ampliamente en las áreas de matemática, estadística, lógica, enseñanza, lingüística, informática, entre otros.
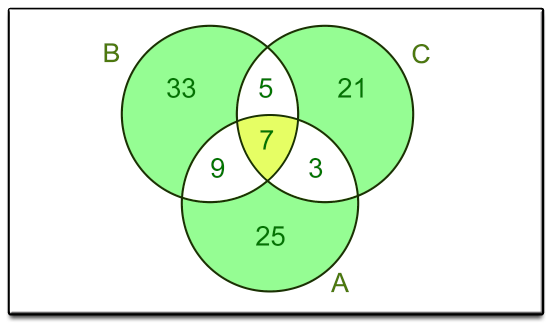 $$A = \{3, 7, 9, 25\}, \quad B = \{5, 7, 9, 33\},\quad C =\{3, 5, 7, 21\}$$
$$A = \{3, 7, 9, 25\}, \quad B = \{5, 7, 9, 33\},\quad C =\{3, 5, 7, 21\}$$
 Comprueba lo aprendido respondiendo a la pregunta.
Comprueba lo aprendido respondiendo a la pregunta.
El conjunto de los números Reales ($\mathbb{R}$) está forman por todos los conjuntos numéricos, recordemos estos conjuntos numéricos:
$\mathbb{N} = \left\lbrace 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,...\right\rbrace$
El conjunto de los números naturales, parece ser el primer conjunto de números de que dispuso el hombre. Estos números llamados números naturales le fueron muy útiles ya que le permitieron realizar operaciones tales como la suma y la multiplicación; es importante notar que la suma o multiplicación de dos elementos cualesquiera de $\mathbb{N}$ da lugar a otro elemento del mismo conjunto, por ejemplo,
$$4 + 7 = 11; \quad 11 \in \mathbb{N}, \qquad 3 \cdot 5 = 15; \quad 15 \in \mathbb{N}$$Sin embargo, esto mismo no sucede con la operación resta o diferencia, pues no siempre la resta de dos elementos de $\mathbb{N}$ da lugar a otro elemento de $\mathbb{N}$.
Es decir el problema de encontrar $a - b$, $a \in \mathbb{N}$, $b \in \mathbb{N}$ sólo se podía resolver en el caso $a$ mayor que o igual a $b$ $(a \geqslant b)$.
 Para poder resolver este problema en cualquier caso fue necesario ampliar el conjunto $\mathbb{N}$, adicionando números negativos (enteros) $-1, -2, -3,...,$ de esta manera se formó el conjunto de los números enteros.
Para poder resolver este problema en cualquier caso fue necesario ampliar el conjunto $\mathbb{N}$, adicionando números negativos (enteros) $-1, -2, -3,...,$ de esta manera se formó el conjunto de los números enteros.
Capitulo I. Los números reales.
Evidentemente el conjunto $\mathbb{N}$ es una parte del conjunto $\mathbb{Z}$; es claro que el conjunto de los enteros es cerrado para las operaciones de suma, resta y multiplicación. Sin embargo, la división de los elementos de $\mathbb{Z}$ no siempre es un elemento de $\mathbb{Z}$, por ejemplo:
$\dfrac{5}{3} \notin \mathbb{Z},\enspace$ es decir que la operación $\displaystyle\frac{a}{b}$ con $a, b \in \mathbb{Z}$ y $b =\not 0$ no siempre es posible en el conjunto de los números enteros. Para poder realizar esta operación fue necesario ampliar el conjunto $\mathbb{Z}$ adicionándo todas las fracciones (o cocientes de dos elementos de $\mathbb{Z}$ con denominador distinto de cero) es decir, a este nuevo conjunto así formado se conoce como el conjunto de los números racionales.
Estos, incluyen a los números naturales $\mathbb{N}$ y los números enteros $\mathbb{Z}$, además, de todas las expresiones de la forma $\displaystyle\frac{a}{b}$ llamadas fracciones.
$\displaystyle \mathbb{Q} = \left\lbrace ...-3, -\frac{5}{2}, -2, -\frac{3}{2}, -1,-\frac{3}{4}, -\frac{1}{2}, 0, \frac{1}{2}, \frac{3}{4}, 1, -\frac{3}{2}, 2, \frac{5}{2},...\right\rbrace$
Los números racionales se representan con la letra ($\mathbb{Q}$), este conjunto se creó debido a las limitaciones de cálculo que presentaban los números naturales ($\mathbb{N}$) y números enteros ($\mathbb{Z}$), para solucionar esta dificultad, se creó el conjunto de los números racionales ($\mathbb{Q}$).
Un número racional es un número que puede expresarse como una fracción, que puede ser exacta o periódica, y se escribe de la forma:
$$\frac{m}{n}=\frac{Numerador}{Denominador}, \quad con \quad b =\not 0 $$
Por otro lado el conjunto $\mathbb{Q}$ es cerrado para las operaciones de suma, resta, multiplicación o división. Es decir: la suma, resta, multiplicación o división de dos números racionales es a su vez un número racional.
En la operación de división se excluye el caso en el cual el denominador es cero. Esto se hace pues si se admitiera la división por cero se podría llegar a un absurdo (la división por cero no existe en los $\mathbb{R}$, por lo tanto, $n \equiv\not 0 $
Las fracciones se representan en la recta numérica, dividiendo cada intervalo de una recta numérica en espacios iguales, que representen números enteros (unidad), por ejemplo,
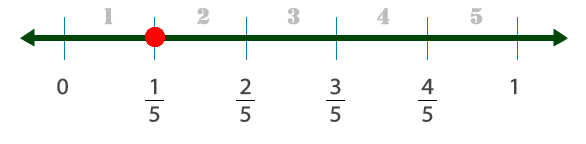
El numerador nos representa la parte que se toma, en la gráfica sería $1$, y el denominador las partes en que se dividió la unidad, para este caso en $5$ partes iguales.
Capitulo I. Los números reales
Cada una de estas subdivisiones representa una fracción con denominador igual al número de partes de la subdivisión. En otras palabras, cuando las divisiones de la unidad coinciden con el denominador de la fracción.
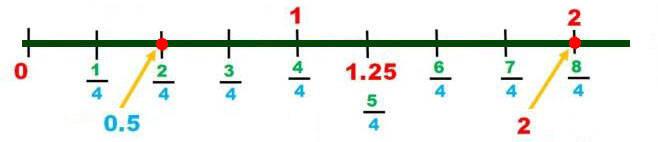
Cada fracción es un número racional y cada número racional consta de infinitas fracciones equivalentes. Los números enteros representados como una fracción, tienen como denominador el número $1$, por ejemplo, $\displaystyle\frac{2}{1} = 2$

¡Recordemos!
 Cuando una fracción $\displaystyle\frac{a}{b}$ es menor que la unidad, se llama fracción propia y está en la recta numérica entre $-1$ y $1$, o se llama impropia, cuando es mayor que la unidad y representa un número llamado mixto, por ejemplo,
Cuando una fracción $\displaystyle\frac{a}{b}$ es menor que la unidad, se llama fracción propia y está en la recta numérica entre $-1$ y $1$, o se llama impropia, cuando es mayor que la unidad y representa un número llamado mixto, por ejemplo,
$$\displaystyle\frac{16}{5} = \textrm{\Huge 3}\dfrac{1}{5}=\frac{(3)(5)+1}{5}=\frac{16}{5}$$

 Herramientas para trabajar con fracciones.
Herramientas para trabajar con fracciones.
$\space$ Descargar para imprimir
 xploremos.
xploremos.
Ingresa la fracción $\displaystyle\frac{a}{b}$, si es un número entero, escribe $b = 1$ y oprime el botón solución, observa su representación en la recta numérica real.
Con el conjunto de los números racionales se pueden resolver gran cantidad de problemas. Sin embargo, pensemos en el siguiente problema muy sencillo que no tiene solución en este conjunto.
Es sabido que en un triángulo rectángulo la suma de los cuadrados de las longitudes de los catetos es igual al cuadrado de la longitud de la hipotenusa (Teorema de Pitágoras).

 ¡Piensa!... Pues bien, miremos la situación problema que se presenta considerando un triángulo rectángulo cuyos catetos tengan de longitud $1$.
¡Piensa!... Pues bien, miremos la situación problema que se presenta considerando un triángulo rectángulo cuyos catetos tengan de longitud $1$.
Capitulo I. Los números reales
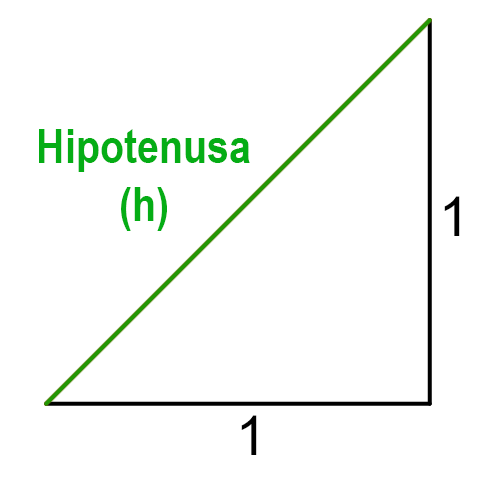 Según lo anterior la hipotenusa de este triángulo tiene como longitud $\sqrt{2}$, pero el número $\sqrt{2}$ no es un número racional, es decir, el problema de hallar la hipotenusa de un triángulo rectángulo cuyos catetos tienen como longitud $1$ no tiene solución en el conjunto $\mathbb{Q}$.
Según lo anterior la hipotenusa de este triángulo tiene como longitud $\sqrt{2}$, pero el número $\sqrt{2}$ no es un número racional, es decir, el problema de hallar la hipotenusa de un triángulo rectángulo cuyos catetos tienen como longitud $1$ no tiene solución en el conjunto $\mathbb{Q}$.
Los números $\sqrt{2}$, $\sqrt{3}$, $\pi$... entre otros, que no son racionales, es decir, aquellos números que no pueden transformarse en una fracción, se conocen como el conjunto de números irracionales.
Este conjunto surgió de la necesidad de reunir a ciertos números que no pertenecen a los conjuntos anteriores; este, está representado por los números decimales infinitos no periódicos, entre ellos se pueden citar a las raíces inexactas, el número $ \pi$ (Pi), entre otros.
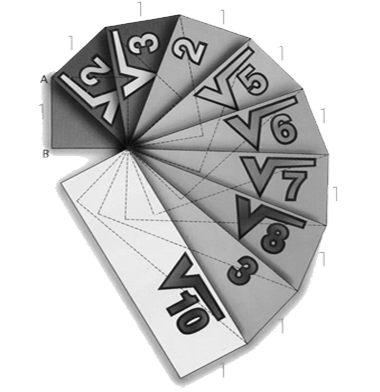
Un número Irracional no se puede expresar como una fracción o como el cociente de dos números, algunos ejemplos:
$$ \pi\approx 3,14159265358979323846…$$ $$ e\approx 2,718281828459045235360…$$
$$\sqrt{2}\approx 1,41421356237309504880...$$
Las raíces inexactas representan números Irracionales.
Su característica principal es que, al expresarlos en forma decimal, su parte decimal no termina ni se repiten, es un decimal infinito (es decir, con infinitas cifras), son decimales no periódicos.
 Los números irracionales $\mathbb{Q^*}$ no deben confundirse con los números racionales $\mathbb{Q}$, porque éstos son números decimales finitos, infinitos periódicos e infinitos mixtos que sí pueden transformarse en una fracción.
Los números irracionales $\mathbb{Q^*}$ no deben confundirse con los números racionales $\mathbb{Q}$, porque éstos son números decimales finitos, infinitos periódicos e infinitos mixtos que sí pueden transformarse en una fracción.Un número Irracional $\mathbb{Q^*}$ no se puede expresar como una fracción o el cociente de dos números.
$$\sqrt{5}\approx 2,236067976...$$
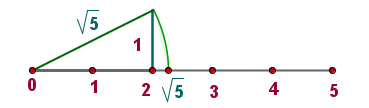
Si el conjunto $\mathbb{Q^*}$ de los números irracionales se amplia agregándole los números racionales $\mathbb{Q}$, se obtiene un conjunto que se denota por la letra $\mathbb{R}$ y se llama el conjunto de los números reales $\mathbb{R}$.
Capitulo I. Los números reales
Representación de los números reales $\mathbb{R}$ en la siguiente imagen:
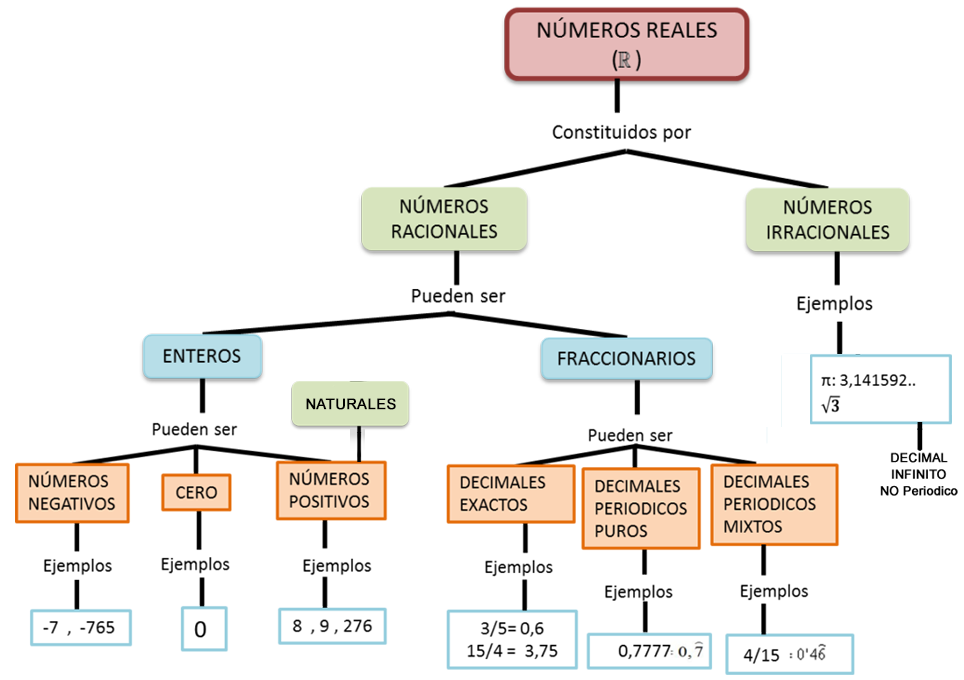
La figura 1.5 representa la gráfica del conjunto de los números Reales, teniendo en cuenta esto, se puede representar gráficamente el conjunto de los números Reales en una recta numérica, en la que cada punto representa un número.
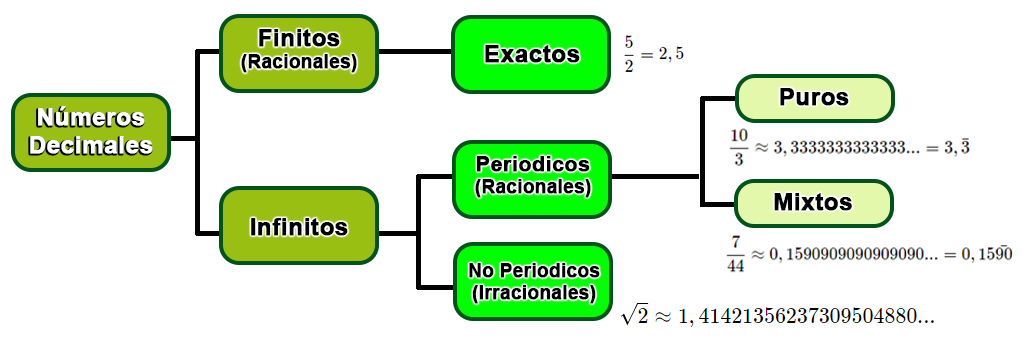
Los números decimales son aquellos que poseen una parte decimal, en contraposición a los números enteros, que carecen de esta, es decir, un número decimal $\textit{\textbf{x}}$ se puede representar como:
$$ x = a,dddddd....\text {donde } \textit{\textbf{a}} \in\mathbb{Z} \text{ y } \textit{\textbf{d}} \text{ dígitos decimales }$$Un número decimal que tiene en su parte decimal dígitos que se repiten infinitamente, se conocen como un decimal Periódico, la parte que se repite se llama Periódo. Su representación se da mediante una barra en la parte superior, en el valor que se repite, por ejemplo:
$$ \frac{1}{6} \approx 0,16666666666666... = 0,1\bar{6}$$ Video. Los decimales, observa el siguiente video para iniciar:
Video. Los decimales, observa el siguiente video para iniciar:
Capitulo I. Los números reales
Observa el esquema de la representación de los números decimales:

Arrastrar los números a cada recuadro según su conjunto numérico, ubicar el número en el conjunto más pequeño al que pertenezca.


¡Recordemos!
Todos los conjuntos numéricos pueden ser representados en la recta numérica. Proyecto Descartes.org.
Proyecto Descartes.org.
 Si se tiene un número decimal exacto, periódico puro o periódico mixto, se puede encontrar la fracción que lo representa, esta fracción se conoce como fracción generatriz.
Si se tiene un número decimal exacto, periódico puro o periódico mixto, se puede encontrar la fracción que lo representa, esta fracción se conoce como fracción generatriz.
por tanto, la fracción generatriz es:
$$ \frac{7}{44} \approx 0,1590909090909090... \quad\Rightarrow \quad \frac{7}{44} = 0,15\bar{90}$$Capitulo I. Los números reales

¡Recuerda!
 Los decimales no exactos y no periódicos tienen una cantidad infinita de cifras decimales, pero ningún conjunto de esas cifras se repite de forma periódica.
Los decimales no exactos y no periódicos tienen una cantidad infinita de cifras decimales, pero ningún conjunto de esas cifras se repite de forma periódica.
 Video. Fracción generatriz, observa y complementa.
Video. Fracción generatriz, observa y complementa.
 Comprueba lo aprendido respondiendo a la pregunta.
Comprueba lo aprendido respondiendo a la pregunta.
Capitulo I. Los números reales

Lea detenidamente el problema, realice los cálculos con su debido procedimiento. Para actualizar otros valores oprime el botón.
Es posible pensar en una representación gráfica de los números reales, esta se hace estableciendo una correspondencia entre los números reales y los puntos de una recta, es decir, que un número real sea representado por un punto de una recta y que cada punto de esa recta represente un número real. A continuación, veamos como establecer esta correspondencia:

Por convención los puntos en la recta a la derecha del cero representan números reales positivos y a la izquierda, números reales negativos.
 Elegimos una unidad de distancia (unidad de medida) arbitraria.
Elegimos una unidad de distancia (unidad de medida) arbitraria.

¡Recordemos!
Los números reales podemos clasificarlos en reales positivos (aquellos que son mayores que cero, a la derecha del cero), reales negativos (menores que cero, a la izquierda del cero) y el cero, es decir, que dado cualquier número real $a$ puede ser: $$a > 0, \quad o\quad a < 0,\quad o\quad a = 0$$Capitulo I. Los números reales
En primer lugar localizamos los puntos correspondientes a los números $1$ y $-1$, al número $1$ corresponderá al punto sobre la recta situado a la derecha del $0$ y a una distancia de $1$ unidad, el número $-1$ será el punto sobre la recta situado a la izquierda del $0$ a una distancia de $1$ unidad.
El número $2$ será el punto sobre la recta situado a la derecha del $0$ y a una distancia de $1$ unidad del punto que representa a $1$, o sea a $2$ unidades de distancia a la derecha del $0$.
El número $-2$ se localizará de manera análoga al $2$ pero naturalmente a la izquierda del $0$.
De esta manera se pueden localizar los números $..., 3, -3, 4, -4,...$ entre otros, es decir todos los números enteros.

 Se observa que la distancia entre cada par de números enteros consecutivos es la misma y que el número de unidades de longitud de cero a cualquier número entero es igual a ese número entero.
Se observa que la distancia entre cada par de números enteros consecutivos es la misma y que el número de unidades de longitud de cero a cualquier número entero es igual a ese número entero.
Los puntos correspondientes a las fracciones están entre los puntos que representan a los números enteros, consideremos la fracción:
$$\displaystyle\frac{m}{n}, \quad con \quad m, n \in \mathbb{Z}, \quad donde \quad n =\not 0$$Fracciones comprendidas entre $0$ y $1$.
Se tiene $\displaystyle\frac{m}{n}$ positiva menor de $1$, es decir, con $m < n$ con $m, n \in \mathbb{Z^+}$. En primer lugar dividimos la unidad elegida en $n$ partes iguales, de estas $n$ partes escogemos las $m$ primeras consecutivas y así este segmento tiene como longitud $\displaystyle\frac{m}{n}$, por tanto, el número $\displaystyle\frac{m}{n}$ será el punto sobre la recta situado a la derecha del $0$ y a una distancia $\displaystyle\frac{m}{n}$.
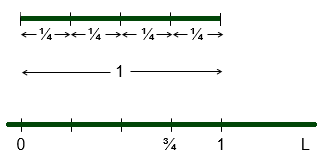 Se divide la unidad en $4$ partes iguales (distancia iguales), se escogen las $3$ primeras consecutivas y la longitud de este segmento es $\displaystyle\frac{3}{4}$ de la unidad, entonces el punto sobre la recta situado a una distancia de $\displaystyle\frac{3}{4}$ a la derecha del $0$ será el representación de dicho número.
Se divide la unidad en $4$ partes iguales (distancia iguales), se escogen las $3$ primeras consecutivas y la longitud de este segmento es $\displaystyle\frac{3}{4}$ de la unidad, entonces el punto sobre la recta situado a una distancia de $\displaystyle\frac{3}{4}$ a la derecha del $0$ será el representación de dicho número.
Capitulo I. Los números reales
Se usa el mismo método anterior, pero en lugar de localizar el punto a la derecha del $0$ se hace a la izquierda.
Sea $m > n$, donde, $\displaystyle\frac{m}{n}$ fracción positiva mayor a $1$, , en primer lugar expresamos la fracción como la suma de un número entero positivo y una fracción comprendida entre $0$ y $1$.
Sea $\displaystyle\frac{m}{n} = k + \frac{m}{n}$, donde $k$ es un entero positivo y $\displaystyle\frac{m}{n}$ es una fracción comprendida entre $0$ y $1$. De ello la fracción $\displaystyle\frac{m}{n}$ está comprendida entre los enteros $k$ y $k + 1$. Entonces el punto representativo de la fracción $\displaystyle\frac{m}{n}$ se localiza tomando a partir del punto que representa al entero $k$ a una distancia de $\displaystyle\frac{m}{n}$ hacia la derecha. (La distancia $\displaystyle\frac{m}{n}$ se obtiene como el caso 1).
Expresamos $\displaystyle\frac{27}{5} = 5 + \frac{2}{5}$, como la suma de un entero positivo $5$ y una fracción comprendida entre $0$ y $1$ (o sea $2/5$), donde se tiene que $\displaystyle\frac{27}{5}$ está comprendida entre los enteros $5$ y $6$:

Por tanto, el punto correspondiente $\displaystyle\frac{27}{5}$ se localizará tomando a partir del punto que representa a $5$ una distancia de $\displaystyle\frac{2}{5}$ hacia la derecha.
Se sigue el mismo procedimiento de la parte 3) pero la localización se hace a la izquierda del $0$. De esta manera se pueden localizar sobre la recta todos los puntos correspondientes a los números racionales, ahora, la pregunta será:
¿Si se localizan sobre la recta todos los números racionales estos agotarán todos los puntos de la recta o por el contrario quedarán "vacios"?
Veamos la siguiente construcción:
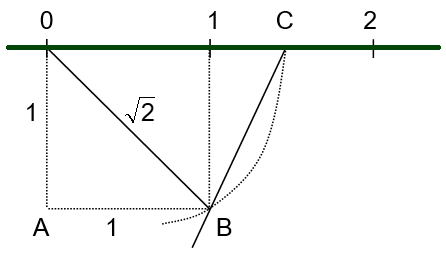
 0B tiene de longitud $\sqrt{2}$, tomando sobre la recta $L$ y a partir del $0$ hacia la derecha una longitud igual a la de 0B se obtiene el punto C corresponde al número $\sqrt{2}$.
0B tiene de longitud $\sqrt{2}$, tomando sobre la recta $L$ y a partir del $0$ hacia la derecha una longitud igual a la de 0B se obtiene el punto C corresponde al número $\sqrt{2}$.
Capitulo I. Los números reales
Pero el punto C sobre la recta no corresponde a un número racional, pues $\sqrt{2}$ no corresponde a un número racional.
De modo que si sobre la recta se han localizado todos los números racionales, han quedado sin embargo "vacios", como el punto C localizado anteriormente.
Estos "vacios" son precisamente los puntos que corresponden a los números irracionales $\mathbb{Q^*}$.
Resumiendo todo lo anterior se puede establecer una correspondencia biunívoca entre el conjunto de los números reales y el conjunto de los puntos de una recta, de tal manera que aun número real se le asocia uno y solo un punto de la recta e inversamente que todo punto de la recta es la representación de uno y solo un número real.

A una tal recta se le denomina la recta numérica o recta real, y al número asociado con un punto se llama la coordenada del punto.
Propiedades de la recta numérica.
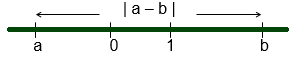


 ¡Piensa!... Al número $\pi$ que tiene infinitos decimales, se le han dedicado millones y millones de horas de estudio. Aunque se han llegado a descubrir unos 2,7 billones de decimales de $\pi$, ni la computadora más poderosa ha sido capaz de calcularlo sin márgenes de error. De acuerdo con la lectura, ¿qué tipo de número es $\pi$?
¡Piensa!... Al número $\pi$ que tiene infinitos decimales, se le han dedicado millones y millones de horas de estudio. Aunque se han llegado a descubrir unos 2,7 billones de decimales de $\pi$, ni la computadora más poderosa ha sido capaz de calcularlo sin márgenes de error. De acuerdo con la lectura, ¿qué tipo de número es $\pi$?
Capitulo I. Los números reales
Una desigualdad es un enunciado matemático que compara dos expresiones (numéricas o algebraicas) usando algún signo de desigualdad $>,<,≥ o ≤$.
En una desigualdad, una expresión de la desigualdad puede ser más grande o más chica que la otra expresión, se utilizan símbolos especiales en estos enunciados.
En general dados $a$, $b$ números reales cualesquiera se dirá que $a$ es menor que $b$ y se escribe $a < b$, donde, se puede representar como $0 < b - a$, por ejemplo: $$2 < 4 \quad puesto \space que \quad 0 < 4 - 2 = 2$$
Son fáciles de demostrar las siguientes propiedades de la relación “menor que” entre números reales:
Si $a < b$ y $b < c$, entonces por la definición se tiene que: $$0 < (b - a) \quad y \quad 0 < (c - b)$$
Pero como la suma de dos números positivos es un número positivo tendremos: $$0 < (b - a) + (c - b)$$ $$0 < -a + c$$
por lo tanto, $a < c$, con lo cual queda demostrado.
Ahora, si $a < b$ y $c < 0$, entonces
$$0 < (b - a) \quad y \quad 0 < (- c)$$Pero como el producto de dos números positivos es positivo tendremos: $$0 < (-c) (b - a)$$ $$0 < ac - bc$$
por tanto, queda demostrado que $bc < ac$.
Esta relación cumple propiedades análogas a la relación “$<$” y son:
Capitulo I. Los números reales
Es un subconjunto de la recta real que contiene a todos los números reales que están comprendidos entre dos cualesquiera de sus elementos llamados límites, que pueden estar incluidos o no en dicho intervalo.

Los intervalos denominados finitos o acotados, pueden ser cerrados, abiertos o semiabiertos.
Estos se pueden representar por medio de la notación de conjuntos o por una desigualdad o usando una gráfica.
Cuando en una desigualdad, los límites inferior o superior se incluyen, o sea, están representados con el simbolo "mayor o igual que" ($\geqslant$) o "menor o igual que" ($\leqslant$), notese esto con un punto cerrado en la recta numérica y un corchete cuando se representa en notación de intervalo.
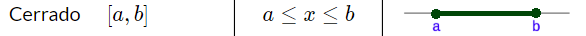
Cuando los límites o un límite no se incluye, se utiliza en la recta un punto abierto o en el intervalo los paréntesis, y la desigualdad se representa con el símbolo "mayor que" ($>$) o "menor que" ($<$).
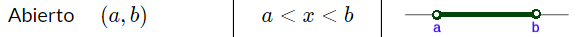
Los intervalos se clasifican en: Intervalos finitos o acotados, es el conjunto de los números comprendidos entre los límites $a$ y $b$, con $a, b, \in \mathbb{R}$ los cuales pueden estar incluidos o no incluidos. Los Intervalos infinito o no acotado, cuando se tiene al menos uno de los extremos infinito, el cual se considera siempre abierto.
| Intervalo con $x \in \mathbb{R}$ | Desigualdad | Gráfico |
|---|---|---|
| Abierto $\ (a, b)$ |  |
|
| Cerrado $\ [a, b]$ |  |
|
| Abierto izquierda $\ (a, b]$ |  |
|
| Abierto derecha $\ [a, b)$ |  |
| Abierto izquierda $\ (a, +\infty)$ |  |
|
| Cerrado izquierda $\ [a, +\infty)$ |  |
|
| Abierto derecha $\ (-\infty, b)$ |  |
|
| Cerrado derecha $\ (-\infty, b]$ |  |
|
| Todos los $\mathbb{R}, \ (-\infty, +\infty)$ |  |
Capitulo I. Los números reales
 xploremos.
xploremos.
Identifiquemos los intervalos acotados y no acotados.
 xploremos.
xploremos.
Los extremos de los intervalos acotados.

Punto abierto ($\color{red} \circ$): No incluye el extremo del intervalo, se representa con paréntesis $(\space)$.
Punto cerrado ($\color{red} \bullet$): Si incluye el extremo del intervalo, se representa con corchetes $[\space]$.
Intervalos acotados, su desigualdad y su representación gráfica, oprime el botón Ejemplos y observa.
Sean $a, b, c \in\mathbb{R}$, entonces, se cumple que:
Capitulo I. Los números reales
$\quad a ≤ b ⇔ a ± c ≤ b ± c$
$\quad c > 0 \quad {\displaystyle \longrightarrow } \quad a ≤ b ⇔ ca ≤ cb$.
$\quad c > 0 \quad {\displaystyle \longrightarrow } \displaystyle \quad a ≤ b ⇔ {a \over c} ≤ {b \over c}$.
$\quad c < 0 \quad {\displaystyle \longrightarrow }\quad a ≤ b ⇔ ca ≥ cb$.
$\quad c < 0 \quad {\displaystyle \longrightarrow }\quad \displaystyle a ≤ b ⇔ {a \over c} ≥ {b \over c}$.

Dado un número real $a$, llamamos valor absoluto de $a$, que se expresa como $|a|$, al número real definido por:
$$|a| = \begin{cases} a &\text{si } a ≥ 0 \\ -a &\text{si } a < 0 \end{cases} $$
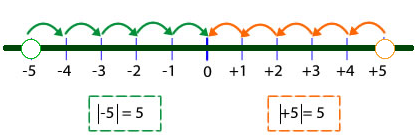
$|-5| = | 5 | = 5$, significa que el valor absoluto de $-5$ es $5$.
$|-10| = | 10 | = 10$, significa que el valor absoluto de $-10$ es $10$
Si $a < 0$ entonces $| a | = - a$, que es mayor que cero o sea que $| a |$ es mayor o igual a cero para cualquier a número real .
Capitulo I. Los números reales
Dado $a > 0$ entonces se tiene que:
si $| x | < a$ necesariamente $-a < x < a$ y recíprocamente, si $- a < x < a$ entonces se debe tener que $| x | < a$.
El valor absoluto de la suma de dos números reales es menor o igual que la suma de los valores absolutos de esos números. Esta es llamada desigualdad triangular.
$$| a + b | ≤ |a| + |b|$$
$|4 + 6| ≤ | 4 | + | 6 |, \quad |10| ≤ 4 + 6, \quad 10 ≤ 10$.
$|10 + (-7)| ≤ | 10 | + | -7 |, \quad |3| ≤ 10 + 7, \quad 3 ≤ 17$.

¡Recordemos!
 Si $a$ y $b$ son del mismo signo, colocamos el signo igual, mientras que si $a$ y $b$ son de diferente signo colocamos el signo del mayor número en valor absoluto.
Si $a$ y $b$ son del mismo signo, colocamos el signo igual, mientras que si $a$ y $b$ son de diferente signo colocamos el signo del mayor número en valor absoluto.


Genere un intervalo o desigualdad oprimiendo el botón Ejercicio, arrastre de forma organizada el circulo al recuadro para expresar la solución.
Verifique oprimiendo el botón Solución para ver si lo has hecho bien, repite los pasos hasta finalizar los 10 ejercicios propuestos.
Capitulo I. Los números reales
Una inecuación es una desigualdad entre dos expresiones algebraicas, donde su solución posee infinitas soluciones. Las inecuaciones se conforman por valores conocidos y desconocidos, estos últimos son llamados incógnitas, por ejemplo,
$$ 4 < x + 2 < 7$$ $$ 2 < x < 5$$
Todos los valores de $x$ entre $2$ y $5$ verifican la desigualdad, por tanto, el conjunto solución de la desigualdad puede verse intuitivamente como el tramo de la recta real entre $2$ y $5$ .
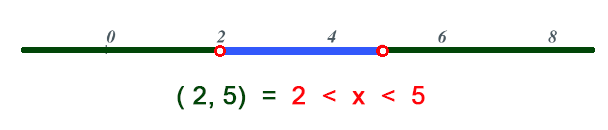
Para resolver una inecuación se hace un proceso similar como al resolver una ecuación, se debe despejar la incógnita o las incógnitas, hasta llegar a determinar el valor de la incógnita.
Si $a,b \in \mathbb{R}$ con $a =\not 0$, cualquiera de las siguientes expresiones se llama inecuación lineal de una variable, inecuaciones del tipo:
$$ax + b < 0 ,\quad x > b, \quad ax < b, \quad ax ≥ b, \quad ax ≤ b$$Primero se aísla la incógnita en un lado de la desigualdad, dejando en el otro solo términos independientes, para ello debe tenerse en cuenta las propiedades de las desigualdades, luego se procede de igual forma que al resolver una ecuación lineal con una incógnita.
 Veamos cómo solucionar una inecuación lineal encontrando los valores de $x$ que satisfacen la desigualdad y la representación de su respectiva solución gráfica:
Veamos cómo solucionar una inecuación lineal encontrando los valores de $x$ que satisfacen la desigualdad y la representación de su respectiva solución gráfica:
$ 3x > 5 - 10 $
$ x > {-5 \over 3}, \quad intervalo: ({-5 \over 3}, +\infty) $

Capitulo I. Los números reales
 xploremos.
xploremos.
Ejemplos de inecuaciones lineales no acotadas.

¡Recordemos!
Este tipo de intervalos aparece cuando se conoce solo uno de los extremos y el otro es el infinito, al no poderse incluir el infinito en el intervalo, estos se consideran siempre abiertos en el infinito.
Se plantean cuatro tipos de inecuaciones lineales que contienen expresiones racionales, tener en cuenta la siguiente indicación:
Primero resuelve los ejercicios propuestos, luego, verifica tus respuestas, oprima el botón solución, observa la solución de la inecuación (desigualdad y representación del intervalo).

 ¡Piensa!... ¿Cuándo se sabe que una inecuación lineal es acotada o no acotada?
¡Piensa!... ¿Cuándo se sabe que una inecuación lineal es acotada o no acotada?
Capitulo I. Los números reales
 xploremos.
xploremos.
Solución paso a paso de inecuaciones lineales no acotadas.
Ejemplos paso a paso, oprime el botón siguiente paso y observa.
Ejemplos de inecuaciones acotadas, que tienen la forma $\quad a \le x \le b$

$ 2 < 3x-7 \land\quad 3x-7\le {2x-7 \over 4}$
$ 9 < 3x \quad\land\quad 12x-28\le 2x-7$
$ {9 \over 3}< x \quad\land\quad 12x - 2x\le 28 - 7$
$ 3 < x \quad\land\quad x\le {21 \over 10}, \quad intervalo: (-\infty, {21 \over 10}) \cup (3, +\infty)$


Observa el ejemplo, resuelve el ejercicio planteado, verifica con el botón solución, para un nuevo ejercicio, oprime el botón ejercicio.
Capitulo I. Los números reales
Para solucionar este tipo de inecuaciones, debemos recordar cómo solucionar una ecuación de 2° grado, teniendo en cuenta si tiene solución o no, analizando el discriminante $d = b^2 -4ac$ que indica que tipo de solución tiene la ecuación cuadrática siguiente:
$$ax^2 + bx + c = 0$$
Con la información anterior, los pasos para encontrar la solución de la inecuación de 2° grado son:
Ubicamos los datos encontrados, sustituimos un valor de cada intervalo en el factor para obtener el signo que lo determina:
Observemos el signo del factor $x - 7$:
Si $x < 7,$ sustituimos $x$ por $1 \quad {\displaystyle \longrightarrow } \quad 1-7 = -6 \quad {\displaystyle \longrightarrow } \quad (-)$.
Si $x > 7,$ sustituimos $x$ por $9 \quad {\displaystyle \longrightarrow } \quad9-7 = 2 \quad {\displaystyle \longrightarrow } \quad (+)$.

Observemos el signo del factor $x + 6$:
Si $x < -6,$ sustituimos $x$ por $-8 \space {\displaystyle \longrightarrow } \space -8+6 = -2 \space {\displaystyle \longrightarrow } \quad (-)$.
Si $x > -6,$ sustituimos $x$ por $2 \quad {\displaystyle \longrightarrow } \quad 2+6 = 8\quad {\displaystyle \longrightarrow } \quad (+)$.
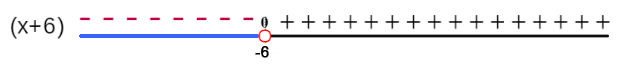

 ¡Piensa!... ¿Que sucede en el caso que la ecuación no tenga solución en los números reales?
¡Piensa!... ¿Que sucede en el caso que la ecuación no tenga solución en los números reales?
Capitulo I. Los números reales
Por lo tanto, la solución de la inecuación $x^2 - x -42 < 0$, son los valores donde los intervalos son negativos:
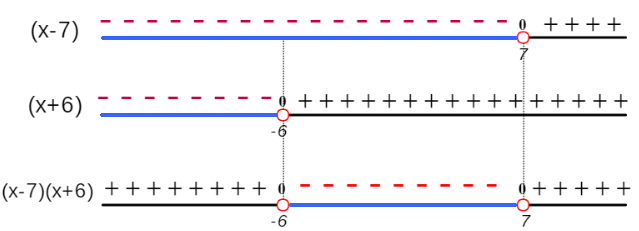
Donde, se tiene que la solución es: $\quad -6 < x < 7 = (-6, 7)$
Si la inecuación fuera $x^2 - x -42 \le 0$, significa que ahora se admiten valores que al evaluar el polinomio el resultado sea cero: $$(-6)^2 - (-6) -42 \le 0$$ $$(7)^2 - (7) -42 \le 0$$ Por tal motivo, se incluye $-6$ y $7$ en la solución: $\quad [-6, 7]$.
Podemos expresar la solución de la inecuación mediante una representación gráfica o un intervalo.

¡Recordemos!
Si la desigualdad tiene este signo $< ó >$, los valores en la recta son un círculo vacío y se ubica en paréntesis en la solución.Si la desigualdad tiene este signo $≥ o ≤$, los valores en la recta son un circulo relleno y se ubica en corchetes en la solución.
 xploremos.
xploremos.
Ejemplos de la solución de una inecuación cuadrática.
Comprueba la solución, toma un valor de cada intervalo, remplace en el polinomio inicial y verifica el signo del resultado obtenido.
Seleccione el signo para cambiar el tipo de desigualdad, oprime el botón ejemplos para ver más ejemplos.
Cuándo tenemos inecuaciones con expresiones racionales se realizan los siguientes pasos:
Capitulo I. Los números reales
 xploremos.
xploremos.
Observa ejemplos de inecuaciones con expresiones racionales:
Comprueba la solución, toma un valor de cada intervalo, remplaza en la expresion inicial y verifica el signo del resultado obtenido, oprime el botón ejemplos para ver más ejemplos.
Para resolver inecuaciones que involucran valor absoluto; expresiones algebraicas de la forma $ax+b$, donde $a, b$ números $\mathbb{R}$ con $a = \not 0$, y $x$ es una variable real, se utiliza la definición de valor absoluto y se aplican algunas de las propiedades, con el fin de facilitar el procedimiento de resolución. Así, siendo $c>0$:
Se aplica la propiedad $|ax + b|≤ c, \enspace$ donde, $\enspace -c ≤ ax + b ≤ c$, entonces, se tiene que: $$-3 ≤ x - 5 ≤ 3$$ $$-3 + 5 ≤ x ≤ 3 + 5$$ $$2 ≤ x ≤ 8,$$
por tanto, la solución gráfica y en intervalo es: $\quad [2, 8]$

Capitulo I. Los números reales
 Ejercicio práctico
Ejercicio práctico
Indicaciones
Resuelve cada una de las siguientes inecuaciones de tipo cuadrática o racional. Expresa la solución como intervalo y su desigualdad.

 Evaluamos lo aprendido
Evaluamos lo aprendido
Prepárate para la evaluación y mide tus conocimientos de lo aprendido en este capítulo, responde las preguntas a continuación:

 Actividad complementaria.
Actividad complementaria.
$\space$ Descargar para imprimir
Capitulo I. Los números reales
 Evaluación. 10 preguntas con límite de tiempo (Máx. 10 minutos)
Clic en el link, responde y envía tus respuestas por correo.
Evaluación. 10 preguntas con límite de tiempo (Máx. 10 minutos)
Clic en el link, responde y envía tus respuestas por correo.
 Tomada de la Red Educativa Digital Descartes.
Tomada de la Red Educativa Digital Descartes.
"Nada acontece sin una razón suficiente.".
Leibniz

DERECHOS BÁSICOS DE APRENDIZAJE (DBA)
DBA.3. Utiliza instrumentos, unidades de medida, sus relaciones y la noción de derivada como razón de cambio, para resolver problemas, estimar cantidades y juzgar la pertinencia de las soluciones de acuerdo al contexto.
DBA.6. Modela objetos geométricos en diversos sistemas de coordenadas (cartesiano, polar, esférico) y realiza comparaciones y toma decisiones con respecto a los modelos.
DBA.7. Usa propiedades y modelos funcionales para analizar situaciones y para establecer relaciones funcionales entre variables que permiten estudiar la variación en situaciones intraescolares y extraescolares.
Derechos Básicos de Aprendizaje - Grado 11°.
DESEMPEÑOS / ESTANDAR
Componente 1 - Pensamiento numérico.
1.4 M.V Utilizo argumentos de la teoría de números para justificar relaciones que involucran números naturales. DBA 7.
Componente 2 - Pensamiento Geométrico.
2.2 M.V Identifico características de localización de objetos geométricos en sistemas de representación cartesiana y otros (polares, cilíndricos y esféricos) y en particular de las curvas y figuras cónicas. DBA 6.
Componente 3 - Pensamiento Métrico.
3.2 M.V Resuelvo y formulo problemas que involucren magnitudes cuyos valores medios se suelen definir indirectamente como razones entre valores de otras magnitudes, como la velocidad media, la aceleración media y la densidad media. DBA 3, 7.
Componente 5 - Pensamiento Variacional.
5.1 M.V Utilizo las técnicas de aproximación en procesos infinitos numéricos. DBA 3.

El desarrollo de estos Estándares Básicos de Competencia permitirá fortalecer los procesos de formulación, modelación y resolución de problemas.
Capitulo II. Funciones
 Mientras que el cálculo diferencial e integral surgió en el siglo $XVII$, el concepto de función vino a conocerse un siglo después, y el de límite entendido de una manera formal y rigurosa sólo a finales del siglo $XIX$, lo cual difiere de la forma como se presenta actualmente el cálculo, en donde primero se enseñan funciones, luego límites y finalmente derivados o integrales.
Mientras que el cálculo diferencial e integral surgió en el siglo $XVII$, el concepto de función vino a conocerse un siglo después, y el de límite entendido de una manera formal y rigurosa sólo a finales del siglo $XIX$, lo cual difiere de la forma como se presenta actualmente el cálculo, en donde primero se enseñan funciones, luego límites y finalmente derivados o integrales.
En la obra Introductio in analysin infinitorum (Latin: Introduction to the Analysis of the Infinite), Leonhard Euler intenta por primera vez dar una definición formal del concepto de función afirmando que: “Una función de cantidad variable es una expresión analítica formada de cualquier manera por esa cantidad variable y por números o cantidades”.
En 1741, por invitación de Federico II el Grande se trasladó a la Academia de Berlín, refinó los métodos y las formas del cálculo integral.

Los resultados novedosos y los cambios en los habituales métodos de demostración geométricos, que sustituyó por métodos algebraicos, se convirtió en herramienta de fácil aplicación a problemas de física.
En 1748 publicó la obra "Introductio in analysim infinitorum", en la que expuso el concepto de función en el análisis matemático, campo en el que así mismo contribuyó de forma decisiva con resultados como el teorema sobre las funciones homogéneas y la teoría de la convergencia.
A lo largo de sus innumerables obras, publicaciones y nuevas técnicas, contribuyó de forma sustancial a la moderna notación matemática de conceptos como función, suma de los divisores de un número y expresión del número imaginario raíz de menos uno. También se ocupó de la teoría de números, campo en el cual su mayor aportación fue la ley de la reciprocidad cuadrática, enunciada en 1783.

Esta definición difiere de la que conocemos, pero siete años después, en el prólogo de sus Instituciones Cálculo diferencial, afirma: “Algunas cantidades en verdad dependen de otras, si al ser combinadas las últimas las primeras también sufren cambio, y entonces las primeras se llaman funciones de las últimas.
Esta denominación es bastante natural y comprende cada método mediante el cual una cantidad puede ser determinada por otras. Así, si $x$ denota una cantidad variable, entonces todas las cantidades que dependen de $x$ están determinadas por $x$ y se les conoce como funciones de $x$”.
Capitulo II. Funciones
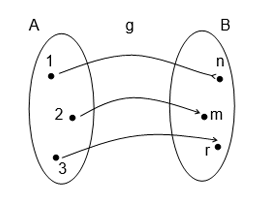
Consideremos los conjuntos $A = \{ 1, 2, 3, 4 \}$ y $B = \{ m, n, r, p \}$, se puede establecer una correspondencia entre los conjuntos $A$ y $B$ de tal manera que a todos y cada uno de los elementos del conjunto $A$ se le asocie un único elemento del conjunto $B$, por ejemplo, una tal correspondencia como la mostrada en la figura:
Es decir, al elemento $1$ de $A$ le asociamos el elemento $n$ de $B$, al elemento $2$ de $A$ le asociamos el elemento $m$ de $B$ y al elemento $3$ de $A$ le asociamos el elemento $r$ de $B$. Este tipo de correspondencia es lo que llamamos una función.

Esto quiere decir que dado un elemento de $A$, a ese elemento dado se le puede hacer corresponder un único elemento de $B$ y que todos los elementos de $A$ deben tener sus correspondientes elementos en $B$.
Las funciones se acostumbra a nombrarlas con letras $f, g, h, F, G,...$
Si designamos por $x$ cualquier elemento de $A$ ($x$ también se acostumbra a llamar la variable independiente) la función $f$ debe asociarse a $x$ un único elemento de $B$ que notaremos $f(x)$ o $y$ ($y$ se acostumbra a llamar la variable dependiente, pues los valores de $y$ dependen de los valores de $x$ de acuerdo con la función $f$), también a $y$ se le conoce como la imagen por la función $f$ del elemento $x$.
El conjunto $A$ se llama dominio de la función y el conjunto $B$ codominio (o rango) de la misma, según esto, si llamamos $g$ a la función siguiente, se tiene que:
Capitulo II. Funciones
 xploremos.
xploremos.
Observa ejemplos de función o no función.
En cada uno de los esquemas, observa si hay o no correspondencia en la función de $A$ en $B$, oprime el botón ejemplos para ver más ejemplos.

Si $f$ está definida en los $\mathbb{R}$ como $f(x) = -4x + 5$, se tiene que para cualquier valor $\mathbb{R}$:
$f(-1)= -4(-1) + 5, \quad$ donde $\quad f(-1) = 9$
$f(2)= -4(2) + 5, \quad$ donde $\quad f(2) = -3$
En otras palabras, estas funciones llamadas funciones matemáticas se representan con ecuaciones, acudiendo a variables y signos aritméticos para expresar la relación existente entre las magnitudes.
Dichas ecuaciones, a su vez, podrán resolverse, despejando sus incógnitas, o bien ser graficadas geométricamente.
Entonces $f$ está definida para todo $x ≥ 0$. (Para que $\sqrt{x}$ sea un número real $x$ tiene que ser no negativo), es decir, $f$ se puede considerar una función de $\quad \ce{\mathbb{R}^* -> \mathbb{R}}, \quad$ en donde $\mathbb{R}^*$ es el conjunto de los números reales mayores o iguales a cero.

¡Recordemos!

$x ≥ 0 \quad$ representa los números $\mathbb{R}$ mayores o iguales a cero, números positivos $(+)$ y el cero.
$x ≤ 0 \quad$ representa los números $\mathbb{R}$ menores o iguales a cero, números negativos $(-)$ y el cero.
Una función se puede determinar mediante tres formas:
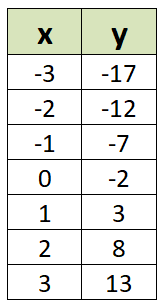
Es una representación de datos, mediante pares ordenados que expresan la relación entre dos variables, para este caso, $x$ y $y$.
Capitulo II. Funciones
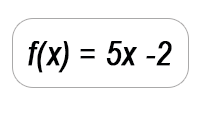
La expresión analítica de una función es una ecuación matemática que relaciona algebraicamente las variables que intervienen.
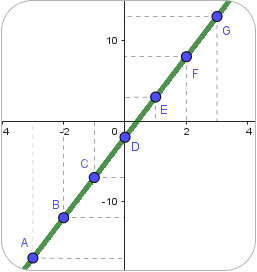
Es un dibujo o boceto que permite conocer intuitivamente el comportamiento de dicha función, se elabora en un plano de coordenadas $(x,y)$.
Gráfica de una función
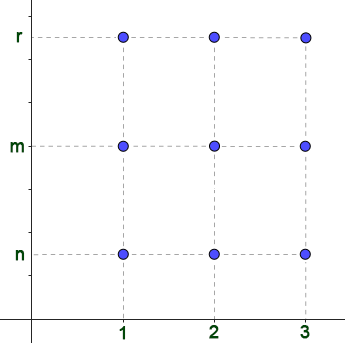 Sean $A = \{1, 2, 3\}$ y $B = \{n, m, r\}$ dos conjuntos que representamos por los puntos tal como se muestra en la figura 2.2,
Sean $A = \{1, 2, 3\}$ y $B = \{n, m, r\}$ dos conjuntos que representamos por los puntos tal como se muestra en la figura 2.2,
Trazando rectas verticales desde los elementos de $A$ y horizontales por los elementos de $B$ como se puede observar en la figura, se determinan seis puntos que son de intersección de estas rectas.
A cada punto podemos asociarle una pareja ordenada tomando como primer elemento de la pareja ordenada el correspondiente del conjunto $A$ por donde se trazó la vertical y como segundo elemento de la pareja ordenada el correspondiente de $B$ por donde se trazó la horizontal.
De esta manera, a partir de los conjuntos $A$ y $B$ se ha construido el conjunto de todas las posibles parejas de los elementos de $A$ y como segundo elemento uno de $B$, como se muestra a continuación:
$$\{(1, n) , (1, m) , (2, m) , (2, n) , (3, m) , (3, n)\}$$
Este nuevo conjunto se llama producto cartesiano de los conjuntos $A$ y $B$ que se denota $A \times B$.
El producto cartesiano entre los conjuntos $A$ y $B$ es: $$A \times B = \{(1, 2) , (1, 4) , (2, 2) , (2, 4) , (3, 2) , (3, 4)\}$$
Como notaremos el conjunto $A \times B$ es diferente de $B \times A$: $$B \times A = \{(2, 1) , (2, 2) , (2, 3) , (4, 1) , (4, 2) , (4, 3)\}$$
El plano cartesiano
Ya vimos que el conjunto de los reales se puede representar por el conjunto de los puntos de una recta.

Tomando dos rectas numéricas, una horizontal y otra vertical que se interceptan en el punto correspondiente a cero de ambas se determina un plano, este plano se llama el plano cartesiano.
Capitulo II. Funciones
 xploremos.
xploremos.
El plano cartesiano o plano de coordenadas rectangulares.
Mueve el punto rojo y observa que a cada punto le corresponde un valor en el plano de coordenadas.
A cada punto de este plano cartesiano se le puede asociar una pareja ordenada de números reales, y dada pareja ordenada de números reales a ella solo le corresponde un único punto del plano.
Dada una pareja ordenada $(a, b)$ de números $\mathbb{R}$, a ella le corresponde un punto $P$ del plano cartesiano, llamadas las coordenadas del punto.
 xploremos.
xploremos.
El plano de coordenadas o cartesiano.
Expresa en palabras, en cada uno de los recuadros, los nombres correspondientes, inicia siempre con letra mayúscula.
Al número $\mathbb{R}$ “$a$” se llama la abscisa del punto y al número $\mathbb{R}$ “$b$” se llama la ordenada del punto. A la recta numérica horizontal se acostumbra llamar el eje de abscisas ($Eje \space x$) y a la recta numérica vertical el eje de ordenadas ($Eje \space y$).

Capitulo II. Funciones
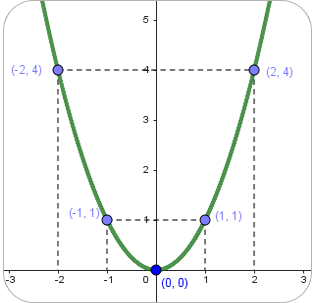
Algunos puntos de la gráfica de esta función están dados por las parejas ordenadas que se representan como: $$(x, y) = (x, g(x))= (x, x^2)$$ $$(1, 1) , (0, 0) , (2, 4) , (-2, 4)$$

¡Definición!
La gráfica de una función debe ser tal que al trazar cualquier vertical ésta corte a lo más en un punto a la gráfica, esto se conoce como el criterio de la recta vertical.
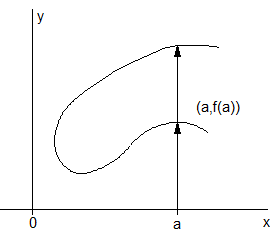
Por ejemplo, la gráfica de la figura no es la de una función pues al punto $a$ le corresponden dos valores $f(a)$, lo cual contradice a la definición de función.
 Comprueba lo aprendido respondiendo a la pregunta.
Comprueba lo aprendido respondiendo a la pregunta.

Una función $f$, expresada de la forma $f(x)$, tiene la ventaja que permitir identificar la variable dependiente $y$, al mismo tiempo informa que la variable independiente es $x$.
Las funciones se clasificación de la siguiente forma:
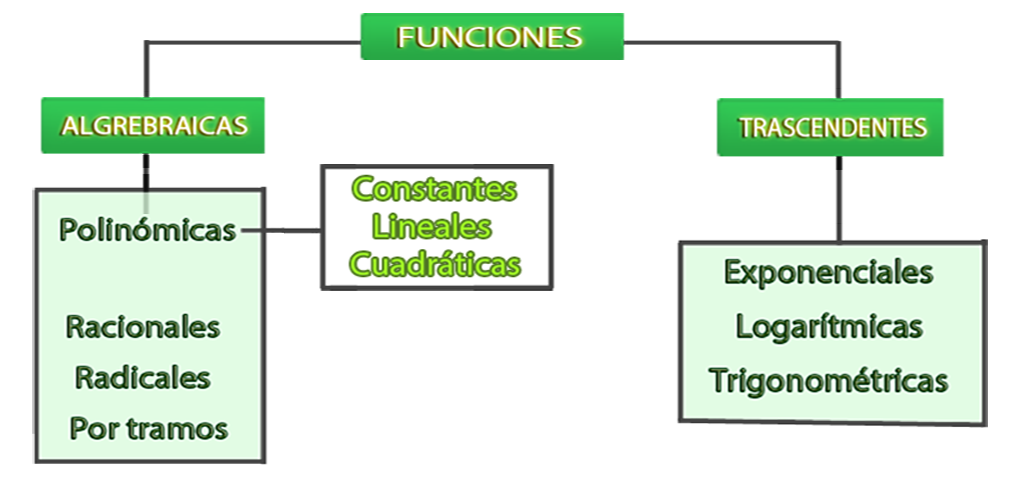
Funciones algebraicas, se obtienen, a partir de operaciones algebraicas, es decir, por un conjunto de números y variables relacionados entre sí por operaciones como la suma, resta, multiplicación, división, potenciación y radicación.
Funciones trascendentes, son aquellas funciones cuya variable contiene expresiones exponenciales, logarítmicas, trigonométricas e inversas.
Capitulo II. Funciones
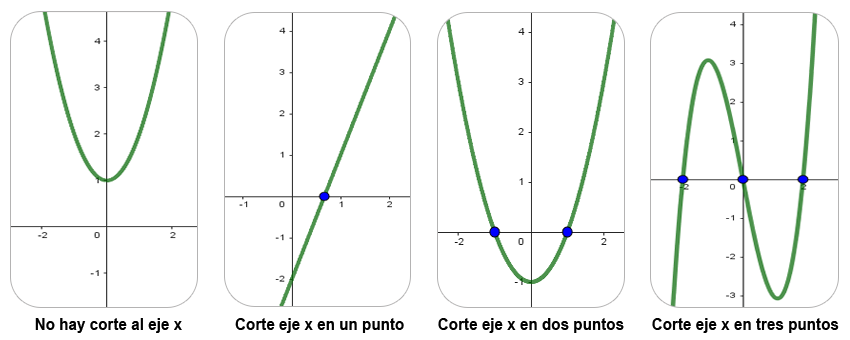
Los puntos de corte de una función $f$ con el $eje \space x$ se encuentran resolviendo la ecuación $f(x) = 0$. Es posible que la gráfica no tenga intersección con los ejes (no corta los ejes), o que presente varias de ellas. A estos cortes o intersecciones con el $eje \space x$, se le denominan ceros de la función.
El punto de corte de una función $f$ con el $eje \space y$ es el punto $(0, f(0))$, solo hay un punto de corte, ya que si no, $f$ no sería función.

¡Recordemos!
Los puntos de corte o intersección con los ejes, hace referencia a las coordenadas $(x,0)$ y $(0,y)$ es decir, son los puntos en que la gráfica de la función $f$ corta el eje $x$ o con el eje $y$.Cuando no es posible utilizar el método analítico para determinar las intersecciones con los ejes, se recurre al método gráfico, buscando los puntos donde la gráfica de la función toca los ejes.
El estudio de la simetría facilita la construcción de la representación gráfica en el plano cartesiano de una función si se reconoce la existencia de una reflexión de una parte de la curva. La gráfica de una función $f$ es simétrica con respecto a:
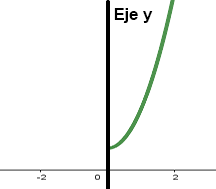 Eje y, si se cumple que:
Eje y, si se cumple que:
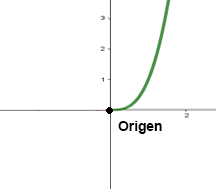 Origen, si se cumple que:
Origen, si se cumple que:

Si se remplaza la variable $x$ por $(-x)$, se obtiene:
$f(-x) = \frac{(-x)}{(-x)^2 - 3}= \frac{-x}{x^2 - 3}=-\frac{x}{x^2- 3} = -f(x)$ por tanto, la función es impar ya que cumple que $f(x) = -f(-x)$, simétrica al origen.
Capitulo II. Funciones
Una función polinómica es una función algebraica, definida a partir de sumas y productos de términos conocidos como monomios, de la forma:
$$f(x) = a_nx^n + a_{n-1}x^{n-1} + ... + a_3x^3 + a_2x^2 + a_1x + a_0 $$Donde, $a_0, a_1...a_n$ son los coeficientes del polinomio, en otras palabras, son los números reales que acompañan a la variable independiente $x$ en los distintos sumandos. Al término $a_0$ se le conoce como término independiente.
El número de coeficientes de una función $f$ polinómica puede ser cualquiera, pero siempre será un número finito. Puede haber coeficientes que "faltan", por ejemplo, $\quad x^3 - 3x + 2, \quad$ falta el término $x^2$, cualquier coeficiente que falta tiene valor $0$.
El polinomio se identifica por el grado $n$, donde, $n$ es el mayor exponente entero no negativo que tiene la variable independiente.


¡Recordemos!
El valor numérico de un polinomio, se obtiene al reemplazar las variables de cada uno de sus términos por valores numéricos y realizar las operaciones indicadas.
El dominio de toda función polinómica es el conjunto de todos los números $\mathbb{R}$, ya que al sustituir la variable $x$ por un número $\mathbb{R}$ cualquiera con $x \in\mathbb{R}$, siempre va a existir $f(x)$.

Polinómio de grado $3$ ($x^3$), el término independiente es $a_0 = -9$, y sus coeficientes son $a_0 = -9, a_1 = 1, a_1 = -2, a_3 = 5$.
Si tomamos a $\quad x = -2$ el valor de $f(x)$ es: $$\quad f(-2) = 5(-2)^3 - 2(-2)^2 + (-2) - 9$$ $$\quad f(-2) = 5(-8) - 2(4) - 2 - 9$$ $$f(-2) = -59$$
Una función polinómica también puede ser una constante, donde, el término independiente está multiplicado por $x^0$. Esta función polinómica se conoce como la función constante, donde, $\enspace y=a_0$
 Comprueba lo aprendido respondiendo a la pregunta.
Comprueba lo aprendido respondiendo a la pregunta.
Capitulo II. Funciones
Una función constante es aquella función $f$ que siempre toma la misma imagen para cualquier valor de la variable independiente $x$, es decir, una función $f$ constante es de la forma $f(x)= b$, donde $b$ es un número real cualquiera.
 xploremos.
xploremos.
La representación gráfica de una función constante es siempre una recta horizontal que corta el $eje \space y$ en el punto $(0,b)$.
Mueve el punto rojo y observa la función constante.
Una función afín es una función polinómica de primer grado, las funciones afines son de la forma:
$$y = mx + b$$Donde, el coeficiente $m$ se le llama pendiente de la recta (grado de inclinación de la línea recta) y $b$ ordenada en el origen, es decir, punto de corte con el $eje \space y$, (punto $(0,b)$).
La representación gráfica de una función afín es una recta que no pasa por el origen de coordenadas, donde $b$ es la ordenada de $x = 0$ (su gráfica es una línea recta).
La expresión algebraica y simplificada de la forma:
$$y = mx$$
Representa una función lineal, es una función de proporcionalidad directa, recta que pasa por el origen de coordenadas, donde, $m$ es la pendiente de la recta ($m$ sería la constante de proporcionalidad).
Las gráficas de las funciones $y = mx + b$ y $y = mx$ son rectas paralelas, que atraviesan al eje de ordenadas ($eje \space y$) a una altura $b$, estas funciones se denominan funciones afines.
Capitulo II. Funciones

El dominio y el rango (o codominio) tanto de la función afín como de la función lineal es el conjunto de todos los números reales, para cualquiera valor de $x \in\mathbb{R}$, siempre $f(x)$ va a existir:
$$ Dom\space f = \mathbb{R}$$ $$Rango \space f = \mathbb{R}$$ xploremos.
xploremos.
La representación gráfica de las funciones lineales $y = mx + b$, $y = mx$, funciones afines, son rectas paralelas.
Mueve los controles de la pendiente $m$ y la ordenada $b$, corte con el $eje \space y$ en el punto $(0,b)$ y observa la función constante.
¿Comó hallar la pendiente $m$ de una finción lineal?
 xploremos.
xploremos.
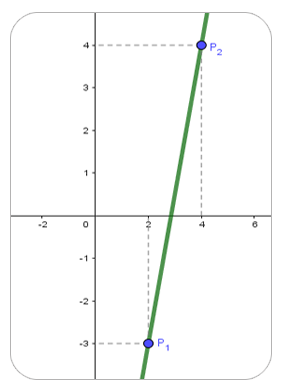
Desplaza el punto rojo o punto azul, observa el resultado de la pendiente $m$ dados dos puntos $\begin{aligned} P_1 (x_1, y_1) \end{aligned}$ y $\begin{aligned} P_2 (x_2, y_2) \end{aligned}$.
Una de las formas de hallar la pendiente $m$ de una recta es tomar dos puntos sobre dicha recta, entonces sean los puntos $\begin{aligned} P_1 (x_1, y_1) \end{aligned}$ y $\begin{aligned} P_2 (x_2, y_2) \end{aligned}$ la pendiente está dada por la expresión: $$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
Capitulo II. Funciones
Primero, la pendiente $\quad m =\displaystyle \frac{y_2 - y_1}{x_2 - x_1} = \frac{4 - (-3)}{4 - 2} = \frac72$
Ulizamos la ecuación punto-pendiente, tomamos cualquiera de los dos puntos:
$$y - y_1 = m (x - x_1) = y - (-3) = \frac72 ( x - 2)$$ $$y + 3 = \frac72 x - \frac{7}{\cancel{2}} (\cancel{2})$$ $$y = \frac72 x - 7 - 3$$por tanto, la ecuación es: $\quad \displaystyle y = \frac72 x - 10$
Además, también se puede saber si dos rectas son paralelas o perpendiculares a partir de sus pendientes:

En otras palabras, dos rectas en el plano son perpendiculares si el producto de sus pendientes $m_1$ y $m_2$ es igual a $-1$.

Lea detenidamente el problema, realice los cálculos con su debido procedimiento. Para actualizar otros valores oprime el botón.
Capitulo II. Funciones
Se denomina función cuadrática o función polinómica de 2° grado (su forma es una parábola) , es decir, una función en la que el término de mayor grado es de exponente dos, donde, la expresión o fórmula general de una función cuadrática está dada por:
$$f(x)=ax^2+bx+c$$ donde, los coeficientes $a$, $b$, y $c$ son números reales con $a =\not 0$.La ecuación de la función cuadrática en forma general está compuesta por los términos:
$ax^2$ el término cuadrático, $bx$ el término lineal y $c$ el término independiente.
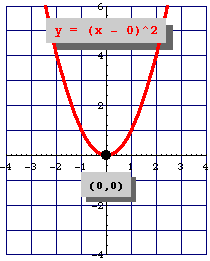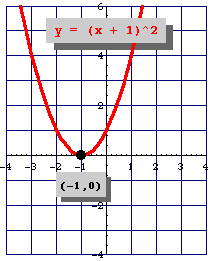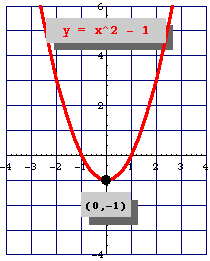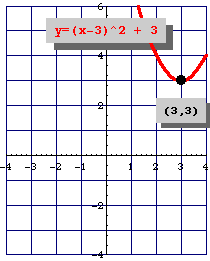
Para poder graficar una función cuadrática es necesario saber las coordenadas del vértice de la parábola.
Con el objeto de analizar mejor esta función la transformamos en la expresión que se conoce como la forma canónica o estándar de la función cuadrática, donde, el punto $(x,y) = V(h, k)$ representa el vértice de la parábola y se expresa como:
$$f(x) = a(x - h)^2 +k$$$h$ y $k$ corresponden respectivamente al punto en el $eje \space x$ y punto en el $eje \space y$ del vértice, es decir, el vértice tiene de coordenadas $(h, k)$, además, el vértice es importante para graficar la función cuadrática.

Para hallar el vértice de una función cuadrática tenemos que calcular la coordenada $x = h$ del punto mediante la siguiente expresión:
$$x=\frac{-b}{2a}$$Para bosquejar la gráfica de la función de 2° grado, con solo el coeficiente $\textit{\textbf{a}}$ (coeficiente cuadrático) se indica hacia donde es la abertura de la función cuadrática, además, si es hay un punto máximo o mínimo en el vértice.
Capitulo II. Funciones
 xploremos.
xploremos.
Elementos de la función cuadrática. Mueve el control $a$, $b$ o $c$, observe los cambios en la gráfica y los datos de la función cuadrática.
El dominio de una función cuadrática siempre es el conjunto de todos los números reales. $$\text{Dom } f=\mathbb{R}$$
El rango está restringido a esos puntos máximos o iguales a la coordenada en $y$ del vértice, o mínimos o iguales, dependiendo si la parábola abre hacia arriba o hacia abajo.
 xploremos.
xploremos.
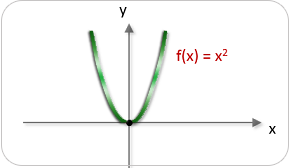
Función cuadrática caso especial, $\quad y =x^2$.
Mueve el control $a$ o modifica el valor de $x$, observe los cambios en la gráfica y los datos de la función cuadrática.
Un caso particular de la función de 2° grado se obtiene cuando el valor del coeficiente cuadrático $a$ es igual a $1$, y los demás coeficientes $b$, $c$ son iguales a $0$, con estos valores se obtiene una parábola con vértice en el origen de coordenadas $(0,0)$ y su expresión es:
$$f(x) = x^2$$Capitulo II. Funciones
Una parábola siempre corta con el eje de ordenadas ($eje \space y$), y esto sucede cuando $x=0$. Por lo tanto, para calcular el punto de corte de una función cuadrática con el $eje \space y$ se debe resolver $f(0)$.

Por otro lado, el punto de corte de una función de 2° grado con el eje de abscisas $(eje \space x)$ se produce cuando $f(x)=0$. Así que para calcular el punto de corte con el $eje \space x$ hay que resolver la ecuación $f(x)=0$.
Características
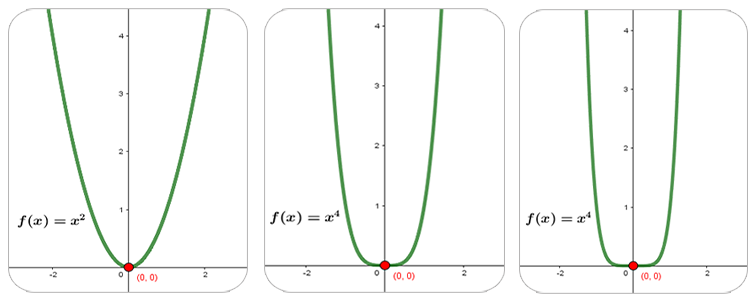
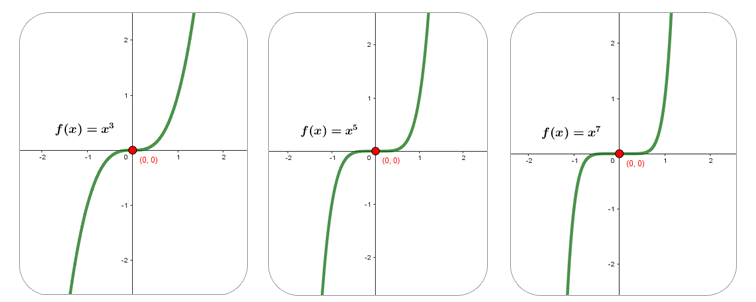
El dominio de una función polinómica siempre es el conjunto de todos los números reales.
 Comprueba lo aprendido respondiendo a la pregunta.
Comprueba lo aprendido respondiendo a la pregunta.
Capitulo II. Funciones

Lea detenidamente el problema, realice los cálculos con su debido procedimiento. Para actualizar otros valores oprime el botón.
Una función racional es una función formada por la división de dos polinomios, es decir, una función racional es una fracción que tiene un polinomio $f(x)$ en el numerador y un polinomio $g(x)$ en el denominador, y se expresa de la forma:
$$y = \frac{f(x)}{g(x)}$$$\displaystyle y = \frac{5x+3}{x^2 - 3}$, $\quad \displaystyle f(x) = \frac{x^2+9}{5x^2 - 3x+8}$, $\quad \displaystyle h(x) = \frac{-2}{x^3 - 6x^2-3}$
 No se puede confundir una función racional con este tipo de expresión $\displaystyle y = \frac{5x + 2}{- 3}$, que tiene el polinomio $g(x)$ de grado 0 (solo un término independiente, función constante $y=b$), y es, por tanto, una función polinómica, función de 1° grado igual a $\displaystyle y = -\frac{5}{3}x - \frac{2}{3}$
No se puede confundir una función racional con este tipo de expresión $\displaystyle y = \frac{5x + 2}{- 3}$, que tiene el polinomio $g(x)$ de grado 0 (solo un término independiente, función constante $y=b$), y es, por tanto, una función polinómica, función de 1° grado igual a $\displaystyle y = -\frac{5}{3}x - \frac{2}{3}$
Capitulo II. Funciones
 xploremos.
xploremos.
Gráfica de una función racional. Ingresa la función a gráficar y pulsa la tecla "enter <┘", oprime el botón ayuda para escribir algunas expresiones de la función, observa el ejemplo, sea la función
 Especial ¡cuidado!, con los signos de agrupación en la escritura de la función.
Especial ¡cuidado!, con los signos de agrupación en la escritura de la función.
Tomada de: Funciones de Norma Patricia Apodaca Álvarez, modificada por el autor.
El dominio de una función racional son todos los números reales excepto aquellos valores que anulan el denominador.
Por lo tanto, un número dividido entre $0$ es una indeterminación que da como resultado infinito $(∞)$, así que una función racional existirá siempre menos cuando el denominador sea $0$.
Entonces, para encontrar el dominio de una función racional debemos encontrar cuándo el denominador es $0$, o sea, $g(x) = 0$, ya que ese punto será el único que no pertenece al dominio de la función.
Para esta función, el valor de $x = 2$ no pertenece al dominio, ya que $\displaystyle f(x) = \frac{3(2) - 2}{(2) - 2} = \frac{4}{0}$ y la división por cero no está definida (no se le puede asignar una imagen al valor de dos); ahora como no hay otro valor real que haga que el denominador sea cero, se puede concluir que el dominio de la función $f(x)$ son todos los números reales diferentes de 2, simbólicamente se expresaría así:
$$dom f = \{ x\in \mathbb{R} \text{ | } x =\not 2 \} = \mathbb{R} - \{ 2 \}$$Se lee: “el dominio de $f$ son todos los $x$ que pertenecen a los reales tales que $x$ sea diferente de dos”

 ¡Piensa!... En general, el rango o codominio de una función racional son todos los números reales menos aquellos valores en los que la función posee una asíntota horizontal. ¿Sabes que son las rectas asíntotas?
¡Piensa!... En general, el rango o codominio de una función racional son todos los números reales menos aquellos valores en los que la función posee una asíntota horizontal. ¿Sabes que son las rectas asíntotas?
Capitulo II. Funciones
 Video. Dominio de una función racional, cuyo denominador se descompone en factores.
Video. Dominio de una función racional, cuyo denominador se descompone en factores.
Existen algunos casos particulares de las funciones racionales que se presentan con frecuencia como son: de proporcionalidad inversa, de proporcionalidad inversa trasladada y homográfica.
 xploremos.
xploremos.
Casos particulares de las funciones racionales. Mueve el control, observa las características de cada función, oprime el botón gráfica si deseas ver los ejemplos de las gráficas.
Tomada de: Funciones de Norma Patricia Apodaca Alvarez, modificada por el autor.
Capitulo II. Funciones
Sea $b>0$ y $b =\not 1$, entonces una función exponencial $y=f(x)$ es una función de la forma: $$ f(x)= b ^x,$$
 donde, $b \in \mathbb R$ se llama base y la variable $x$ es cualquier número real (exponente). Se presentan dos tipos de grafica de la función exponencial, dependiendo del valor de $b$:
donde, $b \in \mathbb R$ se llama base y la variable $x$ es cualquier número real (exponente). Se presentan dos tipos de grafica de la función exponencial, dependiendo del valor de $b$:
Si $b > 1, \quad$ por ejemplo, $f(x) = 5^x$ sus características son:
Si $0 < b < 1, \quad$ por ejemplo, $f(x)= (\frac{2}{5})^x$ sus características son:
 xploremos.
xploremos.
Casos de la función exponencial. Mueve el control, observa las características de cada función, oprime el botón gráfica si deseas ver los ejemplos de las gráficas.
Debemos tener en cuenta que las funciones exponenciales satisfacen las leyes generales de los exponentes. Para recordar estas leyes, las establecemos como reglas.
Capitulo II. Funciones
Para cualquier constante $a > 0$, $b > 0$, y para todo $n$ y $m$:
Propiedades de las funciones exponenciales $\quad y = b^x$El logaritmo es el exponente de una potencia con cierta base, este es un número positivo, es decir, el número y la base de un logaritmo corresponde a números $\mathbb{R^+}$ (números positivos).
El logaritmo de $a$ en base $b$ es otra forma de expresar la potenciación con $b>0$ y $a$ un número $\mathbb{R}$ positivo, se denota como:
$$\log_b(a)= c \quad \text{si y solo si} \quad b^c = a$$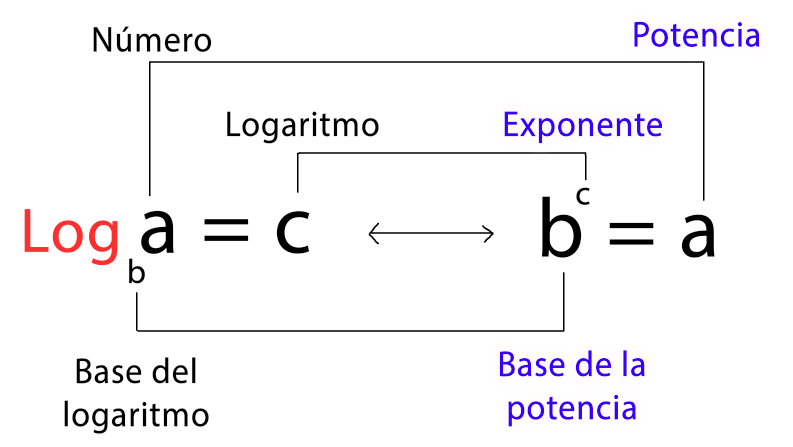

Capitulo II. Funciones
 xploremos.
xploremos.
La función Logaritmica. Mueve el control y observa las gráficas.
Propiedades de la función logaritmo $\quad y = \log_b(x)$
REGLA. Propiedades de los logaritmos.
Si $m$ y $n$ son números positivos y $a$ es un número $\mathbb{R}$, entonces:
$$\log_5 (25)=\log_5(5^2)=2\cdot\log_5(5)=2\cdot(1)=2$$
Capitulo II. Funciones

¡Recursos! $\space$ Uso de la calculadora científica.
 Para el uso de la calculadora científica que en muchas de estas no tienen como hallar el logaritmo en cualquier base, se utiliza el cambio de base con una de las expresiones anteriores.
En la calculadora encontramos dos teclas para calcular logaritmos:
Para el uso de la calculadora científica que en muchas de estas no tienen como hallar el logaritmo en cualquier base, se utiliza el cambio de base con una de las expresiones anteriores.
En la calculadora encontramos dos teclas para calcular logaritmos:
 Con esta tecla se calculan los logaritmos en base $10$, logaritmos decimales.
Con esta tecla se calculan los logaritmos en base $10$, logaritmos decimales.
 Con esta tecla se calculan los logaritmos en base e, logaritmo natural o también conocido como logaritmos neperianos.
Con esta tecla se calculan los logaritmos en base e, logaritmo natural o también conocido como logaritmos neperianos.

Las dos teclas se utilizan también para calcular cualquier logaritmo, por ejemplo,
$$\log_8(4) = \frac{\log(4)}{\log(8)} = \frac23 \approx 0,66666666666666... $$ $\displaystyle \log_8(4) = \frac{\ln(4)}{\ln(8)} = \frac23 $

Indicaciones

Capitulo II. Funciones
¿Cómo se resuelve una ecuación logarítmica o exponencial?
Tomamos logaritmos en base $2$ a ambos lados de la ecuación:
$$\log_2 (2^{x+3}) = \log_2 (126)$$ $$(x+3) \cdot \cancel{\log_2(2)} = \log_2 (126)$$ $$x+3 = \log_2 (126)$$ $$x = \log_2 (126) - 3$$Si deseamos encontrar el valor exacto de la incógnita, se hace un cambio de base y se evalúa en calculadora.
$$x = \log_2{(126)} - 3$$ $$x = {\log{(126)} \over \log{(2)}} - 3$$ $$ x = 3,977279924$$Verifique, sustituyendo el valor hallado en la ecuación inicial.
$$2^{(3,9773)+3} = 126$$
¡Recordemos!
 Siempre se puede verificar el resultado encontrado, sustituyendo este por la incógnita de la ecuación inicial, y se debe cumplir la igualdad.
Siempre se puede verificar el resultado encontrado, sustituyendo este por la incógnita de la ecuación inicial, y se debe cumplir la igualdad.
Despejamos los logaritmos a un solo lado de la ecuación aplicando las leyes para simplificar:
$$ \log{(x+3)}- \log{(x+2)}=5$$ $$ \log{\bigg(\dfrac{x+3}{x+2}\bigg)}=5,$$para eliminar el logaritmo, aplicamos la base en forma exponencial a ambos lados de la ecuación, simplificando asi el logaritmo.
$$ \displaystyle 10^{\log{\big(\frac{x+3}{x+2}\big)}}=10^5$$ $$ \frac{x+3}{x+2}=10^5$$ $$ x+3=10^5 (x+2)$$ $$ x+3=10^5x+(2)10^5$$ $$ x-10^5x=(2)10^5-3$$ $$ x(1-10^5)=200000-3$$ $$ x=\frac{199997}{1-10^5}$$ $$x \approx -1,99999$$Capitulo II. Funciones
 xploremos.
xploremos.
Observa las gráficas de la función logarítmica y exponencial. Mueve los controles, para modificar la base del logaritmo y de la función exponencial, además, los puntos simétricos en cada gráfica.
 ¡Piensa!... Observa las gráficas de las funciones logaritmicas $y=\log_b(x)$ y exponencial $y = b^x$ y responde a las preguntas:
¡Piensa!... Observa las gráficas de las funciones logaritmicas $y=\log_b(x)$ y exponencial $y = b^x$ y responde a las preguntas:
¿Que se puede decir de la gráfica de las dos funciones?,
¿Que sucede en ambas ecuaciones si $b=1$?,
¿Qué pasa si $x=0$ y puede ser $y<0$?
¿Cómo está ubicada la recta $y=x$?

La función logarítmica más utilizada es cuando $b = e$, está función expresada como $\log_e(x)$ utiliza el número $e$ como base y se lee logaritmo natural o neperiano.
La diferencia principal entre los logaritmos naturales y otros logaritmos es la base que se está usando. Los logaritmos principalmente usan una base $10$ (aunque podría ser otro valor para la base), mientras que los logaritmos naturales siempre usan base $e$.
Para la función logaritmo en base $e$ y logaritmo natural, se usará:
$$\log_e(x)=\ln(x),$$ además, de la diferencia en la base (que es grande), las leyes de los logaritmos y logaritmos naturales son las mismas, por ejemplo, $$\ln(e)=\ln_e(e)=1$$ $$\ln(e^3)= \log_e(e^3)= 3$$ $$\ln (1) = \log_e(1) = 0$$Capitulo II. Funciones
Si se necesita convertir entre logaritmo y logaritmo natural, se puedes usar una de las siguientes expresiones:
$$\log_{10} (x) =\log(x)=\frac{\ln(x)}{\ln(10)} \quad\text{ o }\quad \ln(x)=\frac{\log(x)}{\log(e)}$$ Con lo visto hasta ahora, se puede deducir que $y= \log_b(x)$ y $y=b^x$ son funciones inversas, con $b>0$ y $b = \not 1$, como condición esencial, entonces, se tiene que:
$$\log_b(x) =y \quad\quad \text{si y solo si} \quad\quad b^y=x.$$
Con lo visto hasta ahora, se puede deducir que $y= \log_b(x)$ y $y=b^x$ son funciones inversas, con $b>0$ y $b = \not 1$, como condición esencial, entonces, se tiene que:
$$\log_b(x) =y \quad\quad \text{si y solo si} \quad\quad b^y=x.$$
De aqui, se desprende que el dominio de la primera es el rango de la segunda y viceversa.
Como las funciones $\quad y =e^x$, $ \quad y = \ln (x)$ son inversas, entonces, se cumplen también las siguientes propiedades:
$$\ln(e^x) =x \,\,\,\,\, \text{y}\,\,\,\,\, e^{\ln(x)}=x.$$La función $f $ y su inversa son gráficas simétricas con respecto a la recta $y = x$. Para que una función $f$ tenga inversa debe ser uno a uno. Una función es uno a uno si y solo si cada recta horizontal interseca su gráfica en máximo un punto.
No toda función $f$ tiene inversa, pero veamos cuando existe la función inversa.
Una función inversa, que se denota $ f^{-1}(x)$, es una función que parte del rango y llega al dominio. Para hallar la función inversa se procede de la siguiente manera:
Capitulo II. Funciones
 xploremos.
xploremos.
Ingresa las funciones y pulsa la tecla "enter <┘", oprime el botón ayuda para ver como escribir algunas expresiones de las funciones.
Se tiene que si el punto $(a, b)$ pertenece a la función $f$ entonces el punto $(b, a)$ pertenece a la función inversa $f^{-1}$. Esto implica que la gráfica de la función $f$ y la gráfica de su inversa $f^{-1}$ se reflejan con respecto a la recta $y=x$, por lo tanto, son funciones simétricas.

¡Recordemos!
No toda función $f(x)$ tiene función inversa $f^{-1}(x)$.
 $$\text{Dominio } f^{-1} = \text{Rango } f$$ $$\text{Rango } f= \text{Dominio } f^{-1}$$
$$\text{Dominio } f^{-1} = \text{Rango } f$$ $$\text{Rango } f= \text{Dominio } f^{-1}$$
Una función tiene función inversa si se trata de una uno a uno, es decir, si cada valor del conjunto de su dominio le corresponde solamente un único valor de su codominio o rango, por ejemplo,
La función exponencial $y=2^x +1$ sí tiene función inversa porque a cada $x$ le corresponde un único valor de $f(x)$.
En cambio, la función cuadrática $y=x^2$ no posee función inversa ya que tiene varios valores de $x$ cuyas imágenes son iguales, por ejemplo $f(1)=f(3)=2$.
Y, finalmente, se debe tener en cuenta que la función inversa no es lo mismo que la inversa multiplicativa de una función, sino que son dos conceptos diferentes.
$$f^{-1}(x) =\not \frac{1}{f(x)}$$
Capitulo II. Funciones
Una función definida mediante diferentes fórmulas en diferentes partes de su dominio es una función que se conoce como función definida por tramos o a trozos, no es una complicada, simplemente se representa cada tramo por separado en un mismo gráfico y cumple con las propiedades de la función de cada tramo, está se expresa en intervalos de la forma: $$f(x) = \begin{cases} g(x) &\text{si } x < a \\ h(x) &\text{si } x \ge a \end{cases}$$
 xploremos.
xploremos.
Función por tramos. Mueve el control y observa las gráficas.
La imagen de un valor de $x$ se calcula según en qué intervalo se encuentra, por ejemplo, (grafica 1), si $x = 2$ está en el intervalo $[1,4)$, entonces su imagen es $f(2) = (2)^2 - 4(2) + 4 = 0$.
 xploremos.
xploremos.
Problemas. Funciones a tramos y sus gráficas. Oprime el botón ejercicio o gráficas y compara los resultados con su gráfica.


¡Recordemos!
Punto abierto ($\color{red} \circ$): No incluye el extremo del intervalo, se representa con paréntesis $(\space)$.
Punto cerrado ($\color{red} \bullet$): Si incluye el extremo del intervalo, se representa con corchetes $[\space]$.
Capitulo II. Funciones
 Ejercicio práctico
Ejercicio práctico

 Evaluamos lo aprendido
Evaluamos lo aprendido
Prepárate para la evaluación y mide tus conocimientos de lo aprendido en este capítulo, responde las preguntas a continuación:

 Actividad complementaria.
Actividad complementaria.
$\space$ Descargar para imprimir
Capitulo II. Funciones
 Evaluación. 10 preguntas con límite de tiempo (Máx. 10 minutos)
Clic en el link, responde y envía tus respuestas por correo.
Evaluación. 10 preguntas con límite de tiempo (Máx. 10 minutos)
Clic en el link, responde y envía tus respuestas por correo.
 Tomada de la Red Educativa Digital Descartes.
Tomada de la Red Educativa Digital Descartes.
"Nada acontece sin una razón suficiente.".
Leibniz

DERECHOS BÁSICOS DE APRENDIZAJE (DBA)
DBA.3. Utiliza instrumentos, unidades de medida, sus relaciones y la noción de derivada como razón de cambio, para resolver problemas, estimar cantidades y juzgar la pertinencia de las soluciones de acuerdo al contexto.
DBA.4. Interpreta y diseña técnicas para hacer mediciones con nive- les crecientes de precisión (uso de diferentes instrumentos para la misma medición, revisión de escalas y rangos de medida, estimaciones, verificaciones a través de mediciones indirectas).
DBA.6. Modela objetos geométricos en diversos sistemas de coordenadas (cartesiano, polar, esférico) y realiza comparaciones y toma decisiones con respecto a los modelos.
Derechos Básicos de Aprendizaje - Grado 11°.
DESEMPEÑOS / ESTANDAR
Componente 1 - Pensamiento Numérico.
1.4 M.V Utilizo argumentos de la teoría de números para justificar relaciones que involucran números naturales. DBA 7.
Componente 2 - Pensamiento Geométrico.
2.6 M.V Reconozco y describo curvas o lugares geométricos. DBA 6.
Componente 5 - Pensamiento Variacional.
5.2 M.V Interpreto la noción de derivada como razón de cambio y como valor de la pendiente de la tangente a una curva y desarrollo métodos para hallar las derivadas de algunas funciones básicas en contextos matemáticos y no matemáticos. DBA 4.

El desarrollo de estos Estándares Básicos de Competencia permitirá fortalecer los procesos de formulación, modelación y resolución de problemas.
Capitulo III. Límites de funciones
 L'Hôpital, como todos los de su época, por tener títulos de nobleza debía hacer la carrera militar, pero por deficiencias visuales le obligó a cambiar a las matemáticas.
L'Hôpital, como todos los de su época, por tener títulos de nobleza debía hacer la carrera militar, pero por deficiencias visuales le obligó a cambiar a las matemáticas.
Es el autor del primer libro sobre cálculo diferencial, L'Analyse des Infiniment Petits pour l'Intelligence des Lignes Courbes (Análisis de los infinitamente pequeños para el entendimiento de las líneas curvas). Publicado en 1696,
el texto incluye las clases de su profesor, Johann Bernoulli, en donde Bernoulli discute la indeterminación 0/0. Este es el método para resolver estas indeterminaciones a través de derivadas sucesivas que lleva su nombre.
método llamado la Regla de L'Hôpital, que se emplea para calcular el valor límite de una fracción donde numerador y denominador tienden a cero o ambos
tienden a infinito.
En realidad, la mencionada regla fue demostrada por Johann Bernoulli (1667-1748), pero por un acuerdo entre ambos, lo publicó el marqués.


En 1922 se encontraron documentos que apoyaban la tesis de Bernoulli. La creencia generalizada de que L'Hôpital trató de aprovecharse del descubrimiento de la regla que lleva su nombre ha resultado falsa. Publicó su libro anónimamente; en la introducción de este incluyó un agradecimiento a Bernoulli por la ayuda prestada, y nunca dijo ser el descubridor de la regla.
Esta herramienta, conocida como la regla de L'Hôpital, utiliza derivadas para calcular los límites. Con esta regla, se podrán evaluar muchos límites que no son fáciles de determinar.

Entre las curvas estudiadas por L'Hopital están: la cicloide, la epicicloide, la hipocicloide y la serpentina.

En 1694 Bernoulli y L'Hôpital acordaron que L'Hôpital le pagaría trescientos francos anuales para que le transmitiera sus descubrimientos, que L'Hôpital describiría en su libro.
En 1704, tras la muerte de L'Hôpital, Bernoulli reveló la existencia del trato, asegurando que la mayoría de los descubrimientos que aparecían en el libro de L'Hôpital eran suyos.
Capitulo III. Límites de funciones
En el estudio de las sucesiones, se profundizará más en su análisis, abordándolas como un tipo especial de funciones. Cuando se estudian bajo esta forma, vemos que a partir de ellas podemos llegar a obtener una idea intuitiva de límite de una sucesión y luego, aplicando esta idea, obtener lo que compete a límite de una función en forma sencilla y amplia.


¡Recuerda!
Las sucesiones y los límites de una función, son la base para el trabajo de otros temas posteriores, como el referente para las derivadas de funciones.
Iniciemos esta unidad hablando del concepto de sucesión como un tipo especial de función, analicemos el siguiente ejemplo:
Sea $\quad a = \{(1,\frac12), (2,1), (3,\frac32), (4,2), (5,\frac52), (6, \frac72),... \}$
Se observa que la función definida, está denotada como conjunto de parejas ordenadas, y en cada una de ellas las primeras componentes de la pareja ordenada son los números naturales ($\mathbb{N}$), y las segundas componentes son los números reales ($\mathbb{R}$),
Se puede afirmar que son funciones definidas de los naturales en los reales, $\quad f : \ce{\mathbb{N} -> \mathbb{R}} $
Estas formas de funciones reciben el nombre de sucesión de números reales, cuyo dominio es el conjunto de los números $\mathbb{N}$.
Con la función definida $a$, donde, la primera componente de la pareja ordenada siempre son los números naturales y que definimos la sucesión como una función de $\quad \ce{\mathbb{N} -> \mathbb{R}}$, se acostumbra omitir estos elementos (primeras componentes) y determinar la sucesión escribiendo solamente los valores reales sucesivos (segundas componentes).
Sean las funciones definidas $a , b , c$, (segundas componentes de la sucesión), que se escriben como:
$\quad \displaystyle a = \bigg\{\frac12, 1, \frac32, 2, \frac52, \frac72,... \bigg\}$
$\quad b = \{1, \sqrt{2}, \sqrt{3}, 2, \sqrt{5},... \}$
$\quad \displaystyle c = \bigg\{ 0, \frac12, 1, \frac32, 2, \frac52, \frac72,... \bigg\} $
Para la sucesión definida en $a$, podemos hallar todos sus términos, donde, estos elementos se caracterizan por seguir una determinada regla de formación, y se pueden denotar por:
$$a_1,a_2,a_3,a_4,...,a_n$$El entero $n$ recibe el nombre de índice $sub-n$ de $S$, que se expresa como $a_n$. Los términos de la sucesión se forman cuando el índice $n$ toma valores de $1, 2, 3, . . . $.
Capitulo III. Límites de funciones
 Por ejemplo, el número $a_1$ es el primer término, $a_2$ el segundo término, $a_3$ el tercer término y asi hasta llegar al término $a_n$, conocido como el término n-énesimo o término general de la sucesión.
Por ejemplo, el número $a_1$ es el primer término, $a_2$ el segundo término, $a_3$ el tercer término y asi hasta llegar al término $a_n$, conocido como el término n-énesimo o término general de la sucesión.
Veamos entonces cuales son los términos de la sucesión definida en $a$:
$$a_1 = \frac12, \quad a_2 = 1, \quad a_3 = \frac32, \quad a_4 = 2, \quad a_5 = \frac52,..., a_n,... $$Para determinar los términos de una sucesión o el término n-ésimo o término general $(a_n)$, podemos asegurar que una sucesión se puede determinar de dos formas:
Se tiene que la sucesión $a$ sus términos se mueven por medio de una fracción $\frac{p}{q}$, donde, el numerador se observa que aumenta de uno en uno, $p = 1, 2, 3, 4, 5,...,n$, y el denominador no varia, siempre es $q=2$.
$$a= \frac{p}{q} = \frac12, \frac22, \frac32, \frac42, \frac52,...=\bigg\{\frac12, 1, \frac32, 2, \frac52, \frac72,..., a_n = \frac{n}{2},... \bigg\}$$ Nótese que para todo entero positivo $n$ hay un correspondiente número $a_n$ entonces una sucesión se puede definir como una función cuyo dominio es el conjunto de enteros positivos $1. 2, 3, 4, 5,...$.
Nótese que para todo entero positivo $n$ hay un correspondiente número $a_n$ entonces una sucesión se puede definir como una función cuyo dominio es el conjunto de enteros positivos $1. 2, 3, 4, 5,...$.
Se tiene que la sucesión $b$ sus términos se mueven por medio de un aumento de uno en uno, $1, 2, 3, 4, 5,...,n$ y a cada término se aplica la función $f(x)= \sqrt{x}$, obteniendo como término n-ésimo $ b_n = \sqrt{n}$
$$b = \sqrt{1}, \sqrt{2}, \sqrt{3}, \sqrt{4}, \sqrt{5},...$$ $$b=\{1, \sqrt{2}, \sqrt{3}, 2, \sqrt{5},..., \sqrt{n},... \}$$Para los ejemplos anteriores, se tiene que las sucesiones inician ambas en $n=1$, depende de la sucesión, se puede hacer la restricción para que $n$ inicie en cualquier valor entero positivo o natural.
Capitulo III. Límites de funciones
Supongamos que conocemos el término n-ésimo de una sucesión definida $a$ como $\quad \displaystyle a_n=\bigg\{\frac{n}{n+1}\bigg\}$ con $n \in \mathbb{N}$, entonces, los primeros términos de la sucesión se obtienen, reemplazando directa y sucesivamente a $n$ por los números naturales, o sea:
El primer término $\quad a_1 = \displaystyle \frac{1}{1+1}= \frac12$
El segundo término $\quad a_2 = \displaystyle \frac{2}{2+1}= \frac23$
El tercer término $\quad a_3 = \displaystyle \frac{3}{3+1}= \frac34$
El cuarto término $\quad a_4 = \displaystyle \frac{4}{4+1}= \frac45$, y así, sucesivamente, obtenemos la sucesión:
$$a_n= \bigg\{\frac12, \frac23, \frac34, \frac45, \frac56, \frac67,..., \frac{n}{n+1},...\bigg\}_{n=1}$$Para determinar el término n-ésimo o término general, debemos conocer algunos términos consecutivos de la sucesión y analizar que transformación se les realizó a los números naturales (1, 2, 3...) para obtener los términos de la sucesión que son números reales.
 ¡Piensa!... Puedes encontrar el término n-ésimo de la sucesión que inicia en $n=1$ y que por notación seguiremos llamando $S_n$.
$$\quad \displaystyle S_n = \bigg\{ 1, \frac43, \frac32, \frac85, \frac53, \frac{12}{7}, \frac{14}{8},... \bigg\} $$
¡Piensa!... Puedes encontrar el término n-ésimo de la sucesión que inicia en $n=1$ y que por notación seguiremos llamando $S_n$.
$$\quad \displaystyle S_n = \bigg\{ 1, \frac43, \frac32, \frac85, \frac53, \frac{12}{7}, \frac{14}{8},... \bigg\} $$

$a_1=1 \quad\text{transformamos el 1º término: } \quad 2(1) - 1$
$a_2=3 \quad\text{transformamos el 2º término: }\quad 2(2) - 1$
$a_3=5 \quad\text{transformamos el 3º término: }\quad 2(3) - 1$
$a_4=7 \quad\text{transformamos el 4º término: }\quad 2(4) - 1$
.
$a_n=n \quad\text{transformamos el n-ésimo término: }\quad 2(n) - 1$,
por tanto, se tiene que en término n-ésimo es $\quad a_n=\{2n - 1\}$
$$S =\{1, 3, 5, 7, 9, 11,..., (2n - 1),... \}$$Cuando se presentan los términos con alternancia en los signos, positivos y negativos, el término n-ésimo presenta una multiplicación por potencias de la forma $(-1)^n$ o $(-1)^{n-1}$ o $(-1)^{n+1}$.
Este tipo de sucesión genera términos con signos alternantes:
$$S=\bigg\{-\frac{1}{3},\space \frac{2}{3}, -\frac{3}{3},\space \frac{4}{3},\ -\frac{5}{3}, \ \frac{6}{3},\ -\frac{7}{3},... \frac{(-1)^n n}{3}\bigg\}$$Cabe resaltar, que en ocasiones las sucesiones se determinan por sus primeros términos, donde, estos permiten también intuir el valor del término general.
Capitulo III. Sucesiones y Límites
 Muchas sucesiones quedan determinadas por su término general o término e-nésimo, $a_n$, que suele ser una expresión algebraica en términos de la variable indeterminada $n$.
Muchas sucesiones quedan determinadas por su término general o término e-nésimo, $a_n$, que suele ser una expresión algebraica en términos de la variable indeterminada $n$.

Para iniciar, oprime el botón términos y completa la sucesión de números dada, oprime el botón verificar y comprueba tu solución.
Ingresa la regla que genera la sucesión y pulsa la tecla "enter <┘", verifica la respuesta con el botón verificar regla o corrige si encuentras errores. Con el botón Inicio generas una nueva sucesión.
Tomada de: Telesecundaria, autoria ILCE Grupo Descartes, modificado por el autor
Representar gráficamente los términos de una sucesión, permite visualizar e identificar en forma práctica algunas características de estas, además de ser una ayuda importante para el cálculo del límite de ellas.
Teniendo en cuenta que una sucesión es una función de $\ce{\mathbb{N} -> \mathbb{R}}$, podemos hacer la representación gráfica mediante un plano cartesiano (sistema de coordenadas), o sobre una recta numérica.


¡Recuerda!
Si hacemos representación en un plano cartesiano, debemos observar que en las abscisas ($eje \space x$) ubicamos los números naturales y en la ordenada ($eje \space y$) los números reales (términos de la sucesión).
Si la hacemos sobre la recta numérica, en ella representamos los términos de la sucesión, teniendo presente utilizar una unidad de medida adecuada como patrón.
 Comprueba lo aprendido respondiendo a la pregunta.
Comprueba lo aprendido respondiendo a la pregunta.
Capitulo III. Límites de funciones
Practica y analiza lo dicho, observando el siguiente ejemplo:
Una pelota es lanzada desde 2 metros de altura. Rebota en el suelo y en cada rebote alcanza una altura, cuyo valor en metros coincide con los términos de la sucesión definida como $S$ así:
$$S=\bigg\{2, \frac{3}{2},\space \frac{4}{3}, \frac{5}{4},\space \frac{6}{5},..., \frac{100}{101},..., \frac{1000}{1001},... \bigg\}_{n=1}$$Expresemos una fórmula en función de $n$, que permita generalizar los términos de la sucesión dada:
Se observa que en cada rebote la pelota sube a una altura menor que en el rebote anterior y que el numerador que inicia en $2$ y aumenta de uno en uno, además, siempre es una unidad más que el denominador, por tal motivo, se tiene que la expresión para encontrar los terminos de la sucesión es:
$$\qquad\qquad S_n=\frac{n+1}{n}$$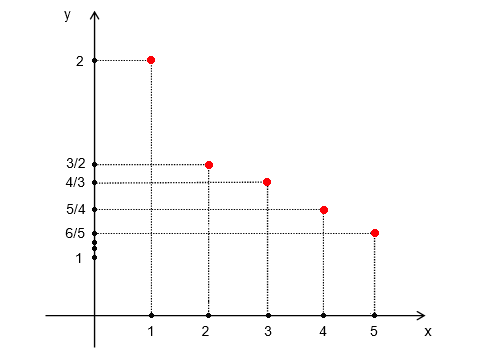
Representación gráfica en el plano cartesiano de los términos de la sucesión de la altura a la que llegaría la pelota en los primeros rebotes.
Hasta el momento hemos estudiado las sucesiones sin tener en cuenta algunas características que tienen sus términos, veamos algunas de las características que pueden tener las sucesiones:
Por medio del siguiente ejemplo vamos a analizar el comportamiento de los términos de una sucesión.
El primer término es $0$; el segundo término es $\displaystyle\frac12$; el tercer término es $1$; el cuarto término es $\displaystyle\frac32$, y así sucesivamente; se observa en los términos que: $$\quad\quad 0<\frac12, \quad \frac12<1, \quad 1<\frac23, \quad \frac32< 2, .....$$
En forma general, se cumple que:
$$S_1 < S_2, \quad S_2 < S_3, \quad S_3 < S_4,..., \quad S_n < S_{n+1},...$$ $$S_1 < S_2 < S_3 < S_4 < S_5 < S_6 < ,..., < S_n < S_{n+1},...$$ Aquí se observa que en la sucesión los términos van aumentando su valor progresivamente; cuando los términos de una sucesión tienen esta característica, la sucesión se llama monótona creciente.
Aquí se observa que en la sucesión los términos van aumentando su valor progresivamente; cuando los términos de una sucesión tienen esta característica, la sucesión se llama monótona creciente.
Analizando el comportamiento de los términos de la sucesión, se tiene que:
El primer término es $5$; el segundo término es $\displaystyle\frac{13}{3}$; el tercer término $\displaystyle\frac{11}{3}$; el cuarto término $3$; y así, sucesivamente; se observa en los términos que:
$$5 > \frac{13}{3}, \quad \frac{13}{3} > \frac{11}{3}, \quad \frac{11}{3} > 3, \quad 3 > \frac{7}{3},...$$En forma general, se cumple que:
$$S_1 > S_2, \quad S_2 > S_3, \quad S_3 > S_4,..., \quad S_n > S_{n+1},...$$ $$S_1 > S_2 > S_3 > S_4 > S_5 > S_6 > ,..., > S_n > S_{n+1},...$$Es decir, los valores de los términos de la sucesión disminuyen progresivamente. Cuando los términos de una sucesión tienen esta cualidad, la sucesión se llama monótona decreciente.
Podemos obtener otra conclusión sobre las sucesiones y es cuando éstas tienen todos sus términos iguales, esté tipo de sucesiones reciben el nombre de sucesiones constantes.
Se puede Verificar por medio de una demostración si una sucesión es monótona creciente o decreciente, veamos el siguiente ejemplo:
Partimos de la siguiente equivalencia:
$$\frac{n}{n+1} < \frac{(n)+1}{(n+1)+1} \\ \frac{n}{n+1} < \frac{n+1}{n+2}$$
Si multiplicamos cruzadamente las fracciones y simplificamos expresiones, obtenemos desigualdades equivalentes:
$$n(n+2) < (n+1)(n+1) \\ \cancel {n^2+2n} < \cancel {n^2+2n}+1 \\ 0<1$$Por tanto, la desigualdad obtenida $0<1$, es verdadera, entonces decimos que la sucesión es creciente.
En conclusión, se tienen las siguientes definiciones:
Una sucesión $S$, es monótona creciente si cada término es mayor o igual que el término inmediatamente anterior.
Simbólicamente:
$S_n$ es monótona creciente si $S_n ≤ S_{n+1}$, para todo $n \in \mathbb{N}$.
Una sucesión $S$, es monótona decreciente si cada término es menor o igual que el término inmediatamente anterior.
Simbólicamente:
$S_n$ es monótona creciente si $S_n ≥ S_{n+1}$, para todo $n \in \mathbb{N}$.
Otro aspecto importante en el estudio de las sucesiones es saber cuáles son los elementos que cierran las sucesiones, en otras palabras, que acotan la sucesión, ya que, de esta forma, podemos establecer con más claridad el espacio donde estas se desarrollan; analicemos esta otra característica con un ejemplo:
Se tiene que los seis primeros términos de la sucesión son:
$$S=\displaystyle\bigg\{\frac12, \space \frac14, \space \frac18, \space \frac{1}{16}, \space \frac{1}{32}, \space \frac{1}{64},...,\frac{1}{2^n},...\bigg\}$$ Se observa que los términos de la sucesión nos damos cuenta de que cada término hallado es menor que $1$, por tal motivo, decimos que $1$ es una cota superior de la sucesión $S=\displaystyle\bigg\{\frac{1}{2^n} \bigg\}$ con $n \in \mathbb{N}$.
Se observa que los términos de la sucesión nos damos cuenta de que cada término hallado es menor que $1$, por tal motivo, decimos que $1$ es una cota superior de la sucesión $S=\displaystyle\bigg\{\frac{1}{2^n} \bigg\}$ con $n \in \mathbb{N}$.
Además, cuando $n$ aumenta, disminuye el valor de cada término y este cada vez se acerca más a cero, lo que indica que $0$ es una cota inferior de la sucesión.
Por tanto, es una sucesión acotada, $\quad 0 < S_n ≤ 1$.
Una sucesión está acotada superiormente si existe algún número real mayor o igual que todos los términos de la sucesión. Es decir, existe $M \in \mathbb{R}$, tal que:
$$\quad\quad S_n ≤ M,\quad \text{para todo } n.$$
Una sucesión está acotada inferiormente si existe algún número real mayor o igual que todos los términos de la sucesión. Es decir, existe $m \in \mathbb{R}$, tal que:
$$\quad\quad m ≤ S_n,\quad \text{para todo } n.$$

 ¡Piensa!... Si Encontramos los primeros términos de la sucesión
$S = \displaystyle\{\frac{2}{n+1}\},\quad$ ¿La sucesión es acotada?
¡Piensa!... Si Encontramos los primeros términos de la sucesión
$S = \displaystyle\{\frac{2}{n+1}\},\quad$ ¿La sucesión es acotada?

Lea detenidamente el problema, realice los cálculos con su debido procedimiento. Para actualizar otros valores oprime el botón.
Analizaremos el concepto de límite de una sucesión, a través de la representación gráfica de ella obre una recta real (recta metrizada), para luego, con base en este análisis, dar una definición formal, realicemos para ello, algunos ejemplos:
Se tiene los primeros términos de la sucesión y su gráfica en la recta real:
$$S=\displaystyle\bigg\{3, \space\frac32, \space 1, \space \frac34, \space \frac{3}{5}, \space \frac{3}{6}, \space \frac{3}{7},...\bigg\}$$
Analizando la gráfica, se observa que los términos de la sucesión se están acercando cada vez más al punto cero. Esto nos indica que a medida que $n$ toma valores grandes, los términos de la sucesión se aproximan al valor $0$.
 Por tanto, se tiene que el límite de la sucesión $S$ es $0$, cuando $n$ toma valores muy grandes, esto se expresa simbólicamente de la forma:
Por tanto, se tiene que el límite de la sucesión $S$ es $0$, cuando $n$ toma valores muy grandes, esto se expresa simbólicamente de la forma:
Está expresión se lee:
El límite de la sucesión $\displaystyle\frac{3}{n+1}$, cuando $n$ tiende a más infinito (${+}\infty$), es igual a cero $0$.
Definición del límite de una sucesión.
El límite de una sucesión es el número al cual se van aproximando los términos de una sucesión.
Si una sucesión $\{S_n\}$, tiene como límite un valor real $L$, este se expresa como:
$$\lim_{n \to \infty}\{S_n\} = L \qquad o \qquad {\{a_n\} \to L} \space cuando \space {n \to \infty}$$Si $n$ toma valores suficientemente grandes, entonces, si $\displaystyle \lim_{n \to \infty}\{S_n\}$ existe, decimos que:
Con base en las definiciones dadas de límite de una sucesión, convergencia y divergencia, podemos analizar otro tipo de sucesiones. Veamos el análisis con algunos ejemplos:
Si hacemos que en la sucesión $S=\displaystyle\bigg\{\frac{3n}{n+1} \bigg\}$, tome valores muy grandes, vemos que los términos de la sucesión se van acercando o aproximando a $3$.
$$S=\displaystyle\bigg\{\frac32, \space \frac63, \space \frac94, \space \frac{12}{5}, \space \frac{15}{6},..., \frac{27}{10}\approx 2,7,..., \frac{90}{31}\approx 2,903,..., \bigg\},$$por tanto, $\quad \displaystyle \lim_{n \to \infty} \bigg\{\frac{3n}{n+1} \bigg\} = 3, \quad$ así, notamos que la sucesión tiende a un valor determinado, el $3$, o sea la sucesión tiene un límite y recibe el nombre de convergente.

Si hacemos que $n$ tome valores muy grandes, vemos que los términos de la sucesión no tienden a ningún valor determinado, entonces, podemos afirmar que la sucesión no tiene límite.
Por tanto, $\quad \displaystyle \lim_{n \to \infty} \{n\} = \text{No existe}, \quad$ este tipo de sucesiones se conocen como divergentes.
Las sucesiones que no son convergentes ni divergentes, se llaman sucesiones oscilantes, sus términos son alternantes, (

Determinar los términos de una sucesión, si está converge o diverge, si crece o decrece, oprime el botón solución y verifica tu respuesta.
Se desarrollará y analizará el concepto de límite que está estrechamente unido al cálculo y proporciona el fundamento para la derivada y la integral.
Iniciamos este estudio analizando varios ejemplos que nos ayuden a interpretar este concepto, y luego dar algunas definiciones con diferentes grados de complejidad.
Dando respuesta a la pregunta, se elabora una tabla de valores para $f(x)$, dando a $x$ valores muy cercanos a $1$. Debemos tener en cuenta que al valor $1$ nos podemos acercar por la izquierda o por la derecha.
Se observa que, en cada uno de los extremos en que nos acercamos al valor de $1$, el valor de $y$ se aproxima o se acerca al valor de $5$.

Veamos el gráfico de la función:
$y = f(x) = 3x + 2$,
según los datos obtenidos en la tabla.
Observando el gráfico, nos damos cuenta de que si nos acercamos al valor de $1$ por la izquierda o por la derecha, la gráfica se aproxima al valor de $5$.
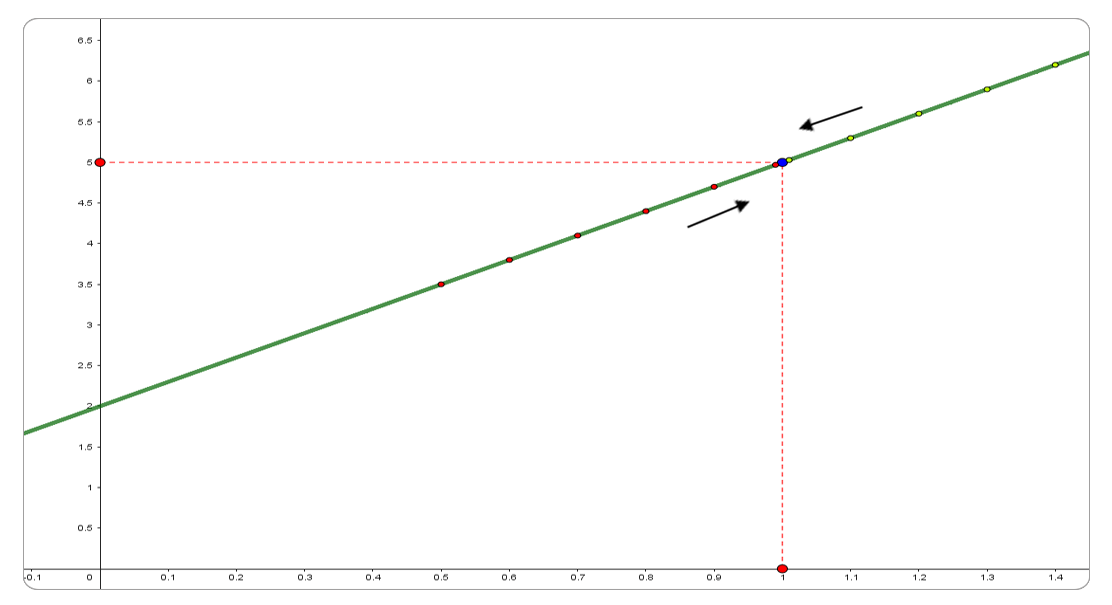
Este resultado se expresa y se denota así:
$$\lim_{x \to{1}}{(3x + 2)} = 5,$$y se lee: el límite de $3x + 2$, cuando $x$ tiende a $1$ es igual a $5$.
 Tomando como base este ejemplo, podemos tener una primera definición muy informal del concepto de límite, a medida que avancemos llegaremos a su definición precisa.
Tomando como base este ejemplo, podemos tener una primera definición muy informal del concepto de límite, a medida que avancemos llegaremos a su definición precisa.
Suponga que $L$ denota un número finito. El concepto de $f(x)$ que tiende a $L$ a medida que $x$ tiende a un número $a$ puede definirse informalmente de la siguiente manera:
Definición informal del concepto de límite.
Sea $f(x)$ una función y $a$ un valor determinado, tal que $a$ pertenezca a un intervalo $(c,b)$ del dominio de $f(x)$, si al aproximarse $x$ hacia $a$, tanto por la izquierda como por la derecha, $f(x)$ tiende a un valor especifico $L$... luego $L$ es el límite de $f(x)$ cuando $x$ tiende a $a$, simbólicamente:
$$\lim_{x \to{a}}{f(x)} = L$$
El propósito de esta unidad es introducir uno de los conceptos más destacados del cálculo: el límite de una función en un punto dado.
Dicho conocimiento es el soporte para el estudio de la derivada de una función y de la integral definida, que se estudiarán en capítulos más adelante.
Estamos en capacidad de evaluar algunos limites por simple intuición, pero es necesario conocer unos teoremas, los cuales no se van a demostrar, porque eso está más allá de los objetivos de este libro de cálculo elemental.
Encontrar límites para la gran mayoría de puntos para una función dada es tan simple como sustituir el número que $x$ se acerca en la función, desarrollaremos algunos ejemplos que nos ayudarán a entender mejor las definiciones.
Como debemos calcular $\quad\displaystyle\lim_{x \to{2}}{f(x)}$, tenemos que $a = 2$, por tanto, evaluando el límite, reemplazamos directamente en $f(x)$ entonces se tiene que:
$$\lim_{x \to{2}}{(2x+1)} = 2(2)+1=4+1=5$$Como debemos calcular $\quad\displaystyle\lim_{x \to{1}}{f(x)}$, tenemos que $a = 1$, por tanto, evaluando el límite, reemplazamos directamente en $f(x)$ entonces se tiene que:
$$\lim_{x \to{1}}{\frac{x^2 + x + 1}{x+1}} = \frac{(1)^2 + (1) + 1}{(1)+1}=\frac32$$Si $f$ es un función y $a$ está definida en el dominio de la función $f$, entonces, $$\lim_{x \to a}{f(x)}= f(a)$$
En conclusión, cuando se evalúa un límite, es evaluar la función en el punto $x$ dado y se simplifican las expresiones resultantes, al evaluar la función siempre el símbolo de límite desaparece.
Puedes estar seguro de que este método funciona siempre y cuando no termines dividiéndolo por cero cuando realices la sustitución.

Para iniciar, lee las indicaciones dadas. Resuelve el límite propuesto y verifica la solución que se dada paso a paso, genera un nuevo ejemplo, oprime el botón Otro ejemplo.
Hay casos en que las funciones no están definidas (en los reales) a la izquierda o a la derecha de un número $a$ determinado, para ello, utilizamos los limites unilaterales, estos, son límites que se acercan por la derecha o izquierda de la función:
Cuando los límites laterales por la izquierda y la derecha existen, pero no son iguales, se dice que la función no tiene límite (figura 3.6).
Así mismo, si la función tiende a $±∞$ en un punto $a$ (figura 3.6, función $y=h(x)$), también se dice que no tiene límite; aunque en esos casos está permitido escribir:
$$\lim_{x \to a}{f(x)}= ±∞ $$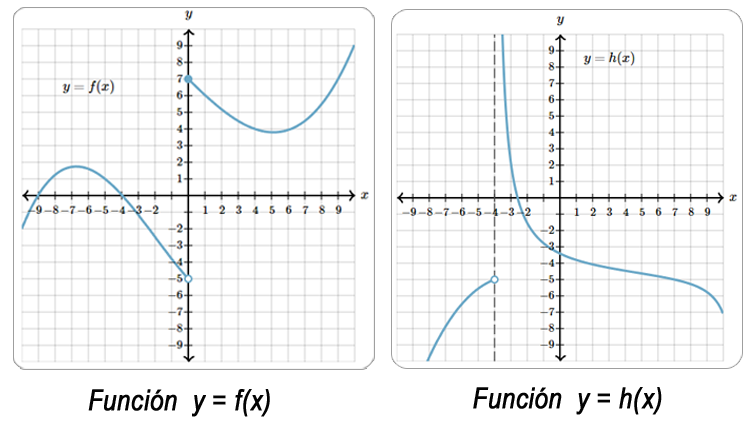
En la figura 3.6, se tiene que en la función $y=f(x)$, el límite $\lim\limits_{x \to{0}}{f(x)}$ no existe, ya que los límites laterales son diferentes,
$$\lim\limits_{x \to{0^-}}{f(x)} = -5 =\not \lim\limits_{x \to{0^+}}{f(x)}=7$$De igual forma, en la figura 3.6, se tiene que en la función $y=h(x)$, el límite tiende a $+∞$ por la derecha, o sea, $\lim\limits_{x \to{-4^+}}{f(x)}$ no tiene límite, y se puede expresar como:
$$\lim\limits_{x \to{-4^+}}{f(x)}= +∞$$
Para comprabar tus resultados, oprime el botón comprobar, genera un nuevo ejercicio, oprime el botón otra función
Escena de José R. Galo Sánchez y Mª José García Cebrián adaptada y modificada por el autor.
 En conclusión, el análisis de límites unilaterales es una técnica utilizada en cálculo para determinar el comportamiento de una función cuando se acerca a un valor $a$ específico desde un solo lado de la función.
En conclusión, el análisis de límites unilaterales es una técnica utilizada en cálculo para determinar el comportamiento de una función cuando se acerca a un valor $a$ específico desde un solo lado de la función.
Propiedades individuales de los límites, sean $f$, $g$ funciones tales que: $\lim\limits_{x \to{a}}{f(x) = L_1}$ y $\lim\limits_{x \to{a}}{g(x) = L_2},$ sea $k$ una constante, entonces, cada una de las siguientes afirmaciones es válida:
$\begin{aligned} \lim\limits_{x \to{2}}{\dfrac{5x^2+x+1}{3x-1}} &= {\dfrac{\lim\limits_{x \to{2}}(5x^2+x+1)}{\lim\limits_{x \to{2}}(3x-1)}} \quad \text{................... ley de cocientes} \\ &={\dfrac{\lim\limits_{x \to{2}}(5x^2) + \lim\limits_{x \to{2}}(x) + \lim\limits_{x \to{2}}(1)}{\lim\limits_{x \to{2}}(3x)- \lim\limits_{x \to{2}}(1)}} \quad\text{.... ley de la suma} \\ &={\dfrac{5(2)^2 + (2) +1}{3(2)-1}}= \frac{23}{5} \quad\text{........... ley de Constantes} \\ \text{y sustitución directa}\end{aligned}$
 No obstante, no todos los límites pueden ser evaluados por una sustitución directa, ya que puede suceder que no podemos hallar el límite al sustituir $x=a$
porque $f(a)$ no está definida en el dominio de la función.
No obstante, no todos los límites pueden ser evaluados por una sustitución directa, ya que puede suceder que no podemos hallar el límite al sustituir $x=a$
porque $f(a)$ no está definida en el dominio de la función.
Cuando resolvemos límites con frecuencia necesitamos operar con el infinito. Sin embargo, debemos recordar que el infinito no es un número. En algunas ocasiones lo vamos a operar como un número con el fin de encontrar límites, no obstante, debemos tener en cuenta que en muchas ocasiones el infinito no se comporta como un número.
Existen algunas ocasiones donde la operación con el infinito está indeterminada. Esta es una de esas ocasiones donde no se comporta como un número.

En muchas ocasiones. se presenta el cálculo de límites de cocientes, diferencias y productos de funciones en los que al reemplazar la variable por el valor al cual tiende se generan indeterminaciones, para resolverlos, se realizan procedimientos algebraicos adecuados que permitan salvar la indeterminación. Algunas de las indeterminaciones que se pueden presentar son del tipo:
$$\frac00, \space \frac{∞}{∞}, \space 0^0, \space ∞^0, \space 0\cdot ∞, \space ∞-∞$$Como primer paso para resolver cualquier límite es sustituir el valor de la variable $x$ por el número al que tienda y ver si se obtiene un valor por sustitución directa.
Es importante conocer el comportamiento de una función $f(x)$, cuando $x$ es un número positivo muy grande o negativo con valor absoluto muy grande, analicemos el comportamiento de una función, cuando $x$ toma valores muy grandes, por ejemplo:
Se tiene la función $f(x)= \dfrac{1}{x+1}$ cuando $x$ toma valores positivos muy grandes y cuando $x$ toma valores negativos de valor absoluto muy grandes.
Veamos los resultados en la tabla después de tabular para valores de $x$ y calculando los de $y$; cuando tenemos valores positivos muy grandes a $x$ y valores negativos con valor absoluto muy grandes, obtenemos la gráfica de la hipérbola que se muestra en la figura 3.8,
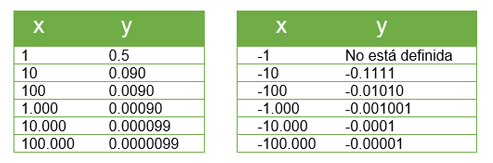
Al observar las tablas se ve que cuando $x$ toma valores positivos muy grandes, la función $f(x)= \dfrac{1}{x+1}$ se acerca al valor cero $(0)$, y cuando $x$ toma valores negativos de valor absoluto grandes, la función $f(x)$ también se acerca al valor cero $(0)$.
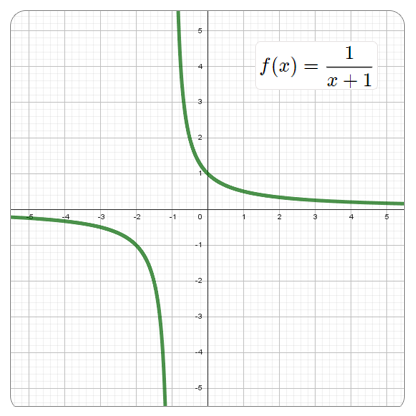

En el caso de la función $f(x)= \dfrac{1}{x+1}$, se expresa el límite como:
$$\quad\lim\limits_{x \to{+∞}}{\bigg(\dfrac{1}{x+1}\bigg)}=0$$Ahora, analicemos el caso para el comportamiento de funciones de la forma $f(x) = x^a$, con $a > 0$, cuando $x$ toma valores positivos muy grandes o valores negativos de valor absoluto muy grandes.
Para analizar este caso también nos valemos por un ejemplo, y a partir de los resultados encontrados, obtendremos reglas o leyes que nos permitan más adelante su aplicación directa.
Sea la función $f(x) = x^2$, analicemos el comportamiento de está cuando $x$ toma valores positivos muy grandes o valores negativos de valor absoluto grandes.
Tabulando la función, se obtienen los siguientes datos de la tabla, y su respectiva gráfica:
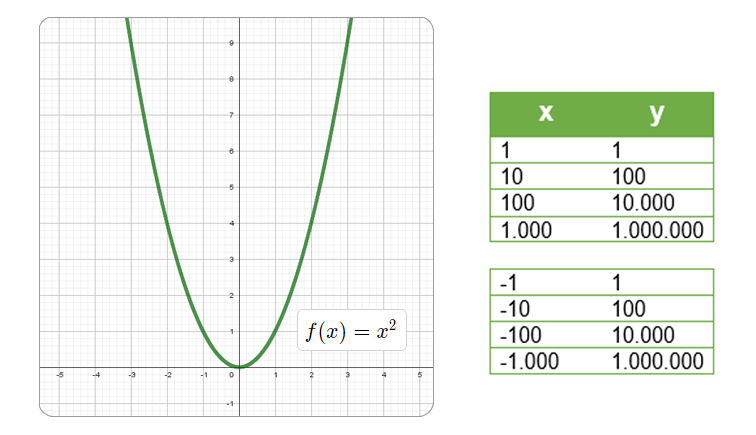
 Si se observan los datos de la tabla, vemos que cuando $x$ toma valores positivos muy grandes o valores absolutos de valor absoluto grandes, $f(x)$ no tiende a un valor determinado si no que aumenta en forma indeterminada, tanto hacia la derecha como hacia la izquierda de la función, lo cual se refeja en la gráfica, entonces se tiene que:
Si se observan los datos de la tabla, vemos que cuando $x$ toma valores positivos muy grandes o valores absolutos de valor absoluto grandes, $f(x)$ no tiende a un valor determinado si no que aumenta en forma indeterminada, tanto hacia la derecha como hacia la izquierda de la función, lo cual se refeja en la gráfica, entonces se tiene que:
Partimos del análisis del siguiente límite $\quad \displaystyle \lim_{x \to \infty} \dfrac{1}{x}$, si $x$ toma valores cada vez más grandes, $\frac{1}{x}$ es más pequeña, por ejemplo,
$$\quad\dfrac{1}{10}= 0,1, \space \dfrac{1}{100}= 0,01, \space \dfrac{1}{10000}= 0,0001$$
Por tanto, si tenemos a $x$ lo suficientemente grande, podemos hacer que $\dfrac{1}{x}$ sea tan cercana a $0$ como queramos, entonces, se tiene que:
$$\lim_{x \to \infty} \frac{1}{x} = 0$$Razonando de igual forma, si $x$ es grande negativa, $\dfrac{1}{x}$ es cercana a cero, por tanto, se obtiene una regla para límites que tienden a $\pm \infty$.
 Si $n$ es un entero positivo, se tiene que:
$$\lim_{x \to \pm\infty} \frac{1}{x} = 0$$
$$\text{si generalizamos, } \quad\lim_{x \to \pm\infty} \frac{1}{x^n} = 0$$
Si $n$ es un entero positivo, se tiene que:
$$\lim_{x \to \pm\infty} \frac{1}{x} = 0$$
$$\text{si generalizamos, } \quad\lim_{x \to \pm\infty} \frac{1}{x^n} = 0$$
Una forma de resolver límites que tienden al infinito, cuando se tiene una función $y=\dfrac{f(x)}{g(x)}$, se debe dividir tanto numerador como denominador por la potencia más grande de $x$ que se encuentre en la función, simplificando expresiones y aplicando las definiciones anteriores.
Dividimos por la mayor potencia de $x$, en este caso $x^2$
$$\lim_{x \to \infty} \dfrac{\dfrac{3x^2-2x+2}{x^2}}{\dfrac{6x^2-x+3}{x^2}} = \lim_{x \to \infty} \dfrac{\dfrac{3x^2}{x^2}-\dfrac{2x}{x^2}+\dfrac{2}{x^2}}{\frac{6x^2}{x^2}-\dfrac{x}{x^2}+\dfrac{3}{x^2}},$$simplificamos cada término que sea posible
$$= \lim_{x \to \infty} \dfrac{\dfrac{3\cancel{x^2}}{\cancel{x^2}}-\dfrac{2\cancel{x}}{x\cancel{^2}}+\dfrac{2}{x^2}}{\dfrac{6\cancel{x^2}}{\cancel{x^2}}-\dfrac{\cancel{x}}{x\cancel{^2}}+\dfrac{3}{x^2}} = \lim_{x \to \infty} \dfrac{\dfrac{3}{1}-\dfrac{2}{x}+\dfrac{2}{x^2}}{\dfrac{6}{1}-\dfrac{1}{x}+\dfrac{3}{x^2}},$$ahora, aplicando las leyes de los límites y distribuyendo en toda la expresión tenemos que:
$$\lim_{x \to \infty} \dfrac{3-\dfrac{2}{x}+\dfrac{2}{x^2}}{6-\dfrac{1}{x}+\dfrac{3}{x^2}} = \dfrac{\lim\limits_{x \to \infty}{3}- \lim\limits_{x \to \infty} \dfrac{2}{x}+ \lim\limits_{x \to \infty} \dfrac{2}{x^2}}{\lim\limits_{x \to \infty} 6 - \lim\limits_{x \to \infty} \dfrac{1}{x} + \lim\limits_{x \to \infty} \dfrac{3}{x^2}}$$y aplicando la definición, $\quad\lim\limits_{x \to \infty} {\dfrac{1}{x^n}} = 0$, obtenemos que:
$$\frac{3 - 0 + 0}{6 - 0 + 0} = \frac{3}{6} = \frac{1}{2}$$Por tanto, el límite existe y es igual a $\quad\lim\limits_{x \to \infty} {\dfrac{3x^2-2x+2}{6x^2-x+3}}=\dfrac{1}{2}$
Dividimos por la mayor potencia de $x$, en este caso $x^3$ $$\lim\limits_{x \to \infty} \dfrac{\dfrac{x^3+x}{x^3}}{\dfrac{4 - 5x}{x^3}} = \lim\limits_{x \to \infty} \dfrac{\dfrac{x^3}{x^3}+\dfrac{x}{x^3}}{\dfrac{4}{x^3}-\dfrac{5x}{x^3}} = \lim\limits_{x \to \infty} \dfrac{\cancel{\dfrac{x^3}{x^3}}+\dfrac{\cancel{x}}{x\cancel{^3}}}{\dfrac{4}{x^3}-\dfrac{\cancel{5x}}{x\cancel{^3}}} = \lim\limits_{x \to \infty} \dfrac{1+\dfrac{1}{x^2}}{\dfrac{4}{x^3}-\dfrac{5}{x^2}}$$
Aplicando las leyes y distribuyendo tenemos que: $$\dfrac{\lim\limits_{x \to \infty} 1+ \lim\limits_{x \to \infty} \dfrac{1}{x}}{4\lim\limits_{x \to \infty} \dfrac{1}{x^3} -5 \lim\limits_{x \to \infty} \dfrac{1}{x^2}} = \dfrac{1 + 0}{4(0) - 5(0)} = \dfrac{1}{0} = \infty,$$
por tanto, el límite no existe.
 Comprueba lo aprendido respondiendo a la pregunta.
Comprueba lo aprendido respondiendo a la pregunta.

Escribe en los recuadros la solución, en este caso, corresponde a una fracción $\dfrac{a}{b}$ y verificar pulsando la tecla "enter <┘", para generar un nuevo ejercicio, oprime el botón otro ejercicio
Escena de Juan Guillermo Rivera adaptada y modificada por el autor.

 ¡Piensa!... ¿Qué se puede deducir al solucionar limites donde $x \to \pm\infty$ de una función racional si en el numerador
y el denominador la máxima potencia es la misma? ¿se pueden deducir una definición con la solución de límites de funciones racionales?
¡Piensa!... ¿Qué se puede deducir al solucionar limites donde $x \to \pm\infty$ de una función racional si en el numerador
y el denominador la máxima potencia es la misma? ¿se pueden deducir una definición con la solución de límites de funciones racionales?
En la solución de límites, se pueden presentar, en algunas ocasiones, formas extrañas que no presentan ni dicen nada. Estas formas extrañas reciben el nombre de formas indeterminadas.
Veamos algunas indeterminaciones que se pueden presentar, ya sean en un punto o en el infinito y las formas de eliminarlas matemáticamente (para eliminar estas indeterminaciones debemos tener bien claros los temas sobre factorización y conjugada de una cantidad), veamos algunos casos que se pueden aplicar:
Descomponemos en factores los polinomios del numerador y del denominador, simplificando los factores comunes.
Primero se evalúa el límite por sustitución directa:
$$\lim_{x \to -4} \frac{x^2-16}{x+4}= \frac{(-4)^2-16}{(-4)+4}=\frac{0}{0},$$factorizamos el numerador utilizando diferencia de cuadrados y simplificamos los factores semejantes,
$$ \lim_{x \to -4} \frac{(x-4)\cancel{(x+4)}}{\cancel{(x+4)}}=\lim_{x \to -4} {(x-4)} = (-4)-4 = -8 $$$$\lim_{x \to -4} \frac{x^2-16}{x+4}= -8 $$
En ocasiones, los límites con indeterminación tienen raíces y en estos casos se dificulta factorizar los polinomios para eliminar factores del numerador y del denominador.
Para esta situación, se utiliza multiplicar el numerador y el denominador por el conjugado del binomio donde esté la raíz.

Si se tiene $\quad \sqrt{a}-\sqrt{b}$, su conjugado será: $\sqrt{a}+\sqrt{b}$, de está forma, al multiplicar por su conjugado, obtenemos que:
$$(\sqrt{a}-\sqrt{b}).(\sqrt{a}+\sqrt{b}) = (\sqrt{a})^2-(\sqrt{b})^2=a-b$$Primero se evalúa el límite por sustitución directa: $$\lim_{x \to 4} \frac{\sqrt{x}-2}{x-4}= \frac{\sqrt{4}-2}{4-4}= \frac{0}{0} $$
Simplificar una expresión que contiene radicales, en este caso, multiplicamos y dividimos toda la función por el conjugado del numerador, o sea, por $({\sqrt{x}+2})$
$$\lim_{x \to 4} \frac{(\sqrt{x}-2)(\sqrt{x}+2)}{(x-4)(\sqrt{x}+2)}= \lim_{x \to 4} \frac{(\sqrt{x})^2-(2)^2}{(x-4)(\sqrt{x}+2)}= $$
$$=\lim_{x \to 4} \frac{\cancel{(x-4)}}{\cancel{(x-4)}(\sqrt{x}+2)}= \frac{1}{\sqrt{4}+2} = \frac{1}{2+2} = \frac{1}{4} $$
Para este caso, realizamos las operaciones matemáticas que se presenten para llegar a una simplificación de una expresión equivalente.
Primero se evalúa el límite por sustitución directa:
$$\lim_{x \to 0} \dfrac{1 + \dfrac{4}{x}}{1 - \dfrac{2}{x}}= \dfrac{1 + \dfrac{4}{0}}{1 - \dfrac{2}{0}} $$Para eliminar la indeterminación en este caso, resolvemos la expresión racional y simplificamos los resultados.
$$\lim_{x \to 0} \dfrac{1 + \dfrac{4}{x}}{1 - \dfrac{2}{x}}= \lim_{x \to 0} \dfrac{\frac{x+4}{x}}{\dfrac{x-2}{x}} = \lim_{x \to 0} \dfrac{\cancel{x}.(x+4)}{\cancel{x}.(x-2)} $$ $$\lim_{x \to 0} \dfrac{x+4}{x-2} = \dfrac{0+4}{0-2} = \dfrac{4}{-2} = -2 $$ $$\lim_{x \to 0} \frac{1 + \dfrac{4}{x}}{1 - \dfrac{2}{x}}= -2$$Estudiaremos algunos límites que llamaremos especiales, que son de gran utilidad para la obtención de otros conceptos; tal es el caso de la derivada de las funciones trigonométricas.
Analicemos y evaluemos estos límites de funciones trigonométricas:
Evaluemos este límite, teniendo en cuenta que el ángulo de $\theta$ se mide en radianes.
Elaboremos una tabla, donde damos a $(\theta)$ valores por la izquierda y por la derecha, próximos a cero, y analicemos que sucede con la función
$$f(\theta) = \dfrac{Sen (\theta)}{\theta}$$Observando la tabla (figura 3.11), notamos que cuando $(\theta)$ toma valores próximos a cero $(0)$ tanto por la derecha como por la izquierda, $f(\theta)$ toma valores cada vez mas cercanos a $1$.
Por lo tanto, podemos asegurar que los límites trigonométricos se pueden calcular a partir de la siguiente fórmula:
 $$\lim\limits_{\theta \to 0} \dfrac{Sen (\theta)}{\theta} = 1$$
$$\lim\limits_{\theta \to 0} \dfrac{Sen (\theta)}{\theta} = 1$$
$$\lim_{\theta \to 0} \frac{Sen(\theta)}{7\theta} = \lim_{\theta \to 0} \frac{1}{7} \frac{Sen(\theta)}{\theta} = \frac{1}{7} \lim_{\theta \to 0} \frac{Sen(\theta)}{\theta} = \frac{1}{7} (1) = \frac{1}{7},$$ por lo tanto, $$\lim_{\theta \to 0} \frac{Sen(\theta)}{7\theta} = \frac{1}{7} $$
$$\lim_{\theta \to 0} \frac{Sen(5\theta)}{2\theta} = \lim_{\theta \to 0} \frac{1}{2} \frac{Sen(5\theta)}{\theta} = \frac{1}{2} \lim_{\theta \to 0} \frac{5}{5}\frac{Sen(5\theta)}{\theta} = $$ $$\frac{1}{2}(5) \bigg(\lim_{\theta \to 0} \frac{Sen(5\theta)}{5\theta} \bigg)= \frac{5}{2}(1) = \frac{5}{2} $$
Si reemplazamos a $\theta$ por cero ($0$) directamente, obtenemos una indeterminación de la forma $\dfrac00$, por lo que tenemos que eliminar dicha indeterminación.
Para eliminar esa indeterminación, multiplicamos y dividimos por la conjugada del numerador,
$$\begin{aligned}\lim\limits_{\theta \to 0} \dfrac{1-Cos(\theta)}{\theta} &= \lim\limits_{\theta \to 0} \dfrac{(1-Cos(\theta))}{\theta}\cdot\dfrac{(1+Cos(\theta))}{1+Cos(\theta)} \\ &= \lim\limits_{\theta \to 0} \dfrac{1-Cos^2(\theta)}{\theta \cdot(1+Cos(\theta))} = \lim\limits_{\theta \to 0} \dfrac{Sen^2(\theta)}{\theta \cdot(1+Cos(\theta))}, \end{aligned}$$distribuyendo el producto y aplicando leyes, tenemos que,
$$\lim\limits_{\theta \to 0} \dfrac{Sen^2(\theta)}{\theta \cdot(1+Cos(\theta))}=\lim\limits_{\theta \to 0} \dfrac{Sen(\theta)}{\theta} \cdot \lim\limits_{\theta \to 0} \dfrac{Sen(\theta)}{1+Cos(\theta)}$$

¡Recuerda!
Una indeterminación no significa que el límite no exista o no se pueda determinar, sino que la aplicación de las propiedades de los límites no es válida y podemos buscar una forma de eliminar esa indeterminación para que el límite exista.
Aplicando la ley de $\lim\limits_{\theta \to 0} \dfrac{Sen (\theta)}{\theta} = 1$ y evaluando el límite, tenemos que,
$$\bigg(\lim\limits_{\theta \to 0} \dfrac{Sen(\theta)}{\theta}\bigg) \cdot \lim\limits_{\theta \to 0} \dfrac{Sen(\theta)}{1+Cos(\theta)}= (1) \cdot \dfrac{Sen(0°)}{Cos(0°)+1}=(1)\cdot(0)$$
Por lo tanto, podemos asegurar que los límites trigonométricos se pueden calcular a partir de la siguiente fórmula:
 $$\lim\limits_{\theta \to 0} \dfrac{1-Cos(\theta)}{\theta} = 0$$
$$\lim\limits_{\theta \to 0} \dfrac{1-Cos(\theta)}{\theta} = 0$$
$$\lim_{x \to 0} \frac{x-x Cos(x)}{3x^2} = \lim_{x \to 0} (x).(\frac{1}{3}).\frac{1-Cos(x)}{x^2} = $$ $$ (\frac{1}{3}) \lim_{x \to 0} \cancel{x}.\frac{1-Cos(x)}{x^{\cancel{2}}} = (\frac{1}{3}) \lim_{x \to 0} \frac{1-Cos(x)}{x} = (\frac{1}{3})(0) = 0,$$ por lo tanto, $$\lim_{x \to 0} \frac{x-x Cos(x)}{3x^2} = 0$$
Sugerencias para calcular límites trigonométricos:

Escribe tu solución, puedes utilizar 2 decimales o fracción $\dfrac{a}{b}$ y verifica, pulsa la tecla "enter <┘", para continuar debe estar correcto.
Cuando la gráfica de una función se acerca a una recta, donde $x$ o $y$ tienden a infinito, dicha recta se llama asíntota de la función, y se clasifican en: verticales, horizontales y/o oblicuas, cabe notar, que no todas las funciones tienen rectas asíntotas.
Se dice que se tiene una asíntota vertical en $x=a$ si se cumple cualquiera de las siguientes afirmaciones:

Hasta el momento hemos analizado el límite de una función $f(x)$ cuando "$x \to a$" un número real $L$, sin embargo, también es posible analizar el comportamiento de una función $f(x)$, cuando $x$ toma valores cada vez más grandes, sean éstos positivos o negativos; es decir cuando ${x \to +\infty}$ o cuando ${x \to -\infty}$.
La recta $y=b$ es una asíntota horizontal de $f(x)$, si se cumple que:
$$ \lim_{x \to \pm\infty}f(x) = b$$Cuando la función $f(x)$ es el cociente de dos polinomios, y el grado del numerador supera en uno al del denominador, entonces, la curva $y=f(x)$ tiene una asíntota oblicua cuya ecuación es la función lineal $\quad y=mx+b, \quad$ con $\quad m =\not 0$, donde:
$$m=\lim_{x \to \infty}\frac{f(x)}{x} \qquad b= \lim_{x \to \infty}(f(x)- m(x))$$ xploremos.
xploremos.
Observa las gráficas de cada asintota, oprime el botón para cada caso. Mueve el punto y observa diferentes funciones.

Verificar si $f(x)$ es continua.
Izquierda, $\displaystyle \lim_{x \to a^-} f(x)=\lim_{x \to -1^-} x^2+1=(-1)^2+1=2$
Derecha, $\displaystyle \lim_{x \to a^+} f(x)=\lim_{x \to -1^+} 2x+4=2(-1)+4=2$
Como los límites laterales son iguales, el $\displaystyle \lim_{x \to -1} f(x)$ existe, además, se cumple que $f(x)=\displaystyle \lim_{x \to -1} f(x)$, entonces, $f(x)$ es continua en $x=-1$.
Si alguna de las condiciones para que una función sea continua no se cumple, se dice que $f$ es discontinua en el punto $x=a$. Una función que presenta discontinuidad, se puede clasificar en:
Discontinuidad removible.
Si se tiene que $f(a)$ no está definida, pero se cumple que el $\displaystyle\lim_{x \to a} f(x)$ existe, se dice que las discontinuidades son removibles o puntuales, para remover está discontinuidad basta con redefinir la función para $x=a$, por ejemplo:
La función cuya gráfica (figura 3.13) se presenta no es continua en el punto $x=0$ debido a que en ese punto la imagen para $x=0$ no está definida, pero el límite si existe, ya que:
$$\lim_{x \to 0^-} f(x)=\lim_{x \to 0^+} f(x)=4$$Si se tiene que $f(a)$ está definida y que el $\displaystyle \lim_{x \to a} f(x)$ existe, pero no se cumple la tercera condición, que $\displaystyle \lim_{x \to a} f(x)= f(a)$, se dice que la función tiene discontinuidad removible, por ejemplo:
La función cuya gráfica (figura 3.13) se presenta no es continua en el punto $x=0$ debido a que en ese punto la imagen para $x=0$ está definida, $$f(0)=2, \space\text{ además, el límite existe, ya que:}$$ $$\lim_{x \to 0^-} f(x)=\lim_{x \to 0^+} f(x)=4$$
$$\text{pero, no se cumple que } \lim_{x \to 0} f(x)= f(0)$$
Discontinuidad no removible.
Si se tiene que no se cumple la condición 2, que: $$\lim_{x \to a} f(x) \space no \space existe$$ se dice que la discontinuidad en NO removible, porque la gráfica de la función presenta un salto, por ejemplo:
La función cuya gráfica (figura3.13) se presenta no es continua en el punto $x=0$ debido a que en ese punto la imagen para $x=0$ está definida, $$f(0)=4$$ pero el límite no existe, ya que:
$$\lim_{x \to 0^-} f(x) \space \cancel{=} \lim_{x \to 0^+} f(x)$$
 Podremos suponer que la existencia de un límite es importante en la continuidad de una función, ya que, una función es continua en un intervalo, si es continua en cada punto de ese intervalo.
Podremos suponer que la existencia de un límite es importante en la continuidad de una función, ya que, una función es continua en un intervalo, si es continua en cada punto de ese intervalo.
Capitulo III. Sucesiones y límites
 Ejercicio práctico
Ejercicio práctico
Indicaciones
Escena de José R. Galo Sánchez y Mª José García Cebrian adaptadas por el autor.
 Evaluamos lo aprendido
Evaluamos lo aprendido
Prepárate para la evaluación y mide tus conocimientos de lo aprendido en este capítulo, responde las preguntas a continuación:

 Actividad complementaria.
Actividad complementaria.
$\space$ Descargar para imprimir
Capitulo III. Sucesiones y límites
 Evaluación. 10 preguntas con límite de tiempo (Máx. 10 minutos)
Clic en el link, responde y envía tus respuestas por correo.
Evaluación. 10 preguntas con límite de tiempo (Máx. 10 minutos)
Clic en el link, responde y envía tus respuestas por correo.
 Tomada de la Red Educativa Digital Descartes.
Tomada de la Red Educativa Digital Descartes.
"Lo que sabemos es una gota,
lo que ignoramos es un océano!.".
Newton

DERECHOS BÁSICOS DE APRENDIZAJE (DBA)
DBA.3. Utiliza instrumentos, unidades de medida, sus relaciones y la noción de derivada como razón de cambio, para resolver problemas, estimar cantidades y juzgar la pertinencia de las soluciones de acuerdo al contexto.
DBA.5. Interpreta la noción de derivada como razón de cambio y como valor de la pendiente de la tangente a una curva y desarrolla métodos para hallar las derivadas de algunas funciones básicas en contextos matemáticos y no matemáticos.
DBA.8. Encuentra derivadas de funciones, reconoce sus propiedades y las utiliza para resolver problemas.
DBA.9. Plantea y resuelve situaciones problemáticas del contexto real y matemático que implican la exploración de posibles asociaciones o correlaciones entre las variables estudiadas.
DESEMPEÑOS / ESTANDAR
Componente 1 - Pensamiento numérico.
1.4 M.V Utilizo argumentos de la teoría de números para justificar relaciones que involucran números naturales. DBA 3, 5.
Componente 3 - Pensamiento métrico y sistemas de medidas.
3.2 M.V Resuelvo y formulo problemas que involucren magnitudes cuyos valores medios se suelen definir indirectamente como razones entre valores de otras magnitudes, como la velocidad media, la aceleración media y la densidad media. DBA 8.
Componente 5 - Pensamiento Variacional.
5.2 M.V Interpreto la noción de derivada como razón de cambio y como valor de la pendiente de la tangente a una curva y desarrollo métodos para hallar las derivadas de algunas funciones básicas en contextos matemáticos y no matemáticos. DBA 4, 9.

El desarrollo de estos Estándares Básicos de Competencia permitirá fortalecer los procesos de formulación, modelación y resolución de problemas.
Derechos Básicos de Aprendizaje.
Capitulo IV. La derivada y antiderivada
Los inventores del Cálculo.
 En el último tercio del siglo XVII, Newton en 1664 - 1666 y Leibniz en 1675 inventaron el Cálculo, ellos hicierón:
En el último tercio del siglo XVII, Newton en 1664 - 1666 y Leibniz en 1675 inventaron el Cálculo, ellos hicierón:
1. Unificaron y resumieron en dos conceptos generales, el de integral y derivada, la gran variedad de técnicas diversas y de problemas que se abordaban con métodos particulares.
2. Desarrollaron un simbolismo y unas reglas formales de cálculo que podían aplicarse a funciones algebraicas y trascendentes, independientes de cualquier significado geométrico, que hacía casi automático, el uso de dichos conceptos generales.
3. Reconocieron la relación inversa fundamental entre la derivación y la integración.


En 1666 el método inverso de fluxiones y la relación entre cuadraturas y fluxiones. En esos dos años también inició las teorías de los colores y de la gravitación universal. Newton tenía 24 años.
Newton desarrolló tres versiones de su cálculo. En la obra De Analysi per aequationes numero terminorum infinitas, que Newton entregó a su maestro Barrow en 1669, y que puede considerarse el escrito fundacional del Cálculo, Newton usa conceptos infinitesimales de manera similar a como hacía el propio Barrow.
Una segunda presentación del Cálculo es la que realiza Newton en el libro Methodus fluxionum et serierum infinitorum, escrito hacia 1671 y que se publicó mucho después en 1736. Newton considera cantidades variables que van fluyendo con el tiempo, a las que llama fluentes.
Newton llamó a nuestra derivada una - fluxión - una razón de cambio o flujo; Leibniz vio la derivada como una razón de diferencias infinitesimales y la llamó el cociente diferencial. Newton hizo sus primeros descubrimientos diez años antes que Leibniz quien, sin embargo, fue el primero en publicar sus resultados.
Los principales datos matemáticos de Newton en el campo del cálculo infinitesimal datan de los llamados Anni Mirabiles 1665 y 1666. La Universidad de Cambridge, en la que Newton se había graduado como bachelor of arts en 1664, estuvo cerrada por la peste esos dos años. Newton pasó ese tiempo en su casa de Woolsthorpe y, como él mismo reconoció cincuenta años después, ése fue el período más creativo de su vida.
A principios de 1665 descubre el teorema del binomio y el cálculo con las series ifinitas. A finales de ese mismo año, el método de fluxiones, es decir, el cálculo de derivadas.
 Un problema que dio origen al concepto de derivada fue el de determinar la velocidad instantánea de un objeto que se mueve de una manera conocida.
Un problema que dio origen al concepto de derivada fue el de determinar la velocidad instantánea de un objeto que se mueve de una manera conocida.
Consideremos, por ejemplo, el caso de una piedra que dejamos caer desde lo alto de un edificio: vemos caer la piedra en línea recta, pero la ecuación que describe la posición de la piedra en cada instante de la caída es:
$$S = f(t) = -\dfrac12 gt^2,$$donde $S$ es el espacio recorrido en metros $(m)$, $t$ es el tiempo transcurrido en segundos $(s)$ y la gravedad $(g)$, $\quad g \approx 10 \space{m}/{s^2}$.
Esta ecuación evidentemente no es de una línea recta, por lo tanto, una cosa es la forma cómo se mueve un objeto y otra la ecuación que describe su posición en un instante dado.
 Supongamos, en general, que un objeto se mueve de acuerdo con la ecuación $S = f(t)$, donde $S$ se mide en metros, $t$ en segundos y la dirección positiva es hacia arriba o hacia la derecha. Supongamos también que la trayectoria del cuerpo es la que muestra la figura.
Supongamos, en general, que un objeto se mueve de acuerdo con la ecuación $S = f(t)$, donde $S$ se mide en metros, $t$ en segundos y la dirección positiva es hacia arriba o hacia la derecha. Supongamos también que la trayectoria del cuerpo es la que muestra la figura.
¿Cuál será la velocidad instantánea de la partícula en el momento $t = t_1$ segundos?
Para contestar la pregunta, supongamos que el objeto ocupa, en el instante $t_1$, la posición $S_1 = f(t)$ y que $h$ segundos después, es decir, en el instante $t_2 = t_1 + h$ ocupa la posición $S_2 = f(t_2) = f(t_1 + h)$.
Con estos dos datos podemos calcular la velocidad media ($V_m$) entre los dos instantes; así:
$$V_{media}= \dfrac{posición_{final}-posición_{inicial}}{tiempo_{final}-tiempo_{inicial}}$$ $$V_m=\dfrac{f(t_1 + h) - f(t_1)}{t_1 + h - t_1} = \dfrac{f(t_1 + h) - f(t_1)}{h}$$Ahora bien, si el valor de “$h$” lo vamos reduciendo cada vez, entonces la diferencia de tiempo entre $t_1$ y $t_1 + h$ es muy pequeña y podemos pensar en definir la velocidad instantánea $(V_i)$ en el tiempo $t_1$ como el límite de la velocidad media cuando "$h$" se aproxima a cero, es decir:
$$V_i = \lim\limits_{h \to 0} \dfrac{f(t_1+h) - f(t_1)}{h}$$ Si una función describe el cambio de posición en el tiempo de un móvil entonces la derivada se podrá interpretar como la velocidad del móvil esto es, el cambio instantáneo de la posición del móvil en el tiempo.
Si una función describe el cambio de posición en el tiempo de un móvil entonces la derivada se podrá interpretar como la velocidad del móvil esto es, el cambio instantáneo de la posición del móvil en el tiempo.
La figura nos describe la trayectoria de la partícula cuando se mueve hacia atrás y hacia delante a lo largo de una recta:

La parte curveada de la trayectoria a en realidad no existe y sólo indica que la partícula invierte el sentido.
Hallemos inicialmente la velocidad instantánea en cualquier momento $t_1$ y, luego, calculemos el valor de dicha velocidad en $t = 4 \space s$ y en $t = 2 \space s$.
$$V_i = \lim\limits_{h \to 0} \dfrac{f(t_1+h) - f(t_1)}{h}$$ $$V_i =\lim_{h \to 0} \frac{2(t_1+h)^2-12(t_1+h)+10-(2{t_1}^2-12t_1+10)}{h}$$ $$V_i =\lim_{h \to 0} \frac{\cancel{2{t_1}^2}+4t_1h + 2h^2-\cancel{12t_1}- 12h +\cancel{10} -\cancel{2{t_1}^2} +\cancel{12t_1}-\cancel{10}}{h}$$ $$V_i =\lim_{h \to 0} \frac{4t_1h + 2h^2 - 12h}{h} = \lim_{h \to 0} \frac{\cancel{h\space}(4t_1+2h-12)}{\cancel{h\space}},$$Evaluando el límite, se tiene que:
$$V_i =\lim\limits_{h \to 0}(4t_1+\cancel{2h}-12)=4t_1-12,$$por tanto, la velocidad instantanea en $t=t_1$ es:
$$ V_i =4t_1-12$$Ahora, calculemos el valor de dicha velocidad en:
Además, la velocidad es cero cuando $\quad 4t_1 – 12 = 0$; es decir, cuando $t_1 = \dfrac{12}{4}= 3 s$, por tanto, en $t= 3\space s$.
Este ejemplo nos muestra que a veces la velocidad puede ser negativa. Para el movimiento horizontal consideramos la velocidad como negativa cuando el objeto se mueve hacia la izquierda y como positiva cuando el objeto se mueve hacia la derecha.
En este caso, el objeto se mueve primero en sentido negativo, y en $t = 3 \space s$, la velocidad es cero al invertir el objeto su sentido.
 En el caso de un objeto que se lanza al aire verticalmente, generalmente consideramos la velocidad como positiva mientras se está elevando, cero en su altura máxima y negativa cuando cae.
En el caso de un objeto que se lanza al aire verticalmente, generalmente consideramos la velocidad como positiva mientras se está elevando, cero en su altura máxima y negativa cuando cae.

¡Recuerda! 
No confundir la rapidez de un objeto con su velocidad. La rapidez es solo el valor absoluto o módulo de la velocidad e indica lo rapido que se mueve el objeto, mientras que la velocidad indica también el sentido del movimiento.
Ahora, vamos a resolver el primero de los problemas que dio lugar al concepto de derivada, el problema de hallar la recta tangente a una curva en un punto específico de la misma.
Comenzaremos recordando que la geometría griega nos dice que:
"Si la curva es una circunferencia, la recta tangente en un punto $P$ la definimos como la recta que tiene un solo punto común con la circunferencia".
Vamos ahora a definir la recta tangente a una curva en un punto $P$ de la misma. Para ello necesitamos hallar la pendiente de dicha recta, pues ya tenemos el punto ($P$) y bastaría simplemente aplicar la ecuación punto – pendiente.
Para hallar la pendiente de la recta tangente a la curva en el punto $P(x, f(x))$ hacemos lo siguiente:
Consideramos sobre la curva otro punto $Q$, distinto de $P$, de abscisa $x_1 = x + h$.
Dibujamos la recta secante $\overline{PQ}$ y llamamos “$\beta$“ el ángulo que forma con la dirección positiva del eje $x$.
Sea $f$ una función continua en $x$ cuya gráfica vemos en la escena:
Desplace el punto $P$ o el punto $Q$, la escena ilustra la pendiente de la recta tangente (recta azul) a una función $y=f(x)$ en el punto $(x,f(x))$ que está dada por $\quad m = \lim\limits_{h \to 0} \dfrac{f(x+h) - f(x)}{h}$.
Por lo tanto, la pendiente de la recta tangente a la curva en P es el límite de la pendiente de la recta secante PQ cuando “h” tiende a cero. Según esto podemos definir la recta tangente como la recta que pasa por $P$ y tiene pendiente $m(x)$ dada por la expresión anterior.
Capitulo IV. La derivada y antiderivada
Los matemáticos del siglo $XVII$ y posteriores encontraron estos problemas fundamentales que dieron lugar al concepto de la derivada, particularmente aquellos que implicaban determinar la intensidad del cambio instantaneo de una variable respecto a otra, estos podían resolverse utilizando el mismo concepto y tuvieron la misma solución, por lo tanto, a la solución de todos estos problemas se le dio el nombre común de derivada, la cual definiremos y trabajaremos en este capítulo.

Definición de la derivada
Sea $f$ una función real, la derivada de $f$ es otra función que simbolizaremos por $f'$ y tal que su valor en cualquier punto $x = x_1$ de su dominio está dado por la expresión:
$$f'(x_1) = \lim\limits_{h \to 0} \dfrac{f(x_1+h) - f(x_1)}{h},$$ siempre que este límite exista.El símbolo utilizado para denotar la derivada es $f'(x)$, esto significa que la derivada es una nueva función que al ser evaluada en un punto particular, es un número que representa la pendiente de la recta tangente a $f(x)$ en ese punto; análogamente si $f(t)$ es la ecuación del movimiento de una partícula, entonces $f'(t)$ evaluada en un tiempo $t$ representa la velocidad instantánea de la partícula en $t$.
Otros símbolos que utilizaremos para denotar la derivada son los siguientes:
aplicando la definición de la derivada, se tiene que:
$$\lim_{h \to 0} \frac{7(x+h)^2+3(x+h)-4-(7x^2+3x-4)}{h}=$$ $$\lim_{h \to 0} \frac{\cancel{7x^2}+14xh+7h^2+\cancel{3x}+3h -\cancel{4\space} -\cancel{7x^2} -\cancel{3x}+\cancel{4\space}}{h}=$$ $$\lim_{h \to 0} \frac{14xh+7h^2+3h}{h} = \lim_{h \to 0} \frac{\cancel{h\space}(14x+7h+3)}{\cancel{h\space}},$$evaluando el límite, se tiene que:
$$\lim_{h \to 0}(14x+\cancel{7h}+3)= 14x+3,$$por tanto, la derivada de la función $f$ es: $\qquad y'=14x+3$
Dada la función de la posición $(S)$: $\quad S = – 16t^2 + 100$.
La velocidad es la derivada de la función de posición, donde la velocidad instantánea, está dada, de acuerdo con la fórmula:
$$S'(t) = V_i = \lim\limits_{h \to 0} \dfrac{S(t_1+h) - S(t_1)}{h}$$ $$V_i =\lim_{h \to 0} \frac{-16(t_1+h)^2-100-(-16{t_1}^2+100)}{h}=$$ $$V_i =\lim_{h \to 0} \frac{-16({t_1}^2+2t_1h +h^2)+\cancel{100} + 16{t_1}^2-\cancel{100}}{h}=$$ $$V_i =\lim_{h \to 0} \frac{\cancel{-16{t_1}^2} - 32t_1h - 16h^2 + \cancel{16{t_1}}^2}{h}=$$ $$V_i =\lim_{h \to 0} \frac{\cancel{h\space} (-32t_1 - 16h)}{\cancel{h\space}}= -32t_1 -16(0) = -32t_1$$Luego, la velocidad instantánea $V_i$ para

Matemáticamente, la velocidad instantánea es la tasa de cambio del desplazamiento con respecto al tiempo en un momento determinado.
$\dfrac{d}{dt} S(t),\space$ derivada del desplazamiento $(S)$ con respecto al tiempo $(t)$.

¡Recuerda! 
En cálculo, la velocidad instantánea es la derivada de la función de la posición con respecto al tiempo o, de forma equivalente, puede definirse como el límite de la velocidad media a medida que el intervalo de tiempo se aproxima a cero.
La aceleración instantánea describe la tasa de cambio de la velocidad de un objeto en un instante determinado, de otra forma, es el límite de la aceleración media a medida que el intervalo de tiempo se aproxima a cero.
$\dfrac{d}{dt} V(t),\space$ derivada de la velocidad $(V)$ con respecto al tiempo $(t)$.
Las fórmulas de la velocidad instantanea y la aceleración instantánea se expresan como:
$$V_i(t) = \dfrac{d}{dt}S(t) = S'(t)$$ $${\Large {a}}(t) = \dfrac{d}{dt}V(t) = V'(t)$$Las derivadas de funciones algebraicas, se han realizado utilizando el límite, que a veces resulta un poco complicado, por tal motivo, se trabajarán algunas propiedades que faciliten el cálculo de estas, para llegar a una solución más rapida, para ello, partiremos de la definición de la derivada $f'(x) = \lim\limits_{h \to 0} \dfrac{f(x+h) - f(x)}{h},$ demostrando una primera propiedad y asumiendo las demas como validas.
Propiedad. Derivada de una potencia de $x$
Si $f(x) = x^n \quad \Rightarrow \quad f'(x) = nx^{n-1}$
Si $f$ es una función tal que $f(x) = x^n$, donde $n \in \mathbb{R}$, entonces, aplicando la definición de la derivada para un punto $x$, se tiene:
$$f'(x) = \lim\limits_{h \to 0} \dfrac{f(x+h) - f(x)}{h}= \lim\limits_{h \to 0} \dfrac{{(x+h)}^n - {(x)}^n}{h},$$desarrollando para ${(x+h)}^n$ el binomio de newton, se tiene:
$$f'(x) = \lim\limits_{h \to 0} \dfrac{x^n + nx^{n-1}h + h^2(...) - x^n}{h} = \lim\limits_{h \to 0} \dfrac{\cancel{h\space} (nx^{n-1} + h(...))}{\cancel{h\space}},$$por tanto, evaluando el límite, $\quad\lim\limits_{h \to 0} {(nx^{n-1} + h(...))} = nx^{n-1}$
En general, si $f(x) = x^n$, entonces, $f'(x) = nx^{n-1}$.
$$\textcolor{ForestGreen}{\Large\star}\quad \text{Si } n = 1, \quad f(x) = x \quad \Rightarrow \quad f'(x) = 1, \text{ porque, } x^{1-1} = x^0 = 1.$$
Propiedad. Derivada de una función constante.
Si $c \in \mathbb{R}$ y $f(x) = c \quad \Rightarrow \quad f'(x) = 0$
Interpretacion geometrica, como la función constante es una línea recta paralela al eje $x$, al hallar su derivada estamos encontrando su pendiente, donde la pendiente de una recta paralela el eje $x$ es cero, por tanto, su derivada será cero.
 La multiplicación de una constante por una función establece que la derivada de una constante multiplicada por una función es igual a la constante multiplicada por la derivada de la función.
La multiplicación de una constante por una función establece que la derivada de una constante multiplicada por una función es igual a la constante multiplicada por la derivada de la función.
Propiedad. Derivada de una suma de funciones.
Si $f$ y $g$ son dos funciones tales que $f'(x)$ y $g'(x)$ existen,
$ y = f(x) + g(x) \quad \Rightarrow \quad y' = f'(x) + g'(x)$
Según esta propiedad, para derivar una suma debemos derivar cada sumando además, esta se puede extenderse a una suma o resta, donde, se pueden tener dos o más sumandos.
$$\textcolor{ForestGreen}{\Large\star}\quad \text{Si } y = f(x) + g(x) – h(x) \quad \Rightarrow \quad y' = f'(x) + g'(x) – h'(x)$$Aplicando la propiedad 3, derivada de suma de funciones, se tiene que: $$f'(x) = \dfrac{d\space (5x^2)}{dx}− \dfrac{d\space (2x)}{dx} + \dfrac{d\space (3)}{dx},$$
propiedad 2, función constante, se tiene que:
$$f'(x) = 5 \cdot\dfrac{d\space (x^2)}{dx}− 2\cdot\dfrac{d\space (x)}{dx} + \cancel{\dfrac{d\space (3)}{dx}}^0,$$propiedad 1, función potencia, se tiene que:
$$f'(x) = 10\cdot x^{2-1}− 2\cdot x^{\cancel{1-1}^0},$$por tanto, la derivada de $f(x)$ es, $\quad f'(x) = 10x -2$
Expresamos a $f$ como una potencia, $\quad f(x) = \sqrt{x} = x^{\frac12},$
aplicando propiedad 1, función potencia, se tiene que:
$$f'(x) = \frac12 x^{\frac12-1} = \frac12\cdot x^{-\frac12}= \frac12\cdot \dfrac{1}{x^{\frac12}},$$por tanto, la derivada de $f(x)$ es, $\quad f'(x) = \dfrac{1}{{2\sqrt{x}}}$
Propiedad. Derivada de un producto de funciones.
Si $f$ y $g$ son dos funciones tales que $f'(x)$ y $g'(x)$ existen,
$ y = f(x) \cdot g(x) \space \Rightarrow \space y' = f'(x)\cdot g(x) + f(x) \cdot g'(x)$
Expresado en palabras, la derivada de un producto de funciones es igual a la derivada de la primera función por la segunda función, más la primera función por la derivada de la segunda función.
Organicemos cada función y su derivada:
$f(x) = 2x^3+5, \quad$ su derivada es:
$f'(x) = 6x^2$.
$g(x) = x^2− 2x, \quad$ su derivada es:
$g'(x) = 2x - 2$.
Expresemos en la formula, $\quad y' = f'(x)\cdot g(x) + f(x) \cdot g'(x)$,
$$y' = 6x^2\cdot (x^2− 2x) + (2x^3+5) \cdot (2x - 2),$$ $$y' = 6x^4− 12x^3 + 4x^4 - 4x^3 +10x -10,$$por tanto, la solución es: $\quad y' = 10x^4− 16x^3 +10x -10$
Propiedad. Derivada de un cociente de funciones.
Si $f$ y $g$ son dos funciones tales que $f'(x)$ y $g'(x)$ existen,
$ y = \dfrac{f(x)}{g(x)} \space \Rightarrow \space y' = \dfrac{f'(x)\cdot g(x) - f(x) \cdot g'(x)}{[g(x)]^2}$
Expresado en palabras, la derivada de un cociente de dos funciones es (la segunda función, por la derivada de la primera función, menos la primera función por la derivada de la segunda función) entre la segunda función al cuadrado.
Organicemos cada función y su derivada:
$f(x) = 2x^3+5, \quad$ su derivada es:
$f'(x) = 6x^2$.
$g(x) = x^2− 2x, \quad$ su derivada es:
$g'(x) = 2x - 2$.
Expresemos en la formula, $\quad y' = \dfrac{f'(x)\cdot g(x) - f(x) \cdot g'(x)}{[g(x)]^2}$,
$$y' = \dfrac{6x^2\cdot (x^2− 2x) - (2x^3+5) \cdot (2x - 2)}{(x^2− 2x)^2}= $$por tanto, la solución es: $\quad y' = \dfrac{2x^4 − 8x^3 - 10x + 10}{(x^2− 2x)^2} $

Problema de la recta tangente, si en el ejemplo anterior, evaluamos a $x$ en la derivada, en un punto dado $P(-1, 1)$, obtenemos la pendiente ($m$) de la recta tangente a la curva $y$ en dicho punto, o sea,
$$ m = y'(-1)$$ $$ m = \dfrac{2x^4 − 8x^3 - 10x + 10}{(x^2− 2x)^2} $$ $$m = \dfrac{2(-1)^4 − 8(-1)^3 - 10(-1) + 10}{[(-1)^2− 2(-1)]^2} =\dfrac{2 + 8 + 10 + 10}{[1+2]^2}= \dfrac{30}{9},$$por tanto, la pendiente de la recta tangente es: $\quad m = \dfrac{10}{3} $
Ahora, conocida la pendiente $(m)$ y el punto $P$, se puede encontrar la ecuación de la recta tangente a la curva $y$ aplicando la expresión punto-pendiente: $$y - y_1 = m(x - x_1)$$
Remplazando el punto y la pendiente en la formula, se tiene que:
$$y - 1 = \dfrac{10}{3}(x + 1) \space \Rightarrow \space y = \dfrac{10}{3}x +\dfrac{10}{3}+1$$Por lo tanto, la ecuación de la recta tangenta a la curva $y = \dfrac {2x^3+5}{x^2− 2x}$ en el punto $P(-1, 1)$ es: $\quad y = \dfrac{10}{3}x +\dfrac{13}{3}$
A continuación puedes ver representadas gráficamente la curva $y$ y su recta tangente en en punto $P$:
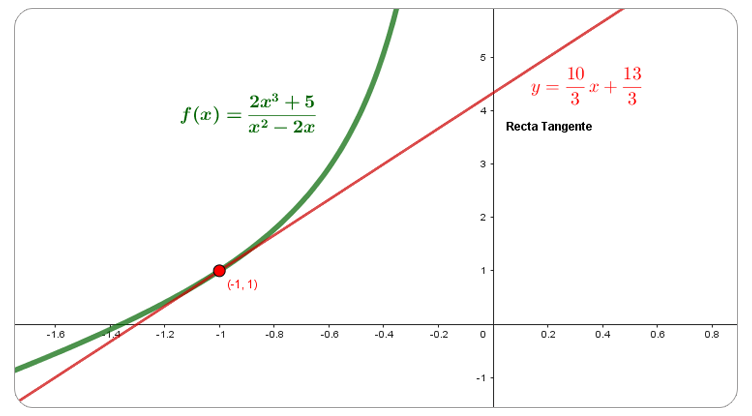

¡Recuerda! 
La ecuación de la recta tangente y la curva siempre tienen un punto en común, que en este caso es $x = -1$. Por tanto, como la curva $y = f(x)$ pasa por este punto, si no se conociera la otra componente, o sea la componente en $y$, podemos hallarla calculando el punto $f(-1)$.
Para terminar el estudio de las propiedades básicas de la derivada nos falta discutir una de las propiedades más importantes de derivadas, llamada la regla de la cadena.
Acá la palabra ”cadena” se refiere a las funciones que se componen de otras funciones como formando una cadena, que definimos como funciones compuestas.
Si se tiene la expresión: $\quad y = f(g(x)), \quad$ una función dentro de otra función, ¿cuál será la derivada de $y$ con respecto a $x$?
Consideremos dos funciones derivables $y = f (u)$ y $u = g (x)$ cuya función compuesta es $\quad y = f(g(x)), \quad$.
Como una derivada indica una “razón de cambio”, podemos decir que:
$\Rightarrow \space y$ cambia $\dfrac{dy}{du}$ veces más rápido que $u$.
$\Rightarrow \space u$ cambia $\dfrac{du}{dx}$ veces más rápido que $x$.
Por lo tanto, parece lógico pensar que: $\quad y$ cambia $\dfrac{dy}{dx}$ veces más rápido que $x$, lo cual equivale a decir:
$$\dfrac{dy}{dx} = \dfrac{dy}{du} \cdot \dfrac{du}{dx}$$Esta expresión es llamada la regla de la cadena.
Propiedad. Regla de la cadena.
Si $y = f (u)$ es una función derivable de $u$ y $u = g (x)$ es una función derivable de $x$, entonces,
$y = f (g (x))$ es una función derivable de $x$ tal que:
$\dfrac{dy}{dx} = \dfrac{dy}{du} \cdot \dfrac{du}{dx}$
Consideremos, por ejemplo la siguiente función:
Una forma de hacerlo sería desarrollando la expresión $(7x – 8)^5$ y luego calcular $\dfrac{dy}{dx}$, pero desarrollar $(7x – 8)^5$ sería muy tedioso por lo cual debemos es más facil utilizar la regla de la cadena para calcular la derivada de esta, que corresponde a una función compuesta.
Esta función podemos expresarla como la compuesta de dos funciones; así:
$u = g(x) = 7x-8,\quad$ derivada de $ u'(x) = 7,$
ahora, $\quad y = f(u) = u^5,\quad$ derivada de $f$, $\quad f'(u) = 5u^4,$
por tanto, $\quad\dfrac{dy}{dx} = f'(u)\cdot u'(x)=5u^4 \cdot 7 $
La derivada de $y = (7x - 8)^5 \space \Rightarrow \space \dfrac{dy}{dx}= 35(7x-8)^4$
La función del ejemplo 4.8, presenta el tipo más común de función compuesta; es decir, funciones de la forma:
$$y = [u(x)]^n$$Este tipo de funciones puede derivarse utilizando un caso particular de la regla de la cadena denominado regla general de la cadena de las potencias, donde se tiene que:
Si $y = [ u (x) ]^n$, donde $u$ es una función derivada de $x$ y $n$ es un número real, entonces: $$\textcolor{ForestGreen}{\Large\star}\quad \text{Si } y = [ u (x) ]^n \quad \Rightarrow \quad \dfrac{dy}{dx} = n [u(x)]^{n-1}\cdot u'(x) $$
Expresemos la raiz como una potencia:
$$\quad y = \sqrt[3]{2x^2+5x-3}=(2x^2+5x-3)^{\frac13}$$Aplicamos regla general de la cadena de las potencias, se tiene que:
$$u(x)= 2x^2+5x-3$$ $$ \text{La derivada de u(x) es: } \quad u'(x)= 4x+5$$ $$\dfrac{dy}{dx} = \dfrac13 \cdot (2x^2+5x-3)^{\frac13-1}\cdot (4x+5)$$por tanto, la derivada de $\quad y = \sqrt[3]{2x^2+5x-3}$
$$\dfrac{dy}{dx} = \dfrac{4x+5}{3(2x^2+5x-3)^{\frac23}}$$Hemos visto que si $f(x)$ es una función, entonces, su derivada $f'(x)$ también es una función.
Si derivamos de nuevo a $f'(x)$, obtenemos la segunda derivada de $f(x)$ y la denotamos $f''(x)$. Si luego derivamos a $f''(x)$, obtenemos la tercera derivada de $f(x)$, la cual denotamos $f'''(x)$, en general:
| Derivadas de orden superior |
|---|
Sea $f$ una función diferenciable en $x$, entonces $\quad y'= f'(x)= \frac{dy}{dx},\hspace{1cm}$ Primera derivada. $\quad y''= f''(x)= \frac{d^2y}{dx^2},\hspace{0.7cm}$ Segunda derivada. $\quad y'''= f'''(x)= \frac{d^3y}{dx^3},\hspace{0.6cm}$ Tercera derivada. |

$f'(x) = 20x^3 -6x^2, \quad$ primera derivada.
$f''(x) = 60x^2 - 12x, \quad$ segunda derivada.
Por tanto, $\quad f''(x) = 120x - 12, \quad$ tercera derivada.

Se tiene la función $S(t)= 5t^2 + 3t – 4$, que representa la posición de una partícula en el instante $t$, entonces, $V= S'(t),\space$ que representa la derivada del desplazamiento $S$ con respecto al tiempo $t$.
Sea $S(t)= 5t^2 + 3t – 4$
$\textcolor{ForestGreen}{\Large\star}\quad $ Velocidad $V(t)$ cuando han transcurrido un tiempo $t = 2$ segundos
$V(t)= S'(t) = 10t+3, \quad \text{donde, }\\ V(2) = 10(2) + 3 = 23 \space m / s \quad \Rightarrow \quad V(2) = 23 \space m / s$
$\textcolor{ForestGreen}{\Large\star}\quad $ Aceleración ${\Large {a}}(t)$ cuando han transcurrido un tiempo $t = 2$ segundos
${\Large {a}}(t) = V' (t)= S''(t),\space$ que representa la segunda derivada del desplazamiento $S$ con respecto al tiempo $t$ o la derivada de la velocidad $V$ con respecto al tiempo $t$.
${\Large {a}}(t)=V'(t)= S''(t) = 10, \quad \text{donde, }\\ {\Large {a}}(2) = 10 \space m / s^2 $
| Funciones | Derivadas | 1. $\quad y=e^x$ | $\space y'=e^x$ |
|---|---|
| 2. $\quad \displaystyle y=b^x,\quad $ con $\quad b \in \mathbb{R}$ | $\space y'=b^x \cdot\ln(b)$ |
| 3. $\quad y=\ln|x|$ | $\space \displaystyle y'=\frac{1}{x}$ |
| 4. $\quad \displaystyle y=\log_b(x),\quad $ con $\quad b \in \mathbb{R}$ | $\space \displaystyle y'=\frac{1}{x\cdot\ln(b)}$ |
Aplicando la derivada de función logarítmica, se tiene que:
$$\frac{dy}{dx}=\frac{1}{x\cdot\ln(3)},$$ahora derivamos de nuevo y hallamos la segunda derivada, donde, reorganizando la expresión se tiene que:
$$\frac{1}{\ln(3)}\cdot \frac{dy}{dx}=\frac{1}{x}=x^{-1},$$por tanto, aplicando regla de la potencia, las segunda derivada es:
$$\frac{1}{\ln(3)}\cdot \frac{d^2y}{dx^2}=\frac{(-1)}{x^2} \quad \Rightarrow \quad \frac{d^2y}{dx^2}=-\frac{1}{\ln(3)x^2}$$Aplicando la derivada de función exponencial, se tiene que:
$$y'=3^x \cdot(\ln(3)) \enspace \Rightarrow \enspace y'=\ln(3) 3^x$$Las propiedades de los logaritmos, pueden ser aplicadas para simplificar una función al momento de obtener su derivada. Estas propiedades se aplican a logaritmos o logarítmos naturales.
Como se tiene una función un poco compleja para derivar, se pueden utilizar las
Aplicando regla de la cadena y derivando a ambos lados:
$$\frac1y \frac{dy}{dx}= \frac15 \bigg(\frac{6x}{3x^2-9}\bigg) - \frac15 \bigg(\frac{4x}{2x^2+4}\bigg)$$ $$\frac{dy}{dx}= \frac{y}{5} \bigg[\bigg(\frac{6x}{3x^2-9}\bigg) - \bigg(\frac{4x}{2x^2+4}\bigg)\bigg]$$ $$y'= \frac15 \sqrt[5]{\dfrac{3x^2-9}{2x^2+4}} \cdot \bigg[\bigg(\frac{6x}{3x^2-9}\bigg) - \bigg(\frac{4x}{2x^2+4}\bigg)\bigg]$$A esta derivada logarítmica se le llama derivada implícita. Se realiza la derivada de una función, en este caso $y$, sin especificar lo que vale $y$ como función de $x$.
 La función exponencial y logarítmica tienen gran cantidad de aplicaciones en la vida cotidiana y no tan cotidiana. Muchos fenómenos naturales y sociales están regidos por leyes en cuya expresión aparece la función exponencial.
La función exponencial y logarítmica tienen gran cantidad de aplicaciones en la vida cotidiana y no tan cotidiana. Muchos fenómenos naturales y sociales están regidos por leyes en cuya expresión aparece la función exponencial.
Este tipo de funciones son de gran importancia en el estudio de la física, la química, la biología, la estadística, la economía y muchas otras aplicaciones.
| Funciones | Derivadas |
|---|---|
| 1. $\quad y=Sen(x)$ | $\space y'=Cos(x)$ |
| 2. $\quad y=Cos(x)$ | $\space y'=-Sen(x)$ |
| 3. $\quad y=Tan(x)$ | $\space y'=Sec^2(x)$ |
| 4. $\quad y=Cot(x)$ | $\space y'=-Csc^2(x)$ |
| 5. $\quad y=Sec(x)$ | $\space y'=Sec(x)Tan(x)$ |
| 6. $\quad y=Csc(x)$ | $\space y'=-Csc(x)Cot(x)$ |
 ¡Piensa!...
¿Por qué?, en las funciones trigonométricas, la derivada de la función $y=Cot(x)$ es igual a $y'=-Csc^2(x).$
¡Piensa!...
¿Por qué?, en las funciones trigonométricas, la derivada de la función $y=Cot(x)$ es igual a $y'=-Csc^2(x).$
Las funciones trigonométricas, $Tan(x)$, $Cot(x)$, $Sec(x)$ y $Csc(x)$ se pueden escribirse en términos de $Sen(x)$ y $Cos(x)$; por lo tanto, para hallar sus derivadas bastará aplicar la derivada de un cociente y utilizar derivadas de $Sen(x)$ y $Cos(x)$.
Veamos que, $\quad y'=-Csc^2(x) \space$ es la derivada de $\space y=Cot(x)$
¿Por qué? $\space$ Tenemos la identidad trigonométrica:
 $$y=Cot(x)=\frac{cos(x)}{sen(x)},$$
entonces, aplicando la propiedad de cociente de funciones, se tiene que:
$$y=Cot(x)=\frac{cos(x)}{sen(x)},$$
entonces, aplicando la propiedad de cociente de funciones, se tiene que:

¡Recuerda!
Tener en cuenta que las funciones trigonométricas con exponentes se pueden expresar de dos formas, por ejemplo,
$$Sen^3(x) =(Sen(x))^3$$La función $f(x)$ se deriva utilizando regla de la cadena:
$\quad f(x) = Cot(u),\quad \text{derivada }\quad f'(u) = -Csc^2(u)$,
donde $\quad u= x^3,\quad \text{derivada }\quad u'(x)= 3x^2$
por tanto, $f'(x)= f'(u)\cdot u'(x)= -Csc^2(u)\cdot(3x^2)$
La derivada de $f(x) = Cot(x^3)\space\Rightarrow \space f'(x)= -(3x^2)Csc^2(x^3)$
A continuación, se presenta un mapa conceptual como resumen del camino que hemos tomado en el estudio de las derivadas:

Selecciona un tipo de función, observa y resuelve el ejercicio propuesto, oprima el botón solución y verificar tu respuesta; genera otro ejercicio, oprima el botón ejercicio o cambia de tipo de función.
Escena de Miguel Ángel Cabezon, licencia CC by-nc-sa, adaptada y modificada por el autor.
Hasta el momento las funciones consideradas las hemos expresado en forma explicita; es decir, la función $f$ está definida por una ecuación de la forma $y = f (x)$ donde la “$y$” aparece de forma despejada, por ejemplo, $\enspace y = 5x^3-2x+1$
Sin embargo, hay expresiones que relacionan a “$x$” y “$y$” mediante ecuaciones de la forma $f(x,y) = 0$. En estos casos, la expresión ha sido definida en forma implicita, por ejemplo, $\enspace 5xy = x^3+y^2$
¿Cómo se halla la derivada implícita $y'=\dfrac{dy}{dx}$ de una función definida implícitamente por $f(x,y)=0$?
Si fuera posible escribir $y$ explícitamente a partir de $f(x,y)=0$, o sea, despejar $y$ en términos de $x$, es posible que sea sencillo hallar $\dfrac{dy}{dx}$ con las propiedades básicas de diferenciación.
 La cuestión es que, no siempre es posible obtener una forma explícita $y=f(x)$, aunque fuera posible despejar $y$ explícitamente, puede suceder que la derivada sea más complicada o dispendiosa.
La cuestión es que, no siempre es posible obtener una forma explícita $y=f(x)$, aunque fuera posible despejar $y$ explícitamente, puede suceder que la derivada sea más complicada o dispendiosa.
Directrices para diferenciación implícita:
Está expresión resulta más complicada expresarla explícitamente, por tal motivo derivamos cada término de la siguiente forma:
Derivar la forma implícita 2$x^3+y^2=6xy$ con respecto a $x$ aplicando las propiedades, cuando se derive a $y$ se multiplica por $\dfrac{dy}{dx}$: $$6x^2+2y \cdot\bigg(\frac{dy}{dx}\bigg)=6(1)y+6x(1).\bigg(\frac{dy}{dx}\bigg)$$ $\hspace{3.8cm}\color{LimeGreen}\uparrow\underline{\color{LimeGreen}\hspace{1.0cm}{\quad\frac{dy}{dx}}\hspace{1.3cm}}\hspace{0.0cm}\uparrow\\$
Ahora, llevamos todos los términos que contengan el factor $\dfrac{dy}{dx}$ al lado izquierdo de la igualdad, los demás al lado derecho: $$2y\bigg(\frac{dy}{dx}\bigg)-6x\bigg(\frac{dy}{dx}\bigg)=6y-6x^2$$
Por último, se factoriza y simplifica, despejando el diferencial $\frac{dy}{dx}$:
$$\bigg(\frac{dy}{dx}\bigg)\cancel{2}(y-3x)=\cancel{6}(y-x^2) \space\Rightarrow \space y'= \frac{dy}{dx}=\frac{3(y-x^2)}{y-3x}$$$$\frac{d}{dx}(x^2+y^2)=\frac{d}{dx}(25) \\ 2x+2y.\bigg(\frac{dy}{dx}\bigg)=0\\ 2y.\bigg(\frac{dy}{dx}\bigg)=-2x$$ $$\frac{dy}{dx}=-\frac{x}{y},$$
por lo tanto, la pendiente de la recta tangente ala curva en el punto $P(3,4)$, $\enspace m=\frac{dy}{dx} \bigg|_{(3,4)}=-\frac{3}{4} \space\Rightarrow \space m=-\frac{3}{4},$
ahora, con la pendiente $m$ y el punto $P$, utilizamos la ecuación punto-pendiente, se tiene: $$y-4=-\frac{3}{4}(x-3)\\ y=-\frac{3}{4}x +\frac{9}{4}+4,$$
entonces, la ecuación de la recta tangente en el punto $P(3,4)$ al círculo $x^2+y^2=25$ es: $$y=-\frac{3}{4}x +\frac{25}{4}$$

 ¡Piensa!... ¿Se puede encontrar la ecuación de la recta normal en el mismo punto
por donde pasa la tangente?
¡Piensa!... ¿Se puede encontrar la ecuación de la recta normal en el mismo punto
por donde pasa la tangente?

Encuentra la derivada implícita de la función que se plantea, oprima el botón solución para verificar tu respuesta.
Para generar un nuevo ejercicio, oprima el botón otro ejercicio.

 Resumen de propiedades y reglas.
Resumen de propiedades y reglas.
$\space$ Descargar para imprimir
En muchas situaciones de la vida real se presentan varias variables, cada una de las cuales están relacionadas con el tiempo y a su vez están relacionadas entre sí a través de alguna ecuación, por ejemplo, el caso de un globo esférico el cual se infla mediante la acción de algún gas.
En este caso el volumen de un globo en un instante $t$ cualquiera es: $\enspace V = \dfrac43 \pi R^3, \enspace$ donde $V$ es el volumen y $R$ el radio.

Las variables $V$ y $R$ están relacionadas mediante la ecuación del volúmen y cada una de ellas está relacionada con el tiempo desde el momento en que se inició el inflado, entonces, las funciones $V$ y $R$ están relacionadas con una tercera variable $t$, el tiempo.
Otro ejemplo similar, puede suceder con el interés producido por un capital determinado a una tabla fija de interés está relacionado con este capital y, a su vez, tanto el capital como los intereses varían con el tiempo.
En estos casos el cálculo diferencial es de gran utilidad para conocer la rapidez con la que están cambiando las variables por unidad de tiempo en un instante particular.
La razón de cambio es la proporción en la que una variable cambia con respecto a otra, de manera más explícita es como en el tiempo unas componentes cambian a medida que el tiempo transcurre.
En conclusión, podemos expresar que, si dos cantidades están relacionadas entre sí, entonces cuando una de ellas cambia con el tiempo, la otra también cambiará, por lo tanto, sus razones de cambio (con respecto al tiempo) están relacionadas entre sí. A está situaciones se les llama razones de cambio relacionadas.
La derivada $\dfrac{dy}{dx}$ de una función $y=f(x)$ es una razón de cambio instantánea con respecto a la variable $x$. Veamos algunos problemas como ejemplo de razón de cambio en un tiempo $t$.
Se debe tener presente que las variables del volumen como el radio varían con el tiempo, esto quiere decir, que $V$ y $R$ son funciones de $t$.
El volumen de una esfera esta dado por la expresión:
$\enspace V = \dfrac43 \pi R^3, \enspace$ entonces, se tiene que la derivada $\dfrac{dV}{dt}$ y $\dfrac{dR}{dt}$ son razones de cambio instantáneas con respecto a la variable $t$.
$\enspace \dfrac{dV}{dt} = \dfrac{4}{\cancel{3}} \pi \cancel{3}R^2 \dfrac{dR}{dt} \quad\Rightarrow \quad \dfrac{dV}{dt} = 4\pi R^2 \dfrac{dR}{dt}$
Se conoce que el volumen aumenta proporcionalmente a razón de $\enspace \dfrac{dV}{dt}=4\space m^3/seg$
Despejando $\dfrac{dR}{dt}$ de la expresión hallada y remplazando los valores dados, se tiene que:
$\dfrac{dV}{dt} = 4\pi R^2 \dfrac{dR}{dt} \enspace\Rightarrow \enspace \dfrac{dR}{dt}=\dfrac{\dfrac{dV}{dt}}{4\pi R^2} \space\Rightarrow \space \dfrac{dR}{dt}=\dfrac{4\space m^3/seg}{4(3.14) (2\space m)^2} $
$\dfrac{dR}{dt}=\dfrac{\cancel{4\space} \dfrac{m^{\cancel{3}}}{seg}}{\cancel{16}\pi \space \cancel{m^2}} = \dfrac{1}{4\pi}\dfrac{m}{seg} \approx 0.080 \space m/seg $

Respuesta. La rapidez con que cambia el radio cuando este es de $2\space m$ es:
$\space\dfrac{dR}{dt} = \dfrac{1}{4\pi} m/seg \approx 0.080 \space m/seg $
El volumen de un cilíndro esta dado por la expresión:
$V = \pi R^2h, \enspace$ donde, se conoce que el volumen se está llenando a razón de $\enspace \dfrac{dV}{dt}=20\space m^3/h \quad$ y el radio $R=4\space m$
Derivando la altura la altura $(h)$ en un instante $t$ (en relación al tiempo) de la expresión del volumen del cilindro, se tiene que:
$\dfrac{dV}{dt} = \pi (4)^2 \dfrac{dh}{dt} \enspace\Rightarrow \enspace \dfrac{dV}{dt} = 16\pi \dfrac{dh}{dt}$
Despejando $\dfrac{dh}{dt}$ y remplazando los valores dados, se tiene que: $\dfrac{dh}{dt} = \dfrac{\cancel{20}^5}{\cancel{16}^4\pi} m/h = \dfrac{5}{4\pi}m/h$
Respuesta. La rapidez con que cambia la altura $h$ en un instante $t$ cualquiera es: $\enspace\dfrac{dh}{dt} = \dfrac{5}{4\pi}m/h \approx 0.40 \space m/h$
Consideremos la ecuación del área de un circulo: $\enspace A = \pi R^2$
Si derivamos respecto a $t$, se tiene que:$\enspace \dfrac{dA}{dt} = 2\pi R\dfrac{dR}{dt},$
donde, tenemos que $\enspace\dfrac{dR}{dt}=1\space cm/seg$ y el radio $r = 4\space cm,$
por tanto, sustituyendo y simplificando los valores, se tiene que: $\enspace \dfrac{dA}{dt} = 2\pi (4\space cm)(1\space \dfrac{cm}{seg})= 8\pi\space cm^2/seg$

Respuesta. El área total circular crece a ritmo de: $$\dfrac{dA}{dt} = 8\pi\space \dfrac{cm^2}{seg} \approx 25.12 \space cm^2/seg $$

Lea detenidamente el problema, realice los cálculos con su debido procedimiento. Para actualizar otros valores oprime el botón.
En esta ultima sección del libro, solo se aboradará el concepto de la antiderivada de funciones algebraicas, también conocida como integral indefinida y sus reglas básicas desde los más simple, ya que es un tema correspondiente al cáculo integral que estudia temas de un nivel más avanzado tratados en los inicios universitarios.
 La antiderivada es la función que resulta del proceso inverso de la derivada, es decir, consiste en encontrar una función que, al ser derivada produce la función dada.
La antiderivada es la función que resulta del proceso inverso de la derivada, es decir, consiste en encontrar una función que, al ser derivada produce la función dada.
El concepto de la antiderivada se abordara para funciones $y=f(x)$, donde $f(x)$ son funciones de tipo algebraicas.

¡Recuerda!
Una función algebraica es aquella que puede expresarse mediante un número finito de términos usando las operaciones básicas de adición, sustracción, multiplicación, división, potenciación y radicación. Un ejemplo de una función de tipo algebraico es: $\quad f(x) = 5x^3 + 2x^2 -x +3$.
Una función $F(x)$ recibe el nombre de antiderivada de $f(x)$ sobre un intervalo $[a, b]$, para todo $x$ que pertenece a un intervalo $[a, b]$:
$$\text{Si } F'(x)=f(x) \space \text {para todo x en I}$$Así, decimos que $F(x)$ es una primitiva de la función $f(x)$ si su derivada es precisamente la función $f(x)$.
Cualquier antiderivada de $f$ debe ser de la forma $H(x)= F(x) + C$ ($C$ es llamada constante de integración), es decir, dos antiderivadas de la misma función pueden diferir a lo más en una constante. por lo tanto, $F(x) + C$ es la antiderivada más genp>eral de $f(x)$.
Integral indefinida de funciones algebraicas
El proceso de encontrar una antiderivada se denomina antidiferenciación o integración, donde, al número $C$ se le denomina constante de integración.
El símbolo $\int$ fue introducido por Leibniz, denominado signo integral, y para denotar la integral indefinida, por conveniencia, se introducirá la notación para una antiderivada de una función.
 La notación $\displaystyle\int f(x)\, dx$ se denomina integral indefinida de $f(x)$ respecto a $x$, la función $f(x)$ se llama integrando.
La notación $\displaystyle\int f(x)\, dx$ se denomina integral indefinida de $f(x)$ respecto a $x$, la función $f(x)$ se llama integrando.
Interpretacion geometrica, la integral indefinida resuelve el problema de encontrar una curva de la cual se conoce su derivada $f(x)$. Dicha curva no es unica. La integral indefinida de $f(x)$ entrega todas las funciones cuya derivada es $f(x)$, donde $\displaystyle \int f(x)\, dx = F(x)+C$, siendo $F(x)$ una antiderivada de $f(x)$
La notación $F(x) + C$ representa una familia de funciones; cada una tiene una derivada igual a $f(x)$, solo cambia la constante $C$, por ejemplo, la antiderivada más general de $f(x)=2x$ es la familia $F(x)=x^2 + C$.
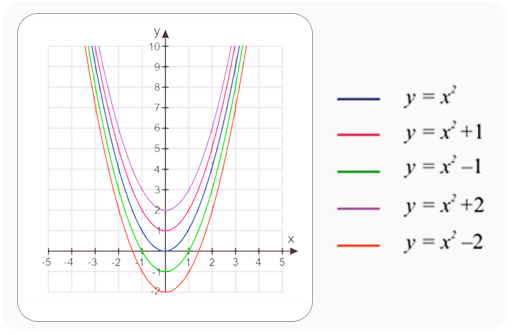
La colección de todas las funciones de la forma $x^2 + C$, donde $C$ es cualquier número real, se conoce como la familia de antiderivadas de $y= 2x$. La figura 4.6 muestra las gráficas de algunas de esta familia de antiderivadas.
 xploremos.
xploremos.
Observar las gráfica de la función propuesta, además, las gráficas de la familia de primitivas generadas de su integral.
Escena de Juan Guillermo Rivera Berrío y Consolación Ruiz Gil, adaptada y modificada por el autor.
La evaluación de integrales indefinidas para algunas funciones de tipo algebraico es un cálculo sencillo. Siempre que se obtiene la derivada de una función, al mismo tiempo se obtiene una fórmula de integración, por ejemplo, para algunas funciones, la evaluación de integrales indefinidas se sigue directamente de las propiedades de los derivados.
La siguiente tabla enumera las integrales indefinidas para este tipo de funciones algebraicas, además, su fórmula derivada.
| Fórmula de integración | Fórmula de derivación |
|---|---|
| 1. $\displaystyle \int x^n\, dx = \frac{x^{n+1}}{n+1} + C$ | $\quad\displaystyle\frac{d}{dx} \frac{x^{n+1}}{n+1} = x^n$ |
| 2. $\displaystyle\int \, dx = x + C$ | $\quad\displaystyle\frac{d}{dx} x=1$ |
| 3. $\displaystyle \int k\, dx = k \int \, dx = k\cdot x + C$ $\enspace$ donde $k$ es cualquier constante. | $\quad\displaystyle\frac{d}{dx}(k) = 0$ |
| 4. $\displaystyle \int kf(x)\, dx = k\cdot F(x) + C$ $\enspace$ donde $k$ es cualquier constante. | $\quad\displaystyle\frac{d}{dx} k\cdot \frac{x^{n+1}}{n+1} = k\cdot x^n$ |
| 5. $\displaystyle\int \frac{1}{x}\, dx = Ln(x) + C$ | $\quad\displaystyle\frac{d}{dx} Ln(x) = \frac{1}{x}$ |
| 6. $\displaystyle\int [f(x)\pm g(x)] \, dx = \int f(x) \, dx \pm \int g(x) \, dx$, $\quad$ donde las constantes $C_1 \pm C_2$ se sustituye por una simple $C$. | |
Aplicando las propiedades básicas de la integral, se tiene que:
Aplicamos propiedad 6, suma o diferencia de funciones,
$$= \int 5x^3 \, dx + \int 2x^2 \, dx - \int x \, dx + \int 4 \, dx ,$$ahora, utilizamos la propiedad 3 de las constantes, y se tiene que:
$$ = 5\int x^3 \, dx + 2\int x^2 \, dx - \int x \, dx + 4\int \, dx ,$$por ultimo, aplicamos propiedad 1, $\displaystyle \int x^n\, dx = \frac{x^{n+1}}{n+1} + C$ para potencias, realizando la integración:
$$ = 5\frac{x^4}{4} + 2\frac{x^3}{3} - \frac{x^2}{2} + 4x + C,$$por tanto, el resultado de la integral es:
$$\int (5x^3 +2x^2-x +4) \, dx = \frac{5}{4}x^4 + \frac{2}{3}x^3 - \frac{1}{2}x^2 + 4x + C$$
¡Recuerda!
Como la integral es el proceso inverso de la derivada (antiderivada), el resultado obtenido al ser derivado, se obtine la función inicial, comprueba estos resultados aplicando la derivada.

Utiliza las formulas y propiedades para calcular la integral indefinida propuesta y verifica el resultado obtenido, oprime el botón solución, para generar un nuevo ejercicio, oprime el botón otro ejercicio y repite los pasos anteriores.
Escena de Juan Guillermo Rivera Berrío, adaptada y modificada por el autor.
Es fundamental tener siempre presente que la integral indefinida de una función es “un conjunto de funciones”.
Capitulo IV. La derivada y antiderivada
 Ejercicio práctico
Ejercicio práctico
Indicaciones

¡Recuerda!
La derivada nos puede dar un valor instantáneo preciso de la tasa de cambio y nos conduce a modelar de forma precisa la cantidad deseada. La integral de una función se puede interpretar geométricamente como el área bajo la curva de una función matemática $f(x)$ trazada como una función de $x$.
 Evaluamos lo aprendido
Evaluamos lo aprendido
Prepárate para la evaluación y mide tus conocimientos de lo aprendido en este capítulo, responde las preguntas a continuación:

 Actividad complementaria.
Actividad complementaria.
$\space$ Descargar para imprimir
Capitulo IV. La derivada y antiderivada
 Evaluación. 10 preguntas con límite de tiempo (Máx. 10 minutos)
Clic en el link, responde y envía tus respuestas por correo.
Evaluación. 10 preguntas con límite de tiempo (Máx. 10 minutos)
Clic en el link, responde y envía tus respuestas por correo.
 Tomada de la Red Educativa Digital Descartes.
Tomada de la Red Educativa Digital Descartes.
Números Naturales, $\ \mathbb{N} = \{1,2,3,4,...\}$
Números Enteros, $\ \mathbb{Z} = \{ ..., - 4 ,-3,-2,-1,0,1,2,3,4,...\}$
Enteros negativos, $\ \mathbb{Z}^- =\{ ..., - 4 ,-3,-2,-1 \}$
Enteros positivos (números naturales), $\ \mathbb{Z}^+ = \{ 1, 2, 3, 4, 5 ,...\}$
Enteros no negativos (números enteros),
$\ \mathbb{Z}^+ \ \cup \ \{0\} = \{0, 1, 2, 3, 4, 5 ,...\}$
Números racionales ($\ \mathbb{Q} \ $),
es un número en la forma $\dfrac{p}{q}$, donde $p$ y $q =\not 0$ son enteros.
Números irracionales ($\ \mathbb{Q^*} \ $),
es un número que no puede escribirse en la forma $\dfrac{p}{q}$, donde $p$ y $q =\not 0$ son enteros.
Números reales ($\ \mathbb{R} \ $), El conjunto $\mathbb{R}$ de números reales es la unión de los conjuntos de números racionales e irracionales.
Leyes de las potencias, $a^n \cdot a^m = a^{n+m}$ $\dfrac{a^n}{a^m} = a^{n-m}$ $(a^n)^m = a^{n\cdot m}$ $\bigg(\dfrac{a}{b}\bigg)^n = \dfrac{a^n}{b^n}$ |
Exponentes racionales y radicales, $\sqrt [n]{a}= a^{\frac{1}{n}}$ $\sqrt [n]{a^m}= (\sqrt [n]{a})^m = a^{\frac{m}{n}}$ $\sqrt [n]{ab}= \sqrt [n]{a} \sqrt [n]{b} = (a b)^{\frac{1}{n}}$ $\sqrt [n]{\dfrac{a}{b}}= \dfrac{\sqrt [n]{a}}{\sqrt [n]{b}}$ |
Repaso para matemáticas.
Propiedades de las desigualdades, Si $\ a > 0 \quad {\displaystyle \longrightarrow } \quad \dfrac{1}{a} > 0. \hspace{1.7cm}$ Si $\ a < 0 \quad {\displaystyle \longrightarrow }\quad \dfrac{1}{a} < 0$ Si $\ a < b \ $ y $\ b < c \quad {\displaystyle \longrightarrow } \quad a < c. \hspace{0.7cm} $ Si $\ a ≤ b \quad \longleftrightarrow \quad a ± c ≤ b ± c$ Si $\ a > 0 \ $ y $ \ b > 0 \quad {\displaystyle \longrightarrow } \quad a ≤ b \quad \longleftrightarrow \quad \dfrac{1}{a} ≥ \dfrac{1}{b}$ Si $\ a ≤ b \ $ y $ \ c ≤ d \quad {\displaystyle \longrightarrow }\quad a + c ≤ b + d $ $\quad c > 0 \quad {\displaystyle \longrightarrow } \quad a ≤ b \quad \longleftrightarrow \quad ca ≤ cb$
$\quad c < 0 \quad {\displaystyle \longrightarrow }\quad a ≤ b \quad \longleftrightarrow \quad ca ≥ cb$
|
|
| Valor absoluto,
$|a| = \begin{cases} a &\text{si } a ≥ 0 \\ -a &\text{si } a < 0 \end{cases} $ |
Desigualdad triangular,
$| a + b | ≤ |a| + |b|$
|
Propiedades del valor absoluto, Si $\ |ax + b|< c, \quad$ entonces $\quad -c < ax + b < c$ Si $\ |ax + b|≤ c, \quad$ entonces $\quad -c ≤ ax + b ≤ c$ Si $\ |ax + b|> c, \quad$ entonces $\quad ax + b > c \quad 0 \quad ax + b < -c$ Si $\ |ax + b|≥ c, \quad$ entonces $\quad ax + b ≥ c \quad 0 \quad ax + b ≥ -c$ |
|
Repaso para matemáticas.
Fórmula cuadrática, Las raíces de una ecuación cuadrática $\quad ax^2 + bx + c= 0 \quad$ con $\quad a=\not 0,$ $ x = \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}$ |
|
| Fórmulas de factorización,
$a^2 - b^2 = (a + b)(a - b)$ $a^3 - b^3 = (a - b)(a^2 + ab + b^2)$ $a^3 + b^3 = (a + b)(a^2 - ab + b^2)$ |
Expansiones binomiales,
$(a \pm b)^2 = a^2 \pm 2ab + b^2$ $(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$ $a^3 + b^3 = (a + b)(a^2 - ab + b^2)$ |
Leyes de los logaritmos, $\hspace{1.5cm} \text{logaritmo natural, } \log_e (x) =\ln(x)$ $\log_b{b}= 1.$ $\hspace{5cm} \ln(e)=\ln_e(e)=1$ $\log_b{b^c}= c$. $\hspace{4.8cm} \ln(e^c)= \log_e(e^c)= c$ $\log_b{1}= 0$. $\hspace{5cm} \ln (1) = \log_e(1) = 0$ $\log_b{(m\cdot n)} = \log_b{(m)} + \log_b{(n)}$. $\log_b{\frac{m}{n}} = \log_b{(m)} - \log_b{(n)}$. $\log_b{(m^n)} = n \log_b{(m)}$. $\log_b\sqrt[n]{m} = {\frac{1}{m}}\cdot \log_b(m)$ Cambio de base, $\ \log_b(m)=\dfrac{\log_n(m)}{\log_n(b)}$ |
Reglas de la derivada.
| Reglas básicas de la derivada | Derivadas | 1.$\quad$ Función potencia de $x$ $\qquad$ Si $\space f(x) = x^n$ | $\ f'(x) = nx^{n-1}$ |
|---|---|
| $\hspace{0.7cm}$ Si $\space f(x) = x$ | $\space f'(x) = 1$ |
| 2. $\quad$ Función constante.
$\qquad$Si $\space c \in \mathbb{R}$ y $f(x) = c$ | $\space f'(x) = 0$ |
| $\hspace{0.7cm}$ Si $\space y = c\cdot f(x)$ | $\space y' = c\cdot f'(x)$ |
| 3. $\quad$ Suma o diferencia de funciones.
$\qquad$ $y = f(x) \pm g(x) \pm ...$ | $y' = f'(x) \pm g'(x) \pm...$ |
| 4. $\quad$ Producto de funciones.
$\qquad$ $y = f(x) \cdot g(x)$ | $y' = f'(x)g(x) + f(x)g'(x)$ |
| 5. $\quad$ División de funciones.
$\qquad$ $y = \dfrac{f(x)}{g(x)}$ | $y' = \dfrac{f'(x)g(x) - f(x)g'(x)}{[g(x)]^2}$ | Derivadas de orden superior |
| $y'= f'(x)= \dfrac{dy}{dx}, \hspace{0.7cm}$ Primera derivada, $y''= f''(x)= \dfrac{d^2y}{dx^2}, \quad$ Segunda derivada, $y'''= f'''(x)= \dfrac{d^3y}{dx^3}, \quad$ Tercera derivada, $\ \ . \ \ . \ \ .$ | |
Reglas de la derivada.
| Regla de la cadena. | |
|---|---|
| 6. $\quad$ Si $\ y = f (u)$ es una función derivable de $u$ y $u = g (x)$ es una función derivable de $x$, entonces, $y = f (g (x))$ es una función derivable de $x$ tal que: | |
si $\ y = [ u (x) ]^n \quad \Rightarrow \quad \dfrac{dy}{dx} = n [u(x)]^{n-1}\cdot u'(x) $ | |
En general, derivadas de las funciones cuando se aplica regla de la cadena: Potencias Logaritmo natural Función exponencial Euler Exponencial Radical Trigonométricas |
| Función Exponencial - logaritmica | Derivadas | 1. $\quad y=e^x$ | $\space y'=e^x$ |
|---|---|
| 2. $\quad \displaystyle y=b^x,\quad $ con $\quad b \in \mathbb{R}$ | $\space y'=b^x \cdot\ln(b)$ |
| 3. $\quad y=\ln|x|$ | $\space \displaystyle y'=\frac{1}{x}$ |
| 4. $\quad \displaystyle y=\log_b(x),\quad $ con $\quad b \in \mathbb{R}$ | $\space \displaystyle y'=\frac{1}{x\cdot\ln(b)}$ |
| Funciones Trigonométricas | Derivadas |
| 1. $\quad y=Sen(x)$ | $\space y'=Cos(x)$ |
| 2. $\quad y=Cos(x)$ | $\space y'=-Sen(x)$ |
| 3. $\quad y=Tan(x)$ | $\space y'=Sec^2(x)$ |
| 4. $\quad y=Cot(x)$ | $\space y'=-Csc^2(x)$ |
| 5. $\quad y=Sec(x)$ | $\space y'=Sec(x)Tan(x)$ |
| 6. $\quad y=Csc(x)$ | $\space y'=-Csc(x)Cot(x)$ |
Reglas de la antiderivada.
| Fórmulas básicas de integración | Fórmula de derivación |
|---|---|
| 1. $\displaystyle \int x^n\, dx = \frac{x^{n+1}}{n+1} + C$ | $\quad\displaystyle\frac{d}{dx} \frac{x^{n+1}}{n+1} = x^n$ |
| 2. $\displaystyle\int \, dx = x + C$ | $\quad\displaystyle\frac{d}{dx} x=1$ |
| 3. $\displaystyle \int k\, dx = k \int \, dx = k\cdot x + C$, $\quad$ donde $k$ es cualquier constante. | $\quad\displaystyle\frac{d}{dx}(k) = 0$ |
| 4. $\displaystyle \int kf(x)\, dx = k\cdot F(x) + C$, $\quad$ donde $k$ es cualquier constante. | $\quad\displaystyle\frac{d}{dx} k\cdot \frac{x^{n+1}}{n+1} = k\cdot x^n$ |
| 5. $\displaystyle\int \frac{1}{x}\, dx = Ln(x) + C$ | $\quad\displaystyle\frac{d}{dx} Ln(x) = \frac{1}{x}$ |
| 6. $\displaystyle\int [f(x)\pm g(x)] \, dx = \int f(x) \, dx \pm \int g(x) \, dx$, $\quad$ donde las constantes $C_1 \pm C_2$ se sustituye por una simple $C$. | |

 Resumen de propiedades y reglas.
Resumen de propiedades y reglas.
$\space$ Descargar para imprimir