Misceláneas. Las Espirales III
Proporcionalidad. Las Espirales III
Entre las innovaciones producidas en el ámbito de la Red Educativa Digital Descartes caben destacar, entre otras, la creación del subproyecto Pisa con ordenador por parte de Mª José García Cebrian y José R. Galo Sánchez, documentado en este Blog por Santos Mondéjar López y la herramienta creada por el profesor Ángel Cabezudo Bueno que nos ha dotado de la posibilidad de analizar un crecimiento espiral y hallar la expresión matemática que mejor lo ajusta. La siguiente imagen enlaza con la miscelánea que explica el proceso de creación de dicha herramienta y el uso de la misma.
En el proceso de recuperación y adaptación de materiales de la Red Descartes que habían quedado obsoletos y en el de creación de nuevos recursos son varios los trabajos que merecen mención especial que ya está reflejada en el Blog, no obstante animamos a los socios y visitantes de nuestra web a usar y estudiar dichos trabajos y emprender tareas de adaptación-creación de: Unidades, Misceláneas, Discursos... para recuperar todo el esfuerzo e ilusión que en su día se invirtió y dotar a la aldea global de herramientas útiles para la enseñanza y el aprendizaje.
Seguimos insistiendo en la necesidad de estar al día de las posibilidades operativas y de uso de los materiales y escenas de la Red Educativa Digital Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS, en especial a estos, que llevan a la información de las funciones matemáticas disponibles para la construcción de escenas.
Antes de comenzar con el análisis de los gráficos incluidos en la escena en estudio vamos a mostrar un vídeo que relaciona los fractales y las espirales con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa.
Los siguientes enlaces nos llevan a páginas donde puede ampliarse el conocimiento de las espirales y el concepto, significado y enfoque del estudio de las mismas.
- Espirales de Antonio Pérez Sanz
- Real Sociedad Matemática Española
- Espirales, fractales, Fibonacci,...
- Visión más espiritual
- Espirales y Laberintos
Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales.
En el artículo anterior nos quedamos estudiando los gráficos introducidos en la escena: puntos, segmentos, líneas, polígonos, textos... etc. Para lo cual abrimos la opción de menú Gráficos y observamos los 26 objetos creados y que muestra la siguiente imagen.
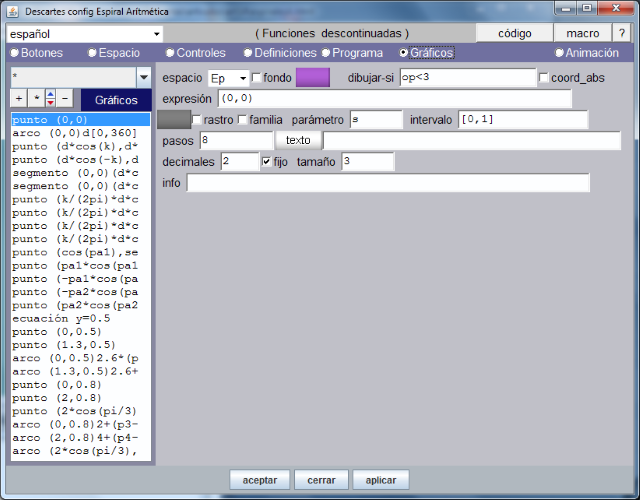
Insistimos en la conveniencia de descargar la escena, abrirla con el editor DescartesJS y analizar detenidamente las propiedades de cada gráfico. Si en este punto se tiene alguna duda el autor o la administración del Blog atenderán las consultas.
El código que corresponde a los gráficos se puede examinar y modificar, abriendo el archivo descargado "espiralesA.html", con un editor de texto plano. Las líneas que corresponden a dichos gráficos son las que comienzan por: <param name="G_x" que en nuestro caso llegan hasta <param name="G_26". Recordamos que se debe tener mucha precaución al editar directamente el código.
Observando la imagen vemos que, en primer lugar, se ha definido un punto en el origen de coordenadas (0,0) que, en esta ocasión, está centrado en la escena. Conviene, si no se tiene práctica, estudiar y probar las diferentes maneras de situar el origen de coordenadas de un espacio y el espacio en si mismo, dentro de la escena. También vemos el espacio donde se representará el punto, su color, tamaño y otra serie de parámetros autoexplicativos y de facil uso.
De los parámetros que ayudan a manejar un punto en la escena uno muy interesante es el de 'familia' que mediante un parámetro (variable) que se introduce en la/s coordenada/s y que se declara en el cuadro de texto "parámetro" (o se acepta el ofrecido por el editor 's') permite introducir simultáneamente tantos puntos como se precise en los lugares definidos por las coordenadas.
La siguiente imagen muestra como se han definido la colección de puntos azules que dibujan la espiral de Aquímedes según la definió el geómetra griego, donde se usa el parámetro global 'familia' con el parámetro o variable 'k '. Recordamos que en su momento definimos el control 'k ' y le asignamos un valor inicial y un valor final. Esta manera de proceder hace que la escena sea interactiva ya que el conrol k puede manipularse al estar presente en la escena en forma de pulsador.
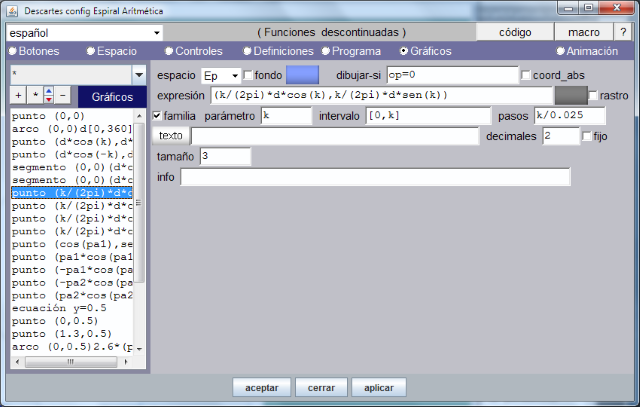
Puesto que disponemos de la escena podemos analizar cada uno de los gráficos cambiando los valores de sus parámetros y observando el efecto de las modificaciones para así aprender a configurar escenas con el editor de código.
Con objeto de practicar con los condicionales hemos elaborado la siguiente escena para su análisis. Es una pequeña aplicación donde se hace una breve introducción al estudio de la distribución de la proporción humana en superficies lisas mediante triángulos, rectángulos, rombos y otras figuras derivadas.
También, en la misma dirección, hemos creado, con el programa GeoGebra, una breve aplicación que muestra como obtener dos triángulos cordobeses a partir de un folio DIN A4.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo la espiral de Teodoro entre sus funcionalidades, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Miscelánea: Las espirales II
Proporcionalidad. Las Espirales II
Entre las innovaciones producidas en el ámbito de la Red Educativa Digital Descartes cabe destacar el impresionante impulso que ha tenido el estudio generalizado de las espirales logarítmicas y la particularización al caso de las gnomónicas entre las que se han destacado las de proporción Divina y Humana. En esta línea el profesor Ángel Cabezudo Bueno ha dotado a la espiral humana de una nueva envoltura aproximándola gnomónicamente mediante funciones exponenciales. Estas son, con sus propias palabras, las razones que aporta para llevar a cabo la acción a la vez que ofrece unas instrucciones de uso de la escena que ha creado.
Espiral gnomon-exponencial y su correspondiente espiral logarítmica
Aparte de la proporción áurea o divina hemos venido trabajando con la proporción cordobesa por ser más natural o humana.
Nos llamó la atención la proporción cordobesa e investigamos de ella algunas cuestiones:
- ¿Cuál es su espiral obtenida al modo con que se obtiene la espiral de Durero en relación a la proporción Áurea?
- El gnomon áureo es un cuadrado y la espiral puede construirse fácilmente con regla y compás, pues basta dibujar un cuadrante de circunferencia haciendo centro en un vértice y conectando los dos vértices opuestos. Repitiendo este proceso sobre los sucesivos gnómones podemos obtener una versión muy aproximada de la espiral logarítmica correspondiente.
Queriendo hacer extensivo este procedimiento con el gnomon cordobés de lados desiguales nos fijamos en la elipse como curva que nos aproxima a la logarítmica correspondiente. El único inconveniente es que no se puede construir fácilmente, aunque sea de forma aproximada, con regla y compás. Además, piénsese que hay que dibujar cuatro arcos de elipse para cada vuelta de espiral. No obstante pudimos ver su dibujo utilizando DescartesJS, nuestra habitual herramienta matemática. - Otras espirales basadas en el modelo gnomon-elipse se han podido así mismo dibujar y aunque su estética no nos ha disgustado además de cumplir con la condición de ser derivables en los puntos de enlace de los arcos de elipse, hemos querido probar otras aproximaciones.
Pensando que el modelo gnomon-exponencial, que consiste en trazar arcos de exponencial en vez de arcos de elipse, debería de dar resultados mejores me he puesto a hacer unos cálculos y al ver que la cosa iba saliendo bien pasé a programar una escena con Descartes.
Debo advertir que esta escena ha estado orientada a hacer algunas averiguaciones en relación con este modelo gnomo-exponencial y hacer algunas comparaciones con lo que ya teníamos, es decir la construcción con el modelo gnomon-elipse y la espiral logarítmica. Por tanto he descuidado, en esta ocasión, la utilización de recursividad para obtener vértices y longitudes de los lados de los sucesivos gnómones dado que este problema ya lo tenemos resuelto (sendas escenas una del profesor José Galo Sánchez y otra mía) y queriendo ver enseguida resultados he trabajado con los valores de estos elementos en los cuatro primeros gnómones (de 0 a π/2, de π/2 a π , de π a 3π/2 y de 3π/2 a 2π), completando así una vuelta de espiral. Bien es cierto que han bastado estos cuatro gnómones para observar la recurrencia al calcular los parámetros de la exponencial en cada gnomon:
![]()
A esta, en coordenadas polares, que formalmente es la misma que la de la correspondiente espiral logarítmica, le aplicamos las condiciones de contorno al gnomon donde va a ser trazada. Es decir para un gnomon de lados a y b cuyo radio vector debe de rotar entre Θ y Θ+Π/2 le imponemos las siguientes dos condiciones:
- Para el ángulo Θ se debe cumplir que r = a
- Para el ángulo Θ+π/2, se debe cumplir que r = b
Con estas dos condiciones podemos determinar los parámetros m y n. Resulta que
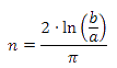
es una constante para todos los gnómones puesto que 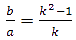 para cualesquiera a y b siendo k=razón de proporcionalidad (k=1,307 para la cordobesa, k=1,618 para la áurea, etc.)
para cualesquiera a y b siendo k=razón de proporcionalidad (k=1,307 para la cordobesa, k=1,618 para la áurea, etc.)
Los valores de m siguen esta ley de recurrencia: 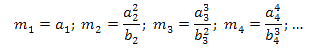 .......
.......
O bien teniendo en cuenta que 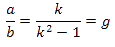 podemos escribir
podemos escribir![]() ........
........
La curva resultante es derivable en los puntos de empalme.
Un cambio de base c ≠ e en la exponencial es posible
r= m0·cn0·θ (2)
verificándose que ![]()
Para el caso k=1,618 (áurea), tenemos a = b (gnomon cuadrado) y la exponencial se convierte en circular pues ![]() con lo que la ecuación polar ahora es
con lo que la ecuación polar ahora es
r = m (3)
Con el modelo gnomon-elipse la traza circular era un caso de elipse y con el modelo gnomon-exponencial la traza circular es un caso de exponencial.
Veamos algunas imágenes captadas de la escena que nos permite hacer algunos comentarios y de paso explicar algo de la funcionalidad de la misma:
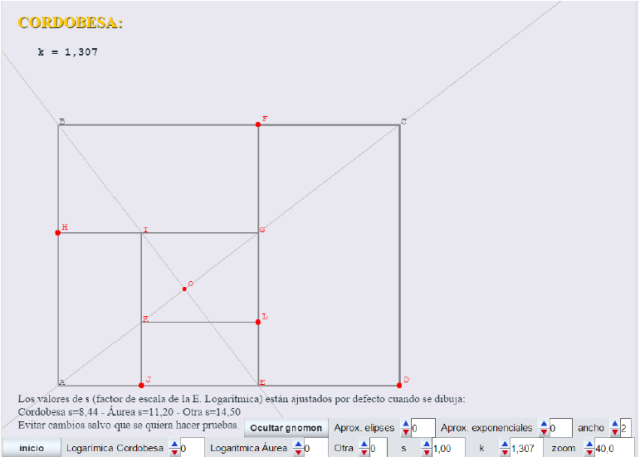
- EDCF (polo en E)
- GFBH (polo en G)
- IHAJ (polo en I)
- FJEL (polo en F)
-
-
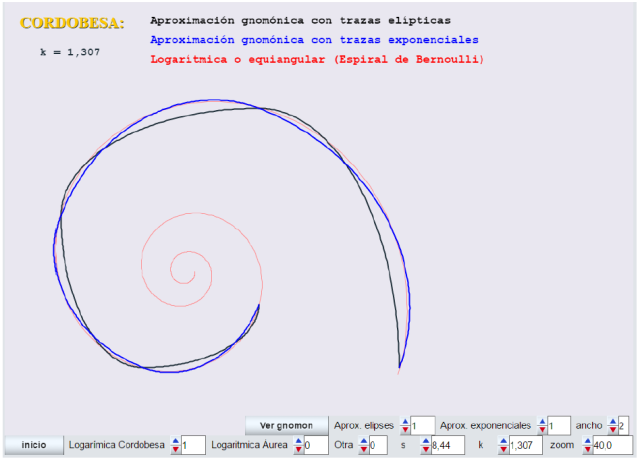
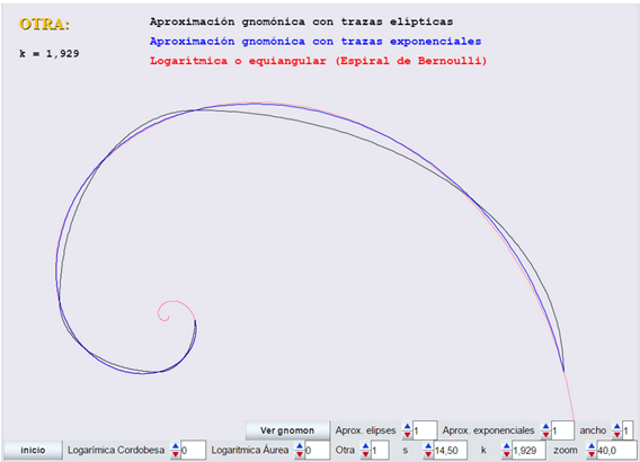
- El control k proporciona sucesivamente K=1,307 (cordobesa), k=1,618 (áurea), k=1,929 (otra).
- Las correspondientes espirales logarítmicas a estos tres valores de k se obtienen poniendo a 1 su control que excluye al resto: Logarítmica Cordobesa, Logarítmica áurea y Otra logarítmica
- Se pueden representar para cierto valor de k, sus aproximadas espirales gnomónica-con-elipses y gnomónica-con-exponenciales.
- Las espirales para cierto k se pueden superponer para hacer comparaciones.
-
- Se representan sólo cuatro gnómones a partir del rectángulo ABCD:
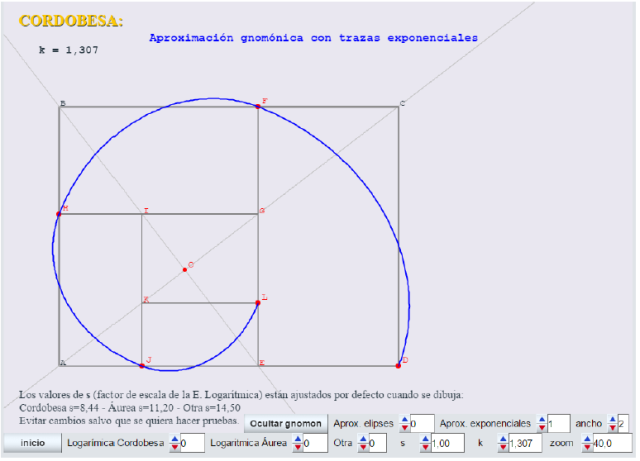
-
-
- El control ancho permite tres anchos de punto (1, 2, 3) de las curvas aproximadas. El ancho de la logarítmica es 1 fijo (se observa mejor la diferencia con ancho 1).
- El parámetro s es un factor de escala de la espiral logarítmica, que facilita el ajuste a los vértices de los gnómones. Están fijados por defecto para cada una de las tres espirales.
-
Observar la buena aproximación que se consigue con el modelo gnomon-exponencial para la cordobesa.
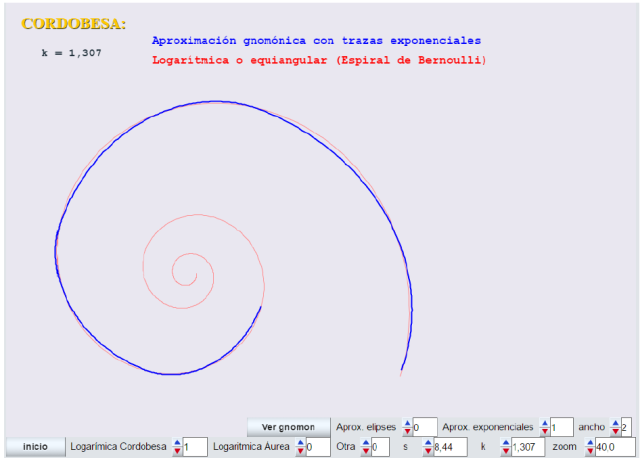
El modelo gnomon-elipse para valores de k menores que 1,618 (áurea) no es muy bueno. Este es el caso de la cordobesa.
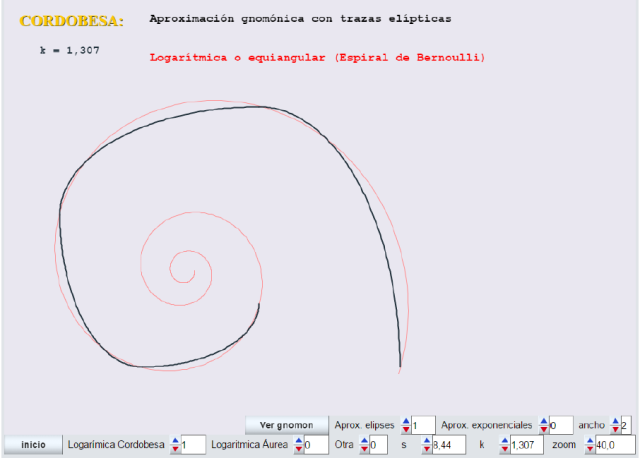
En la siguiente imagen podemos ver una comparativa de las tres espirales para el caso k=1,307 (cordobesa) al dibujarlas juntas.
Ver el buen acoplamiento de las trazas exponenciales para k=1,929 (otra)
Animamos a colaborar con los compañeros que están trabajando en el proyecto ed@d en moodle. El material que están elaborando puede suponer una mejora extraordinaria en la labor educativa con un aumento significativo en la cantidad y calidad de la información expuesta y en la comunicación alumno-alumno, profesor-alumno y viceversa.
Seguimos insistiendo en la necesidad de estar al día de las posibilidades operativas y de uso de los materiales y escenas de la Red Educativa Digital Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS, en especial a estos que llevan a la información de cómo crear animaciones y juegos interactivos para el aula.
Antes de comenzar con el desarrollo de las aplicaciones de la Proporcionalidad vamos a mostrar el vídeo que el profesor Antonio Pérez Sanz elaboró para el programa + por - de TVE.
Los siguientes enlaces nos llevan a páginas donde puede ampliarse el conocimiento de las espirales y el concepto, significado y enfoque del estudio de las mismas.
Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales:
Recordamos que la miscelánea que vamos a elaborar estará enfocada a mostrar el proceso de planificación y realización de dicha miscelánea teniendo en cuenta que los objetivos didácticos de cara al alumnado son: las aplicaciones de la proporcionalidad, el potencial de uso de las funciones trigonométricas elementales, logarítmicas y exponenciales, las ecuaciones paramétricas de una curva, la ecuación polar, las aplicaciones de la derivada y cualquier otro relacionado con el tema de estudio.
No debe olvidarse que estamos estudiando una de las aplicaciones del concepto de Proporcionalidad siguiendo algunos de los materiales que están disponibles en el Proyecto Descartes y, eventualmente, algún otro contenido que por su indudable interés lo merezca.
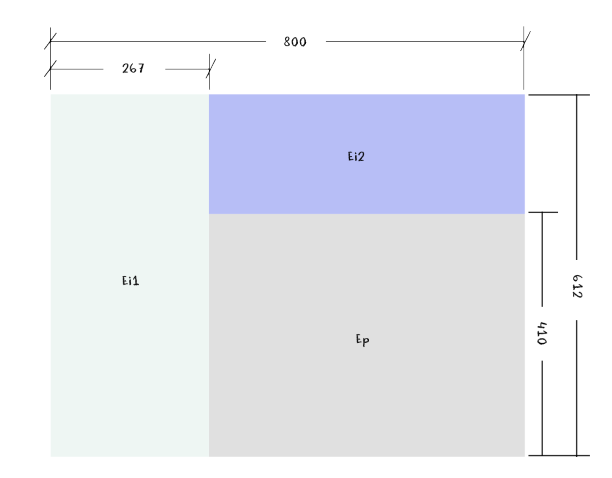
También recordamos que al escenario donde va a desarrollarse la acción (E1) le hemos asignado unas dimensiones de 800x612 y dentro de este espacio general definiremos tres espacios rectangulares según muestra la siguiente imagen.
En el artículo anterior se mostró la manera en que se había realizado la siguiente escena
hasta la creación, configuración y posicionamiento del control de tipo menú y de nombre "Espiral". La siguiente imágen muestra todos los controles necesarios para hacer que la escena funcione.
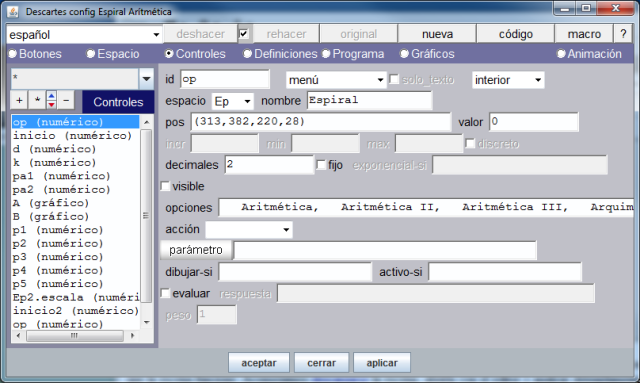
Aconsejamos descargar la escena, abrirla con el editor DescartesJS y analizar detenidamente las propiedades de cada control. Si en este punto se tiene alguna duda el autor o la administración del Blog atenderán las consultas.
El código que corresponde a los controles se puede examinar, y modificar, abriendo el archivo descargado "espiralesA.html", con un editor de texto plano. Las líneas que corresponden a dichos controles son las que comienzan por: <param name="C_x" que en nuestro caso llegan hasta <param name="C_16". Recordamos que se debe tener mucha precaución al editar directamente el código.
Ahora, seleccionando en el editor de código la opción Definiciones, observamos
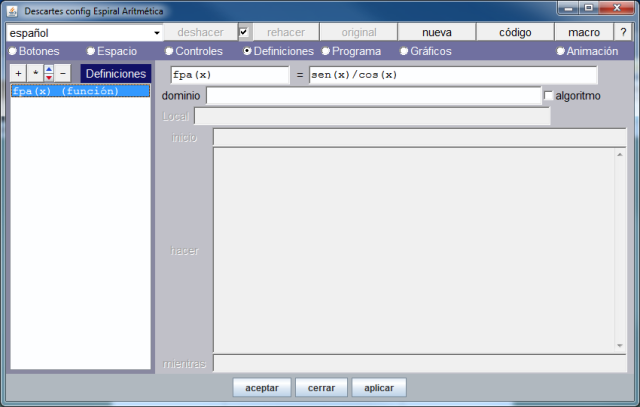
Se ha definido la función fpa que calcula la tengente de un ángulo dado en radianes para facilitar el dibujo de las familias de puntos.
En la opción Programa aún no se ha definido nada y en Gráficos se han definido varios puntos, segmentos etc... como puede comprobar el lector si abre dichas opciones de menú. En el próximo artículo explicaremos cada uno de los gráficos definidos.
Más adelante, cuando la primera fase esté completa, implementaremos los espacios informativos con los detalles de cada espiral y veremos la manera de sincronizar las distintas partes de la información.
Queremos adelantar, por si el lector desea hacer prácticas por su cuenta y luego comprobar los resultados, que una vez analizada la escena tal como está ahora, vamos a integrar en ella esta otra.
dedicada a la espiral de Teodoro

Pitágoras
En próximas entradas continuaremos con el paso a paso de la escena, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Miscelánea: Las Espirales.
Proporcionalidad. Espirales Aritméticas
Afortunadamente continúan las innovaciones en las posibilidades operativas y de uso de los materiales y Escenas de la Red Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS para intentar estar al día de las mismas, fundamentalmente a estos, que llevan a la información sobre cómo comunicar las escenas con el HTML y viceversa, y las escenas entre si y a estos otros que ilustran la manera de integrar el cálculo simbólico en las escenas.
También queremos animar a colaborar con los compañeros que están trabajando en el proyecto ed@d en moodle. El material que se está elaborando puede suponer una mejora extraordinaria en la labor educativa con un aumento significativo en la cantidad y calidad de la información expuesta y en la comunicación alumno-alumno, profesor-alumno y viceversa.
En este artículo nos vamos a centrar en la creación de una miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirá, estudiará y representará alguna de las siguientes espirales:
- Espiral Aritmética o de Arquímedes
- Espirales arquimedianas. Envolventes Uniformes de: 2, 3, 4, ..., n centros. (Enlace cambiado el 16 de agosto de 2023 al quedar roto el original)
- Espiral de litius
- Espiral de Fermat
- Espiral de Pitágoras (de Teodoro, de caracol...)
- Espilral de Ulam
- Espiral de Cornu
- Espiral de Durero
- Espiral de Fibonacci (Enlace cambiado el 16 de agosto de 2023 al quedar roto el original)
- Espiral Hiperbólica (Enlace cambiado el 16 de agosto de 2023 al quedar roto el original)
- Espiral Logarítmica (Enlace cambiado el 16 de agosto de 2023 al quedar roto el original)
- Espiral de Parker (del viento solar)
- Espiral Cordobesa
Cada elemento de la lista anterior enlaza con una página que puede contener o enlazar a: la definición, la ecuación en polares, las ecuaciones paramétricas, la gráfica y otras características de cada espiral, por lo que la miscelánea que vamos a elaborar estará enfocada a mostrar el proceso de planificación y realización de dicha miscelánea teniendo en cuenta que los objetivos didácticos de cara al alumnado son: las aplicaciones de la proporcionalidad y el potencial de uso de las funciones trigonométricas elementales, logarítmicas y exponenciales.
Aprovecharemos este artículo, los siguientes y la miscelánea que elaboraremos, para la presentación de la espiral Cordobesa, particularización de las espirales gnomónicas y fruto de un largo y laborioso trabajo colaborativo, aún vigente, que nuestro compañero, Ángel Cabezudo Bueno, ha concretado, provisionalmente, con éxito.
No debe olvidarse que estamos estudiando una de las aplicaciones del concepto de Proporcionalidad siguiendo algunos de los materiales que están disponibles en el Proyecto Descartes y, eventualmente, algún otro contenido que por su indudable interés lo merezca.
LAS ESPIRALES ARITMÉTICAS
Al escenario donde va a desarrollarse la acción (E1) le hemos asignado unas dimensiones de 800x612 y dentro de este espacio general definiremos tres espacios rectangulares según muestra la siguiente imagen.

Los espacios Ei1 y Ei2 son, fundamentalmente, informativos aunque, eventualmente, pueden alojar algún elemento interactivo como un botón o un campo de texto. En el espacio Ep es donde se desarrollarán las acciones principales de la primera escena que está dedicada a la espiral Aritmética (de Arquímedes) y al grupo de espirales uniformes de 2, 3,...,n centros.
Comenzaremos trabajando de una forma peculiar, crearemos un solo espacio, el Ep, de dimensiones: 533x410 (conviene observar que 533 y 410 son, aproximadamente, el 67% de 800 y de 612 respectivamente) desarrollaremos todas las acciones de la primera escena que tienen lugar en este espacio con sus interrelaciones y, una vez finalizado este proceso, añadiremos los espacios Ei1 y Ei2, los dotaremos de contenido, y sincronizaremos la acción.
La base teórica de todo el trabajo para esta primera escena va a ser la observación de Arquímedes que originó la espiral que lleva su nombre:"Imaginaos una línea que gira con velocidad constante alrededor de un extremo, manteniéndose siempre en un mismo plano, y un punto que se mueve a lo largo de la línea con velocidad lineal constante: ese punto describirá una espiral"

Creamos el espacio Ep de 533x410 y en él vamos a representar lo descrito en la definición de tres maneras diferentes con objeto de practicar con las funciones seno y coseno y el concepto de proporcionalidad.
- Partiendo de dos segmentos horizontales superpuestos. Uno que gira a derechas y otro que gira a izquierdas.
- Partiendo de dos segmentos horizontales unidos por el punto fijo que giran en el sentido opuesto a las agujas del reloj.
- Partiendo de dos segmentos verticales superpuestos. Uno que gira a derechas y otro que gira a izquierdas.
Consideramos las dos opciones posibles de giro del segmento y algunas de las composiciones que seguramente son conocidas por todos pues son de uso habitual.
También, en esta primera escena, vamos a mostrar la construcción de las espirales uniformes de dos y tres centros lo que unido a las explicaciones informativas que se incluirán en su momento bastará para aprender a construir una espiral uniforme de cualquier número de centros. Esto hace que para mantener el carácter didáctico del código convenga añadir un nuevo espacio, que superpuesto al anterior se hará visible cuando el primero esté oculto.
Para conseguir lo expuesto necesitaremos definir algunos controles de distinto tipo, algún vector, varias funciones, diversos algoritmos de cálculo y bastantes gráficos.
Vamos a mostrar lo que queremos conseguir y luego veremos, paso a paso como lo hemos realizado.
El siguiente vídeo muestra como se ha realizado la escena anterior.
En próximas entradas continuaremos con el paso a paso de la escena, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Respecto al trabajo de investigación sobre las espirales gnomónicas en general y sobre la Cordobesa, en particular, que se está desarrollando, queremos mostrar los siguientes avances y animar a aportar alguna ayuda en el proceso de generalización emprendido.
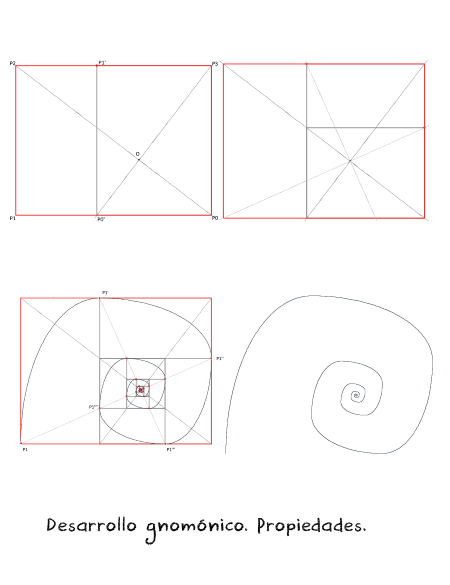
La siguiente escena muestra el avance realizado respecto a las iniciales.Espirales. Proceso de generalización
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Escenas. Misceláneas. Discursos. Unidades.
Proporcionalidad. Las Espirales
Debido a que, afortunadamente, continúan las innovaciones en las posibilidades operativas y de uso de los materiales y Escenas de la ReDescartes aconsejamos acudir a los contenidos de la Documentación técnica de la herramienta de autoría DescartesJS para intentar estar al día de las mismas, fundamentalmente a estos, que llevan a la información sobre cómo comunicar las escenas con el HTML y viceversa, y las escenas entre sí, a estos otros que ilustran la manera de integrar el cálculo simbólico en las escenas, quedando pendientes los enlaces a algunos de los contenidos de las siguientes novedades:
- Se han publicado nuevos recursos en el subproyecto de Competencias que han sido encargados por el INEE. Son pruebas liberadas del programa PISA para la nueva evaluación de PISA con ordenador.
- Integración de escenas descartes-JS en un paquete Scorm para su uso en Moodle (la profesora Elena Alvarez ha incorporado un ejemplo de integración de Descartes con Moodle mediante un paquete Scorm) y Ficheros de "Juegos Didácticos" para plataformas educativas. de Enric Ripoll Mira
- Experiencia con atención personalizada en matemáticas mediante libro digital en el aula de informática de Juan José López
- ed@d en moodle de Emilio Pazo Núñez.
- Lupa cartesiana de Juan Guillermo Rivera Berrío
este último ya disponible y algunos de los anteriores llevan la documentación incluida o ya están parcialmente disponibles en los foros de la ReDescartes.
En esta ocasión, tal como indica el título, vamos a hacer un recorrido por el concepto de Proporcionalidad siguiendo algunos de los materiales que están disponibles en el Proyecto Descartes y, eventualmente, enlazaremos algún otro contenido por su indudable interés.
El objetivo de incluir el uso y análisis de Unidades Cartesianas sobre la Proporcionalidad es, además del evidente relacionado con el tema, el de aprender a generar una, o varias Misceláneas a partir de dichas unidades o simplemente, a extraer escenas aisladas para un uso ágil y puntual como ejemplo de apoyo a un aspecto concreto de uso o aplicación del concepto en estudio.
El siguiente vídeo muestra la manera de realizar esta acción y de hacer operativo el objeto derivado de la Unidad o Miscelánra.
Antes de continuar conviene observar la manera en que la profesora Antolina Muñoz Huertas enfoca el tema de la Proporcionalidad en la unidad  que publicó en el año 2002 y que he adaptado a DescartesJS debido a la importancia del concepto y a la claridad y sencillez con que se expone. Y también porque de esta Unidad, tal y como más tarde haremos con otros trabajos del profesor José R. Galo Sánchez, vamos a extraer escenas para su posible uso de forma individual.
que publicó en el año 2002 y que he adaptado a DescartesJS debido a la importancia del concepto y a la claridad y sencillez con que se expone. Y también porque de esta Unidad, tal y como más tarde haremos con otros trabajos del profesor José R. Galo Sánchez, vamos a extraer escenas para su posible uso de forma individual.
Una escena tratada aisladamente puede cubrir varios objetivos; unos relacionados con un concepto, por ejemplo la proporcionalidad, otros con una aplicación del concepto p.e. el número de oro y otros con el uso del código que hace comportarse a la escena de la forma que lo hace.
En todos los casos al ser un objeto simple es facil abordar su estudio desde cualquier punto de vista.
El número de oro.
La escena sacada tal cual de la Unidad anterior muestra, de forma dinámica e intuitiva, como dividir un segmento en partes que verifiquen la proporción Divina. Cierto que podemos añadir muchos aspectos que la mejoren hasta convertirla en una excelente Miscelánea, pero en esta ocasión queremos que permanezca tal cual está en origen para así comprender las explicaciones que se dan en el vídeo incluido en este artículo.
A continuación se enlaza una Miscelánea que complementa la Unidad anterior, pues introduce la proporción Humana o Cordobesa y que ha sido creada con objetivos fundamentalmente formativos.
Las dos escenas siguientes están sacadas de la excelente Unidad  creada por José R. Galo y la tercera es una escena simple que, en su día, se creó para practicar con el Teorema de Pitágoras y con las funciones Trigonométricas: seno, coseno, tangente, arcotangente...
creada por José R. Galo y la tercera es una escena simple que, en su día, se creó para practicar con el Teorema de Pitágoras y con las funciones Trigonométricas: seno, coseno, tangente, arcotangente...
Rectángulo cordobés I
Rectángulo cordobés II
Espiral por puntos.
En esta otra escena, de utilidad si nos planteamos el tema de la proporcionalidad de manera algo más avanzada, tenemos una herramienta que puede ayudar a la confección de espirales logarítmicas, arquimedianas, uniformes de doble centro... y con muy pocas modificaciones de cualquier otro tipo.
Espiral logarítmica
Estando a punto de cerrar este artículo nos llega la noticia de que el profesor Ángel Cabezudo Bueno ha culminado un laborioso trabajo colaborativo y ha dado forma a la Espiral Cordobesa. Aunque dedicaré el próximo artículo a este logro a continuación expongo una escena, aún provisional, con la construción, mediante gnomones, de la espiral.
Espiral cordobesa mediante gnomones
En próximas entradas continuaremos analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Cálculo simbólico en escenas DescartesJS: Introducción.
La siguiente escena es el ejemplo desarrollado de la implementación del cálculo simbólico dentro de escenas DescartesJS. Realizado por Elena E. Álvarez Sáiz, es un completo estudio que la autora ha realizado de la situación, ampliando los comandos utilizados a más de 400 y detallando la manera de proceder en una amplísima documentación parte de la cual se enlaza al principio del artículo.
De este impresionante avance se ha dicho, entre otras cosas, lo siguiente:
¡Felicitaciones Elena!
Antes de despedir este artículo quisiera hacer mención al impresionante trabajo que hace ya algún tiempo presentaron Deyanira Monroy y José Luis Abreu con el nombre de ConGeo para darlo a conocer a aquellos que aún no lo usan y enviarle a sus autores la petición de incluir en descartes-min.js algunos de los comandos como: Punto Medio, Mediatriz, Bisectriz,... cosa que algún creador de escenas agradecería.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Misceláneas. X
Audios y Vídeos Interactivos con Descartes
Continuación de la práctica (3)
Debido a las recientes innovaciones en las posibilidades operativas de las Escenas aconsejamos estudiar los contenidos de la Documentación técnica de la herramienta de autoría DescartesJS, fundamentalmente estos, que llevan a la información sobre cómo comunicar las escenas con el HTML y viceversa, y las escenas entre sí.
Continuando con la práctica, recordamos que ya hemos definido en los espacios: E1, E2 y E3, algunos de los gráficos (textos) y controles necesarios para dirigir y complementar el flujo de la actividad, y también hemos definido los algorítmos y la animación que controlan la reproducción del vídeo. Ahora, siguiendo con el paso 10 y aunque ya se indicó que podía hacerse en el paso 6, crearemos los mensajes que serán visibles según la respuesta sea correcta; o no, tal y como muestra el siguiente vídeo.
Ya podemos abrir el archivo index.html creado con cualquier navegador para ver la escena funcionando de la forma prevista.
En próximas entradas continuaremos analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Cálculo simbólico en escenas DescartesJS: Introducción.
La siguiente escena es un ejemplo de la implementación del cálculo simbólico dentro de escenas DescartesJS. Este ejemplo, realizado por Elena E. Álvarez Sáiz, es una propuesta para evaluación de la viabilidad de la utilidad que aún está en fase de prueba (Al enviar este artículo nos llega el completo estudio que la autora ha realizado de la situación, ampliando los comandos utilizados a más de 400 y detallando la manera de proceder en una amplísima documentación, situación que recogeremos en próximos artículos).
De este impresionante logro se ha dicho lo siguiente:
"Continuamos con los avances basados en la comunicación escena-html y adelantamos una escena desarrollada por Elena Álvarez en la que, utilizando esa comunicación, se integra el cálculo simbólico (en este caso el CAS de Geogebra) en Descartes. La documentación explicando todo el proceso en detalle, estará pronto. Éste es sólo un ejemplo de lo que se puede hacer. ¡Muchísimas gracias Elena por compartir tu creatividad y tu buen saber y hacer! y por abrir una nueva línea de posibilidades.
Lo importante es que, en general, se puede integrar cualquier módulo CAS que esté en js o que disponga de un API. O una librería de cálculo numérico, o con bases de datos, o... ¡imaginación al poder! Al comunicarse Descartes con el exterior se ha abierto un amplio mundo de interacciones.
El esquema es siempre igual: un html que incluye todo lo relativo al módulo que se quiere integrar (bien sea un vídeo como en los vídeos interactivos, o un CAS como es en este caso, o una librería de cálculo numérico, o una base de datos o...) y una escena que envía a ese html una petición, éste actúa y envía la respuesta a la escena. También hay que tener presente conseguir el objetivo de que el módulo html no haya que tocarlo para nada, que sea una caja negra o interface ajeno al desarrollador que quiere usarlo.
La línea anterior coincide conceptualmente con otra que están desarrollando nuestros colegas en México, donde se están elaborando módulos (teclado, herramientas geométricas, tiza --tipo PDI--) donde se utiliza la comunicación escena con escena. Pronto os presentaremos estas utilidades.
Espero que os guste e incentive vuestra creatividad. ¡Ánimo y a preparar nuevos modelos! ¡Quedamos a la espera de vuestros ejemplos! (José R. Galo)"
"Sencillamente genial :-) ( Josep Mª Navarro Canut )"
"¡Felicitaciones Elena!
Has hecho realidad un viejo sueño de incorporar la potencialidad de GeoGebra a Descartes. Se despejan nuevos horizontes para el diseño de nuevas y más impactantes escenas de Descartes. (Juan Rivera )"
"Me alegra muchísimo esta gran noticia es como unir dos compuestos químicos esenciales. Fantástico! Y además se abren muchas e interesantes posibilidades para poner a prueba la creatividad...
Enhorabuena y gracias por el esfuerzo, es lo mínimo que podemos ofrecer los que estamos sin colaborar de una forma tan activa, enriquecedora y generosa. ( Luis Javier Rodríguez González)"
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo