Mostrando artículos por etiqueta: Hipias
Misceláneas. Lugares geométricos. Cuadraturas V. La cuadratura del círculo.
Como prólogo a un breve estudio sobre la cuadratura del círculo, hemos analizado la manera de cuadrar algunos polígonos y hecho una breve reflexión sobre los teselados. En particular se ha visto, entre otros asuntos, el método general de cuadrar los polígonos regulares y referente a las teselaciones se ha mostrado, entre otras, la manera de teselar un triángulo cordobés con una sucesión de triángulos cordobeses.
Dentro del tema que nos ocupa: los Lugares geométricos también, en su día, estudiamos las Trisectrices de Hipias y Nicomedes y en otros artículos se han expuesto misceláneas y escenas que desarrollan la espiral de Arquímedes y la cuadratriz de Dinostrato; no obstante en la presente entrada volvemos a insistir en el estudio de las primeras curvas mecánicas o lugares geométricos creados por estos autores por su evidente interés y para animar a la conversión en misceláneas de las escenas que aún no lo son.
Anteriormente hemos enlazado el extraordinario trabajo del profesor Fernando Bombal sobre la cuadratura del círculo, volvemos a hacerlo y en el leemos:
Recomendamos la lectura completa del documento así como el análisis de su extensa bibliografía.
También en entradas anteriores hemos enlazado con el blog de Miguel Ángel Morales Medina, en esta ocasión lo hacemos al básico pero minucioso artículo sobre la cuadratura del círculo: ¿Quién dijo que la cuadratura del círculo era imposible?.
A continuación y también como prolegómeno al estudio de la cuadratura del círculo enlazamos con dos pequeños trabajos sobre la cuadratura de las lúnulas: el primero de ellos creado con DescartesJS y el segundo con el programa GeoGebra.
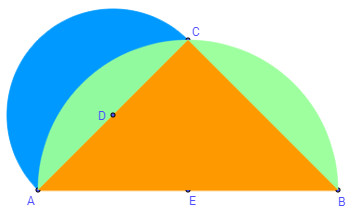
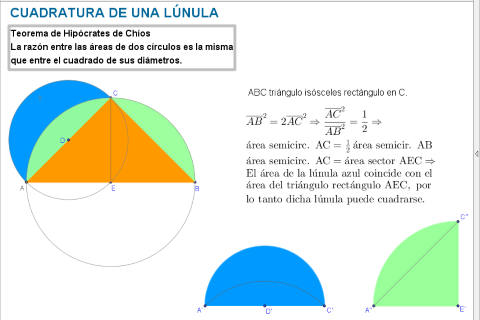
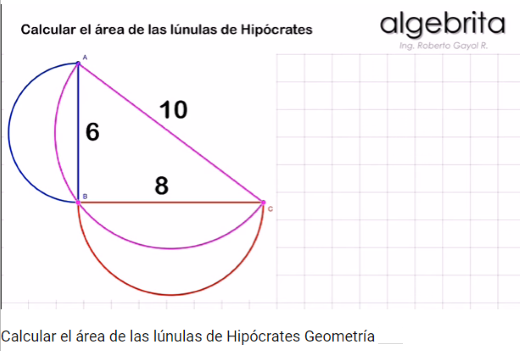
- Cuadratura de una lúnula I: Con la ayuda de dos semicírculos creamos una lúnula y aplicando el teorema de Hipócrates de Chios encontramos, según se muestra en la siguiente escena interactiva, un triángulo de igual área que dicha lúnula. Cuadrando el triángulo obtenemos la cuadratura de la lúnula.
Escena desarrollada con DescartesJS.
- Cuadratura de una lúnula II: actuando de forma análoga a como hemos hecho en la escena anterior obtenemos la cuadratura de una lúnula con el programa GeoGebra
Las escenas que se exponen a continuación son recreaciones de otras ya expuestas en este blog y tienen como objetivo refrescar la memoria sobre las curvas mecánicas mencionadas anteriormente.
Todos los trabajos dejan, para quien tenga interés en el tema, una buena cantidad de opciones de ampliación y mejora.
La trisectriz de Hípias
La trisectriz - cuadratriz de Hípias - Dinostrato
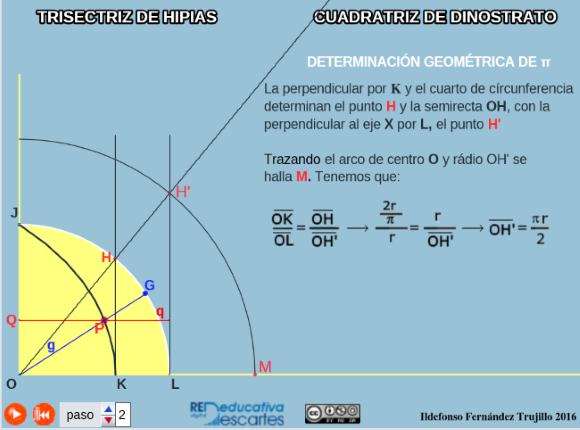
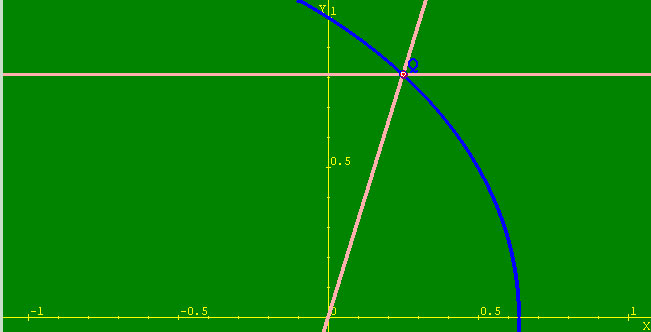
En la siguiente escena se determina un segmento relacionado directamente con el número π utilizando la trisectriz - cuadratriz de Hípias - Dinostrato
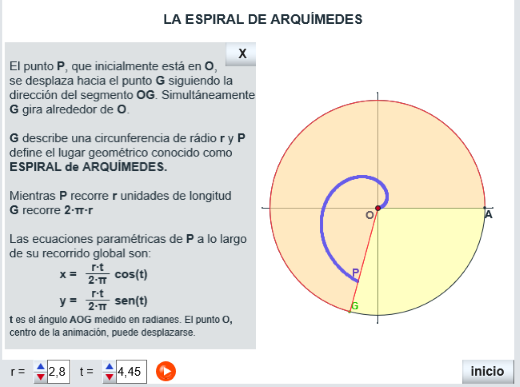
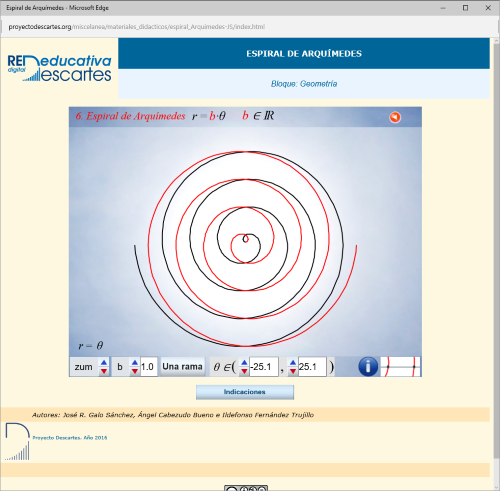
Las siguientes utilidades muestran: la primera, además de las ecuaciones paramétricas de la espiral, la manera como se genera el lugar geométrico conocido como espiral de Arquímedes y la otra la determinación de un segmento de longitud raiz cuadrada de π, en esta ocasión mediante la mencionada espiral de Arquímedes y la ecuación cartesiana de dicho lugar geométrico.
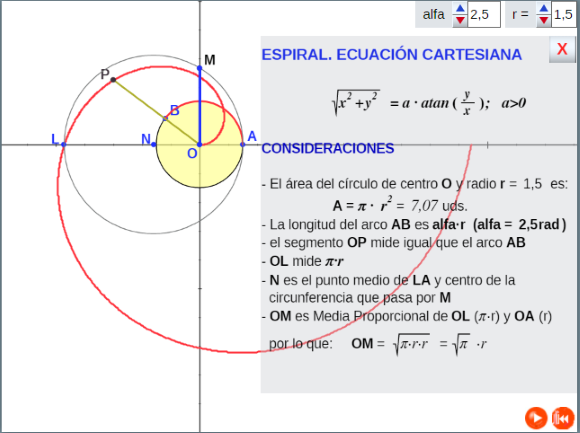
deducción de raiz de π con la espiral de Arquímedes
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra la deducción, paso a paso, del área de las lúnulas de Hipócrates.
,Continuando con la creación de la miscelánea "Las Espirales" sugerimos completar su elaboración extrayendo el contenido relacionado con las cuadraturas estudiadas para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos. Cuadraturas"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La cuadratura del círculo: Historia de una obsesión.
XIV Programa de Promoción de la Cultura Científica y Tecnológica.
Rev. Real Acad. Ci. Exact. Fis. Nat. (Esp) Vol. 105, Nº 2 (2012), 241-258
Fernando Bombal - Cuadraturas
Prof. Esteban Rubén Hurtado Cruz. Facultad de Ciencias UNAM. Cálculo Diferencial e Integral II - Páginas en GeoGebra de Vicente Martín Torres López
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
Lugares geométricos: Trisectrices de Hipias y Nicomedes.
Continuamos con el estudio de los lugares geométricos y en esta entrada volvemos a desarrollar una aproximación al conocimiento genérico de los conocidos como "Trisectriz (Cuadratriz) de Hipias" y "Concoide (Trisectriz) de Nicomedes" que son las curvas resultantes del trabajo de estos sabios griegos para resolver el problema de la trisección de un ángulo.
Dentro del amplio grupo de cicloides y demás ll.gg. retomamos el análisis de los mencionados anteriormente por su especial interés debido a que cronológicamente estas curvas están, después de la circunferencia, entre las primeras que fueron creadas y descritas.
Para llevar a la práctica el estudio remitimos a la publicación en el Blog de dos escenas que los generan de forma interactiva. Se aconseja ver los detalles de estas utilidades, repitiendo la animación, hasta comprender el proceso de creación de los ll.gg. Son escenas basadas en la obra del profesor Pedro González Enríquez, trabajo que está en proceso de adaptación a las nuevas versiones del editor DescartesJS; no obstante, debido a su interés, las siguientes imágenes enlazan directamente con cada uno de los trabajos en su estado actual.
Estudio de la Trisectriz (Cuadratriz) de Hipias.
Estudio de la Concoide de Nicomedes
Animamos a conocer las nuevas caractrísticas del editor DescartesJS. Exponemos otra vez el ejemplo sobre probabilidad publicado en la entrada anterior como ilustración de lo que se puede hacer, en muy pocos minutos, reutilizando la documentación que aporta.
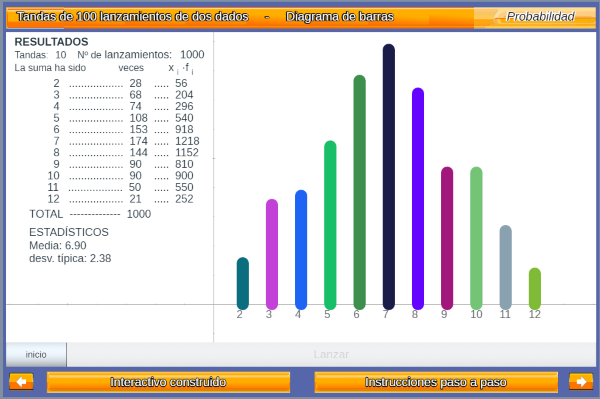
Introducción al concepto de probabilidad
Como en anteriores ocasiones notamos que las utilidades mostradas son fácilmente adaptables y admiten las modificaciones y/o ampliaciones que se consideren convenientes para los propósitos particulares de uso.
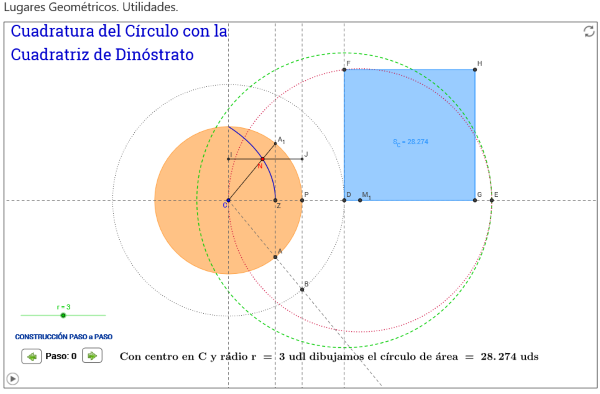
Las siguientes imágenes enlazan con pequeñas herramientas realizadas con el programa GeoGebra en las que se recrea el proceso de generación de la Concoide de Nicomedes, la trisectriz de Hipias y el uso por parte de Dinostrato de dicha trisectriz para hallar la cuadratura del círculo. Como ya se ha explicado esto se hace con el doble propósito de profundizar en el estudio de dichas curvas y ahondar en el conocimiento de ambas plataformas: GeoGebra y DescartesJS de forma paralela para lograr los objetivos señalados en entradas anteriores.
Estudio de la Trisectriz (Concoide) de Nicomedes.
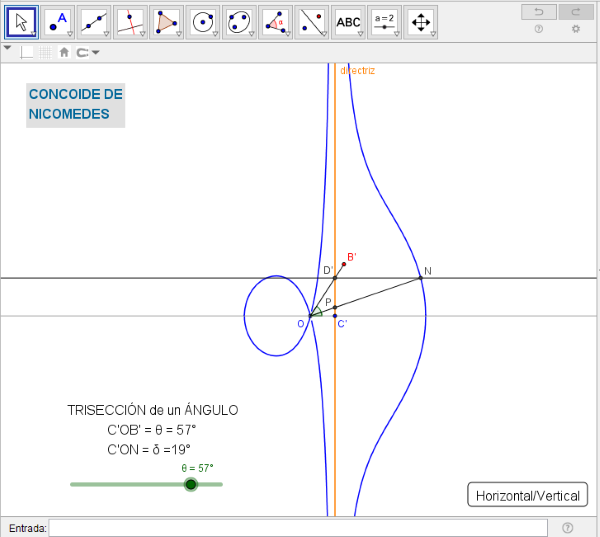
hoja de trabajo de la Concoide
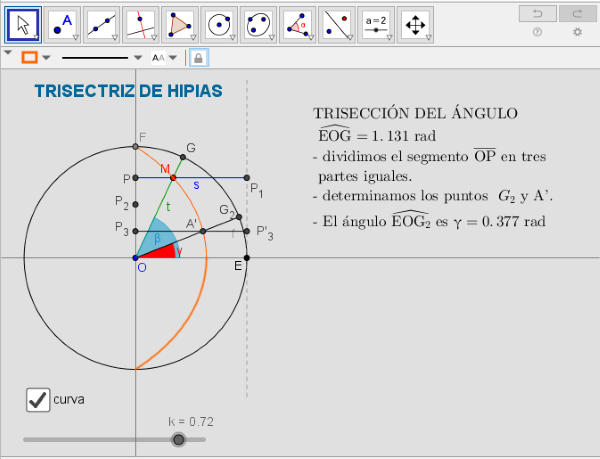
La siguiente imagen es un vínculo a la utilidad que muestra la generación del l.g. "Trisectriz de Hipias" y su uso como trisector de ángulos agudos.
Tiene especial interés la consideración de que según el procedimiento mostrado, cuando el segmento horizontal que se desplaza verticalmente y el que gira alrededor de O, centro del círculo, son ambos horizontales ( k = 0), el punto M intersección de los mismos (generador del l.g.) está indefinido. Esta situación no interfiere en nada a la trisección pues ahí el ángulo a trisecar vale 0 rad, pero si es transcendental considerar la distancia, en ese instante de horizontalidad, del hipotético punto M, deducido por la tendencia de la curva antes y después de ese instante, al centro del círculo.
Dinostrato, entre otros, consideró la tendencia de la curva y llegó a la conclusión de que cuando k → 0 entonces d(O,M) → 2·r/π, hecho que le permitió cuadrar el círculo usando la trisectriz.
La herramienta enlazada comprueba lo anterior al hacer k = 0.
Estudio de la Trisectriz de Hipias.
Proponemos al lector el análisis de las utilidades anteriores, su modificación y mejora con objeto de lograr un profundo conocimiento de ambas plataformas y así potenciar la inclusión del cálculo simbólico en escenas DescartesJS de forma eficaz.
Esta vez en la sección de vídeo hemos elegido uno que muestra la creación de la Concoide de Nicomedes paso a paso. Consideramos que su uso en centros bilingües es muy adecuado por la claridad de la exposición.
Concoide de Nicomedes
Continuando con la creación de la miscelánea "Las Espirales" sugerimos completar su elaboración extrayendo el contenido relacionado con los lugares geométricos estudiados para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografia:
- Unidad para el taller de 4º de la E.S.O. "Curvas clásicas en coordenadas paramétricas" del profesor: Ricardo Sarandeses Fernández, que está en proceso de adaptación a la nueva versión del editor DescartesJS.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
Proporcionalidad. Las Espirales IX
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca el subproyecto TELESECUNDARIA.
En palabras del encargado de la presentación del subproyecto en el Blog, Ángel Cabezudo Bueno, "Telesecundaria es una modalidad de los estudios de educación secundaria en el Sistema Educativo de México dirigido a estudiantes adolescentes de 12 a 15 años que viven en comunidades dispersas que carecen de escuela de secundaria.
Se utilizan para ello los avances en tecnologías de la información y comunicación (TIC) como recurso para acercar esta formación a los jóvenes y puedan concluir su educación básica.
En este subproyecto de RED Descartes se han recogido objetos de la Telesecundaria desarrollando los correspondientes materiales con la herramienta Descartes. Las asociaciones de Colombia y España han sido las encargadas de preparar la adaptación a DescartesJS y en consecuencia todos podrán ser consultados en cualquier dispositivo con sistema operativo que admita un navegador compatible con HTML5." los primeros materiales pueden verse y descargarse siguiendo el enlace gráfico siguiente.
Dentro de nuestro ámbito local queremos destacar, entre otros, los siguiente materiales:
- Todos los creados para el subproyecto COMPETENCIAS. Debido a la creciente internacionalización de nuestro sistema educativo, progresiva integración en la comunidad europea, conviene que la manera de evaluar competencias en los ámbitos externos sea conocido con objeto de participar en igualdad de condiciones. Un acercamiento a estos procedimientos lo ofrecen los materiales del proyecto Competencias.
- La Miscelánea sobre la espiral de Arquímedes que sigue la corriente de mostrar los conceptos complicados, composición de movimientos, mediante la visualización del hecho de forma que es posible intervenir en la escena modificando los parámetros que la definen, con lo que la comprensión del concepto se facilita sobremanera, por lo tanto la miscelánea que se presenta es, por derecho propio, un objeto educativo lúdico e interactivo con un potencial formativo sobresaliente; no obstante en esta ocasión queremos enfocar el proceso de creación de la espiral desde el punto de vista de la definición de un lugar geométrico.
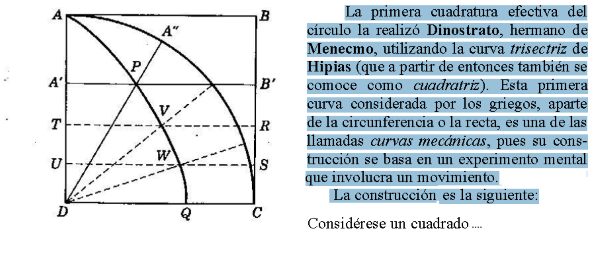
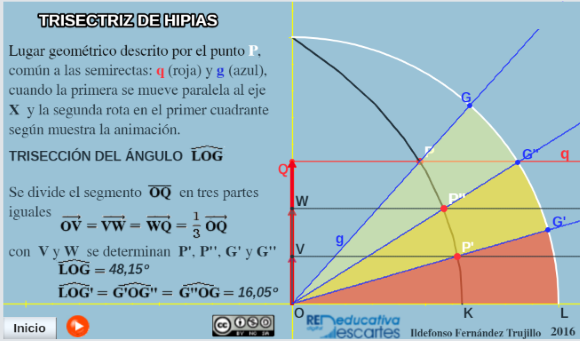
La miscelánea anterior muestra, paso a paso, la creación de un lugar geométrico (l.g.) por un punto que se mueve linealmente en un segmento mientras este gira alrededor de uno de sus extremos. Existen otros muchos lugares geométricos, entre los clásicos y más conocidos destaca la Trisectriz de Hipias que junto con la espiral de Arquímedes se ha usado, además de para otras utilidades, para la trisección de cualquier ángulo. A la Trisectriz de Hipias también se la llama Cuadratriz de Dinóstrato debido a que este geómetra usó el l.g. para la cuadratura del círculo. La Trisectriz (o Cuadratriz) es el l.g. generado por el punto común a dos segmentos uno de los cuales gira alrededor de uno de sus extremos y el otro se desplaza horizontalmente según muestran las siguientes escenas:
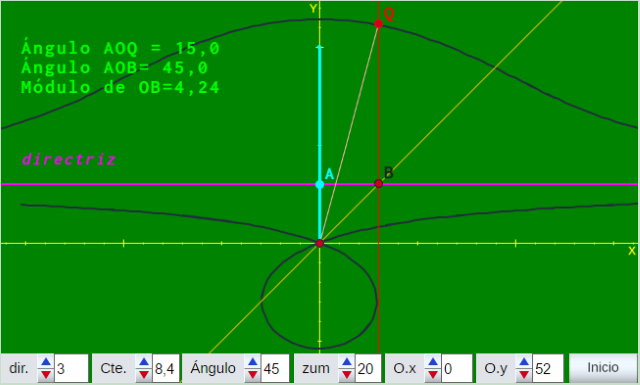
- La Trisectriz de Hipias que muestra, mediante una animación, la definición de la curva
- La trisección de un ángulo mediante la Trisectriz de Hipias. También se basa en una animación, en la primera parte se dibuja la curva y a continuación se muestra y explica, de forma dinámica, la trisección de un ángulo. La animación puede detenerse/reanudarse en cualquier instante.
- La cuadratura del círculo mediante la Cuadratriz de Dinóstrato (Primera Parte). Esta escena se basa en un pulsador que muestra, según se pulsa, la explicación del proceso para cuadrar el círculo. También tiene una animación que vuelve a construir la curva. La animación puede activarse/detenerse en cualquier instante.
Conviene analizar las escenas anteriores, reproducirlas y/o mejorarlas y ver la forma de integrarlas en la miscelánea sobre las espirales.
En próximas entradas en el Blog completaremos el estudio de uso de la Cuadratriz y veremos la manera de trisecar un ángulo y cuadrar el círculo con la espiral de Arquímedes.
En esta ocasión, en la sección de vídeo, hemos elegido uno muy particular que muestra la manera de dibujar la Trisectriz de Hipias (Cuadratriz de Dinóstrato) con ¿regla y compás? con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa. Buscando en internet se pone de manifiesto el enorme interés que suscitan, aún hoy en día, los problemas clásicos de la Geometría Griega.
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral de Fermat" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:
- Hemos creado la siguiente escena: Espiral de Fermat
- Inclusión del código de la escena anterior en el de la miscelánea en proyecto.
La escena del proyecto puede verse a continuación:
Y desde este enlace descargar el proyecto con la espiral de Fermat incluida.
También, relacionado con el tema de los lugares geométricos (l.g.) y sus utilidades hemos incluido dos trabajos, realizados con el programa GeoGebra, uno muestra el uso de la espiral de Arquímedes para la trisección de un ángulo y en el otro, enlazado en la imagen que sigue a la trisección, se lleva a cabo la cuadratura de un círculo de forma dinámica.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Bibliografía.- Para la realización de esta entrada y siguientes ha sido de gran ayuda la siguiente información:
- El trabajo sobre las TRISECTRICES de Pedro González Enríquez.
- Cuadratura de un círculo con la Cuadratriz de Dinóstrato
- Cuadratura de un círculo
Ildefonso Fernández Trujillo. Blog ReDescartes 2016