Mostrando artículos por etiqueta: Arquímedes
Misceláneas. Lugares geométricos. Cuadraturas V. La cuadratura del círculo.
Como prólogo a un breve estudio sobre la cuadratura del círculo, hemos analizado la manera de cuadrar algunos polígonos y hecho una breve reflexión sobre los teselados. En particular se ha visto, entre otros asuntos, el método general de cuadrar los polígonos regulares y referente a las teselaciones se ha mostrado, entre otras, la manera de teselar un triángulo cordobés con una sucesión de triángulos cordobeses.
Dentro del tema que nos ocupa: los Lugares geométricos también, en su día, estudiamos las Trisectrices de Hipias y Nicomedes y en otros artículos se han expuesto misceláneas y escenas que desarrollan la espiral de Arquímedes y la cuadratriz de Dinostrato; no obstante en la presente entrada volvemos a insistir en el estudio de las primeras curvas mecánicas o lugares geométricos creados por estos autores por su evidente interés y para animar a la conversión en misceláneas de las escenas que aún no lo son.
Anteriormente hemos enlazado el extraordinario trabajo del profesor Fernando Bombal sobre la cuadratura del círculo, volvemos a hacerlo y en el leemos:
Recomendamos la lectura completa del documento así como el análisis de su extensa bibliografía.
También en entradas anteriores hemos enlazado con el blog de Miguel Ángel Morales Medina, en esta ocasión lo hacemos al básico pero minucioso artículo sobre la cuadratura del círculo: ¿Quién dijo que la cuadratura del círculo era imposible?.
A continuación y también como prolegómeno al estudio de la cuadratura del círculo enlazamos con dos pequeños trabajos sobre la cuadratura de las lúnulas: el primero de ellos creado con DescartesJS y el segundo con el programa GeoGebra.
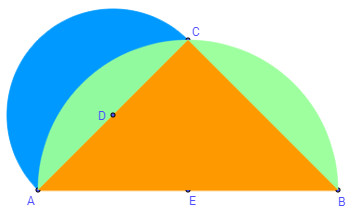
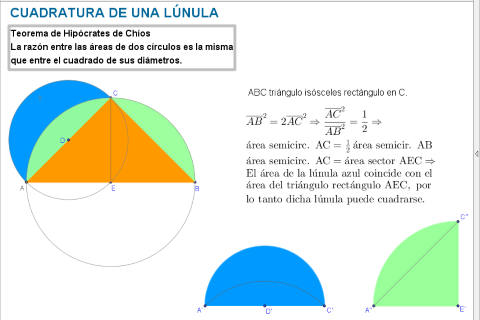
- Cuadratura de una lúnula I: Con la ayuda de dos semicírculos creamos una lúnula y aplicando el teorema de Hipócrates de Chios encontramos, según se muestra en la siguiente escena interactiva, un triángulo de igual área que dicha lúnula. Cuadrando el triángulo obtenemos la cuadratura de la lúnula.
Escena desarrollada con DescartesJS.
- Cuadratura de una lúnula II: actuando de forma análoga a como hemos hecho en la escena anterior obtenemos la cuadratura de una lúnula con el programa GeoGebra
Las escenas que se exponen a continuación son recreaciones de otras ya expuestas en este blog y tienen como objetivo refrescar la memoria sobre las curvas mecánicas mencionadas anteriormente.
Todos los trabajos dejan, para quien tenga interés en el tema, una buena cantidad de opciones de ampliación y mejora.
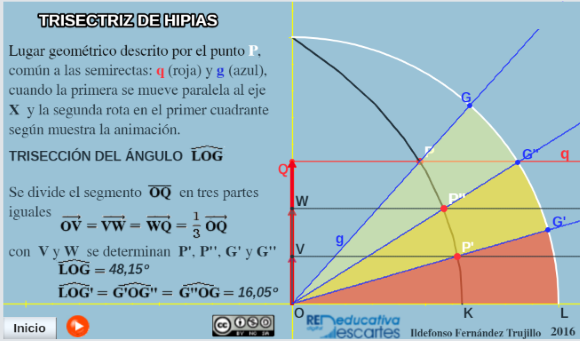
La trisectriz de Hípias
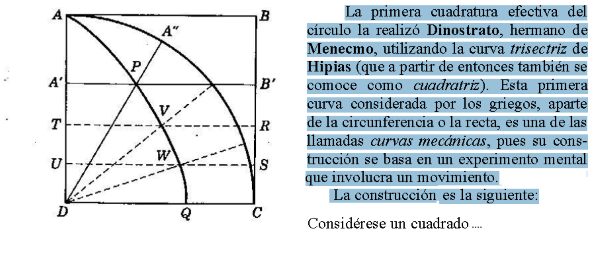
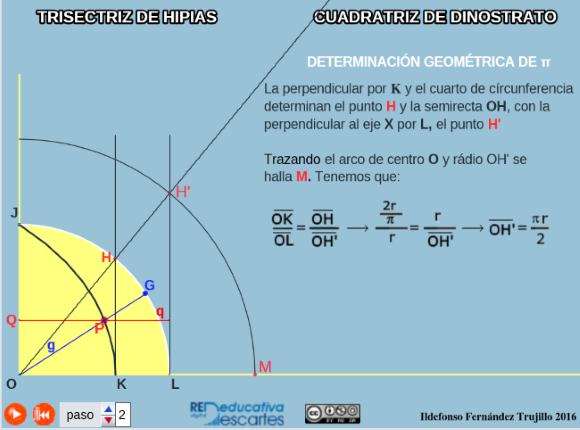
La trisectriz - cuadratriz de Hípias - Dinostrato
En la siguiente escena se determina un segmento relacionado directamente con el número π utilizando la trisectriz - cuadratriz de Hípias - Dinostrato
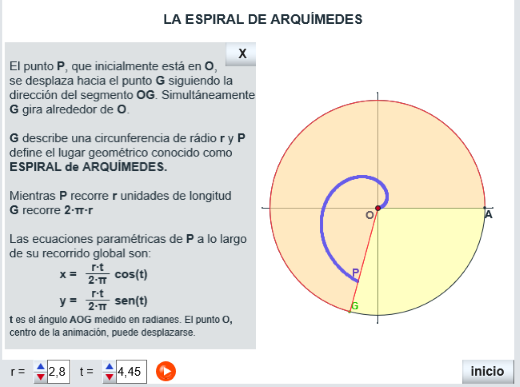
Las siguientes utilidades muestran: la primera, además de las ecuaciones paramétricas de la espiral, la manera como se genera el lugar geométrico conocido como espiral de Arquímedes y la otra la determinación de un segmento de longitud raiz cuadrada de π, en esta ocasión mediante la mencionada espiral de Arquímedes y la ecuación cartesiana de dicho lugar geométrico.
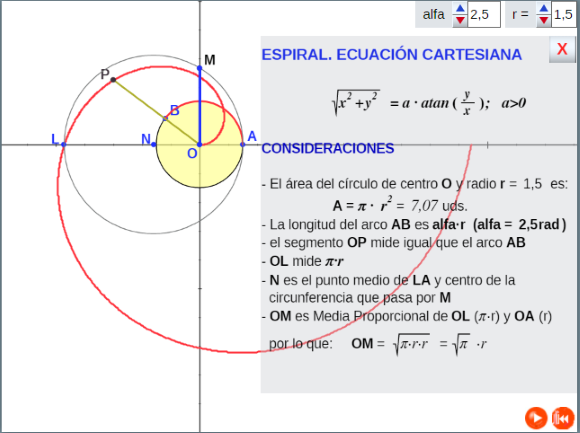
deducción de raiz de π con la espiral de Arquímedes
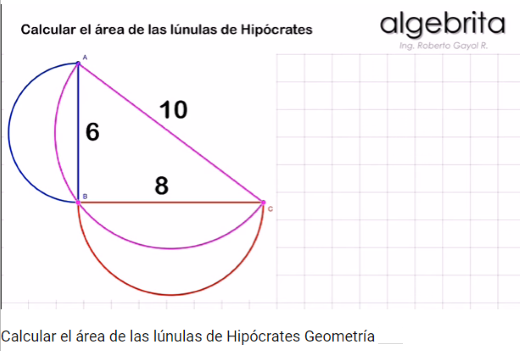
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra la deducción, paso a paso, del área de las lúnulas de Hipócrates.
,Continuando con la creación de la miscelánea "Las Espirales" sugerimos completar su elaboración extrayendo el contenido relacionado con las cuadraturas estudiadas para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos. Cuadraturas"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La cuadratura del círculo: Historia de una obsesión.
XIV Programa de Promoción de la Cultura Científica y Tecnológica.
Rev. Real Acad. Ci. Exact. Fis. Nat. (Esp) Vol. 105, Nº 2 (2012), 241-258
Fernando Bombal - Cuadraturas
Prof. Esteban Rubén Hurtado Cruz. Facultad de Ciencias UNAM. Cálculo Diferencial e Integral II - Páginas en GeoGebra de Vicente Martín Torres López
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
Proporcionalidad. Las Espirales XI
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades a los subproyectos: TELESECUNDARIA, GEOgráfica-GEOevaluación y PLANTILLAS.
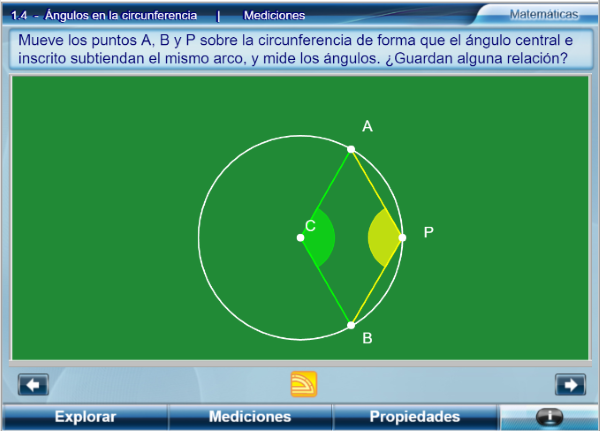
Como muestra enlazamos la unidad sobre Ángulos en la circunferencia, del subproyecto TELESECUNDARIA,
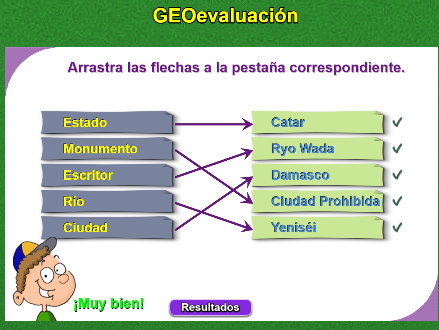
la GEOevaluación de Asia
y los ejemplos de Puzle de intercambio de imágenes tipo 2 donde Descartes realiza directamente el troceado en 4x4 de las imágenes, del subproyecto PLANTILLAS.
Dentro de nuestro ámbito local destacan, entre otras, las Misceláneas sobre las espirales y los lugares geométricos, todas ellas de indudable valor en cuanto establecen un hito en el estudio de estos objetos matemáticos. Se muestran y/o enlazan a continuación: una escena prolegómeno del estudio del l.g. "Concoide de Nicomedes" para más adelante ver su uso en la trisección de un ángulo, una miscelánea, que es un estudio riguroso y completo sobre las espirales logarítmicas y una segunda que complementa a la anterior. La excelente documentación aportada por ambas es una extraordinaria introducción a estudios más complejos de estos objetos y a la creación de utilidades educativas, dinámicas e interactivas.
Artículos anteriores mostraban, paso a paso y exhaustivamente, escenas interactivas con la creación de lugares geométricos (l.g.) por un punto, el actual muestra, según hemos visto, la creación de la Concoide de Nicomedes que es un l.g. definido por dos puntos, cuya posición depende del desplazamiento de un tercer punto por un eje. En próximas entradas se mostrará como trisecar un ángulo agudo con la Concoide.
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra con una belleza y claridad incuestionables la relación de la espiral con el origen del conocimiento tanto física como metafísicamente y son de especial relevancia la calidad de las fotografias y composiciones expuestas. El objetivo de este vídeo es el de apreciar distintas formas de enfocar el tema que nos ocupa: "Las Espirales.
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral Logarítmica" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:
- Hemos creado la siguiente escena: Espiral Logarítmica
- Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto.
La escena del proyecto puede verse a continuación:
Desde este enlace puede descargarse el proyecto de miscelánea con la espiral Logarítmica incluida.
También, relacionado con el tema de los lugares geométricos (l.g.) y sus utilidades, hemos incluido el trabajo realizado con el programa GeoGebra donde se muestra la construcción de la Concoide de Nicomedes para, más tarde, usarla en la trisección de un ángulo.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Proporcionalidad. Espirales Aritméticas
Afortunadamente continúan las innovaciones en las posibilidades operativas y de uso de los materiales y Escenas de la Red Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS para intentar estar al día de las mismas, fundamentalmente a estos, que llevan a la información sobre cómo comunicar las escenas con el HTML y viceversa, y las escenas entre si y a estos otros que ilustran la manera de integrar el cálculo simbólico en las escenas.
También queremos animar a colaborar con los compañeros que están trabajando en el proyecto ed@d en moodle. El material que se está elaborando puede suponer una mejora extraordinaria en la labor educativa con un aumento significativo en la cantidad y calidad de la información expuesta y en la comunicación alumno-alumno, profesor-alumno y viceversa.
En este artículo nos vamos a centrar en la creación de una miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirá, estudiará y representará alguna de las siguientes espirales:
- Espiral Aritmética o de Arquímedes
- Espirales arquimedianas. Envolventes Uniformes de: 2, 3, 4, ..., n centros. (Enlace cambiado el 16 de agosto de 2023 al quedar roto el original)
- Espiral de litius
- Espiral de Fermat
- Espiral de Pitágoras (de Teodoro, de caracol...)
- Espilral de Ulam
- Espiral de Cornu
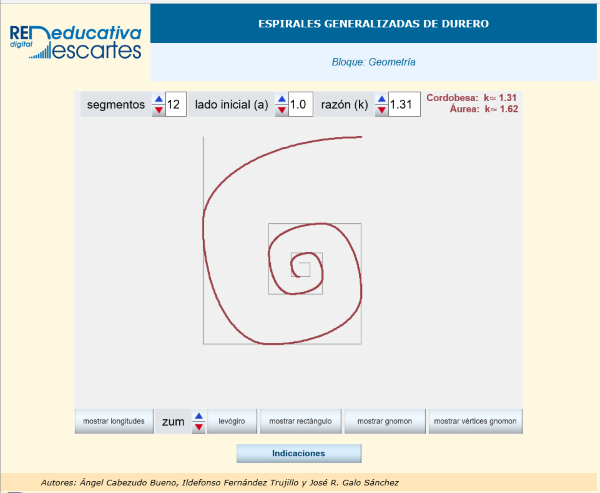
- Espiral de Durero
- Espiral de Fibonacci (Enlace cambiado el 16 de agosto de 2023 al quedar roto el original)
- Espiral Hiperbólica (Enlace cambiado el 16 de agosto de 2023 al quedar roto el original)
- Espiral Logarítmica (Enlace cambiado el 16 de agosto de 2023 al quedar roto el original)
- Espiral de Parker (del viento solar)
- Espiral Cordobesa
Cada elemento de la lista anterior enlaza con una página que puede contener o enlazar a: la definición, la ecuación en polares, las ecuaciones paramétricas, la gráfica y otras características de cada espiral, por lo que la miscelánea que vamos a elaborar estará enfocada a mostrar el proceso de planificación y realización de dicha miscelánea teniendo en cuenta que los objetivos didácticos de cara al alumnado son: las aplicaciones de la proporcionalidad y el potencial de uso de las funciones trigonométricas elementales, logarítmicas y exponenciales.
Aprovecharemos este artículo, los siguientes y la miscelánea que elaboraremos, para la presentación de la espiral Cordobesa, particularización de las espirales gnomónicas y fruto de un largo y laborioso trabajo colaborativo, aún vigente, que nuestro compañero, Ángel Cabezudo Bueno, ha concretado, provisionalmente, con éxito.
No debe olvidarse que estamos estudiando una de las aplicaciones del concepto de Proporcionalidad siguiendo algunos de los materiales que están disponibles en el Proyecto Descartes y, eventualmente, algún otro contenido que por su indudable interés lo merezca.
LAS ESPIRALES ARITMÉTICAS
Al escenario donde va a desarrollarse la acción (E1) le hemos asignado unas dimensiones de 800x612 y dentro de este espacio general definiremos tres espacios rectangulares según muestra la siguiente imagen.
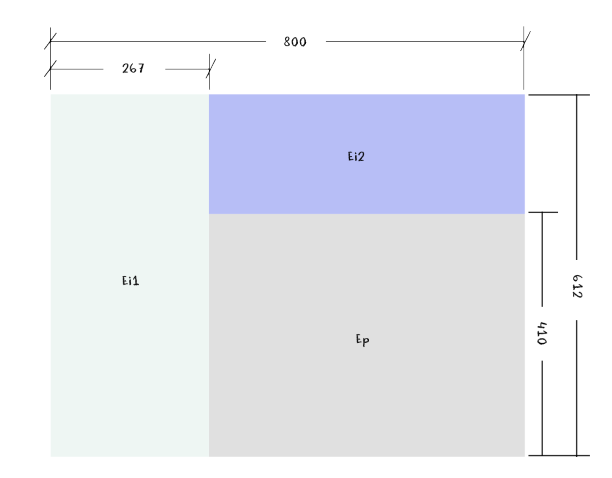
Los espacios Ei1 y Ei2 son, fundamentalmente, informativos aunque, eventualmente, pueden alojar algún elemento interactivo como un botón o un campo de texto. En el espacio Ep es donde se desarrollarán las acciones principales de la primera escena que está dedicada a la espiral Aritmética (de Arquímedes) y al grupo de espirales uniformes de 2, 3,...,n centros.
Comenzaremos trabajando de una forma peculiar, crearemos un solo espacio, el Ep, de dimensiones: 533x410 (conviene observar que 533 y 410 son, aproximadamente, el 67% de 800 y de 612 respectivamente) desarrollaremos todas las acciones de la primera escena que tienen lugar en este espacio con sus interrelaciones y, una vez finalizado este proceso, añadiremos los espacios Ei1 y Ei2, los dotaremos de contenido, y sincronizaremos la acción.
La base teórica de todo el trabajo para esta primera escena va a ser la observación de Arquímedes que originó la espiral que lleva su nombre:"Imaginaos una línea que gira con velocidad constante alrededor de un extremo, manteniéndose siempre en un mismo plano, y un punto que se mueve a lo largo de la línea con velocidad lineal constante: ese punto describirá una espiral"

Creamos el espacio Ep de 533x410 y en él vamos a representar lo descrito en la definición de tres maneras diferentes con objeto de practicar con las funciones seno y coseno y el concepto de proporcionalidad.
- Partiendo de dos segmentos horizontales superpuestos. Uno que gira a derechas y otro que gira a izquierdas.
- Partiendo de dos segmentos horizontales unidos por el punto fijo que giran en el sentido opuesto a las agujas del reloj.
- Partiendo de dos segmentos verticales superpuestos. Uno que gira a derechas y otro que gira a izquierdas.
Consideramos las dos opciones posibles de giro del segmento y algunas de las composiciones que seguramente son conocidas por todos pues son de uso habitual.
También, en esta primera escena, vamos a mostrar la construcción de las espirales uniformes de dos y tres centros lo que unido a las explicaciones informativas que se incluirán en su momento bastará para aprender a construir una espiral uniforme de cualquier número de centros. Esto hace que para mantener el carácter didáctico del código convenga añadir un nuevo espacio, que superpuesto al anterior se hará visible cuando el primero esté oculto.
Para conseguir lo expuesto necesitaremos definir algunos controles de distinto tipo, algún vector, varias funciones, diversos algoritmos de cálculo y bastantes gráficos.
Vamos a mostrar lo que queremos conseguir y luego veremos, paso a paso como lo hemos realizado.
El siguiente vídeo muestra como se ha realizado la escena anterior.
En próximas entradas continuaremos con el paso a paso de la escena, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Respecto al trabajo de investigación sobre las espirales gnomónicas en general y sobre la Cordobesa, en particular, que se está desarrollando, queremos mostrar los siguientes avances y animar a aportar alguna ayuda en el proceso de generalización emprendido.
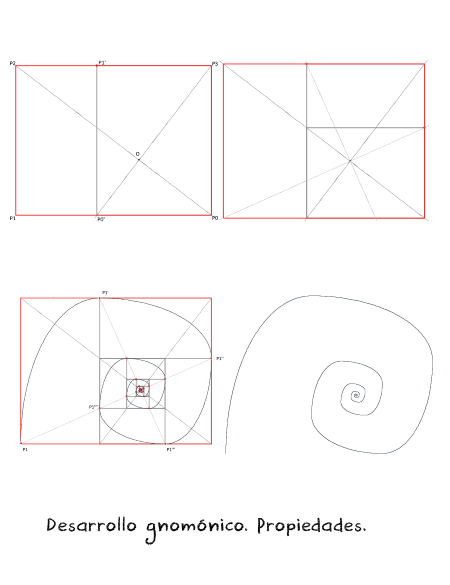
La siguiente escena muestra el avance realizado respecto a las iniciales.Espirales. Proceso de generalización
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo