Mostrando artículos por etiqueta: universidad
 Título: Interpretación geométrica de la derivada direccional
Título: Interpretación geométrica de la derivada direccional
Sección: Miscelánea
Bloque: Análisis
Unidad: Derivación de funciones
Nivel/Edad: Universitario (18 o más) años
Idioma: Castellano
Autoría: Elena E. Álvarez Sáiz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm
Este material está publicado bajo una licencia:

Creative Commons Atribución-NoComercial- CompartirIgual 3.0.
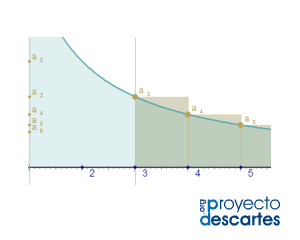 Título: Resto enésimo: criterio integral
Título: Resto enésimo: criterio integral
Sección: Miscelánea
Bloque: Análisis
Unidad: Integración de funciones
Nivel/Edad: Universitario (18 o más) años
Idioma: Castellano
Autoría: Elena E. Álvarez Sáiz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm
Este material está publicado bajo una licencia:

Creative Commons Atribución-NoComercial- CompartirIgual 3.0.
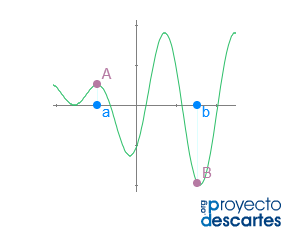 Título: Teorema de Bolzano. Método de la bisección
Título: Teorema de Bolzano. Método de la bisección
Sección: Miscelánea
Bloque: Análisis
Unidad: Límites y continuidad de funciones
Nivel/Edad: Universitario (18 o más) años
Idioma: Castellano
Autoría: Elena E. Álvarez Sáiz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm
Este material está publicado bajo una licencia:

Creative Commons Atribución-NoComercial- CompartirIgual 3.0.
Descartes en la Universidad. Miscelánea: Extremos de funciones de dos variables. Método del Hessiano
Acceso a la miscelánea: Extremos de funciones de dos variables. Método del Hessiano.
En esta escena se muestra cómo realizar el estudio de los extremos relativos de una función diferenciable de dos variables.
Introducida la expresión de una función diferenciable y de sus derivadas parciales primeras, se puede analizar en primer lugar, qué puntos tienen el plano tangente horizontal (condición necesaria para que un punto sea extremo). Posteriormente, el método del hessiano permitirá determinar cuáles de esos puntos son máximos o mínimos relativos.
Este método se justifica utlilizando el polinomio de Taylor de la función de grado 2 centrado en el punto en el que se está realizando el análisis.
El vídeo siguiente explica el funcionamiento de esta escena.
Acceso a la miscelánea: Extremos de funciones de dos variables. Método del Hessiano.
Se presenta la miscelánea:Gradiente y curvas de nivel
En esta escena se muestra la propiedad siguiente del gradiente: el vector gradiente de una función de dos variables en un punto P es ortogonal a la curva de nivel C que pasa por dicho punto, esto significa que es ortogonal al vector tangente a la curva C en el punto P.
La miscelánea se puede configurar modificando el valor de la función e introduciendo o bien un punto P, o bien un valor de k de manera que al hallar la intersección de la gráfica de la función con el plano z=k nos permita determinar la curva de nivel. En el primer caso, cuando se da las coordenadas del punto P, la curva de nivel se obtiene considerando k como el valor f(P).
A partir de estos datos se representa, por un lado, la superficie de la función, y por otro, la curva de nivel. Se tiene además la posibilidad de incluir las coordenadas de un vector cualquiera para comprobar que únicamente será ortogonal a la curva de nivel en el punto, cuando sea proporcional al gradiente en dicho punto.
En la miscelánea se ha incluido también un botón que, al pulsar sobre él, nos conduce a la demostración de esta propiedad del gradiente.
El vídeo siguiente explica el funcionamiento de esta escena.
Acceso a la miscelánea:Gradiente y curvas de nivel
El proyecto Un_100 comprende 101 unidades didácticas del nivel universitario en las áreas de Matemáticas y de Física. Es un proyecto que ha contado con el patrocinio de varias instituciones mejicanas y la participación en su desarrollo de otras de Chile, Colombia, España y México. Todas las unidades tienen un mismo esquema o plantilla común, con un diseño gráfico genérico, y sobre él cada desarrollador ha incorporado los contenidos y ha elaborado su secuencia didáctica personal. Se distinguen cuatro fases o momentos: Motivación, Inicio, Desarrollo y Cierre, y se complementa con un acceso a la documentación de la unidad en la que además se incluyen los créditos.
El tema de esta unidad es la representación de la muestra de una población.
Se trata de que el usuario adquiera experiencia en el uso del concepto de muestreo.
Se parte de una pregunta de investigación, cuál es la altura de los niños o de las niñas de una cierta edad o nivel educativo en una determinada comunidad y se pasa después a su desarrollo en dos partes, en la primera se indaga cuál debe ser el tamaño de la muestra para que sea representativa y en la segunda parte la relación entre el tamaño de la muestra y la dispersión de la población. En ambos casos el usuario puede configurar la población y la muestra y observar los resultados que se muestran con los datos estadísticos y las gráficas correspondientes para un mejor análisis
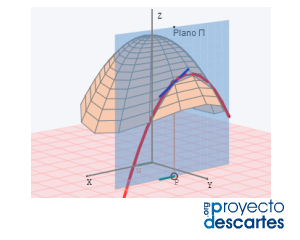
Se presenta la miscelánea: Interpretación geométrica de la derivada direccional
Igual que ocurría en el caso de la derivada de una función de una variable en un punto, la derivada direccional de una función f de dos variables en un punto P es la pendiente de una recta. En este caso se trata de la recta tangente a la superficie, gráfica de la función f, en el punto f(P) que además está contenida en el plano vertical que contiene al punto P y a la dirección.
Como las derivadas direccionales en las direcciones paralelas al eje X y al eje Y son las derivadas parciales, la escena también permite mostrar su interpretación geométrica.
Introduciendo la expresión de la función y las coordenadas del punto, la miscelánea guía en la construcción de la recta tangente cuya pendiente coincide con la derivada direccional que se elija.
El vídeo siguiente explica el funcionamiento de esta escena.
Acceso a la miscelánea: Interpretación geométrica de la derivada direccional
Se trata de una unidad perteneciente al proyecto Un_100, un proyecto de la Red Educativa Digital Descartes que recoge unidades didácticas interactivas de matemáticas y física para un nivel de Bachillerato y Universidad.
En la elaboración de las unidades de este proyecto han participado académicos de México, España, Colombia y Chile.
El objetivo de esta unidad es presentar cuatro conceptos fundamentales del cálculo: el límite, la derivada, la integral y el teorema fundamental del cálculo. El alumno podrá experimentar con los interactivos observando que el cálculo se basa en problemas de resolver límites, ya sea el límite de la suma de polígonos para el caso de la integral, o el límite de la pendiente de dos puntos arbitrariamente cercanos en una curva, para la derivada. Se explica que el teorema fundamental del cálculo permite relacionar a la derivada e integral como funciones inversas.
Se presenta la miscelánea: Resto de Lagrange
Esta escena analiza el resto de la aproximación de una función derivable n veces en un punto a por su polinomio de Taylor de grado n a partir de la expresión del resto debida a Lagrange.
Esta expresión es una generalización del teorema del valor medio del cálculo diferencial y permite, en algunos casos, acotar el error de la aproximación de una función por su polinomio de Taylor.
Para la utilización de esta miscelánenea se debe introducir la expresión de la función, su derivada de orden n y los puntos a y x que se corresponden, respectivamente, con el punto en el que se hace el desarrollo y el punto en el que se quiere estudiar la aproximación. A partir de estos datos se puede calcular el polinomio de Taylor de cualquier grado centrado en el punto a siempre que la función sea suficientemente derivable en un dicho punto.
El vídeo siguiente explica el funcionamiento de esta escena.
Acceso a la miscelánea: Resto de Lagrange
Se presenta la miscelánea: Polinomios de Taylor
Con esta escena se pueden obtener los polinomios de Taylor hasta el grado 4 de cualquier función que sea lo suficientemente derivable en un punto a.
Se representa además, en una misma gráfica, la función y los distintos polinomios de Taylor calculando sus valores en puntos x que son próximos al punto en el que se hace el desarrollo, punto a. El objetivo es poder observar la tesis del teorema de Taylor viendo que el valor de la función en un punto x se puede aproximar por el valor que toman los distintos polinomios de Taylor en dicho punto. Puede también comprobarse que esta aproximación es mejor cuanto mayor sea el grado del polinomio y cuanto más próximo esté x del punto a.
El vídeo siguiente explica el funcionamiento de esta escena.
Enlace a la miscelánea: Polinomios de Taylor







