Mostrando artículos por etiqueta: universidad
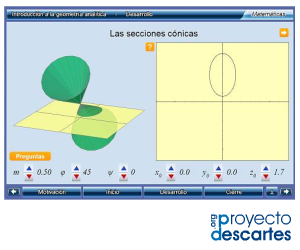
Título: Introducción a la geometría analítica
Sección: Un_100
Bloque: Geometría
Unidad: Geometría analítica plana
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: José Luis Abreu León y Alejandro Radillo Díaz
Diseño funcional: José Luis Abreu León y Alejandro Radillo Díaz
Programación: José Luis Abreu León y Alejandro Radillo Díaz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
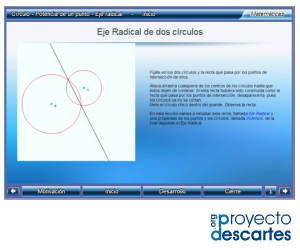
Título: Círculo, potencia, eje radical
Sección: Un_100
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Carlos Hernández Garciadiego
Diseño funcional: Carlos Hernández Garciadiego
Programación: Carlos Hernández Garciadiego
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
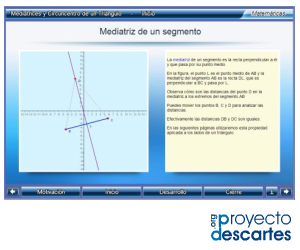
Título: Mediatrices y circuncentro de un triángulo
Sección: Un_100
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Carlos Hernández Garciadiego
Diseño funcional: Carlos Hernández Garciadiego
Programación: Carlos Hernández Garciadiego
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
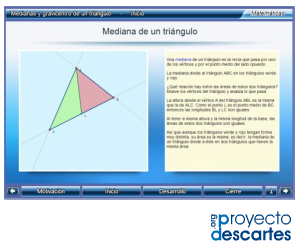
Título: Medianas y gravicentro de un triángulo
Sección: Un_100
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Universidad y Bachillerato (16 años en adelante)
Idioma: Castellano
Diseño del contenido: Carlos Hernández Garciadiego
Diseño funcional: Carlos Hernández Garciadiego
Programación: Carlos Hernández Garciadiego
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
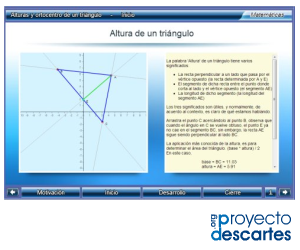
Título: Alturas y ortocentro de un triángulo
Sección: Un_100
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Universidad y Bachillerato (16 años en adelante)
Idioma: Castellano
Diseño del contenido: Carlos Hernández Garciadiego
Diseño funcional: Carlos Hernández Garciadiego
Programación: Carlos Hernández Garciadiego
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
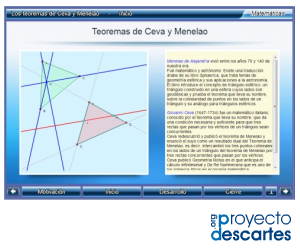
Título: Los teoremas de Ceva y Menelao
Sección: Un_100
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Carlos Hernández Garciadiego
Diseño funcional: Carlos Hernández Garciadiego
Programación: Carlos Hernández Garciadiego
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: El Teorema de Pick
Sección: Un_100
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Joel Espinosa Longi
Diseño funcional: Joel Espinosa Longi
Programación: Joel Espinosa Longi
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: El cono y la esfera según Arquímedes
Sección: Un_100
Bloque: Geometría
Unidad: Geometría métrica tridimensional
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: José Luis Abreu León
Diseño funcional: José Luis Abreu León
Programación: José Luis Abreu León
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
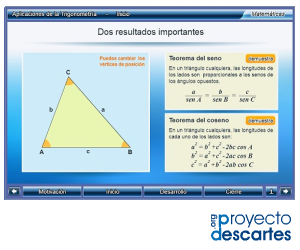
Título: Aplicaciones de la trigonometría
Sección: Un_100
Bloque: Geometría
Unidad: Trigonometría
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: María José García Cebrian
Diseño funcional: María José García Cebrian
Programación: María José García Cebrian
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
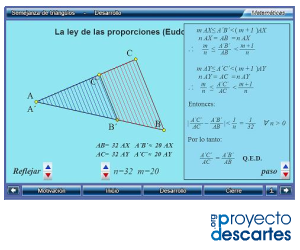
Título: Semejanza de triángulos
Sección: Un_100
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: José Luis Abreu León y Alejandro Radillo Díaz
Diseño funcional: José Luis Abreu León y Alejandro Radillo Díaz
Programación: José Luis Abreu León y Alejandro Radillo Díaz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional