Mostrando artículos por etiqueta: universidad
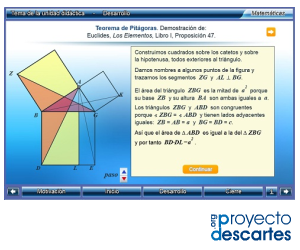
Título: Áreas y Perímetros
Sección: Un_100
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Jose Luis Abreu León y Leticia Monserrat Vargas Rocha
Diseño funcional: José Luis Abreu León y Leticia Monserrat Vargas Rocha
Programación: José Luis Abreu León y Leticia Monserrat Vargas Rocha
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
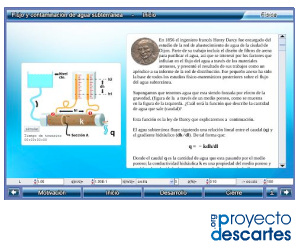
Título: Flujo y contaminación de agua subterránea
Sección: Un_100
Bloque: Geología
Unidad: Geofísica
Nivel/Edad: Universidad y Bachillerato (16 años en adelante)
Idioma: Castellano
Diseño del contenido: Oliver López Corona y Elvia Ramírez Carrillo
Diseño funcional: Oliver López Corona
Programación: Oliver López Corona
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
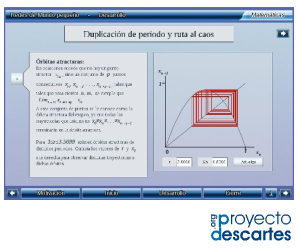
Título: Caos Determinista
Sección: Un_100
Bloque: Geometría
Unidad: Fractales y caos
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Daniel Monsivais Velázquez
Diseño funcional: Daniel Monsivais Velázquez
Programación: Daniel Monsivais Velázquez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
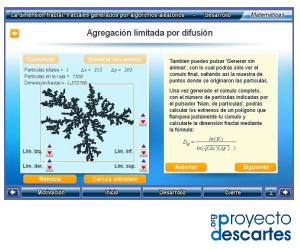
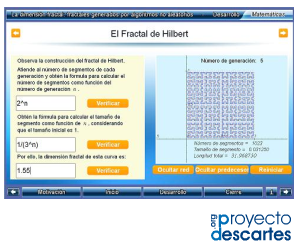
Título: La dimensión fractal: fractales generados por algoritmos aleatorios
Sección: Un_100
Bloque: Geometría
Unidad: Fractales y caos
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Alejandro Radillo Díaz
Diseño funcional: Alejandro Radillo Díaz
Programación: Alejandro Radillo Díaz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: La dimensión fractal: fractales generados por algoritmos no aleatorios
Sección: Un_100
Bloque: Geometría
Unidad: Fractales y caos
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Alejandro Radillo Díaz
Diseño funcional: Alejandro Radillo Díaz
Programación: Alejandro Radillo Díaz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
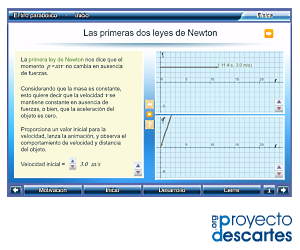
Título: El tiro parabólico
Sección: Un_100
Bloque: Los movimientos
Unidad: Cinemática
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: José Luis Abreu, Alejandro Radillo Díaz
Diseño funcional: José Luis Abreu, Alejandro Radillo Díaz
Programación: José Luis Abreu, Alejandro Radillo Díaz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
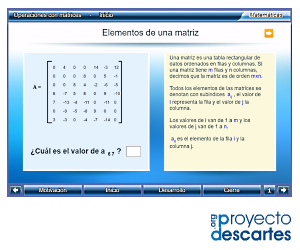
Título: Operaciones con matrices
Sección: Un_100
Bloque: Álgebra
Unidad: Álgebra Lineal
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Juan Guillermo Rivera Berrío
Diseño funcional: Carlos Mario Restrepo Restrepo
Programación: Héctor Javier Herrera
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
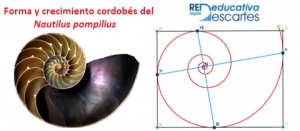
Hay una tendencia a tratar de asociar o encontrar en todo aquello que es bello la proporción áurea o divina, o a construir objetos a partir de esta razón porque se presuponen serán apreciados como bellos por el simple hecho de seguir dicha pauta. Esto, como no, también ha acontecido con la modelación matemática de la concha del Nautilus pompilius sobre la que suele afirmarse que su forma y crecimiento es áureo. Sin embargo, en este artículo se muestra y se analiza en detalle cómo dicha concha lo que realmente sigue es un patrón ubicado en la denominada proporción cordobesa o humana. Con apoyo en un recurso interactivo desarrollado con la herramienta Descartes se motiva el análisis y comportamiento y se procede a partir de la yocto-yotta realidad observada a construir el modelo matemático, el cual se detalla ampliamente.
Pulsando sobre la siguiente imagen se accede a dicho recurso interactivo que se aborda o plantea en seis fases:
- Ajuste de la concha por una espiral logarítmica.
- Ajuste del sifúnculo por una espiral logarítmica.
- Ajuste global por una familia de espirales cordobesas.
- Mejora del modelo discreto.
- Aproximación de los septos.
- Modelo matemático del Nautilus pompilius.
|
|
En cada fase se dispone de un botón de información que, al pulsarlo, da acceso a un detalle de las propiedades que pueden inducirse a partir de la interacción con la escena. |
 |
| Y en el botón de indicaciones se aborda una introducción, los objetivos, las instrucciones de uso en cada fase y finalmente se enlaza un artículo donde se detalla el análisis matemático realizado. Este artículo está embebido a continuación o bien puede abrirse y/o descargarse desde este enlace. |
En las conclusiones del artículo anterior afirmamos:
A través del detallado y progresivo análisis realizado hemos ido construyendo la base teórica o modelo matemático que soporta a la bella morfología del Nautilus Pompilius y hemos tratado del encontrar el modelo de crecimiento que conduce a poder explicar y a comprender por qué adquiere esa forma. Desde su inicio la espiral logarítmica cordobesa tomó presencia y a medida que la mirada se deslizaba hacia algún nuevo detalle esta espiral ha vuelto a imponer su presencia marcándonos y alumbrándonos el camino del descubrimiento y de la adquisición del conocimiento. La belleza del Nautilus pompilius se sustenta en la proporción cordobesa o humana y todo punto de su concha o del interior ha quedado determinado por la intersección de dos espirales cordobesas. El germen o base inicial matemática que explica el por qué acontece todo lo observado, se ha ubicado en el crecimiento gnomónico de un triángulo cordobés, las propiedades de éste se trasladan al desarrollo y comportamiento global detectado y modelado.
Deseamos que nuestro trabajo de investigación satisfaga tu curiosidad y te animamos a interactuar con nosotros bien realizando algún comentario en este blog (los comentarios no se publicarán directamente sino que pasan por una moderación previa a su publicación) o bien escribe al correo de nuestra RED Descartes: descartes@proyectodescartes.org.
Título: Sobre el crecimiento cordobés del Nautilus Pompilius
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Universidad (18 años o más)
Idioma: Castellano
Autoría: José R. Galo Sánchez, Ángel Cabezudo Bueno e Ildefonso Fernández Trujillo
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional