Mostrando artículos por etiqueta: descartesjs

 ¡Ya está aquí el Número 10 de la Revista Digital Red Descartes!
¡Ya está aquí el Número 10 de la Revista Digital Red Descartes! 

Celebramos 5 años de innovación educativa con una edición especial llena de ideas, recursos y experiencias que transforman la enseñanza.
En este número encontrarás:
 Juegos didácticos adaptativos AJDA
Juegos didácticos adaptativos AJDA La revolución de los libros interactivos en matemáticas
La revolución de los libros interactivos en matemáticas IA generativa aplicada a la educación: análisis y herramientas
IA generativa aplicada a la educación: análisis y herramientas Matemáticas, arte y belleza: espiral de Durero, ternas pitagóricas y planteamiento académico y gráfico del Teorema de Pitágoras
Matemáticas, arte y belleza: espiral de Durero, ternas pitagóricas y planteamiento académico y gráfico del Teorema de Pitágoras Proyectos, investigación y creatividad educativa en acción
Proyectos, investigación y creatividad educativa en acciónNuestra revista es interactiva: no solo se lee, ¡se explora! Videos, escenas dinámicas, animaciones y recursos DescartesJS la convierten en una experiencia única para docentes, estudiantes y apasionados de la educación digital.
 Disponible gratis, abierto y con licencia Creative Commons.
Disponible gratis, abierto y con licencia Creative Commons.
Los contenidos incluidos están accesibles en línea pulsando sobre la siguiente imagen, también puede consultarlos en formato pdf y si lo desea descargarlos en su ordenador.
|
Para acceder al décimo número pulse sobre la imagen |
|
Este número refleja un compromiso constante por parte de la Red Descartes: integrar lo mejor de la tecnología al servicio de una educación más inclusiva, creativa y personalizada. Invitamos a nuestros lectores a interactuar, experimentar y reflexionar con cada una de las propuestas, siempre con el espíritu de compartir conocimiento y construir comunidad.
Confiamos en que este décimo número satisfaga el interés de múltiples lectores y resulte atractivo y variado.
Recuerde que puede aportar sus comentarios y observaciones, su retroalimentación es importante para nosotros. ¡Conecte con RED Descartes! Y si desea compartir, sus artículos serán muy bienvenidos ¡queremos leer, interactuar y aprender contigo!
¡Quedán invitados a publicar sus artículos en nuestra revista! Como referencia para la composición de su contenido pueden consultar las "Normas de publicación" y para cualquier duda o propuesta quedamos atentos en nuestra dirección de correo Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo..
Divulgamos en este artículo el acceso a la Defensa del Trabajo Final Integrador de la Maestría en Enseñanza en Escenarios Digitales, aprobada por Resolución Ministerial RM 1053/24, perteneciente a la AUSA (Asociación de Universidades Sur Andina, Argentina) de la profesora Dª. Fabiana Andrea González, experiencia basada en la problemática de la brecha educativa en matemática entre el nivel medio y el nivel superior, con especial foco en los estudiantes ingresantes a la Facultad de Ciencias Económicas (FCE) de la Universidad Nacional de la Patagonia San Juan Bosco (UNPSJB), sede Trelew, en Argentina. A partir del diagnóstico realizado, se identificaron dificultades significativas en el desempeño de los estudiantes de primer año, vinculadas a la falta de conocimientos matemáticos básicos y a la ausencia de estrategias adecuadas para el aprendizaje de la disciplina.
En respuesta a esta situación, se propone el diseño de un Libro Digital Interactivo (LDI) como una estrategia didáctico pedagógica innovadora para mejorar la enseñanza y el aprendizaje de la matemática preuniversitaria, diseñando la misma como una experiencia de aprendizaje contextualizada. Este recurso integra elementos multimedia y actividades interactivas que favorecen la autonomía del estudiante y promueven un aprendizaje más dinámico y significativo. A su vez, el LDI de la RED Descartes se enmarca dentro del concepto de Recursos Educativos Abiertos (REA), lo que permite su libre acceso y reutilización en diferentes contextos educativos, permitiendo adecuarlo a los requerimientos de los estudiantes.
El estudio resalta la importancia de la incorporación de herramientas didáctico-digitales al servicio de proyectos educativos en el proceso de enseñanza-aprendizaje y el rol fundamental del docente como creador de contenido digital.
Los resultados obtenidos permiten concluir que la utilización de materiales digitales interactivos, como estrategia didáctica en el nivel superior, puede contribuir a reducir la brecha educativa en matemática, mejorar la retención de los estudiantes y fortalecer su desempeño en los primeros años de la universidad.
A continuación insertamos la presentación utilizada por la maestranda para defender su Trabajo Final Integrador, que enlazamos y cuya lectura recomendamos. A su vez, ofrecemos el audiovisual con su intervención ante el tribunal.
Diseño de un Libro Digital Interactivo (RED Descartes) como estrategia para la enseñanza-aprendizaje de Matemática Básica en la Educación Superior, es el título de este gran Trabajo Final Integrador cuya reflexión final destaca la importancia de estar relacionados con la comunidad educativa global a través de redes como RED Descartes. Formar parte de una red educativa global ofrece diversas ventajas y oportunidades:
- Intercambiar conocimientos, al interactuar con docentes de otras universidades en todo el mundo, se abre la puerta a un intercambio valioso de conocimientos. Cada institución puede tener enfoques y perspectivas únicas que enriquecen la comprensión colectiva.
- Compartir experiencias con colegas de diferentes lugares permite aprender de los desafíos y éxitos de otros, lo que puede ayudar a mejorar las prácticas pedagógicas y encontrar soluciones innovadoras.
- Compartir recursos educativos. Acceder a materiales y herramientas digitales amplía el abanico de recursos a utilizar por los docentes.
- Participar en redes educativas globales ofrece oportunidades constantes de capacitación continua y desarrollo profesional. Esto es esencial en un entorno educativo en constante evolución.
En resumen, formar parte de comunidades educativas globales como RED Descartes no sólo amplía el horizonte de posibilidades para mejorar la enseñanza y el aprendizaje, sino que también fomenta la colaboración y la construcción de una red profesional sólida y diversificada.
Desde RED Descartes trasladamos nuestra más sincera enhorabuena a la nueva Mg. Ing. Fabiana Andrea GONZÁLEZ y mostramos todo el agradecimiento por su colaboración para la publicación y divulgación de esta experiencia.
¿Quieres aprender a crear libros interactivos que faciliten tu labor docente y cautiven a tu alumnado y a tus lectores? Únete a nuestro curso y descubre cómo utilizar las herramientas de inteligencia artificial y DescartesJS para diseñar libros interactivos educativos y páginas dinámicas.
Queda abierto el plazo de inscripción gratuita a la II Edición del Curso para el "Diseño de libros interactivos con DescartesJS y herramientas de Inteligencia Artificial", una acción formativa que se enmarca en el programa de Educación Abierta desarrollado entre redes docentes de Colombia, México y España, fundamentalmente, aunque contamos con la participación de profesorado de otros países de habla hispana, portuguesa e inglesa.
Está dirigido a docentes de cualquier etapa educativa, infantil, primaria, educación secundaria obligatoria, bachillerato, formación profesional, enseñanzas de régimen especial y universidad, y de cualquier materia o especialidad, en activo o no, así como a profesionales vinculados a la educación o formación y a diseñadores y desarrolladores interesados en libros y objetos interactivos, utilizando una metodología activa, concretamente Clase Invertida y Aprendizaje Basado en Proyectos (Tareas), pues desde la primera sesión cada participante comenzará a diseñar y editar su primer libro interactivo, recibiendo sesiones quincenales por videoconferencia, que serán grabadas y compartidas con todos los participantes y asesorados por docentes de las redes mencionadas.
El curso comienza el próximo día 17 de octubre y finaliza el 13 de febrero de 2026, impartiéndose las sesiones de 7 AM a 8 AM en el horario oficial de Colombia, de acuerdo al siguiente calendario previsto y contenidos a tratar:
Para cualquier consulta o aclaración, puedes contactar con nosotros en la dirección de correo Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
| ACCESO AL FORMULARIO DE INSCRIPCIÓN |
Este formulario estará abierto hasta el día 10 de octubre o hasta cubrir disponibilidad.
Toda la información sobre el curso se encuentra disponible, como no puede ser de otra manera, en el formato libro interactivo, ofreciendo allí, conforme a la metodología, los contenidos y tareas de la primera sesión. Así, tenemos:
- Metodología
- Programación detallada
- Prepárate para la primera sesión
- Descarga el libro plantilla
- Trabajos en la primera sesión
- Estructura del libro
Relación de recursos de gran interés
Documentación y vídeos del curso
"Diseño de libros interactivos con DescartesJS y herramientas de IA"
Recursos y tutoriales previos:

Los vídeos con la grabación de cada sesión del curso, que se imparte por videoconferencia según el calendario establecido, se irán publicando progresivamente a continuación:´
- Vídeo de la 1ª sesión (17 de octubre 2025). Presentación de la 1ª sesión.
- Vídeo de la 2ª sesión (31 de octubre 2025). Presentación de la 2ª sesión.
- Vídeo de la 3ª sesión (14 de noviembre 2025). Presentación de la 3ª sesión.
- Vídeo de la 4ª sesión (28 de noviembre 2025). Presentación de la 4ª sesión.
- Vídeo de la 5ª sesión (12 de diciembre 2025). Presentación de la 5ª sesión.
- Vídeo de la 6ª sesión (16 de enero 2026). Presentación de la 6ª sesión.
- Vídeo de la 7ª sesión (30 de enero 2026). Presentación de la 7ª sesión.
- Vídeo de la 8ª sesión (27 de febrero 2026).
Recursos ofrecidos durante la primera sesión
- Editores de texto plano
- Notepad++
- Sublime Text
- Phoenix Code
- Visual Studio
- Explicación sobre la instalación y uso de editores de texto plano para el libro interactivo
- En este video te explicamos cómo descargar y usar un editor de código para archivos HTML y CSS, necesario para editar los libros interactivos. Se incluyen dos editores adicionales: Sublime Text y Visual Studio.
- Tutoriales y manuales
- Diseño de libros interactivos (Segunda edición)
- Manual HTML5 (Una guía completa para dominar HTML desde cero)
- Manual CSS Manual CSS (Domina el diseño y estilo de tus páginas web)
- Manual de Visual Estudio Code (Guía completa para principiantes)
- Manual Phoenix Code (Guía completa para evitar errores y trabajar eficientemente)
- Manual Notepad++ (Guía completa para programar sin errores con Notepad++)
- Referencia de entidades HTML (Símbolos matemáticos, letras griegas,...)
- Manual de referencia KaTeX (Símbolos y funciones matemáticas para nuestros libros interactivos)
- ¿Qué debe contener el prefacio de un libro interactivo de RED Descartes? (Archivo PDF)
- Flujo de trabajo de la primera sesión (Archivo PPTX)
- Sobre Inteligencia Artificial
- Herramientas de IA para la enseñanza
- IA Generativas (Últimos desarrollos o actualizaciones)
- La importancia del prompt en la generación de imágenes con IA (Archivo PDF)
- Manual de usuario NotebookLM (Transforme la enseñanza con Inteligencia Artificial)
- Escritor de libros
Recursos ofrecidos durante la segunda sesión
- Tutoriales y manuales
- Flujo de trabajo de la segunda sesión (Archivo PPTX)
Recursos ofrecidos durante la tercera sesión
- Editores
- Tutoriales y manuales
Título: Memorias del curso "Diseño de objetos interactivos con DescartesJS e IA"
Sección: iCartesiLibri
Bloque: Formación
Unidad: Formación docente
Nivel/Edad: Universidad (18 años o más)
Idioma: Castellano
Autores: Carlos Alberto Rojas Hincapié, Juan Guillermo Rivera Berrío y Jesús Manuel Muñoz Calle
ISBN: 978-84-10368-26-2
![]() Haz clic aquí para ver una versión en pdf
Haz clic aquí para ver una versión en pdf
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
En esta novena edición de la Revista Digital Red Descartes, continuamos nuestra apuesta por la innovación educativa mediante el uso creativo e intencionado de herramientas digitales interactivas. Este número destaca por su enfoque en la inteligencia artificial y la gamificación, abordando sus aplicaciones tanto desde una perspectiva técnica como pedagógica.
Los artículos que conforman este número ofrecen un recorrido diverso: desde el enriquecimiento de actividades gamificadas con IA y el diseño de chatbots con DescartesJS y Pollinations, hasta propuestas que combinan narrativa educativa, imágenes generadas por IA y animaciones. También se exploran nuevas formas de autoría digital mediante pequeñas herramientas creadas con DescartesJS, así como análisis críticos sobre sesgos sociales en modelos lingüísticos y la influencia de las tecnologías emergentes en la vida de las mujeres.
Además, compartimos valiosas experiencias en el aula, donde docentes y estudiantes han integrado con éxito los recursos de Descartes para enriquecer sus prácticas pedagógicas. Asimismo, se presentan investigaciones que evidencian el impacto positivo del uso de contenidos digitales interactivos diseñados con DescartesJS en diversos contextos educativos.
Los contenidos incluidos están accesibles en línea pulsando sobre la siguiente imagen, también puede consultarlos en formato pdf y si lo desea descargarlos en su ordenador.
|
Para acceder al noveno número pulse sobre la imagen |
|
Este número refleja un compromiso constante por parte de la Red Descartes: integrar lo mejor de la tecnología al servicio de una educación más inclusiva, creativa y personalizada. Invitamos a nuestros lectores a interactuar, experimentar y reflexionar con cada una de las propuestas, siempre con el espíritu de compartir conocimiento y construir comunidad.
Confiamos en que este noveno número satisfaga el interés de múltiples lectores y resulte atractivo y variado.
Recuerde que puede aportar sus comentarios y observaciones, su retroalimentación es importante para nosotros. ¡Conecte con RED Descartes! Y si desea compartir, sus artículos serán muy bienvenidos ¡queremos leer, interactuar y aprender contigo!
¡Quedán invitados a publicar sus artículos en nuestra revista! Como referencia para la composición de su contenido pueden consultar las "Normas de publicación" y para cualquier duda o propuesta quedamos atentos en nuestra dirección de correo Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo..
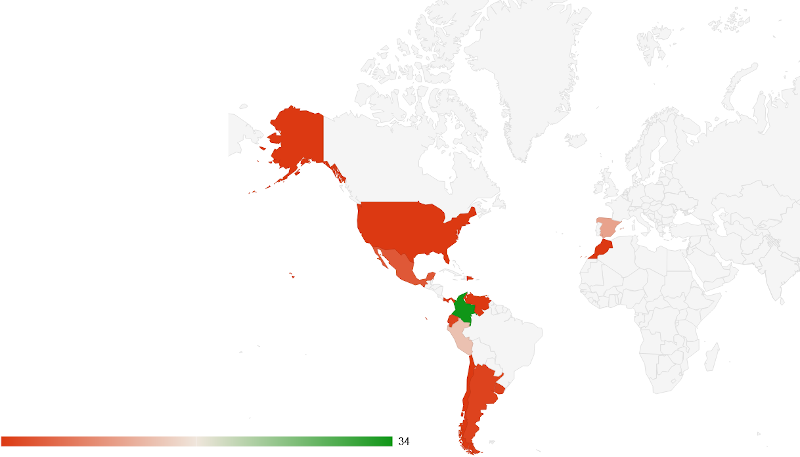
Comienza la I Edición del Curso para el Diseño de Objetos interactivos con DescartesJS e IA, que forma parte del programa de Educación Abierta de RED Descartes y cuenta con participantes distribuidos en tres continentes y doce países, todos profesionales de la educación que comprenden diversas etapas educativas y una amplia gama de especialidades. Como viene siendo habitual, compartimos el diagrama de sectores con el porcentaje de personas inscritas según el país de origen:
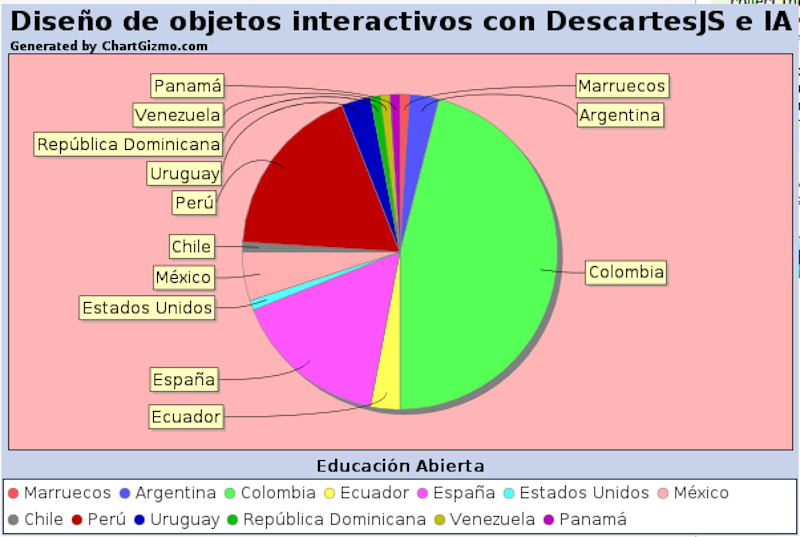
Nuestra gran experiencia y trayectoria en el desarrollo de acciones formativas nos ha encaminado a convocar un curso bastante demandado en el que se aúnan las herramientas de inteligencia artificial para la enseñanza y la potente herramienta de autor DescartesJS, de software libre, promovida y soportada por nuestra asociación en colaboración con instituciones y organizaciones de Colombia y México, fundamentalmente.
Pues bien, una vez han sido atendidas todas las inscripciones de forma personalizada y cada participante ha recibido las debidas instrucciones iniciales y los recursos y materiales para la primera sesión, corresponde, en el marco del programa de Educación Abierta de nuestra red, compartir la información con nuestros seguidores, usuarios y personas interesadas en aprender de forma independiente. Así que, en primer lugar, proporcionamos la
para continuar con el resto de recursos:
- Descarga el software libre DescartesJS para tu sistema operativo
- Tutorial sobre DescartesJS - Nivel I
- Herramientas de Inteligencia Artificial para la enseñanza
- Lista en Youtube con vídeos de apoyo
- Descripción detallada de cada sesión
Los vídeos con la grabación de cada sesión del curso, que se imparte por videoconferencia según el calendario establecido, se irán publicando progresivamente en la página denominada
Diseño de objetos interactivos con DescartesJS e IA
Vídeos del curso "Diseño de objetos interactivos con DescartesJs e IA"
Presentación
Recursos y tutoriales previos:
- Descarga el software libre DescartesJS para tu sistema operativo
- Tutorial sobre DescartesJS - Nivel I
- Herramientas de Inteligencia Artificial para la enseñanza
- Lista en Youtube con vídeos de apoyo
- Descripción detallada de cada sesión

Los vídeos con la grabación de cada sesión del curso, que se imparte por videoconferencia según el calendario establecido, se irán publicando progresivamente a continuación:
- Vídeo de la 1ª sesión (11 de abril 2025). Presentación de la 1ª sesión. Resumen sesión 1.ª
- Vídeo de la 2ª sesión (25 abril 2025). Presentación de la 2ª sesión.
- Vídeo de la 3ª sesión (9 de mayo 2025). Presentación de la 3ª sesión.
- Vídeo de la 4ª sesión (23 de mayo 2025). Presentación de la 4ª sesión.
- Vídeo de la 5ª sesión (6 de junio 2025). Presentación de la 5ª sesión.
- Vídeo de la 6ª sesión (20 de junio de 2025). Presentación de la 6ª sesión.
- Vídeo de la 7ª sesión (4 de julio de 2025). Presentación de la 7ª sesión .
- Vídeo de la 8ª sesión (18 de julio de 2025).. Presentación de la 8ª sesión .
El nuevo Marco de Referencia para la Competencia Digital Docente recoge, en el área 2 dedicada a contenidos digitales, entre sus elementos específicos:
- "Utilización de herramientas de autor para la modificación, diseño y creación de contenidos educativos digitales nuevos o derivados de otros contenidos..."
- "Aplicación de criterios de calidad de los contenidos educativos digitales para su adaptación al alumnado con el que se trabaja y a los fines perseguidos".
- "Respeto de los derechos de autor y de las limitaciones de la propiedad intelectual aplicadas al ámbito educativo para la reutilización y la creación de contenidos..."
Pues bien, desde RED Descartes te ofrecemos la posibilidad de abordar estos elementos específicos, como mínimo, aprendiendo el manejo de la herramienta de autor DescartesJS, un software libre y multipropósito con el que podrás crear tus propios contenidos interactivos para cualquier materia, respetando los derechos de autor y compartiéndolos en entornos seguros con una licencia Creative-Commons. Pero, además, conocerás y podrás aprovechar el enorme potencial de la Inteligencia Artificial en el ámbito educativo usando herramientas que te facilitarán la práctica docente hasta límites insospechados.
Queda abierto, por tanto, el plazo de inscripción gratuita a la I Edición del Curso para el Diseño de objetos interactivos con IA y DescartesJS, una acción formativa que se enmarca en el programa de Educación Abierta desarrollado entre redes docentes de Colombia, México y España, fundamentalmente, aunque contamos con la participación de profesorado de otros países de habla hispana, portuguesa e inglesa. Un curso que tiene como objetivo principal diseñar recursos educativos abiertos en formato de escenas interactivas con la herramienta de autor Descartes JS y en formato web con herramientas de Inteligencia Artificial (WebSim, Claude 3.7, vo de Vercel, Pollinations, entre otras), que permitan poner de manifiesto que es posible dar una respuesta positiva y asequible a los retos educativos intrínsecos al paradigma educativo emergente.
Está dirigido a docentes de cualquier etapa educativa, infantil, primaria, educación secundaria obligatoria, bachillerato, formación profesional, enseñanzas de régimen especial y universidad, y de cualquier materia o especialidad, en activo o no, así como a profesionales vinculados a la educación o formación y a diseñadores y desarrolladores interesados en objetos interactivos, utilizando una metodología activa, concretamente Clase Invertida y Aprendizaje Basado en Proyectos (Tareas), pues desde la primera sesión cada participante comenzará a diseñar y editar su primer recurso interactivo, recibiendo sesiones quincenales por videoconferencia, que serán grabadas y compartidas con todos los participantes y asesorados por docentes de las redes mencionadas.
El curso comienza el próximo día 11 de abril y finaliza el 18 de julio de 2025, impartiéndose las sesiones de 7 AM a 8 AM en el horario oficial de Colombia, de acuerdo al siguiente calendario previsto y contenidos a tratar:
Para cualquier consulta o aclaración, puedes contactar con nosotros en la dirección de correo Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
| ACCESO AL FORMULARIO DE INSCRIPCIÓN |
Este formulario estará abierto hasta el día 6 de abril o hasta cubrir disponibilidad.
Recursos que utilizaremos:
- Descarga el software libre DescartesJS para tu sistema operativo.
- Tutorial sobre DescartesJS - Nivel I
- Herramientas de Inteligencia Artificial para la enseñanza
- Lista en Youtube con vídeos de apoyo
| DESCRIPCIÓN DETALLADA DE CADA SESIÓN |
| PRIMERA SESIÓN - Introducción (11 de abril) |
Tarea: Generar un cuestionario con IA |
| SEGUNDA SESIÓN - Espacios (25 de abril) |
Tarea: Diseñar una escena con dos espacios (ver tarea aquí) |
| TERCERA SESIÓN - Imágenes (9 de mayo) |
Tarea: Diseñar un presentador de diapositivas con cualquier herramienta |
| CUARTA SESIÓN - Elementos mínimos de programación 1 (23 de mayo) |
Tarea: Resolver los problemas 6 y 7 propuestos aquí |
| QUINTA SESIÓN - Elementos mínimos de programación 2 (6 de junio) |
Tarea: Resolver el problema 10 propuesto aquí |
| SEXTA SESIÓN - Controles (20 de junio) |
Tarea 1: Diseñar una actividad similar a la propuesta aquí Tarea 2: Diseñar con IA una actividad que incluya dos tipos de controles (zum y menú, por ejemplo) |
| SÉPTIMA SESIÓN - Audios y videos (4 de julio) |
Tarea: Diseñar un video interactivo con IA o DescartesJS |
| OCTAVA SESIÓN - Familias de gráficos (18 de julio) |
|
Diseño paso a paso de una escena interactiva de secuencias temporales Tarea: Diseño de una escena interactiva de 4 secuencias temporales |
¡Ya está aquí el número 8 de la "Revista Digital de la RED Descartes"!
En esta nueva edición, consolidamos nuestro compromiso con la educación y la innovación tecnológica. Este número está repleto de artículos fascinantes que abarcan desde estrategias didácticas en geometría hasta aplicaciones educativas de inteligencia artificial.
Destacamos algunos artículos como:
“La maqueta como estrategia didáctica en el aprendizaje de la semejanza de figuras”, una experiencia práctica para explorar conceptos de geometría.
“Plantillas generadas con inteligencia artificial”, que nos introduce en la creación de recursos educativos personalizados con IA.
“El juego del dominó y su relación con la teoría de grafos”, que demuestra cómo un juego tradicional puede convertirse en una herramienta pedagógica.
Además, exploramos nuevas herramientas digitales, simulaciones y actividades interactivas que enriquecen la enseñanza, como cuestionarios sonoros, calculadoras educativas y más.
¡Te invitamos a descubrir, aprender e innovar con nosotros!
Presentación de la Revista por los locutores de NotebookLM
Accede ahora a la revista completa y sigue siendo parte de esta revolución educativa interactiva.
Los contenidos incluidos están accesibles en línea pulsando sobre la siguiente imagen, también puede consultarlos en formato pdf y si lo desea descargarlos en su ordenador.
|
Para acceder al octavo número pulse sobre la imagen |
|
Confiamos en que este octavo número satisfaga el interés de múltiples lectores y resulte atractivo y variado.
Recuerde que puede aportar sus comentarios y observaciones, su retroalimentación es importante para nosotros. ¡Conecte con RED Descartes! Y si desea compartir, sus artículos serán muy bienvenidos ¡queremos leer, interactuar y aprender contigo!
¡Quedán invitados a publicar sus artículos en nuestra revista! Como referencia para la composición de su contenido pueden consultar las "Normas de publicación" y para cualquier duda o propuesta quedamos atentos en nuestra dirección de correo Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo..