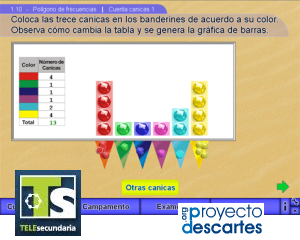
Polígono de frecuencias
Título: Polígono de frecuencias
Sección: Telesecundaria
Bloque: Estadística y probabilidad
Unidad: Estadística descriptiva
Nivel/Edad: 2º y 3º ESO (13-15 años)
Idioma: Castellano
Autoría: Carlos Alberto Jaimes Vergara (ILCE Grupo Descartes).
 Haz clic aquí para ver la documentación
Haz clic aquí para ver la documentación
![]() Haz clic en la imagen para abrir una muestra de este recurso
Haz clic en la imagen para abrir una muestra de este recurso
Puedes encontrar todos los recursos de Telesecundaria en
https://proyectodescartes.org/Telesecundaria/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
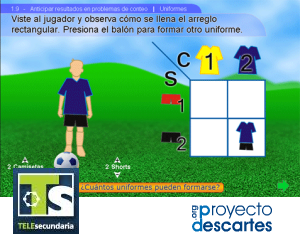
Anticipar resultados en problemas de conteo
Título: Anticipar resultados en problemas de conteo
Sección: Telesecundaria
Bloque: Álgebra
Unidad: Combinatoria
Nivel/Edad: 2º y 3º ESO (13-15 años)
Idioma: Castellano
Autoría: Carlos Alberto Jaimes Vergara (ILCE Grupo Descartes).
 Haz clic aquí para ver la documentación
Haz clic aquí para ver la documentación
![]() Haz clic en la imagen para abrir una muestra de este recurso
Haz clic en la imagen para abrir una muestra de este recurso
Puedes encontrar todos los recursos de Telesecundaria en
https://proyectodescartes.org/Telesecundaria/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
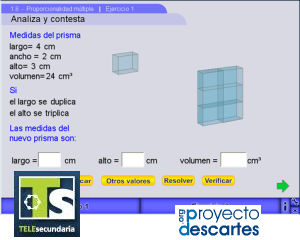
Proporcionalidad múltiple
Título: Proporcionalidad múltiple
Sección: Telesecundaria
Bloque: Álgebra
Unidad: Números y operaciones
Nivel/Edad: 2º y 3º ESO (13-15 años)
Idioma: Castellano
Autoría: Erika Paulina Tovilla Quesada (ILCE Grupo Descartes).
 Haz clic aquí para ver la documentación
Haz clic aquí para ver la documentación
![]() Haz clic en la imagen para abrir una muestra de este recurso
Haz clic en la imagen para abrir una muestra de este recurso
Puedes encontrar todos los recursos de Telesecundaria en
https://proyectodescartes.org/Telesecundaria/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
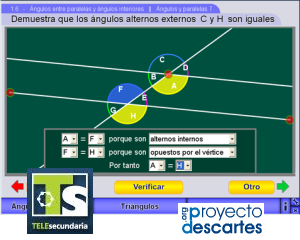
Ángulos entre paralelas y ángulos interiores
Título: Ángulos entre paralelas y ángulos interiores
Sección: Telesecundaria
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: 2º y 3º ESO (13-15 años)
Idioma: Castellano
Autoría: María Lourdes Velasco Arregui (ILCE Grupo Descartes).
 Haz clic aquí para ver la documentación
Haz clic aquí para ver la documentación
![]() Haz clic en la imagen para abrir una muestra de este recurso
Haz clic en la imagen para abrir una muestra de este recurso
Puedes encontrar todos los recursos de Telesecundaria en
https://proyectodescartes.org/Telesecundaria/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
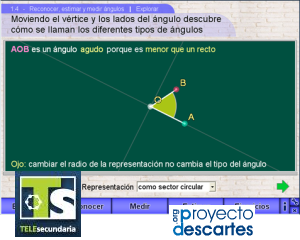
Reconocer, estimar y medir ángulos
Título: Reconocer, estimar y medir ángulos
Sección: Telesecundaria
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: 2º y 3º ESO (13-15 años)
Idioma: Castellano
Autoría: José Luis Abreu León (ILCE Grupo Descartes).
 Haz clic aquí para ver la documentación
Haz clic aquí para ver la documentación
![]() Haz clic en la imagen para abrir una muestra de este recurso
Haz clic en la imagen para abrir una muestra de este recurso
Puedes encontrar todos los recursos de Telesecundaria en
https://proyectodescartes.org/Telesecundaria/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)


 CONTACTO
CONTACTO
