Unidad 1.4Reconocer, estimar y medir ángulosReferencia curricular
PropósitoQue el alumno conozca los nombres de los diferentes tipos de ángulos y aprenda a reconocerlos, a medirlos con el transportador y a estimar a "ojo de buen cubero" su medida en grados. El ejercicio que aparece al final de la unidad tiene el propósito de que los alumnos practiquen la medición de ángulos haciéndolo con los ángulos interiores de un triángulo arbitrario y aprendan, como preparación para las siguientes unidades, que la suma de los ángulos interiores de un triángulo es 180 grados. Instrucciones GeneralesEsta unidad tiene cinco apartados, todos ellos, excepto el tercero constan de una sola escena:
1. Explorar Se puede navegar entre los apartados o escenas con el menú de la parte inferior.
Este menú aparece a lo largo de toda la unidad y conserva su funcionalidad.
Uso de campos de textoEn algunas escenas aparecen campos de texto para que el usuario escriba en ellos valores o expresiones numéricas. La forma de uso de estos campos es la siguiente: Uso de tablasPara introducir valores es necesario ir dando clic en cada una de las celdas donde se tiene que colocar el resultado, y para comprobar los resultados introducidos hay que presionar el botón Verificar. Las respuestas correctas aparecerán en color verde y las incorrectas en rojo. Uso de calculadoraAl hacer doble clic en un campo de texto o en una de las celdas de una tabla aparecerá una calculadora o un teclado virtual.
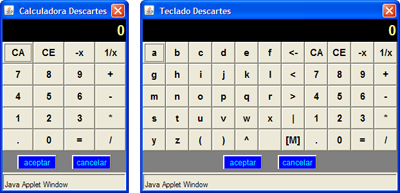
En ambos casos al terminar de introducir los datos se debe presionar el botón Aceptar; en este momento desaparecerá la calculadora y aparecerá el último resultado escrito en ella. 1. ExplorarEn la primera escena aparece un pizarrón con un ángulo dibujado que está formado por un vértice llamado O y dos lados uno de cuyos extremos es el vértice O y los otros dos se llaman A y B. El usuario puede mover libremente (arrastrándolo con el ratón) el vértice, puede alargar los lados del ángulo arrastrando los puntos A y B, También puede abrir y cerrar el ángulo arrastrando los lados sin tocar los puntos O, A y B. En la parte superior del pizarrón aparece una descripción del ángulo que lo clasifica en agudo, recto, obtuso, llano, cóncavo y completo, dando además la relación que tienen con los ángulos rectos. Abajo del pizarrón aparece un menú que permite al usuario elegir entre cuatro tipos diferentes de representación gráfica del ángulo: como sector circular, como arco de circunferencia, como región entre dos semirrectas o ninguna. El usuario puede cambiar libremente la representación sin que esto altere el ángulo. También puede modificar el radio de la representación gráfica sin que el ángulo se altere. En la parte inferior del pizarrón aparece una advertencia fija de que el tipo de ángulo no cambia si se cambia su representación.
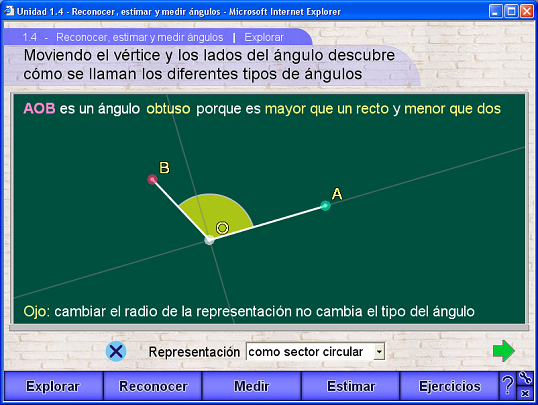
Dibujadas en un tono gris discreto, aparecen dos rectas perpendiculares que pasan por el vértice y una de ellas siempre contiene al punto A. Estas rectas pueden ocultarse o pintarse pulsando el botón circular azul. Las rectas sirven para comparar los ángulos con uno o dos ángulos rectos, que es la base de la clasificación en agudos, rectos, obtusos, llanos, cóncavos y completos. Nota 1: En esta unidad hemos adoptado la convención de que los ángulos se miden a partir del primero de sus lados y en la dirección contraria al movimiento de las manecillas del reloj. Para indicar cual es el primero de los lados de un ángulo usamos normalmente una letra. La nomenclatura AOB que se utiliza en la primera escena obedece a la convención en la que un ángulo se denota con tres letras, la primera indica el primer lado, la segunda el vértice y la tercera el segundo lado. Nota 2: El concepto de ángulo es difícil de definir. Euclides lo definía como la "inclinación mutua de dos líneas". La Real Academia de la Lengua Española lo define como: "Figura geométrica formada por dos líneas que parten de un mismo punto". La opinión del autor es que sigue siendo mejor la definición de Euclides, aunque peque de imprecisa. Lo importante es que señala en la dirección correcta. El ángulo no es la figura, sino la apertura (Euclides dice inclinación) entre los lados de esa figura formada por dos segmentos unidos en un vértice. Pero además el ángulo tiene una dirección, es importante indicar cual es el primero de sus lados y cual el segundo. Por este motivo se utilizan a veces representaciones geométricas, incluso a veces se usan flechas en los arcos para indicar el sentido. Nota 3: Las representaciones usadas para los ángulos en esta unidad interactiva no son las únicas que se utilizan en la práctica para los ángulos, a veces se utilizan otras y a veces no se representan gráficamente. La intención de mostrar estas tres representaciones es fomentar que los alumnos dejen de identificar al ángulo con su representación y lleguen a comprender que el ángulo es un concepto que no depende de su representación. En el caso de los ángulos completos (y sólo en este caso) se requiere de una representación gráfica adecuada (arco o sector circular) para distinguir entre el ángulo agudo de cero grados y el completo. Nota 4: La clasificación de ángulos que se enseña en esta unidad no depende de la medida en grados sino de cómo se comparan los ángulos con uno o dos ángulos rectos. Es, básicamente, la clasificación de Euclides. Para ello es imprescindible tener claro que un ángulo recto no se define como uno de 90 grados sino como el ángulo que forman entre sí dos rectas perpendiculares, es decir dos rectas que al cortarse forman cuatro ángulos iguales. Sugerencias didácticasEn primer lugar se sugiere arrastrar el lado B del ángulo abriéndolo y observando la descripción que aparece en la parte superior del pizarrón. Habrá que hacer movimientos muy delicados para lograr un ángulo recto, uno llano o uno completo. Es importante no hacer referencia a los grados que pueda medir un ángulo sino solo prestar atención a su comparación con uno o dos ángulos rectos. Luego conviene girar también el lado B y repetir el ejercicio moviendo el lado A para mostrar que el primer lado del ángulo puede apuntar en cualquier dirección y no "a la derecha" como a veces se piensa. Finalmente se sugiere hablar en clase de que el tipo (y la medida) del ángulo es independiente de la representación, es decir no depende ni de la representación gráfica, ni de la longitud de los lados, sólo de su "inclinación mutua". 2. 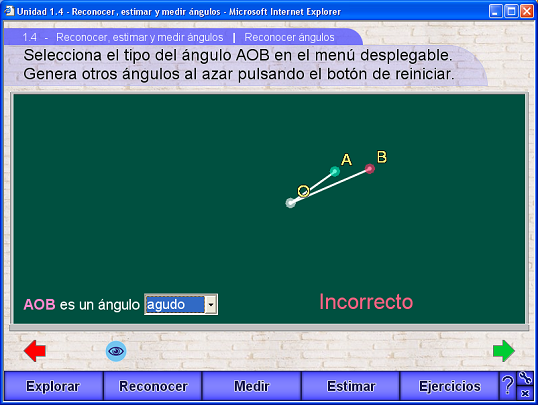ReconocerLa segunda escena presenta un ángulo AOB construido al azar y con una representación gráfica también elegida al azar. En la parte inferior del pizarrón aparece un menú en el que hay que seleccionar el tipo de ángulo de que se trate. El programa responde indicando si la respuesta fué incorrecta, en cuyo caso hay que elegir otra opción hasta obtener la correcta, y cuando se selecciona la opción correcta el programa así lo indica y presenta un botón de reiniciar con el que se puede generar otro ángulo al azar. En esta escena el usuario no puede cambiar el ángulo pero sí puede modificar la longitud de sus lados y el radio de la representación gráfica.
Sugerencias didácticasSe sugiere generar un ángulo al azar y pasar a un alumno a responder la pregunta. Cuando haya respondido correctamente se pasa otro alumno a que genere un nuevo ángulo al azar y seleccione el tipo. En algún momento se puede preguntar al alumno si puede cambiar el tipo del ángulo alargando los lados o el radio de la representación y generar así una discusión sobre si un ángulo es mayor que otro porque sus lados sean más largos o porque el radio del sector que lo representa sea mayor y llegar a la conclusión de que no es así. 3. MedirEl apartado de Medir tiene dos escenas casi idénticas. En ambas se presenta un ángulo y se pide al usuario que lo mida con un transportador. En la primera escena se pueden usar dos transportadores diferentes, uno de 180 grados y otro de 360. Se espera que cuando haya que medir un ángulo cóncavo el usuario utilice el de 360 grados. En la segunda escena sólo puede usarse el transportador de 180 grados, lo cual obligará, cuando el ángulo que se desea medir es cóncavo, a medir el ángulo recorrido en sentido inverso y obtener la medida del otro tomando la diferencia con 360.
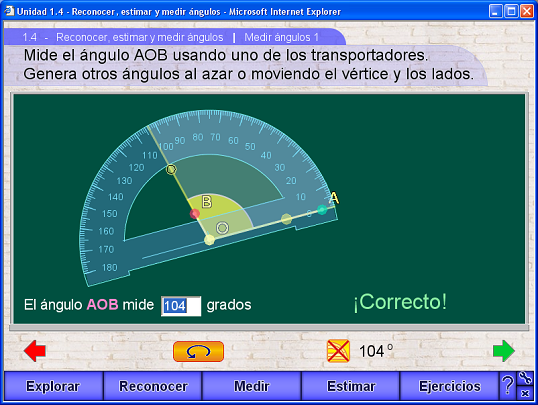
Los dos transportadores funcionan igual. Tienen tres controles, uno en el centro que debe colocarse en el vértice del ángulo, otro que apunta a la marca de cero grados y que debe usarse para orientar el transportador en la dirección del lado inicial. El tercer control sirve para alinearlo con el segundo lado del ángulo. El objetivo en la medición es entonces formar con estos controles el mismo ángulo que el que se desea medir y leer la medida viendo al número de la escala circular al que apunta el tercer control, o bien leyendo el valor cómodamente abajo del pizarrón. Los controles del transportador tienen "imanes", es decir, son atraídos por los elementos del ángulo. Si el control del centro pasa cerca del vértice del ángulo, éste lo atrapa. De la misma manera, los otros dos controles son atraídos por los lados del ángulo. Esto permite hacer un ajuste perfecto, que con un transportador físico no es posible. En la parte baja del pizarrón hay un campo de texto en el que el usuario debe escribir el resultado de su medición y hay un botón de Verificar que hay que pulsar para comprobar la medición. El programa responde diciendo si la medición es incorrecta o correcta y en este caso cambia el botón de Verificar por uno gráfico de Reiniciar que al pulsarse genera aleatoriamente otro ángulo. En algunas ocasiones los ángulos aparecerán sin una representación gráfica, y en esos casos el usuario deberá recurrir a la nomenclatura de los lados para saber cuál es el ángulo que debe medir. Sugerencias didácticasSe sugiere al maestro enseñar una o dos veces cómo se usa el transportador para medir un ángulo y posteriormente pasar uno a uno a varios alumnos al pizarrón para que ellos mismos hagan la medición. Cuando aparezca un ángulo cóncavo, el maestro puede sugerir utilizar el transportador de 360 grados para medirlo. Cuando el grupo haya dominado la técnica para medir ángulos con los dos transportadores, conviene pasar a la segunda escena de medición en la que además de obtener una medida con el transportador de 180 grados, será necesario hacer una resta para obtener el resultado. 4. EstimarAl igual que en las escenas de medir en ésta aparecen ángulos al azar que ahora el usuario deberá estimar, es decir, adivinar su valor escogiendo el que cree correcto de una lista. La escena genera ángulos que son múltiplos de 15 grados, con lo cual es relativamente fácil, pero no trivial, adivinar a simple vista la medida del ángulo.
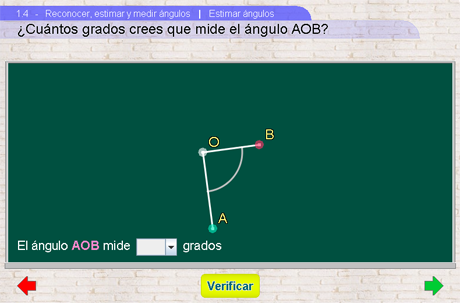
El objetivo de esta escena es que los alumnos adquieran una idea intuitiva de cuánto mide un ángulo por su aspecto. Es muy fácil adivinar ciertas medidas como las de 90 o 45 grados porque el de 90 es un ángulo recto y el de 45 es la mitad de uno recto. Pero el ser humano tiene la capacidad de estimar, a veces con bastante precisión, otros valores intemedios. La escena pretende ayudar a desarrollar esta habilidad, no porque sea un sustituto de las mediciones precisas sino porque estas medidas de ángulos suelen usarse en el lenguaje diaro para describir calles, construcciones, etcétera. Sugerencias didácticasSe sugiere que el maestro vaya generando nuevos ángulos al azar y pregunte al grupo cuánto miden. Puede elegir la repuesta de algún alumno en particular y si no es correcta preguntar al grupo si creen que el valor correcto debe ser mayor o menor. 5. EjerciciosEjercicio 1 En esta escena se pide al usuario medir, usando el transportador, los ángulos internos de unos triángulos que el programa genera al azar. El usuario debe poner los valores medidos usando unos pulsadores. Los triángulos generados tienen ángulos cuyas medidas son múltiplos de 5 grados. Si se ponen las medidas correctas y se pulsa el botón Verificar el programa responde que los resultados son correctos y muestra que la suma de los ángulos internos es 180 grados.
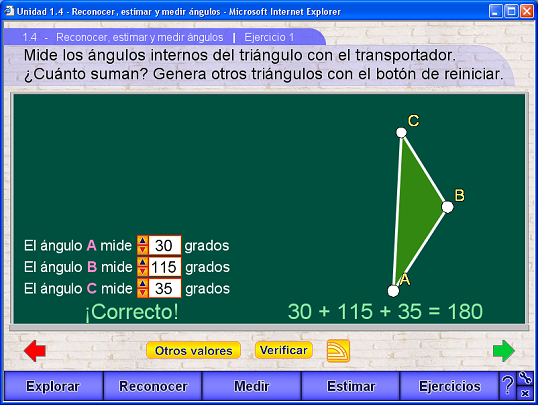
El botón de Reiniciar siempre está visible y activo para que el maestro pueda pulsarlo varias veces hasta que salga un triángulo sobre el que le interese particularmente hacer el ejercicio. Sugerencias didácticasComo en los ejercicios de Medir, aquí se sugiere pasar a los alumnos usar el transportador, quizás un alumno distinto para cada ángulo. La dificultad adicional, relativa a los ejercicios anteriores, es que aquí no hay un solo vértice sino tres y el alumno debe saber en cuál poner el centro y cómo acomodar los brazos del transportador para medir el ángulo que se le pida. Una vez hechas las mediciones, antes de pulsar el botón de Verificar conviene preguntar al grupo si hay un error y si observan alguna relación curiosa entre los tres valores. El objetivo es llegar a conjeturar que la suma de los ángulos es 180 grados y que ésa es precisamente igual a la medida de un ángulo llano, igual también a la suma dos ángulos rectos. Después de varios ejercicios, el maestro puede pasar a dos alumnos a medir los primeros dos ángulos y luego a un tercero pedirle que sin medir, diga cuánto debe medir el ángulo que falta. Nota: Se han eliminado dos actividades con tablas Créditos
Autor Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes. Sus contenidos se distribuyen bajo una licencia de  La unidad utiliza Descartes que es software libre. Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)
|
Brinda acceso a la ayuda de las escenas interactivas
éste tendrá la misma función que presionar la tecla Intro.
