Unidad 1.6Ángulos entre paralelas y ángulos interiores(Ángulos entre una transversal y dos paralelas y ángulos interiores de triángulos y cuadriláteros)Referencia curricularPropósito
Que el alumno deduzca las relaciones entre los ángulos que se forman
entre dos paralelas cortadas por una transversal y justifique las
relaciones de las medidas de los ángulos interiores de un triángulo, un
paralelogramo y un cuadrilátero en general. Instrucciones generalesLa unidad se divide en tres apartados :
1. Ángulos y paralelas
2. Triángulos 3. Cuadriláteros Se puede navegar entre los apartados (grupos de escenas) con el menú de la parte inferior.
Este menú aparece a lo largo de toda la unidad y conserva su funcionalidad.
1. Ángulos y paralelasEste apartado tiene una secuencia de siete escenas en las que se presenta una argumentación paso a paso para llegar a la igualdad de las parejas de ángulos que son alternos internos, correspondientes o alternos externos. Ángulos y paralelas 1
Esta escena y la siguiente son exploratorias y pretenden que los alumnos encuentren algunas de las parejas de ángulos iguales que se forman cuando una recta intersecta a dos paralelas. Las rectas se pueden mover con los controles que tienen a la orilla del pizarrón. Con el botón Mover ángulos se habilita el movimiento de los ángulos, pero a la vez se desactivan el desplazamiento de las rectas y los pulsadores del radio. Los ángulos se pueden trasladar y rotar mediante los controles. El botón Cambiar ángulos muestra a la pareja de ángulos complementarios. Por último, el botón Colocar rectas permite mover de nuevo las rectas, y rehabilita los pulsadores del radio.
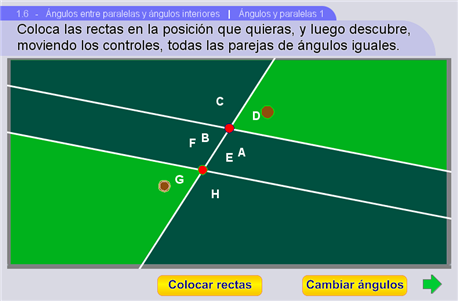
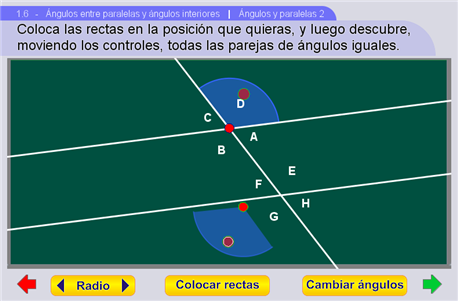
En esta escena los ángulos se representan por regiones completas que pueden arrastrarse y colocarse en otros sitios para comprobar que ciertos pares de ángulos son iguales. Ángulos y paralelas 2 Esta escena es exploratoria y busca que los alumnos encuentren algunas de las parejas de ángulos iguales que se forman cuando una recta intersecta a dos paralelas. Las rectas se pueden mover con los controles que tienen a la orilla del pizarrón, y los pulsadores de la parte baja cambian el tamaño del radio de los sectores que representan los ángulos. Con el botón Mover ángulos se habilita el movimiento de los ángulos, pero a la vez se desactivan el desplazamiento de las rectas y los pulsadores del radio. Los ángulos se pueden trasladar y rotar mediante los controles. El botón Cambiar ángulos muestra a la pareja de ángulos complementarios. Por último, el botón Colocar rectas permite mover de nuevo las rectas, y rehabilita los pulsadores del radio.
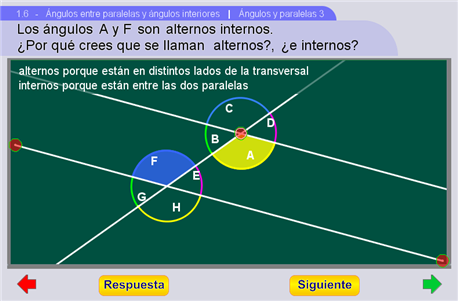
Sugerencias didácticasConviene que los alumnos dibujen en su cuaderno una recta que corte a dos paralelas, nombren los ángulos y hagan una lista de las parejas de ángulos iguales que encuentren para trabajar con ellas en las siguientes escenas. Ángulos y paralelas 3 En esta escena aparecen algunas parejas de ángulos iguales, se les asigna el nombre: alternos internos, alternos externos y correspondientes, y se pide reflexionar sobre los nombres que se les dan a dichos ángulos, de manera que en lo sucesivo identifiquen el nombre con la posición relativa que guardan los ángulos. Los botones en esta escena son para obtener una respuesta a las preguntas que se plantean y para cambiar la pareja de ángulos que se muestran. Las imágenes son dinámicas. Con los controles que tiene una de las rectas en las orillas del pizarrón se puede cambiar la pendiente de las rectas paralelas. La otra paralela se puede trasladar moviendo el control que está en la intersección.
Sugerencias didácticasConviene que en su lista de ángulos iguales los alumnos identifiquen a las parejas de alternos internos, alternos externos y correspondientes, observando su dibujo. Ángulos y paralelas 4 Esta escena también es exploratoria y busca que los alumnos observen que, cuando una transversal cruza dos rectas, si la pareja de ángulos internos de un mismo lado no suma 180 grados, las rectas no son paralelas. O lo que es equivalente, para que las rectas sean paralelas dichos ángulos deben sumar 180 grados. Aleatoriamente aparecen dos rectas intersectadas por una tercera y arcos que representan algunos de los ángulos que se forman en la intersección. Dos de las rectas tienen pendiente aleatoria y son fijas, mientras que a la tercera se le puede cambiar la pendiente moviendo verticalmente los controles que están junto a la orilla del pizarrón.
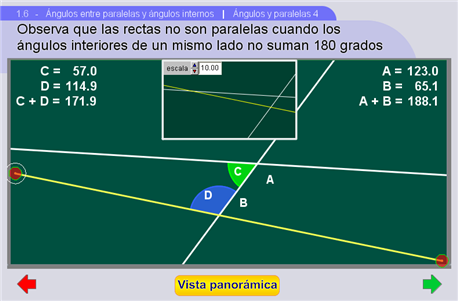
En las esquinas de arriba del pizarrón se muestra la medida de los ángulos interiores que se forman de cada lado y su suma. Se pide que se observe que si estas sumas no son 180 grados, entonces estas dos últimas rectas se van a cruzar (no son paralelas). Para ello el botón Vista panorámica abre una ventana donde se puede cambiar la escala y/o mover el espacio a la derecha y la izquierda para encontrar el punto donde las rectas se cruzan. Sugerencias didácticasLa afirmación que se hace en esta escena es el contenido del Quinto Postulado de Euclides. El objetivo del apartado no es informativo, sino que pretende hacer verosímil lo que se asegura, ya que en las siguientes escenas se parte de este postulado para demostrar la igualdad de los ángulos alternos internos, alternos externos o correspondientes. Para ello es conveniente que los estudiantes observen en la vista panorámica lo que ocurre tanto cuando la suma de los ángulos no es igual a 180 grados, como cuando si lo es. 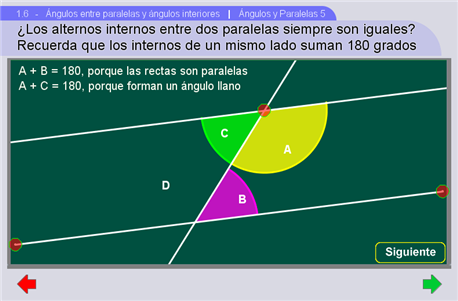(ver la Nota al final de este documento) Ángulos y paralelas 5 En esta escena aparecen dos paralelas cruzadas por otra recta, y delineados los arcos que representan a los ángulos internos. Con los controles las rectas paralelas se pueden acercar/alejar y rotar. Así mismo, la pregunta: "¿Los alternos internos entre dos paralelas siempre son iguales?"; únicamente es para motivar y generar la inquietud entre los alumnos sobre éste hecho. Si bien ésta pregunta no se responde explícitamente en un campo verificador propiamente de la escena, en cambio, los contenidos del interactivo si responden implícitamente a ésta cuestión. Se piden argumentos para demostrar que los ángulos alternos internos son iguales. El botón Explicación da una demostración ilustrada y paso a paso. En cada una de las etapas se pide al estudiante la justificación de la afirmación. La pregunta se responde pulsando sobre el botón ¿por qué? El botón Cambiar ángulos presenta la demostración para la otra pareja de ángulos internos.
Sugerencias didácticasPrimero debe quedar claro lo que se pide, identificando los ángulos cuya igualdad se quiere demostrar. Antes de pasar a los alumnos al pizarrón se sugiere que discutan entre ellos y propongan argumentos. Puede ayudar que se recuerde que los ángulos internos de un mismo lado suman 180 grados y ubicarlos en la imagen. Ángulos y paralelas 6 En esta escena aparece la misma figura que en la anterior, pero ahora se pide una justificación de que dos ángulos correspondientes sean iguales. El botón Qué sabemos muestra/oculta dos afirmaciones que ya se justificaron previamente:
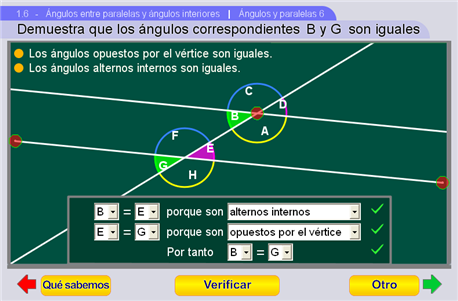
El botón Argumenta abre el texto para que con los pulsadores se llenen las afirmaciones de la justificación. El botón Verificar indica si las afirmaciones son correctas y si el argumento demuestra lo que se pide.
El botón Otro cambia las rectas y la pareja de correspondientes para la que se pide la demostración. Sugerencias didácticasPrimero debe quedar bien identificado lo que se pide y lo que se puede usar. Y como siempre es conveniente que, antes de pasar al pizarrón a los alumnos, ellos discutan y propongan argumentos. Ángulos y paralelas 7 Como en la escena anterior, en esta aparece la figura de dos rectas paralelas cruzadas por una tercera, pero ahora se pide una justificación de que dos ángulos alternos externos dados sean iguales. El botón Qué sabemos muestra/oculta tres afirmaciones que ya se justificaron previamente:
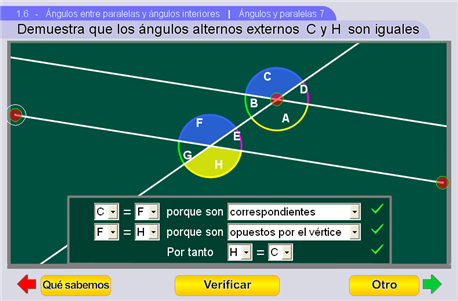
El botón Argumenta abre el texto para que con los pulsadores se completen las afirmaciones de la justificación. El botón de Verificar indica si las afirmaciones son correctas y si el argumento demuestra lo que se pide.
El botón Otro sólo cambia las rectas y la pareja de ángulos correspondientes con la que se ilustra la demostración. Sugerencias didácticasComo en las escenas anteriores, primero hay que identificar exactamente lo que se pide y lo que se puede usar. Además es muy recomendable que los alumnos discutan y propongan argumentos antes de pasarlos al pizarrón. La demostración en este caso usa una pareja de correspondientes y una de opuestos por el vértice.
Hay otra posibilidad utilizando dos parejas de opuestos por el vértice y una de alternos internos.
2. TriángulosEste apartado consta de una sola escena, en la que se buscan argumentos que justifiquen que los ángulos interiores de un triángulo suman 180 grados Los botones bajo el pizarrón muestran una construcción que sugiere los argumentos. El botón Explicación muestra los argumentos paso a paso.
Sugerencias didácticasInicialmente los alumnos deben intentar dar una explicación sin ayuda alguna. Luego se pueden
mostrar las construcciones, una a una, para sugerirles posibles argumentos.
La explicación debe usarse solamente como última instancia y para corroborar.
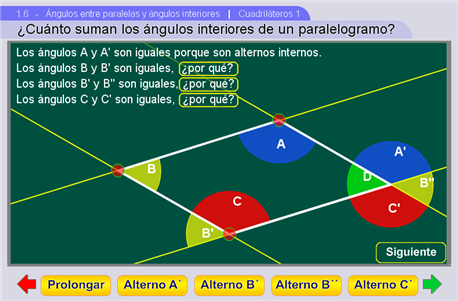
3. CuadriláterosEste apartado consta de dos escenas, en la que se buscan argumentos que justifiquen que los ángulos interiores de un paralelogramo y de un cuadrilátero en general suman 360 grados. Cuadriláteros 1 En la escena aparece un paralelogramo que cambia con los controles. Se pregunta cuánto vale la suma de sus ángulos. Los botones bajo el pizarrón muestran, paso a paso, una construcción que sugiere cuales pueden ser los argumentos. El botón Explicación muestra un texto en el que los argumentos aparecen paso a paso.
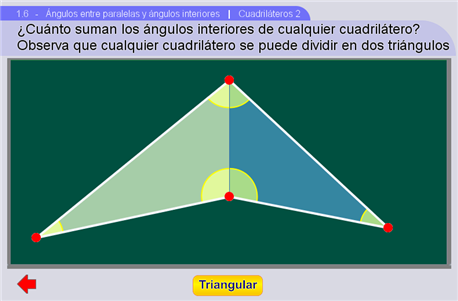
Sugerencias didácticasRepetimos: Inicialmente los alumnos deben intentar dar una explicación sin ayuda alguna. Luego se pueden mostrar las construcciones, una a una, para sugerirles posibles argumentos. La explicación debe usarse solamente como última instancia y para corroborar. Cuadriláteros 2
En la escena aparece un cuadrilátero que cambia con los controles. Se pregunta cuánto vale la suma de sus ángulos. El botón Triangular divide el cuadrilátero en dos triángulos.
Sugerencias didácticasInicialmente los alumnos deben intentar dar una argumentación sin ayuda alguna. Luego se puede mostrar la triangulación para sugerir que como:
Nota sobre el Quinto PostuladoEuclides en el siglo III a.C compiló en un tratado de 13 libros un conjunto de principios fundamentales de las matemáticas y la geometría, llamado Los Elementos. El tratado es relevante porque se desarrolla siguiendo el método de razonamiento deductivo, en donde una conclusión debe derivarse necesariamente de ciertas premisas. De tal manera Euclides desarrolló la geometría en base a 23 definiciones, 8 nociones comunes y 5 postulados. Las definiciones son descripciones, por ejemplo:
Las nociones comunes son, por ejemplo:
Los cinco postulados son:
Este Quinto Postulado fue históricamente polémico, pues no parecía tan natural como los otros. Los matemáticos buscaron demostrarlo usando los otros cuatro. No lo lograron, pero consiguieron postulados que lo pueden sustituir. El más conocido es el de Ptolomeo: "Por un punto exterior a una recta sólo se puede trazar una paralela" Subyacente al Quinto Postulado está el hecho de que Los Elementos desarrollan la geometría del plano. Siguiendo otra línea, que toma de manera abstracta las definiciones, nociones comunes y postulados y eliminando el Quinto Postulado y sus equivalencias, Gauss y Lobachevsky encontraron otras geometrías : la esférica y la hiperbólica. En la primera no existen paralelas (todas las rectas se cruzan) , y en las segunda por un punto pasan infinidad de paralelas. En la Red hay mucha información acerca de Euclides, Los Elementos, el Quinto Postulado y las geometrías no euclidianas.
CréditosAutora Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes. Sus contenidos se distribuyen bajo una licencia de  La unidad utiliza Descartes que es software libre. Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)
|
Brinda acceso a la ayuda de las escenas interactivas
