Proporcionalidad. Las espirales XIII
Proporcionalidad. Las Espirales XIII
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades a los subproyectos: TELESECUNDARIA, GEOgráfica-GEOevaluación y PLANTILLAS.
Como muestra enlazamos la unidad sobre Probabilidad, del subproyecto TELESECUNDARIA,
la GEOevaluación de Francia.
y los cinco ejemplos de plantillas transparentes, de los que enlazamos el primero.
Dentro de nuestro ámbito local destacan, entre otras, la permanente actualización del Proyecto ED@D en particular los materiales de 2º y 4º LOMCE y LOE y la experiencia: Aprendemos a resolver problemas con Descartes y Wiris
Aprendemos a resolver problemas con Descartes es una iniciativa del Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija, realizada con alumnos y alumnas de 4º ESO durante el curso escolar 2015/2016, basada en la experiencia para el "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes"
Continuando con el estudio de los l.g. y sus utilidades se expone a continuación una escena con el primero de los métodos para duplicar un cubo, esto es, dado un cubo de arista a y volumen V halla, mediante la Duplicatriz de Hipócrates, un segmento de longitud a'= a·21/3 que será la arista del cubo de volumen V' = 2·V.
La escena, en primer lugar, construye dinámicamente la curva duplicatriz pulsando en el botón ![]() , en el momento en que la recta MA corta a la recta PO (M = C y A = B) se activa el botón de información que al pulsarlo deja ver un breve texto con la definición del l.g. y una demostración, que usa la construcción de Platón, del hecho de la duplicidad. En cualquier instante puede detenerse la animación mediante el botón
, en el momento en que la recta MA corta a la recta PO (M = C y A = B) se activa el botón de información que al pulsarlo deja ver un breve texto con la definición del l.g. y una demostración, que usa la construcción de Platón, del hecho de la duplicidad. En cualquier instante puede detenerse la animación mediante el botón ![]() .
.
La escena es facilmente adaptable y admite las modificaciones y/o ampliaciones que el usuario considere convenientes para su uso personal.
En el siguiente trabajo se muestra la forma en que se genera el l.g. conocido como Cisoide de Diocles y la manera de encontrar con dicha curva el segmento que sirva de arista al cubo que doble en volumen a uno inicial dado.
En esta ocasión, en la sección de vídeo, hemos elegido la primera parte del que se ha mostrado en las últimas entradas. El objetivo de este vídeo es el de apreciar distintas formas de enfocar el tema que nos ocupa: "Las Espirales.
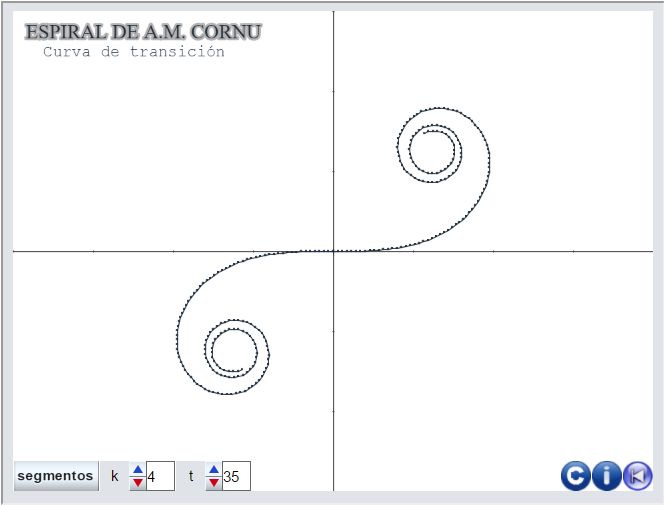
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral de Cornu" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:
- Hemos creado la siguiente escena: Espiral de Cornu (pulsad sobre la imagen para acceder a ella). Debemos advertir que, tal y como hemos procedido, esta realiza cálculos intensivos con números extremadamente grandes y pequeños, lo que hace que la ejecución de la misma sea muy lenta. Esta manera de proceder tiene la intención de hacer visible la sensibilidad de las aproximaciones polinómicas y sus efectos secundarios según muestra el trabajo posterior realizado con GeoGebra y que puede reproducirse con la escena actual con unas pocas modificaciones.
- Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto.
La escena del proyecto puede verse a continuación:
Desde este enlace puede descargarse el proyecto de miscelánea con la espiral de Cornu incluida.
En el siguiente trabajo realizado con GeoGebra, al activar la animación puede observarse como se genera el lugar geométrico conocido como curva Duplicatriz. En primer lugar se obtienen las dos medias proporcionales, propuestas por Hipócrates, entre dos segmentos de longitudes a y 2·a, donde a es la longitud de la arista del cubo inicial. A continuación la curva determina el segmento que se usará de arista del cubo de volumen doble al primero. Para la demostración se usa la composición de triángulos rectángulos semejantes atribuida a la escuela platónica.
De los recursos de la web de GeoGebra hemos tomado como origen para el análisis de las características de la aproximación polinómica de las integrales de Fresnel el "material-956849" y entre otras hemos encontrado ocurrencias como las que se exponen a continuación, que se ponen en evidencia pulsando el botón 'GO'.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- Documentación de Yuli Andrea Rodríguez Rodríguez y Benjamin R. Sarmiento Lugo
- El problema de la Duplicación del cubo de Juana Contreras S. y Claudio del Pino O. Instituto de Matemática y Física. Universidad de Talca.
- Una aproximación a la curva de transición Clotoide vista desde Mathematica de:
Luís Blanch, Emilio Checa, Josefa Marín
Universitat Politecnica de Valencia
Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo., Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo., Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo. - Problema de la duplicación del cubo de Juan Pablo Mora.
- Y otros documentos buscados en Internet.
Ildefonso Fernández Trujillo
Proporcionalidad. Las espirales XII
Proporcionalidad. Las Espirales XII
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades a los subproyectos: TELESECUNDARIA, GEOgráfica-GEOevaluación y PLANTILLAS.
Como muestra enlazamos la unidad sobre Crecimiento Exponencial, del subproyecto TELESECUNDARIA,
la GEOevaluación de los estados y ciudades de México.
y el ejemplo de: Asocia parejas de imágenes y textos (2).
Dentro de nuestro ámbito local destacan, entre otras, la permanente actualización del Proyecto ED@D en particular los materiales de 2º y 4º LOMCE y las adaptaciones de los trabajos de Javier de la Escosura Caballero: "Geometría dinámica del trángulo" que enlazamos a continuación
y el de Cuadrilateralia, donde se fomenta el estudio y conocimiento de las características matemáticas de los objetos mediante la manipulación virtual de los mismos y que enlazamos con la imagen siguiente.
Continuando con el estudio de los l.g. y sus utilidades se expone a continuación una escena con el primero de los métodos para trisecar un ángulo con la Concoide de Nicomedes. El ángulo a trisecar es el formado por el eje polar y la recta que une el polo con el punto que se desplaza por la directriz.
El análisis de la escena y su modificación, fundamentalmente en la situación del tercio del ángulo mencionado anteriormente, nos lleva a descubrir interesantes características de la Concoide. También son interesantes las modificaciones funcionales que mejoren las prestaciones de la utilidad.
Mencionar, por último, que la escena es copia de la que en su día publicó el profesor Pedro González Enríquez en su trabajo sobre las trisectrices.
Entradas anteriores mostraban, paso a paso y exhaustivamente, escenas interactivas con la creación de lugares geométricos (l.g.) por uno y dos puntos y algunas de las utilidades de los l.g. generados por un punto, en la actual comenzamos a mostrar algunos de los usos de la Concoide.
En esta ocasión, en la sección de vídeo, hemos elegido, debido a su calidad e interés, el mismo que en la entrada anterior, que muestra con una belleza y claridad incuestionables la relación de la espiral con el origen del conocimiento tanto física como metafísicamente y son de especial relevancia la calidad de las fotografías y composiciones expuestas. El objetivo de este vídeo es el de apreciar distintas formas de enfocar el tema que nos ocupa: "Las Espirales.
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral de Lituus" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:
- Hemos creado la siguiente escena: Espiral de Lituus
- Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto.
La escena del proyecto puede verse a continuación:
Desde este enlace puede descargarse el proyecto de miscelánea con la espiral de Lituus incluida.
También, relacionado con el tema de los lugares geométricos (l.g.) y la trisección del ángulo, hemos incluido los trabajos realizados con el programa GeoGebra donde se muestran dos metodos para trisecar un ángulo con la Concoide de Nicomedes.
Método 1.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Misceláneas. Las espirales XI
Proporcionalidad. Las Espirales XI
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades a los subproyectos: TELESECUNDARIA, GEOgráfica-GEOevaluación y PLANTILLAS.
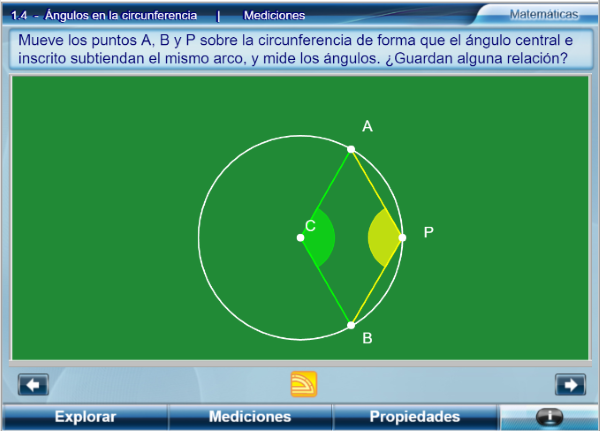
Como muestra enlazamos la unidad sobre Ángulos en la circunferencia, del subproyecto TELESECUNDARIA,
la GEOevaluación de Asia
y los ejemplos de Puzle de intercambio de imágenes tipo 2 donde Descartes realiza directamente el troceado en 4x4 de las imágenes, del subproyecto PLANTILLAS.
Dentro de nuestro ámbito local destacan, entre otras, las Misceláneas sobre las espirales y los lugares geométricos, todas ellas de indudable valor en cuanto establecen un hito en el estudio de estos objetos matemáticos. Se muestran y/o enlazan a continuación: una escena prolegómeno del estudio del l.g. "Concoide de Nicomedes" para más adelante ver su uso en la trisección de un ángulo, una miscelánea, que es un estudio riguroso y completo sobre las espirales logarítmicas y una segunda que complementa a la anterior. La excelente documentación aportada por ambas es una extraordinaria introducción a estudios más complejos de estos objetos y a la creación de utilidades educativas, dinámicas e interactivas.
Artículos anteriores mostraban, paso a paso y exhaustivamente, escenas interactivas con la creación de lugares geométricos (l.g.) por un punto, el actual muestra, según hemos visto, la creación de la Concoide de Nicomedes que es un l.g. definido por dos puntos, cuya posición depende del desplazamiento de un tercer punto por un eje. En próximas entradas se mostrará como trisecar un ángulo agudo con la Concoide.
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra con una belleza y claridad incuestionables la relación de la espiral con el origen del conocimiento tanto física como metafísicamente y son de especial relevancia la calidad de las fotografias y composiciones expuestas. El objetivo de este vídeo es el de apreciar distintas formas de enfocar el tema que nos ocupa: "Las Espirales.
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral Logarítmica" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:
- Hemos creado la siguiente escena: Espiral Logarítmica
- Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto.
La escena del proyecto puede verse a continuación:
Desde este enlace puede descargarse el proyecto de miscelánea con la espiral Logarítmica incluida.
También, relacionado con el tema de los lugares geométricos (l.g.) y sus utilidades, hemos incluido el trabajo realizado con el programa GeoGebra donde se muestra la construcción de la Concoide de Nicomedes para, más tarde, usarla en la trisección de un ángulo.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Misceláneas. Proporcionalidad. Las Espirales X
Proporcionalidad. Las Espirales X
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades al subproyecto TELESECUNDARIA.
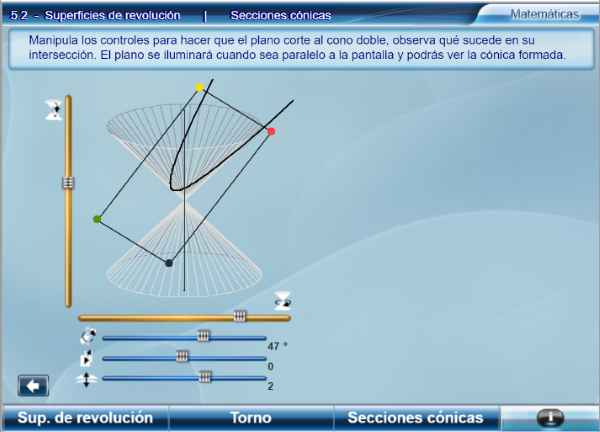
Como muestra, enlazamos la unidad sobre superficies de revolución
También es continuo el flujo de aportación de unidades al apartado GEOevaluación del subproyecto GEOgráfica
En esta ocasión enlazamos la Evaluación de los Estados Unidos de América
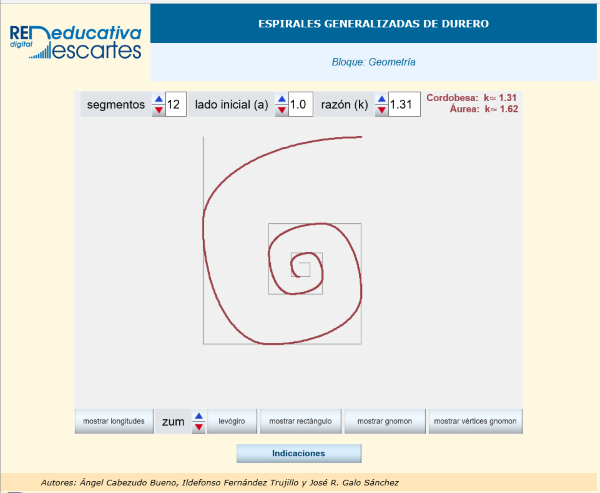
Dentro de nuestro ámbito local destacan, entre otras, las Misceláneas sobre las espirales, todas ellas de indudable valor en cuanto establecen un hito en el estudio de estos lugares geométricos aunque, en particular, es de especial interés la creada por Ángel Cabezudo Bueno ya que, además de ser la primera de la serie actual, entronca directamente con la fuente origen de dicha serie, el trabajo de José R. Galo Sanchez sobre las proporciones, la belleza en las Matemáticas y la espiral Cordobesa y es consecuencia de la acertada propuesta de espiral gnomónica Cordobesa, ambas: propuesta y miscelánea se muestran y/o enlazan a continuación.
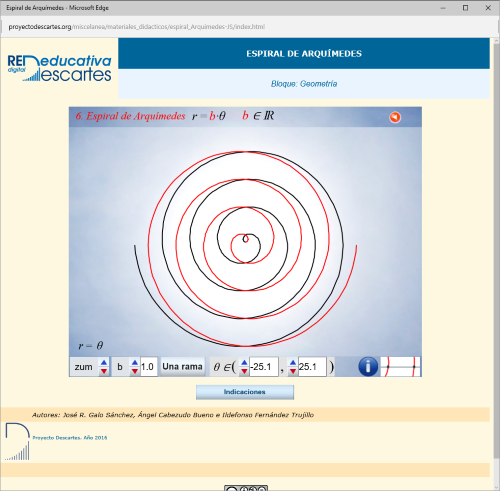
El artículo anterior mostraba, paso a paso y exhaustivamente escenas interactivas con la creación de un lugar geométrico (l.g.) por un punto común a dos segmentos y por un punto que se mueve linealmente en un segmento mientras este gira alrededor de uno de sus extremos, el actual vuelve a construir la espiral de Arquímedes y también paso a paso e interactivamente muestra como trisecar un ángulo cualquiera y como hallar la cuadratura de cualquier círculo.
A continuación se exponen las escenas interactivas.
- Generación del lugar geométrico conocido como espiral de Arquímedes.
- Trisección de un ángulo mediante la espiral de Arquímedes.
- La cuadratura del círculo mediante la espiral de Arquímedes.
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra la relación de la espiral con la orografía y la interpretación de las señales cosmológicas por las diferentes culturas con objeto de apreciar distintas formas de enfocar el tema que nos ocupa.
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral Hiperbólica" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:
- Hemos creado la siguiente escena: Espiral Hiperbólica
- Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto. Dejamos para los lectores interesados la inclusión total y/o personalizada de esta opción.
La escena del proyecto puede verse a continuación:
Desde este enlace puede descargarse el proyecto de miscelánea con la espiral Hiperbólica incluida.
También, relacionado con el tema de los lugares geométricos (l.g.) y sus utilidades, hemos incluido los siguientes trabajos realizados con el programa GeoGebra: en el primero se muestra el uso de la espiral de Arquímedes para la trisección de un ángulo y en el segundo para la cuadratura del círculo.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Proporcionalidad. Las Espirales IX. Lugares Geométricos
Proporcionalidad. Las Espirales IX
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca el subproyecto TELESECUNDARIA.
En palabras del encargado de la presentación del subproyecto en el Blog, Ángel Cabezudo Bueno, "Telesecundaria es una modalidad de los estudios de educación secundaria en el Sistema Educativo de México dirigido a estudiantes adolescentes de 12 a 15 años que viven en comunidades dispersas que carecen de escuela de secundaria.
Se utilizan para ello los avances en tecnologías de la información y comunicación (TIC) como recurso para acercar esta formación a los jóvenes y puedan concluir su educación básica.
En este subproyecto de RED Descartes se han recogido objetos de la Telesecundaria desarrollando los correspondientes materiales con la herramienta Descartes. Las asociaciones de Colombia y España han sido las encargadas de preparar la adaptación a DescartesJS y en consecuencia todos podrán ser consultados en cualquier dispositivo con sistema operativo que admita un navegador compatible con HTML5." los primeros materiales pueden verse y descargarse siguiendo el enlace gráfico siguiente.
Dentro de nuestro ámbito local queremos destacar, entre otros, los siguiente materiales:
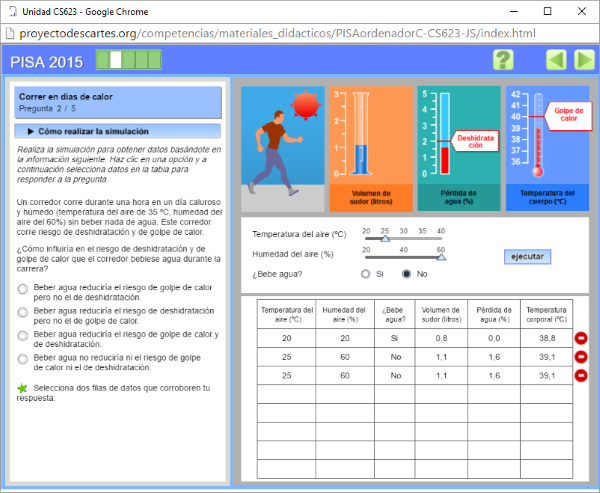
- Todos los creados para el subproyecto COMPETENCIAS. Debido a la creciente internacionalización de nuestro sistema educativo, progresiva integración en la comunidad europea, conviene que la manera de evaluar competencias en los ámbitos externos sea conocido con objeto de participar en igualdad de condiciones. Un acercamiento a estos procedimientos lo ofrecen los materiales del proyecto Competencias.
- La Miscelánea sobre la espiral de Arquímedes que sigue la corriente de mostrar los conceptos complicados, composición de movimientos, mediante la visualización del hecho de forma que es posible intervenir en la escena modificando los parámetros que la definen, con lo que la comprensión del concepto se facilita sobremanera, por lo tanto la miscelánea que se presenta es, por derecho propio, un objeto educativo lúdico e interactivo con un potencial formativo sobresaliente; no obstante en esta ocasión queremos enfocar el proceso de creación de la espiral desde el punto de vista de la definición de un lugar geométrico.
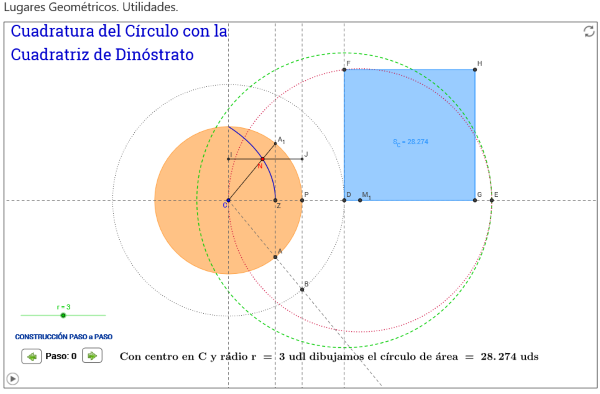
La miscelánea anterior muestra, paso a paso, la creación de un lugar geométrico (l.g.) por un punto que se mueve linealmente en un segmento mientras este gira alrededor de uno de sus extremos. Existen otros muchos lugares geométricos, entre los clásicos y más conocidos destaca la Trisectriz de Hipias que junto con la espiral de Arquímedes se ha usado, además de para otras utilidades, para la trisección de cualquier ángulo. A la Trisectriz de Hipias también se la llama Cuadratriz de Dinóstrato debido a que este geómetra usó el l.g. para la cuadratura del círculo. La Trisectriz (o Cuadratriz) es el l.g. generado por el punto común a dos segmentos uno de los cuales gira alrededor de uno de sus extremos y el otro se desplaza horizontalmente según muestran las siguientes escenas:
- La Trisectriz de Hipias que muestra, mediante una animación, la definición de la curva
- La trisección de un ángulo mediante la Trisectriz de Hipias. También se basa en una animación, en la primera parte se dibuja la curva y a continuación se muestra y explica, de forma dinámica, la trisección de un ángulo. La animación puede detenerse/reanudarse en cualquier instante.
- La cuadratura del círculo mediante la Cuadratriz de Dinóstrato (Primera Parte). Esta escena se basa en un pulsador que muestra, según se pulsa, la explicación del proceso para cuadrar el círculo. También tiene una animación que vuelve a construir la curva. La animación puede activarse/detenerse en cualquier instante.
Conviene analizar las escenas anteriores, reproducirlas y/o mejorarlas y ver la forma de integrarlas en la miscelánea sobre las espirales.
En próximas entradas en el Blog completaremos el estudio de uso de la Cuadratriz y veremos la manera de trisecar un ángulo y cuadrar el círculo con la espiral de Arquímedes.
En esta ocasión, en la sección de vídeo, hemos elegido uno muy particular que muestra la manera de dibujar la Trisectriz de Hipias (Cuadratriz de Dinóstrato) con ¿regla y compás? con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa. Buscando en internet se pone de manifiesto el enorme interés que suscitan, aún hoy en día, los problemas clásicos de la Geometría Griega.
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral de Fermat" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:
- Hemos creado la siguiente escena: Espiral de Fermat
- Inclusión del código de la escena anterior en el de la miscelánea en proyecto.
La escena del proyecto puede verse a continuación:
Y desde este enlace descargar el proyecto con la espiral de Fermat incluida.
También, relacionado con el tema de los lugares geométricos (l.g.) y sus utilidades hemos incluido dos trabajos, realizados con el programa GeoGebra, uno muestra el uso de la espiral de Arquímedes para la trisección de un ángulo y en el otro, enlazado en la imagen que sigue a la trisección, se lleva a cabo la cuadratura de un círculo de forma dinámica.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Bibliografía.- Para la realización de esta entrada y siguientes ha sido de gran ayuda la siguiente información:
- El trabajo sobre las TRISECTRICES de Pedro González Enríquez.
- Cuadratura de un círculo con la Cuadratriz de Dinóstrato
- Cuadratura de un círculo
Ildefonso Fernández Trujillo. Blog ReDescartes 2016
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)




















 CONTACTO
CONTACTO
