
La “Revista Digital Red Descartes” tiene como objetivo principal la difusión de todo lo concerniente al proyecto Descartes ―proyecto educativo de ámbito global que persigue la mejora de la educación apoyándose en las tecnologías de la información y de la comunicación (TIC) y en las del aprendizaje y el conocimiento (TAC)―, pero con visión abierta a acoger todo aquello que signifique un gran avance en el ámbito educativo con herramientas y recursos similares.
Nuestra revista se caracteriza y distingue por ser una publicación interactiva, es decir, aporta como elemento identificador el que dentro de su contenido aparecen elementos que dan respuesta adecuada, contextualizada, a las acciones que sobre ellos realice el lector/actor. Esa interactividad es identificadora del aporte que suministran los recursos desarrollados con nuestra herramienta Descartes, pero sin exclusividad a ellos. Nuestra línea de trabajo está abierta a cualquier recurso promotor del aprendizaje y del conocimiento, aunque tengamos obviamente nuestra predilección personal básica por lo que promovemos, desarrollamos y difundimos.
Así pues, abrimos una nueva línea de trabajo, inmersa en nuestro sello editorial y servicio altruista, con vocación de seguir transmitiéndoles interés por la educación y, en particular, con la utilización de los recursos educativos interactivos de nuestro proyecto Descartes, desarrollados con la herramienta homónima: Descartes, y en una revista con soporte en los “Libros interactivos de RED Descartes”. Confiamos poder rebatir a Quintiliano cuando afirmaba: “Facilius est multa facere quam diu” ―Es más fácil hacer muchas cosas que hacer una durante mucho tiempo―.
EDITORIAL
En esta décima edición de la Revista Digital Red Descartes, celebramos cinco años de difusión ininterrumpida de innovación educativa, creatividad tecnológica y reflexión pedagógica.
Los artículos reunidos abordan líneas diversas, pero unidas por un hilo común: la integración entre pedagogía e innovación. Iniciamos con una mirada al valor educativo de los juegos AJDA como herramientas adaptativas que personalizan la experiencia de aprendizaje y promueven la inclusión. Continuamos con una reflexión sobre la revolución de los libros interactivos en la enseñanza de las matemáticas, ejemplo claro de cómo la interactividad y el diseño didáctico pueden renovar las metodologías tradicionales.
El desarrollo del conversor de ficheros AJDA nos recuerda el potencial de la inteligencia artificial generativa para apoyar la labor docente. Y, en ese mismo ámbito de la IA, el análisis comparativo entre Nano Banana y Seedream 4.0 ofrece una visión crítica sobre las tendencias actuales en generación de imágenes por IA, un campo que abre nuevas posibilidades para la educación visual y la creatividad digital.
La sección matemática de este número se enriquece con los estudios sobre la espiral de Durero, las ternas pitagóricas y la generalización del teorema de Pitágoras, ejemplos de cómo el rigor matemático puede dialogar con el arte, la historia y la estética. La nota creativa “Hechizos digitales” nos recuerda que la educación también puede ser mágica cuando la imaginación y la tecnología se encuentran.
Este número es, en esencia, un homenaje a la perseverancia de una comunidad que cree en la colaboración, en el conocimiento compartido y en el poder de la tecnología para educar mejor. Agradecemos a todos los autores, editores y colaboradores que han hecho posible este recorrido de cinco años, demostrando que la innovación educativa es, sobre todo, una obra colectiva.
SUMAR
| 06 | Los juegos AJDA como juegos didácticos adaptativos Jesús M. Muñoz Calle (Sevilla - España) |
| 16 | Transformando el Aprendizaje: La Revolución de los libros interactivos en la enseñanza de las Matemáticas Carlos Alberto Rojas Hincapié Medellín - Colombia |
| 26 | Conversor de ficheros de preguntas de juegos AJDA Jesús M. Muñoz Calle (Sevilla - España) |
| 40 | Análisis y crítica de la espiral de Durero José R. Galo Sánchez (Córdoba - España) |
| 50 | Análisis Comparativo: Nano Banana versus Seedream 4.0 en la generación y edición de imágenes por IA Juan Guillermo Rivera Berrío (Medellín - Colombia) |
| 58 | El teorema de Pitágoras y su generalización. Interpretaciones de Euclides y Byrne. Ángel Cabezudo Bueno y José R. Galo Sánchez Valladolid y Córdoba - España |
ARIO
| Ternas pitagóricas: una fórmula, muchas miradas Elena E. Álvarez Saiz (Santander - España) |
68 |
| DescartesJS es "de cine" José Antonio Salgueiro González Lebrija - España |
78 |
| Hechizos digitales: cómo creé un libro de brujas con IA Juan Guillermo Rivera Berrío (Medellín - Colombia) |
86 |
| Un repaso por los archivos incrustables en DescartesJS Joel Espinosa Longi (Ciudad de México - México) |
94 |
| Blue Sea: El barco autónomo que revaloriza la FP Canaria Juan Jorge Becerra Rodríguez Las Palmas de Gran Canaria - España |
108 |
| Publicaciones iCartesiLibri Segundo semestre 2025 |
122 |
Los juegos adaptativos son herramientas tecnológicas que ajustan su contenido, dificultad y dinámica a las necesidades y niveles de habilidad de cada usuario en función de sus respuestas y de su progreso. Estos juegos se diseñan para ofrecer una experiencia de aprendizaje personalizada, lo que puede ayudar a mejorar la motivación y el compromiso de los estudiantes.
Una de las características inherentes de los juegos didácticos digitales del Proyecto AJDA es que estos sean adaptables a las necesidades específicas del alumnado al que están destinados.

Comentaremos las principales ventajas que presentan los juegos didácticos adaptativos:
Red Descartes 2025/Año 5, núm. 10

Red Descartes 2025/Año 5, núm. 10

Red Descartes 2025/Año 5, núm. 10
Comentaremos algunas de las características de los juegos didácticos del Proyecto AJDA que hacen que estos sean adaptativos:
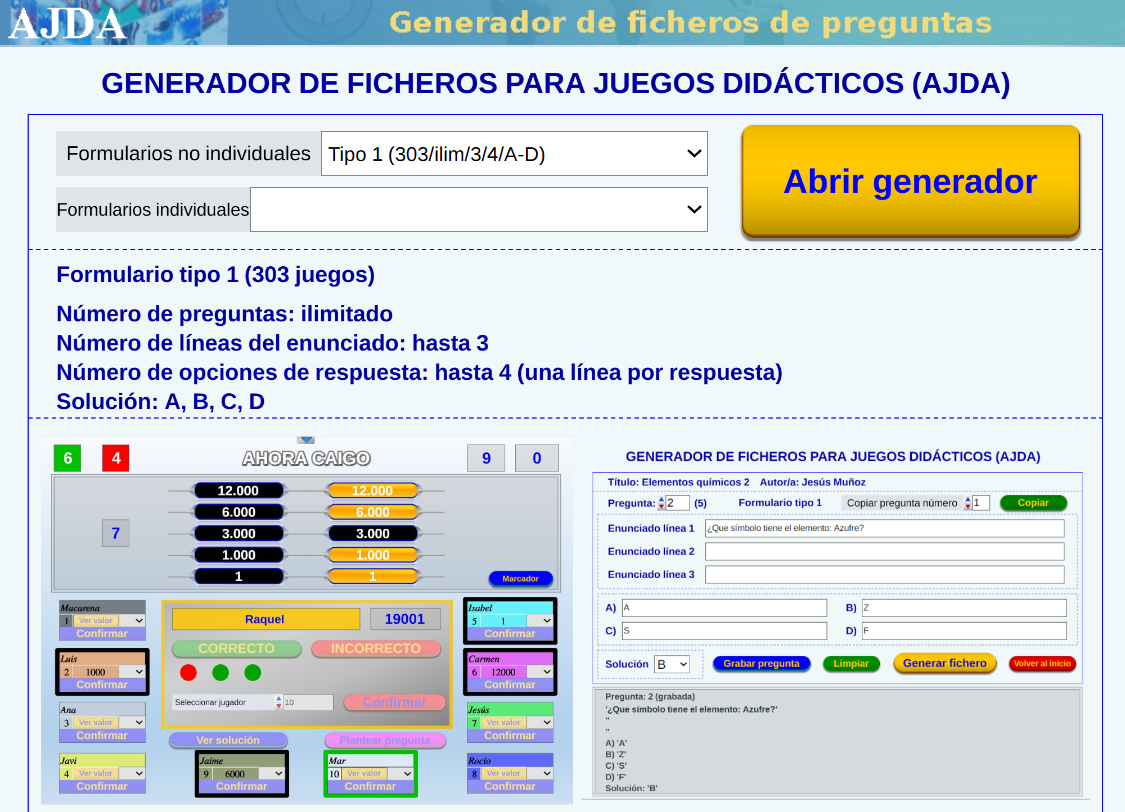
Red Descartes 2025/Año 5, núm. 10
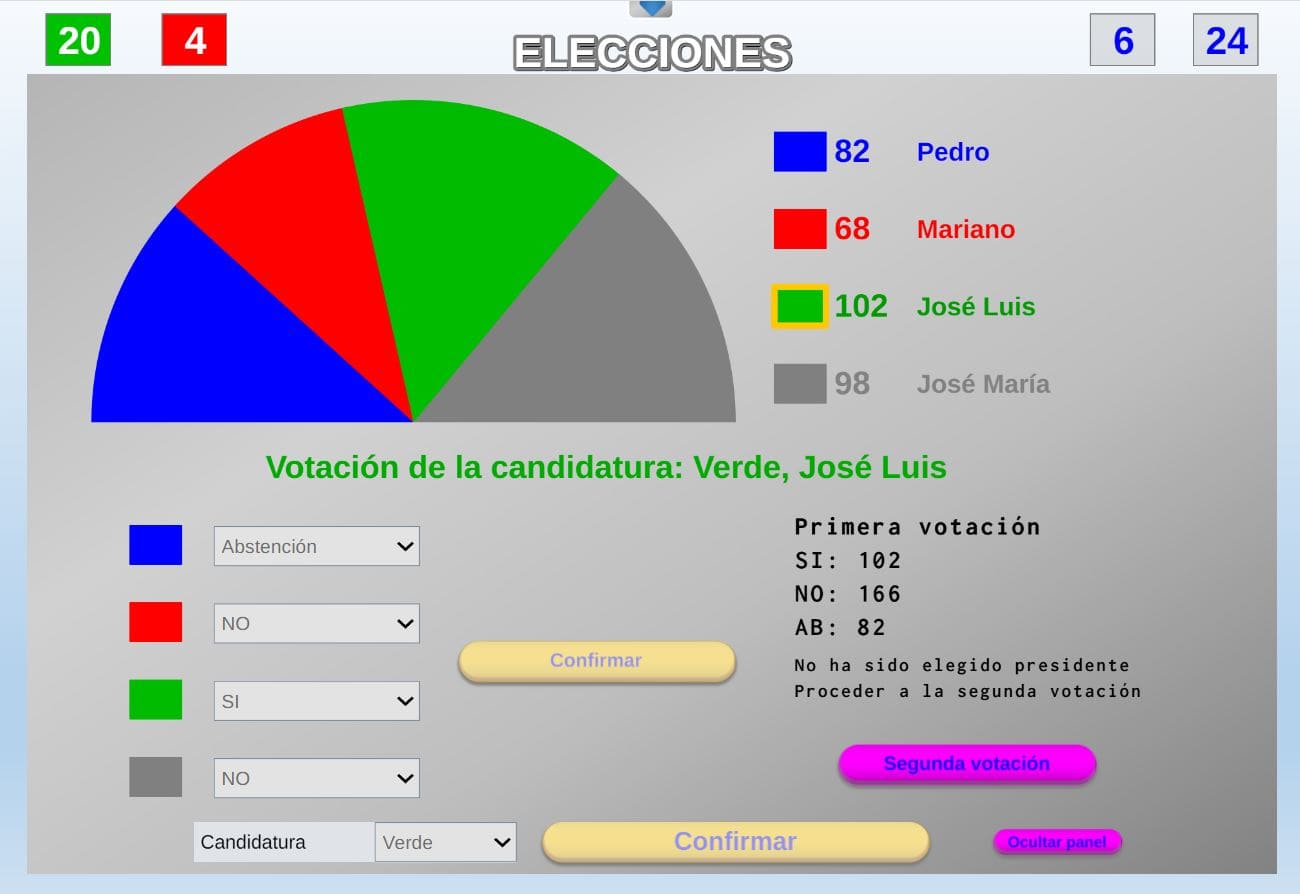
Además, en cualquier momento de la partida se puede generar un fichero de texto con los resultados que se van produciendo en cada momento.
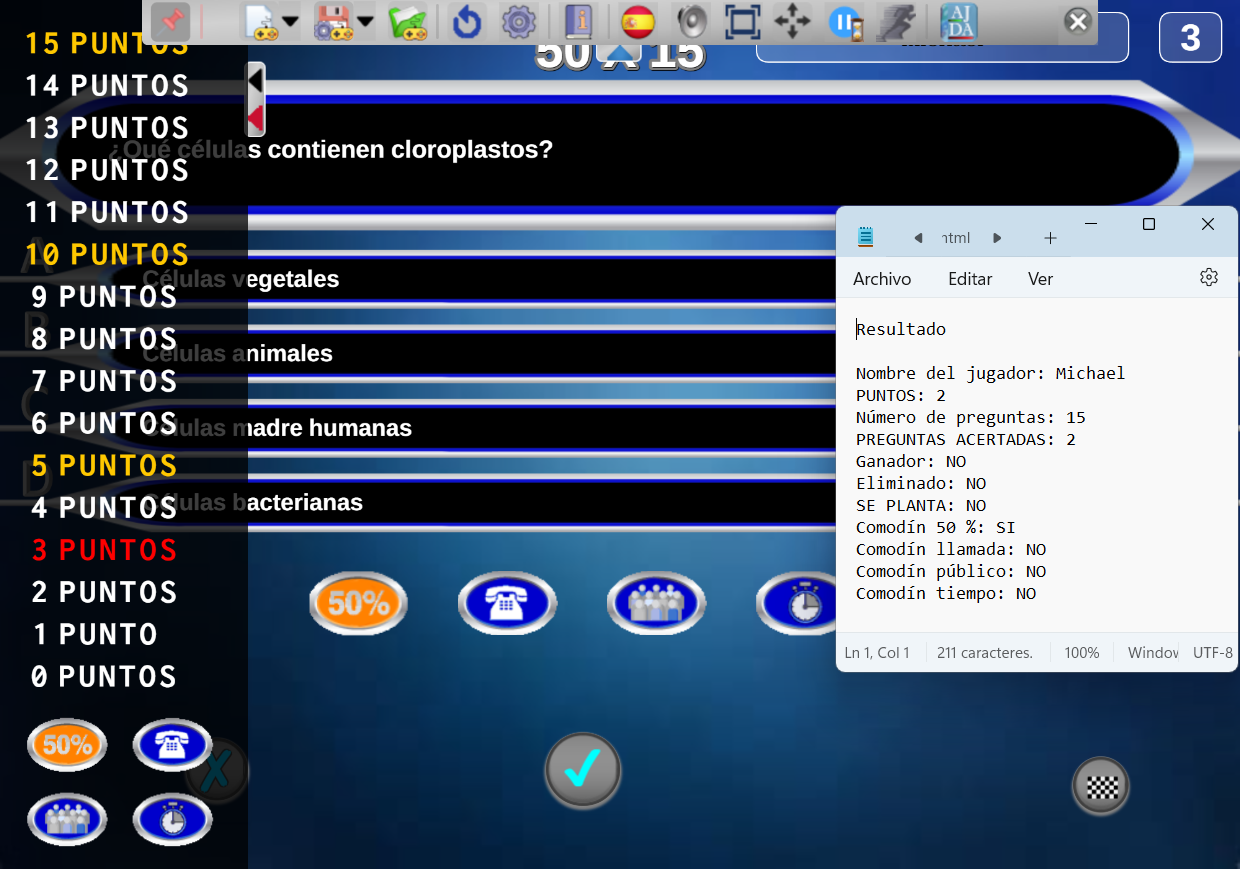
Red Descartes 2025/Año 5, núm. 10
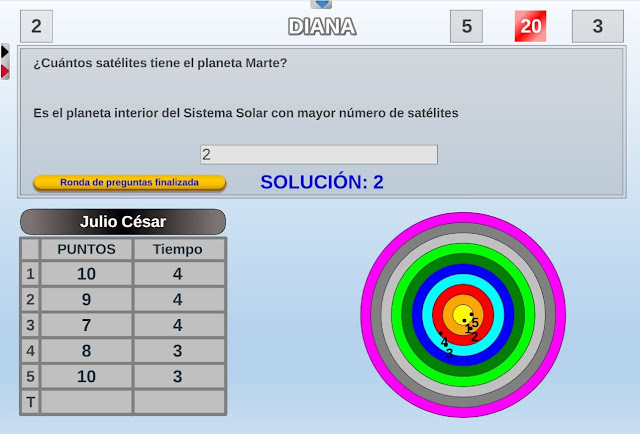
Esto puede ayudar a reducir la brecha existente para el alumnado que tiene dificultades con la lengua.
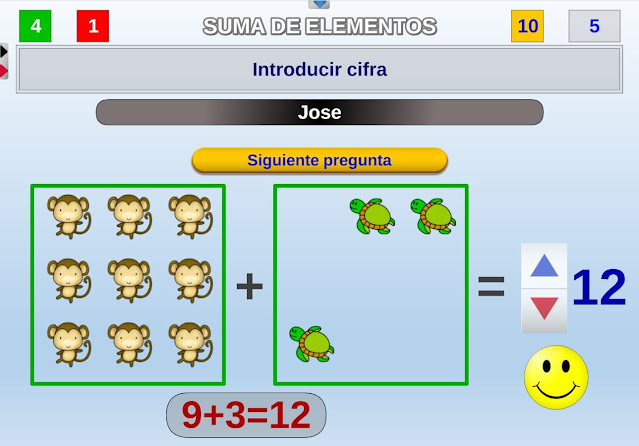
Red Descartes 2025/Año 5, núm. 10
Los recursos pueden configurarse para adaptarse a estilos visuales, auditivos o kinestésicos. Los recursos pueden configurarse para adaptarse a estilos visuales, auditivos o kinestésicos.
Red Descartes 2025/Año 5, núm. 10

Red Descartes 2025/Año 5, núm. 10
Red Descartes 2025/Año 5, núm. 10
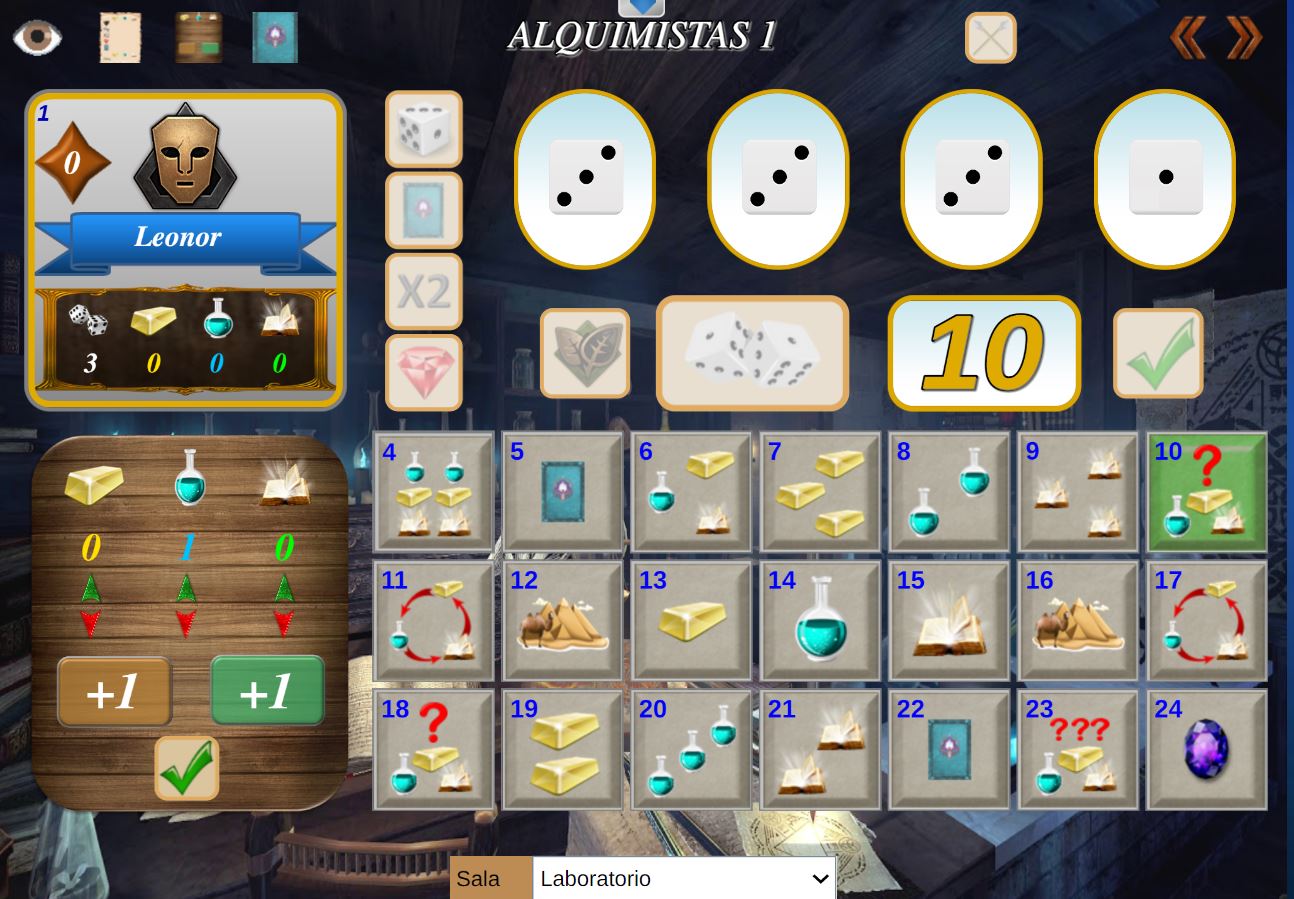
Para finalizar y como conclusión, el Proyecto AJDA se presenta como una propuesta innovadora que introduce juegos didácticos adaptativos en la educación, con el propósito de impulsar un aprendizaje más inclusivo y efectivo. La combinación de tecnología y gamificación no solo enriquece la experiencia del alumnado en su diversidad, sino que proporciona también a los docentes nuevas herramientas para enseñar de manera más dinámica y personalizada, contribuyendo así a la transformación y mejora del proceso educativo.
Red Descartes 2025/Año 5, núm. 10
En la búsqueda de mejorar la enseñanza de las matemáticas, la tecnología ofrece herramientas innovadoras que pueden revolucionar la forma en que los docentes transmiten los conceptos y los estudiantes los comprenden. Los libros interactivos de aprendizaje para la enseñanza de las matemáticas son una de estas herramientas, y en este artículo te presento cómo pueden transformar tus clases y motivar a tus estudiantes.
En la era digital, la educación está experimentando una transformación significativa. Los libros de texto tradicionales están siendo complementados o incluso reemplazados por recursos interactivos que facilitan un aprendizaje más dinámico y atractivo.
Un complemento para la creación de estos recursos educativos es la herramienta de Autor DescartesJS, es una de las herramientas que está a la vanguardia de este cambio, permitiendo la creación de libros interactivos de aprendizaje que integran elementos multimedia y actividades interactivas. En este artículo, exploraremos cómo los libros interactivos desarrollados con DescartesJS están revolucionando la forma en que enseñamos y aprendemos matemáticas.
Red Descartes 2025/Año 5, núm. 10
Ventajas de los Libros Interactivos

Los libros interactivos han tenido un impacto notablemente positivo en el proceso de enseñanza-aprendizaje de las matemáticas, mejorando significativamente la comprensión de los estudiantes. Aquí se detallan algunos de los principales beneficios y cómo han contribuido a este cambio:
Red Descartes 2025/Año 5, núm. 10
Los estudiantes reciben comentarios inmediatos sobre sus respuestas, lo que les permite corregir errores al momento y comprender mejor los conceptos.
Red Descartes 2025/Año 5, núm. 10

Mi experiencia docente y potencial pedagógico en el uso de recursos educativos
Desde mi experiencia como docente de matemáticas, he identificado que el diseño y uso de recursos didácticos interactivos, como son los libros digitales interactivos de aprendizaje, representa una estrategia eficaz para mejorar la comprensión y la motivación de los estudiantes. La naturaleza abstracta de muchos conceptos matemáticos requiere enfoques que promuevan la visualización, la manipulación y la exploración activa de los contenidos.
Red Descartes 2025/Año 5, núm. 10
En este sentido, los libros interactivos permiten integrar elementos visuales, simulaciones dinámicas, retroalimentación inmediata y actividades autoevaluativas, lo cual fortalece la participación del estudiante en su propio proceso de aprendizaje. Además, estos recursos ofrecen la posibilidad de adaptar los contenidos a diferentes ritmos y estilos de aprendizaje, facilitando así una enseñanza más inclusiva. Diseñar estos materiales desde la perspectiva de un docente permite incorporar las dificultades reales que enfrentan los alumnos en el aula, así como proponer secuencias didácticas contextualizadas y alineadas con los objetivos curriculares.
Soy un educador colombiano especializado en el área de las matemáticas, reconocido por mi trabajo en la creación y distribución de recursos educativos digitales, más específicamente en la elaboración de libros digitales que complementan mi quehacer docente. Soy autor de varios libros interactivos y materiales didácticos dirigidos a mejorar la enseñanza de las matemáticas y otras disciplinas en niveles de educación básica, media y universitaria.
He diseñado y difundido una serie de libros electrónicos interactivos concebidos como herramientas pedagógicas de apoyo tanto para docentes como para estudiantes. Estos recursos han demostrado ser particularmente valiosos en contextos de emergencia educativa, como durante periodos de contingencia sanitaria, así como en situaciones donde los estudiantes enfrentan barreras para acceder a la educación presencial. Su formato digital e interactivo permite mantener la continuidad del proceso de enseñanza-aprendizaje fuera del aula convencional, ofreciendo contenidos accesibles, actividades autoguiadas y recursos multimedia que fomentan la autonomía del estudiante. Además, al estar disponibles en línea o mediante descarga, estos libros favorecen una mayor flexibilidad educativa y
Red Descartes 2025/Año 5, núm. 10
contribuyen a reducir brechas en el acceso al conocimiento, especialmente en entornos donde las condiciones no siempre permiten una participación presencial constante.
Desde hace más de trece años formo parte activa de la Red Educativa Descartes, una comunidad dedicada a la innovación pedagógica mediante el desarrollo de recursos educativos digitales. Uno de los ejes centrales de sus proyectos es la creación de libros digitales interactivos y multimedia que no solo facilitan la comprensión conceptual de los contenidos, sino que también están diseñados para centrarse en el aprendizaje activo del estudiante. Estos materiales promueven la autonomía, el pensamiento crítico y el desarrollo de competencias clave, con el objetivo de formar personas capaces de aprender a lo largo de la vida y de afrontar de manera reflexiva y eficaz los retos de su trayectoria personal y profesional.
Mi producción de libros digitales educativos

El complemento de mi labor como docente de Matemáticas se ha materializado en la creación de una serie de libros interactivos concebidos como herramientas accesibles, dinámicas y centradas en el estudiante y docentes. Estos materiales integran elementos multimedia, actividades autoevaluativas y simulaciones que promueven la exploración activa de los conceptos matemáticos, favoreciendo la autonomía y el pensamiento crítico.
El primer libro que elaboré en esta línea fue "Matemáticas Básicas", orientado a fortalecer los conocimientos fundamentales en estudiantes de nivel de básica secundaria.
Red Descartes 2025/Año 5, núm. 10

A partir de allí, he desarrollado otros títulos que responden a diferentes necesidades del currículo escolar, como "Función lineal y cuadrática", "Geometría Plana. Fundamentos para Secundaria & Media", "Matemáticas de secundaria: Grado 8 -9 ", "Cálculo Diferencial e integral", entre otros, cada uno estructurado con un enfoque pedagógico centrado en la resolución de problemas, la visualización de conceptos abstractos y la aplicación contextualizada de la matemática.

Red Descartes 2025/Año 5, núm. 10

El más reciente de estos trabajos es "Matemáticas de Media: Grado 11", pensado para estudiantes que se preparan para enfrentar retos académicos de mayor complejidad, incluyendo las pruebas estandarizadas de final de ciclo escolar.
Diseñado bajo los lineamientos de los Estándares Básicos de Competencia y los Derechos Básicos de Aprendizaje de Matemáticas para el grado 11° establecidos por el Ministerio de Educación Nacional de Colombia. Contiene cuatro capítulos temáticos del área de cálculo; incluye, además, actividades de exploración, actividades de construcción, talleres, juegos, el editor de GeoGebra, objetos interactivos diseñados con DescartesJS y actividades evaluativas, los cuales se presentan de modo agradable, que garantizan el aprendizaje al aumentar la motivación cuando se utiliza en ordenadores o diferentes dispositivos móviles.

Paralelamente, me encuentro actualmente en la fase de diseño de un nuevo libro titulado "Los Números del Sistema Solar", una propuesta interdisciplinaria que une la astronomía con la matemática, destinada a despertar el interés por la ciencia a través de actividades lúdicas, exploratorias y contextualizadas en el entorno del universo.
Red Descartes 2025/Año 5, núm. 10
Este proyecto busca integrar el conocimiento científico con competencias matemáticas clave, en un formato accesible y altamente interactivo, alineado con los principios del aprendizaje activo y significativo.
Estos libros han sido ampliamente utilizados tanto en entornos presenciales como en modalidades a distancia, especialmente durante periodos de contingencia, ofreciendo una alternativa pedagógica eficaz para asegurar la continuidad educativa. Asimismo, la posibilidad de compartir estos materiales a través de plataformas abiertas ha permitido que otros docentes los adopten, adapten y utilicen, fortaleciendo el trabajo colaborativo y el acceso equitativo a recursos educativos de calidad.
En conclusión, los libros interactivos de aprendizaje han transformado la enseñanza y el aprendizaje de las matemáticas al proporcionar una experiencia educativa más activa, personalizada y motivadora. Han mejorado la comprensión de los estudiantes al ofrecer interactividad, retroalimentación inmediata, adaptación personalizada y visualización de conceptos abstractos, entre otros beneficios.
Red Descartes 2025/Año 5, núm. 10
Bibliografía
Red Descartes 2025/Año 5, núm. 10
Uno de los aspectos más destacados de los juegos didácticos del Proyecto AJDA es su capacidad para personalizar contenidos mediante la creación de ficheros de preguntas adaptados a las necesidades del usuario. Estos ficheros pueden ser archivados, clasificados y reutilizados, lo que fomenta una experiencia de aprendizaje propia más dinámica y versátil.
El Proyecto AJDA ofrece un generador de ficheros de preguntas que facilita la creación de contenido de manera sencilla, a través de formularios diseñados específicamente para cada uno de los diferentes tipos de juegos. Estos formularios están optimizados para adaptarse a los distintos formatos de preguntas compatibles con la diversidad de juegos AJDA y para simplificar su elaboración y tratamiento.
Los archivos utilizados por los juegos AJDA están en formato TXT o texto plano y son completamente editables con cualquier procesador de textos, aunque se recomienda utilizar el generador proporcionado por el Proyecto para evitar errores y garantizar una mejor integración y funcionalidad. Este formato, exclusivo de los juegos AJDA, ha sido diseñado para garantizar su simplicidad y flexibilidad.
Red Descartes 2025/Año 5, núm. 10
Con el propósito de ampliar las posibilidades de uso, mejorar la compatibilidad y fomentar la reutilización de estos contenidos, se ha desarrollado un conversor de ficheros para el Proyecto AJDA. Este conversor, creado con el apoyo de diversas inteligencias artificiales generativas, representa un avance en la gestión de contenidos personalizados. Pulsando sobre la siguiente imagen se accede a la página principal del conversor.
En esta página, al seleccionar el formulario correspondiente al tipo de fichero deseado, se mostrarán sus características junto con una imagen representativa de un juego AJDA de ese tipo y una captura de pantalla del conversor. Al hacer clic en el botón Abrir conversor, se abrirá una nueva ventana con el conversor específico para el tipo seleccionado.
Red Descartes 2025/Año 5, núm. 10
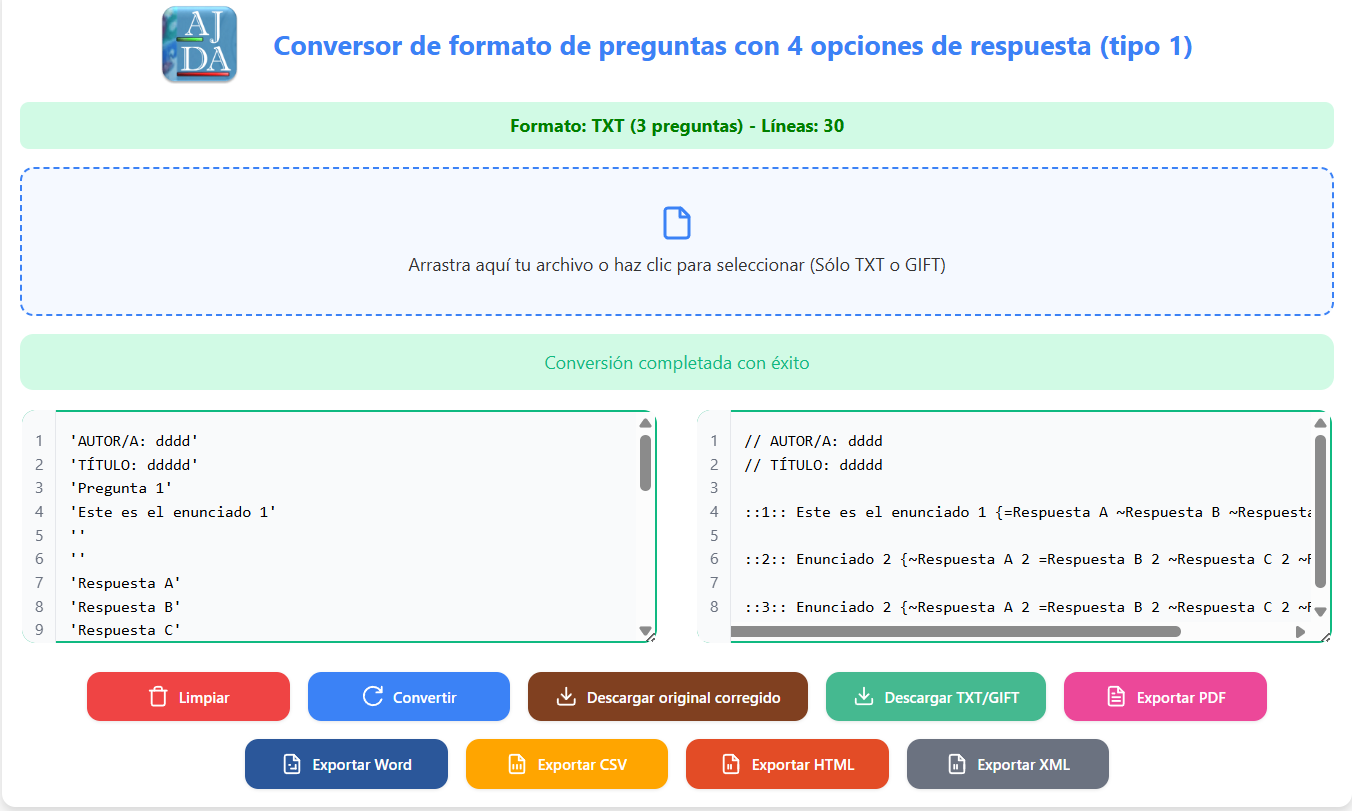
Los conversores de los diferentes tipos comparten un diseño uniforme. En la parte superior se encuentran el logotipo de AJDA, el título y una breve descripción del conversor. Justo debajo, una línea indica el formato y muestra un fondo de color verde, naranja o rojo, dependiendo de la idoneidad del archivo seleccionado.
A continuación, se encuentra el área destinada para seleccionar o arrastrar los archivos de entrada. Debajo de esta, hay una sección dedicada a visualizar posibles errores detectados durante el proceso.
En la parte inferior, se presentan dos campos de texto numerados: el de la izquierda muestra el contenido de entrada, que puede ser modificado manualmente, y el de la derecha contiene el contenido de salida generado por el conversor.
Por último, en el pie de la página, se encuentra una barra de herramientas con botones para realizar acciones clave como conversión, descarga, exportación y limpieza de los datos.
Red Descartes 2025/Año 5, núm. 10
Los ficheros de entrada admiten dos formatos: el formato TXT, propio de los juegos didácticos AJDA, y el formato GIFT (General Import Format Technology), un estándar ampliamente utilizado para crear preguntas de evaluación en plataformas educativas como Moodle.
El formato GIFT se caracteriza por su simplicidad, permitiendo redactar preguntas de manera rápida y sencilla a través editores de texto básicos. Su alta compatibilidad con Moodle facilita la importación y exportación de cuestionarios, además de permitir la edición masiva, lo que lo convierte en una herramienta ideal para agilizar y organizar la creación de evaluaciones.
Los datos pueden ingresarse mediante un archivo o copiando y pegando directamente en el campo de texto izquierdo del conversor. Si se detectan errores, estos serán señalados para su corrección.
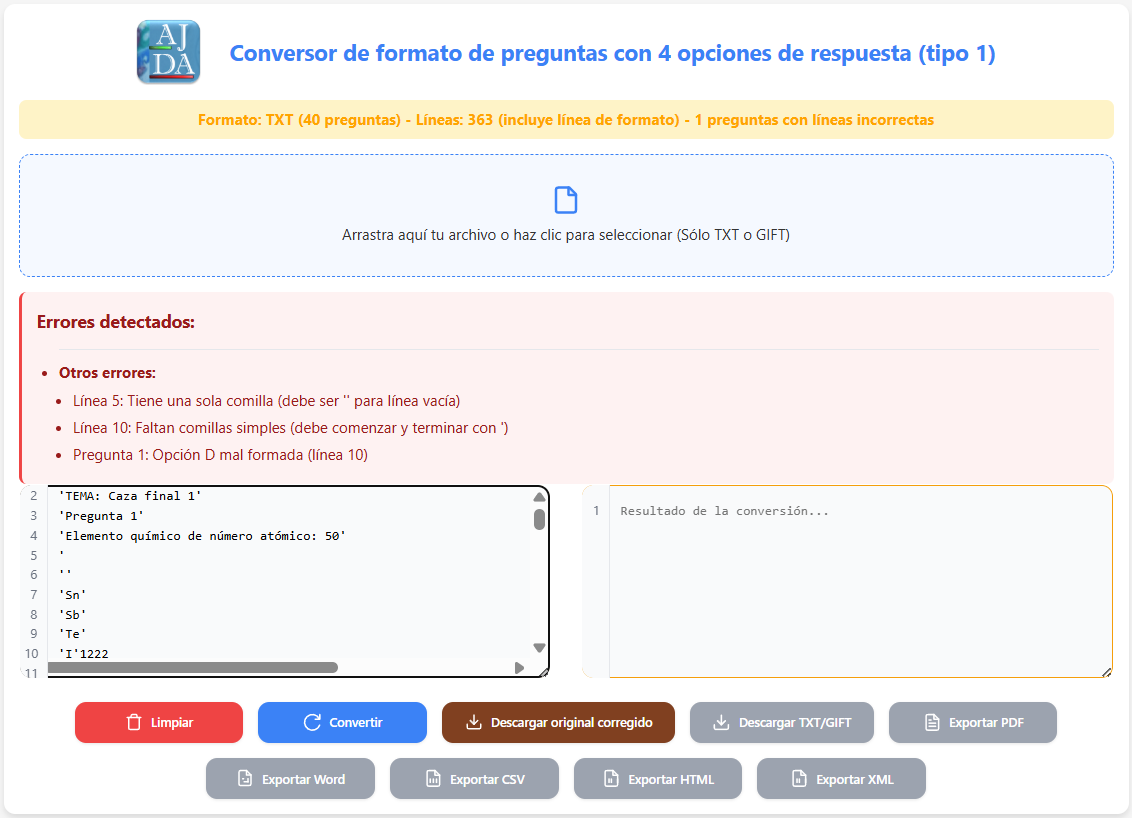
Red Descartes 2025/Año 5, núm. 10
Si se detectan errores graves, la línea de formato debajo del título se resaltará en rojo y no será posible realizar la conversión. Para errores corregibles, la línea se mostrará en naranja, permitiendo subsanarlos directamente en el campo de texto izquierdo. Una vez corregidos, los errores dejarán de mostrarse. Si el color es verde, significa que no se han encontrado errores y la conversión puede realizarse sin inconvenientes.
Al presionar el botón Convertir, el archivo en formato TXT de AJDA se transformará al formato GIFT, o viceversa. El resultado de la conversión se mostrará en el campo de texto derecho.
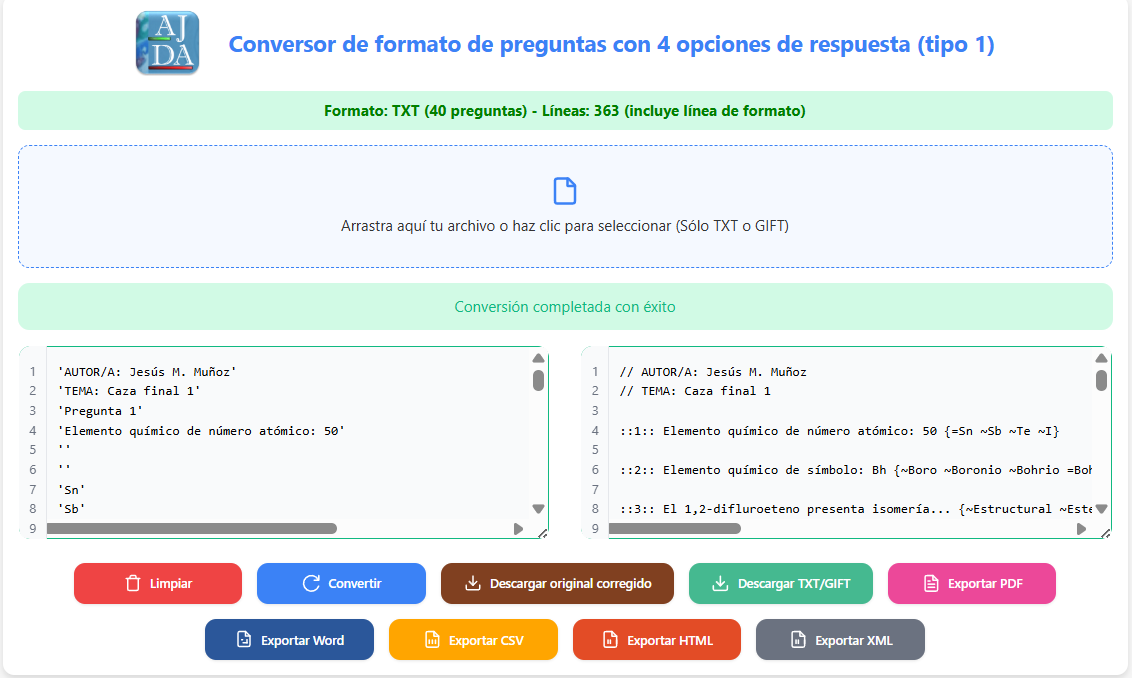
Después de la conversión, es posible descargar tanto el archivo original como el convertido. Además, se puede exportar el contenido a siguientes formatos: PDF, Word, CSV, HTML y XML.
Para los formatos PDF, Word y HTML se ha buscado que la presentación sea la más adecuada.
Red Descartes 2025/Año 5, núm. 10
A continuación, presentamos un ejemplo de conversión de archivos del tipo 16, diseñado para emparejar dos columnas de 10 elementos cada una. El proceso comienza con un archivo en formato TXT, que luego es convertido al formato GIFT.
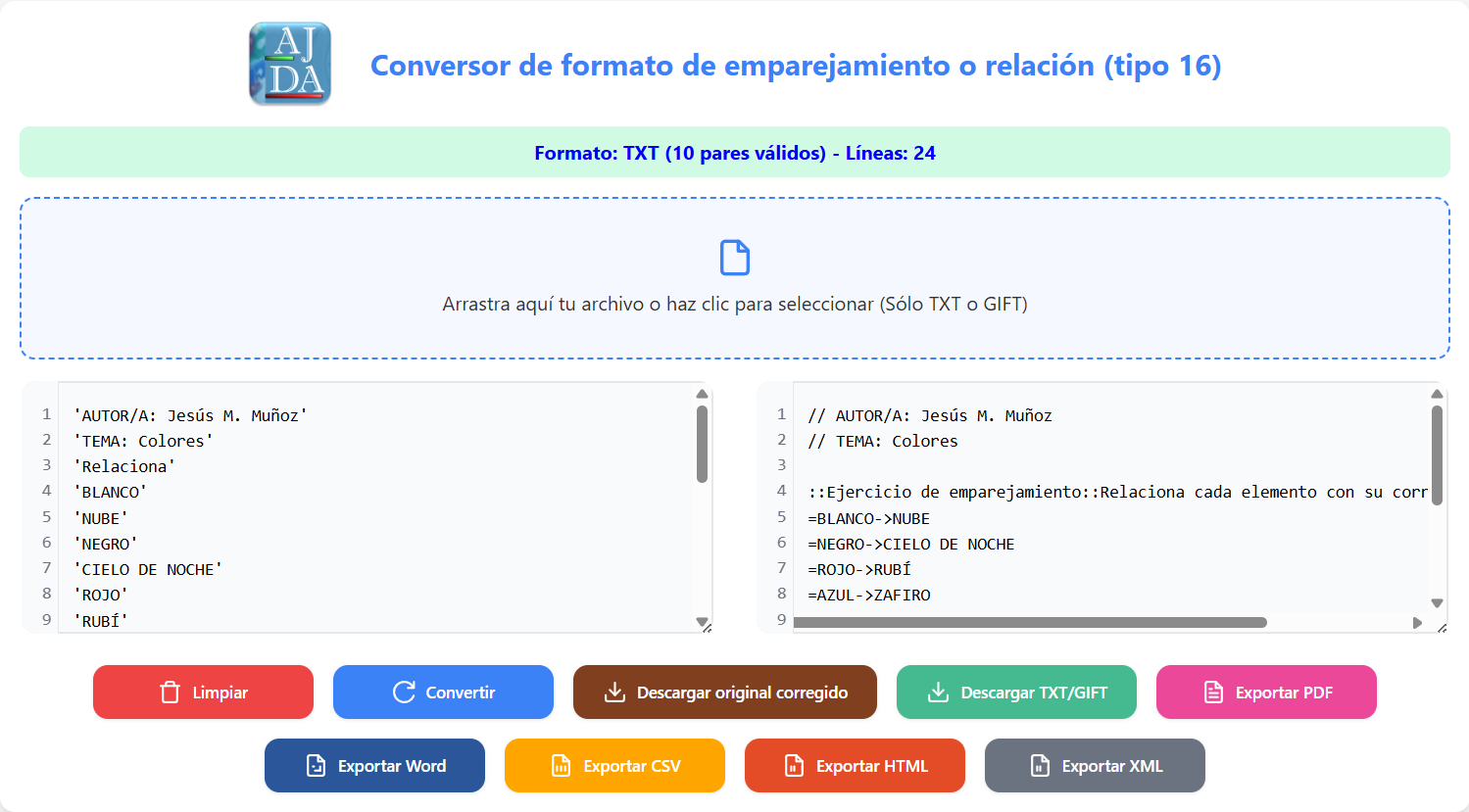
Posteriormente realizamos la exportación a Word, PDF y HTML.
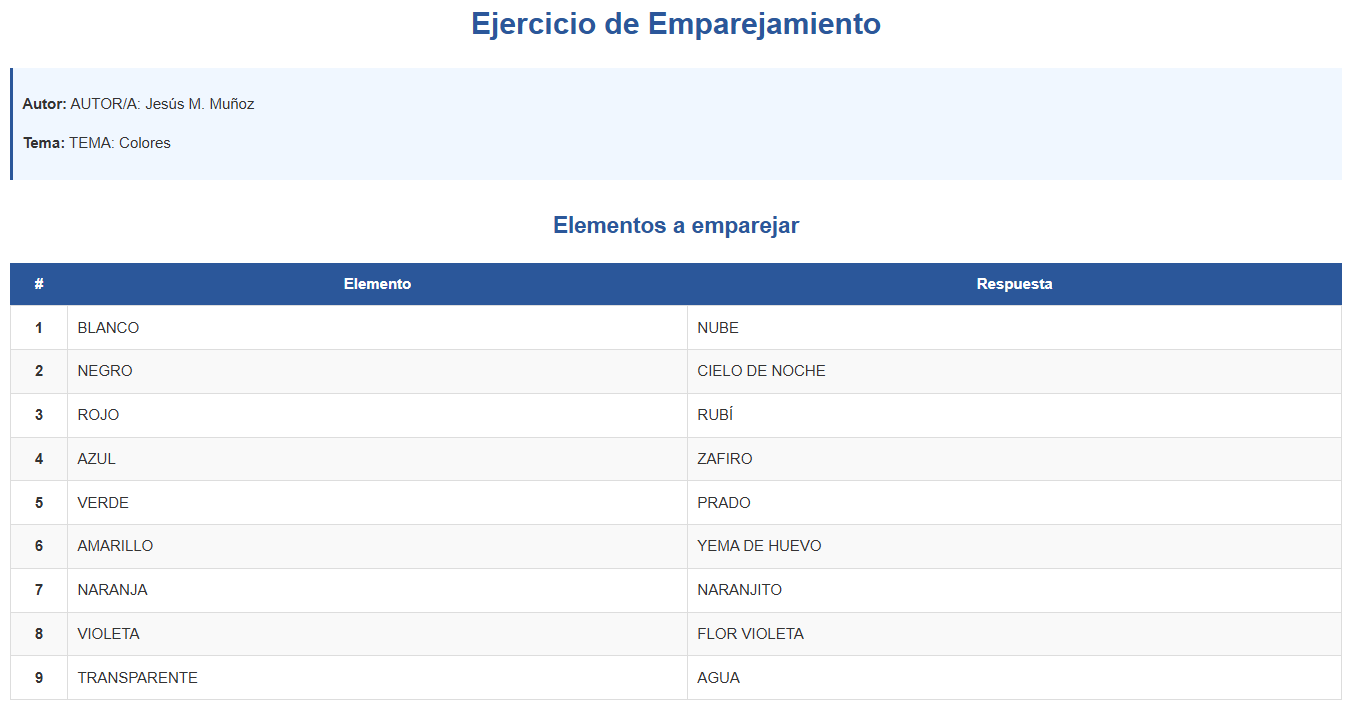
Red Descartes 2025/Año 5, núm. 10
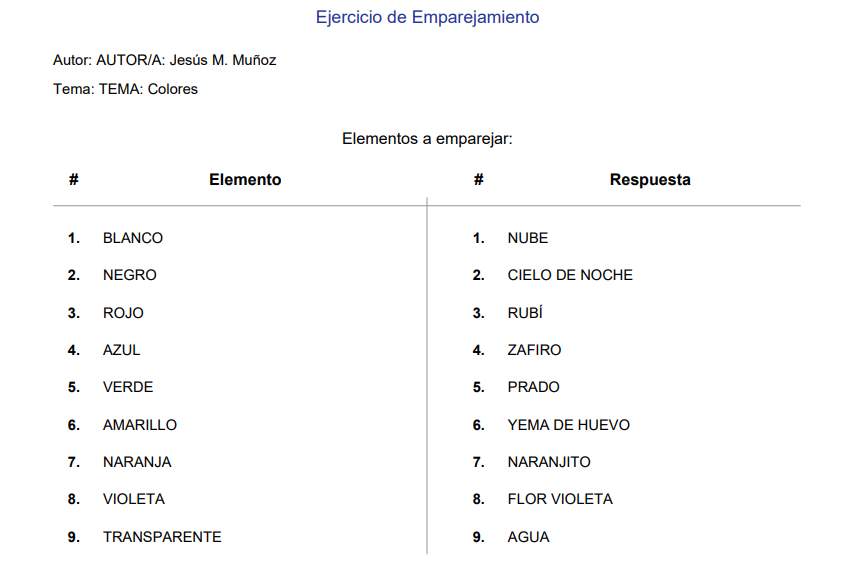
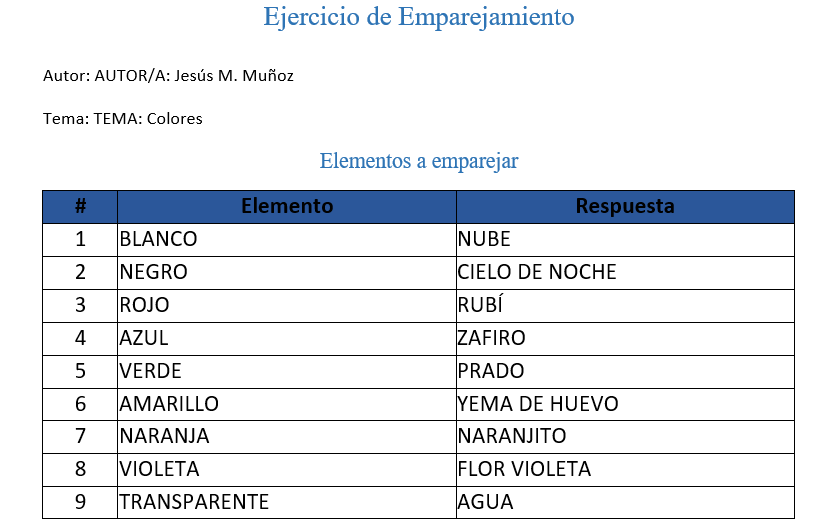
Red Descartes 2025/Año 5, núm. 10
Realizamos una realización de los formatos utilizados en el conversor:
El siguiente vídeo ofrece una explicación sencilla sobre cómo utilizar el conversor.
Red Descartes 2025/Año 5, núm. 10
En este apartado, nos centraremos en el diseño de los 54 conversores desarrollados con el apoyo de diversas herramientas de inteligencia artificial generativa. El proceso comenzó con la creación de la estructura y presentación base del conversor, sobre la cual se incorporaron las distintas funcionalidades. Durante este desarrollo, se destacaron los siguientes aspectos clave:
Red Descartes 2025/Año 5, núm. 10
Después del diseño, fue necesario realizar pruebas utilizando diversas inteligencias artificiales generativas para abordar las siguientes dificultades encontradas:
Red Descartes 2025/Año 5, núm. 10
Otro aspecto especialmente relevante es la elaboración del prompt. Aunque este elemento siempre es importante, en este caso resultó fundamental, requiriendo un ajuste minucioso para lograr los resultados deseados.
Para ilustrar la relevancia de incluir instrucciones detalladas, presentamos el prompt específico que utilizamos para generar el conversor del tipo Super frase. Como punto de partida para esta generación, se tomó como base el conversor ya desarrollado y finalizado en el archivo tipo-10.html.
Incluimos el prompt exactamente como se introdujo en la inteligencia artificial, sin corregir erratas ni modificar el texto, con el fin de reflejar con la mayor fidelidad posible el proceso realizado.
Partiendo del conversor adjunto tipo-10.html necesito generar otro llamado tipo super_frase. También te adjunto un fichero TXT para que veas como debe quedar el resultado. Necesito que me generes el código completo del conversor tipo super_frase con las mismas funcionalidades, tipo de notificaciones de error, estilo y los mismos enlaces relativos a las imágenes y a los ficheros js que el tipo-10.html que te adjunto, pero con las siguientes diferencias:
Red Descartes 2025/Año 5, núm. 10
Red Descartes 2025/Año 5, núm. 10
Tras recibir estas instrucciones, en aproximadamente 10 minutos generó un código de unas 2.500 líneas, sobre el cual fue necesario solicitar cinco correcciones específicas para que el conversor funcionara correctamente.
A modo de conclusión, presentamos un resumen de los aspectos más relevantes de este proceso:
Red Descartes 2025/Año 5, núm. 10
Este proyecto es un claro ejemplo de colaboración imprescindible entre inteligencia humana y artificial, donde ambas se complementan y resultan esenciales para su realización.

Red Descartes 2025/Año 5, núm. 10
Si aborda una búsqueda literaria o pregunta a un buscador o a una inteligencia artificial sobre "La espiral de Durero", con alta probabilidad se verá derivado a una curva plana que se enmarca en una sucesión de rectángulos y obtendrá una imagen análoga a la siguiente:
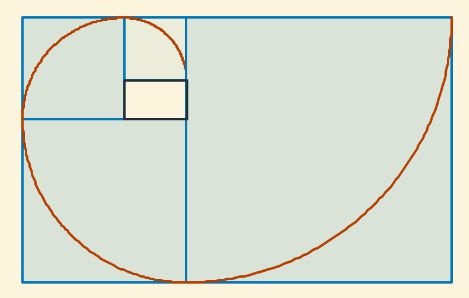
Fig. 1. Representación usual actual de "La espiral de Durero".
Pero si consultamos la fuente original, es decir, la espiral que describe Durero en el libro I de "De la Medida", verá que este artista dibuja una espiral con aspecto diferente o al menos que difiere de la representación anterior (Fig. 2).
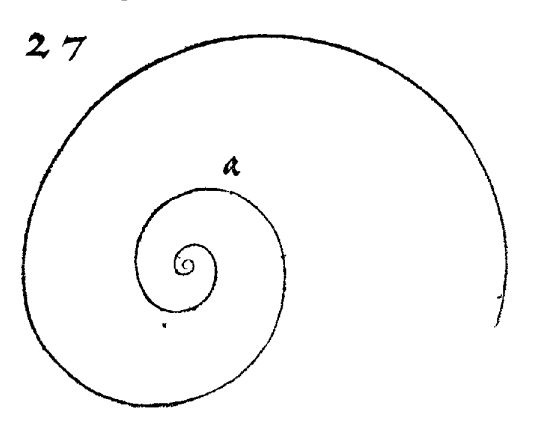
Fig. 2. Espiral dibujada por Durero en el libro I "De la Medida".
Red Descartes 2025/Año 5, núm. 10
Si siente inquietud acerca de la relación que existe entre esas dos espirales ha llegado al sitio adecuado. Aquí le explicaré el vínculo matemático, el cordón umbilical que une a ambas y cómo una recoge la esencia primigenia, el ser, de la otra. Esta explicación la he recogido en una escena interactiva que he titulado "Crítica de la pseudoespiral de Durero" y que nos servirá de guía expositiva. El detalle matemático puede consultarlo en el documento de indicaciones, accesible al pulsar el botón etiquetado con la letra i.

Fig. 3. Escena interactiva "Crítica de la pseudoespiral de Durero.
Pulse sobre la imagen para acceder.
Si se siguen las instrucciones dadas por Durero rápidamente se observará que no se concretan, que son ambiguas y obligan al lector o reproductor de ellas a tomar decisiones para intentar reproducir lo que Durero posiblemente quiso dibujar, según la imagen que elaboró, aunque no lo detalló en su guía constructiva. En la escena podrá ir paso a paso y ver cuáles son los criterios por los que yo he optado y también cómo queda abierto el estudio para otras posibles opciones que serán objeto de un trabajo posterior.
Red Descartes 2025/Año 5, núm. 10
Interpretando las instrucciones iniciales de Durero podemos dibujar una curva que es concatenación de arcos de circunferencias (en concreto consideramos cuadrantes) afectados por un factor reductor de 0,5 que conforman una "espiral hacia dentro": Realmente no es una espiral propiamente, sino una pseudoespiral, ya que es una curva definida a trozos (ver Fig.4, izqda.). Continuando con las siguientes instrucciones que aporta este artista obtenemos una pseudoespiral "hacia fuera" formada también por cuadrantes de circunferencia con un factor amplificador de 1,5 (ver Fig.4, dcha.).
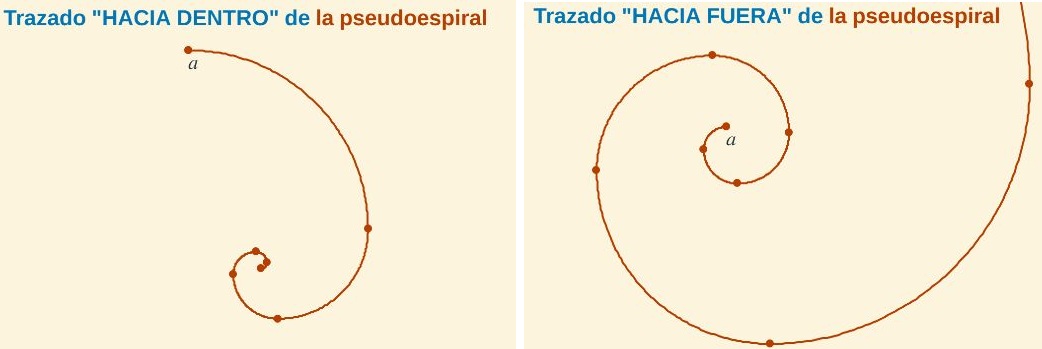
Fig. 4. Izq.: Espiral "hacia dentro", dcha.: Espiral "hacia fuera", según las indicaciones iniciales de Durero
y forzada interpretación del autor de este artículo.
Concatenando ambas obtenemos la pseudoespiral de Durero:
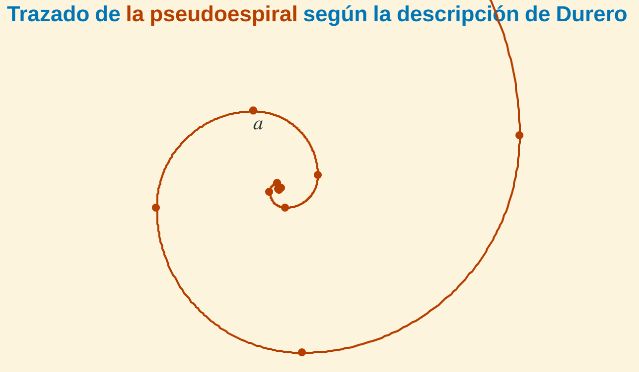
Fig. 5. La pseudoespiral de Durero acorde con las indicaciones dadas por Durero
e interpretación del autor de este artículo
Red Descartes 2025/Año 5, núm. 10
Abordando un análisis personal de esta construcción y realizando una crítica de la misma, podemos afirmar lo siguiente:
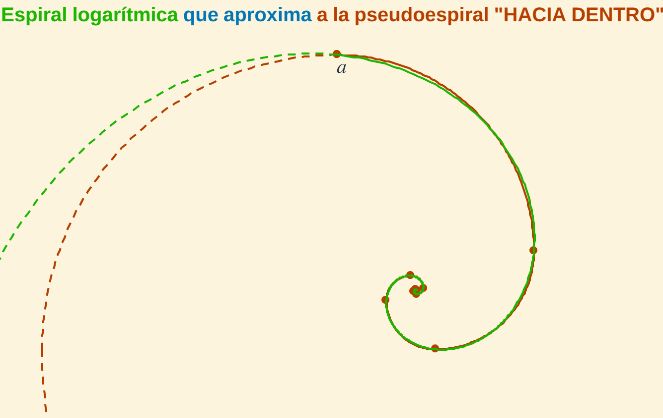
Fig. 6. Espiral logarítmica que aproxima a la pseudoespiral de Durero "hacia dentro".
Red Descartes 2025/Año 5, núm. 10
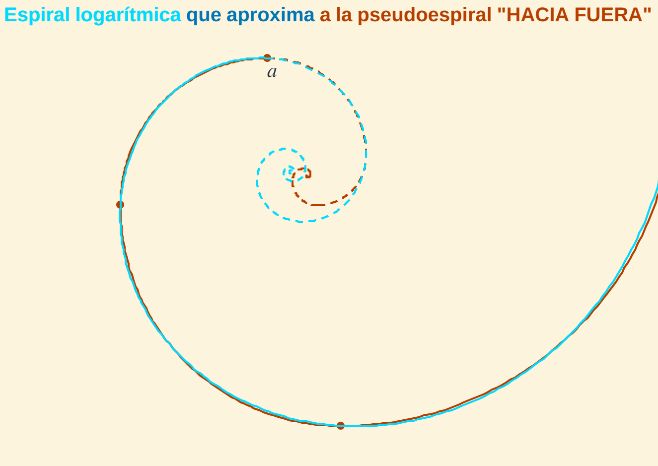
Fig. 7. Espiral logarítmica que aproxima a la pseudoespiral de Durero "hacia fuera".
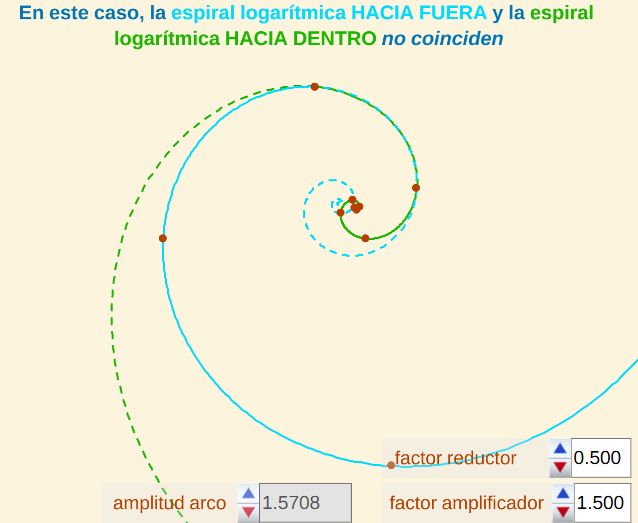
Fig. 8. La espiral logarítmica "hacia dentro" y la espiral logarítmica "hacia fuera" no coinciden, pues se tiene que $1,5 (1 - 0,5) ≠ 1$.
Red Descartes 2025/Año 5, núm. 10
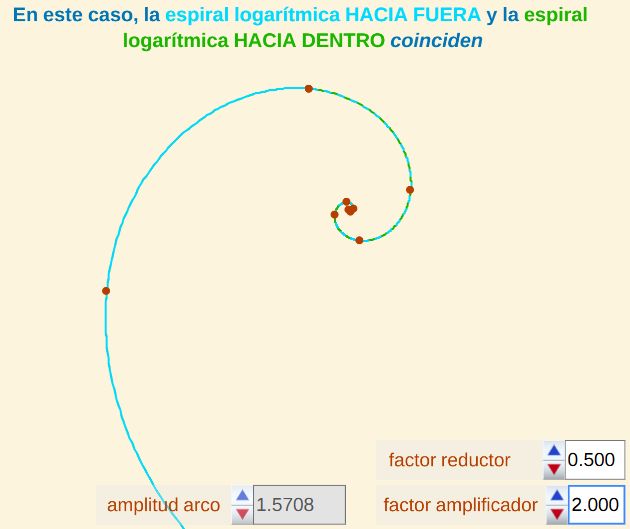
Fig. 9. La Espiral logarítmica "hacia dentro" y la espiral logarítmica "hacia fuera" sí coinciden, pues se verifica que: $2 (1 - 0,5) = 1$.
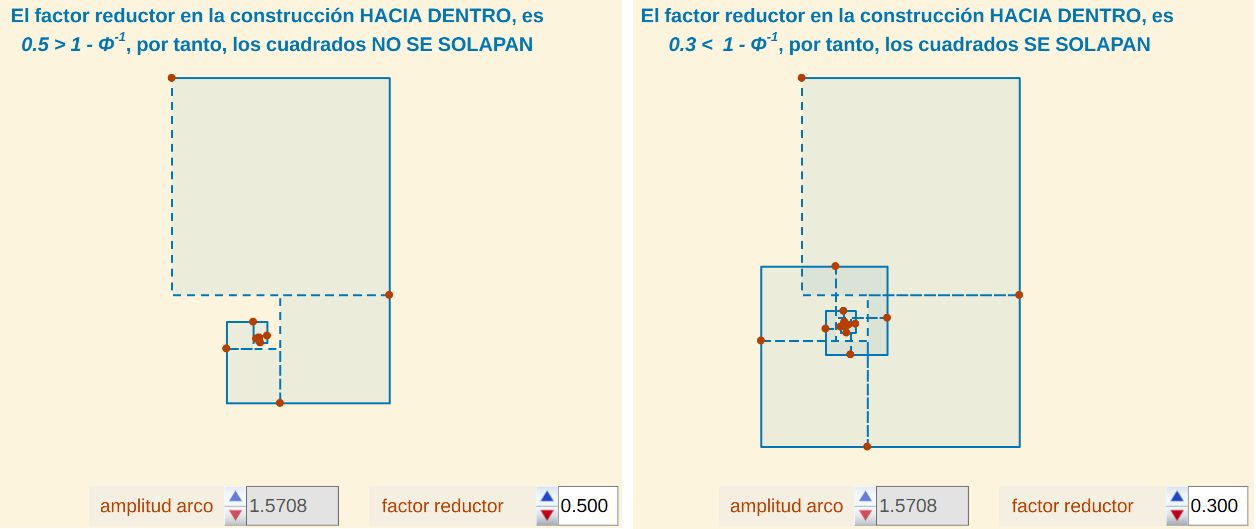
Fig. 10. Condición para que haya solapamiento en la construcción de la pseudoespiral de Durero "hacia dentro".
Red Descartes 2025/Año 5, núm. 10
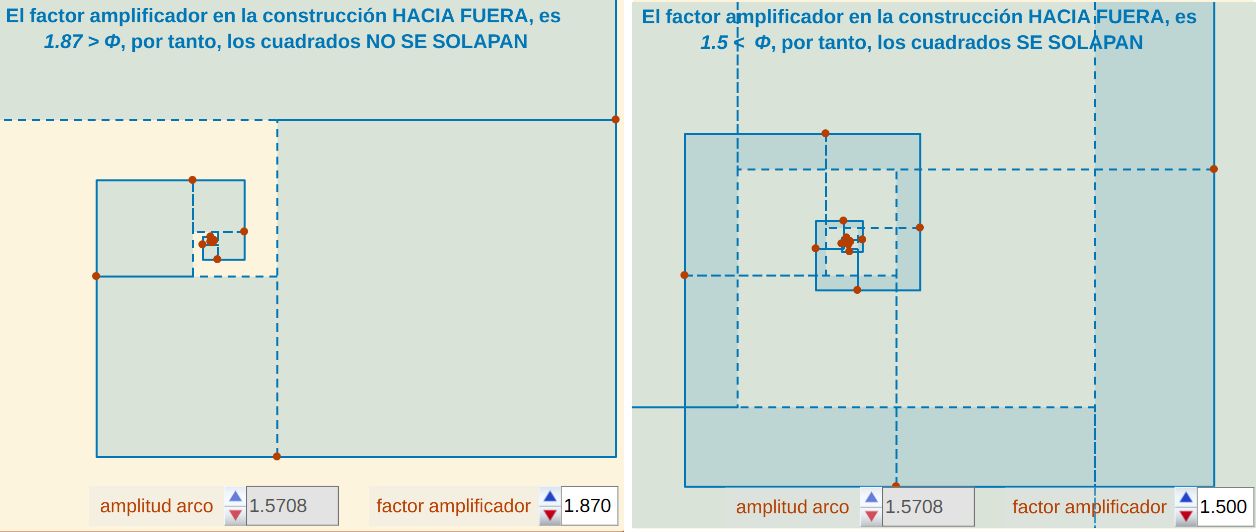
Fig. 11. Condición para que haya solapamiento en la construcción de la pseudoespiral de Durero "hacia fuera".
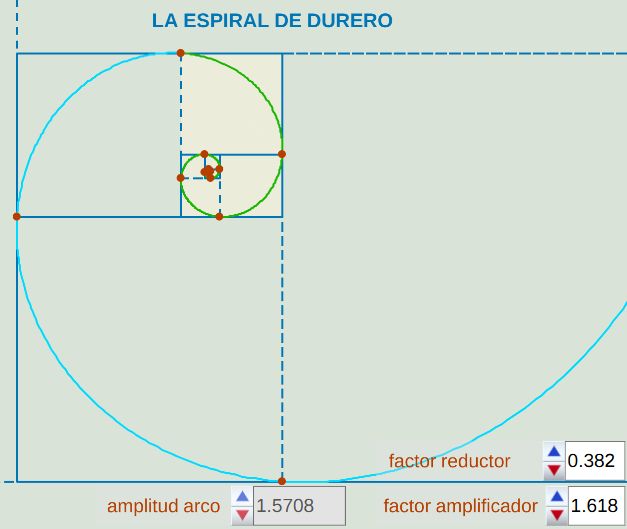
Fig. 12. La actualmente denominada como espiral de Durero.
Red Descartes 2025/Año 5, núm. 10
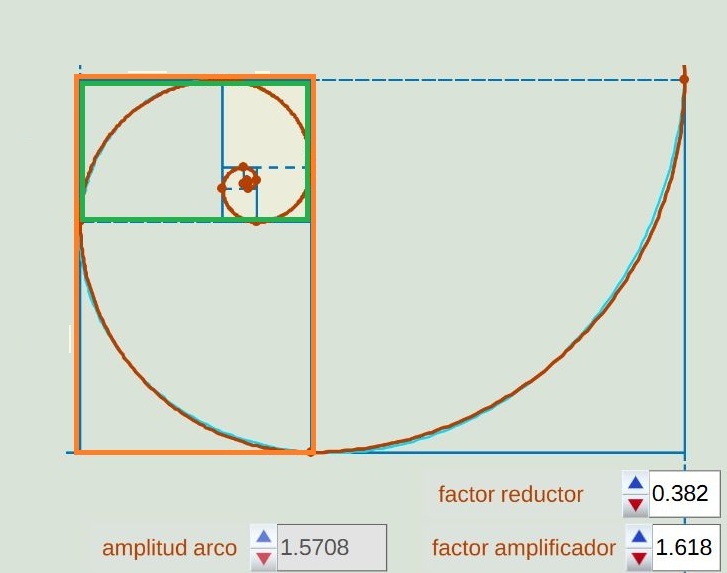
Fig. 13. Sucesión de rectángulos áureos en la construcción de la espiral de Durero.
Insistamos en que la "espiral de Durero", realmente no es una espiral, pero sí aproxima a la espiral logarítmica áurea cuya ecuación es: $$ \rho = a \, \Phi^{2 \frac{\theta}{\pi}}$$ siendo $a$ un factor de escala. La "espiral de Durero" es una curva inscrita tangencialmente en la sucesión de rectángulos áureos de la construcción, pero la espiral logarítmica áurea interseca a dichos rectángulos en los extremos de los arcos de circunferencia.
Red Descartes 2025/Año 5, núm. 10
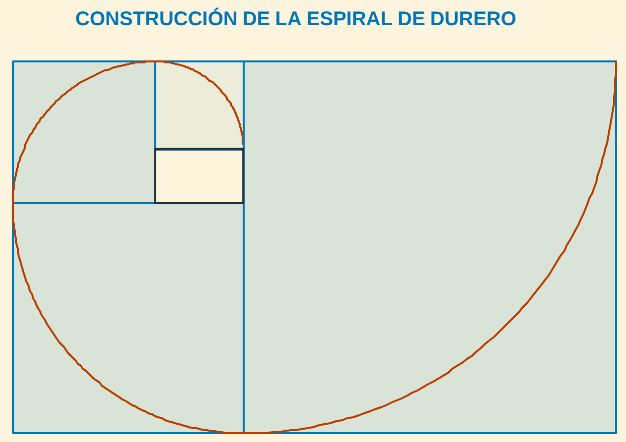
Fig. 14. Construcción de la "espiral de Durero" a partir de un rectángulo áureo.
Si he cumplido el objetivo planteado, usted, paciente lector, ya conoce la relación que existe entre el dibujo que realizó Durero en el siglo XVI y la actual "espiral de Durero" y, quizás tenga interés en saber el porqué matemático de lo aquí indicado. Si es así, puede acudir a las indicaciones de la escena interactiva y satisfacer su curiosidad.
Red Descartes 2025/Año 5, núm. 10

Fig. 15. Alberto Durero, autorretrato con abrigo de piel, óleo sobre tabla de madera (fuente: Britannica, Licencia CC) .
Red Descartes 2025/Año 5, núm. 10
Este artículo proporciona un análisis detallado y comparativo de "Nano Banana" y "Seedream 4.0", dos de los modelos de inteligencia artificial más avanzados en el ámbito de la generación y edición de imágenes. Ambos sistemas, lanzados en 2025, representan la vanguardia en la creación de contenido visual asistida por IA, pero ofrecen características, fortalezas y enfoques distintos que los hacen adecuados para diferentes necesidades creativas y profesionales. El artículo explora sus capacidades, diferencias clave y casos de uso, ofreciendo una perspectiva integral para comprender su impacto en el panorama digital.
Nano Banana (Google/Gemini 2.5 Flash Image)
Red Descartes 2025/Año 5, núm. 10

Red Descartes 2025/Año 5, núm. 10
Seedream 4.0 (ByteDance/Volcano Engine)
Red Descartes 2025/Año 5, núm. 10

Diferencias clave y comparación
Red Descartes 2025/Año 5, núm. 10
Red Descartes 2025/Año 5, núm. 10
En este ejercicio, ambos modelos conservan los rasgos del personaje, como también el tamaño, posición del personaje y el texto solicitado; sin embargo, si se observan con más detalle las imágenes generadas, Nano Banana presenta algunas deficiencias (Amplía las escenas y mueve la barra vertical deslizante, para apreciar los resultados obtenidos con mayor detalle).
Red Descartes 2025/Año 5, núm. 10
Perspectivas y matices
La elección entre Nano Banana y Seedream 4.0 a menudo depende de los requisitos específicos del proyecto. Mientras que Nano Banana, con su enfoque en la consistencia de personajes y la edición conversacional, es ideal para el prototipado de contenido social y el uso dentro de la aplicación Gemini, Seedream 4.0 se perfila como una herramienta más potente para la producción de imágenes de alta resolución, listas para campañas, con ediciones iterativas y precisas.
Muchos profesionales optan por utilizar ambos, aprovechando la fiabilidad y coherencia de Nano Banana para ciertas tareas y la resolución superior y flexibilidad artística de Seedream 4.0 para otras. Seedream 4.0 ha mostrado un fuerte impulso en las clasificaciones, a menudo superando a Nano Banana en las tareas de texto a imagen y edición de imágenes, aunque Nano Banana sigue siendo una herramienta fundamental para aquellos que priorizan la coherencia y la facilidad de uso dentro de las aplicaciones de Google.
Conclusión
Tanto Nano Banana como Seedream 4.0 representan avances significativos en la inteligencia artificial de generación y edición de imágenes. Nano Banana, el modelo de Google, destaca por su coherencia, fiabilidad y capacidades de edición conversacional, siendo una herramienta robusta para el ajuste y la transformación de imágenes con un enfoque en el realismo. Seedream 4.0 de ByteDance, por otro lado, lidera en alta resolución (hasta 4K), flexibilidad artística y la capacidad de generar múltiples salidas consistentes simultáneamente. La decisión de utilizar uno sobre el otro a menudo recae en la prioridad entre la consistencia en ediciones digitales de menor resolución (Nano Banana) o la creación
Red Descartes 2025/Año 5, núm. 10
de activos de alta resolución y estéticamente diversos para usos comerciales y artísticos (Seedream 4.0).
Fuentes consultadas
Red Descartes 2025/Año 5, núm. 10
El Teorema de Pitágoras es, posiblemente, el resultado matemático más "conocido" tanto por legos como expertos, al menos como sabedores de su existencia, aunque incluso no se sea capaz de dar un enunciado correcto y ni siquiera se sepa el porqué de su importancia ni su aplicación. Un resultado con más de dos mil años de antigüedad y que fue recogido y divulgado por Euclides en "Los Elementos”. Es una propiedad que está indisolublemente ligada a la perpendicularidad que condiciona nuestras vidas y nuestro entorno, dado que estamos sujetos a la fuerza gravitatoria y, de ahí, su máxima importancia en cualquier construcción o diseño ergonómico que permita satisfacer nuestras necesidades de movilidad y acomodación. ¿Quién no ha visto la representación geométrica de este Teorema?:
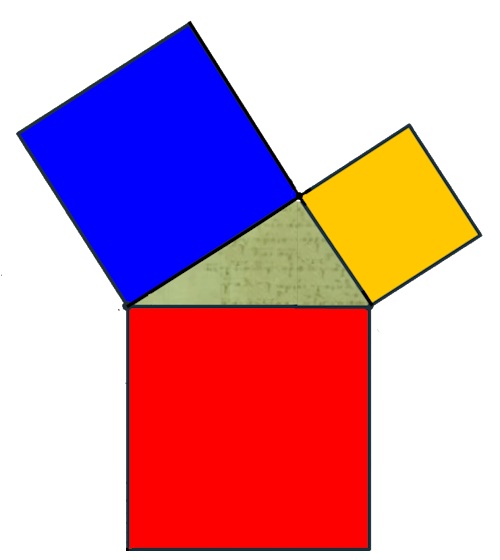
Fig. 1. Representación geométrica del Teorema de Pitágoras.
Red Descartes 2025/Año 5, núm. 10
o ¿quién no ha visto en algún momento su más críptica representación algebraica?:
$$a^2+b^2=c^2$$Fig. 2. Representación algebraica del Teorema de Pitágoras
Pero menos divulgado, aunque Euclides también lo incluye en el libro VI de los Elementos, es la "Generalización del Teorema de Pitágoras" donde se extiende el resultado a cualquier terna de figuras semejantes que se dibujen sobre los catetos y la hipotenusa de un triángulo rectángulo. Euclides, en su demostración, hace una representación gráfica con rectángulos, pero realmente la realiza de manera general.
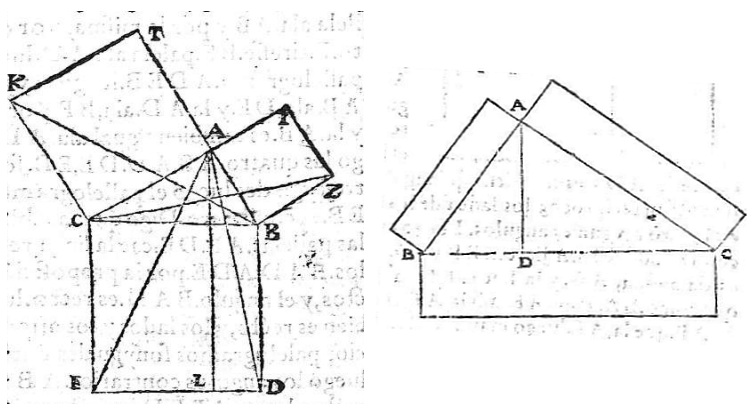
Fig. 3. Ilustraciones originales de los Elementos.
Izq. Teorema de Pitágoras. Dcha. Generalización del teorema de Pitágoras.
El artista renacentista Alberto Durero mostró un profundo interés por la geometría, un conocimiento que se revitalizó en Europa gracias a la primera edición impresa de los Elementos de Euclides. Esta edición, publicada en 1482, se basó en la traducción y comentarios
Red Descartes 2025/Año 5, núm. 10
del matemático Campano de Novara. A su vez, el trabajo de Campano se fundamentó en versiones árabes, una de las cuales fue la influyente traducción que realizó en el siglo XII Adelard de Bath. Adelard de Bath tradujo la obra de un texto en árabe andalusí, y se suele novelar indicando que lo obtuvo por espionaje de la biblioteca de Madīnat az-Zahrā (Medina Azahara) en Córdoba.
Durero, formador de artesanos a los que dedicó sus libros —conocidos colectivamente como los libros "De la Medida"—, fundamentales para la construcción de formas y la perspectiva, también refleja la generalización del Teorema de Pitágoras y dibuja los casos particulares de triángulos y cuadrados en dicha construcción sobre un triángulo rectángulo.
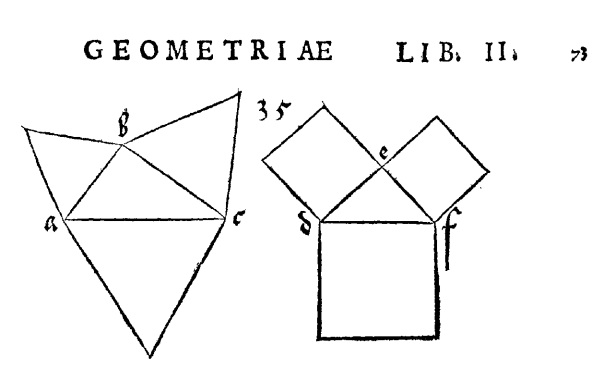
Fig. 4. Ilustraciones de Albert Durero en el libro II de la Medida.
Izq. Generalización del Teorema de Pitágoras con triángulos. Dcha. teorema de Pitágoras con cuadrados.
En la siguiente imagen podemos observar otras muestras de este resultado:
Red Descartes 2025/Año 5, núm. 10
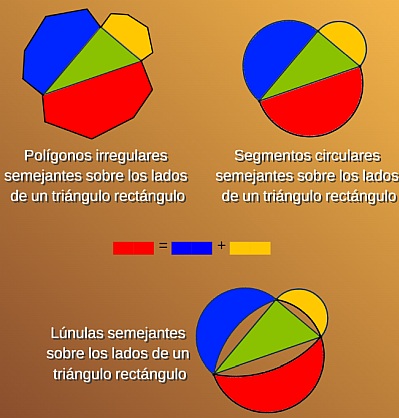
Fig. 5. Otros ejemplos de la generalización del Teorema de Pitágoras.
Para quienes estén interesados en profundizar sobre este tema hemos desarrollado dos recursos interactivos, dos misceláneas, enlazadas posteriormente en este artículo, que se adentran en estos contenidos, detallándolos. Les invitamos a interactuar con ellas.
Motivación
Los logros, avances y resultados en la ciencia, en general, y en las matemáticas, en particular, suelen presentarse y enseñarse de manera aislada, desconectadas del hilo histórico-cultural que ha sido el germen o génesis de estos. Sin embargo, el conocimiento de la causa o motivo que provoca el abordaje de un problema o cuestión, ayuda a comprender el porqué de su planteamiento, el contexto y la dificultad inherente al momento en el que se abordó su análisis y el cómo o procedimiento que llevó a su obtención e incluso el porqué.
Red Descartes 2025/Año 5, núm. 10
En la primera escena interactiva (pulse sobre la imagen de la Fig. 6) buscamos ubicar el Teorema de Pitágoras en el hito histórico en el que éste se academiza, es decir, su inclusión en “Los Elementos” de Euclides pues se constata y está ampliamente documentado que éste era un resultado conocido y usado en diversas civilizaciones previas.
Los Elementos, segundo libro más publicado en la historia después de la Biblia, introduce el sistema axiomático euclidiano que durante siglos ha servido y que, actualmente, aún sirve como guía o camino para el desarrollo de las teorías matemáticas y para su enseñanza, si bien Gödel con su famoso Teorema de la incompletitud pone parcialmente en solfa la lógica deductiva de los mismos.
Contexto y procedimiento
El Teorema de Pitágoras es una proposición o propiedad que puede demostrarse dentro del sistema axiomático euclidiano y, aquí, buscamos mostrar cuál es el proceso o procedimiento para aceptar como cierta cualquier proposición matemática en un sistema axiomático. Esto requiere acudir a la base conceptual que da origen al sistema y, junto a los resultados que previamente hemos admitido o demostrado, proceder a la construcción de un nuevo conocimiento mediante un razonamiento lógico contrastado o, al menos, que es aceptado por pares (pareja de personas versadas o expertas en el tema que lo valoran como correcto). En concreto, nos centraremos en el Teorema de Pitágoras y se aborda la deducción lógica que realizó Euclides en sus libros, apoyándose en las 23 definiciones que le sirvieron como punto de partida para fijar los objetos matemáticos básicos con los que iniciar el trabajo, en las cinco definiciones comunes (axiomas) con las que aportó las relaciones imprescindibles para el trabajo con dichos objetos y para la construcción de otros nuevos, y en los cinco postulados —que constituyen los cimientos de la Geometría euclidiana (Fig. 7) y, a su vez, los que al no cumplirse o negarlos conducen a las geometrías no euclidianas—, todo junto al uso de proposiciones demostradas con anterioridad a dicho Teorema.
Red Descartes 2025/Año 5, núm. 10

Fig. 6. Demostración euclidiana del Teorema de Pitágoras (escena interactiva).
Pulse sobre la imagen para acceder.
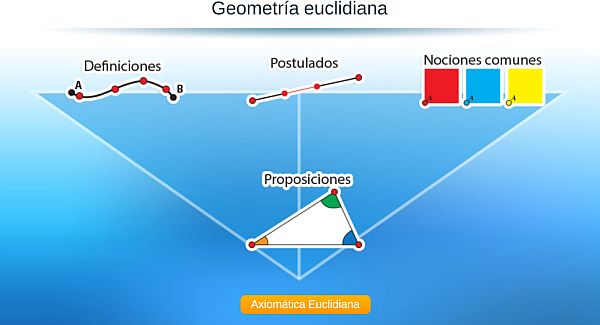
Fig. 7. Sistema axiomático euclidiano.
Recurso procedente del Proyecto Descartes (Red Descartes).
Pulse sobre la imagen para acceder.
Red Descartes 2025/Año 5, núm. 10
La segunda escena interactiva (pulse sobre la imagen de la Fig. 8) nos permite adentrarnos en la Proposición 31 del Libro VI, de los Elementos, la cual es un testimonio de la brillantez de Euclides al generalizar el Teorema de Pitágoras sin el uso de un sistema algebraico moderno. Su demostración se basa en una profunda comprensión de la semejanza de figuras y un uso meticuloso de las propiedades de las proporciones, herramientas que le permitieron establecer relaciones cuantitativas entre magnitudes geométricas como líneas y áreas. Al establecer las proporciones a través la Proposición 31 del Libro VI, y luego aplicar el Corolario de VI.19, Euclides muestra que la figura sobre la hipotenusa se divide, en términos de área, en dos partes cuyas áreas son proporcionales a las figuras similares sobre los catetos: "En los triángulos rectángulos, la figura descrita sobre el lado opuesto al ángulo recto es igual a la suma de las figuras similares y descritas de forma similar sobre los lados que contienen el ángulo recto".

Fig. 8. Acceso a la miscelánea "generalización euclidiana del teorema de Pitágoras" (escena interactiva).
Pulse sobre la imagen para acceder.
Red Descartes 2025/Año 5, núm. 10
La Proposición 19 del Libro VI y su corolario, con su formulación específica, son pilares fundamentales que vinculan las razones de los lados con las razones de las áreas de figuras semejantes, permitiendo a Euclides llegar a esta poderosa generalización.
El discurso anterior lo hemos planteado ubicándonos en el planteamiento académico y axiomático de Euclides y, si ha interactuado con las escenas para seguir paso a paso el razonamiento deductivo de la demostración habrá podido ubicarse en la dificultad que conlleva la necesaria notación y la expresión literaria de la lógica empleada y, quizás, haya podido sentirse incómodo, más si se posiciona como un alumno que se inicia en este críptico aprendizaje.
En 1847, Oliver Byrne publicó su libro "The First six books of the Elements of Euclid whith coloured diagrams and symbols" en el que, como él indica, el uso de diagramas coloreados y símbolos en lugar de letras facilita el aprendizaje a los estudiantes. El libro de Byrne puede considerarse una revolucionaria propuesta innovadora en la enseñanza de las Matemáticas ya que sustituye el usual sistema literal e introduce atractivos elementos gráficos coloreados que le sirven de soporte y medio para abordar las demostraciones matemáticas de manera visual y por ende evitando la, muchas veces, farragosa expresión escrita que requiere una interpretación de lo leído, es decir, pone en práctica el conocido dicho: "más vale una imagen que mil palabras". De hecho, basta ver por primera vez una página de este precioso libro de Byrne (ver la Fig. 9) para sentirse atraído con su diseño y verse sorprendido por el potencial comunicador y didáctico que encierra. El libro de Byrne podemos consultarlo en español en la versión elaborada por Nicholas Rougeux, y nosotros aquí introduciremos algo más de interactividad.
Red Descartes 2025/Año 5, núm. 10

Fig. 9. Demostración del teorema de Pitágoras según Byrne. Pulse sobre la imagen para verlo en el libro de Byrne.
Si antes hemos buscado introducir al lector en el academicismo euclidiano, ahora buscaremos mostrarle cómo Euclides puede adentrarse en el aula de una manera didáctica, aproximándonos al aprendiz, pero respetando al gran maestro y referente. Para ello, hemos desarrollado otras dos escenas interactivas (ver la Fig. 10 y la 11) que abordan las demostraciones gráficas del Teorema de Pitágoras y de su generalización. Le invitamos, de nuevo, a acceder y a interactuar con ellas.
Comparando las demostraciones en sus versiones clásicas con las gráficas, podrá experimentar la dureza que pueden encerrar algunos argumentos literarios matemáticos y el lenguaje matemático en sí —una posible causa de la desmotivación de nuestro alumnado— y cómo esta aspereza puede ser salvada con métodos didácticos innovadores. El academicismo euclidiano y, en general, de nos, los matemáticos, siendo en nuestra profesión necesario, esencial, imprescindible y loable, pensamos ha de saber reconducirse cuando lo que se desea es enseñar y divulgar el conocimiento. Byrne así lo entendió y nos marcó un esplendoroso camino del que aprender y tratar de adaptar, más en estos tiempos en los que las herramientas tecnológicas son una ayuda innegable e imprescindible que no se pueden obviar en nuestra labor docente.
Red Descartes 2025/Año 5, núm. 10

Fig. 10. Acceso a la miscelánea "Byrne y su demostración gráfica del teorema de Pitágoras".
Pulse sobre la imagen para acceder.

Fig. 11. Acceso a la miscelánea "Byrne y su demostración gráfica de la generalización del teorema de Pitágoras".
Pulse sobre la imagen para acceder.
Red Descartes 2025/Año 5, núm. 10
Introducción histórica
Una terna pitagórica es un trío de enteros positivos $(a,b,c)$ que cumple la igualdad $a^2+b^2=c^2$. Se dice primitiva si $a, b, c$ no comparten divisores comunes, es decir, si $mcd(a,b,c)=1$. Se pueden construir infinitas ternas no primitivas multiplicando una primitiva por un entero positivo.
Aunque su nombre evoca el famoso teorema de Pitágoras (siglo VI a. C.), el conocimiento de estas relaciones cuadráticas es milenario. La prueba más notable de su antigüedad se halla en Mesopotamia con la tablilla babilónica Plimpton 322 (1800–1600 a. C.) que registra algunas ternas, evidenciando así un conocimiento de sus propiedades anterior a la era griega.

En la tradición matemática griega, las ternas son abordadas por autores como Nicómaco de Gerasa (siglo I a. C) y padre de Aristóteles o Diofanto de Alejandría (siglo III a. C.) en su Arithmetica (II.8).
Red Descartes 2025/Año 5, núm. 10
Sin embargo, es Euclides quien desarrolla el tratamiento más completo principalmente en el libro X de los Elementos. Sus consideraciones sobre conmensurabilidad y las identidades geométricas que usa, permiten una parametrización completa y rigurosa de las ternas primitivas.
El generador de Euclides
Euclides establece que cualquier terna pitagórica se puede generar a partir de dos enteros \(p>q>0\) de la forma siguiente siguiente
\[(a,b,c)=\big(p^2-q^2,\;2pq,\;p^2+q^2\big).\]Si, además, \(\operatorname{mcd}(p, q)=1\) y \(p,q\) tienen paridad opuesta (uno par y el otro impar), la terna es primitiva, las no primitivas son múltiplos de ellas \(k(a,b,c)\).
Algebraicamente, es sencillo ver que de esta forma se generan ternas pitágoricas al cumplirse:
\[(p^2-q^2)^2+(2pq)^2=(p^2+q^2)^2.\]Partiendo de la fórmula de Euclides, recorremos distintas estrategias de generación de ternas y veremos que, aunque parten de ideas variadas, se reducen al mismo esquema.
Rectas racionales en el círculo unidad
Siglos después de Euclides, la conexión entre las ternas y la geometría volvió a hacerse explícita en la obra de Diofanto de Alejandría.
Red Descartes 2025/Año 5, núm. 10
En el problema II.8 de la Arithmetica, su libro más célebre, Diofanto plantea descomponer un cuadrado dado en la suma de dos cuadrados. Su procedimiento equivale a buscar puntos racionales \((x, y)\) de la circunferencia unidad \(x^2 + y^2 = 1\); es decir, una parametrización racional de la circunferencia unidad. Si \(\left(\frac{a}{c}\right)^2 + \left(\frac{b}{c}\right)^2 = 1\), entonces \(a^2 + b^2 = c^2\) para enteros \(a, b, c\) lo que permite obtener ternas pitagóricas.
El método consiste en:
Considerando $ t=\frac{m}{n}$ y operando, la terna pitagórica generada es:
$$a = m^2 - n^2, \quad b = -2mn, \quad c = m^2 + n^2.$$Dado que las ternas pitagóricas se definen con enteros positivos, bastaría tomar el valor absoluto de \(b\), lo que permitiría obtener la fórmula de Euclides: \((m^2 - n^2, 2mn, m^2 + n^2)\). La única diferencia es que la pendiente \(t\) necesaria para generarla es la opuesta, lo que refleja la simetría de la circunferencia.
Red Descartes 2025/Año 5, núm. 10
Generación mediante números complejos
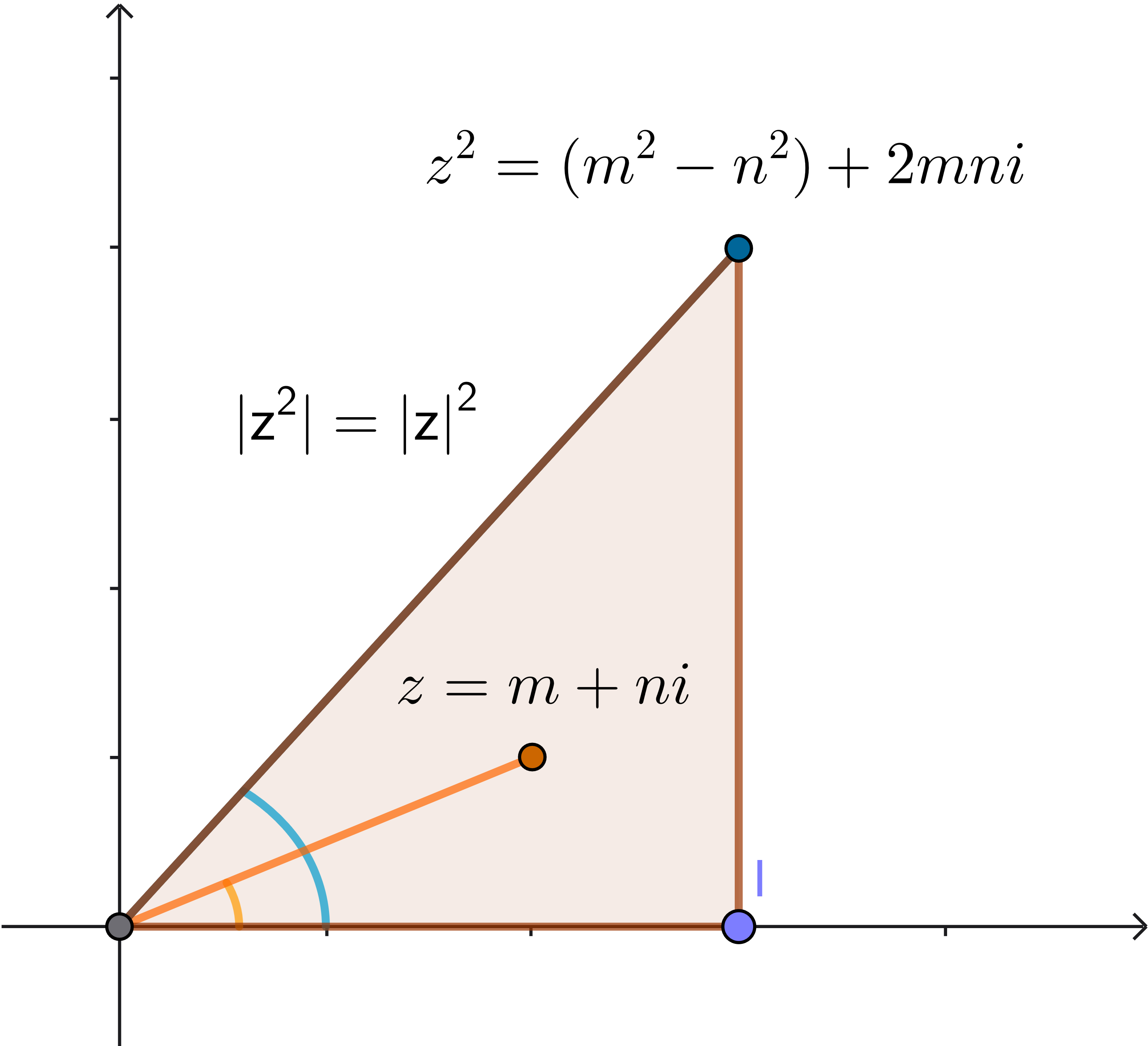
Otra perspectiva es considerar la aritmética de los números complejos. Se considera para ello un número complejo \(z\) con componentes los enteros positivos \(m\) y \(n\):
$$z = m + ni$$
Para generar la terna pitagórica, se calcula el cuadrado de este número complejo, \(z^2\):
$$z^2 = (m + ni)^2 = m^2 + 2m(ni) + (ni)^2 =(m^2-n^2) + 2mni$$Ahora, teniendo en cuenta que \(|z^2| = |z|^2\), se tendrá que
$$\sqrt{(m^2 - n^2)^2 + (2mn)^2}= m^2 + n^2$$ $$(m^2 - n^2)^2 + (2mn)^2 = (m^2 + n^2)^2$$Si definimos los lados de la terna como: $a = m^2 - n^2, \quad b = 2mn, \quad c = m^2 + n^2$ obtenemos la terna pitagórica \((a, b, c)\) que satisface \(a^2 + b^2 = c^2\).
Red Descartes 2025/Año 5, núm. 10
En el siguiente video se puede ver la visualización de todas las ternas pitagóricas considerando esta interpretación.
Este método considera dos fracciones racionales cuyo producto es \(2\): \(\tfrac{m}{n}\) y \(\tfrac{2n}{m}\). Sumando a cada una de ellas \(2\) unidades, obtenemos:
$$\begin{aligned} \frac{m}{n} + 2 &= \frac{m+2n}{n} \\ \frac{2n}{m} + 2 &= \frac{2(n+m)}{m} \end{aligned}$$Al multiplicar en cruz, esto es, tomando el numerador multiplicado por el denominador de la otra fracción, se generan los lados de la terna:
Red Descartes 2025/Año 5, núm. 10
$$a=m(m+2n),\qquad b=2n(m+n),\qquad c=m^2+2n^2+2mn$$
Se puede comprobar que esta terna \((a, b, c)\) satisface \(a^2+b^2=c^2\).
Este método es una reformulación de la fórmula de Euclides, donde
$$\begin{aligned} p &= m+n \\ q &= n \end{aligned}$$Generación mediante números de Fibonacci
Se aborda en este apartado cómo generar ternas pitagóricas a partir de la sucesión de Fibonacci. Esta sucesión fue establecida por Leonardo de Pisa, matemático del siglo XVIII, también conocido como Fibonacci. Se define de forma recurrente como: \(F_1=1, F_2=1, F_3=2, F_4=3, F_5=5, F_6=8, \ldots\), donde \(F_n = F_{n-1} + F_{n-2}\).
Una fórmula para generar una terna pitagórica \((a, b, c)\) utilizando cuatro números consecutivos de Fibonacci es la siguiente:
$$a = F_{n} F_{n+3}$$ $$b = 2 F_{n+1} F_{n+2}$$ $$c = F_{n+1}^2 + F_{n+2}^2$$
Alternativamente, también podría considerarse
$$a = F_{n} F_{n+3} \quad b = 2 F_{n+1} F_{n+2} , \quad c = F_{n} F_{n+2} + F_{n+1}F_{n+3}$$
o también:
$$a = F_n F_{n+3}, \quad b = 2 F_{n+1} F_{n+2}, \quad c = F_{2n+3}$$Red Descartes 2025/Año 5, núm. 10
Generación con catetos consecutivos: \((x, x+1, z)\)
El caso de ternas con catetos consecutivos, como \((3, 4, 5)\) o \((20, 21, 29)\), es particularmente interesante. Este tipo de terna se genera con una ecuación diofántica conocida como la Ecuación de Pell.
Para que los catetos sean consecutivos, sus fórmulas en el generador de Euclides deben diferir en 1: \(x^2+(x+1)^2=z^2\). Operando,
\[ 2x^2+2x+1=z^2 \;\Longleftrightarrow\; (2x+1)^2-2z^2=-1. \]Definiendo \(u=2x+1\) llegamos a la ecuación de Pell negativa siguiente $ u^2-2z^2=-1$. Resolviendo esta ecuación, nos dará las parejas $(u,z)$ y de cada una se recuperaría $x=\frac{u-1}{2}$ obteniéndose la terna pitagórica $(x,x+1,z)$.
Puede demostrarse que las ternas $(x_k, y_k, z_k)$ se generan mediante las siguientes relaciones de recurrencia, donde el punto de partida es la terna primitiva más pequeña \((3, 4, 5)\):
$$\begin{aligned} x_{k+1} &= 3x_k + 2z_k + 1 \quad y_{k+1} = x_{k+1} \\ z_{k+1} &= 4x_k + 3z_k + 2 \end{aligned}$$Las soluciones de Pell generan una simple recurrencia de Euclides \((m,n)\) que produce todas las ternas con catetos consecutivos:
$$m_{k+1}=2m_k+n_k,\qquad n_{k+1}=m_k\,\qquad (m_0,n_0)=(2,1)$$Cada paso da una nueva terna \((m_k^2-n_k^2,\;2m_kn_k,\;m_k^2+n_k^2)\) con \(|b-a|=1\).
Red Descartes 2025/Año 5, núm. 10
Esta secuencia genera todas y solo las ternas pitagóricas primitivas en las que los catetos son consecutivos, demostrando que este caso específico también está completamente contenido dentro de la estructura general definida por Euclides.
Método platónico
El método platónico, que Proclo (siglo V d. C.) atribuyó a Platón, es el procedimiento más antiguo conocido en la tradición griega para generar ternas de forma sistemática. Es un caso particular del método de Euclides tomando un entero positivo $m$ y $n=1$.
Método de Dickson
El método de Leonard Eugene Dickson (1920) es una herramienta puramente algebraica que genera todas las ternas pitagóricas a partir de una sencilla identidad. Se basa en encontrar tres enteros positivos \(r, s, t\) que satisfagan la condición clave: $r^2 = 2st$.
Si se cumple esta condición, la identidad que garantiza la terna es:
$$(r+s)^2 + (r+t)^2 = (r+s+t)^2$$Las ternas pitagóricas \((a, b, c)\) se construyen entonces con los siguientes lados: $a = r+s, \quad b = r+t, \quad c = r+s+t$.
Red Descartes 2025/Año 5, núm. 10
Una elección útil de los parámetros que garantiza que se cumpla $r^2=2st$ es: $ r = 2mn \,\,\,\,\, s = m^2 \,\,\,\, t = 2n^2$.
Al sustituir estos valores en las fórmulas de Dickson:
$$\begin{aligned} a &= r+s = 2mn + m^2 \quad b = r+t = 2mn + 2n^2 \\ c &= r+s+t = 2mn + m^2 + 2n^2 \end{aligned}$$Considerando \(p=m+n\), \(q=n\) se llega a Euclides. Es primitiva si \(\operatorname{mcd}(m,n)=1\) y hay paridad opuesta.
Método del gnomon (diferencia de cuadrados)
Este método utiliza dos cuadrados encajados. Una exterior de lado \((u+v)\) y el interior de lado \((u-v)\) con \(u>v\). El gnomon, la “L” restante, tiene área \((u+v)^2-(u-v)^2=4uv=(2\sqrt{uv})^2\). Por tanto
\[(u+v)^2=(u-v)^2+\big(2\sqrt{uv}\big)^2.\]Considerando \(u=m^2\), \(v=n^2\) aparece la fórmula de Euclides:
$$(m^2+n^2)^2=(m^2-n^2)^2+(2mn)^2\Rightarrow (m^2-n^2,\,2mn,\,m^2+n^2)$$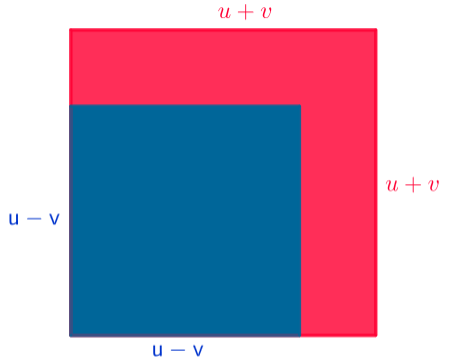
Red Descartes 2025/Año 5, núm. 10
En el siguiente interactivo, se puede explorar dinámicamente las distintas formas de generar ternas pitagóricas vistas en este artículo y su relación con el generador de Euclides.
\[(a,b,c)=\big(m^2-n^2,\;2mn,\;m^2+n^2\big),\qquad m>n>0.\]Referencias
[1] Fallas, J. J. (2009). Ternas pitagóricas: métodos para generarlas y algunas curiosidades. Revista Digital: Matemática, Educación e Internet, 9(2), 1-21.Red Descartes 2025/Año 5, núm. 10
Introducción
Generalmente, cuando se presentan recursos educativos abiertos generados con la herramienta de autor Descartes, se espera encontrar un recurso interactivo para la materia de Matemáticas, pues fue ese el origen del Proyecto Descartes. Sin embargo, Descartes es una potente herramienta de autor multipropósito que permite desarrollar objetos educativos interactivos en cualquier área de conocimiento. Por su parte, DescartesJS es un intérprete de Descartes que es compatible HTML5, consecuentemente las escenas interactivas desarrolladas con Descartes se visualizan en todos los dispositivos, ordenador, tableta o smartphone, independientemente del sistema operativo que porte. Pero, ¿cómo unimos Descartes y cine?
Cine y educación
Es un proyecto promovido e impulsado en España por docentes de todas las etapas educativas con el apoyo logístico y organizativo de empresas del mundo cinematográfico, cuyo objetivo primordial es que "el cine tenga en las aulas la relevancia que merece como patrimonio cultural indiscutible en una sociedad inmersa en el lenguaje audiovisual". Entre las acciones encaminadas para ello destacan el preestreno simultáneo y gratuito, en una veintena de ciudades, de una película de actualidad a la que asisten todos los miembros de la Tribu 2.0, esa tribu que se necesita para educar y que abarca representantes
Red Descartes 2025/Año 5, núm. 10
institucionales y políticos, profesionales de la enseñanza, alumnado, familias y toda la ciudadanía. A su vez, el alumnado, bajo la dirección y coordinación de sus profesores y profesoras, realizan y desarrollan actividades a priori relacionadas con la temática de la película, para conocimiento de su entorno social, geográfico, histórico, etc.; también actividades in situ, como reportajes periodísticos o entrevistas a los asistentes, y otras actividades a posteriori, básicamente para compartir y difundir lo aprendido, siempre en relación con el currículo, a través de un blog colaborativo dedicado a cada noche o matinal de cine y educación, empleando herramientas gratuitas de la denominada Web 2.0 y las redes sociales.
Recientemente, en nuestra sección dedicada a la formación en comunicación audiovisual, hemos publicado la obra "Cine y educación en Lebrija (2010 - 2012)", que tiene por objeto recopilar y difundir en soporte único la experiencia y los productos de cultura digital generados en Lebrija (España), una de las ciudades activamente implicadas y participantes en este sensacional proyecto durante un trienio, que también están disponibles en los blogs colaborativos dedicados a cada película y compartidos entre todas las ciudades.

Red Descartes 2025/Año 5, núm. 10



DescartesJS y ... ¡acción!
Un grupo de alumnos y alumnas de 1º ESO (12 - 13 años) realiza una selección de diez directores y directoras de cine en España con su filmografía más conocida, que se recogen en una infografía diseñada con DescartesJS.
Red Descartes 2025/Año 5, núm. 10
Red Descartes 2025/Año 5, núm. 10
Con una evaluación tipo Jinich, actividad que consiste en asociar un enunciado dado con su término correspondiente, tres alumnas de la misma edad nos proponen localizar al director o directora de cine a través del título de una de sus películas.
La barra que aparece en la parte inferior de este recurso interactivo, que se ha denominado Barra Jinich, se muestra inicialmente en un avance del 50%, que irá creciendo hasta el extremo verde o decreciendo (más rápido) hasta el extremo rojo, según el resultado de nuestras respuestas.
Red Descartes 2025/Año 5, núm. 10
Dicho funcionamiento es el siguiente: Si tenemos 10 preguntas, por cada respuesta correcta la barra avanza en un 5%; si es incorrecta, retrocede el doble, es decir un 10%. Si la barra llega al extremo rojo, aparece un botón para reiniciar la prueba.
Otro equipo de alumnos y alumnas de la misma clase se decantó por diseñar un cuestionario relacionado con la temática tratada, dando lugar al siguiente recurso interactivo, también diseñado con DescartesJS:
Red Descartes 2025/Año 5, núm. 10
Todo es posible con DescartesJS
Celia y Esperanza, alumnas de 3º ESO C del IES Bajo Guadalquivir de Lebrija, diseñaron de forma colaborativa una línea de tiempo dedicada a la filmografía de Ken Loach, usando la herramienta 2.0 TimeRime que, desgraciadamente, ha desaparecido.
En reconocimiento a su gran trabajo, hemos intentado restaurar su producto final utilizando una línea de tiempo diseñada con la herramienta de autor DescartesJS.
Todos los recursos insertados o embebidos en nuestros libros pueden visualizarse a pantalla completa sin más que pulsar en la flecha que aparece en la esquina superior derecha de los mismos. Recomendamos hacerlo en este caso para una mejor visualización, donde encontramos año, título de la película, sinopsis y un tráiler.
Red Descartes 2025/Año 5, núm. 10
¿Y tú?
Si deseas diseñar recursos interactivos para tu alumnado con esta potente herramienta de autor y de software libre, te recomendamos:

Red Descartes 2025/Año 5, núm. 10
Introducción
El avance de la inteligencia artificial (IA) ha transformado significativamente los procesos creativos en diversos campos, incluido el editorial. Este artículo describe la experiencia de desarrollo del libro “Brujas: mitos y leyendas”, un proyecto que integra contenidos culturales y narrativos con herramientas de IA, aplicadas a la generación de texto, ilustración y diseño editorial. El objetivo es reflexionar sobre el potencial de estas tecnologías en la producción de obras literarias y visuales, así como documentar las etapas del proceso, los recursos utilizados y los desafíos encontrados. A través de este caso práctico, se busca aportar una perspectiva sobre el uso ético, creativo y técnico de la IA en la creación de contenido cultural.
Selección del título del libro
y de los capítulos
Mediante la herramienta "Escritor de libros", de la siguiente página, enviamos el mensaje "Brujas" que, por ser tan general, nos propuso cuatro posibles títulos, de los cuales escogimos "Brujas: mitos y leyendas". Posteriormente, le enviamos este título y le pedimos que nos diera los títulos para 8 capítulos. Su respuesta fue: Introducción; Orígenes del mito; La Edad Media y la caza de brujas; Magia, pócimas y rituales, entre otros.
Red Descartes 2025/Año 5, núm. 10
Red Descartes 2025/Año 5, núm. 10
Imágenes de portada y de carátulas de capítulo
Dado que el libro se está usando como modelo para el curso "Diseño de libros interactivos con DescartesJS y herramientas de IA", decidimos usar dos clases de carátulas. La primera, con imagen cuadrada de 582x582 pixeles y, la segunda, con imágenes tipo portarretrato de 640x825 pixeles.

Para la generación de las imágenes, usamos las siguientes herramientas de IA: Pollinations AI (Flux y GPT Image), ChatGPT, Ideogram, NightCafé y Grok. Obtenidas las imágenes, diseñamos la portada y las carátulas de libro, dejando tres páginas en blanco en cada capítulo.
Red Descartes 2025/Año 5, núm. 10
Contenidos de cada capítulo
En la herramienta "Diseñador de libros digitales - V2, se ingresa el título del capítulo y, al menos, tres títulos de subcapítulo; por ejemplo, para el capítulo 1, obtuvimos:
Red Descartes 2025/Año 5, núm. 10
Los resultados obtenidos con la herramienta anterior, nos ahorraron mucho trabajo de investigación sobre el tema del libro; no obstante, como lo dice la advertencia, revisamos y verificamos información clave como fechas, nombres, lugares, eventos y otra información sensible que, de no ser revisada, pudo dar origen a la divulgación de información errónea o de alucinaciones.
Algunas de las imágenes generadas, también las incorporamos a nuestro libro y otras la generamos con herramientas generadoras de imagen como Meta, Grok, Ideogram, Imagen 4 de Google, entre otras.
Red Descartes 2025/Año 5, núm. 10
La herramienta "Diseñador de libros digitales - V2 incluye un selector con nueve diferentes recuadros o cajas. Diseñamos una imagen con cuatro de estos estilos de cajas, luego subimos esa imagen a ChatGPT y le pedimos "En la imagen puedes observar cuatro modelos de contenedores diseñados con estilos CSS, puedes darme los estilos de otros cuatro modelos, que sean llamativos por su estética y diseño".
De esa forma, obtuvimos cajas diferentes para cada capítulo, más como ejercicio modelo para los participantes del curso de diseño de libros interactivos, pues lo usual es usar uno o dos modelos en un libro, sin embargo:
Otro uso es para romper la monotonía visual en libros extensos o educativos, pues los estilos variados ayudan a mantener el interés y la atención del lector.
Red Descartes 2025/Año 5, núm. 10
Objetos interactivos
La inclusión de objetos interactivos no es un gran problema, pues las Herramientas de IA, nos permite incorporar al libro quices y puzles. Pero, ¿cómo incluir quices con preguntas sobre lo tratado en el libro? He aquí el procedimiento:
El primer quiz lo presentamos al final del capítulo 2, generándolo así:
¡sencillo y rápido el procedimiento!
Otra intervención que hicimos con Google AI Studio, fue con el "presentador de felinos", pidiéndole: "Haz una versión en la que las imágenes y los textos estén en una misma ventana (imágenes arriba y textos abajo), de tal forma que ocupen un ancho máximo de 540px; para ello, reduce el tamaño de los textos.
Nuestro trabajo más laborioso, fue cambiar imágenes y textos, hasta lograr la presentación que se muestra en la siguiente página.
¡Eso es todo!... bueno...casi todo, si se me escapó algo, consulten el libro aquí.
Red Descartes 2025/Año 5, núm. 10
Red Descartes 2025/Año 5, núm. 10
Las escenas educativas e interactivas creadas con la herramienta de autor DescartesJS son, en esencia, una página HTML, por lo que es necesario utilizar un navegador de internet para su uso y visualización, lo cual impone restricciones sobre las funcionalidades y características que una escena puede tener. En particular, una restricción que surge al abrir las páginas web localmente, es el acceso al contenido de archivos externos; esta restricción la imponen los navegadores con la finalidad de proteger a los usuarios de la ejecución no autorizada de código potencialmente malicioso, o el acceso a archivos que contengan información sensible del usuario.
La gran mayoría de las escenas de DescartesJS buscan que puedan ser visualizadas y utilizadas localmente, es decir, sin la necesidad de un servidor en internet para funcionar, por lo que DescartesJS ofrece la posibilidad de incrustar el contenido de archivos externos en la página HTML de tal manera que sean accesibles para una escena interactiva. Revisaremos los distintos tipos de archivos que se pueden incrustar en una escena.
Vectores y matrices
En DescartesJS, dentro de los elementos de tipo definición, existen los vectores y las matrices, que son un tipo de objeto que permite almacenar (bajo un
Red Descartes 2025/Año 5, núm. 10
mismo identificador) múltiples valores, y permiten asignar y acceder a estos valores por medio de índices. Los valores pueden asignarse directamente en el vector o matriz correspondiente, o leyendo los datos desde un archivo externo cuya ruta se especifica en el parámetro archivo.
De forma predeterminada, el editor de DescartesJS lee el contenido del archivo especificado en la ruta del parámetro archivo e incrusta la información dentro del HTML de la escena interactiva, este comportamiento se puede configurar desde el menú Opciones en el submenú Agregar al HTML, donde se puede marcar sí se agrega o no el contenido de los archivos asociados a diversos elementos.
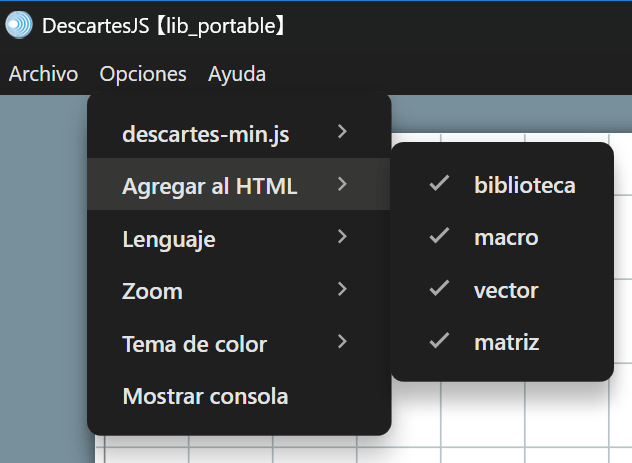
Cuando se tiene marcada la opción de Agregar al HTML para vectores y/o matrices, dentro del contenido de la página HTML de la escena interactiva se crean etiquetas <script> con un tipo type="descartes/vectorFile" para vectores, o en el caso de matrices type="descartes/matrixFile", cuyo contenido es la información del archivo asociado, y adicional a esto se incluye en su parámetro id la ruta del archivo correspondiente.
Red Descartes 2025/Año 5, núm. 10
Para un vector que en su parámetro archivo tiene asignada la ruta los_datos_del_vector.txt, se agrega un <script> con una estructura como la siguiente:
<script type="descartes/vectorFile" id="los_datos_del_vector.txt">... aquí va el contenido del archivo ...</script>
Y de forma similar, para una matriz cuyo parámetro archivo tiene la ruta los_datos_de_la_matriz.txt, se crear lo siguiente:
<script type="descartes/matrixFile" id="los_datos_de_la_matriz.txt">... aquí va el contenido del archivo ...</script>
Para el contenido de los vectores se especifica un valor en cada línea del archivo, siendo el orden de aparición el valor del índice asociado, por ejemplo, para asignar los valores V[0]=0, V[1]='hola' y V[2]=12.34, se tendría el siguiente contenido:
<script type="descartes/vectorFile" id="datos.txt">0'hola'12.34</script>
El identificador al cual se asignan los valores se obtiene de la definición del vector que esta leyendo el archivo, por lo que el mismo archivo se puede usar para asignar los valores a vectores con diferentes identificadores.
Red Descartes 2025/Año 5, núm. 10
Para las matrices se utiliza el formato conocido como CSV (Comma Separated Values) donde cada línea del archivo de texto especifica los valores de una columna de la matriz, separando los valores de cada fila por medio de comas.
Por ejemplo, para especificar los siguientes valores a una matriz M1[0,0]=1, M1[0,1]=2, M1[0,2]=3, M1[0,3]=4, M1[0,4]=5, M1[1,0]='a', M1[1,1]='b', M1[1,2]='c', M1[1,3]='d', M1[1,4]='e', M1[2,0]=1.11, M1[2,1]=2.22, M1[2,2]=3.33, M1[2,3]=4.44 y M1[2,4]=5.55, se haría de la siguiente forma:
<script type="descartes/matrixFile" id="archivo.txt">1,2,3,4,5'a','b','c','d','e'1.11,2.22,3.33,4.44,5.55</script>
Nota: algo importante a considerar para valores numéricos, es que la representación del punto flotante o coma flotante depende del valor del parámetro signo decimal de la escena, en el caso del ejemplo anterior el signo decimal es el punto, por lo que la coma (,) funciona como separador.
En caso de que la escena utilice la coma decimal, entonces el separador de los valores es el punto y coma (;). El ejemplo anterior usando la coma como separador decimal quedaría de la siguiente manera:
<script type="descartes/matrixFile" id="archivo.txt">1;2;3;4;5'a';'b';'c';'d';'e'1,11;2,22;3,33;4,44;5,55</script>
Red Descartes 2025/Año 5, núm. 10
Bibliotecas
En las definiciones existen los objetos de tipo biblioteca, estos elementos se crearon con la finalidad de conjuntar diversas definiciones en un archivo de texto, que pueden compartirse entre varias escenas. Por ejemplo, si se desarrolla un conjunto de funciones para realizar operaciones con números complejos, y estas funciones se quieren utilizar en múltiples escenas, en lugar de copiar y pegar las funciones en cada escena, simplemente se incluye y utiliza la misma biblioteca, lo que facilita en gran medida la reutilización y mantenimiento del código.
La forma en la que se crean y editan las bibliotecas es igual a como se crean y editan las definiciones, ya que un elemento de tipo biblioteca simplemente ofrece un espacio aislado donde viven las definiciones que se quieren compartir.
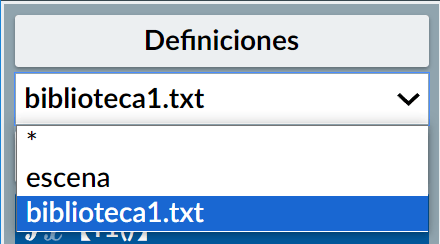
Definiciones.Sí ya se cuenta con una escena cuyas definiciones se quieren usar como biblioteca, se puede usar la opción para exportar la escena actual como biblioteca.
Red Descartes 2025/Año 5, núm. 10
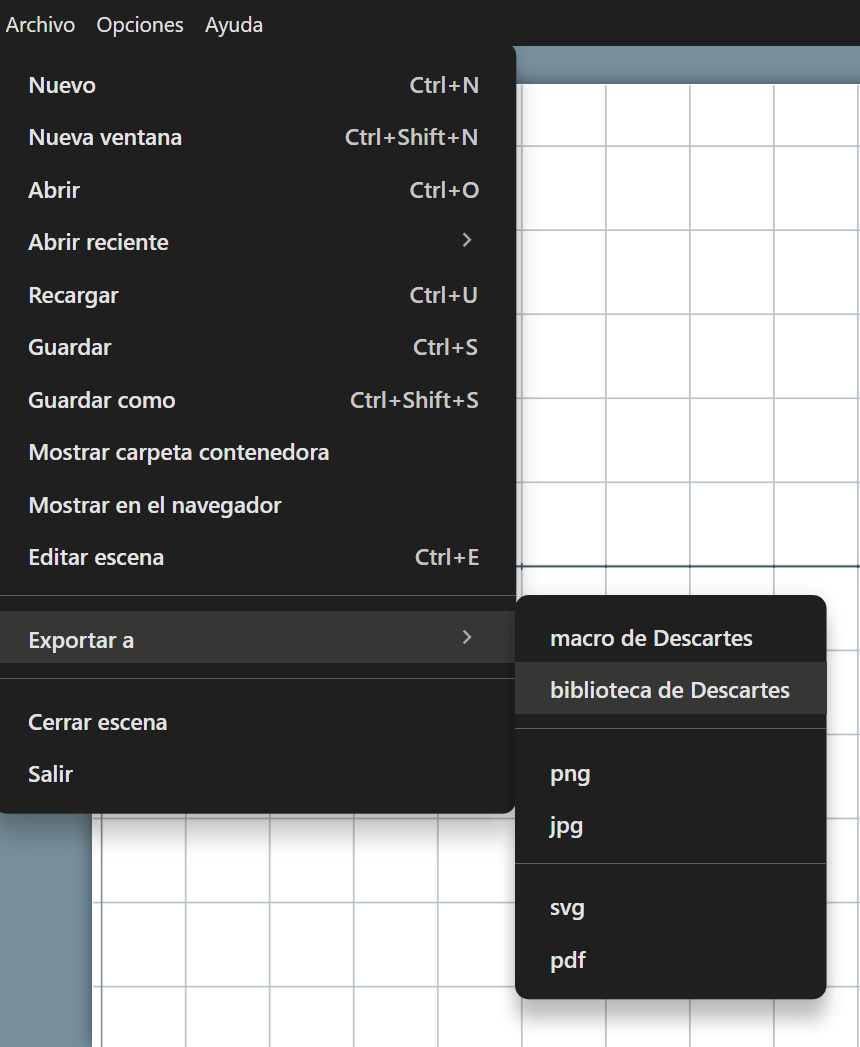
Cuando se activa la opción de agregar una biblioteca al HTML, está se incrusta en la escena agregando un <script> con el tipo type="descartes/library", con el identificador igual a la ruta del archivo de la biblioteca.
Por ejemplo, una biblioteca que contiene la función identidad f(x) = x, la matriz M con tres filas y tres columnas con los valores M[0,0]=1, M[1,0]=2, M[2,0]=3, M[0,1]=4, M[1,1]=5, M[2,1]=6, M[0,2]=7, M[1,2]=8, M[2,2]=9, el vector V de longitud tres con los valores V[0]=0, V[1]=1, V[2]=2 y la variable var = 3.14, se genera el siguiente <script>:
Red Descartes 2025/Año 5, núm. 10
<script type="descartes/library" id="biblioteca.txt">id='f(x)' algoritmo='no' expresión='x' tipo='función'id='M' matriz='sí' evaluar='una-sola-vez' columnas='3' filas='3' expresión='M[0,0]=1;M[1,0]=2;M[2,0]=3;M[0,1]=4;M[1,1]=5;
M[2,1]=6;M[0,2]=7;M[1,2]=8;M[2,2]=9;' tipo='matriz'id='V' vector='sí' evaluar='una-sola-vez' tamaño='3' expresión='V[0]=0;V[1]=1;V[2]=2' tipo='vector'id='var' expresión='3.14' tipo='variable'</script>
Macros
Los macros son muy similares a las bibliotecas, en el sentido de que permiten empaquetar o encapsular múltiples elementos en un archivo externo, favoreciendo la reutilización de código entre múltiples escenas. Los macros además de definiciones, pueden empaquetar algoritmos y elementos gráficos (tanto 2D como 3D), lo que los hace ideales para construir representaciones complejas de objetos gráficos.
La principal diferencia con las bibliotecas, además de poder incorporar diversos tipos de elementos, es que un macro es un elemento gráfico que tiene asociado un identificador, y a todos los elementos encapsulados en un macro se les agrega como prefijo el valor de su parámetro nombre seguido de un punto; esto permite reutilizar el archivo de un macro en múltiples instancias, sin que sus definiciones interfieran entre sí.
Debido a que los macros son elementos más complejos que pueden contener diversos tipos elementos de una escena de DescartesJS, para su creación se recomienda utilizar la opción de exportar una escena a un macro.
Red Descartes 2025/Año 5, núm. 10
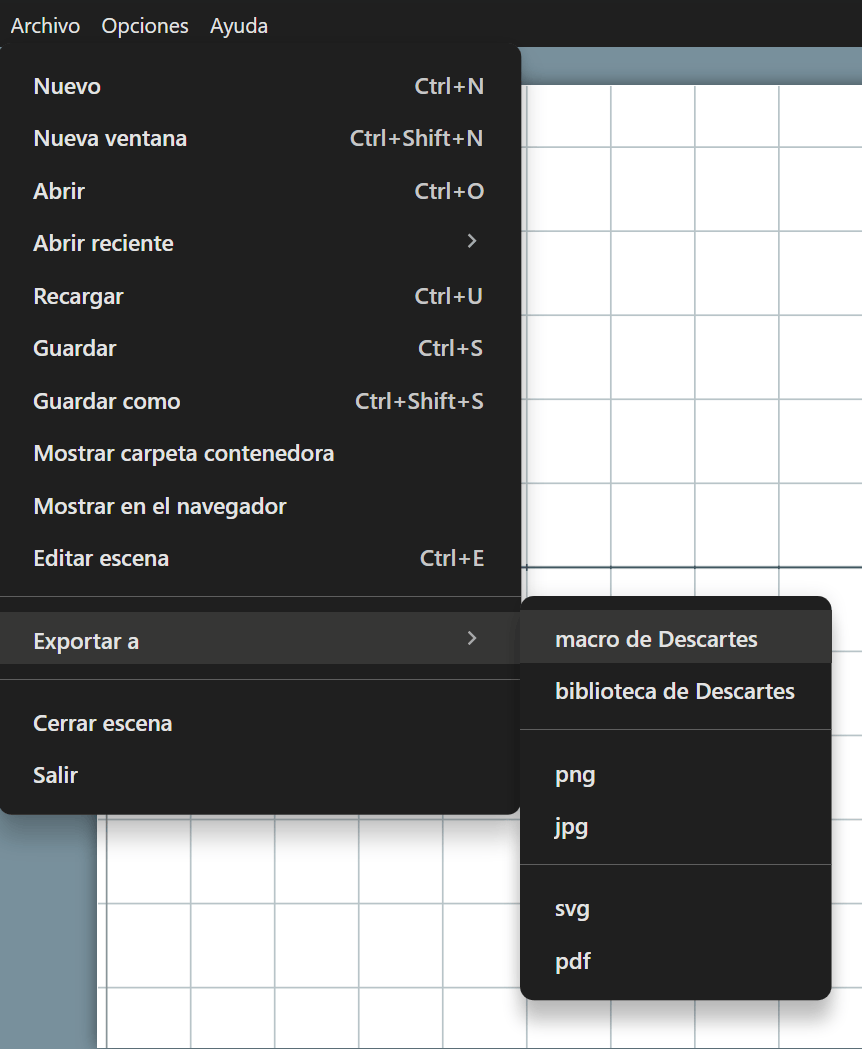
En el siguiente código se muestra el contenido de un macro sencillo que incluye el algoritmo de INICIO donde se define la variable radio=1 y un gráfico de tipo arco que dibuja un circulo rojo centrado en el origen y que utiliza el valor de la variable radio:
<script type="descartes/macro" id="circulo.txt">id='INICIO' algoritmo='sí' evaluar='una-sola-vez' hacer='radio=1'tipo='arco' color='ff0000' coord_abs='no' centro='(0,0)' radio='radio' inicio='0' fin='360' relleno='ff0000' ancho='1'</script>
Red Descartes 2025/Año 5, núm. 10
Archivos de texto generales
Todos los elementos anteriores (vector, matrices, bibliotecas y macros) son elementos que el editor DescartesJS puede incorporar de forma automática (sí se activa la opción correspondiente), debido a que su contenido se espera que sea estático, es decir, que no cambia con el tiempo durante la ejecución de una escena. Pero hay otras funcionalidades de las escenas que permiten acceder a contenido de archivos externos, el cual puede ser variable.
En particular existe la función _Load_(nombre_del_archivo) que se encarga de leer el contenido textual del archivo especificado como parámetro, esta función suele utilizarse en escenas en línea para acceder a contenido generado por algún servidor o especificado de forma interactiva por el usuario, por lo que incrustar el contenido automáticamente en la escena no es realmente viable. Aún así, existe la posibilidad de construir escenas que requieran de archivos externos ubicados siempre en la misma ruta y con la misma información, por ejemplo, archivos de configuración, por lo que en este caso sí es viable incrustar el contenido de los archivos para permitir que la escena se visualice y funcione de forma local.
Para incluir el contenido textual de un archivo dentro del HTML de una escena de DescartesJS, es necesario editar de forma manual su contenido para agregar un <script> con el tipo type="descartes/archivo" y especificando la ruta con el identificador del <script>, por ejemplo:
<script type="descartes/archivo" id="config.txt">... Contenido textual del archivo ...</script>
Red Descartes 2025/Año 5, núm. 10
Imágenes
Las imágenes de mapas de bits, es decir, aquellas con formato jpg, png, gif, webp, se almacenan con una representación binaria. Las páginas HTML están construidas por medio de texto y el uso de imágenes se realiza utilizando mecanismos que ofrece el navegador para cargar, interpretar y dibujar los diversos formatos de imágenes que soporta; estos mecanismos por lo general involucran la ruta a archivos externos donde se localiza el contenido binario de una imagen.
Debido a lo anterior, con los mecanismos tradicionales si una escena interactiva hace uso de imágenes, es necesario compartir el archivo HTML y todos los archivos de las imágenes que utilice. En versiones recientes del intérprete de DescartesJS, se incorporó la posibilidad de incrustar imágenes dentro del contenido de una página HTML, esto mediante el uso de lo que se conoce como la codificación en base64, la cual permite convertir información binaria a una cadena de texto. Esta adición es útil si se busca crear una escena interactiva autocontenida, donde solo sea necesario compartir un único archivo HTML.
Por ejemplo, para codificar la siguiente imagen de un corazón, en formato jpg, con una resolución de 24×24 píxeles.

Se tiene la siguiente representación textual en base64:
Red Descartes 2025/Año 5, núm. 10
data:image/jpeg;base64,/9j/4AAQSkZJRgABAQEASABIAAD/2wBDAAYEBQYFBAYGBQYHBwYIChAKCgkJChQODwwQFxQYGBcUFhYaHSUfGhsjHBYWICwgIyYnKSopGR8tMC0oMCUoKSj/2wBDAQcHBwoIChMKChMoGhYaKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCj/wgARCAAYABgDAREAAhEBAxEB/8QAFwAAAwEAAAAAAAAAAAAAAAAABAUGA//EABcBAQEBAQAAAAAAAAAAAAAAAAMFAgT/2gAMAwEAAhADEAAAAbwu8bKk6LDKPGnIxovmmz406Bpn/8QAHBAAAgICAwAAAAAAAAAAAAAAAQQCAxIUExUi/9oACAEBAAEFArr7ps87+VN90GWDpN5xwXO62QCOt9AAD//EACURAAECBAYCAwAAAAAAAAAAAAEAAwIREjEEExQhQlEVYSNB8P/aAAgBAwEBPwFphqBoPYie9gFkYKWbWaeuSdYajaL2HntcFMjVs6flDb32FRFVRLdPDSM6flFf10ECQZheT2rp+S1X77RJJmV//8QAHxEAAQMEAwEAAAAAAAAAAAAAAgABEhARI0EDEyEy/9oACAECAQE/AXInKIqXJ82TETFEkWMpadX2hyFLTU6dX8p//8QAIhAAAQMDBAMBAAAAAAAAAAAAAQADEQISEwQhQWEUMWLR/9oACAEBAAY/AixpA3NABrqr46WHA3k95d8cIMasNzWJoqo56R1MSy7Ac+TwVfcLIm6doQ1MQy1Ib+jyVB3BWPLV4k3Ye/xQNgF//8QAIBABAAICAQQDAAAAAAAAAAAAAQARMUEhUWFxgbHR8P/aAAgBAQABPyHlsEerYAb3OzfJ9i9V7xLbBW9Uyh3uWMxLC0OPDqfnSF30lDMS0pTjw6jMQFI4ZX4COy89VQmICgME/9oADAMBAAIAAwAAABAEMtFf/8QAHhEBAQEAAgMBAQEAAAAAAAAAAREhADFBUYFxYbH/2gAIAQMBAT8QWiGklZ2q0Ac9/OfHmTX+TzevFvFohhJS9IkEXPd/nDMMu30Hf0uj8w3nkGpJt6k7tycN02bPQN/S6vzTeGkicrr5+HudYy+s6ziJKvP/xAAeEQACAgICAwAAAAAAAAAAAAAAAREhMVFhkUFx8P/aAAgBAgEBPxB4hrLZfRO7gWIbw0P2TjTIRah+ic7Y0moZn7MfeOBJJQj/xAAdEAEAAwEBAAMBAAAAAAAAAAABESExAEFRcZHw/9oACAEBAAE/ELFKE31gKjWRW9/H1Hm/pPw11ClOa6wUA2yK3ndL/YUexZBm2oP4VDCfipc5HO2X+wo8iQHdpEFW0HkGkR079bv0n7X1ib2+FaQeAKADDv/Z
En este ejemplo se utiliza una imagen de baja resolución y en formato jpg, ya que la representación textual en base64 puede ser muy larga, por lo general aumenta el tamaño de almacenamiento un tercio más que la versión binaria de la imagen.
Red Descartes 2025/Año 5, núm. 10
Para incrustar la imagen en una escena de DescartesJS, basta con incluir la cadena de texto anterior dentro de un <script> con tipo type="descartes/imagen", y similar a los otros archivos, en el parámetro id se escribe la ruta de la imagen.
<script type="descartes/imagen" id="corazon.jpg">... Contenido en base64 de la imagen ...</script>
Y para usarla se agrega un gráfico de tipo imagen de la forma usual, haciendo que el parámetro archivo tenga la misma ruta que se utilizó para el id del <script>.
Para convertir una imagen en su representación textual en base64 se recomienda el sitio https://www.base64-image.de/, desde donde se puede realizar la conversión de forma sencilla, simplemente arrastrando la imagen que se quiere convertir y pulsando el botón copy image, para luego pegar el contenido dentro del <script>.
Red Descartes 2025/Año 5, núm. 10
Si se utiliza otro servicio o método para generar la codificación en base64 (por ejemplo, Conversor de Archivos a Base64), es importante tener en cuenta que al inicio de la cadena que representa una imagen debe aparecer: data:image/jpeg;base64, para una imagen en formato jpg, data:image/png;base64, para png, data:image/gif;base64, para un gif, y data:image/webp;base64, para imágenes en formato webp; esta información permite al navegador interpretar correctamente el tipo de imagen presente en el texto codificado.
Respecto a las imágenes vectoriales en formato SVG, como este tipo de imágenes están codificadas de forma textual tenemos dos formas de incrustarlas en una escena de DescartesJS, una es utilizando la codificación base64 de la misma manera que con las imágenes anteriores, garantizando que al inicio aparezca data:image/svg+xml;base64,, por ejemplo:
data:image/svg+xml;base64,PHN2ZyB3aWR0aD0iMjQiIGhlaWdodD0iMjQiIGZpbGw9IiNmZjAwMDAiIHZlcnNpb249IjEuMSIgdmlld0JveD0iMCAwIDI0IDI0IiB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciPjxyZWN0IHdpZHRoPSIyNCIgaGVpZ2h0PSIyNCIgZmlsbD0iI2ZmZiIgc3Ryb2tlLWxpbmVjYXA9InJvdW5kIiBzdHJva2UtbGluZWpvaW49InJvdW5kIiBzdHJva2Utd2lkdGg9IjIiIHN0eWxlPSJwYWludC1vcmRlcjpzdHJva2UgZmlsbCBtYXJrZXJzIi8+PHBhdGggZD0ibTEyIDIxYy03LjMwNC02LjU0OS0xMC05LjI2OS0xMC0xMi44NSAwLTMuMTU2IDIuMzQ0LTUuNSA1LjUtNS41IDIuNDI4IDAgMy45MjYgMS40MjUgNC41IDIuMSAwLjU3NDgtMC42NzYyIDIuMDczLTIuMSA0LjUtMi4xIDMuMTU2IDAgNS41IDIuMzQ0IDUuNSA1LjUgMCAzLjU2NS0yLjY0NiA2LjI1Ny0xMCAxMi44NXptMC0yLjdjNi40NTUtNS43ODIgOC03Ljg5MyA4LTEwLjE1IDAtMi4wMTQtMS40ODYtMy41LTMuNS0zLjUtMS41ODIgMC0zLjA0OSAwLjk3OTUtMy41NSAyLjM1aC0xLjljLTAuNTAxNS0xLjM3MS0xLjk2OS0yLjM1LTMuNTUtMi4zNS0yLjAxNCAwLTMuNSAxLjQ4Ni0zLjUgMy41IDAgMi4yNTcgMS41NDcgNC4zNjkgOCAxMC4xNXoiLz48L3N2Zz4K
Red Descartes 2025/Año 5, núm. 10
La otra forma es utilizar directamente la información textual que contiene la imagen SVG, pero incluyendo al inicio data:image/svg+xml,, es decir, sin la parte que hace referencia a la codificación en base64 (;base64), por ejemplo:
data:image/svg+xml,<svg width="24" height="24" fill="#ff0000" version="1.1" viewBox="0 0 24 24" xmlns="http://www.w3.org/2000/svg"><rect width="24" height="24" fill="#fff" stroke-linecap="round" stroke-linejoin="round" stroke-width="2" style="paint-order:stroke fill markers"/><path d="m12 21c-7.304-6.549-10-9.269-10-12.85 0-3.156 2.344-5.5 5.5-5.5 2.428 0 3.926 1.425 4.5 2.1 0.5748-0.6762 2.073-2.1 4.5-2.1 3.156 0 5.5 2.344 5.5 5.5 0 3.565-2.646 6.257-10 12.85zm0-2.7c6.455-5.782 8-7.893 8-10.15 0-2.014-1.486-3.5-3.5-3.5-1.582 0-3.049 0.9795-3.55 2.35h-1.9c-0.5015-1.371-1.969-2.35-3.55-2.35-2.014 0-3.5 1.486-3.5 3.5 0 2.257 1.547 4.369 8 10.15z"/></svg>
En ambos ejemplos de imágenes SVG, se representa un corazón rojo con fondo blanco .
Red Descartes 2025/Año 5, núm. 10
Este artículo se adentra en el proyecto 'Blue Sea', mostrando cómo la Formación Profesional (FP) se convierte en un laboratorio de innovación, aplicando la electrónica, la programación y la geolocalización satelital para abordar retos de sostenibilidad marina y demostrar el potencial del trabajo colaborativo en el entorno educativo y empresarial canario.
Misión, contexto y visión social
Con el espíritu de vanguardia tecnológica y compromiso social, nace la iniciativa de crear un Sistema de Navegación Autónomo aplicado a un barco. El proyecto tiene como objetivo desarrollar una embarcación capaz de recorrer grandes distancias y recopilar una amplia variedad de datos de gran utilidad para posteriores análisis, incluyendo mediciones de temperaturas, corrientes, detección de plásticos, monitoreo de bancos de peces u observaciones de fondos marinos.
Red Descartes 2025/Año 5, núm. 10
Este desarrollo se enmarca en la visión de que la Formación Profesional en Canarias puede ser un ámbito donde generar iniciativas que sean capaces de revalorizarla, apostando por la calidad en la enseñanza de contenidos prácticos y la **eficiencia energética**.
La Travesía Inaugural
Como primer gran hito técnico y de navegación, se ha planificado que el barco autónomo complete la travesía desde **Playa del Juncal en Agaete (Gran Canaria) hasta El Porís en Tenerife** (aproximadamente 71 km). Este trayecto servirá para validar la autonomía, la precisión de la navegación y la fiabilidad de los sistemas de comunicación frente a desafíos como las corrientes marinas y el tráfico marítimo.
Red Descartes 2025/Año 5, núm. 10
El proyecto Blue Sea se convierte en un reto ejemplar dentro de la metodología de Aprendizaje Colaborativo Basado en Retos (ACBR), ofreciendo a los estudiantes un desafío complejo y real. El barco autónomo funciona como un desafío de ACBR porque:
Red Descartes 2025/Año 5, núm. 10
Presentamos nuestro Proyecto "Blue Sea"
Red Descartes 2025/Año 5, núm. 10
Funcionamiento del Blue Sea
El sistema de navegación autónoma está compuesto por múltiples subsistemas que trabajan en conjunto para proporcionar capacidades de navegación, propulsión, comunicación y gestión energética.
El sistema utiliza un microcontrolador Arduino como unidad central de control, integrando sensores, actuadores y sistemas de comunicación para lograr la autonomía en la navegación.
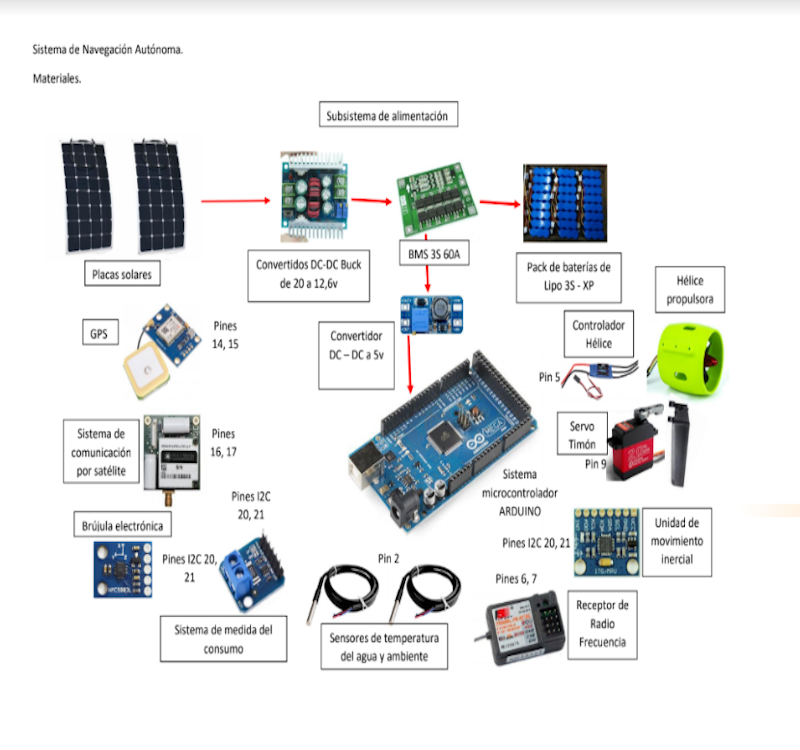
Red Descartes 2025/Año 5, núm. 10
Red Descartes 2025/Año 5, núm. 10
El corazón de la inteligencia del Blue Sea reside en una placa Arduino Mega microcontrolada, que actúa como Unidad Central de Procesamiento (CPU) de la embarcación. Este sistema opera bajo un lazo de control continuo, procesando datos de múltiples sensores para ejecutar la lógica de navegación:
Red Descartes 2025/Año 5, núm. 10
La motricidad se logra mediante un **motor *brushless*** (sin escobillas) acoplado a un sistema de reductora, lo que garantiza un alto par a bajas revoluciones, crucial para la navegación lenta y eficiente. La innovación clave es el Acoplamiento Magnético:
Red Descartes 2025/Año 5, núm. 10
El objetivo es la autosuficiencia total. El sistema de alimentación se diseña en torno a la eficiencia y redundancia energética:
Red Descartes 2025/Año 5, núm. 10
La clave para el seguimiento global del Blue Sea es la comunicación redundante y robusta:
Red Descartes 2025/Año 5, núm. 10
El proyecto fue desarrollado y documentado gracias a la colaboración de los siguientes miembros del IES Politécnico Las Palmas:
Este proyecto ha sido posible gracias al apoyo y la financiación de:
Dirección General de Formación Profesional y Educación de Adultos del Gobierno de Canarias
Las Palmas de Gran Canaria(España)
2023
Red Descartes 2025/Año 5, núm. 10
Red Descartes 2025/Año 5, núm. 10
El diseño modular del 'Blue Sea' facilita su replicación en cualquier centro con especialidades en electrónica, informática o mantenimiento. Los subsistemas críticos que sirven de base son:
Red Descartes 2025/Año 5, núm. 10
Para replicar el proyecto en su centro:
El verdadero valor de 'Blue Sea' radica en que entrena a los estudiantes para ser innovadores ante los retos de la Economía Azul, el sector estratégico que busca un desarrollo marítimo sostenible. Estos desafíos incluyen:
El 'Blue Sea' se erige como un modelo de excelencia que no solo forma técnicos competentes, sino innovadores preparados para el desarrollo sostenible del futuro marítimo canario.
Red Descartes 2025/Año 5, núm. 10
Red Descartes 2025/Año 5, núm. 10
Red Descartes 2025/Año 5, núm. 10
Red Descartes 2025/Año 5, núm. 10
El artículo y los anexos deben enviarse en una archivo zip, a través de un enlace (vía hosting o Google Drive, por ejemplo).
Los artículos deben abordar temas como:
El o los autores podrán sugerir revisores, indicando los datos de contacto (nombre y dirección de correo).
Los editores del Consejo Editorial, en primera instancia, valorarán los artículos para verificar que cumplen con los objetivos de publicación de la revista, si el concepto es positivo se asignarán mínimo dos revisores quienes evaluarán el artículo y harán las recomendaciones pertinentes, entre ellas la aceptación o no de su publicación.
Red Descartes 2025/Año 5, núm. 10