Juan Guillermo Rivera Berrío
Red Educativa Digital Descartes
Córdoba (España)
2023
Título de la obra:
Estática
Libro interactivo para ingenieros
Autor:
Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Foto portada: Bixby Creek Bridge, Monterey, United States, Cody Hiscox, en Unplash.
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-75-2

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual
Foto tomada en Cleveland, Estados Unidos por Lance Anderson, Unplash.
En este libro, exploraremos los fundamentos teóricos y prácticos de la estática, una rama importante de la mecánica que se enfoca en el estudio del equilibrio de fuerzas y objetos estables en reposo. A través de una serie de lecciones detalladas y ejemplos prácticos, los estudiantes aprenderán cómo aplicar conceptos fundamentales como la ley de acción y reacción de Newton, la resolución de fuerzas y la distribución de cargas en estructuras complejas. Ya sea que estés interesado en la ingeniería civil, mecánica o aeroespacial, este libro te brindará una base sólida para comprender y diseñar estructuras y sistemas estables.
Los capítulos que desarrollaremos son los siguientes:
Para ilustrar mejor la información suministrada en este libro, hemos incluido, entre otros elementos multimedia, los siguientes:

Imagen de portada: Puente, Pexels.
Imagen de esta página: Edificio en Milán, foto de Mikita Yo, en Unsplash.
La Estática es una rama de la mecánica que se enfoca en el estudio del equilibrio de los cuerpos rígidos. Esta área se centra en el análisis de las fuerzas que actúan sobre los objetos en reposo, y cómo estas fuerzas se equilibran para mantener el objeto en su lugar. La Estática es esencial para la comprensión de muchos fenómenos físicos en la vida cotidiana. En la estática, se utilizan ecuaciones y principios físicos para resolver problemas relacionados con el equilibrio de los cuerpos rígidos.
En Ingeniería Civil, el estudio de los Sistemas Estructurales requiere poseer una base teórico-práctica de los conceptos de la Mecánica Estática para así lograr un mejor entendimiento de los problemas asociados al análisis de las Estructuras. Si llevamos esto a la práctica, se tiene que esta rama de la Mecánica es en efecto una introducción al Análisis Estructural (steemit).
Para el estudio de la estática, necesitamos tener claro algunos conceptos que, seguramente, ya habrás estudiado en cursos previos. Sin extendernos es grandes descripciones, presentamos los primeros conceptos que usarás en los diferentes capítulos de este libro.
Espacio. En física, el espacio es una entidad geométrica en la que interactúan los objetos físicos y en el que los sucesos que ocurren tienen una posición y dirección. El espacio físico es habitualmente concebido con tres dimensiones lineales, aunque los físicos
modernos usualmente lo consideran, con el tiempo, como una parte de un infinito continuo de cuatro dimensiones conocido como espacio-tiempo, que en presencia de materia es curvoEn 1905, Einstein llegó a la conclusión, por razones experimentales, de que el escenario en el que se desarrollan los aconteceres del mundo tiene cuatro dimensiones, y que el espacio y el tiempo están inextricablemente relacionados, hasta el punto de que las medidas de las longitudes de los cuerpos y la duración de los acontecimientos están conectados entre sí y dependen del estado de movimiento del observador
Pero, no te preocupes, pues en este libro no nos ocuparemos del continuo espacio-temporal. Sólo tienes que preocuparte por el espacio tridimensional, en general, y del espacio en dos dimensiones, en particular y, para facilitar más tu estudio de la estática, las dimensiones de nuestro espacio son muy limitadas, comparadas con la dimensiones ilustradas en el siguiente video:
Masa y peso. La masa y el peso a menudo se usan indistintamente en la conversación diaria. Por ejemplo, nuestros registros médicos a menudo muestran nuestro peso en kilogramos, pero nunca en las unidades correctas de newtons. En física, sin embargo, hay una distinción importante. El peso es la atracción de la Tierra sobre un objeto. Depende de la distancia desde el centro de la Tierra. A diferencia del peso, la masa no varía con la ubicación, es la misma en la Tierra, en la órbita o en la superficie de la Luna
La definición más amplia de peso en este sentido es que el peso de un objeto es la fuerza gravitacional del cuerpo grande más cercano, como la Tierra, la Luna o el Sol. Esta es la definición más común y útil de peso en física (Ibid.).
Fuerza. La fuerza es la acción de un cuerpo sobre otro, es la acción que intenta o logra cambiar el estado de reposo o movimiento de un cuerpo. En este sentido vemos que las fuerzas no aparecen solas, debe existir la interacción de dos cuerpos. Podemos decir también que la fuerza es la resistencia que hace un cuerpo a la acción o interacción con otro cuerpo
Leyes de Newton. Las leyes de Newton son tres principios fundamentales de la física que explican cómo se mueven los cuerpos y cómo las fuerzas interactúan entre ellos. Estas leyes fueron enunciadas por el físico inglés Sir Isaac Newton en el siglo XVII. A continuación se describen las tres leyes de Newton:
La tercera ley de Newton representa una cierta simetría en la naturaleza: las fuerzas siempre ocurren en pares, y un cuerpo no
Retrato de Isaac Newton (1642-1727), foto de Godfrey Kneller, Dominio público.
puede ejercer una fuerza sobre otro sin experimentar una fuerza en sí misma. A veces nos referimos a esta ley en términos generales como "acción-reacción", donde la fuerza ejercida es la acción y la fuerza experimentada como consecuencia es la reacción. La tercera ley de Newton tiene usos prácticos para analizar el origen de las fuerzas y comprender qué fuerzas son externas a un sistema, tal como ocurre en las estructuras que analizaremos en este libro.
En el siguiente objeto interactivo, diseñado por Carlos Alberto Serrato Hernández, podrás manipular la masa de un objeto que es empujado por una persona. Se observan las fuerzas de acción y reacción que intervienen en este evento.
La ley de gravitación de Newton. La fuerza con la que se atraen dos objetos es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa. Es decir, cuanto más grande sea la masa de los objetos, mayor será la fuerza gravitatoria que ejercen entre sí y, por otro lado, cuanto mayor sea la distancia entre los objetos, menor será la fuerza gravitatoria. La fórmula matemática para la ley de la Gravitación Universal es la siguiente:
$$F = G\frac{Mm}{r^2}\tag{1.2}$$Donde $F$ es la fuerza gravitatoria, $M$ y $m$ son las masas de los objetos, $r$ es la distancia entre ellos, y $G$ es la constante de gravitación universal. Esta ley es fundamental para explicar el movimiento de los cuerpos en nuestro sistema solar y otros sistemas en el universo.
Peso. A partir de la ecuación 1.2 y definiendo la gravedad como $g = GM/r^2$, podemos expresar el peso (Weight), así:
$$W = mg \tag{1.3}$$El valor $g$, en la tierraPara la mayoría de los cálculos de ingeniería, $g$ se determina al nivel del mar y a una latitud de $45\degree$, la cual se considera como la “ubicación estándar"
Un objeto interactivo interesante es "Gravedad y órbitas" desarrollado en Phet Interactive Simulations.
En la siguiente escena interactiva, mueve el sol, la tierra, la luna y la estación espacial para ver cómo afecta sus fuerzas gravitatorias y trayectorias orbitales. ¡Visualiza los tamaños y las distancias entre los diferentes cuerpos celestes y desactiva la gravedad para ver lo que pasaría sin ésta!
Todos los objetos interactivos, los puedes ampliar haciendo clic en la esquina superior derecha de la escena.
Los sistemas de unidades consisten en conjuntos de patrones estándar destinados a medir las distintas magnitudes que se usan en ciencia e ingeniería. Se basan en el patrón de unas pocas magnitudes consideradas fundamentales, y a partir de ellas se deriva el resto.
Hay varios sistemas de unidades que se utilizan para la medición. El más común es el Sistema Internacional de Unidades (SI)La Conferencia General de Pesos y Medidas, autoridad internacional acerca del tema, propuso en 1960 la creación del Système International d’Unités, abreviado como SI, tanto en francés como en castellano., que se basa en el metro ($m$) para medir longitud, el kilogramo ($kg$) para medir la masa y el segundo ($s$) para el tiempo. Otro sistema que se utiliza con frecuencia es el Sistema Inglés o, mejor, "Sistema de uso común en Estados Unidos", que se basa en la pulgada, el pie, y el slug para la masa, como elementos principales para la medición.
Las unidades del SI son parte del sistema métrico, que es conveniente para cálculos científicos y de ingeniería porque las unidades se clasifican por factores de 10. La Tabla 1.1 enumera los prefijos y símbolos métricos utilizados para indicar varios factores de 10 en unidades SI. Por ejemplo, un centímetro es una centésima de un metro (en símbolos, $1\;cm = 10^{-2}\;m$) y un kilómetro es de mil metros ($1\;km = 10^3\;m$). De manera similar, un megagramo es un millón de gramos ($1\;Mg = 10^6\;g$), un nanosegundo es una milmillonésima de segundo ($1\;ns = 10^{-9}\;s$) y un terámetro es un billón de metros
($1\;Tm= 10^{12}\;m$).
| Forma exponencial | Prefijo | Símbolo SI | |
|---|---|---|---|
| Múltiplo | |||
| 1 000 000 000 000 | $10^{12}$ | tera | T |
| 1 000 000 000 | $10^9$ | giga | G |
| 1 000 000 | $10^6$ | mega | M |
| 1 000 | $10^3$ | kilo | k |
| Submúltiplo | |||
| 0.01 | $10^{-2}$ | centi | c |
| 0.001 | $10^{-3}$ | mili | m |
| 0.000 001 | $10^{-6}$ | micro | $\mu$ |
| 0.000 000 001 | $10^{-9}$ | nano | n |
Como ejercicio, convirtamos la masa de $1.93\times10^{13}\; kg$ a $Tg$.
Inicialmente, convertimos a gramos ($g$):
$$1.93\times10^{13}\; kg = 1.93\times10^{13}\times 10^3\; g = 1.93\times10^{16}\;g$$De la Tabla 1.1 sabemos que $1\:Tg = 10^{12}\;g$, entonces:
$$1.93 \times 10^{16} \;g = 1.93 \times 10^{4} \times \textcolor{red}{10^{12}\;g} = 1.93\times10^{4}\;Tg$$Consideremos un ejemplo de cómo convertir unidades. Supongamos que queremos convertir $80 \;kg$ a toneladas métricas. Lo primero que debes hacer es listar las unidades que tienes y las unidades a las que deseas convertir. En este caso, tenemos unidades en kilogramos y
queremos convertir a toneladas. Luego, necesitamos determinar un factor de conversión que relacione kilogramos a toneladas. Un factor de conversión es una proporción que expresa cuántos de una unidad son iguales a otra unidad. Por ejemplo, hay $12$ pulg. en $1$ pie, $100\; cm$ en $1 \;m$, $60 \;s$ en $1 \;min$, y así sucesivamente. Consulta las tablas de conversión para obtener una lista más completa de los factores de conversión. En este caso, sabemos que hay $1000 \;kg$ en $1 \;ton$. Ahora podemos configurar nuestra conversión de unidad. Escribimos las unidades que tenemos y luego las multiplicamos por el factor de conversión para que las unidades se cancelen, como se muestra a continuación:
$$80\;\cancel{\textcolor{red}{kg}}\times \frac{1\;ton}{1000\;\cancel{\textcolor{red}{kg}}} = 0.080\;ton$$Ten en cuenta que la unidad kilogramo no deseada se cancela, dejando solo la unidad tonelada deseada. Puedes usar este método para convertir cualquier tipo de unidad.
En cualquier momento puedes consultar las tablas de conversión de unidades en la caja de harramientas de este libro.
La densidad del hierro es $7.86 \;g/cm^3$ en condiciones estándar. Convierte ésto a $kg/m^3$.
Necesitamos convertir gramos a kilogramos y centímetros cúbicos a metros cúbicos. Los factores de conversión que necesitamos son $1\;kg = 10^3\;g$ y $1\;cm = 10^{-2}\;m$. Sin embargo, estamos tratando con
centímetros cúbicos ($cm^3 = cm \times cm \times cm$), por lo que tenemos que usar el factor de la segunda conversión tres veces (es decir, tenemos que ponerlo en el cubo). La idea es aún multiplicar por los factores de conversión de tal forma que cancelen las unidades de las que queremos deshacernos e introduzcan las unidades que queremos conservar.
Solución
$$\begin{split} 7.86\frac{\textcolor{red}{\cancel{g}}} {\textcolor{green}{\cancel{cm^3}}} \times \frac{kg}{10^3\textcolor{red}{\cancel{g}}} \times \bigg(\frac{\textcolor{green}{\cancel{cm}}}{10^{-2}m} \bigg)&= \frac{7.86}{10^3\times 10^{-6}}kg/m^3\\ &= 7.86\times 10^3kg/m^3 \end{split}$$Las conversiones de unidades pueden no parecer muy interesantes, pero no hacerlas puede ser costoso. Un ejemplo famoso de esta situación fue visto con Mars Climate Orbiter. Esta sonda fue lanzada por la NASA el 11 de diciembre de 1998.

El 23 de septiembre de 1999, mientras intentaba guiar la sonda hacia su órbita planeada alrededor de Marte, la NASA perdió el contacto con ella. Investigaciones posteriores mostraron que un software llamado SM_FORCES (o "fuerzas pequeñas") registraba los datos de rendimiento del propulsor en las unidades inglesas de libra-segundos (lb-s). Sin embargo, otras piezas de software que utilizaron estos valores para las correcciones de los cursos esperaban que se grabasen en las
unidades SI de newton-segundos (N-s), tal como se establece en los protocolos de la interfaz del software. Este error provocó que la sonda siguiera una trayectoria muy diferente de la que la NASA pensó que estaba siguiendo, lo que probablemente causó que la sonda se quemara en la atmósfera marciana o se disparara al espacio. Esta falla en prestar atención a las conversiones de unidades costó cientos de millones de dólares, sin mencionar todo el tiempo invertido por los científicos e ingenieros que trabajaron en el proyecto
Existe una gran variedad de aplicativos gratuitos, en línea, para realizar conversiones. Uno de ellos es Js Measurements Converters, que hemos modificado así:
Como ejercicio, convierte $2\;km/h$ a $pie/s$; para ello, debes seleccionar como unidad de medida la velocidad.
¿No encontraste la unidad $pie/s$?, pues trata de hacerlo con $pie/h$ y luego divide por 3600. Lo mejor, como ingeniero, es que hagas tus cálculos. Observa:
Un objeto va a la siguiente velocidad $2 \;km/h$ ¿Cuál es la velocidad en $pies/s$?
Solución
Consultando las tablas de conversión, obtenemos:
$$\begin{split} 2\frac{\textcolor{red}{\cancel{km}}} {\textcolor{green}{\cancel{h}}} \times \frac{10^3\;\textcolor{orange}{\cancel{m}}}{\textcolor{red}{\cancel{km}}} \times \frac{\textcolor{green}{\cancel{h}}}{3600\;s}\times \frac{pies}{0.3048\;\textcolor{orange}{\cancel{m}}} &= \frac{2\times 10^3}{1097.28}pies/s\\ &= 1.82\;pies/s \end{split}$$En realidad, el resultado presenta varias cifras decimales: 1.822688... ¿cuántas cifras debemos tener en cuenta?
En ingeniería, es una práctica normal expresar las respuestas finales en tres (y algunas veces cuatro) cifras significativas, porque los valores dados de entrada para geometría, cargas, propiedades de los materiales y otras cantidades comúnmente se dan con esta precisión (1Libarary).
Los parámetros del diseño definitivo deben determinarse con tanta exactitud como sea posible para lograr el diseño óptimo. En este sentido, una cifra significativa, o dígito significativo, se define como un dígito que se considera confiable como resultado de una medición o cálculo (Ibid.).
En nuestro ejemplo anterior, la respuesta la dimos con tres cifras significativas (1.82), lo cual podría ser suficiente; sin embargo, en algunos cálculos de ingeniería quizá sean necesarias más cifras significativas. Por ejemplo, cuando nos dicen que una persona mide $6\;pies$, en el SI esa medida sería $6\times 0.3048\;m = 1.8288\; m$ que, en general, asumimos como $1.8\;m$. Pero, si este valor corresponde a la longitud de un elemento estructural, quizá los $2\;cm$ eliminados sea un error significativo.

Una recomendación, es usar la notación de científica para expresar un resultado. Lo anterior requiere que los números se redondeen al número apropiado de dígitos significativos y después se expresen en potencias de 10. Por ejemplo, $113,700$ lo podríamos escribir como $11.37 \times 10^3$ o, redondeando, $11.4 \times 10^3$. No obstante, el uso de calculadoras y computadores, ha facilitado el cálculo ingenieril, lo que minimiza este tipo de preocupaciones.
Foto de Karolina Grabowska, Pexels.
Las Torres Petronas, situadas en Kuala Lumpur, capital de Malasia (foto de Engin Akyurt, en Pixabay).
Puente en puesta de sol, foto de Foundry Co, en Pixabay.
Una fuerza es una magnitud física que describe la capacidad de un objeto o un sistema para ejercer una acción sobre otro objeto o sistema. En términos más generales, una fuerza es cualquier interacción que pueda producir un cambio en el movimiento o la forma de un objeto. Las fuerzas se miden en unidades de newton (N) en el Sistema Internacional de Unidades (SI), y se representan gráficamente mediante vectores que indican su dirección, magnitud y sentido. La comprensión de las fuerzas es fundamental para el estudio de la mecánica, la física de la materia y otros campos relacionados con la interacción entre objetos físicos. En la mecánica de materiales, el análisis de las fuerzas es esencial para poder entender cómo se producen los desplazamientos, las deformaciones y los esfuerzos en los diferentes elementos estructurales, y cómo estos se relacionan con las cargas aplicadas.
Una definición intuitiva de fuerza puede seer un empujón o un tirón, que tiene tanto magnitud como dirección (por lo tanto, es una cantidad vectorial). La fuerza puede ser representada por vectores o expresada como un múltiplo de una fuerza estándar. El empujar o tirar de un objeto puede variar considerablemente en magnitud o dirección. Por ejemplo, un cañón ejerce una gran fuerza sobre una bala de cañón que se lanza al aire. Por el contrario, la Tierra ejerce solo una pequeña atracción hacia abajo sobre una pulga.
Los vectores son esenciales para la ingeniería. Muchas cantidades físicas fundamentales son vectores, incluidos el desplazamiento, la velocidad, la fuerza y los campos eléctricos y magnéticos. Los productos escalares de vectores definen otras cantidades físicas escalares fundamentales, como la energía. Los productos vectoriales de vectores definen todavía otras cantidades físicas de vectores fundamentales, como el par motor y el momento angular. En otras palabras, los vectores son una parte de la física de forma muy parecida a como las oraciones son una parte de la literatura.
Los vectores son cantidades euclidianas que tienen representaciones geométricas como flechas en una dimensión (en una línea), en dos dimensiones (en un plano) o en tres dimensiones (en el espacio). Se pueden sumar, restar o multiplicar. Este capítulo, en gran parte, es tomado del libro Física - Volumen I.
Muchas cantidades físicas pueden especificarse dando un número único y la unidad apropiada. Por ejemplo, "un período de clase dura $50\; min$" o "el tanque de gasolina de mi automóvil tiene $65 \;L$" o "la distancia entre dos postes es de $100 \;m$". Una cantidad física que se puede especificar completamente de esta manera se denomina cantidad escalar.
Un escalar es un sinónimo de "número"
El tiempo, la masa, la distancia, la longitud, el volumen, la temperatura y la energía son ejemplos de cantidades escalares. Las cantidades escalares que tienen las mismas unidades físicas se pueden sumar o restar de acuerdo con las reglas habituales del
álgebra para los números. Por ejemplo, una porción de maíz de $60$ calorías seguida de una porción de donas de $200$ calorías da $60\;cal + 200\;cal = 260\;cal$ de energía. Sin embargo, muchas cantidades físicas no se pueden describir completamente con solo un número de unidades físicas. Por ejemplo, cuando una Guardia Costera despacha un barco para una misión de rescate, el equipo debe conocer no solo la distancia a la señal de socorro, sino también la dirección desde la cual llega la señal.
Las cantidades físicas especificadas completamente dando un número de unidades (magnitud) y una dirección se llaman cantidades vectoriales. Ejemplos de cantidades de vectores incluyen desplazamiento, velocidad, posición, fuerza y torque. En el lenguaje de las matemáticas, las cantidades de vectores físicos están representadas por objetos matemáticos llamados vectores (Figura 2.1). Podemos sumar o restar dos vectores, y podemos multiplicar un vector por un escalar o por otro vector, pero no podemos dividir por un vector. La operación de división por un vector no está definida.
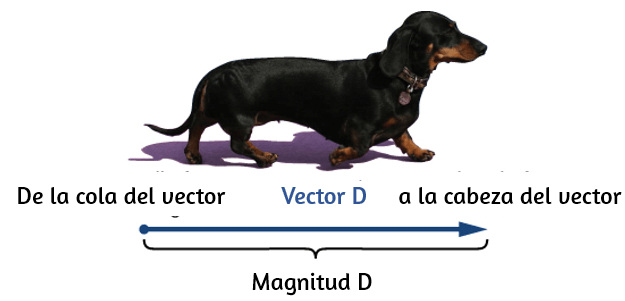
En este capítulo, para distinguir entre un vector y una cantidad escalar, adoptamos la convención común de una letra en negrita con una flecha encima que denota a un vector, y una letra sin una flecha que denota a un escalar. Por ejemplo, una distancia de $2.0\; km$, que es una cantidad escalar, se denota por $d = 2.0\; km$, mientras que un desplazamiento de $2.0 \;km$ en alguna dirección, que es una cantidad vectorial, se denota por $\bold{\vec{d}}$. Sin embargo, para los demás capítulos usaremos la letra en negrita para distinguir los vectores.
Supongamos que le dices a un amigo en un viaje de campamento que has descubierto un fabuloso agujero para pescar a $6\; km$ de tu tienda. Es poco probable que tu amigo pueda encontrar el hoyo fácilmente a menos que también comuniques la dirección en la que se puede encontrar con respecto a tu campamento. Puedes decir, por ejemplo, "Camina unos $6\; km$ al noreste de mi tienda". El concepto clave aquí es que debe dar no una sino dos datos de información, a saber, la distancia o magnitud ($6\; km$) y la dirección (Noreste).
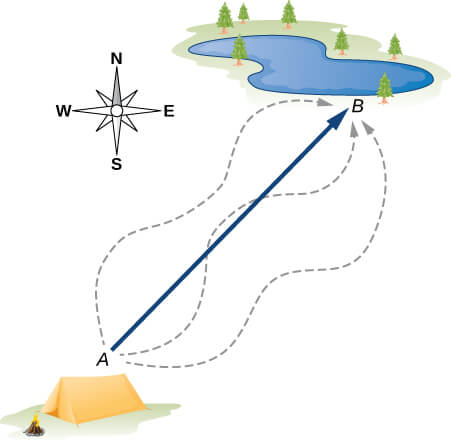
El desplazamiento es un término general usado para describir un cambio de posición, como durante un viaje desde la tienda de campaña hasta el agujero de pesca. El desplazamiento es un ejemplo de una cantidad vectorial. Si caminas desde la tienda (ubicación A) hasta el agujero (ubicación B), como se muestra en la Figura 2.2, el vector $\bold{\vec{D}}$, que representa tu desplazamiento, se dibuja como la flecha que se origina en el punto $A$ y termina en el punto $B$. La punta de flecha marca el final del vector. La dirección del vector de desplazamiento $\bold{\vec{D}}$ es la dirección de la flecha. La longitud de la flecha representa la magnitud $D$ del vector $\bold{\vec{D}}$ Aquí, $D = 6\; km$. Como la magnitud de un vector es su longitud, que es un número positivo, también se indica colocando la notación del valor absoluto alrededor del símbolo que denota el vector; entonces, $D = |\bold{\vec{D}}|$.
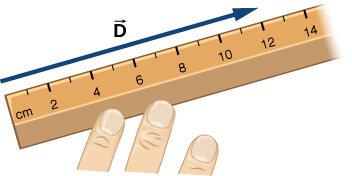
Para resolver un problema vectorial gráficamente, necesitamos dibujar el vector $\bold{\vec{D}}$ a escala. Por ejemplo, si asumimos que $1$ unidad de distancia ($1 km$) está representada en el dibujo por un segmento de línea de longitud $u = 2 \;cm$, entonces el desplazamiento total en este ejemplo está representado por un vector de longitud $d = 6u = 6(2 \;cm) = 12 \;cm$, como se muestra en la Figura 2.3.
Observa que aquí, para evitar confusiones, utilizamos $D = 6\;km$ para denotar la magnitud del desplazamiento real y $d = 12 \;cm$ para indicar la longitud de su representación en el dibujo.
Supongamos que tu amigo camina del campamento en $A$ al estanque de pesca en $B$ y luego regresa del estanque de pesca en $B$ al campamento en $A$. La magnitud del vector de desplazamiento $\bold{\vec{D}}_{AB}$ de $A$ a $B$ es la misma que la magnitud del vector de desplazamiento $\bold{\vec{D}}_{BA}$ de $B$ a $A$ (equivale a $6 km$ en ambos casos), por lo que podemos escribir $\bold{\vec{D}}_{AB} = \bold{\vec{D}}_{BA}$. Sin embargo, el vector $\bold{\vec{D}}_{AB}$ no es igual al vector $\bold{\vec{D}}_{BA}$ porque estos dos vectores tienen diferentes direcciones: $\bold{\vec{D}}_{AB} \ne \bold{\vec{D}}_{BA}$. En la Figura 2.2, el vector $\bold{\vec{D}}_{BA}$ estaría representado por un vector con un origen en el punto $B$ y un extremo en el punto $A,$ indicando el vector $\bold{\vec{D}}_{BA}$ apunta al suroeste, que es exactamente $180\degree$ opuesto a la dirección del vector $\bold{\vec{D}}_{AB}$. Decimos que el vector $\bold{\vec{D}}_{BA}$ es antiparalelo al vector $\bold{\vec{D}}_{AB}$ y escribes $\bold{\vec{D}}_{BA} = -\bold{\vec{D}}_{AB}$, donde el signo menos indica la dirección antiparalela (Estática una fuerza de tracción es antiparalela a una fuerza de compresión).
Se dice que dos vectores que tienen direcciones idénticas son vectores paralelos, lo que significa que son paralelos entre sí.
Los vectores pueden multiplicarse por escalares, sumarse a otros vectores o restarse de otros vectores. Podemos ilustrar estos conceptos vectoriales usando un ejemplo del viaje de pesca que se ve en la Figura 2.4.
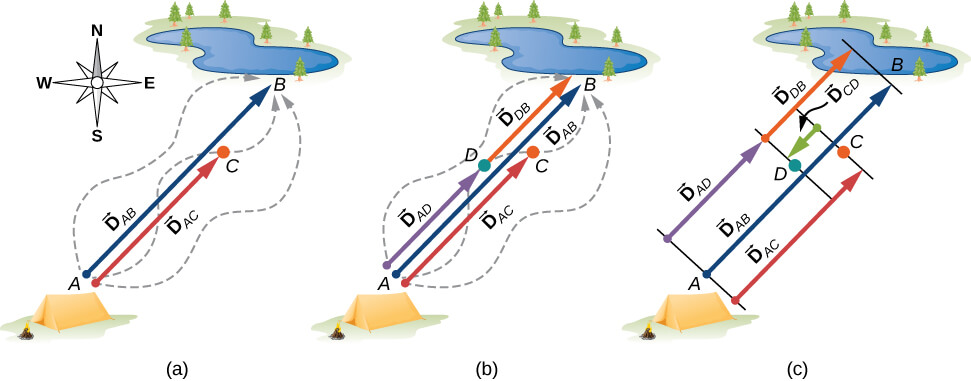
Supongamos que tu amigo sale del punto $A$ (el campamento) y camina en dirección al punto $B$ (el estanque de pesca), pero, en el camino, se detiene para descansar en algún punto $C$ ubicado a tres cuartas partes de la distancia entre $A$ y $B$, comenzando desde el punto $A$ (Figura 2.6 (a)). ¿Cuál es su vector de desplazamiento $\bold{\vec{D}}_{AC}$ cuando alcanza el punto $C$? Sabemos que si camina todo el camino hasta $B$, su vector de desplazamiento relativo a $A$ es $\bold{\vec{D}}_{AB}$, que tiene una magnitud $D_{AB} = 6 \;km$ y una dirección noreste. Si camina solo una fracción de $0.75$ de la distancia total, manteniendo la dirección
noreste, en el punto $C$ debe ser $0.75 D_{AB} = 4.5 \;km$ lejos del campamento en $A$. Entonces, su vector de desplazamiento en el punto de descanso $C$ tiene una magnitud $D_{AC} = 4.5\; km = 0.75D_{AB}$ y es paralela al vector de desplazamiento $\bold{\vec{D}}_{AB}$. Todo esto se puede establecer de manera sucinta en la forma de la siguiente ecuación vectorial:
$$\bold{\vec{D}}_{AC} = 0.75\bold{\vec{D}}_{AB}$$En una ecuación vectorial, ambos lados de la ecuación son vectores. La ecuación anterior es un ejemplo de un vector multiplicado por un escalar positivo (número) $\alpha = 0.75$. El resultado, $\bold{\vec{D}}_{AC}$, de dicha multiplicación es un nuevo vector con una dirección paralela a la dirección del vector original $\bold{\vec{D}}_{AC}$.
En general, cuando un vector $\bold{\vec{A}}$ se multiplica por un escalar positivo $\alpha$, el resultado es un nuevo vector $\bold{\vec{B}}$ que es paralelo a $\bold{\vec{A}}$
$$ \bold{\vec{B}} = \alpha\bold{\vec{A}} \tag{2.1}$$La magnitud $|\bold{\vec{B}}|$ de este nuevo vector se obtiene multiplicando la magnitud $|\bold{\vec{A}}|$ del vector original, según lo expresado por la ecuación escalar: $$\bold{\vec{B}} = |\alpha|\bold{\vec{A}} \tag{2.2} $$
La siguiente escena interactiva representa la multiplicación del vector por un escalar. Cambia el valor de $\alpha$.
Recuerda que puedes abrir el objeto interactivo en una ventana emergente, haciendo clic en la esquina superior derecha de la escena
Si el escalar $\alpha$ es negativo en la ecuación 2.1, entonces la magnitud $|\bold{\vec{B}}|$ del nuevo vector todavía está dado por la ecuación 2.2, pero la dirección del nuevo vector $\bold{\vec{B}}$ es antiparalelo a la dirección de $\bold{\vec{A}}$. Estos principios se ilustran en la Figura 2.5 (a) mediante dos ejemplos en los que la longitud del vector $\bold{\vec{A}}$ es de $1,5$ unidades.
Cuando $\alpha = 2,$ el nuevo vector $\bold{\vec{B}} = 2\bold{\vec{A}}$ tiene longitud $B = 2A = 3.0 \text{ unidades}$ (dos veces más largas que el vector original) y es paralela al vector original. Cuando $\alpha = -2$, el nuevo vector $\bold{\vec{C}} = -2\bold{\vec{A}}$ y tiene longitud $C = |-2|A = 3.0 \text{ unidades}$ (el doble de longitud que el original vector) y es antiparalelo al vector original.
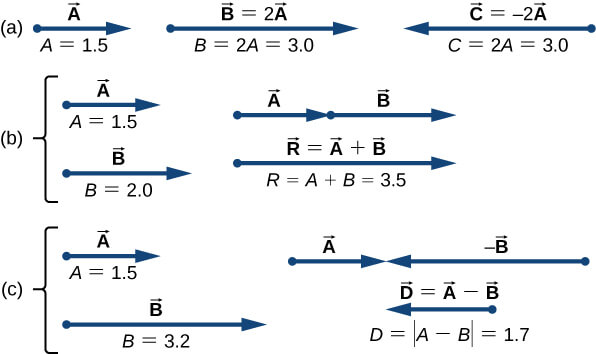
Ahora supongamos que tu compañero de pesca sale del punto $A$ (el campamento), caminando en dirección al punto $B$ (el agujero), pero se da cuenta que perdió su caja de aparejos cuando se detuvo para descansar en el punto $C$ (ubicado a tres cuartos de distancia entre $A$ y $B$, comenzando desde $A$). Entonces, se da vuelta y retrocede sus pasos en dirección al campamento y encuentra la caja en el camino en algún punto $D$ a solo $1.2 km$ del punto $C$ (ver Figura 2.4 (b)). ¿Cuál es su vector de desplazamiento $\bold{\vec{D}}_{AD}$ cuando encuentra la caja en el punto $D$?
¿Cuál es el vector de desplazamiento $\bold{\vec{D}}_{DB}$ del punto $D$ al agujero?
Ya hemos establecido que en el punto de reposo $C$ el vector de desplazamiento es $\bold{\vec{D}}_{AC} = 0.75\bold{\vec{D}}_{AB}$. Comenzando en el punto $C$, camina hacia el sudoeste (hacia el campamento), lo que significa que el nuevo vector de desplazamiento $\bold{\vec{D}}_{CD}$ desde el punto $C$ al punto $D$ es antiparalelo a $\bold{\vec{D}}_{AB}$. Su magnitud $\bold{\vec{D}}_{|CD|}$ es $\bold{\vec{D}}_{CD} = 1.2km = 0.2\bold{\vec{D}}_{AB}$, entonces el segundo vector es $\bold{\vec{D}}_{CD} = -0.2\bold{\vec{D}}_{AB}$. El desplazamiento total $\bold{\vec{D}}_{AD}$ relativo al campamento es la suma vectorial de los dos vectores de desplazamiento: $\bold{\vec{D}}_{AC}$ (desde el camping hasta el punto de descanso) y $\bold{\vec{D}}_{CD}$ (desde el punto de descanso hasta el punto donde él encuentra su caja).
$$\bold{\vec{D}}_{AD} = \bold{\vec{D}}_{AC} + \bold{\vec{D}}_{CD}\tag{2.3}$$La suma de dos (o más) vectores se llama vector resultante o, para abreviar, la resultante. Dado que se conocen los vectores en el lado derecho de la ecuación 2.3, entonces:
$$\begin{split} \bold{\vec{D}}_{AD} &= \bold{\vec{D}}_{AC} + \bold{\vec{D}}_{CD}\\ &= 0.75\bold{\vec{D}}_{AB} - 0.2\bold{\vec{D}}_{AB}\\ &= (0.75 - 0.2)\bold{\vec{D}}{AB} = 0.55\bold{\vec{D}}_{AB} \tag{2.4} \end{split}$$Cuando tu amigo finalmente llega al estanque en $B$, su vector de desplazamiento $\bold{\vec{D}}_{AB}$ del punto $A$ es la suma vectorial del vector de desplazamiento$\bold{\vec{D}}_{AD}$ del punto $A$ al punto $D$ y el vector de desplazamiento $\bold{\vec{D}}_{DB}$ del punto $D$ al agujero de pesca: $\bold{\vec{D}}_{AB} = \bold{\vec{D}}_{AD} + \bold{\vec{D}}_{BD}$ (ver Figura 2.4 (c)). Esto significa que el vector de desplazamiento $\bold{\vec{D}}_{DB}$ es la diferencia de dos vectores:
$$\bold{\vec{D}}_{DB} = \bold{\vec{D}}_{AB} - \bold{\vec{D}}_{AD} = \bold{\vec{D}}_{AB} + (-\bold{\vec{D}}_{AD})\tag{2.5}$$Cuando dos vectores $\bold{\vec{A}}$ y $\bold{\vec{B}}$ se encuentran a lo largo de una línea (es decir, en una dimensión), como en el ejemplo de acampada, su resultante $\bold{\vec{R}} = \bold{\vec{A}} + \bold{\vec{B}}$ y su diferencia $\bold{\vec{D}} = \bold{\vec{A}} - \bold{\vec{B}}$, se encuentran en la misma dirección.
En general, en una dimensión, así como en dimensiones superiores, como en un plano o en el espacio, podemos agregar cualquier número de vectores y podemos hacerlo en cualquier orden porque la adición de vectores es conmutativa,
$$\bold{\vec{A}} + \bold{\vec{B}}= \bold{\vec{B}} + \bold{\vec{A}}\tag{2.6}$$y asociativa,
$$(\bold{\vec{A}}+ \bold{\vec{B}}) + \bold{\vec{C}} = \bold{\vec{A}} + (\bold{\vec{B}} + \bold{\vec{C}})\tag{2.7}$$Además, la multiplicación por un escalar es distributiva:
$$\alpha_1\bold{\vec{A}} + \alpha_2\bold{\vec{A}} = (\alpha_1+ \alpha_2)\bold{\vec{A}}\tag{2.8}$$Al agregar muchos vectores en una dimensión, es conveniente usar el concepto de un vector unitario, que se denota con un símbolo de letra con un sombrero, como $\^{\bold{u}}$, tiene una magnitud de uno y no tiene ninguna unidad física, por lo que $|\^{\bold{u}}| \equiv u = 1$. El único papel de un vector unitario es especificar la dirección. Por ejemplo, en lugar de decir que el vector $\bold{\vec{D}}_{AB}$ tiene una magnitud de $6.0 km$ y una dirección del noreste, podemos introducir un vector unitario $\bold{\^{u}}$ que apunta al noreste y decir sucintamente que $\bold{\vec{D}}_{AB} = (6.0 \;km)\bold{\^{u}}$. Entonces, la dirección del sudoeste simplemente está dada por el vector unitario $\bold{\^{u}}$. De esta forma, el desplazamiento de $6.0 \;km$ en dirección suroeste se expresa mediante el vector
$$\bold{\vec{D}}_{BA} = (-6.0 \;km)\bold{\^{u}}$$La regla de adición para dos vectores en un plano no es tan simple como la regla para la adición de vectores en una dimensión. Tenemos que usar las leyes de la geometría para construir los vectores resultantes, seguidos de la trigonometría para encontrar las magnitudes y direcciones del vector. Este enfoque geométrico se usa comúnmente en navegación (Figura 2.6).
Para una construcción geométrica de la suma de dos vectores en un plano, seguimos la regla del paralelogramo. Supongamos que dos vectores $ \bold{\vec{A}}$ y $\bold{\vec{B}}$ están en las posiciones arbitrarias que se muestran en la Figura 2.7.

Traslada cualquiera de ellos en paralelo al comienzo del otro vector, de modo que después de la traslación, ambos vectores tengan su origen en el mismo punto. Ahora, al final del vector $\bold{\vec{A}}$ dibujamos una línea paralela al vector $\bold{\vec{B}}$ y al final del vector $\bold{\vec{B}}$ dibujamos una línea paralela al vector $\bold{\vec{A}}$ (las líneas discontinuas en la Figura 2.7). De esta forma, obtenemos un paralelogramo. Del origen de los dos vectores dibujamos una diagonal que es la resultante $\bold{\vec{R}}$ de los dos vectores: $\bold{\vec{R}} = \bold{\vec{A}} + \bold{\vec{B}}$ (Figura 2.7 (a)).
La otra diagonal de este paralelogramo es la diferencia vectorial de los dos vectores $\bold{\vec{D}} = \bold{\vec{A}} - \bold{\vec{B}}$, como se muestra en la Figura 2.7 (b). Observa que el final del vector diferencia se coloca al final del vector $\bold{\vec{A}}$.
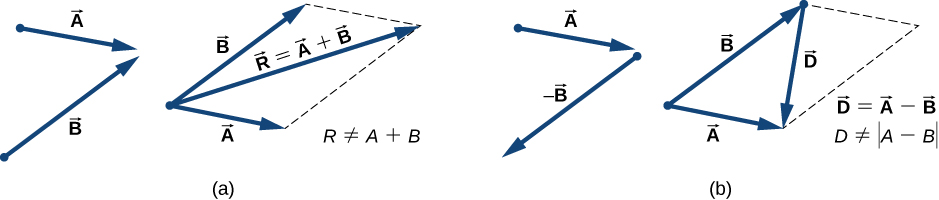
De la regla del paralelogramo se desprende que ni la magnitud del vector resultante ni la magnitud del vector diferencia se pueden expresar como una suma o diferencia simple de magnitudes A y B, porque la longitud de una diagonal no se puede expresar como una simple suma de longitudes laterales, tenemos que usar leyes de trigonometría para triángulos.
Observa los siguientes vídeos y escenas interactivas diseñadas con el editor DescartesJS.
Haz clic sobre la imagen para reproducir el video o en el botón "Otro video", para ver otro método. En los vídeos se muestran tres métodos para sumar vectores en el plano que, para este caso, corresponden a fuerzas aplicadas en un elemento mecánico. El primer método es el del paralelogramo, y los otros dos están asociados al método del polígono, que consiste en unir cabezas con colas para, posteriormente, conformar el polígono con el vector o fuerza resultante.
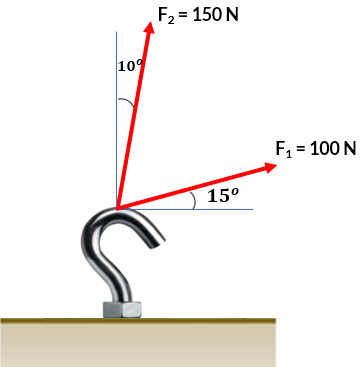
El gancho de la figura está sometido a dos fuerzas, $\bold{\vec{F}_1}$ y $\bold{\vec{F}_2}$. Determina la magnitud y la dirección de la fuerza resultante.
Solución
El ángulo entre las dos fuerzas se obtiene así: $90\degree - 15\degree - 10\degree = 65\degree$. Ahora, obtenemos el otro ángulo del paralelogramos, así: $(360\degree - 2\times 65\degree)/2 = 115\degree$
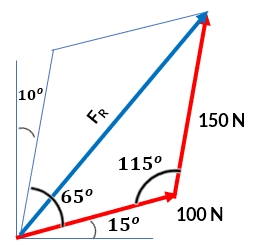
La magnitud de la fuerza resultante, la hallamos por la ley del coseno:
$$\begin{aligned} F_R &= \sqrt{(100\;N)^2 + (150\;N)^2 -2(100\;N)(150\;N)cos\;115\degree}\\ &= 212.6\;N \end{aligned} $$Para hallar la dirección ($\phi$) de $\bold{\vec{F}_R}$, hallamos el ángulo $\theta$ y le sumamos $15\degree$, tal como se ilustra en la siguiente figura:
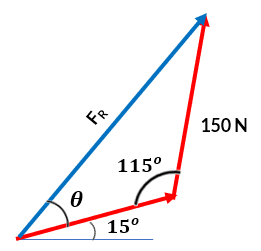
$\theta$ lo hallamos aplicando la ley de los senos:
$$\frac{sen\;\theta}{150\;N} = \frac{sen\;115\degree}{212.6\;N}$$ $$\begin{aligned} sen\;\theta &= \frac{150\;N}{212.6\;N}sen\;115\degree\\ \theta &= 39.8\degree \end{aligned}$$Finalmente:
$$\phi = 39.8\degree + 15\degree = 54.8\degree$$Las proyecciones de una fuerza sobre los ejes $x$ y $y$ se conocen como las componentes rectangulares de la fuerza, las cuales se pueden representar mediante notación escalar o con notación vectorial.
Por ejemplo, si se aplica una fuerza de $100 \;N$ en un ángulo de $30\degree$ con la horizontal, entonces sus componentes rectangulares son $86,6 \;N$ y $50 \;N$.
Un vector $\bold{\vec{F}}$ en un plano se describe mediante un par de coordenadas. La coordenada $x$ del vector $\bold{\vec{F}}$ se denomina componente $x$ y la coordenada $y$ del vector $\bold{\vec{F}}$ se denomina componente $y$. La componente $x$ del vector es denotada por $\bold{\vec{F}}_x$. La componente $y$ del vector es denotada por $\bold{\vec{F}}_y$. En el sistema cartesiano, las componentes $x$ e $y$ del vector son las proyecciones ortogonales de este vector en los ejes $x$ e $y$, respectivamente. De esta manera, siguiendo la regla de paralelogramo para la suma de vectores, cada vector en un plano cartesiano puede expresarse como la suma de vectores de sus componentes de vector:
$$\bold{\vec{F}} = \bold{\vec{F}}_x + \bold{\vec{F}}_y\tag{2.10}$$Es costumbre denotar la dirección positiva en el eje $x$ por el vector unitario $\hat{\bold{i}}$ y la dirección positiva en el eje $y$ por el vector unitario $\hat{\bold{j}}$. Los vectores unitarios de los ejes, $\hat{\bold{i}}$ y $\hat{\bold{j}}$, definen dos direcciones ortogonales en el plano. Como se muestra en el interactivo 2.3, las componentes rectangulares $x$ e $y$ de un vector ahora se pueden escribir en términos de los vectores unitarios de los ejes:
$$ \bold{\vec{F}}_x = F_x\hat{\bold{i}}\\ \bold{\vec{F}}_y = F_y\hat{\bold{j}}\tag{2.11}$$En la siguiente escena interactiva, desplaza el vector $\bold{\vec{F}}$ para que observes las componentes rectangulares del vector en cualquier dirección.
Los vectores $\bold{\vec{F}}_x$ y $\bold{\vec{F}}_y$ definidos por la ecuación 2.11 son las componentes rectangulares del vector $\bold{\vec{F}}$. Los números $F_x$ y $F_y$ que definen las componentes del vector en la Ecuación 2.11 son las componentes escalares del vector $\bold{\vec{F}}$. Combinando la Ecuación 2.10 con la Ecuación 2.11, obtenemos:
Si tenemos varias fuerzas concurrentes, como las mostradas en las siguiente figura, podemos expresar cada fuerza de acuerdo a la ecuación 2.12, así:
$$\bold{\vec{F}_1} = F_{1x}\^{\bold{i}} + F_{1y}\^{\bold{j}}\\ \bold{\vec{F}_2} = -F_{2x}\^{\bold{i}} + F_{2y}\^{\bold{j}}\\ \bold{\vec{F}_3} = -F_{3x}\^{\bold{i}} - F_{3y}\^{\bold{j}}$$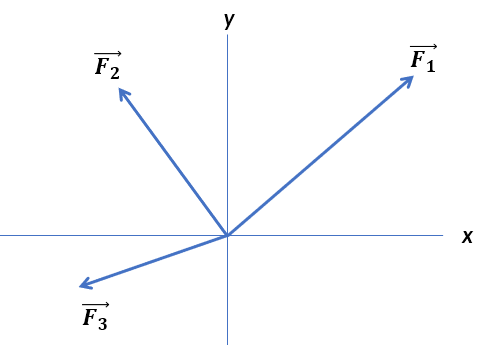
La fuerza resultante en notación vectorial, sería:
$$\begin{aligned} \bold{\vec{F}_R} &= \bold{\vec{F}_1} + \bold{\vec{F}_2} + \bold{\vec{F}_3}\\ &= F_{1x}\^{\bold{i}} + F_{1y}\^{\bold{j}} -F_{2x}\^{\bold{i}} + F_{2y}\^{\bold{j}} -F_{3x}\^{\bold{i}} - F_{3y}\^{\bold{j}}\\ &= (F_{1x} -F_{2x}-F_{3x})\hat{\bold{i}} + (F_{1y} +F_{2y}-F_{3y})\hat{\bold{j}}\\ &= F_{Rx}\hat{\bold{i}} + F_{Ry}\hat{\bold{j}} \end{aligned}$$En notación escalar, podemos escribir para cada componente:
Expresiones que nos llevan a concluir:
$$\bold{F_{Rx} = \Sigma F_x}\\ \bold{F_{Ry} = \Sigma F_y}\tag{2.13}$$En la Figura 2.8 se ilustra la fuerza resultante con sus componentes rectangulares y el ángulo $\theta$ que forma con el eje $x$, por lo tanto:
$$F_R = \sqrt{(F_{Rx})^2+ (F_{Ry})^2}$$ $$\theta = tan^{-1}\bigg|\frac{F_y}{F_x} \bigg|$$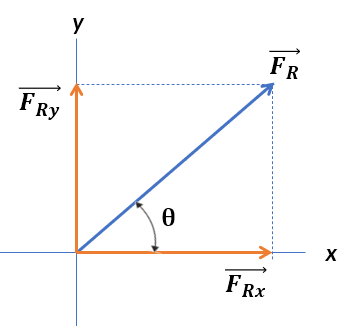
Veamos un ejemplo de aplicación de las expresiones anteriores:
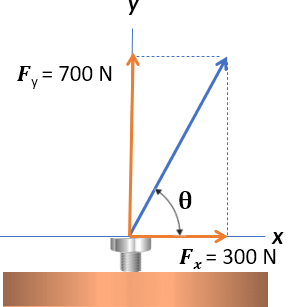
Una fuerza
$\bold{\vec{F}} = (300 \;N)\hat{\bold{i}} + (700 \;N)\hat{\bold{j}}$
se aplica a un perno, tal como se indica en la figura. Calcula la magnitud de la fuerza y el ángulo que forma con la horizontal.
Solución
Usando las expresiones anteriores, calculamos:
$$\theta = tan^{-1}\bigg|\frac{F_y}{F_x}\bigg| = tan^{-1}\bigg|\frac{700\;N}{300\;N}\bigg| = 66.8\degree$$Las magnitud de la fuerza, la podemos calacular así:
$$F = \sqrt{F_x^2 + F_y^2} = \sqrt{(300\;N)^2 + (700\;N)^2} = 761.6\;N$$O, también, usando la expresión:
$$F = \frac{F_y}{sen\;\theta} = \frac{700\;N}{sen\;66.8\degree } = 761.6\;N$$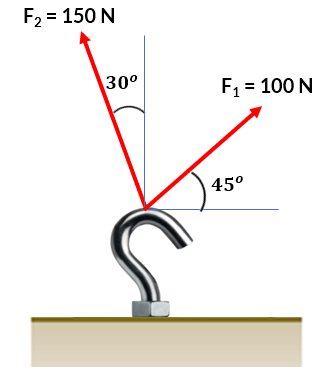
El gancho de la figura está sometido a dos fuerzas, $\bold{\vec{F}_1}$ y $\bold{\vec{F}_2}$. Determina la magnitud y la dirección de la fuerza resultante.
Usa la ecuación 2.13.
Solución
Hallamos, inicialmente, las componentes rectangulares de la fuerza resultante, asumiendo $\bold{\vec{F}_{Rx}}$ positivo a la derecha ($\rarr +$), y $\bold{\vec{F}_{Ry}}$ hacia arriba ($\uarr +$).
$$\begin{aligned} F_{Rx} &= \sum F_x\\ &= 100\;cos\;45\degree\; N - 150\; cos\;60\degree\; N\\ &= -4.29\;N \end{aligned}$$ $$\begin{aligned} F_{Ry} &= \sum F_y\\ &= 100\;sen\;45\degree \; N + 150\; sen \;60\degree\; N\\ &= 200.61\;N \end{aligned}$$Calculamos la magnitud de la fuerza resultante:
$$\begin{aligned} F_R &= \sqrt{(F_{Rx})^2+ (F_{Ry})^2}\\ &= \sqrt{(-4.3\;N)^2+ (200.6\;N)^2}\\ &= 200.66\;N \end{aligned}$$Finalmente, la dirección de la fuerza resultante ($\theta$):
$$\begin{aligned} \theta &= tan^{-1}\Big|\frac{F_y}{F_x} \Big|\\ &= tan^{-1}\frac{200.61\;N}{4.29\;N}\\ &\approx 89\degree \end{aligned}$$Dado que $F_{Rx}$ es negativa y $F_{Ry}$ positiva, $F_R$ se encuentra en el segundo cuadrante del plano cartesiano, por lo que $\theta = 89\degree$ es con respecto al eje x negativo, tal como lo ilustra la siguiente gráfica:
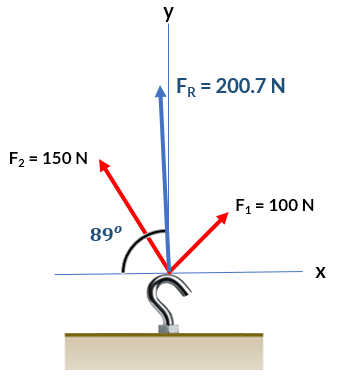
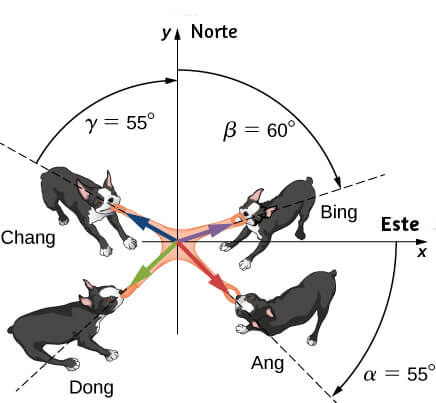
Cuatro perros llamados Ang, Bing, Chang y Dong juegan un juego de tira y afloja con un juguete. Ang tira del juguete en dirección $\alpha = 55\degree$ al sureste, Bing tira en dirección $\beta = 60\degree$ al noreste, y Chang tira en dirección $\gamma = 55\degree$ al noroeste.
Ang tira fuertemente con una fuerza de $160.0\;N$. Bing tira incluso más fuerte que Ang con una fuerza de $B = 200.0 \;N$, y Chang tira con una fuerza de $C = 140.0 \;N$. Cuando Dong tira del juguete de tal manera que su fuerza equilibra la resultante de las otras tres fuerzas, el juguete no se mueve en ninguna dirección. ¿Con qué fuerza y en qué dirección debe Dong tirar del juguete para que esto suceda?
Solución
Calculamos las componentes rectangulares de la fuerza resultante cuando están tirando Ang ($\bold{\vec{F}_A}$), Bing ($\bold{\vec{F}_B}$) y Chang ($\bold{\vec{F}_C}$), asumiendo $\bold{\vec{F}_{Rx}}$ positivo a la derecha ($\rarr +$), y $\bold{\vec{F}_{Ry}}$ hacia arriba ($\uarr +$):
$$\begin{cases} F_{Ax} = \;\;(160\;N)cos(55\degree) = +91.8\;N\\ F_{Ay} = -(160\;N)sen(55\degree) = -131.1\;N \end{cases}$$ $$\begin{cases} F_{Bx} = \;\;\; (200\;N)cos(30\degree) = 173.2\;N\\ F_{By} = \;\;\; (200\;N)sen(30\degree) = 100.0\;N \end{cases}$$ $$\begin{cases} F_{Cx} = -(140\;N)cos(145\degree) = -114.7\;N\\ F_{Cy} = \;\;(140\;N)sen(145\degree) = 80.3\;N \end{cases}$$Ahora calculamos los componentes escalares del vector resultante: $\bold{\vec{F}_R}= \bold{\vec{F}_A} + \bold{\vec{F}_B} + \bold{\vec{F}_C}$.
$$F_{Rx} = F_{Ax} + F_{Bx} + F_{Cx} = 91.8 \;N + 173.2\; N − 114.7\; N = 150.3\;N\\ F_{Ry} = F_{Ay} + F_{By} + F_{Cy} = −131.1\; N + 100.0 \;N + 80.3\; N = 49.2\;N$$El vector antiparalelo a $\bold{\vec{F}_R}$ es la fuerza con la cual debe tirar Dong:
$$\bold{\vec{F}_D} = -\bold{\vec{F}_R} = -F_{Rx}\hat{\bold{i}} - F_{Ry}\hat{\bold{j}} = (-150.3\hat{\bold{i}} - 49.2\hat{\bold{j}}) \;N$$La magnitud de la fuerza de tracción de Dong es
$$\begin{split} D &= \sqrt{D_x^2 + D_y^2}\\ &= \sqrt{(-150.3)^2 + (-49.2)^2}N\\ &= 158.1 N \end{split}$$La dirección de la fuerza de tracción de Dong es
$$\theta = tan^{-1}\Big|\frac{F_{Dy}}{F_{Dx}}\Big| = tan^{-1}\bigg|\frac{-49.2N}{-150.3N}\bigg| = 18.1\degree$$Encuentra la magnitud del vector $\bold{\vec{F}_C}$ que satisface la ecuación
$2\bold{\vec{F}_A} - 6\bold{\vec{F}_B} + 3\bold{\vec{F}_C} = 2\hat{\bold{j}}$,
donde $\bold{\vec{F}_A} = \hat{\bold{i}} - 2\hat{\bold{k}}$ y $\bold{\vec{F}_B} = -\hat{\bold{j}} + \hat{\bold{k}}/2$.
Solución
$$\begin{split} 2\bold{\vec{F}_A} - 6\bold{\vec{F}_B} + 3\bold{\vec{F}_C} &= 2\hat{\bold{j}}\\ 3\bold{\vec{F}_C} &= 2\hat{\bold{j}} - 2\bold{\vec{A}} + 6\bold{\vec{B}}\\ \bold{\vec{F}_C} &= (2/3)\hat{\bold{j}} - (2/3)\bold{\vec{A}} + 2\bold{\vec{B}}\\ \bold{\vec{F}_C} &= (2/3)\hat{\bold{j}} -(2/3)(\hat{\bold{i}}- 2\^{\bold{k}}) +2(-\hat{\bold{i}} + \hat{\bold{k}}/2)\\ \bold{\vec{F}_C} &= (2/3)\hat{\bold{j}} - (2/3)\hat{\bold{i}} + (4/3)\hat{\bold{k}} -2\hat{\bold{j}} +\hat{\bold{k}}\\ \bold{\vec{F}_C} &= -(2/3)\hat{\bold{i}} +(2/3-2)\hat{\bold{j}} + (4/3+1)\hat{\bold{k}}\\ \bold{\vec{F}_C} &= -(2/3)\hat{\bold{i}} -(4/3)\hat{\bold{j}} +(7/3)\hat{\bold{k}} \end{split}$$Los componentes son $F_{Cx} = -2/3, F_{Cy} = -4/3$, y $F_{Cz} = 7/3$; por lo tanto, su magnitud es:
$$F_C= \sqrt{F_{Cx}^2 + F_{Cy}^2 + F_{Cz}^2} = \sqrt{(-2/3)^2 + (-4/3)^2 + (7/3)^2} = \sqrt{\frac{23}{3}}$$
Interactúa, inicialmente, con el siguiente objeto interactivo. Observa las componentes rectangulares de la fuerza $\bold{\vec{F}}$ y los vectores unitarios, puedes modificar los valores de a, b y c. Mueve el objeto con clic izquierdo sostenido.
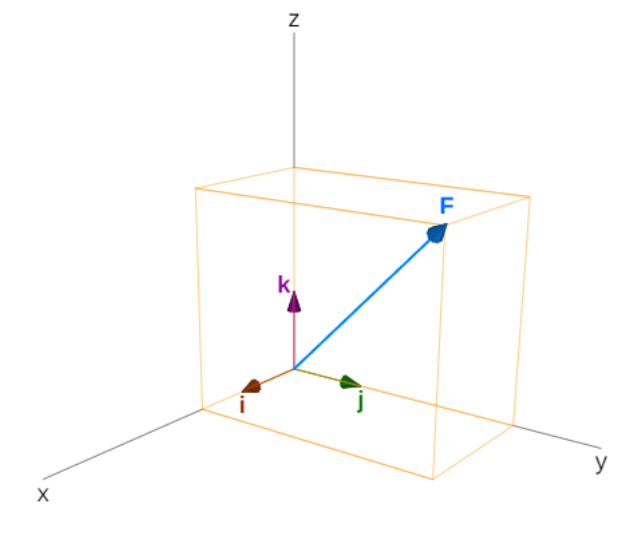
Para especificar la posición de un punto en el espacio, necesitamos tres coorde- nadas $(x, y, z)$, donde las coordenadas $x$ e $y$ especi- fican ubicaciones en un plano, y la coordenada $z$ da una posición vertical por encima o debajo del plano. El espacio tridimensional tiene tres direcciones ortogonales, por lo que no necesitamos dos sino tres vectores unitarios para definir un sistema de coordenadas tridimensional. En el sistema de coordenadas cartesianas, los primeros dos vectores unitarios son el vector unitario del eje $x$ $\^{\bold{i}}$ y el del eje $y$ $\^{\bold{j}}$. El tercer vector unitario $\^{\bold{k}}$ es la dirección del eje $z$. El orden en que los ejes están etiquetados, que es el orden en que aparecen los tres vectores unitarios, es importante pues define la orientación del sistema de coordenadas.
El orden $x-y-z$, que es equivalente al orden $\^{\bold{i}} - \^{\bold{j}} - \^{\bold{k}}$, define el sistema de coordenadas según la regla de la mano derecha (orientación positiva), esta orientación se conoce como sistema dextrógiro.
En el espacio tridimensional, el vector fuerza $\bold{\vec{F}}$ tiene tres componentes de vector: el componente $\bold{\vec{F}}_x = F_x\^{\bold{i}}$, que es la parte del vector $\bold{\vec{F}}$ a lo largo del eje $x$; el componente $y$ $\bold{\vec{F}}_y = F_y\^{\bold{j}}$, que es la parte de $\bold{\vec{F}}$ a lo largo del eje $y$; y el componente $z$ $\bold{\vec{F}}_z = F_z\^{\bold{k}}$, que es la parte del vector a lo largo del eje $z$.
Un vector en el espacio tridimensional es la suma del vector de sus tres componentes del vector.
$$\bold{\vec{F}} = F_x\^{\bold{i}} + F_y\^{\bold{j}} + F_z\^{\bold{k}}\tag{2.14}$$y su magnitud, similar al espacio bidimensional, es:
$$F = \sqrt{F_x^2 + F_y^2 + F_z^2}\tag{2.15}$$Esta expresión para la magnitud del vector proviene de aplicar el teorema de Pitágoras dos veces. Como se ve en el objeto interactivo 2.4, la diagonal en el plano $xy$ tiene una longitud $F_h = \sqrt{F_x^2 + F_y^2}$ y su cuadrado se suma al cuadrado $F_z^2$ para dar $F^2$
Ten en cuenta que cuando el componente $z$ es cero, el vector se encuentra completamente en el plano $xy$ y su descripción se reduce a dos dimensiones.
La dirección de una fuerza $\bold{\vec{F}}$, en un espacio 3D, se define mediante los ángulos directores coordenados $\alpha$ (alfa), $\beta$ (beta) y $\gamma$ (gamma), medidos entre la cola de $\bold{\vec{F}}$ y los ejes $x, y, z$ positivos, pues se localizan en la cola de $\bold{\vec{F}}$, ( ver el interactivo 2.5).
En el siguiente objeto interactivo, haz clic en las casillas de verificación para observar los ángulos directores y la componente rectangular correspondiente. Estos ángulos son los que se forman entre la fuerza $\bold{\vec{F}}$ y sus componentes rectangulares $\bold{\vec{F}_x}, \bold{\vec{F}_y}, \bold{\vec{F}_z}$.
De acuerdo a los triángulos rectángulos, mostrados en el interactivo, obtenemos las siguientes expresiones:
$$cos\;\alpha = \frac{F_x}{F}\;\;\;\;\;cos\;\beta = \frac{F_y}{F}\;\;\;\;\;cos\;\gamma = \frac{F_z}{F}\tag{2.16}$$En muchas situaciones físicas, a menudo necesitamos saber la dirección de un vector. Por ejemplo, podemos querer saber la dirección de un vector de campo magnético en algún punto o la dirección del movimiento de un objeto. Ya dijimos que la dirección viene dada por un vector unitario, que es una entidad adimensional, es decir, no tiene unidades físicas asociadas. Cuando el vector en cuestión se encuentra a lo largo de uno de los ejes en un sistema cartesiano de coordenadas, la respuesta es simple, porque entonces su unidad de vector de dirección es paralela o antiparalela a la dirección del vector unitario de un eje. Por ejemplo, la dirección del vector $\bold{\vec{F}}= -5 \hat{\bold{i}}\;N$ es el vector unitario $\bold{\vec{u}_F} = -\hat{\bold{i}}$. La regla general para encontrar el vector unitario de dirección $\hat{\bold{u}_F}$ para cualquier vector $\bold{\vec{F}} $ es dividirlo por su magnitud $F$:
$$\bold{\hat{u}_F} = \frac{\bold{\vec{F}}}{F}\tag{2.17}$$De la ecuación 2.14, sabemos que $\bold{\vec{F}} = F_x\hat{\bold{i}} + F_y\hat{\bold{j}} + F_z\hat{\bold{k}}$, por lo tanto:
$$\bold{\hat{u}_F} = \frac{\bold{\vec{F}}}{F} = \frac{F_x}{F}\hat{\bold{i}} + \frac{F_y}{F}\hat{\bold{j}} + \frac{F_z}{F}\hat{\bold{k}} \tag{2.18}$$Reemplazando la ecuación 2.16 en la 2.18:
$$\bold{\hat{u}_F} = cos\;\alpha\hat{\bold{i}} + cos\;\beta\hat{\bold{j}} + cos\;\gamma\hat{\bold{k}} \tag{2.19}$$Si conocemos la magnitud y los ángulos directores coordenados, $\bold{\vec{F}}$ puede expresarse así:
$$\bold{\vec{F}} = F\bold{\hat{u}_F} = Fcos\;\alpha\hat{\bold{i}} + Fcos\;\beta\hat{\bold{j}} + Fcos\;\gamma\hat{\bold{k}} $$Despejando las componentes rectangulares de la fuerza en la ecuación 2.16 y reemplazando en la expresión anterior, obtenemos:
$$\bold{\vec{F}} =F_x\hat{\bold{i}} + F_y\hat{\bold{j}} + F_z\hat{\bold{k}}\tag{2.20}$$Una fuerza de $800\;lb$ forma ángulos de $120\degree, 60\degree$ y $30\degree$ con los ejes $x, y$ y $z$, respectivamente. Encuentra las componentes $F_x, F_y$ y $F_z$ de la fuerza y exprésala en notación vectorial.
Solución
De la ecuación 2.16, podemos hallar estas componentes:
$$F_x = Fcos\;\alpha = 800\;lb\;cos\;120\degree = -500\;lb\\ F_y = Fcos\;\beta = 800\;lb\;cos\;60\degree = 500\;lb\\ F_z = Fcos\;\gamma = 800\;lb\;cos\;30\degree = 866\;lb$$Reemplazando en la ecuación 2.20, obtenemos la notación vectorial:
$$\bold{\vec{F}} =-(500\;lb)\hat{\bold{i}} + (500\;lb)\hat{\bold{j}} + (866\;lb)\hat{\bold{k}}$$La fuerza resultante de un sistema de fuerzas concurrentes en el espacio 3D es similar a cómo se calcula en un espacio bidimensional (ver apartado 2.4.3), agregando la tercera componente rectangular.
En el siguiente ejemplo calculamos la fuerza resultante. Lo ilustramos con una escena interactiva, para una mayor comprensión.
Halla la magnitud y los ángulos directores coordenados de la fuerza resultante en la siguiente figura, donde $\bold{\vec{F}_1} = (60\;lb)\hat{\bold{j}} + (80\;lb)\hat{\bold{k}}$ y $\bold{\vec{F}_2} = (50\;lb)\hat{\bold{i}} - (100\;lb)\hat{\bold{j}} + (100\;lb)\hat{\bold{k}}$.
Haz clic en el botón "Muestra $F_R$, para ver el vector de la fuerza resultante.
Solución
Sabemos que $\bold{\vec{F}_R} = \bold{\vec{F}_1} + \bold{\vec{F}_2}$, entonces:
$$\begin{aligned} \bold{\vec{F}_R} &= (60\;lb)\hat{\bold{j}} + (80\;lb)\hat{\bold{k}} + (50\;lb)\hat{\bold{i}} - (100\;lb)\hat{\bold{j}} + (100\;lb)\hat{\bold{k}}\\ &= (50\;lb)\hat{\bold{i}} - (40\;lb)\hat{\bold{j}} + (180\;lb)\hat{\bold{k}} \end{aligned}$$Calculemos la magnitud de $\bold{\vec{F}_R}$:
$$F_R = \sqrt{(50\;lb)^2 + (-40\;lb)^2 + (180\;lb)^2} = 191\;lb$$Ahora, usamos las ecuaciones 2.18 y 2.19, para hallar los ángulos directores:
$$\begin{aligned} \frac{\bold{\vec{F}}}{F} &= \frac{F_x}{F}\hat{\bold{i}} + \frac{F_y}{F}\hat{\bold{j}} + \frac{F_z}{F}\hat{\bold{k}}\\ &= \frac{50\;lb}{191\;lb}\hat{\bold{i}} - \frac{40\;lb}{191\;lb}\hat{\bold{j}} + \frac{180\;lb}{191\;lb}\hat{\bold{k}}\\ &= 0.2618\hat{\bold{i}} - 0.2094\hat{\bold{j}} + 0.9424\hat{\bold{k}} \end{aligned}$$De la ecuación 2.19, sabemos que los coeficientes de la expresión anterior, son los cosenos directores, entonces:
$$cos\;\alpha = 0.2618\;\;\; \rarr\;\;\; \alpha = 74.8\degree\\ cos\;\beta = -0.2094\;\;\; \rarr\;\;\; \beta = 102.1\degree\\ cos\;\gamma = 0.9424\;\;\; \rarr\;\;\; \gamma = 19.5\degree$$Verifica, visualmente, estos resultados en el interactivo 2.6; por ejemplo, rota el objeto interactivo hasta que sólo se vea el plano yz, luego haz clic en el botón "Muestra $F_R$ y observa que el ángulo $\beta$ es mayor de $90\degree$.
Por lo general, la cola de una fuerza no se encuentra en el origen de coordenadas, por lo que hay que hallar las componentes escalares del vector posición, que llamaremos $\bold{\vec{u}_F}$. Observa, en el siguiente objeto interactivo, una fuerza cuya cola está en el punto $A$, el cálculo del vector posición y del vector fuerza, lo explicamos a continuación.
En general, se define el vector posición como el vector que está dirigido entre dos puntos $A$ y $B$ (Figura 2.10). Por la regla del triángulo o, de otra forma, por la reglas del paralelogramo:
$$\bold{\vec{r}_A} + \bold{\vec{r}} = \bold{\vec{r}_B}$$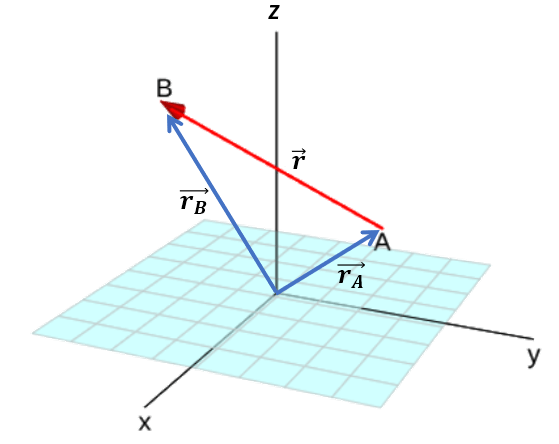
Despejamos $\bold{\vec{r}}$ y lo llamamos $\bold{\vec{AB}}$:
$$\bold{\vec{r}} = \bold{\vec{AB}} = \bold{\vec{r}_B} - \bold{\vec{r}_A} = (x_B\hat{\bold{i}} + x_B\hat{\bold{j}} + x_B\hat{\bold{k}}) - (x_A\hat{\bold{i}} + x_A\hat{\bold{j}} + x_A\hat{\bold{k}}) $$ $$\bold{\vec{AB}} =(x_B - x_A)\hat{\bold{i}} + (y_B - y_A)\hat{\bold{j}} + (z_B - z_A)\hat{\bold{k}}\tag{2.21}$$Que es el vector posición en la dirección $AB$
El vector unitario en la dirección de la fuerza, sería:
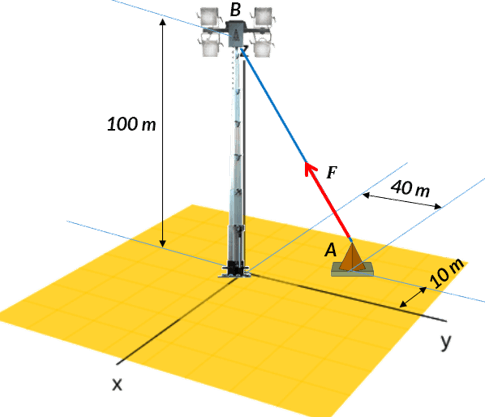
$$\bold{\vec{u}_F} = \frac{\bold{\vec{AB}}}{AB}$$El alambre de una torre está anclado en $A$ como se muestra en la figura 2.8. La tensión en el alambre es de $1000\; N$. Halla las componentes $F_x, F_y$ y $F_z$ de la fuerza que actúa en $A$ y el vector unitario en la dirección de la fuerza.
Solución
Hallamos, inicialmente, el vector posición con la ecuación 2.21, con $A = (-10, 40, 0)$ y $B = (0, 0, 100)$
Ahora, calculamos $AB$ y el vector unitario en la dirección de $\bold{\vec{u}_F}$:
$$\begin{aligned} AB &= \sqrt{10^2 + (-40)^2 + 100^2}\\ &= 108.2\;m \end{aligned}$$ $$\begin{aligned} \bold{\vec{u}_F} &= \frac{\bold{\vec{AB}}}{AB}\\ &=\frac{10\hat{\bold{i}} - 40\hat{\bold{j}} + 100\hat{\bold{k}}}{108.2}\\ &= 0.0924\hat{\bold{i}} - 0.3697\hat{\bold{j}} + 0.9242\hat{\bold{k}} \end{aligned}$$La fuerza tiene una magnitud de $1000\;N$, que multiplicada por el vector unitario se obtiene la fuerza en notación vectorial:
$$\begin{aligned} \bold{\vec{F}} &= 1000\bold{\vec{u}_F}\\ &= 92.42\hat{\bold{i}} - 369.7\hat{\bold{j}} + 924.2\hat{\bold{k}} \end{aligned}$$Por lo tanto, las componente rectangulares de $\bold{\vec{F}}$, son:
$$F_x = 92.42\;N\\ F_y = -369.7\;N\\ F_z = 924.2\;N$$Verifica estos resultados en el interactivo 2.7. Usa el Zoom y no olvides ingresar los $1000\;N$ de la fuerza... ¡No pongas la N!.
Punto Cero de Medellín (Colombia). Foto de Yimi Correa, en Wikimedia Commons (CC BY-SA 3.0).
Escultura en bronce de Fernando Botero en Plaza Botero, Medellín (Colombia). Foto de Julián Zapata, en Pixabay.
Una partícula se encuentra en equilibrio si la suma vectorial de las fuerzas es igual a cero. Aquí aplica la primera Ley de Newton, pues la partícula no experimenta una fuerza neta, su aceleración cero hace que permanezca en reposo o en movimiento rectilíneo uniforme. Las fuerzas que actúan sobre la partícula pueden incluir fuerzas gravitacionales, fuerzas aplicadas externamente y fuerzas de reacción.
A continuación, presentamos cuatro objetos interactivos tomados en la Unidad Didáctica Interactiva "Estática de una partícula", del Proyecto Un_100Este proyecto comprende 101 unidades didácticas del nivel universitario en la áreas de Matemáticas y de Física. Es un proyecto que ha contado con el patrocinio de varias instituciones mejicanas y la participación en su desarrollo de otras de Chile, Colombia, España y México., publicado en la Red Educativa Digital Descartes y en el portal Prometeo de la UNAM de México.
Con el primer objeto interactivo repasamos las componentes rectangulares de una fuerza, incluyendo la determinación gráfica de la resultante de fuerzas, usando el método de "cabeza y cola"; en el segundo se presenta el vector fuerza como múltiplos de los vectores unitarios y se dan las condiciones para que una partícula esté en equilibrio; el tercero presenta ejemplos de aplicación y el último propone varios ejercicios interactivos.
La imagen de abajo, es una representación de una partícula sometida a seis fuerzas, las cuales se anulan y, por tanto, la partícula está en equilibrio.
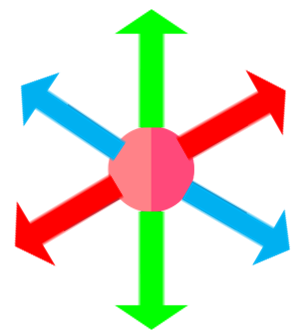
Haz clic en el botón naranja, en la primera escena interactiva
Un vector se puede multiplicar por otro vector pero no se puede dividir por otro vector. Hay dos tipos de productos de vectores usados ampliamente en física e ingeniería. Un tipo de multiplicación es una multiplicación escalar de dos vectores. Tomar un producto escalar de dos vectores da como resultado un número (un escalar), como su nombre lo indica. Los productos escalares se utilizan para definir las relaciones de trabajo y energía. Por ejemplo, el trabajo que una fuerza (un vector) realiza en un objeto mientras causa su desplazamiento (un vector) se define como un producto escalar del vector fuerza con el vector desplazamiento. Un tipo de multiplicación bastante diferente es una multiplicación vectorial de vectores. Tomar un producto vectorial de dos vectores devuelve como resultado un vector, como su nombre lo sugiere. Los productos de vectores se utilizan para definir otras cantidades de vectores derivados. Por ejemplo, al describir las rotaciones, una cantidad vectorial llamada par se define como un producto vectorial de una fuerza aplicada (un vector) y su distancia desde el pivote a la fuerza (un vector). Es importante distinguir entre estos dos tipos de multiplicaciones de vectores porque el producto escalar es una cantidad escalar y un producto vectorial es una cantidad vectorial.
El producto escalar $\bold{\vec{A}}\cdot \bold{\vec{B}}$ de dos vectores es un número definido por la ecuación
$$\bold{\vec{A}}\cdot \bold{\vec{B}} = ABcos\phi\tag{3.1}$$donde $\phi$ es el ángulo entre los vectores (que se muestra en la Figura 3.1). El producto escalar también se denomina producto punto debido a la notación dada.
En la definición del producto escalar, la dirección del ángulo $\phi$ no importa, y se puede medir desde cualquiera de los dos vectores a la otra porque $cos\phi = cos (-\phi) = cos (2\pi-\phi)$. El producto escalar es un número negativo cuando $90\degree \lt \phi \lt 180\degree$ y es un número positivo cuando $0\degree \lt \phi \lt 90\degree$. Además, el producto escalar de dos vectores paralelos es $\bold{\vec{A}}\cdot \bold{\vec{B}} = ABcos0\degree = AB$, y el producto escalar de dos vectores antiparalelos es $\bold{\vec{A}}\cdot \bold{\vec{B}} = ABcos180\degree = -AB$. El producto escalar de dos vectores ortogonales desaparece: $\bold{\vec{A}}\cdot \bold{\vec{B}}= ABcos90\degree = 0$.
El producto escalar de un vector consigo mismo es el cuadrado de su magnitud:
$$\bold{\vec{A}}^2 \equiv \bold{\vec{A}}\cdot \bold{\vec{A}} = AAcos0 = A^2\tag{3.2}$$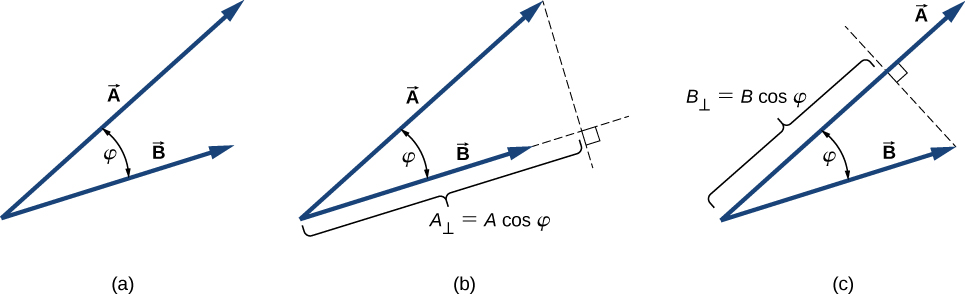
El producto punto. Para los vectores mostrados en la figura, encuentra el producto escalar $\bold{\vec{A}}\cdot \bold{\vec{F}}$
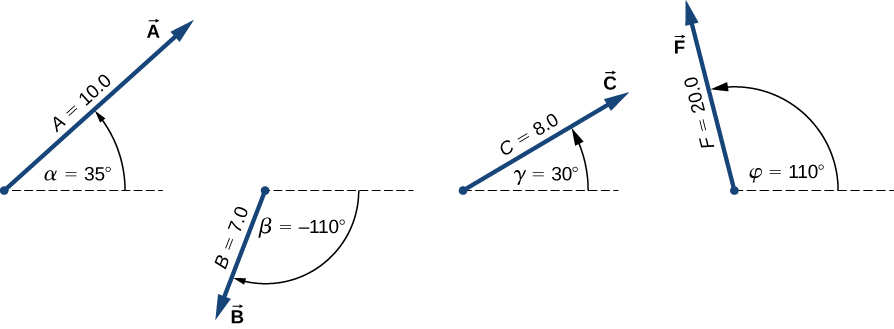
Solución
De la figura, las magnitudes de los vectores $\bold{\vec{A}}$ y $\bold{\vec{F}}$ son $A = 10.0$ y $F = 20.0$. El ángulo $\theta$, entre ellos, es la diferencia: $\theta = \phi - \alpha = 110\degree - 35\degree = 75\degree$. La sustitución de estos valores en la Ecuación 3.1 da el producto escalar. Un cálculo directo nos da
$$\bold{\vec{A}}\cdot \bold{\vec{F}}= AFcos\theta = (10.0)(20.0)cos75\degree = 51.76$$En el sistema de coordenadas cartesianas, los productos escalares del vector unitario de un eje con otros vectores unitarios de otros ejes siempre desaparecen porque son ortogonales:
$$\^{\bold{i}}\cdot \^{\bold{j}} = |\^{\bold{i}}|\cdot|\^{\bold{j}}|cos90\degree = (1)(1)(0) = 0\\ \^{\bold{i}}\cdot \^{\bold{k}} = |\^{\bold{i}}|\cdot|\^{\bold{k}}|cos90\degree = (1)(1)(0) = 0\\ \^{\bold{k}}\cdot \^{\bold{j}} = |\^{\bold{k}}|\cdot|\^{\bold{j}}|cos90\degree = (1)(1)(0) = 0\tag{3.3}$$En estas ecuaciones, usamos el hecho de que las magnitudes de todos los vectores unitarios son uno: $|\^{\bold{i}}| = |\^{\bold{j}}| = |\^{\bold{k}}| = 1$. Para los vectores unitarios de los ejes, la Ecuación 3.2 da las siguientes identidades:
$$\^{\bold{i}}\cdot \^{\bold{i}} = i^2 = \^{\bold{j}}\cdot \^{\bold{j}} = j^2 = \^{\bold{k}}\cdot \^{\bold{k}} = k^2 \tag{3.4}$$La multiplicación escalar de vectores es conmutativa,
$$\bold{\vec{A}}\cdot \bold{\vec{B}} = \bold{\vec{B}}\cdot \bold{\vec{A}}\tag{3.5}$$y obedece a la ley distributiva:
$$\bold{\vec{A}}\cdot (\bold{\vec{B}} + \bold{\vec{C}}) = \bold{\vec{A}}\cdot \bold{\vec{B}} + \bold{\vec{A}}\cdot \bold{\vec{C}} \tag{3.6}$$Cuando los vectores en la Ecuación 3.1 se presentan en sus componentes rectangulares,
$$\bold{\vec{A}} = A_x\^{\bold{i}} + A_y\^{\bold{j}}+ A_z\^{\bold{k}}\\ \bold{\vec{B}} = B_x\^{\bold{i}} + B_y\^{\bold{j}}+ B_z\^{\bold{k}}$$podemos calcular su producto escalar de la siguiente manera:
$$\begin{split} \bold{\vec{A}}\cdot\bold{\vec{B}} &= (A_x\^{\bold{i}} + A_y\^{\bold{j}} + A_z\^{\bold{k}})\cdot(B_x\^{\bold{i}} + B_y\^{\bold{j}} + B_z\^{\bold{k}})\\ &= A_x B_x\bold{i}\cdot\bold{i} + A_x B_y\bold{i}\cdot\bold{j} + A_x B_z\bold{i}\cdot\bold{k}\\ & \;\;\;\;\; + A_y B_x\bold{j}\cdot\bold{i} + A_y B_y\bold{j}\cdot\bold{j} + A_y B_z\bold{j}\cdot\bold{k}\\ & \;\;\;\;\; + A_z B_x\bold{k}\cdot\bold{i} + A_z B_y\bold{k}\cdot\bold{j} + A_z B_z\bold{k}\cdot\bold{k} \end{split}$$Como los productos escalares de dos vectores unitarios de diferentes ejes dan cero, y los productos escalares de los mismos vectores unitarios dan uno (ver las ecuaciones 3.3 y 3.4), solo hay tres términos distintos de cero en la anterior expresión.
Por lo tanto, el producto escalar se simplifica a
$$\bold{\vec{A}}\cdot \bold{\vec{B}} = A_xB_x + A_yB_y + A_zB_z\tag{3.7}$$Podemos usar la Ecuación 3.7 para el producto escalar en términos de los componentes escalares para encontrar el ángulo entre dos vectores. Cuando dividimos la Ecuación 3.1 por $AB$, obtenemos la ecuación para $cos\phi$, en la cual reemplazamos la Ecuación 3.7:
$$cos\phi = \frac{\bold{\vec{A}}\cdot \bold{\vec{B}}}{AB} = \frac{A_xB_x + A_yB_y + A_zB_z}{AB}\tag{3.8}$$El ángulo $\phi$ entre los vectores $\bold{\vec{A}}$ y $\bold{\vec{B}}$ se obtiene calculando el coseno inverso de la expresión en la Ecuación 3.8.
Tres perros están tirando de un palo en diferentes direcciones. El primer perro tira con fuerza $\bold{\vec{F}}_1 = (10.0\^{\bold{i}} - 20.4\^{\bold{j}} + 2.0\^{\bold{k}}N$, el segundo perro tira con fuerza $\bold{\vec{F}}_2 = (- 15.0\^{\bold{i}} - 6.2\^{\bold{i}})N$, y el tercer perro tira con fuerza $\bold{\vec{F}}_3 = (5.0\^{\bold{i}} + 12.5\^{\bold{j}})N$. ¿Cuál es el ángulo entre las fuerzas $\bold{\vec{F}}_1$ y $\bold{\vec{F}}_2$?
Solución
Las componentes del vector de fuerza $\bold{\vec{F}}_1$ son $F_{1x} = 10.0 N, F_{1y} = -20.4N$, y $F_{1z} = 2.0N$, mientras que las del vector de fuerza $\bold{\vec{F}}_2$ son $F_{2x} = - 15.0 N, F_{2y} = 0.0 N$, y $F_{2z} = -6.2N$.
El cálculo del producto escalar de estos vectores y sus magnitudes, y su sustitución en la ecuación 3.8 da el ángulo de interés.
Las magnitudes de las fuerzas $\bold{\vec{F}}_1$ y $\bold{\vec{F}}_1$ son
$$\begin{split} F_1 &= \sqrt{F_{1x}^2 + F_{1y}^2 + F_{1z}^2}\\ &= \sqrt{10.0^2 + 20.4^2 +2.0^2}N = 22.8N \end{split}$$ y $$\begin{split} F_2 &= \sqrt{F_{2x}^2 + F_{2y}^2 + F_{2z}^2}\\ &= \sqrt{15.0^2 + 6.2^2}N = 16.2N \end{split}$$
La sustitución de los componentes escalares en la ecuación 3.7 da como resultado el producto escalar
$$\begin{split} \bold{\vec{F}}_1\cdot \bold{\vec{F}}_2 &= F_{1x}F_{2x} + F_{1y}F_{2y} + F_{1z}F_{2z}\\ &= (10.0 N)(−15.0 N) + (−20.4 N)(0.0 N)\\ & \;\;\;\;+ (2.0 N)(−6.2 N)\\ &= -162.4N^2 \end{split}$$Finalmente, sustituyendo en la ecuación 3.8 obtenemos el ángulo
$$\begin{split} cos\phi &= \frac{\bold{\vec{F}}_1\cdot \bold{\vec{F}}_2}{F_1F_2}\\ &=\frac{(-162.4)N^2}{(22.8 N)(16.2 N)} = -0.439 \end{split}$$Luego
$$\phi = cos^{-1}(-0.439) = 116.0\degree$$El trabajo de una fuerza
Cuando una fuerza $\bold{\vec{F}}$ tira de un objeto y causa su desplazamiento $\bold{\vec{D}}$, decimos que la fuerza realiza un trabajo.
La cantidad de trabajo que hace la fuerza es el producto escalar $\bold{\vec{F}}\cdot\bold{\vec{D}}$. Si el palo del ejemplo anterior se mueve momentáneamente y se desplaza por el vector $\bold{\vec{D}}= (- 7.9\^{\bold{j}} - 4.2\^{\bold{k}})\;cm$, ¿cuánto trabajo realiza el tercer perro en el ejemplo anterior?
Solución
Calculamos el producto escalar del vector de desplazamiento $\bold{\vec{D}}$ con el vector de fuerza $\bold{\vec{F}}_3 = (5.0\^{\bold{i}} + 12.5\^{\bold{j}})\; N$, que es la tracción del tercer perro.
Usemos $W_3$ para denotar el trabajo hecho por la fuerza $\bold{\vec{F}}_3$ en el desplazamiento $\bold{\vec{D}}$.
Calcular el trabajo es una aplicación directa del producto escalar:
$$\begin{split} W_3 &= \bold{\vec{F}}_3\cdot \bold{\vec{D}}\\ &= F_{3x}D_x + F_{3y}D_y + F_{3z}D_z\\ &= (5.0\; N)(0.0 \;cm) + (12.5 \;N)(−7.9 \;cm) + (0.0 \;N)(−4.2 \;cm)\\ &= −98.7 \;N\cdot cm \end{split}$$El producto vectorial de dos vectores $\bold{\vec{A}}$ y $\bold{\vec{B}}$ se denota como $\bold{\vec{A}}\times \bold{\vec{B}}$ y a menudo se denomina producto cruz. El producto vectorial es un vector que tiene su dirección perpendicular a ambos vectores $\bold{\vec{A}}$ y $\bold{\vec{B}}$.
En otras palabras, el vector $\bold{\vec{A}}\times \bold{\vec{B}}$ es perpendicular al plano que contiene los vectores $\bold{\vec{A}}$ y $\bold{\vec{B}}$, como se muestra en la Figura 3.2.
La magnitud del producto vectorial se define como
$$\bold{\vec{A}}\times \bold{\vec{B}} = ABsen\phi\tag{3.9}$$donde el ángulo $\phi$, entre los dos vectores, se mide del vector $\bold{\vec{A}}$ (primer vector en el producto) al vector $\bold{\vec{B}}$ (segundo vector en el producto), como se indica en la Figura 3.2, y está entre $0\degree$ y $180\degree$. De acuerdo con la Ecuación 3.9, el producto vectorial desaparece para pares de vectores que son paralelos $(\phi = 0\degree)$ o antiparalelos $(\phi = 180\degree)$ porque $sen\;0\degree = sen\;180\degree = 0$.
En la línea perpendicular al plano que contiene los vectores $\bold{\vec{A}}$ y $\bold{\vec{B}}$ hay dos direcciones alternativas, arriba o abajo, como se muestra en la Figura 3.2, y la dirección del producto vectorial puede ser cualquiera de ellas. En la orientación estándar a la derecha, donde el ángulo entre vectores se mide en sentido antihorario desde el primer vector, el vector $\bold{\vec{A}}\times \bold{\vec{B}}$ apunta hacia arriba, como se ve en la Figura 3.2 (a). Si invertimos el orden de la multiplicación, de modo que ahora $\bold{\vec{B}}$ es primero en el producto, entonces el vector $\bold{\vec{B}}\times \bold{\vec{A}}$ debe apuntar hacia abajo, como se ve en la Figura 3.2 (b).
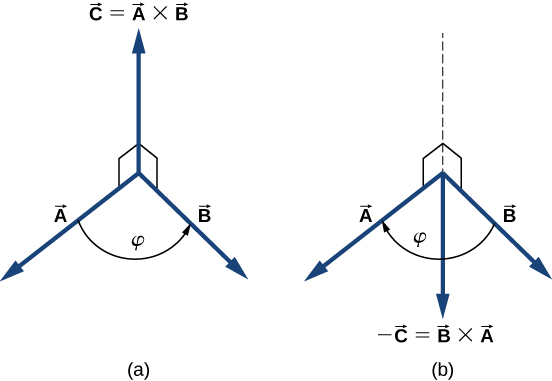
Esto significa que los vectores $\bold{\vec{A}}\times \bold{\vec{B}}$ y $\bold{\vec{B}}\times \bold{\vec{A}}$ son antiparalelos entre sí y que la multiplicación vectorial no es conmutativa, sino anticommutativa. La propiedad anticomutativa significa que el producto vectorial invierte el signo cuando el orden de multiplicación se invierte:
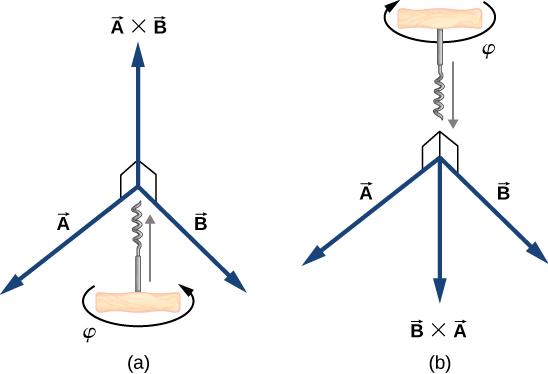
$$\bold{\vec{A}}\times \bold{\vec{B}} =-\bold{\vec{B}}\times \bold{\vec{A}}\tag{3.10}$$La regla de sacacorchos de la mano derecha es un mnemotécnico utilizado para determinar la dirección del producto vectorial. Como se muestra en la Figura 3.3, se coloca un sacacorchos en una dirección perpendicular al plano que contiene los vectores $\bold{\vec{A}}$ y $\bold{\vec{B}}$, y su mango gira en la dirección del primer vector al segundo vector. La dirección del producto cruz viene dada por la progresión del sacacorchos.
En la escena interactiva anterior, hemos recreado la regla de la mano derecha (sin el sacacorchos).
El momento de una fuerza
La ventaja mecánica que proporciona una herramienta familiar llamada llave (figura 3.4), depende de la magnitud $F$ de la fuerza aplicada, de su dirección con respecto al mango de la llave, y de cuán lejos de la tuerca se aplica esta fuerza.
La distancia $R$ desde la tuerca hasta el punto donde se une el vector de fuerza $\bold{\vec{F}}$ está representado por el vector radial $\bold{\vec{R}}$. La cantidad de vector físico que hace que la tuerca gire se llama torque, par o momento (que denotaremos por $\bold{\vec{M}}$), y es el producto vectorial de la distancia del pivote a la fuerza:
$$\bold{\vec{M}}= \bold{\vec{R}}\times \bold{\vec{F}}$$Para aflojar una tuerca oxidada, se aplica una fuerza de $20.00 \;N$ al mango de la llave a un ángulo $\phi = 40\degree$ y a una distancia de $0.25 \;m$ de la tuerca, como se muestra en la figura 3.4 (a). Encuentra la magnitud y dirección del momento aplicado a la tuerca. ¿Cuál sería la magnitud y la dirección del momento si la fuerza se aplicara en el ángulo $\phi = 45\degree$, como se muestra en la figura 3.4 (b)? ¿Para qué valor de ángulo $\phi$ tiene el momento la mayor magnitud?
Solución
Adoptamos el marco de referencia que se muestra en la figura 3.4, donde los vectores $\bold{\vec{R}}$ y $\bold{\vec{F}}$ se encuentran en el plano $xy$ y el origen está en la posición de la tuerca. La dirección radial a lo largo del vector $\bold{\vec{R}}$ (apuntando desde el origen) es la dirección de referencia para medir el ángulo $\phi$ porque $\bold{\vec{R}}$ es el primer vector en el producto vectorial $\bold{\vec{M}} = \bold{\vec{R}}\times \bold{\vec{F}}$. El vector $\bold{\vec{M}}$ debe estar a lo largo del eje $z$ porque este es el eje que es perpendicular al plano $xy$, donde están ambos $\bold{\vec{R}}$ y $\bold{\vec{F}}$.
Para calcular la magnitud $M$, usamos la Ecuación 3.9. Para encontrar la dirección de $\bold{\vec{M}}$, usamos la regla de sacacorchos o de la mano derecha (Figura 3.3).
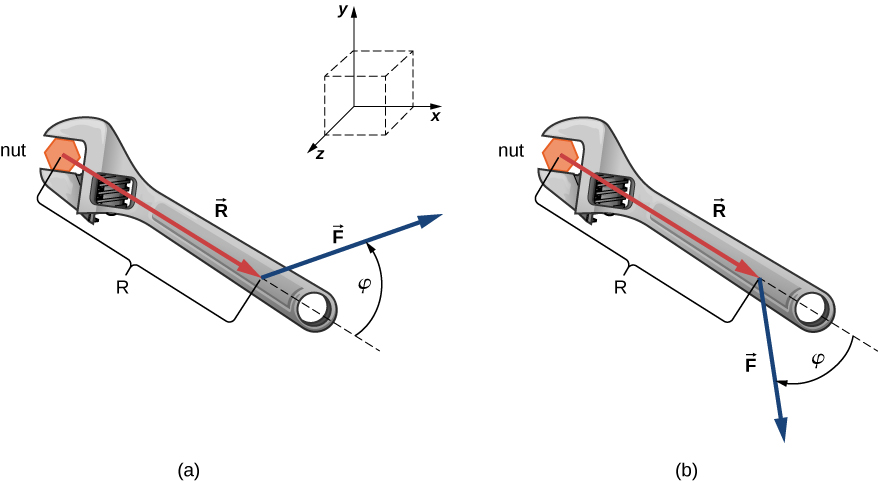
Para la situación en (a), la regla del sacacorchos da la dirección de $\bold{\vec{R}}\times \bold{\vec{F}}$ en la dirección positiva del eje $z$. Físicamente, significa que el torque $\bold{\vec{M}}$ señala fuera de la página, perpendicular al mango de la llave. Identificamos $F = 20.00 \;N$ y $R = 0.25 \;m$, y calculamos la magnitud usando la Ecuación 3.9:
$$\begin{split} M = |\bold{\vec{R}}\times \bold{\vec{F}}| &= RFsen\phi\\ &= (0.25 \;m)(20.00 \;N)sen\;40\degree\\ &= 3.21 \;N\cdot m \end{split}$$Para la situación en (b), la regla del sacacorchos da la dirección de $\bold{\vec{R}}\times \bold{\vec{F}}$ en la dirección negativa del eje $z$. Físicamente, significa que el torque $\bold{\vec{M}}$ apunta a la página, perpendicular al mango de la llave. La magnitud de este par es
$$\begin{split} M = |\bold{\vec{R}}\times \bold{\vec{F}}| &= RFsen\phi\\ &= (0.25 \;m)(20.00 \;N)sen\;45\degree \\ &= 3.53 \;N\cdot m \end{split}$$El momento tiene el mayor valor cuando $sen\phi = 1$, que ocurre cuando $\phi = 90\degree$. Físicamente, significa que la llave inglesa es más efectiva, dándonos la mejor ventaja mecánica, cuando aplicamos la fuerza perpendicular al mango de la llave. Para la situación en este ejemplo, este valor de mejor momento es
$$M_{\text{óptimo}} = RF = (0.25\; m)(20.00\;N) = 5.00\;N\cdot m$$
Similar al producto punto, el producto cruz tiene la siguiente propiedad distributiva
$$\bold{\vec{A}}\times (\bold{\vec{B}} + \bold{\vec{C}}) = \bold{\vec{A}}\times \bold{\vec{B}} + \bold{\vec{A}}\times \bold{\vec{C}}\tag{3.11}$$La propiedad distributiva se aplica con frecuencia cuando los vectores se expresan en sus componentes rectangulares, en términos de los vectores unitarios de los ejes cartesianos.
Cuando aplicamos la definición del producto cruz, ecuación 3.9, a los vectores unitarios $\^{\bold{i}}, \^{\bold{j}}$ y $\^{\bold{k}}$ que definen las direcciones positivas $x, y$, y $z$ en el espacio, encontramos que
$$\^{\bold{i}}\times \^{\bold{i}} = \^{\bold{j}}\times \^{\bold{j}} = \^{\bold{k}}\times \^{\bold{k}} = 0\tag{3.12}$$Todos los demás productos cruz de estos tres vectores unitarios deben ser vectores de magnitudes unitarias, porque $\^{\bold{i}}, \^{\bold{j}}$ y $\^{\bold{k}}$ son ortogonales.
Por ejemplo, para el par $\^{\bold{i}}$ y $\^{\bold{j}}$, la magnitud es $|\^{\bold{i}}\times \^{\bold{j}}| = ijsen90\degree = (1)(1)(1) = 1$. La dirección del producto vectorial $\^{\bold{i}}\times \^{\bold{j}}$ debe ser ortogonal al plano $xy$, lo que significa que debe estar a lo largo del eje $z$. Los únicos vectores unitarios a lo largo del eje $z$ son $-\^{\bold{k}}$ o $+ \^{\bold{k}}$. Por la regla de la mano derecha, la dirección del vector $\^{\bold{i}}\times \^{\bold{j}}$ debe ser paralela al eje $z$ positivo. Por lo tanto, el resultado de la multiplicación $\^{\bold{i}}\times \^{\bold{j}}$ es idéntico a $\^{\bold{k}}$. Podemos repetir un razonamiento similar para los pares restantes de vectores unitarios. Los resultados de estas multiplicaciones son
$$\^{\bold{i}}\times \^{\bold{j}} = \^{\bold{k}}\\ \^{\bold{j}}\times \^{\bold{k}} = \^{\bold{i}}\\ \^{\bold{k}}\times \^{\bold{i}} = \^{\bold{j}}\tag{3.13}$$Observa que en la ecuación 3.13, los tres vectores unitarios $\^{\bold{i}}, \^{\bold{j}}$ y $\^{\bold{k}}$ aparecen en el orden cíclico que se muestra en un diagrama en la figura 3.5(a). El orden cíclico significa que en la fórmula del producto, $\^{\bold{i}}$ sigue a $\^{\bold{k}}$ y está antes de $\^{\bold{j}}$, o $\^{\bold{k}}$ sigue a $\^{\bold{j}}$ y viene antes de $\^{\bold{i}}$ o $\^{\bold{j}}$ sigue a $\^{\bold{i}}$ y viene antes de $\^{\bold{k}}$. El producto cruz de dos vectores unitarios diferentes es siempre un tercer vector unitario. Cuando dos vectores unitarios en el producto cruz aparecen en el orden cíclico, el resultado de dicha multiplicación es el vector unitario restante, como se ilustra en la figura 3.5(b). Cuando los vectores unitarios en el producto cruz aparecen en un orden diferente, el resultado es un vector unitario que es antiparalelo al vector unitario restante, es decir, el resultado es con el signo menos, como se muestra en los ejemplos de la figura 3.5(c) y figura 3.5(d).
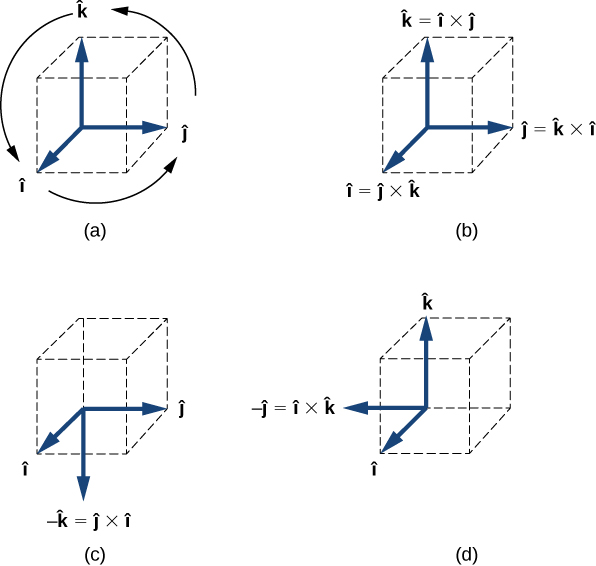
Supongamos que queremos encontrar el producto cruzado $\bold{\vec{A}}\times \bold{\vec{B}}$ para los vectores $\bold{\vec{A}} = A_x\^{\bold{i}} + A_y\^{\bold{j}} + A_z\^{\bold{k}}$ y $\bold{\vec{B}} = B_x\^{\bold{i}} + B_y\^{\bold{j}} + B_z\^{\bold{k}}$. Podemos usar la propiedad distributiva y los resultados en la Ecuación 3.12 y la Ecuación 3.13 para que realizar las siguientes operaciones algebraicas:
Al realizar las operaciones algebraicas que involucren el producto cruz, ten mucho cuidado de mantener el orden correcto de multiplicación porque el producto cruz es anticommutativo. agrupando los términos que contienen un vector unitario común y factorizando, obtenemos la siguiente expresión muy útil para el cálculo del producto cruz:
$$\begin{split} \bold{\vec{C}} &= \bold{\vec{A}}\times \bold{\vec{B}}\\ &= (A_yB_z - A_zB_y)\^{\bold{i}} + (A_zB_x - A_xB_z)\^{\bold{j}}\\ & \;\;\;\;\; + (A_xB_y - A_yB_x)\^{\bold{k}}\tag{3.14} \end{split}$$En esta expresión, los componentes escalares del vector de producto cruz son
$$C_x = A_yB_z - A_zB_y\\ C_y = A_zB_x - A_xB_z\\ C_z = A_xB_y - A_yB_x\tag{3.15} $$En el apartado anterior, indicamos que el torque o momento está dado por la expresión $\bold{\vec{M}}= \bold{\vec{R}}\times \bold{\vec{F}}$. El momento de una fuerza $\bold{\vec{F}}$ con respecto al punto $O$, o con respecto al eje del momento que pasa por $O$ y es perpendicular al plano que contiene a $O$ y a $\bold{\vec{F}}$, lo denotaremos como:
$$\bold{\vec{M}_o}= \bold{\vec{R}}\times \bold{\vec{F}}\tag{3.16}$$
A continuación, presentamos cuatro objetos interactivos tomados de la Unidad Didáctica Interactiva "Momento de una fuerza respecto a un punto", del Proyecto Un_100, diseñada por el autor de este libro y publicada en la Red Educativa Digital Descartes y en el portal Prometeo de la UNAM de México.
A continuación, presentamos tres ejemplos de aplicación, tres de ellos son escenas interactivas tomadas de la Unidad Didáctica Interactiva "Momento de una fuerza respecto a un punto", del Proyecto Un_100.
En el apartado 3.3.2, evidenciamos que el momento tiene el mayor valor cuando $sen\phi = 1$, que ocurre cuando $\phi = 90\degree$. Físicamente, significa que una llave (como la de la figura 3.7) es más efectiva, dándonos la mejor ventaja mecánica, cuando aplicamos la fuerza perpendicular al mango de la llave. En general, para cualquier eje, el valor escalar del momento está dado por:
$$M = Fd\tag{3.17}$$ En la ecuación 3.17, $d$ es la distancia del eje a la línea de acción de la fuerza.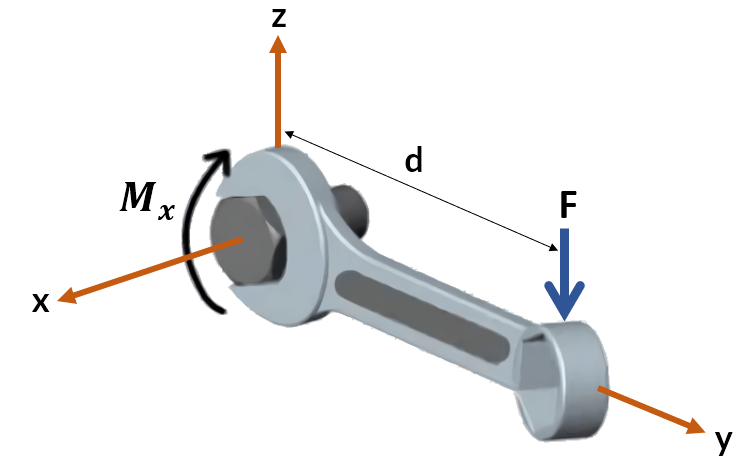
Cuando un cuerpo rígido está sometido a diferentes fuerzas externas, se presentan diferentes tipos de reacciones en los sooportes o apoyos que tiene el cuerpo rígido. Presta atención al siguiente video (creado por el autor de este libro), para que te familiarices con las reacciones, que seguiremos usando en el resto de apartados.
En conclusión, si un apoyo evita la traslación del cuerpo rígido en una dirección cualquiera, entonces se genera una fuerza de reacción en esa dirección. Si el apoyo evita una rotación, se genera un momento sobre el cuerpo rígido.
En el video 3.1, se describen los diagramas de cuerpo libre para una viga simplemente apoyada con carga puntual y carga distribuida, además de usar las ecuaciones de equilibrio del cuerpo rígido, que explicaremos en el apartado 3.8. En general, en el diagrama de cuerpo libre se sustituyen los apoyos por la reacciones. Observa la siguiente escena interactiva:
Observa las cinco escenas en el siguiente objeto interactivo, que hacen parte de la Unidad Didáctica Interactiva "Equilibrio de Cuerpo Rígido", del Proyecto Un_100, diseñada por el autor de este libro.
Viga empotrada con carga puntual
Viga simplemente apoyada con carga puntual
Encuentra las reacciones en la siguiente viga, usando: a) Ecuaciones de equilibrio, b) El método explicado en el video 3.1
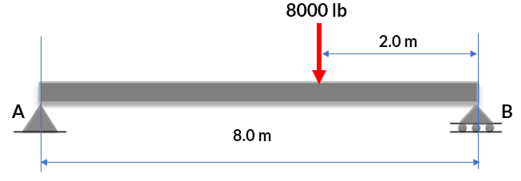
Solución
En primer lugar, dibujamos el diagrama de cuerpo libre:
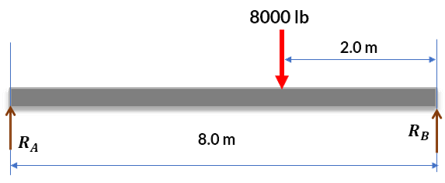
a) Por ecuaciones de equilibrio
Sumamos momentos con respecto al punto $A$
$$\begin{aligned} \bold{\curvearrowleft^+ \sum M_A} &= 0\\ 8R_B - 6\cdot 8000\;lb &=0\\ R_B &= \frac{48000\;lb}{8}\\ R_B &= 6000\;lb \end{aligned}$$Sumamos las fuerzas verticales
$$\begin{aligned} \bold{\uparrow^+ \sum F_y} &= 0\\ R_A + R_B - 8000 &= 0\\ R_A &= 8000 - 6000\\ R_A &= 2000\;lb \end{aligned}$$Observa que para hallar $R_A$ solo usamos las unidades al final, pues al tener unidades consistentes podemos obviarlas durante el cálculo.
b) Usando el método del video
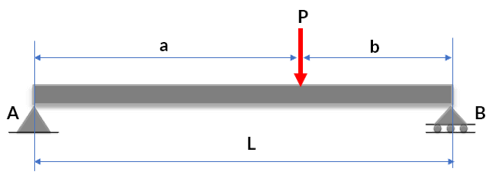
Basta usar las expresiones: $R_A = (Pb/L) = (8000\cdot 2)/8 = 2000\;lb$ y $R_A = (Pa/L) = (8000\cdot 6)/8 = 6000\;lb$.
Encuentra las reacciones en el siguiente cuerpo rígido (problema 5.91 de Hibbeler
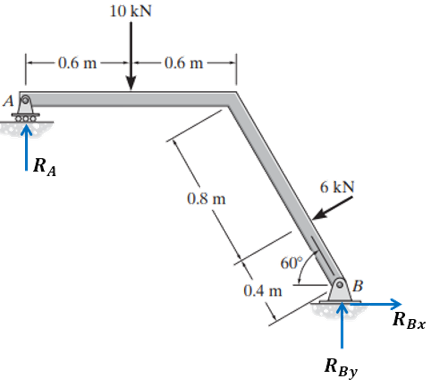
Si hallamos momentos en el punto $B$, podemos hallar $R_A$:
$$\begin{aligned} \bold{\curvearrowleft^+ \sum M_B} &= 0\\ -(1.2+1.2cos\;60\degree)R_A + 10(0.6+1.2cos\;60\degree)+0.4\cdot 6 &=0\\ R_A &= \frac{12 + 2.4}{1.8}\\ \color{blue}\bold{R_A} &= 8\;kN\\ \end{aligned}$$Ahora, podemos hallar $R_{By}$, sumando las fuerzas verticales:
$$\begin{aligned} \bold{\uparrow^+ \sum F_y} &= 0\\ R_A + R_{By} - 10 -6sen\;30\degree &= 0\\ R_{By} &= 10+3-8\\ \color{blue}\bold{R_{By}} &= 5\;kN \end{aligned}$$Fnalmente, podemos hallar $R_{Bx}$, sumando las fuerzas horizontales:
$$\begin{aligned} \bold{\rarr^+ \sum F_x} &= 0\\ R_{Bx} -6cos\;30\degree &= 0\\ R_{Bx} &= 6cos\;30\degree\\ \color{blue}\bold{R_{Bx}} &= 5.2\;kN \end{aligned}$$Las componentes rectangulares de la fuerza de $6\;kN$, se pueden obtener determinando el ángulo que forma con la horizontal, el cual es $30\degree$
Ahora, ya podrás entender, en parte, el video presentado en el prefacio.
Torre Eiffel (foto de Karolina Edi Nugraha, Pixabay).
Imagen de portada: Ilustración del juguete roly-poly "Weeble" (imagen de KDS444, en Wikimedia, CC BY-SA 3.0).
Imagen de esta página: Torre de Pisa (foto de Chiper Catalin, en Pexels).
En el estudio de la mecánica de sólidos y estructuras, existen fenómenos físicos que se caracterizan por la distribución de fuerzas a lo largo de un área determinada. Estas fuerzas, conocidas como fuerzas distribuidas, son de vital importancia para comprender el comportamiento y la respuesta de los materiales y sistemas ante cargas externas.
El concepto de centroide juega un papel fundamental en el análisis de fuerzas distribuidas, ya que nos permite determinar el punto de aplicación de una fuerza equivalente, que resume el efecto de la distribución continua de cargas sobre un elemento o una estructura. El centroide se define como el centro geométrico de un área, considerando la ponderación de las distintas secciones de acuerdo a su geometría y magnitud de la carga.
Al comprender cómo se distribuyen las fuerzas a lo largo de un elemento, podemos determinar con mayor precisión el comportamiento estructural y predecir cómo responderá frente a las cargas externas. Además, el análisis de los centroides y las fuerzas distribuidas nos permite calcular magnitudes importantes, como momentos de inercia, momentos estáticos y esfuerzos internos, que son cruciales para el diseño y la optimización de estructuras.
El centro de gravedad, también conocido como centro de masas, es un punto en un cuerpo o sistema donde el peso se distribuye uniformemente. Es el punto donde se puede considerar que la fuerza de la gravedad está concentrada. La ubicación del centro de gravedad depende de la distribución de la masa dentro del sistema. Si un objeto se encuentra en equilibrio, su centro de gravedad estará ubicado directamente sobre su base de soporte (como el caso del muñeco bobo en la figura 4.1). Si el centro de gravedad se encuentra fuera de la base de soporte, el objeto tenderá a inclinarse o volcar. El conocimiento del centro de gravedad es crucial en el diseño de estructuras, vehículos y objetos que deben mantener un equilibrio estable (observa el video 4.1).
En la figura 4.2, presentamos un cuerpo en el cual cada partícula tiene un peso que representamos como $\Delta W_1, \Delta W_2, \Delta W_3, \cdots \Delta W_i$, fuerzas dirigidas al centro de la Tierra, que supondremos paralelas. La fuerza resultante $W = \sum\Delta W_i$ se aplica en el centro de gravedad del cuerpo.
Este punto de aplicación se puede encontrar con la condición de equilibrio de momentos con respecto a los ejes $x$ e $y$. Punto que denotaremos como $(\={x},\={y})$.
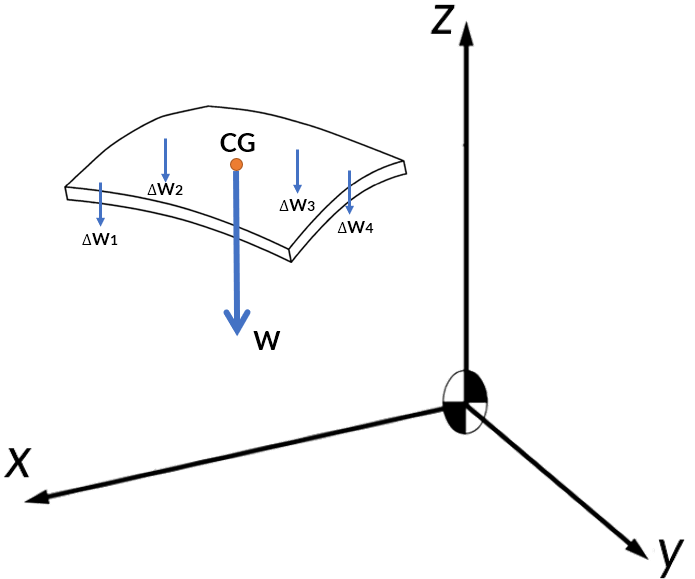
Por sumatoria de momentos, obtenderíamos:
$$\sum M_y:\;\;\; \={x}W = x_1W_1 + x_2W_2 + x_3W_3 + \cdots + x_nW_n\\ \sum M_x:\;\;\; \={y}W = y_1W_1 + y_2W_2 + y_3W_3 + \cdots + y_nW_n\tag{4.1}$$En general, para todas las partículas del cuerpo:
$$\color{#0089cd}{W = \int dW}\;\;\;\;\; \color{#C9913F}{\={x}W = \int xdW} \;\;\;\;\; \={y}W = \int ydW \tag{4-2}$$Supongamos que el cuerpo de la figura 4.2 es una placa plana de espesor uniforme; por lo tanto, el peso lo podemos expresar como $W = \gamma tA$, donde $\gamma$ es el peso específico del cuerpo y $t$ el espesor. Al reemplazar en las ecuaciones 4.2, obtenemos:
$$\={x} = \frac{\displaystyle\int xdA}{\displaystyle\int dA}\;\;\;\;\;\={y} = \frac{\displaystyle\int ydA}{\displaystyle\int dA}\tag{4.3}$$Que son las coordenadas del centro geométrico de la placa, también conocido como centroide de área. Si el cuerpo es uniforme y de espesor delgado, el centroide coincide con el centro de gravedad.
El centroide de un área puede ser considerado como su centro geométrico. Si se tiene una placa delgada y uniforme, entonces el centroide sería el mismo que el centro de masa para esta placa delgada.
En placas delgadas que presenten uno o más ejes de simetría, el centroide se encuentra en un eje de simetría o en la intersección de dichos ejes. Por ejemplo, en un paralelogramo el centroide se encuentra en la intersección de las diagonales (ver puntos naranja en la figura 4.3):
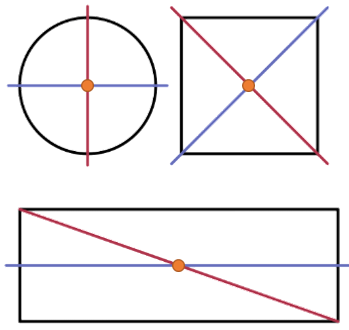
Esta propiedad que tienen algunas placas delgadas con ejes de simetría, es útil para el cálculo de centroides usando la ecuación 4.3, tal como lo evidenciaremos en el siguiente ejemplo en el cual hallaremos el centroide de un triángulo rectángulo.
Halla las coordenadas del centroide correspondiente al triángulo mostrado en la siguiente figura:
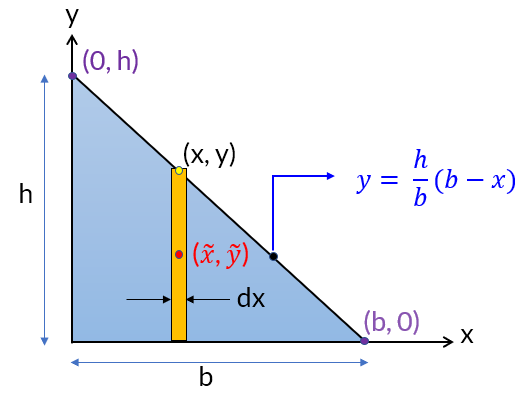
La figura la hemos preparado para aplicar las ecuaciones 4.3, he iniciaremos con el cálculo de $\={x}$:
$$\={x} = \frac{\displaystyle\int xdA}{\displaystyle\int dA} = \frac{\displaystyle\int xdA}{A}$$Sabemos que $A=\frac{bh}{2}$, $y = \frac{h}{b}(b-x)$ y $dA = ydx$.
Hallemos, entonces, la integral del numerador:
Por lo tanto,
$$\={x} = \frac{\displaystyle\int xdA}{A} = \frac{\displaystyle\frac{b^2h}{6}}{\displaystyle\frac{bh}{2}} = \bold{\color{#0089cd}\frac{b}{3}}$$Para el cálculo de $\={y}$ usaremos el mis diferencial de área:
$$\={y} = \frac{\displaystyle\int \tilde{y}dA}{A}$$Observa, en la figura, que $\tilde{x} = x$ y $\tilde{y} = y/2$, este último porque el centroide de $dA$ se encuentra en la intersección de las diagonales del rectángulo, entonces:
$$\={y} = \frac{\displaystyle\int_0^h \tilde{y}dA}{A} = \frac{\displaystyle\int_0^b\Big[\frac{h}{2b}(b-x)\Big]\Big[\frac{h}{b}(b-x)\Big]dx}{A}$$Resolviendo la integral y simplificando:
$$\bold{\color{#0089cd}\={y} = \frac{h}{3}}$$Para un triángulo rectángulo, demostramos que el centroide se encuentra a un tercio de la altura y a un tercio de la base; es decir, a un tercio de cualquiera de los catetos:
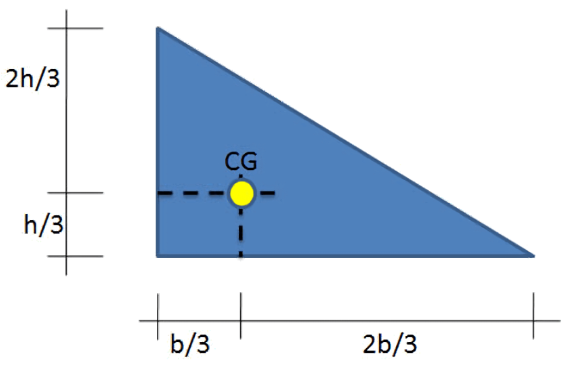
Para un triángulo cualquiera, el centroide es el baricentro del triángulo; es decir, donde las medianas del triángulo se intersecan.
Si conocemos las coordenadas de los vértices del triángulo, el centroide se puede calcular así:
$$(\={x}, \={y}) = \Big(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\Big)\tag{4.4}$$En el siguiente interactivo, mueve los vértices y verifica la expresión anterior o, si lo deseas, las expresiones encontradas para triángulos rectángulos (figura 4.4).
En una placa delgada compuesta de triángulos, rectángulos u otras formas comunes, en los que se saben la ubicación de cada una de esas partes, es posible no recurrir a la integración para determinar el centroide de la placa; para ello recurrimos al uso de las sumatorias discretas ($\sum$), en lugar de las sumatorias continuas ($\int$), así:
$$\={x} = \frac{\sum \tilde{x_{ci}}A_i}{A}\;\;\;\;\;\={y} = \frac{\sum \tilde{y_{ci}}A_i}{A}\tag{4.5}$$En ingeniería interesa conocer el centroide en las secciones transversales de elementos como vigas, columnas, viguetas o perfiles metálicos. En estos últimos, las secciones suelen tener la forma de una I, una C o una T como la de la siguiente figura:
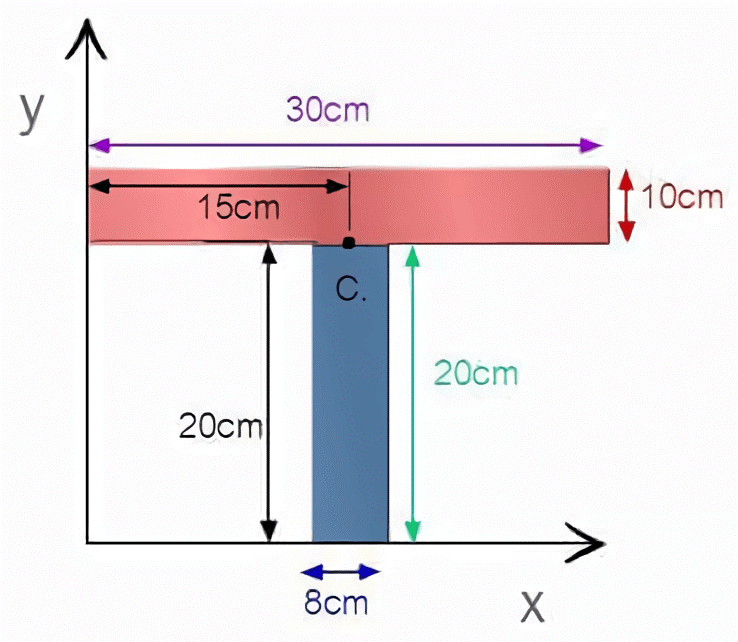
En este caso, solo tendríamos que hallar $\={y}$, pues $\={x}$ se encuentra en el eje de simetría. A continuación, presentamos dos objetos interactivos, en el segundo resolvemos el caso de la figura 4.5.
En el primer objeto interactivo, fue posible dividir el área en triángulos y aplicar la ecuación 4.4, para calcular el centroide del polígono.
En el segundo objeto interactivo, se presenta la sección transversal de una viga, la cual podemos modificar cambiando las dimensiones de los patines (superior e inferior) y del alma, conformando perfiles "I", "T" o rectangulares, el cálculo del centroide se realiza usando las ecuaciones 4.5. Verifica que para una sección rectangular el centroide se encuentra en $h/2 = (hps + ha + hpi)/2$.
Hagamos el cálculo de $\={y}$ para el perfil de la figura 4.5:
$$\begin{aligned} \={y} &= \frac{\sum \tilde{y_{ci}}A_i}{A}\\ &= \frac{y_{c\; alma}\cdot A_{alma} + y_{c \;patín \;superior}\cdot A_{c\; alma}}{A_{total}}\\ &= \frac{10(20\cdot 8) + 25(30\cdot 10)}{20\cdot 8 + 30\cdot 10}\\ &= \frac{9100}{460}\\ &= \color{red}{19.8\; cm} \end{aligned}$$Que coincide con el primer resultado mostrado en el objeto interactivo de la página anterior.
El cálculo de $\={y}$, en perfiles como los anteriores, los vamos a usar en el diseño de vigas, para separar zonas de tracción y compresión, a través de una superficie llamada plano neutro.
En las ecuaciones 4.5 hay que poner cuidado cuando se presentan orificios (área negativa). Observa el siguiente ejemplo.
Halla las coordenadas del centroide correspondiente a la siguiente área compuesta:
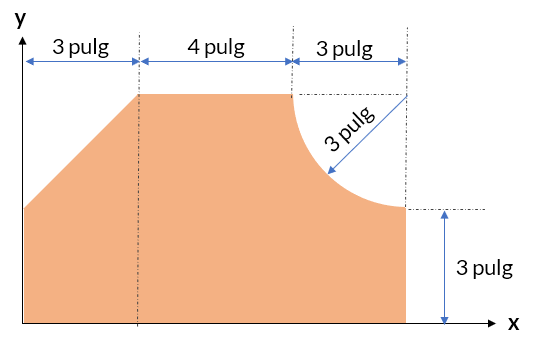
Solución
Podemos dividir el área en cuatro regiones, tal como se indica en la figura 4.5, una de ellas es un vacío ($A_4$), correspondiente a un cuarto de círculo, que se debe restar al rectángul $A_3$.
Hallemos, inicialmente el área total:
$$\begin{aligned} A &= A_1 + A_2 + A_3 - A_4\\ &= 3\cdot 10 + 3\cdot 3/2 + 3\cdot 7 - \pi (3)^2/4\\ &= \color{red}{48.43\;pulg^2} \end{aligned}$$ Para usar las ecuaciones 4.5, debemos conocer el centroide de un cuarto de círculo; para ello, consulta la tabla de centroides en la caja de herramientas.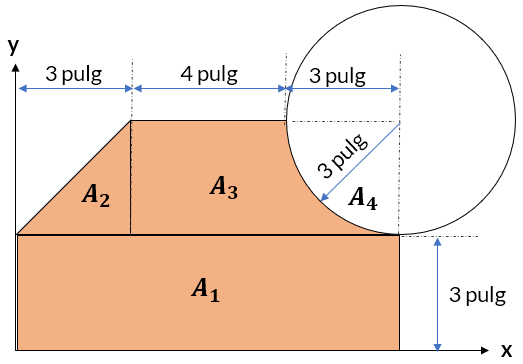
| Región | $A_i$ | $x_{ci}$ | $y_{ci}$ | $x_{ci}A_i$ | $y_{ci}A_i$ |
|---|---|---|---|---|---|
| $A_1$ | $30.0$ | $5.0$ | $1.5$ | $150$ | $45$ |
| $A_2$ | $4.5$ | $2.0$ | $4.0$ | $9$ | $18$ |
| $A_3$ | $21.0$ | $6.5$ | $4.5$ | $136.5$ | $94.5$ |
| $A_4$ | $-7.07$ | $8.73$ | $4.73$ | $-61.72$ | $-33.44$ |
| $\sum$ | $48.43$ | $233.78$ | $124.1$ |
Finalmente,
$$\={x} = \frac{\sum \tilde{x_{ci}}A_i}{A}\;\;\;\;\;\={y} = \frac{\sum \tilde{y_{ci}}A_i}{A}$$ $$\bold{\color{red}{\={x} = 4.83\; pulg\;\;\;\;\;\={y} = 2.56\;pulg}}$$Observa el siguiente video, realizado por el autor de este libro:
Notaste que la posición de la fuerza resultante es $\={x}$:
$$\={x} = \frac{\displaystyle\int xdA}{\displaystyle\int dA} = \frac{\displaystyle\int xdA}{A}$$Y, además, que la fuerza resultante es el área bajo la curva:
$$F_R = \int_A dA = A\tag{4.6}$$En el mundo real, se presentan situaciones donde se hacen presentes las fuerzas o cargas distribuidas. Existen muchas posibles distribuciones de fuerzas. Presiona sobre las imágenes, para que conozcas algunas de esas distribuciones.
A continuación, observa algunos ejemplos tomados de la Unidad Didáctica Interactiva "Fuerzas distribuidas", del Proyecto Un_100.
En mecánica de materiales, los momentos de inercia son propiedades físicas que describen cómo se distribuye la masa alrededor del eje de un elemento estructural y cómo esta distribución de masa afecta a su resistencia a la flexión.
El momento de inercia de la sección transversal de un elemento estructural, también conocido como momento de inercia de área, se representa comúnmente con el símbolo "I" y se calcula integrando la función que describe la distribución de masa de la sección transversal respecto al eje de referencia. Este momento de inercia se utiliza para determinar la resistencia a la flexión y deflexión de las vigas cuando se somete a cargas externas.
El momento polar de inercia, representado comúnmente por el símbolo "J", se utiliza para analizar la resistencia a la torsión de una viga. Este momento de inercia se obtiene calculando la suma de los momentos de inercia de cada elemento diferencial de masa de la sección transversal alrededor del eje de referencia.
El momento de inercia refleja la distribución de masa de un cuerpo o de un sistema de partículas en rotación, respecto a un eje de giro. El momento de inercia solo depende de la geometría del cuerpo y de la posición del eje de giro; pero no depende de las fuerzas que intervienen en el movimiento.
En el apartado anterior, definimos en la ecuación 4.3, que:
$$\={y}A = \displaystyle\int ydA$$La expresión de la derecha de la ecuación, se conoce como primer momento de área.
Los momentos de inercia de un área diferencial $dA$ con respecto a los ejes $x$ e $y$ se definen como un segundo momento de área:
$$\color{blue}I_x = \displaystyle\int_A y^2dA \;\;\;\;\; \color{red}I_y = \displaystyle\int_A x^2dA \color{black}\tag{4.7}$$El momento polar de inercia describe la distribución de área de un objeto con respecto a un punto en su plano. El momento polar de inercia también puede ser descrito como la resistencia de un eje o viga a deformarse por torsión.
El momento polar de inercia con respecto al punto $o$ o, si se prefiere, con respecto al eje $z$ (figura 4.7), está dado por la siguiente expresión:
$$J_o = I_x + I_y = \int_A x^2 dA + \int_A y^2 dA = \int_A r^2 dA = \tag{4.8}$$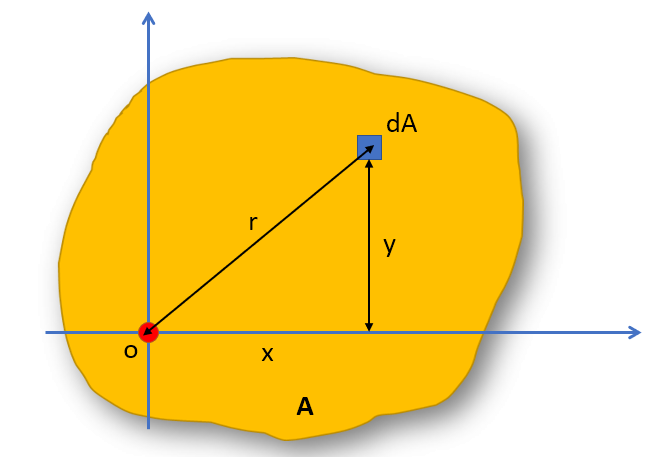
En el siguiente objeto interactivo, determinamos $J$ para un círculo.
Al calcular el momento de inercia $I$ con respecto a un eje arbitrario AA' (ver figura 4.8), observamos que $y = y'+d$. Entonces podemos escribir:
$$I = \int_A y^2dA = \int_A (y' + d)^2dA$$ $$= \int_A y'^2 dA + 2d\int_A y'dA + d^2\int_A dA$$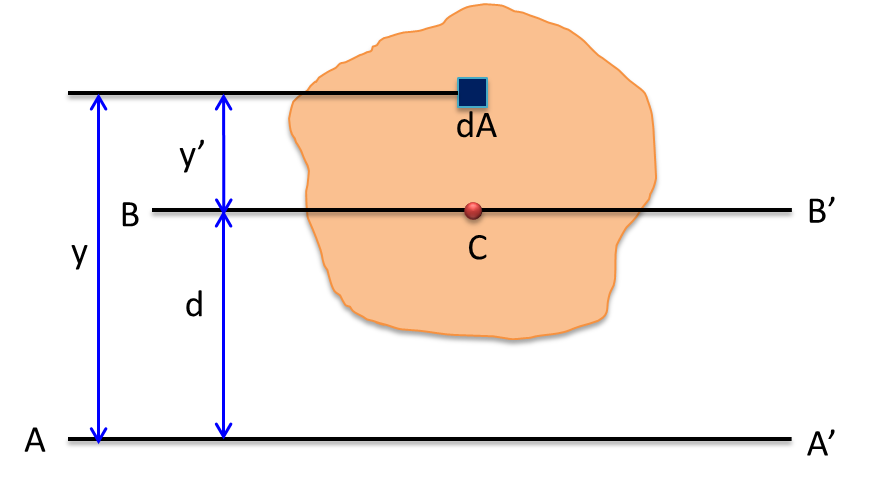
La primera integral es el momento de inercia con respecto al eje centroidal $BB'( I_{x'})$. La segunda es el primer momento de área con respecto a $BB'$ que sería cero por estar el centroide en $BB'$, la tercera es el área de la figura.
Finalmente, obtenemos la expresión: $\bold{\color{blue}{I = I_x + Ad^2}}$, que define el teorema de los ejes paralelos.
Determina el momento de inercia del triángulo con respecto al eje centroidal $BB'$. Usa el teorema de los ejes paralelos.
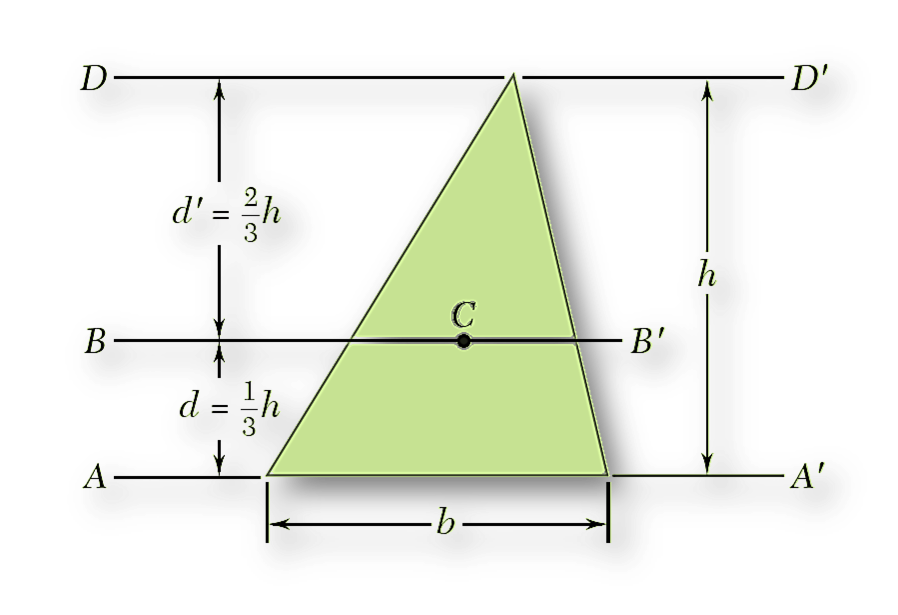
Solución
Ya hemos hallado el momento de inercia con resepcto a $AA'$: $\bold{\color{blue}{I_{AA'} = \frac{bh^3}{12}}}$.
Aplicando el teorema de los ejes paralelos, tenemos:
$$I_{AA'} = I_{BB'} + Ad^2$$Despejando, tenemos:
$$I_{BB'} = I_{AA'} - Ad^2 = \frac{bh^3}{12}- \frac12 bh\Big(\frac13 h\Big)^2 = \frac{1}{36}bh^3$$Vigas de sección transversal en $I$, en Illinois (foto de M dorothy, Wikimedia, CC BY-SA 3.0).
Imagen de portada: Empire Station Complex (imagen de Jim Henderson, en Wikimedia, CC BY-SA 4.0).
Imagen de esta página: Aramadura De Howe. Puente de Clark, río Pemigewasset en Clark's Trading Post (foto de Chiper Catalin, en Wikimedia, Dominio público).
Las armaduras o celosías son estructuras formadas por barras rectas interconectadas en nodos, ya sean de madera o metálicas, ensambladas entre sí para soportar las cargas de la estructura y garantizar su estabilidad. Pueden ser utilizadas en puentes, techos y otras estructuras que necesitan soportar grandes cargas. Las barras trabajan predominantemente a compresión o tracción presentando comparativamente flexiones pequeñas.
La siguiente imagen, es un ejemplo de armadura tipo Warren o armadura equilátera patentada por el ingeniero británico James Warren en 1848. Haz clic sobre la imagen, para que observes el puente Wills Creek Bollman diseñado con la armadura Warren (foto de Jet Lowe, dominio público).

Tal como lo muestra la foto de la Figura 5.1, las estructuras se construyen a partir de varias armaduras unidas entre sí, formando una armadura en 3D. No obstante, cada una de ellas está diseñada para soportar cargas en su propio plano, por lo que en este capítulo nos ocuparemos del análisis de armaduras bidimensionales.
La siguiente imagen, es un ejemplo de armadura tipo Howe inventada por William Howe en 1840 y ampliamente utilizada como puente a mediados y finales del siglo XIX. Haz clic sobre la imagen, para que observes un ejemplo de uso en un techo (foto de HandWiki, CC BY-SA 3.0).
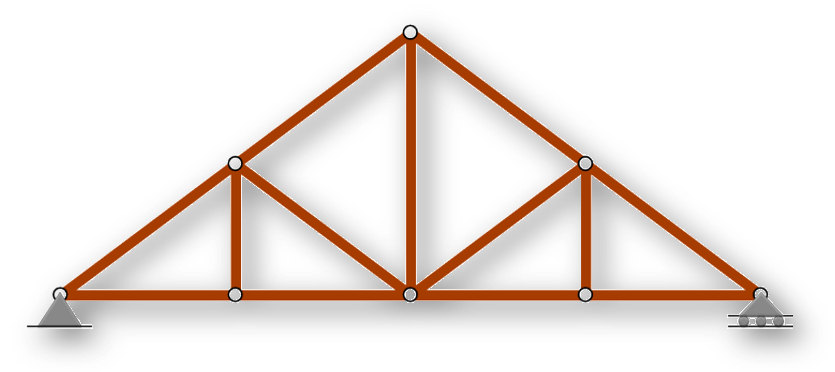
Existen otros tipos de armaduras, las cuales se usan según algunas condiciones, tales como la longitud (en puentes, por ejemplo) o su altura (en techos, por ejemplo). En la siguiente página, presentamos varios ejemplos, que incluye armaduras tipo Pratt, Howe, K, Warren y Waddell.
Puedes observarlas haciendo clic sobre cada imagen.
La armadura más simple y estable es el triángulo. Definimos una armadura simple aquella que comienza con un elemento triangular y se expande al añadirle dos miembros y un nodo. En el siguiente objeto interactivo, observa cómo se genera la armadura Warren de la Figura 5.1; para ello, añadiendo dos barras con el control:
Para estas armaduras, el número de barras (m) y el número de nodos (n) se relacionan por la ecuación:
$$m = 2n – 3$$En el siguiente video, José Luperi nos resume, en parte, lo que hemos descrito de las armaduras:
Este método de análisis es muy útil para hallar las fuerzas en los barras de las armaduras, se considera el equilibrio del nodo o pasador. Todas las fuerzas que actúan en la armadura se muestran en un diagrama de cuerpo libre, incluyendo fuerzas externas y reacciones en los apoyos. Usamos, entonces las ecuaciones de equilibrio: $\sum F_x = 0$ y $\sum F_y = 0$ para hallar las fuerzas desconocidas actuando en las barras.
Con estas dos hipótesis, se concluye que los miembros actuarán como miembros de dos fuerzas dirigidas a lo largo del eje del miembro; es decir, están cargados a tracción o compresión. Es común diseñar los miembros a compresión mas gruesos para evitar el pandeo.
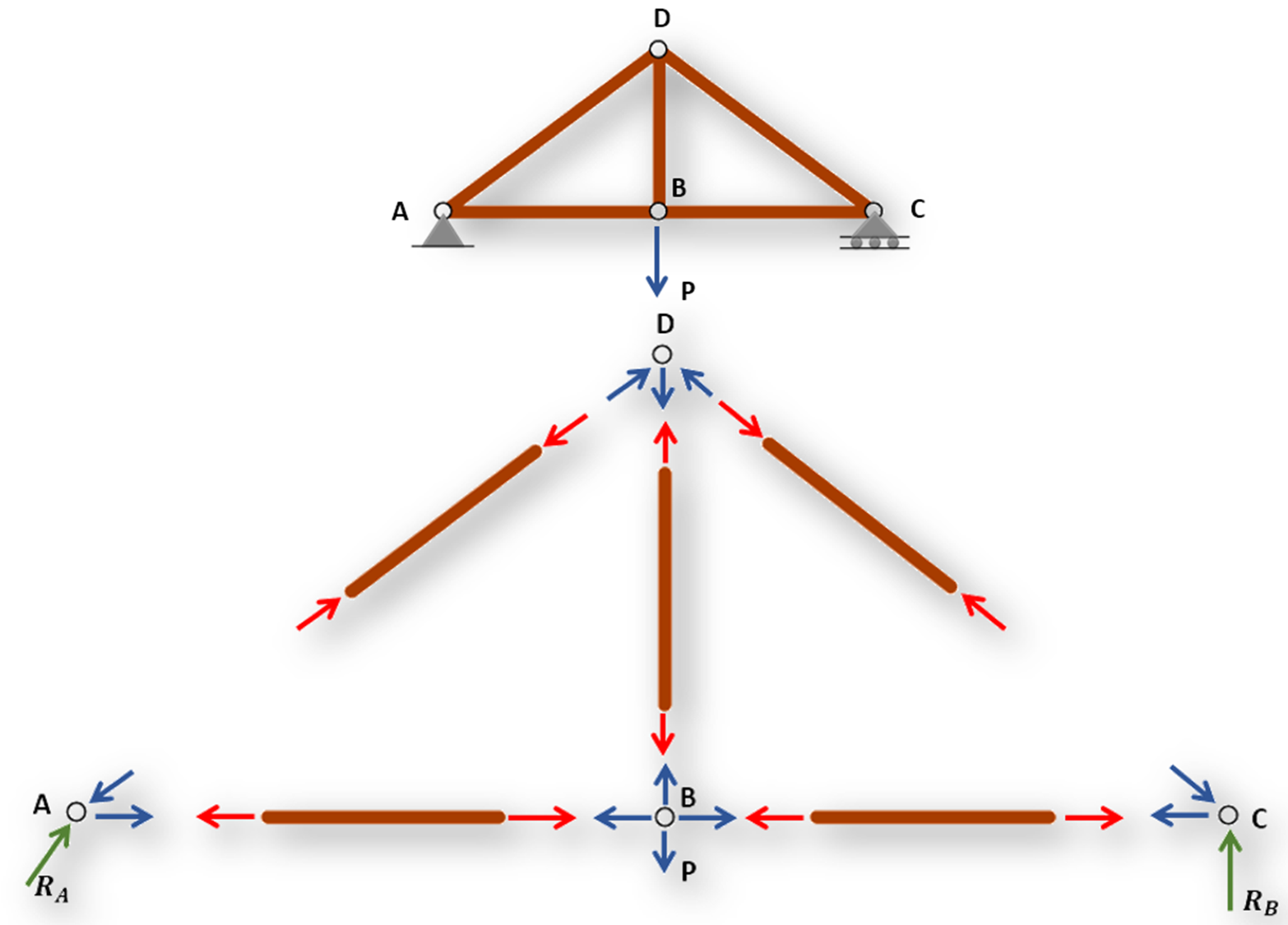
En el ejemplo 5.1, hallamos las fuerzas en las barras de la armadura que se muestra en la figura 5.4.
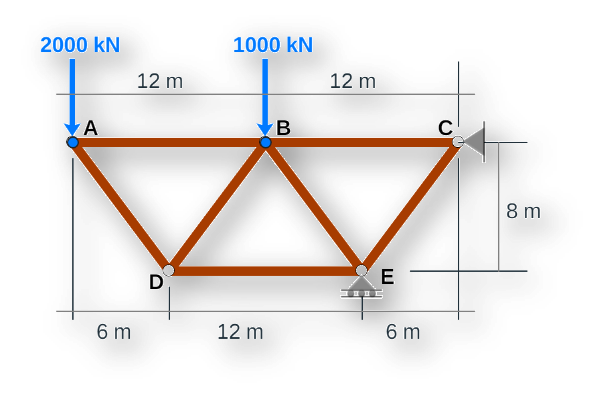
En cada nodo usamos las condiciones de equilibrio, para hallar las fuerzas, tal como se muestra en la figura 5.5.
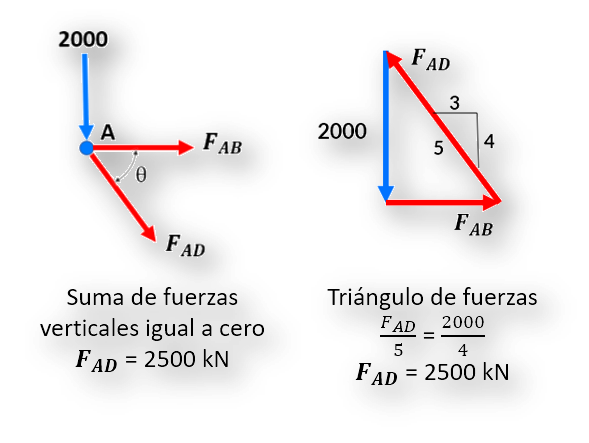
Observa que el triángulo se forma uniendo cabeza y cola de los vectores, lo que nos permite evidenciar que $F_{AD}$ es una fuerza de compresión y $F_{AB}$ de tracción. Obviamente, este método no siempre es tan sencillo de usar, por lo que las ecuaciones de equilibrio es la mejor opción. Veamos un ejemplo:
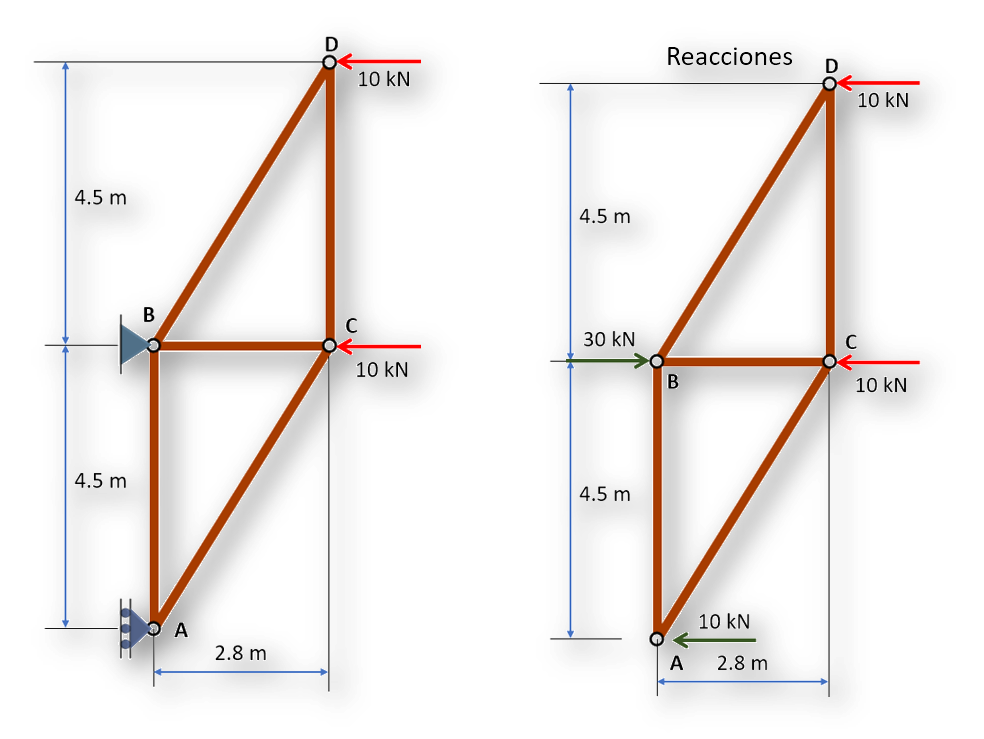
Solución
Nodo A
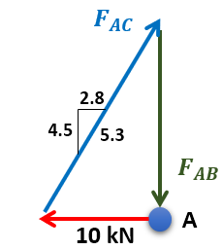
Nodo D
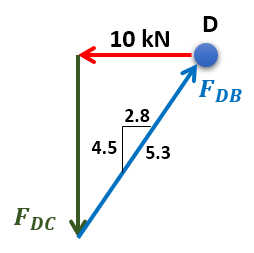
Nodo B
$\sum F_x = 0 \rarr +$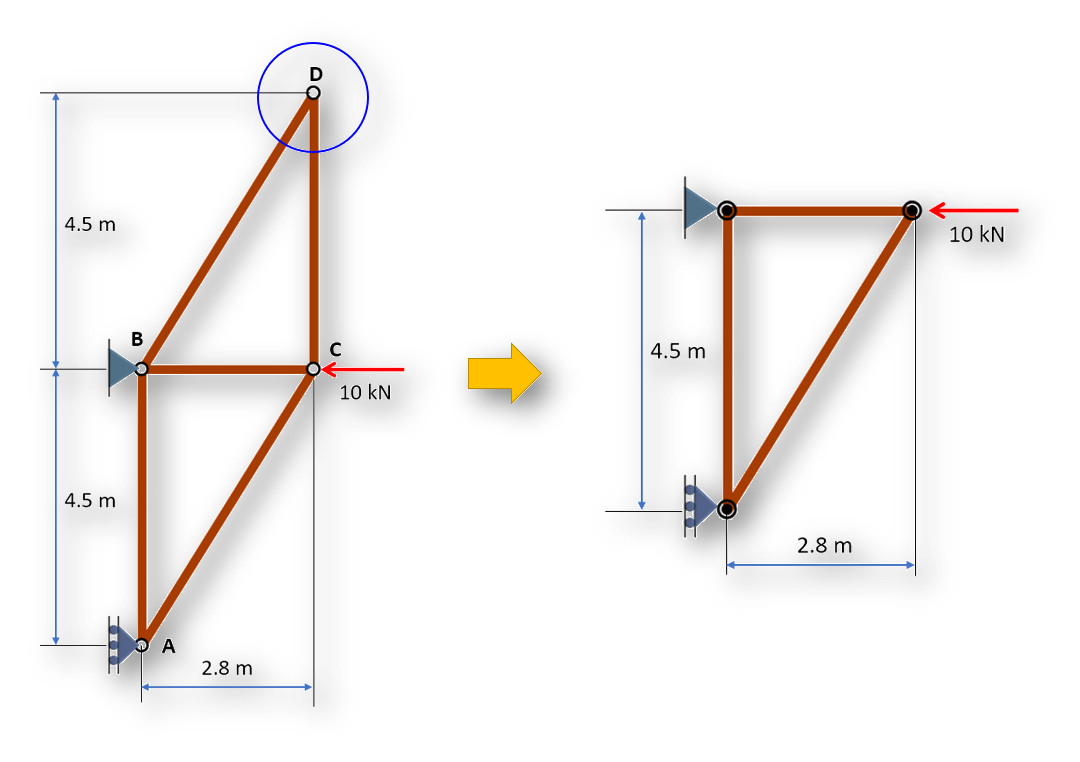
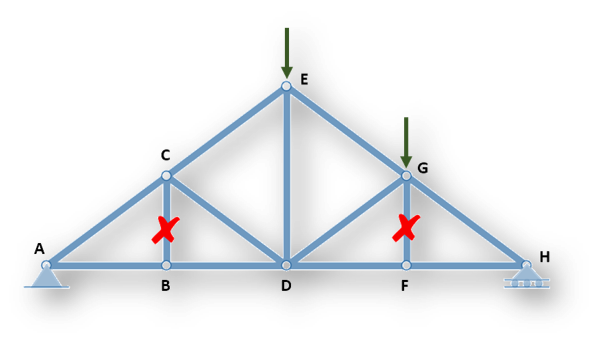
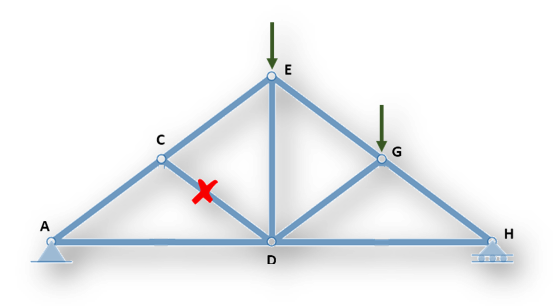
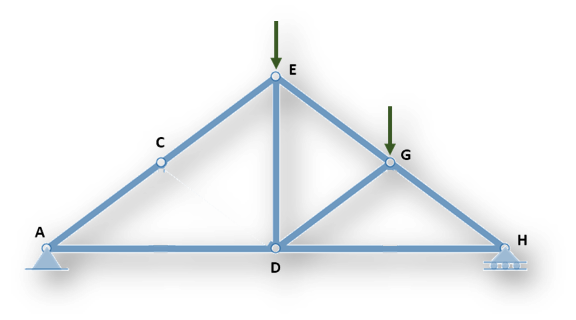
En el siguiente video, José Luperi explica el método de las secciones (lo que el llama esfuerzos corresponde las fuerzas):
El método de las secciones es un proceso que se usa para resolver las fuerzas desconocidas que actúan sobre miembros de una armadura. El método consiste en cortar la armadura en secciones individuales y analizar cada sección como un cuerpo rígido separado.
El método suele ser la forma más rápida y sencilla de determinar las fuerzas desconocidas que actúan en un miembro específico de la armadura.
Si la armadura está en equilibrio, entonces cualquier sección de la armadura está, también, en equilibrio.
Halla la fuerza en la barra BC ($F_{BC}$) por el método de las secciones.
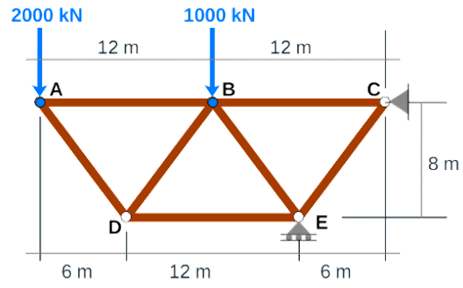
Solución
Las fuerzas en las barras de este armadura, las calculamos en el Ejemplo 5.1, obteniendo $F_{BC} = 5250\;kN$ a tracción.
Ahora, si aplicamos el método de las secciones, podemos hacer un corte como lo muestra la Figura 5.10. Una primera alternativa, sería usar dos ecuaciones de equilibrio como $\sum F_y = 0$, para hallar $F_{BE}$ y, luego, $\sum M_D = 0$, para hallar $F_{BC}$.
Sin embargo, si usamos la ecuación $\sum M_E = 0$, encontramos directamente $F_{BC}$:
$$\begin{aligned} \bold{\curvearrowleft^+ \sum M_E} &= 0\\ 18(2000) + 6(1000) - 8F_{BC} &= 0\\ F_{BC} &= \frac{42000\;kN}{8}\\ F_{BC} &= 5250\;kN \end{aligned}$$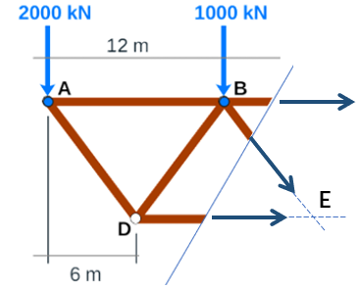
Por ser el resultado positivo, la fuerza sobre la barra $BC$ es a tracción, confirmando el resultado obtenido en el Ejemplo 5.1.
Halla la fuerza en la barra CE ($F_{CE}$) por el método de las secciones.
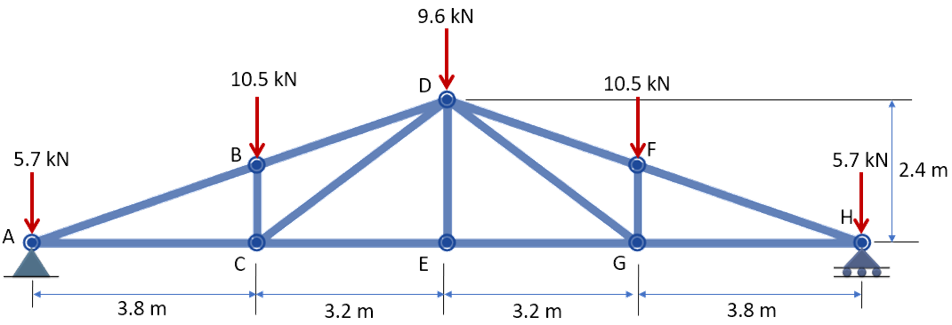
Solución
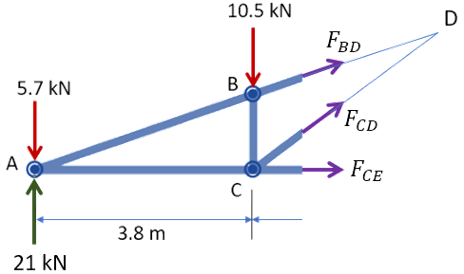
Por simetría de geométrica y de distribución de cargas, las reacciones $A_Y$ y $H_y$ son iguales a $21\;kN$. Haciendo un corte, como lo muestra la figura, podemos hallar $F_{CE}$, así:
El Dambergwarte en St. Ulrich bei Steyr es una estructura de madera de 1972, que tiene 36 m de altura (foto de Isiwal, Wikimedia, CC BY-SA 4.0).