Ejercicios propuestos - Capítulo II

Fuerzas

1. Un pronóstico del tiempo indica que la temperatura se prevé que sea de -5°C al día siguiente. ¿Es esta temperatura un vector o una cantidad escalar?

2. ¿Cuáles de los siguientes es un vector?: la altura de una persona, la altitud en el monte Everest, la velocidad de una mosca, la edad de la Tierra, el punto de ebullición del agua, el costo de un libro, la población de la Tierra o la aceleración de la gravedad.

3. Si dos vectores son iguales, ¿qué puedes decir sobre sus componentes? ¿Qué puedes decir sobre sus magnitudes? ¿Qué puedes decir sobre sus direcciones?

4. Si los vectores $\bold{\vec{A}}$ y $\bold{\vec{B}}$ son ortogonales, ¿cuál es la componente de $\bold{\vec{B}}$ a lo largo de la dirección de $\bold{\vec{A}}$? ¿Cuál es la componente de $\bold{\vec{A}}$ en la dirección de $\bold{\vec{B}}$?

5. Un peatón camina 6.0 km al este y luego 13.0 km al norte. Usa un método gráfico para encontrar el desplazamiento resultante del peatón y la dirección geográfica.

6. Para los vectores dados en la siguiente figura, usa un método gráfico para encontrar los siguientes resultados:
(a) $\bold{\vec{A}} + \bold{\vec{B}}$, (b) $\bold{\vec{C}} + \bold{\vec{B}}$, (c) $\bold{\vec{C}} + \bold{\vec{F}}$, (d)$\bold{\vec{A}} - \bold{\vec{B}}$, (e) $\bold{\vec{D}} - \bold{\vec{F}}$, (f) $\bold{\vec{A}} + 2\bold{\vec{F}}$, (g) $\bold{\vec{A}} - 2\bold{\vec{D}} + 2\bold{\vec{f}}$



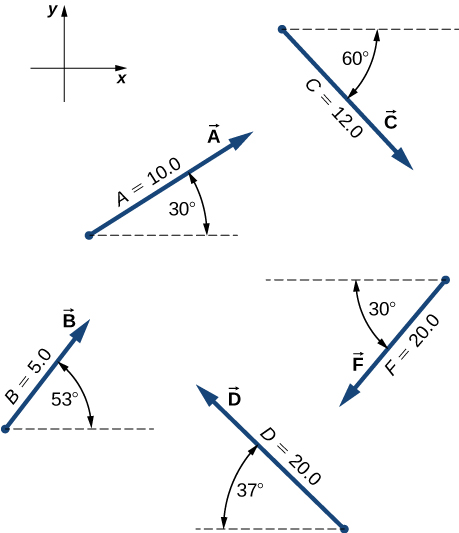
7. Para los vectores $\bold{\vec{A}} = -\hat{\bold{i}} - 4\hat{\bold{j}}$ y $\bold{\vec{B}}= -3\hat{\bold{i}} - 2\hat{\bold{j}}$, calcula (a) $\bold{\vec{A}} + \bold{\vec{B}}$, su magnitud y ángulo de dirección, y (b) $\bold{\vec{A}} - \bold{\vec{B}}$, su magnitud y ángulo de dirección.

8. Si $F_x = 3\;N$ y $F_y = 5\;N$, expresa $\bold{\vec{F}}$ en notación vectorial.

9. Dada $\bold{\vec{F}} = \hat{\bold{i}} + 2\hat{\bold{j}}$, encuentra un vector unitario con la misma dirección que $\bold{\vec{F}}$

10. Encuentra el vector $\bold{\vec{F}}$ cuya magnitud es $70\;N$ y vector $\bold{\vec{u}_F} = 3\hat{\bold{i}} + 4\hat{\bold{j}}$.

11. Si $F = 200\;lb$ y forma un ángulo de $30\degree$ con la horizontal, calcula sus componentes rectangulares.

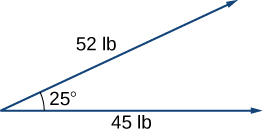
12. Dos fuerzas, una fuerza horizontal de $26 \;lb$ y otra de $45 \;lb$, actúan sobre el mismo objeto. El ángulo entre estas fuerzas es de $55\degree$. Encuentra la magnitud y el ángulo de dirección del eje x positivo de la fuerza resultante que actúa sobre el objeto (Redondear a dos decimales).

13. Dos fuerzas, una fuerza horizontal de $45 \;lb$ y otra de $52 \;lb$, actúan sobre el mismo objeto. El ángulo entre estas fuerzas es de $25\degree$. Encuentra la magnitud y el ángulo de dirección del eje x positivo de la fuerza resultante que actúa sobre el objeto (Redondear a dos decimales).



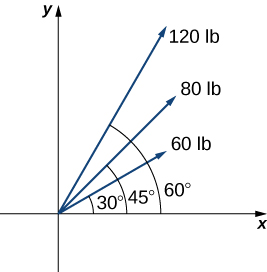
14. Tres fuerzas con magnitudes de $80 \;lb, 120 \;lb$ y $60 \;lb$ actúan sobre un objeto en, ángulos de $45\degree, 60\degree$ y $30\degree$, respectivamente, con el eje x positivo. Encuentra la magnitud y el ángulo de dirección con el eje x positivo de la fuerza resultante (Redondear a dos decimales).



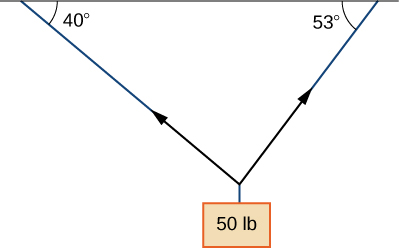
15. Un cable cuelga un peso de $50\; lb$ para que las dos porciones del cable formen ángulos de $40\degree$ y $53\degree$, respectivamente, con la horizontal. Encuentra las magnitudes de las fuerzas de tensión $\bold{\vec{T}_1}$ y $\bold{\vec{T}_2}$ en los cables si la fuerza resultante que actúa sobre el objeto es cero (Redondear a dos decimales)



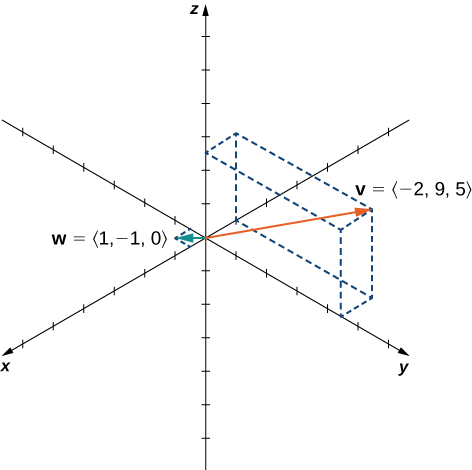
16. Sean $\bold{\vec{v}} = -2\hat{\bold{i}} + 9\hat{\bold{j}} + 5\hat{\bold{k}}$ y $\bold{\vec{w}} = \hat{\bold{i}} - \hat{\bold{j}}$. Encuentra: $3\bold{\vec{v}} - 2\bold{\vec{w}}$ y un vector unitario en la dirección de $\bold{\vec{v}}$



17. Una fuerza $\bold{\vec{F}}$ de $50\;kN$ actúa sobre una partícula en la dirección del vector $\bold{\vec{OP}} = 3\hat{\bold{i}} + 4\hat{\bold{j}} + 0\hat{\bold{k}}$. Expresa la fuerza en notación vectorial y encuentra el ángulo entre la fuerza $\bold{\vec{F}}$ y la dirección positiva del eje x. Expresa la respuesta en grados redondeados al entero más cercano.

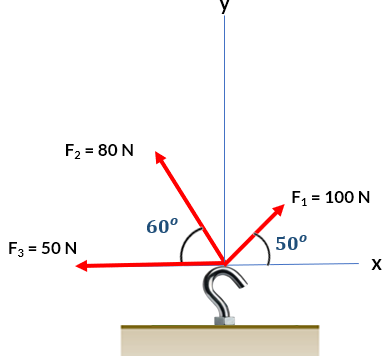
18. Tres fuerzas actúan sobre un gancho se muestra en la figura. Halla la resultante de las fuerzas sobre el gancho.



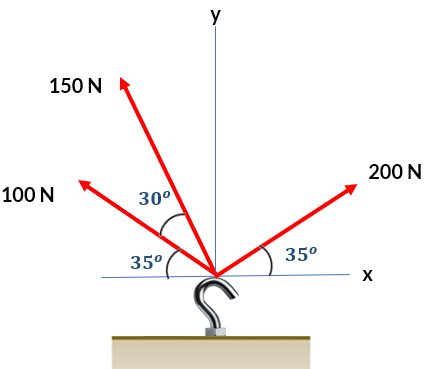
19. Halla la resultante de las tres fuerzas mostradas en la figura:



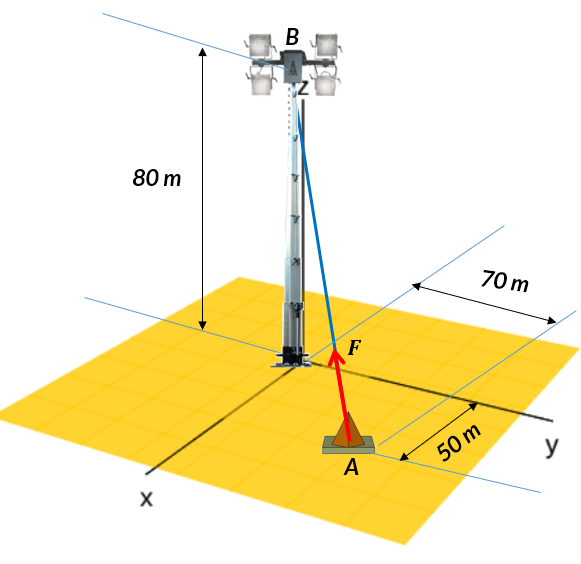
20. El alambre de una torre está anclado en $A$ como se muestra en la figura. La tensión en el alambre es de $500\; N$. Halla las componentes $F_x, F_y$ y $F_z$ de la fuerza que actúa en $A$ y el vector unitario en la dirección de la fuerza.