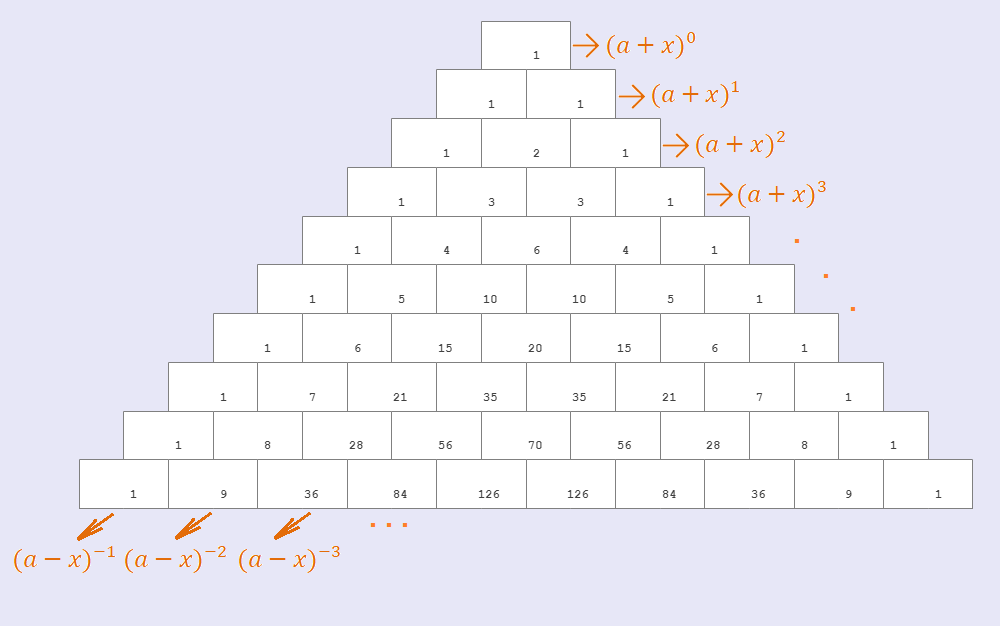Mostrando artículos por etiqueta: Pascal
En el número 106 de la revista Epsilon (ISSN: 2340-714X) de la Sociedad Andaluza de Educación Matemática Thales se ha publicado el artículo titulado "Congruencias en el triángulo de Pascal y el rectángulo de Newton" cuyo autor es nuestro socio José R. Galo Sánchez. Un trabajo de investigación, que como se refleja en la filiación de la autoría, ha sido desarrollado dentro de nuestra RED Descartes.
Este trabajo fue prepublicado en nuestro blog en tres artículos en los que el autor divulgaba la investigación realizada:
- El paralelogramo de Newton el 6 de marzo de 2020.
- El rectángulo de Newton como "simétrico" del triángulo de Pascal el 27 de marzo de 2020.
- Congruencias en el triángulo de Pascal el 24 de abril de 2020.
y, posterioriormente compiló el artículo que sometido a revisión por pares se ha publicado en la revista indicada.
En el resumen se indica :
"El rectángulo de Newton surge como extensión del actualmente denominado triángulo de Pascal partiendo de la versión escalonada de Stifel. Sin embargo, si se parte del esquema organizativo aportado por Pascal entonces el rectángulo de Newton se obtiene mediante una simple simetría signada. Así pues, basta estudiar las congruencias con cero de los números combinatorios y en su análisis aportamos que éstas se ubican en una sucesión de triángulos básicos que se distribuyen de manera periódica. En base a esa periodicidad se incluye un criterio que permite determinar directamente la congruencia de un número combinatorio."
El plantemiento conceptual que sigue, puede sintetizarse en:
- Presentación del conocido triángulo de Pascal en su representación actual como triángulo isósceles escalonado y como triángulo rectángulo que es la original de Pascal, y presentación del menos divulgado rectángulo de Newton.
- Reducción del rectángulo de Newton al de Pascal mediante una simetría signada.
- Muestra de las congruencias con cero en el triángulo de Pascal y revisión de resultados previos de otros autores. Esos resultados se presentan normalmente de manera algebraica y, en general, son oscuros y difíciles de interpretar por profanos dada la abstracción que suele introducir el Álgebra, pero aquí son visualizados geométricamente quedando mostrados de manera diáfana tanto para legos como para ilustrados.
- Finalmente se enuncian algebraicamente los resultados obtenidos por el autor, los cuales muestran la periodicidad de las congruencias módulo p de los números combinatorios y la regla que permite su determinación directa a partir de la descomposición p-ádica del índice superior e inferior, y se visualiza el porqué de ese resultado.
Todo está aderezado por numerosas escenas interactivas que permiten al interesado reproducir la investigación y cómo, apoyándose en ellas, puede potenciarse la reflexión que permite alcanzar la meta lograda. ¡Acceda pulsando sobre la siguiente imagen!
 Pulsa sobre la imagen para abrir la escena
Pulsa sobre la imagen para abrir la escena
Os incluimos a continuación dicho artículo y os invitamos a su lectura, a que realicéis observaciones y comentarios al mismo y a que lo divulguéis a través de vuestras redes sociales y profesionales. También a que, usando los recursos interactivos ahí enlazados y disponibles en nuestra web, abordéis actividades en vuestra aulas en las que divulgar el Triángulo de Pascal, el rectángulo de Newton y las curiosas congruencias que acontecen en ellos y a la vez que podáis promover en vuestro alumnado la inquietud básica, la chispa a partir de la cual se cataliza la vocación investigadora.
Los cilindros generalizados, los conos generalizados y las superficies tangenciales son los tres tipos de superficies regladas desarrollables. Todas ellas pueden obtenerse a partir de una curva directriz sobre la que desplazando una recta se genera la superficie, de ahí que a la recta se le denomine generatriz. En el caso de los cilindros todas las rectas tienen la misma dirección, en los conos todas pasan por un punto que es el vértice y en las superficies tangenciales son las rectas tangentes a la curva directriz. Todas ellas pueden parametrizarse como:
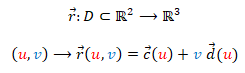
donde 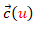 es la curva directriz y
es la curva directriz y 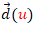 es la dirección de la generatriz. En el artículo "Superficies desarrollables con Descartes" detallé todos estos aspectos e indiqué que en las misceláneas allí compartidas la curva directriz que había considerado era plana y, por tanto, procedería abordar una extensión que contemplara que fuera tridimensional. También planteé abordar una miscelánea en la que se obtuvieran superficies tangenciales y el desarrollo plano de las mismas. Todo ello es lo que aquí presento.
es la dirección de la generatriz. En el artículo "Superficies desarrollables con Descartes" detallé todos estos aspectos e indiqué que en las misceláneas allí compartidas la curva directriz que había considerado era plana y, por tanto, procedería abordar una extensión que contemplara que fuera tridimensional. También planteé abordar una miscelánea en la que se obtuvieran superficies tangenciales y el desarrollo plano de las mismas. Todo ello es lo que aquí presento.
Cilindros y conos generalizados
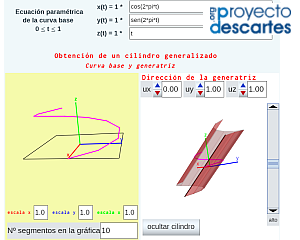
En la miscelánea "Construyo mis cilindros generalizados con curva base 3D" se abordan las superficies que pueden parametrizarse como 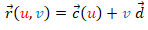 . El usuario define su curva directriz tridimensional
. El usuario define su curva directriz tridimensional 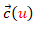 y la dirección de la generatriz que es constante y puede simular la generación del cilindro, obtener su desarrollo plano e imprimirlo si lo desea. En el caso en el que la curva directriz es plana, imprimiendo la base, se tiene una guía sobre la que proceder a la reproducción física del cilindro a partir del desarrollo impreso, pero en el caso de curva tridimensional no siempre será fácil esa construcción ya que no dispone de la reproducción física tridimensional de la curva directriz en la que poder apoyarse para poder plegar el desarrollo. Se requeriría abordar una impresión 3D de la directriz o bien construir la superficie lateral de un prisma cuya base inferior fuera plana y la superior siguiera el perfil de la curva directriz que serviría como soporte sobre el que apoyar y construir el cilindro. Ambas opciones son accesibles, pero no se contemplan en este recurso interactivo.
y la dirección de la generatriz que es constante y puede simular la generación del cilindro, obtener su desarrollo plano e imprimirlo si lo desea. En el caso en el que la curva directriz es plana, imprimiendo la base, se tiene una guía sobre la que proceder a la reproducción física del cilindro a partir del desarrollo impreso, pero en el caso de curva tridimensional no siempre será fácil esa construcción ya que no dispone de la reproducción física tridimensional de la curva directriz en la que poder apoyarse para poder plegar el desarrollo. Se requeriría abordar una impresión 3D de la directriz o bien construir la superficie lateral de un prisma cuya base inferior fuera plana y la superior siguiera el perfil de la curva directriz que serviría como soporte sobre el que apoyar y construir el cilindro. Ambas opciones son accesibles, pero no se contemplan en este recurso interactivo.
Pulsa sobre la imagen para acceder a la escena interactiva
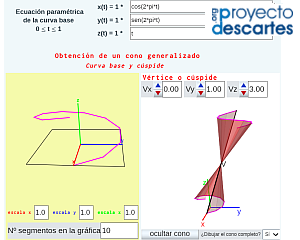
Con identica funcionalidad tenemos la miscelánea "Construyo mis conos generalizados con curva base 3D" correspondiente a la parametrización 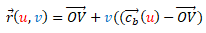 . En ella, definiendo la curva directriz tridimensional y el vértice se procede a generar el cono y a obtener su desarrollo plano. En este caso la reproducción material del cono, gracias a la referencia del vértice, puede ser más sencilla.
. En ella, definiendo la curva directriz tridimensional y el vértice se procede a generar el cono y a obtener su desarrollo plano. En este caso la reproducción material del cono, gracias a la referencia del vértice, puede ser más sencilla.
Pulsa sobre la imagen para acceder a la escena interactiva
El desarrollo de las dos escenas anteriores a partir de las escenas análogas de base plana no requirió mucho trabajo porque realmente estaban diseñadas para ello y practicamente lo que había era una restricción de la curva directriz estableciendo que la tercera componente fuera nula. El pimer objetivo planteado se alcanzó sin un coste excesivo.
Superficies tangenciales
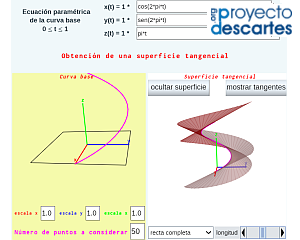
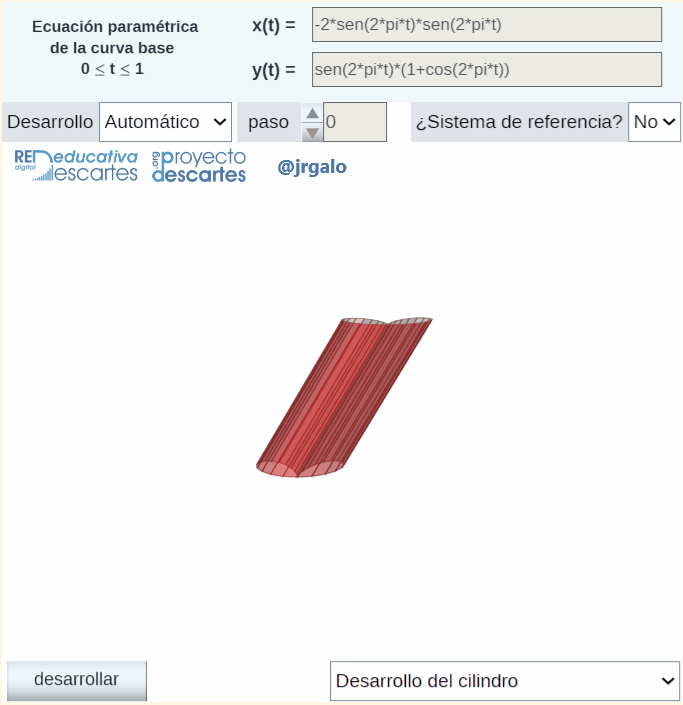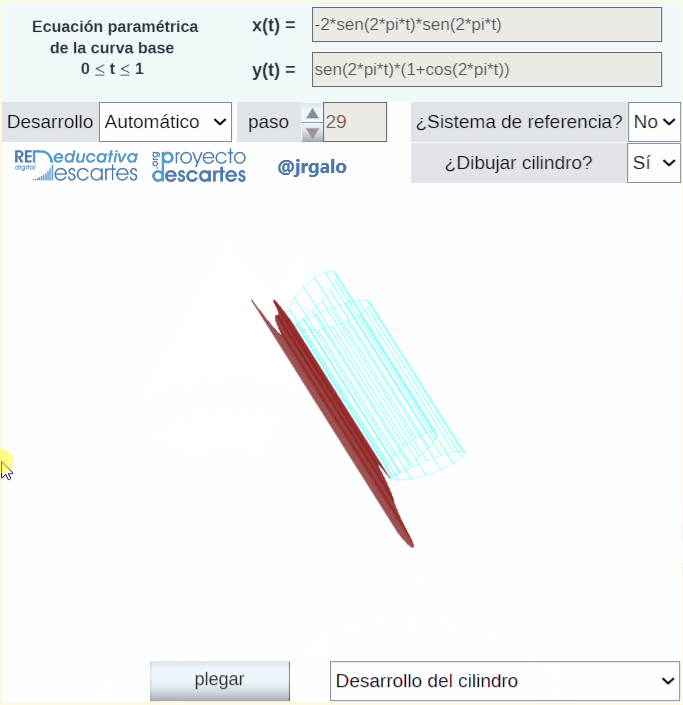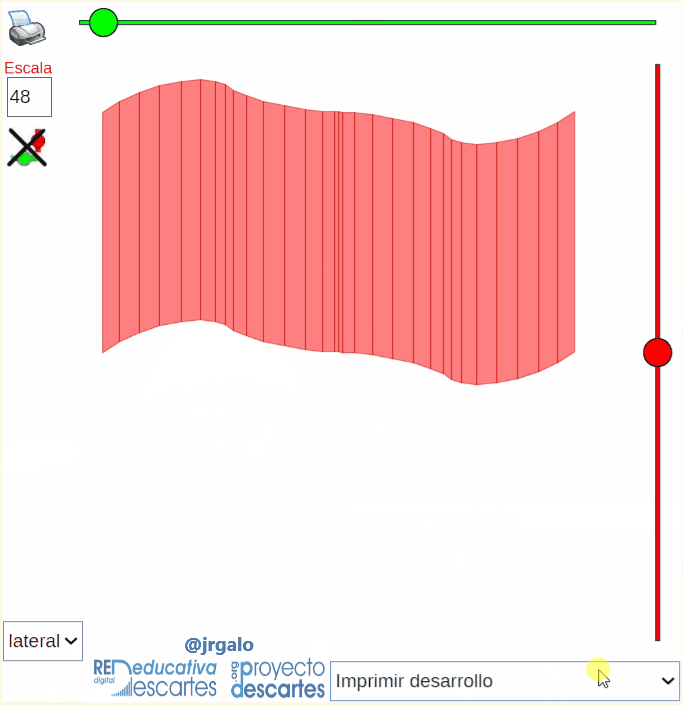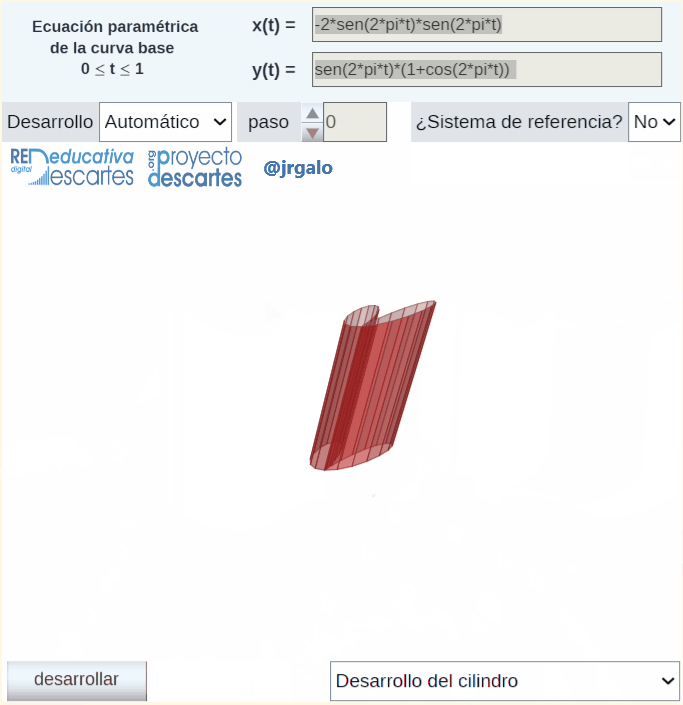
El segundo objetivo era desarrollar la miscelánea "Construyo mis superficies tangenciales" asociada a las parametrizaciones del tipo 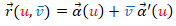 y en las que en cada punto de la curva directriz la generatriz sigue la dirección de la recta tangente a dicha directriz. He aquí la miscelánea:
y en las que en cada punto de la curva directriz la generatriz sigue la dirección de la recta tangente a dicha directriz. He aquí la miscelánea:
Pulsa sobre la imagen para acceder a la escena interactiva
En ella hay que detallar y aclarar algunas cuestiones:
- El usuario define la curva directriz y ésta, teóricamente, ha de ser diferenciable para que en todo punto esté definida la recta tangente que es la generatriz de la superficie.
- A nivel interno en la escena interactiva se trabaja a nivel discreto, es la realidad computacional. Por tanto, realmente, lo que se tiene es que la curva directriz es una poligonal y para segmentos de longitud pequeña la dirección de estos son buenas aproximaciones de la recta tangente. Consecuentemente en cada nodo de esa poligonal (punto de la curva directriz) se puede optar por considerar la dirección de la tangente bien por la del segmento anterior a ese nodo (que se corresponde con diferencias finitas regresivas) o la del segmento posterior (diferencias progresivas) o la media aritmética de ellas (diferencias centradas). En la escena se ha optado por considerar la tangente asociada a las diferencias regresivas
- En toda superficie tangencial los puntos singulares son los puntos de la curva directriz (arista de retroceso) que se corresponden con el valor del parámetro v = 0 y la superficie está formada por dos hojas (v < 0 y v > 0) —en la escena se ha indicado como semirrecta negativa y semirrecta positiva—.
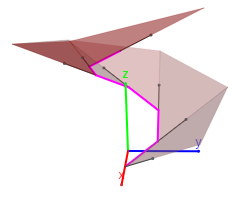
- Para aproximar cada una de las hojas de la superficie, entre cada dos tangentes consecutivas de la poligonal aproximante citada se considera el ángulo plano que forman ambas (en la escena un triángulo). Obviamente a medida que se consideran más número de segmentos la aproximación es mejor. Ver las siguientes imágenes:
 |
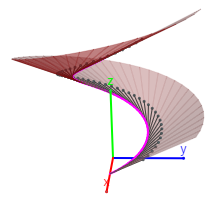 |
| Aproximación con seis segmentos | Aproximación con cincuenta segmentos |
- La aproximación indicada es similar a la que se efectúa en el caso de los cilindros que se aproximan por prismas y para los conos aproximados por pirámides. Y a partir de ésta la obtención dinámica del desarrollo plano y éste en sí es algo inmediato con la parafernalia técnica que habitualmente empleo.
En la animación siguiente se refleja parte de lo que puedes abordar y obtener con esta escena interactiva.
Pulsa sobre la imagen para ampliarla
Te invito a construir ¡tus superficies regladas desarrollables!
tanto de manera virtual como real.
En este artículo se describen y clasifican las superficies regladas desarrollables poniendo de manifiesto que éstas son cilindros, conos y superficies tangenciales. Y, mediante el uso de Descartes, se permite al usuario abordar la construcción virtual de "su" cilindro y cono personalizado, pero también se le da la posibilidad de convertirlo en un objeto tridimensional tangible sin más que proceder a la obtención automática de su desarrollo plano y, mediante su impresión en papel, proceder a su construcción.
Superficies regladas desarrollables
Una superficie es reglada si está constituida por una familia de rectas. Todas estas superficies se pueden parametrizar como:
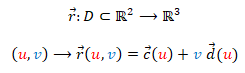 (1)
(1)
donde 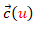 y
y 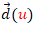 son curvas en el espacio tridimensional. La primera es la curva base o curva directriz y la segunda es el vector director de cada una de las rectas (generatriz). Efectivamente, fijado un valor del parámetro u puede observarse que la expresión obtenida es la ecuacion de una recta y, variando u, geométricamente lo que se puede interpretar es que se va recorriendo cada punto de la curva base
son curvas en el espacio tridimensional. La primera es la curva base o curva directriz y la segunda es el vector director de cada una de las rectas (generatriz). Efectivamente, fijado un valor del parámetro u puede observarse que la expresión obtenida es la ecuacion de una recta y, variando u, geométricamente lo que se puede interpretar es que se va recorriendo cada punto de la curva base 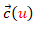 y por él pasa una recta cuya dirección viene dada por
y por él pasa una recta cuya dirección viene dada por 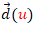 .
.
También puede expresarse de manera equivalente como:
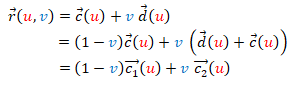 (2)
(2)
que algebraicamente representa, para cada valor de u, a una recta (o un segmento si consideramos 0 ≤ v ≤ 1), pero en este caso lo que se pone de manifiesto es que esa recta se apoya en un punto de la curva 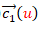 y en otro de la
y en otro de la 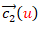 .
.
El ejemplo más simple de superficie reglada es un plano, pero entre otras, también lo son los cilindros, los conos, la banda de Moebius, el hiperboloide, etc.
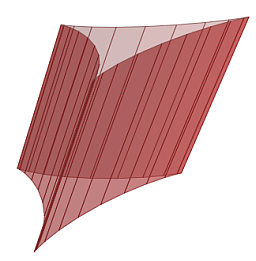 |
 |
| Cilindro generalizado | Cono generalizado |
 |
 |
| Banda de Möbius | Hiperboloide |
Una herramienta matemática que permite caracterizar la curvatura de cualquier superficie regular es la denominada curvatura de Gauss, y se verifica que dicha curvatura es invariante por isometrías. Todas las superficies regladas cumplen que su curvatura de Gauss es menor o igual que cero y, en particular, que la curvatura de Gauss de un plano es identicamente nula. En base a lo anterior, todas las superficies regladas que tienen curvatura cero son isométricas con el plano y son denominadas como superficies desarrollables ya que, consecuentemente, pueden construirse a partir de su desarrollo plano.
En la parametrización (1) la condición de curvatura nula equivale a que el denominado parámetro de distribución sea nulo, y éste viene dado por:
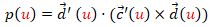 (3)
(3)
o en el caso de la parametrización (2) como:
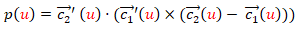 (4)
(4)
De (4) se observa que para que la superficie reglada sea desarrollable tiene que ocurrir que para todo u el vector tangente a la curva 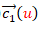 , el vector tangente a
, el vector tangente a 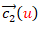 y el vector director de la recta que une a ambas curvas sean coplanarios al ser el producto mixto de los tres cero, o dicho de otra forma que el plano tangente es constante lo largo de cada recta generatriz.
y el vector director de la recta que une a ambas curvas sean coplanarios al ser el producto mixto de los tres cero, o dicho de otra forma que el plano tangente es constante lo largo de cada recta generatriz.
Pero un análisis más detenido de cuándo es identicamente nulo el parámetro de distribución nos puede permitir clasificar a las superficies desarrollables. Así en la expresión (3):
- Si
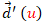 es identicamente nulo, entonces
es identicamente nulo, entonces 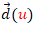 es un vector constante, es decir que todas las rectas tienen la misma dirección y la superficie es un cilindro generalizado de ecuación
es un vector constante, es decir que todas las rectas tienen la misma dirección y la superficie es un cilindro generalizado de ecuación 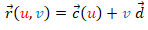 .
. - Si
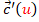 es idénticamente nulo, entonces
es idénticamente nulo, entonces 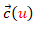 es el vector de posición de un punto V y la superficie desarrollable es un cono generalizado de vértice V, cuya ecuación sería
es el vector de posición de un punto V y la superficie desarrollable es un cono generalizado de vértice V, cuya ecuación sería 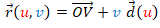 . También puede expresarse en función de una curva base como
. También puede expresarse en función de una curva base como 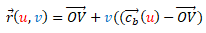 .
. - En cualquier otro caso se demuestra que es una superficie tangencial, que mediante un cambio de parámetro se puede expresar como
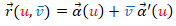 .
.
- Si
Superficies desarrollables con Descartes
En el proyecto "El metro: patrón inexacto para medir exactamente", que en el año 2004 contó con una ayuda de la Junta de Andalucía (España) para la elaboración de materiales y recursos educativos digitales, desarrollamos con Descartes en su versión Java algunos objetos educativos interactivos sobre conos y cilindros generalizados incluyendo la posibilidad de obtener su desarrollo plano. En este año 2020 hemos procedido a adaptarlos a DescartesJS y a mejorar sus posibilidades, en particular en lo relativo a forma de obtener ese desarrollo plano, a incluir la posibilidad de su impresión y consecuentemente a la posibilidad de su reproducción tangible tridimensional. Estos recursos actualizados están publicados en el subproyecto "misceláneas" de la RED Descartes y los enlazamos a continuación aquí en dos triadas de imágenes que respectivamente se corresponden con cilindros y conos generalizados.
En la primera triada correspondiente a los cilindros tenemos:
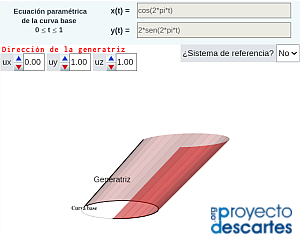
- "Cilindro generalizado" donde se muestra la construcción de un cilindro tomando como curva base una elipse y en la que podemos cambiar la dirección de la recta generatriz. La escena permite reproducir la generación del cilindro mediante desplazamiento de la generatriz sobre la curva base; simular y obtener el desarrollo plano; imprimir dicho desarrollo y el de las bases del cilindro. Adicionalmente, dado el contexto en el que se desarrolló originalmente esta escena —el metro—, se puede obtener un sistema de referencia basado en meridianos y paralelos.
- "Ejemplos de cilindros generalizados" donde se puede elegir diferentes curvas base (circunferencia, elipse, parábola, rama de hipérbola, segmento, cardiode, deltoide, bifolium, astroide, bicircular) y reproducir las acciones indicadas en la escena anterior.
- "Construyo mis cilindros" que como indica el título permite al usuario definir la curva base en coordenadas paramétricas y la dirección de la generatriz que desee y con ellas construir su cilindro generalizado. De nuevo puede realizar de manera virtual interactiva las acciones ya indicadas, pero también procediendo a la impresión del desarrollo pasar a disponer de la versión tangible de "su" cilindro. Para cada curva base cambiando el número de segmentos que se desean considerar en la representación se obtienen diferentes cilindros, para simular el caso continuo basta seleccionar un número de segmentos suficientemente elevado.
 |
 |
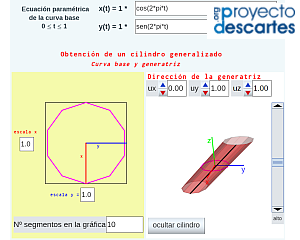 |
| Cilindro generalizado | Ejemplos de cilindros generalizados | Construyo mis cilindros |
De manera análoga en la triada correspondiente a los conos generalizados tenemos:
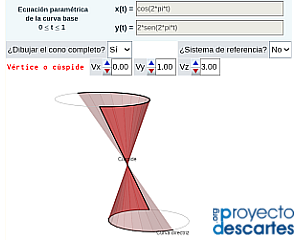
- "Cono generalizado" en el que se muestra la construcción de un cono tomando como curva base una elipse y en la que podemos cambiar su vértice. La escena interactiva permite reproducir la generación del cono mediante desplazamiento de la generatriz sobre la curva base; visualizar el cono completo; simular y obtener el desarrollo plano; imprimir dicho desarrollo y el de la base del cono. Adicionalmente, dado el contexto en el que se desarrolló originalmente esta escena —el metro—, se puede obtener un sistema de referencia basado en meridianos y paralelos.
- "Ejemplos de conos generalizados" donde se puede elegir diferentes curvas base (las mismas que en el caso de los cilindros) y reproducir las acciones indicadas en la escena anterior.
- "Construyo mis conos" que permite al usuario definir la curva base y el vértice y construir su cono generalizado tanto virtual como tangible..
 |
 |
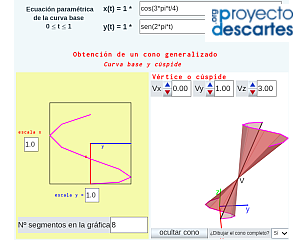 |
| Cono generalizado | Ejemplos de conos generalizados | Construyo mis conos |
En estos objetos interactivos se ha considerado que la curva base es una curva plana, así pues, he de ponerme la tarea de incorporar la tridimensionalidad de la curva base y presentarlo en un próximo artículo en este blog. Y, adicionalmente, este trabajo debería incoporar el caso de superficies tangenciales que implictamente, a priori, entraña cierta dificultad si se deja libertad de definición al usuario, pero sobre ello ya hablaremos.
Finalizo reseñando que para la obtención automática y animada del desarrollo plano del cilindro y el cono se aplica la rotación de Rodrigues descrita en un artículo anterior de este blog. Lo que se hace es plantearlo como el desarrollo plano de un prisma o una pirámide que se ajuste suficientemente al cilindro o cono dado. En la animación siguiente se refleja el desarrollo plano de un cilindro generalizado en el que su base es la curva denominada bifolium.
Pulsa sobre la imagen para ampliarla
Bibliografía
Lucas, E. (2017). Superficies regladas [Trabajo fin de grado]. Universidad de Murcia.
Rosado, E (2010). Superficies regladas [Apuntes docentes]. Universidad Politécnica Madrid.
En el artículo "El rectángulo de Newton como «simétrico» del triángulo de Pascal" llegamos a la conclusión de que si conocemos las congruencias con cero de los coeficientes en el Triángulo de Pascal, según la orientación dada por Pascal a su triángulo, entonces, por simetría, tenemos las correspondientes al rectángulo de Newton. Eso es lo que se refleja en la siguiente imagen.
Imagen de las congruencias con cero módulo dos de los coeficientes binomiales en el rectángulo de Newton.
Simetría respecto a esas congruencias en el Triángulo de Pascal
En este artículo vamos a centrarnos en analizar cuándo un coeficiente binomial es divisible por un determinado número primo, un problema sobre el que podemos encontrar bastantes resultados con fundamento aritmético y algebraico. Aquí, nos centraremos en aquellos resultados que nos permitan determinar y visualizar gráficamente esas congruencias, es decir, poder obtener el gráfico de la imagen anterior, u otros análogos, sin necesidad de calcular el coeficiente binomial y determinar su congruencia u obtener ésta mediante una recurrencia.
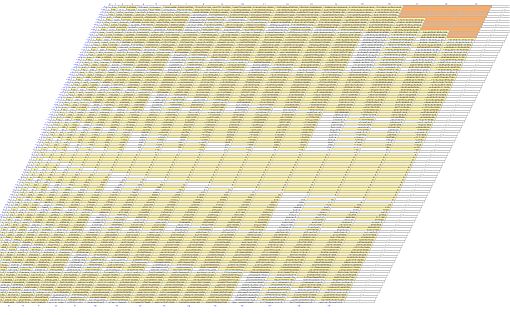
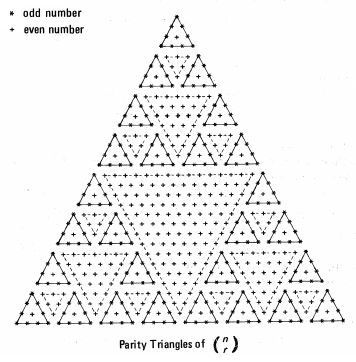
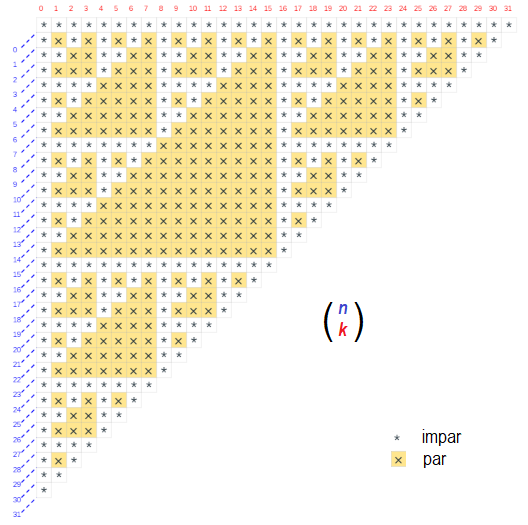
La primera representación gráfica de estas congruencias puede situarse en un brevísimo artículo de Kung (1976). Esa gráfica se muestra en la siguiente imagen, la situada a la izquierda, y en la de la derecha se refleja la gráfica análoga, pero mostrándola según la orientación original de Pascal y coloreando en naranja los números combinatorios pares (en ella cada número se determina observando el correspondiente índice superior en color azul y en rojo el inferior):
 |
 |
|
Triángulos de paridad en el Triángulo de Pascal. Kung, S. H. L. (1976). |
Triángulos de paridad en el Triángulo de Pascal en su orientación original |
Kung adicionalmente afirma, sin incluir la demostración, que para i entero no negativo:
- Si n = 2i y 1 ≤ k ≤ n-1, entonces
 es par.
es par. - Si n = 2i-1 y 0 ≤ k ≤ n, entonces
 es impar.
es impar.
Y ello se observa en las imagenes anteriores ya que para n = 0, 3, 7, 15, 31, todos los símbolos en esas filas o diagonales, respectivamente, son asteriscos (números impares). Y para n = 2, 4, 8, 16, 32, son todos cruces (números pares), salvo el primero y el último.
Ese es un breve artículo, pero que marca unas pautas que son extrapolables a la obtención de patrones en las congruencias con cero módulo otros números primos. De hecho, ese resultado es un caso particular de los dos que fueron enunciados en 1947 por N. J. Fine en su artículo "Binomial coefficients modulo prime", si bien el primero de ellos (según Joris et al. en un artículo de 1985) ya lo formuló Ram en 1909 (B. RAM, Common factors of n!/m!(n-m)!, (m= 1, 2 ,..., n- l), J. Indian Marh. Club (Madras) 1 (1909), 39-43):
- La condición necesaria y suficiente para que todos los coeficientes binomiales
 con 0 < k < n, sea divisible por un primo p es que n sea una potencia de p.
con 0 < k < n, sea divisible por un primo p es que n sea una potencia de p. - La condición necesaria y suficiente para que ningún coeficiente binomial de índice superior n, con n = n0 + n1 p + n2 p2 + ⋅⋅⋅ + nm pm, siendo 0 ≤ nr < p y nr > 0, sea divisible por p es que nr = p - 1 para r < m.
Veamos cómo se reflejan estos resultados de una manera gráfica en las dos imágenes siguientes:
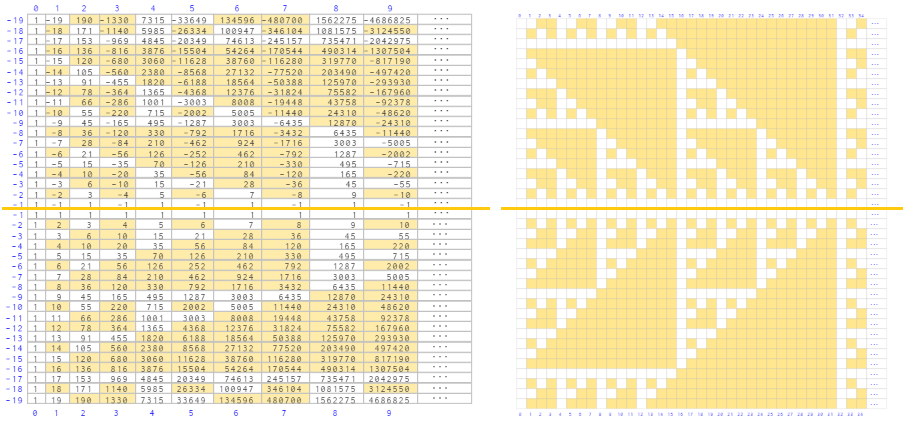
- En la imagen izquierda, se refleja gráficamente el primer resultado cuando p = 3, mostrándose todas las líneas en las que todos los números combinatorios son divisibles por 3, salvo el primero y el último. Esas líneas se corresponden con
 con 0 < k < n y n = 30, 31, 32, 33,... Gráficamente vienen a ser las "hipotenusas" de los triángulos rectángulos que particionan al triángulo de Pascal y que lo muestran a diferentes escala y posteriormente utilizaremos esta analogía y terminología coloquial para ubicar y describir otros resultados.
con 0 < k < n y n = 30, 31, 32, 33,... Gráficamente vienen a ser las "hipotenusas" de los triángulos rectángulos que particionan al triángulo de Pascal y que lo muestran a diferentes escala y posteriormente utilizaremos esta analogía y terminología coloquial para ubicar y describir otros resultados. - En la de la derecha se reflejan aquellas líneas en las que ningún número combinatorio es divisible por 3. En la parte superior de esa imagen se reflejan las separaciones entre esas filas (por falta de espacio tipográfico no se refleja el caso 30) y a la derecha se muestra la descomposición p-ádica del índice n correspondiente a los números combinatorios de cada una de esas líneas (expanda la imagen pulsando sobre ella para verlo). Por ejemplo, para 53 = 2 30 + 2 31 + 2 32 + 1 33 y eso nos muestra el camino de "saltos" de amplitud potencias de tres que se han de dar para, partiendo de 0, llegar a 53 (dos de amplitud 30, dos de 31, dos de 32 y uno de 33). Es decir, logramos mostrar visualmente, geométricamente, lo que queda escondido en un abstracto resultado algebraico, el cual puede ser chocante a cualquiera que accede a él por primera vez. Emulando a nuestro alumnado a la pregunta: ¿a quién se le ocurre que la descomposición p-adica da respuesta a este problema? le mostramos que el resultado algebraico, posiblemente, fue consecuencia de su visualización y la "pureza" matemática procedió a esconderlo.
En la miscelánea del final de este artículo podemos reproducir las situaciones descritas para cualquier primo hasta el 31 y en este enlace se tiene un muestrario rápido de las mismas.
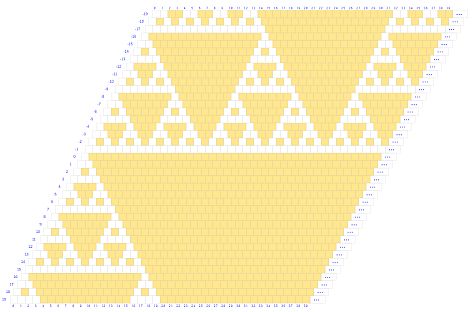
Y justamente, en base a la observación de esos patrones geométricos, podemos visualizar y deducir la propiedad que nos permite detectar todas las hipotenusas de todos los triángulos rectángulos isósceles que muestran esas congruencias. Podemos ver cómo hay triángulos de diferente tamaño, siendo pa-1 el tamaño de las hipotenusas respectivas, y cada uno de ellos tienen una distribución periódica en horizontal y vertical con un periodo pa. Por ejemplo, en la siguiente imagen se reflejan en color naranja los números combinatorios congruentes con cero módulo 5 y se observan tres tipos de triángulos según su tamaño: los de hipotenusa 4 = 51-1, los de 24 = 52-1 y parcialmente (en la esquina inferior derecha) el de 124 = 53-1. La hipotenusa del primero se ha reflejado en color verde y el triángulo se repite periódicamente en horizontal y vertical con un periodo 5, según se ve en dicha imagen. La del segundo está reflejada en color violeta y se repite también periódicamente con periodo 52, y así sería de manera análoga y sucesiva.
 Periodicidad en las hipotenusas de los triángulos congruentes
Periodicidad en las hipotenusas de los triángulos congruentes
Lo anterior, ahora le invito a que mire con ojos algebraicos, queda englobado en el resultado que enuncio a continuación:
p es divisor de todos los números combinatorios 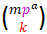 con m, a, k ∈ ℕ, 0 < k < mpa y k no divisible por pa (1)
con m, a, k ∈ ℕ, 0 < k < mpa y k no divisible por pa (1)
Este resultado personal puede relacionarse o considerarse como una reinterpretación —que se centra, enfoca y destaca el aspecto de periodicidad— del aportado por Ram (1909) —del que puede verse la demostración realizada por Albree (1972)— que afirma:
Para cualquier entero positivo n , pr = mcd {  con 0 < k < n, y mcd (k, p)=1 } donde p es primo, r es un entero positivo y pr divide a n.
con 0 < k < n, y mcd (k, p)=1 } donde p es primo, r es un entero positivo y pr divide a n.
Y ¿por qué les remarco que es de gran interés determinar esas hipotenusas? La respuesta también puede visualizarse en la imagen anterior y lo detallamos a continuación ya que conocida una hipotenusa de números congruentes con 0 módulo p,  con r < k < s, por la propiedad de los números combinatorios que relaciona los de índice superior n+1 con los de índice n,
con r < k < s, por la propiedad de los números combinatorios que relaciona los de índice superior n+1 con los de índice n,
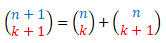
se deduce que los números combinatorios que componen el triángulo rectángulo T(n; r, s)
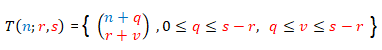 (2)
(2)
—ver imagen siguiente— son también congruentes con 0 módulo p. La justificación es simple, dado que la suma de dos números divisibles por p es un número divisible por p.
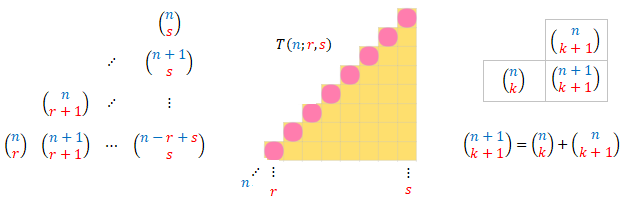 Transmisión de la congruencia en las hipotenusas a los triángulos rectángulos
Transmisión de la congruencia en las hipotenusas a los triángulos rectángulos
Joris et al. (1985) abordan un estudio más profundo al que necesitamos aquí de las propiedades de estos triángulos y a él dirigimos a quienes estén interesados en incrementar su conocimiento en este tema.
Combinando (1) y (2), concluyo que los números combinatorios congruentes con 0 módulo p siguen un patrón de triángulos "rectángulos" T(pa; 1, pa-1) cuyas hipotenusas están constituidas por los números combinatorios 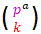 con a, k ∈ ℕ, 0 < k < pa.
con a, k ∈ ℕ, 0 < k < pa.
 Patrón de triángulos T(pa; 1, pa-1) con p=3 y a = 1,2, y 3
Patrón de triángulos T(pa; 1, pa-1) con p=3 y a = 1,2, y 3
distribuyéndose de forma periódica según el esquema:
T(m pa; 1+k pa, (1+k)pa-1) con 0 ≤ k < m y a, m ∈ ℕ
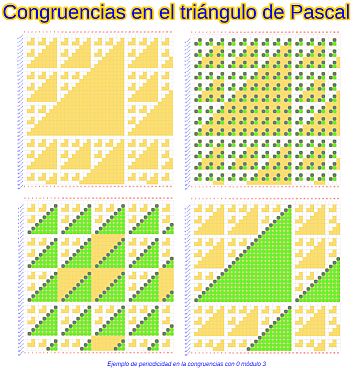
Eso es lo que se observa en el siguiente mosaico de imágenes donde se refleja:
-
- imagen superior izquierda: números combinatorios congruente con 0 módulo 3 en color naranja.
- imagen superior derecha: triángulos congruentes con T(31; 1, 31-1) en color verde claro y las hipotenusas en verde oscuro, y desplazamiento periódico en horizontal y vertical con periodo 3.
- imagen inferior derecha: triángulos congruentes con T(32; 1, 32-1) en color verde claro y las hipotenusas en verde oscuro, y desplazamiento periódico en horizontal y vertical con periodo 32.
- imagen inferior derecha: triángulos congruentes con T(33; 1, 33-1) en color verde claro y las hipotenusas en verde oscuro, y desplazamiento periódico en horizontal y vertical con periodo 33.
 Esquema de periodicidad de los triángulos T(pa; 1, pa-1) con p=3 y a = 1, 2, y 3
Esquema de periodicidad de los triángulos T(pa; 1, pa-1) con p=3 y a = 1, 2, y 3
Así pues la reproducción de todas las congruencias con 0 es una mera reiteración gráfica, periodicidad, de esos triángulos básicos citados.
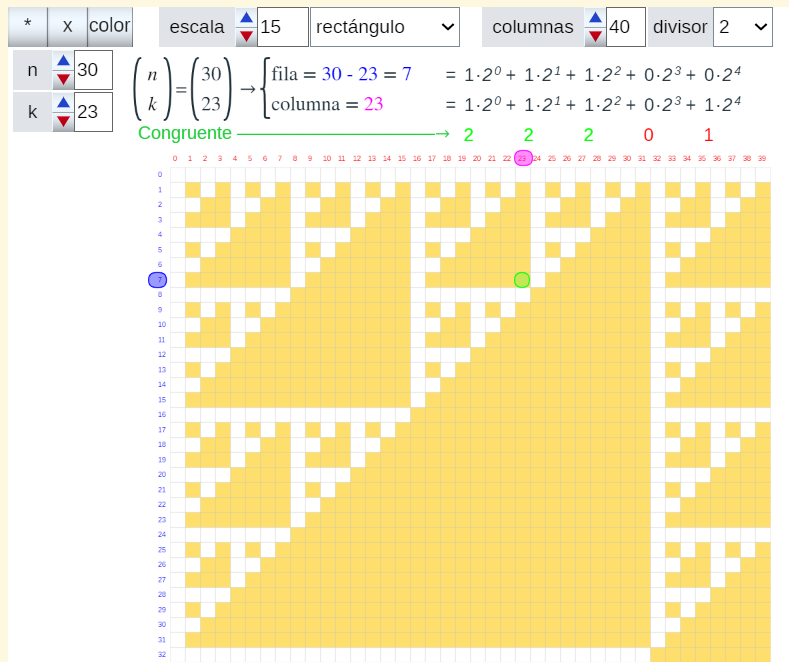
Pero dado un número combinatorio  ¿podemos saber si es o no congruente con 0 módulo p sin necesidad de calcularlo, de una manera sencilla, rápida y sin aplicar recursividad, o lo que es equivalente, sin basarse en diagonales, es decir, en números combinatorios con índice superior menor que n? ¡Veamos que sí! y para ello nos vamos a basar en la posición relativa (fila y columna) que ocupa cada número combinatorio en el triángulo de Pascal original. Observemos que el número
¿podemos saber si es o no congruente con 0 módulo p sin necesidad de calcularlo, de una manera sencilla, rápida y sin aplicar recursividad, o lo que es equivalente, sin basarse en diagonales, es decir, en números combinatorios con índice superior menor que n? ¡Veamos que sí! y para ello nos vamos a basar en la posición relativa (fila y columna) que ocupa cada número combinatorio en el triángulo de Pascal original. Observemos que el número  ocupa la fila n-k y la columna k, que todos los números combinatorios de índice n cumplen que la suma de la fila y la columna que ocupan es n, y que los números combinatorios del triángulo rectángulo T(n; r, s) cumplen que la suma de la fila y la columna de todos ellos es mayor o igual que n. Con este dato y en base a la periodicidad podemos afirmar lo siguiente:
ocupa la fila n-k y la columna k, que todos los números combinatorios de índice n cumplen que la suma de la fila y la columna que ocupan es n, y que los números combinatorios del triángulo rectángulo T(n; r, s) cumplen que la suma de la fila y la columna de todos ellos es mayor o igual que n. Con este dato y en base a la periodicidad podemos afirmar lo siguiente:
Dado el número combinatorio  , consideremos la descomposición p-ádica de n-k y de k
, consideremos la descomposición p-ádica de n-k y de k
n-k = a0 + a1 p + a2 p2+ ⋅ + am pm
k = b0 + b1 p + b2 p2+ ⋅ + bm pm
con m = max (ent(logp(n-k)), ent(logp(k)) ), 0 ≤ aj, bj < p, se verifica que:
 es divisible por p si y solo si aj + bj ≥ p al menos para algún j, 0 ≤ j ≤ m.
es divisible por p si y solo si aj + bj ≥ p al menos para algún j, 0 ≤ j ≤ m.
Además, para los valores de j en los que aj + bj ≥ p, entonces  está en un triángulo T(pj+1; 1, pj+1-1) de números congruentes con 0 módulo p.
está en un triángulo T(pj+1; 1, pj+1-1) de números congruentes con 0 módulo p.
En la siguiente escena se puede reproducir visualmente todos los resultados indicados anteriormente y profundizar en el conocimiento de las interioridades del Triángulo de Pascal.
Pulsa sobre la imagen para abrir la escena
En la imagen anterior se observa como el número combinatorio 30 sobre 23 es congruente con cero módulo 2 y forma parte de un triángulo rectángulo básico de hipotenusa 1 , otro de hipotenusa 3 y otro de hipotenusa 7 (para éste último es evidente, para los dos anteriores haga traslaciones de los triángulos básicos, según el periodo antes indicado, y verá que ese número combinatorio está incluido en ellos). Todo se obtiene sin más que observar la relación de los coeficientes en la descomposición 2-ádica de la fila y columna que ocupa, ya que en este caso, para las tres primeras potencias de 2 la suma de los coeficientes es mayor o igual que el valor del módulo (en este caso 2).
Llegados a esta meta, estando aún confinados por la pandemia del COVID-19, cabe preguntarse si este artículo, y los dos anteriores publicados en este blog sobre este tema, tendrá o no continuidad... el tiempo lo dirá o quizás la necesidad de cambiar de temática para relajar la mente en otros ámbitos lo interrumpa. Tenga o no alguna nueva adenda, gracias a todos los que habéis dedicado parte de vuestro tiempo en leer lo descrito y los nuevos resultados hallados y expuestos en esta trilogía.
En el artículo anterior "El paralelogramo de Newton" se mostró la ampliación que realizó Newton del triángulo de Pascal y cómo, ésta, le condujo a extender la expresión de las potencias binomiales al caso de exponentes enteros negativos. En este artículo mostramos cómo el esquema organizativo con el que Pascal divulgó su triángulo es más adecuado que el que usó Newton (versión escalonada de Stifel), pues conocido el primero, el segundo se obtiene por una simple reflexión y, por tanto, las congruencias existentes entre los coeficientes binomiales en el rectángulo de Newton queda reducida a realizar una simetría de las congruencias del triángulo de Pascal.
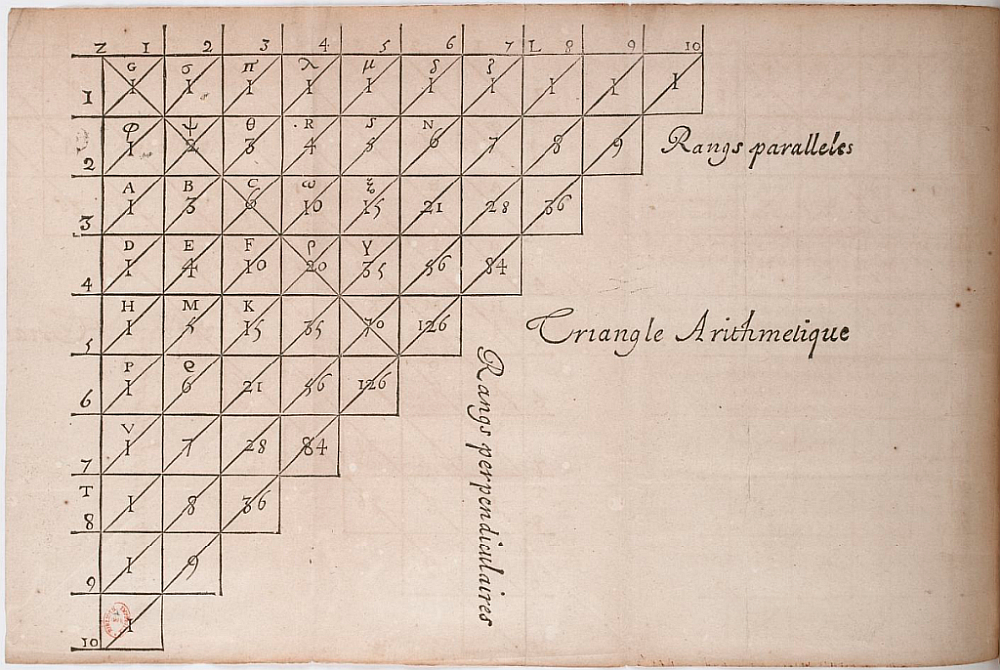
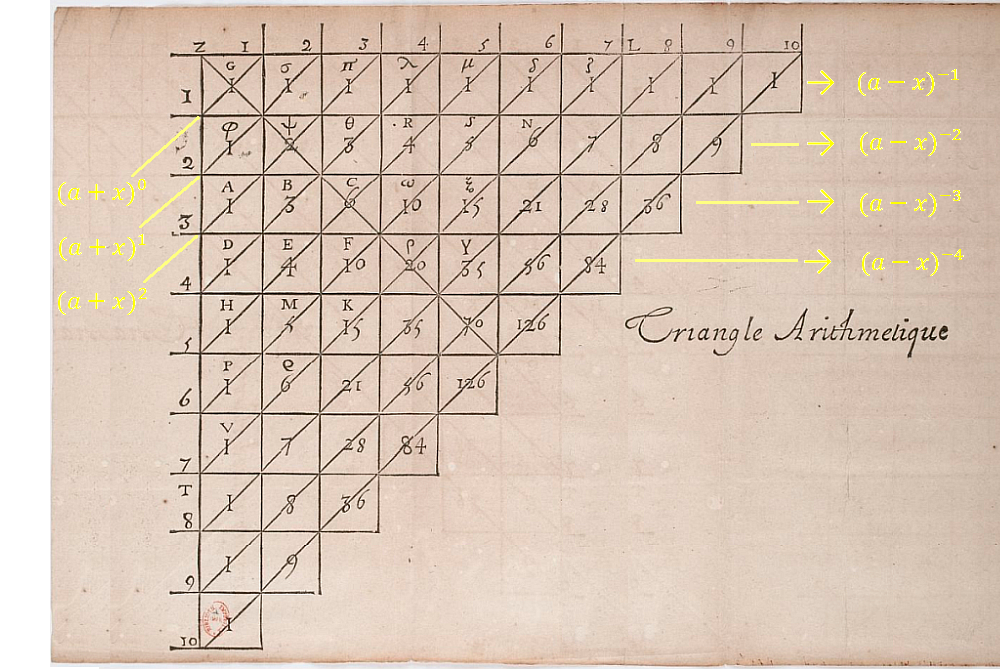
Pascal, en su libro Traité du triangle arithmétique (1665) analizó las propiedades del triángulo aritmético que quedó finalmente ligado a su nombre. La forma en que lo organizó y presentó es la reflejada en la siguiente imagen que he tomado de dicho libro, que es de dominio público:
El triángulo aritmético de Pascal reflejado en su libro Traité du triangle arithmétique
Esa presentación difiere de la forma usual que actualmente suele utilizarse que lo muestra como un triángulo isósceles:
El triángulo de Pascal en su presentación como triángulo isósceles
Y también difiere de la usada por Newton como base para su extensión ya que usó un triángulo rectángulo completado con ceros para obtener un rectángulo: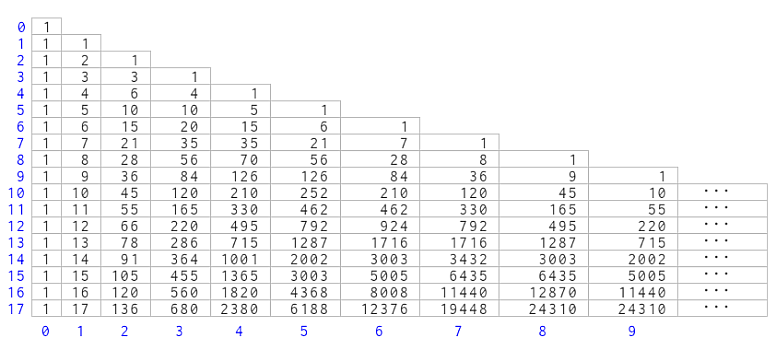
Presentación del triángulo de Pascal para abordar la extensión de Newton
Esta versión escalonada aparece en el libro Arithmetica Integra (1544) de Michael Stifel (1487-1567), en el reverso de la página 44:
Presentación realizada por Stilfel y usada por Newton para su extensión
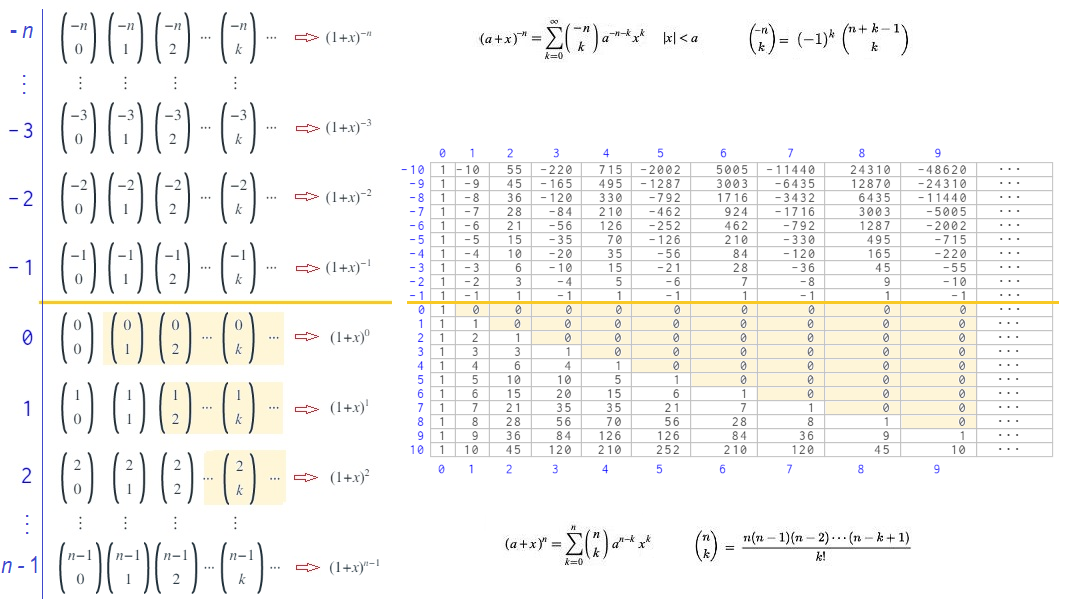
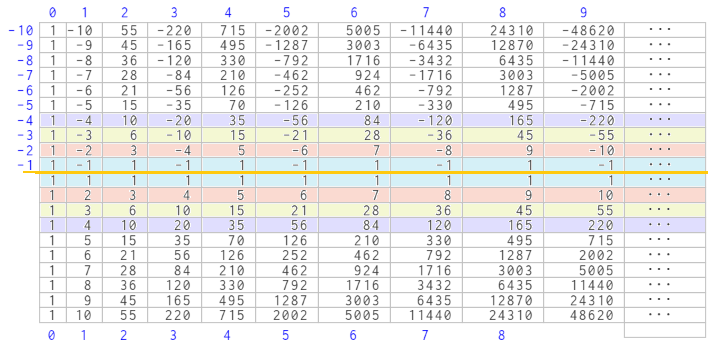
Esa extensión, que detallamos en el artículo previo citado, podemos resumirla en la siguiente imagen. En ella, reseñemos que cada fila del rectángulo se corresponde con los coeficientes binomiales del desarrollo de la potencia de un binomio. La fila numerada con el entero n se corresponde con los coeficientes del desarrollo de (a+x)n, por ejemplo, para n = -1 son los coeficientes de (a+x)-1 y para n = 2 los de (a+x)2.
El paralelogramo de Newton y el desarrollo binomial
Al expresar los coeficientes binomiales de índice superior negativo en base a otros de índice superior positivo: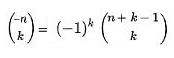 , podemos observar la relación existente entre los coeficientes en el rectángulo de Newton correspondientes a la extensión realizada por él y los ubicados en la zona de partida de Pascal. Seleccionada una columna, salvo un posible cambio de signo, los coeficientes de la extensión de Newton (filas etiquetadas con números negativos) se corresponden con los del triángulo de Pascal, pero con una traslación en la numeración de las filas. Por ejemplo, para la columna 3 los coeficientes de la zona correspondiente a la extensión de Newton son {-1, -4, -10, -20, -35, -56, -84, ...} que se corresponden con las filas numeradas respectivamente como {-1, -2, -3, -4, -5, -6, -7, ...}, y los coeficientes en la zona del triángulo de Pascal son {1, 4, 10, 20, 35, 56, 84 ,...} pero trasladadas en este caso dos posiciones, pues aquí sendas filas se correponden con {3, 4, 5, 6, 7, 8, 9, ...}. Así pues, si quitásemos todos los ceros y ocupáramos esos huecos trasladando los números de cada columna hacia arriba, obtendríamos una tabla simétrica respecto a la línea de separación existente entre la fila 0 y la -1 (salvo el signo de los coeficiente que para columnas impares será negativo y para las pares positivo), de esta manera conocidos los coeficientes del triángulo de Pascal tenemos también los correspondientes al rectángulo de Newton y consecuentemente bastaría sólo obtener el primero.
, podemos observar la relación existente entre los coeficientes en el rectángulo de Newton correspondientes a la extensión realizada por él y los ubicados en la zona de partida de Pascal. Seleccionada una columna, salvo un posible cambio de signo, los coeficientes de la extensión de Newton (filas etiquetadas con números negativos) se corresponden con los del triángulo de Pascal, pero con una traslación en la numeración de las filas. Por ejemplo, para la columna 3 los coeficientes de la zona correspondiente a la extensión de Newton son {-1, -4, -10, -20, -35, -56, -84, ...} que se corresponden con las filas numeradas respectivamente como {-1, -2, -3, -4, -5, -6, -7, ...}, y los coeficientes en la zona del triángulo de Pascal son {1, 4, 10, 20, 35, 56, 84 ,...} pero trasladadas en este caso dos posiciones, pues aquí sendas filas se correponden con {3, 4, 5, 6, 7, 8, 9, ...}. Así pues, si quitásemos todos los ceros y ocupáramos esos huecos trasladando los números de cada columna hacia arriba, obtendríamos una tabla simétrica respecto a la línea de separación existente entre la fila 0 y la -1 (salvo el signo de los coeficiente que para columnas impares será negativo y para las pares positivo), de esta manera conocidos los coeficientes del triángulo de Pascal tenemos también los correspondientes al rectángulo de Newton y consecuentemente bastaría sólo obtener el primero. 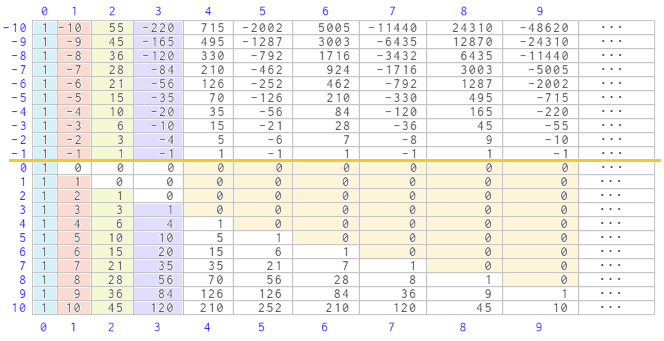
Relación entre los coeficientes binomiales de índice superior negativo con los de índice superior positivo
También podemos establecer otra relación: los coeficientes de la fila -1 se corresponden (en valor absoluto) con los de la columna 0 en la zona del triángulo de Pascal, los de la fila -2 con los de la columna 1 y, en general, la fila -n con la columna n-1. Destacamos estas filas pues cada una de ellas nos aporta los coeficientes del desarrollo binomial con exponente negativo.
Y por la simetría del triángulo de Pascal también tendremos que los coeficientes de la fila -1 se corresponden (en valor absoluto) con los de la diagonal 0 en la zona del triángulo de Pascal, los de la fila -2 con los de la diagonal 1 y, en general, la fila -n con la diagonal n-1.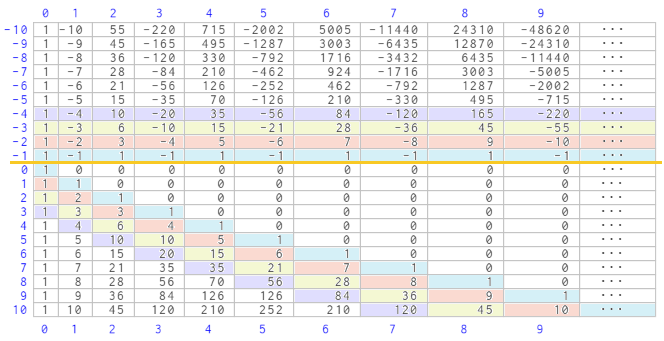
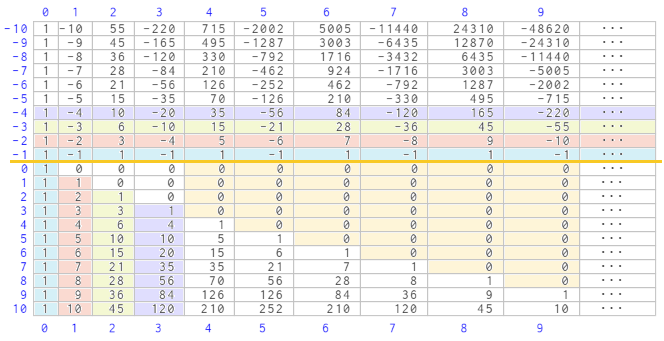
Y omitiendo los ceros y trasladando las columnas hacia arriba para ocupar los huecos, obtenemos la siguiente distribución simétrica (en valor absoluto, insisto). Y en esa imagen hemos omitido la numeración de las filas en la parte inferior ya que esos coeficientes ya no se corresponden con los números combinatorios del triángulo de Pascal por filas, sino que esos coeficientes están ordenados según la estructura original adoptada por Pascal.
La relación observada en las imagenes anteriores se justifica sin más que detallar la relación existente entre los coeficientes binomiales que ahí están involucrados, y eso es lo que reflejamos a continuación. En el recuadro izquierdo tenemos los coeficientes del rectángulo de Newton, destacando en color naranja la ampliación de los números combinatorios con índice superior positivo o nulo y con índice inferior de mayor valor que el superior, cuyo valor es cero. En el cuadro intermedio se han omitido esos números nulos y se han compactado las columnas para ocupar los huecos. Y en el marco derecho se han expresado los coeficientes binomiales de índice negativo según su equivalencia con los números combinatorios y ahí puede comprobarse la simetría de los coeficientes que ya hemos indicado.
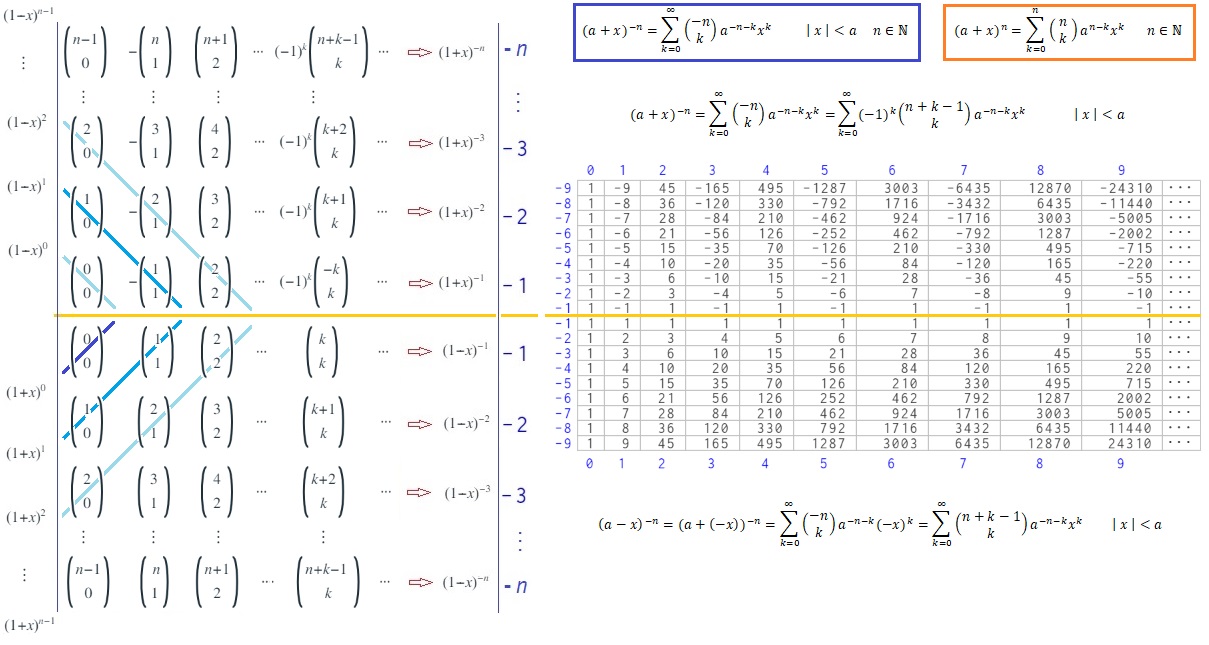
Y con esto ¿a qué hemos llegado? Pues observemos la siguiente imagen que tiene un contenido denso, pero que sirve de resumen.
Coeficientes binomiales y binomio de Newton con exponente natural y entero
En la parte izquierda se reflejan los coeficientes binomiales obtenidos en el cuadro anterior, donde podemos destacar que:
- Cada fila de la parte superior del rectángulo de Newton —por ejemplo la etiquetada en color azul como -n, ubicada encima de la línea naranja— se corresponde con los coeficientes del desarollo del binomio de (a+x)-n, tal y como indicamos en el artículo anterior.
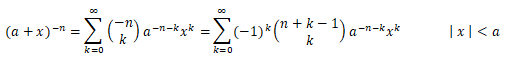
- Cada fila de la parte inferior, que es el triángulo de Pascal en su orientación original, se corresponde con los coeficientes del desarollo del binomio de (a-x)-n, pues tenemos que:
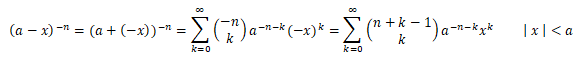
- Cada una de las "diagonales" inferiores y superiores, coloreadas en tonos azules, se corresponden respectivamente con los coeficientes binomiales de (a+x)n y (a-x)n.
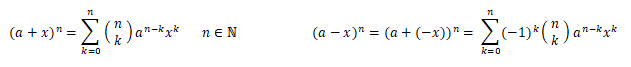
Así pues, como indicaba al inicio, basta tener el triángulo de Pascal para obtener todos los desarrollos binomiales con exponente natural y entero. En la posición original de Pascal, las filas son los coeficientes del desarrollo de (a-x)-n y a partir de este desarrollo el de (a+x)-n basta obtenerlo como (a-(-x))-n, y las diagonales son los coeficientes del desarrollo de (a+x)n y el desarrollo de (a-x)n se obtiene como (a+(-x))n.
Coeficientes binomiales del desarrollo del binomio de Newton con exponente natural y entero en el Triángulo de Pascal
Llegados a este punto, identificados el significado y posición de estos coeficientes binomiales, aquellos que no se acostumbren a esta posición pueden hacer un giro de vértice el del ángulo recto en el triángulo anterior y ángulo -45º y ubicarlo en la posición usual actual. Aquí lo tiene a continuación, ya hemos justificado que es autosuficiente, pero no sólo enseñe cuáles son los coeficientes de las potencias de exponente natural ¡hágalo también con los de exponente entero negativo!
Coeficientes binomiales del desarrollo del binomio de Newton con exponente natural y entero en el Triángulo de Pascal
Obviamente la presentación y orientación es a gusto del lector, pero en la posición dada por Pascal acontece que si conocemos las congruencias con cero de los coeficientes en el Triángulo de Pascal, entonces por simetría tenemos las correspondientes al rectángulo de Newton, tal y como lo observamos en la siguiente imagen.
Imagen de las congruencias con cero módulo dos de los coeficientes binomiales en el rectángulo de Newton. Simetría respecto a esas congruencias en el Triángulo de Pascal
Esa simetría no acontece para congruencias con resto no nulo y módulo superior a dos, dado que en las columnas impares hay un cambio de signo en los valores de los coeficientes... Pero la profundización en estas congruencias tendremos que dejarlas para un tercer artículo, al que os emplazo dentro de unos días.
En la miscelánea "El rectángulo de Newton como «simétrico» del triángulo de Pascal" puede observarse lo antes descrito.
Nota bene: Eli Maor en su libro "e: historia de un número" (1994) describe que Newton en 1665 estuvo recluido durante dos años con motivo de la "gran peste de Londres" y que, durante ese tiempo, formó sus ideas sobre el universo y puso los fundamentos de lo que sería un cambio en el curso de la ciencia. Maor, también nos detalla que fue en esta época cuando procedió a la extensión del triángulo de Pascal y a la expansión de la potencia de un binomio a potencias de exponente entero y racional. Trescientos cincuenta y cinco años después, actualmente, estamos en un periodo de reclusión mundial a causa de la pandemia del "Coronavirus COVID-19" y aquí, en este artículo, recordando su "rectángulo".
El "triángulo de Pascal o de Tartaglia" es ampliamente conocido tanto por las curiosas propiedades que en él pueden encontrarse como por su aplicación en el desarrollo algebraico de la potencia de un binomio. Suele aprenderse ligado a lo que usualmente se enseña con el nombre de "binomio de Newton" y que se identifica con la potencia de un binomio cuyo exponente es un número natural. Pero quien enunció o al menos divulgó este desarrollo particular, relacionándolo con ese triángulo, fue Pascal y de ahí que se denomine a dicho triángulo con su nombre. No obstante, el "triángulo de Pascal" ya era conocido, siglos antes, por matemáticos persas y chinos. Según Maor (1994) la aportación concreta de Newton en el contexto del desarrollo binomial se sitúa en el caso del desarrollo con exponentes racionales y con exponentes enteros y únicamente llegó a conjeturarla sin llegar a abordar o al menos divulgar su demostración. Actualmente este resultado es un caso particular del denominado "Teorema binomial".
Newton abordó la extensión del triángulo de Pascal efectuando un cálculo hacia atrás, de manera que se mantuviera la misma propiedad recursiva de que un elemento de una fila sea el resultado de la suma de dos de la fila anterior siguiendo la propiedad que se verifica entre los números combinatorios.
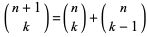
Con esta extensión recursiva en sentido inverso, Newton construye nuevas filas, cada una de las cuales tiene infinitos números y cuya escritura conduce a la forma de un "paralelogramo" (o si se desea puede mostrarse, en particular, como un rectángulo) y cada una de ellas puede asociarse a filas que se corresponderían con números "combinatorios" cuyo índice superior serían números enteros negativos.
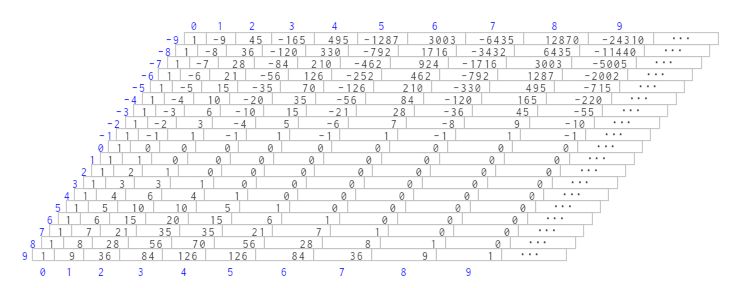
A su vez, Newton hace corresponder los números ubicados en cada fila con los coeficientes del desarrollo de la potencia de un binomio cuyo exponente ya no sólo sería un número natural, sino que en general puede ser un número entero. Y, consecuentemente, a todos los números del paralelogramo de Newton los denominaremos coeficientes binomiales (pierde sentido asociarlo con el número de combinaciones). El desarrollo del binomio conduce a un número finito de sumandos cuando el exponente es natural e infinitos (una serie) cuando es un entero negativo.
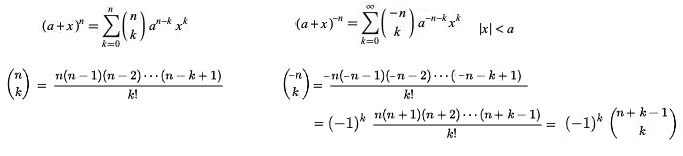
En la miscelánea "Extensión del triángulo de Pascal: El paralelogramo de Newton" se muestran los coeficientes binomiales de dicho paralelogramo. Pulsando el botón "indicaciones" de este recurso se pueden consultar algunos detalles adicionales.
Pulsa sobre la imagen para abrir la escena
La representación de dicho paralelogramo numérico entraña dos dificultades principales a medida que se incrementa la cantidad de números a visualizar. Por un lado, el espacio que necesita ocupar la escritura de cada coeficiente binomial que progresiva y rápidamente va aumentando, al ser mayor el número de cifras que lo constituyen. Y, por otro, el tiempo de cálculo necesario para ubicar, desplazar y representar en la tabla dichos coeficientes y para poder escalarla (si se desea). Adicionalmente, el cálculo de los coeficientes conduce a números enteros que superan el número designado como MAX_SAFE_INTEGER y que en javascript es 253-1 (algo superior a 9 mil billones); así pues, en esos casos no se refleja el coeficiente y se colorea la casilla donde iría ubicada con un fondo rojizo.
En dicha escena se pueden visualizar, mediante colores, pautas geométricas de cómo se distribuyen dichos coeficientes cuando se plantean congruencias numéricas respecto a un divisor y resto seleccionado. No obstante, estas distribuciones pueden observarse mejor si no se muestran los valores de los coeficientes y ello es lo que se aborda en la miscelánea: "Congruencias en el paralelogramo de Newton"
Pulsa sobre la imagen para abrir la escena
En este caso (ver las indicaciones incluidas en la miscelánea) la dificultades siguen centrándose en el espacio necesario para representar el paralelogramo cuando el número de filas y columnas considerado es elevado, pero al no reflejarse el número en sí, cada uno de estos coeficientes ocupa el mismo espacio y puede escalarse hasta el extremo de que ocupe un único píxel. Por otro lado, el cálculo de las congruencias puede hacerse de manera recursiva sin necesidad de calcular el coeficiente y consecuentemente no se ve afectado por lo indicado sobre el máximo entero admisible en javascript. Obviamente, las necesidades computacionales son elevadas y, por defecto, en la escena se ha limitado el número de filas y columnas a 400, pero editando la escena puede cambiarse.
Para evitar que cada interesado tenga que dedicar tiempo en la generación de las imágenes de las congruencias, he preparado un muestrario de consulta para las congruencias con los números primos hasta el treinta y uno, representando los coeficientes binomiales de índice superior en el rango desde -999 a 999 y de índice inferior de 0 a 999. Éste está accesible en la miscelánea: "Muestrario de congruencias en el paralelogramo de Newton", pudiéndose ampliar las imágenes ahí incluidas.
Pulsa sobre la imagen para abrir la escena
En un próximo artículo en este blog, mostraré que si retomamos el esquema organizativo original que Pascal (Traité du triangle arithmétique, 1665) utilizó al presentar y analizar las propiedades de este triángulo numérico, entonces los patrones de las congruencias que se observan en él son mas fáciles de identificar y pautar, y la extensión de estos a los coeficientes binomiales con índice superior un entero negativo se realiza de manera trivial.
Finalmente, quienes deseen aplicar los coeficientes binomiales y practicar con el desarrollo algebraico de potencias de un binomio pueden usar las siguientes misceláneas:
Ejercicios de desarrollo algebraico usando el "Binomio de Newton"
Pulsa sobre la imagen para abrir la escena
Ejercicios del "binomio de Newton" con exponente entero
Pulsa sobre la imagen para abrir la escena