Mostrando artículos por etiqueta: Descartes
Cuarta sesión (27 de agosto de 2021)
|
4A.
4B. Agenda de la cuarta sesión. Libro interactivo con el guión de la sesión.
|
Tercera sesión (13 de agosto de 2021)
|
3A.
3B. Agenda de la tercera sesión. Documento pdf con el guión de la sesión y enlaces usados o recomendados.
Vídeo de apoyo Uso de viñetas con imágenes: |
Segunda sesión (30 de julio de 2021)
|
2A.
2B. Agenda de la segunda sesión. Documento pdf con el guión de la sesión y enlaces usados o recomendados.
Vídeos de apoyo Google como servidor: https://www.youtube.com/watch?v=xv-URqFtr60 Imágenes animadas: https://www.youtube.com/watch?v=J-KDmBCNm-w Tabla de contenido: https://www.youtube.com/watch?v=jOauL-piook Editores HTML: https://www.youtube.com/watch?v=TlL0et79vgo Estilos: https://www.youtube.com/watch?v=8oawkkSGUdU Archivo de estilos: https://www.youtube.com/watch?v=biQVKma3WZk Ayuda con los colores Colores CSS: Combinaciones de colores: https://www.colorcombos.com/color-schemes/2/ColorCombo2.html |
Coincidiendo con el 8º aniversario de RED Descartes, y con el objetivo de actualizar algunas de nuestras producciones audiovisuales, hemos decidido editar y compartir con todos nuestros usuarios y seguidores el siguiente vídeo, que hemos denominado ¿Por qué me gusta Descartes?, donde socios y miembros de la RED Descartes de cinco países responden escuetamente a la pregunta formulada aportando su personal valoración, además de poner rostro y voz a nuestra red con una representación de la misma. Una red docente bien conectada que, con sólidos pilares asentados entre Colombia, España y México, se va extendiendo a otros países de lenguas hispana y portuguesa.
Desde Brasil, Colombia, Costa Rica, España y México, podemos conocer las valoraciones de diferentes perfiles o roles en RED Descartes, como desarrollador y documentalista de la herramienta de autor Descartes JS y del código para la edición y diseño de libros interactivos, autores y creadores de recursos educativos abiertos con Descartes JS y sus libros interactivos, coordinadores y formadores del programa de Educación Abierta, traductor de los recursos a portugués de Brasil y docentes de primaria, secundaria obligatoria, bachillerato y universidad de distintas especialidades.
Quiero aprovechar la efemérides para recordar la trayectoria profesional del profesorado de RED Descartes quien, además de una dilatada experiencia docente, fue pionero en la investigación sobre la incorporación generalizada de las TIC en el aula durante el año 2005, dio lugar a una de las primeras redes docentes oficiales en España, se formó, generó recursos y colaboró en la implantación del programa Escuela 2.0 hasta evolucionar y coordinar la red de Buenas PrácTICas 2.0. Prácticamente, la totalidad de sus miembros han desempeñado o desempeñan funciones directivas en sus respectivos centros de destino, poseen gran experiencia en la coordinación de proyectos de colaboración escolar, tanto en el marco de eTwinning como en el eliminado Programa ARCE, de agrupaciones o redes de centros educativos de distintas comunidades autónomas. Además, han desempeñado funciones de tutorización o coordinación de cursos de formación en línea de INTEF y de sus administraciones autonómicas respectivas y, hoy en día, constituidos como organización no gubernamental, ponen todos sus conocimientos y empeño en trabajar de forma altruista para y por la comunidad educativa de la aldea global, lema de RED Descartes.
Saludo inicial
|
0.
|
Primera sesión (16 de julio de 2021)
|
1A.
1B.
|
La segunda edición del curso "Edición de libros interactivos" de la RED Descartes (segundo semestre de 2021) se desarrolló según la siguiente planificación:
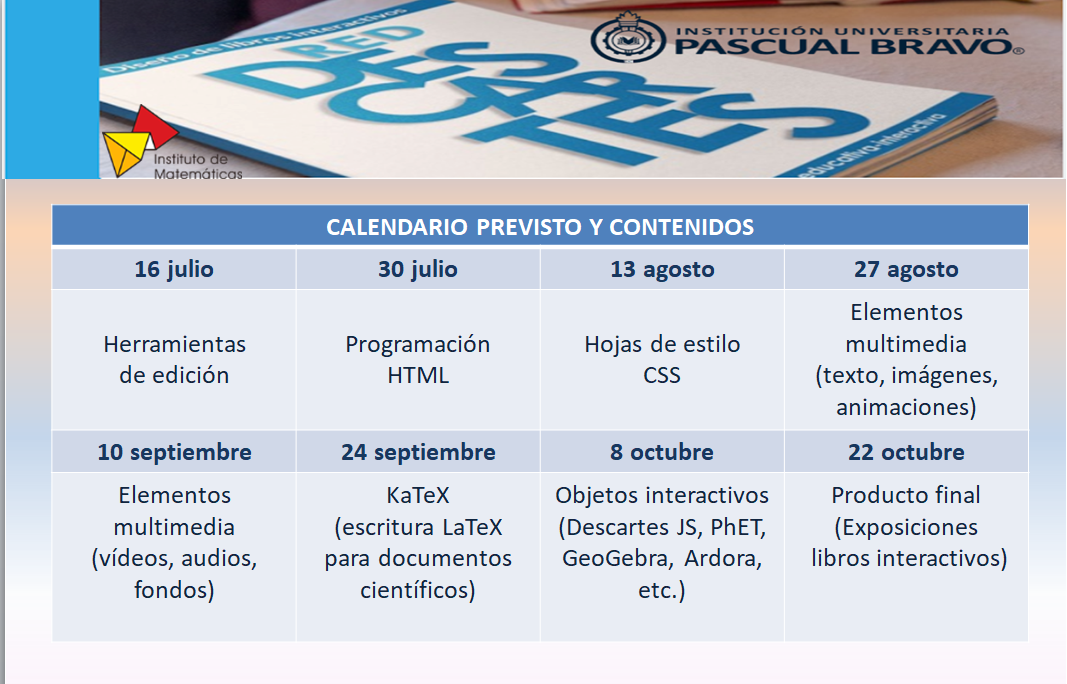
- Primera sesión (16 de julio de 2021).
- Segunda sesión (30 de julio de 2021).
- Tercera sesión (13 de agosto de 2021).
- Cuarta sesión (27 de agosto de 2021).
- Quinta sesión (10 de septiembre de 2021).
- Sexta sesión (24de septiembre de 2021).
- Séptima sesión (8 de octubre de 2021).
- Octava y última sesión (22 de octubre de 2021).
- Resultados de aprendizaje (5 de noviembre de 2021).
Página inicial curso "Edición de libros interactivos"
|
|
Curso de libros interactivos |
|
- La plantilla o plantillas del libro interactivo. Acceda, mire, observe y descargue la plantilla que vaya a usar.
En el curso se comienza con una plantilla básica (Mi_libro) que puede ver aquí y también descargarla desde acá. - Necesita un editor de texto plano para poder editar ficheros en código html, puede ser el bloc de notas de Windows o TextEdit de iOS, pero le recomendamos Notepad++ o Sublime text porque estos colorean las etiquetas y faclitan la edición. Por favor, descargue el que vaya a usar.
Comience su auto-formación
Lea e interactúe con el libro "Curso de libros interactivos", antes enlazado. También puede descargarlo.
¿Alguna ayuda adicional?
- Puede escribirnos a Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo..
- Puede inscribirse a los cursos de formación en línea cuando se convoquen (ver convocatoria de la segunda edición).
- Puede consultar los vídeos grabados en las sesiones de la segunda edición del curso en línea que ha sido promovido por la Institución Universitaria Pascual Bravo (IUPB) de Medellín (Colombia), por RED Descartes de Colombia y RED Descartes España y que está dirigido e impartido por el Dr. Rivera, vicerrector de la IUPB y presidente de la RED Descartes de Colombia.
Vídeos de la segunda edición en línea del curso "Edición de libros interactivos"
(Pulse sobre la imagen)
En el número 106 de la revista Epsilon (ISSN: 2340-714X) de la Sociedad Andaluza de Educación Matemática Thales se ha publicado el artículo titulado "Congruencias en el triángulo de Pascal y el rectángulo de Newton" cuyo autor es nuestro socio José R. Galo Sánchez. Un trabajo de investigación, que como se refleja en la filiación de la autoría, ha sido desarrollado dentro de nuestra RED Descartes.
Este trabajo fue prepublicado en nuestro blog en tres artículos en los que el autor divulgaba la investigación realizada:
- El paralelogramo de Newton el 6 de marzo de 2020.
- El rectángulo de Newton como "simétrico" del triángulo de Pascal el 27 de marzo de 2020.
- Congruencias en el triángulo de Pascal el 24 de abril de 2020.
y, posterioriormente compiló el artículo que sometido a revisión por pares se ha publicado en la revista indicada.
En el resumen se indica :
"El rectángulo de Newton surge como extensión del actualmente denominado triángulo de Pascal partiendo de la versión escalonada de Stifel. Sin embargo, si se parte del esquema organizativo aportado por Pascal entonces el rectángulo de Newton se obtiene mediante una simple simetría signada. Así pues, basta estudiar las congruencias con cero de los números combinatorios y en su análisis aportamos que éstas se ubican en una sucesión de triángulos básicos que se distribuyen de manera periódica. En base a esa periodicidad se incluye un criterio que permite determinar directamente la congruencia de un número combinatorio."
El plantemiento conceptual que sigue, puede sintetizarse en:
- Presentación del conocido triángulo de Pascal en su representación actual como triángulo isósceles escalonado y como triángulo rectángulo que es la original de Pascal, y presentación del menos divulgado rectángulo de Newton.
- Reducción del rectángulo de Newton al de Pascal mediante una simetría signada.
- Muestra de las congruencias con cero en el triángulo de Pascal y revisión de resultados previos de otros autores. Esos resultados se presentan normalmente de manera algebraica y, en general, son oscuros y difíciles de interpretar por profanos dada la abstracción que suele introducir el Álgebra, pero aquí son visualizados geométricamente quedando mostrados de manera diáfana tanto para legos como para ilustrados.
- Finalmente se enuncian algebraicamente los resultados obtenidos por el autor, los cuales muestran la periodicidad de las congruencias módulo p de los números combinatorios y la regla que permite su determinación directa a partir de la descomposición p-ádica del índice superior e inferior, y se visualiza el porqué de ese resultado.
Todo está aderezado por numerosas escenas interactivas que permiten al interesado reproducir la investigación y cómo, apoyándose en ellas, puede potenciarse la reflexión que permite alcanzar la meta lograda. ¡Acceda pulsando sobre la siguiente imagen!
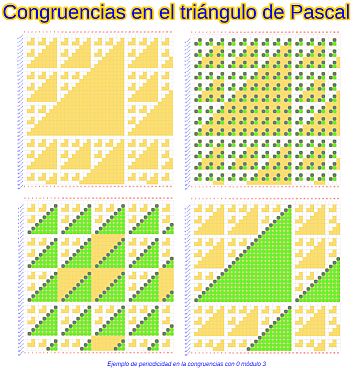Pulsa sobre la imagen para abrir la escena
Os incluimos a continuación dicho artículo y os invitamos a su lectura, a que realicéis observaciones y comentarios al mismo y a que lo divulguéis a través de vuestras redes sociales y profesionales. También a que, usando los recursos interactivos ahí enlazados y disponibles en nuestra web, abordéis actividades en vuestra aulas en las que divulgar el Triángulo de Pascal, el rectángulo de Newton y las curiosas congruencias que acontecen en ellos y a la vez que podáis promover en vuestro alumnado la inquietud básica, la chispa a partir de la cual se cataliza la vocación investigadora.
