Mostrando artículos por etiqueta: Descartes
abre en una ventana nueva
A) Curso “Diseño de libros interactivos con IA y DescartesJS” (Octubre 2024 a febrero de 2025)
Pulse sobre la imagen para acceder a los contenidos
Vídeo de introducción
B) Para la formación en la "Edición de libros interactivos" de RED Descartes pulse sobre la siguiente imagen de cada una de las ediciones celebradas:
Acceso a la quinta edición del curso (octubre 2023 a febrero de 2024) ⇒
Acceso a la cuarta edición del curso ⇒
Acceso a la tercera edición del curso ⇒
Acceso a la segunda edición del curso ⇒
C) Para formación específica en la herramienta DescartesJS puede acceder a los siguientes recursos:
- Curso de "Diseño de objetos interactivos con DescartesJS"
-
Octubre 2022 a marzo de 2023
Acceso a la segunda edición del curso ⇒
- Libros interactivos del proyecto iCartesiLibri:
|
|
|
- Documentación de Descartes JS en pdf, con actividades y enlaces a ejemplos
- Curso del subproyecto Aplicación de Juegos Didácticos en el Aula
|
|
Acceso al blog de documentación  abre en una ventana nueva |
||
|
|
1. Texto del artículo o artículos seleccionados donde se describe el objeto de interés seleccionado por el usuario. Al final de cada artículo se dispone de un grupo de campos mediante los cuales se puede realizar un comentario, éste no se publica de manera automática sino que necesitará ser moderado por el administrador del blog de documentación. 2. Menú de acceso a los artículos clasificado en seis bloques principales:
3. Campo de búsqueda. Introduciendo una palabra o palabras permite localizar aquellos artículos que contienen dichas palabras. 4. Categorías. Cada artículo es clasificado por su autor o autores de acuerdo a determinadas categorías, en este selector puede elegirse una categoría y acceder a todos los artículos incluidos en ella. El selector aporta una estadística del número de artículos en cada categoría. 5. Etiquetas. En esta sección se presenta una nube con las etiquetas asignadas por los autores a los artículos, el tamaño de la etiqueta es proporcional a la frecuencia de su uso. 6. Entradas recientes. Se reflejan lso últimos artículos incluidos en la documentación. 7. Comentarios recientes. Se aporta una relación de los últimos comentarios efectuados a algún artículo. 8. Utilidades. En este apartado se cuenta con un enlace para acceder aI blog como editor, con enlaces para la sindicación de contenidos RSS y un enlace al sitio de wordpress.org organización que desarrolla y mantiene el software del blog que utilizamos. |
|||||||||||||||||||
Este mes vamos a ver un vídeo de 4ºESO Opción A, correspondiente a proporcionalidad:
En este vídeop hemos tratado los siguientes apartados:
1.Proporcionalidad directa e inversa
Proporcionalidad directa
Proporcionalidad inversa
Repartos proporcionales
Proporcionalidad compuesta
2.Porcentajes
Porcentajes
Aumentos y disminuciones
Porcentajes sucesivos
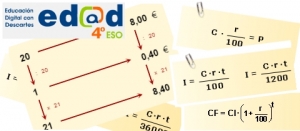
3.Interés simple y compuesto
Interés simple
Interés compuesto
Tasa anual equivalente (T.A.E.)
Capitalización
La posibilidad de comunicar escenas Descartes con páginas html facilita incorporar resultados obtenidos de la ejecución de comandos Geogebra e incluso construcciones completas que pueden ser manipuladas desde la propia escena.
En este artículo se presenta una primera escena de ejemplo que utiliza los resultados de tres comandos Geogebra: Derivada, Integral y Circunferencia. Estos tres comandos tienen en común que su ejecución devuelve un único valor que puede enviarse a la escena Descartes como una cadena de caracteres. En próximos artículos se verá cómo incorporar los resultados de comandos que devuelven una lista de datos o una lista de listas.
Para poder comprender el código con el que se establece la comunicación desde Descartes, se recuerda la sintáxis de los comandos Geogebra que se utilizan en este ejemplo:
- Derivada[función,orden].
Por ejemplo: Derivada[cos(x),2] calcula la segunda derivada de la función cos(x)
- Integral[función,extremo_Inf,extremo_Sup].
Por ejemplo: Integral[cos(x),1,2] calcula la integral definida de la función cos(x) en el intervalo [1,2]
- Circunferencia[Punto1,Punto2,Punto3].
Por ejemplo: Circunferencia[(0,0),(1,1),(2,2)] calcula la ecuación de la circunferencia que pasa por los puntos A=(0,0), B=(1,1) y C=(2,2).
La escena Descartes que se presenta en este artículo incluye cuatro espacios.
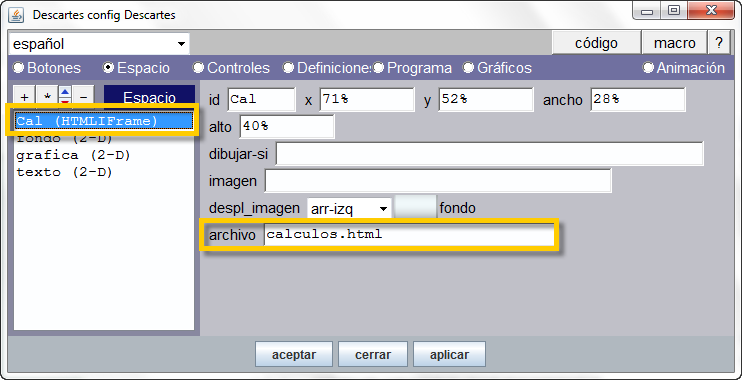
Uno de ellos es un espacio HTMLFrame que tiene como identificador el nombre Cal y será el que permitirá la comunicación con la página calculos.html que está vinculada a este espacio a través del parámetro 'archivo'.
La página calculos.html incluye el código javascript necesario para poder enviar y recibir datos de la construcción Geogebra que está embebida en ella. Esta página no necesita ser modificada y debe incorporarse en el mismo directorio que la página que contenga la escena Descartes (de no ser así se tendrá que modificar la ruta de acceso a ella en el parámetro 'archivo' del espacio HTMLFrame).
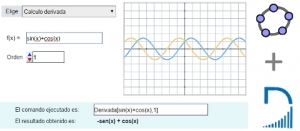
El funcionamiento de la escena Descartes que se presenta como ejemplo es sencilla. Elegida una de las tres opciones del menú, se inicia la comunicación con Geogebra. Si la opción elegida del menú es 'Calculo de la Derivada' se ejecuta la función Calculo1(), si se elige la opción 'Circunferencia por tres puntos' la función a ejecutar será Calculo2() y en el caso de que la opción sea 'Cálculo de la integral de un intervalo' la función asociada es Calculo3().
Las tres funciones tienen un código similar, en primer lugar construyen una cadena de caracteres con la sintásis del código Geogebra a ejecutar y después inician la comunicación enviando a la página incluida en el espacio Cal el evento 'evalua' pasándole como parámetro esta cadena de caracteres. Por ejemplo, el código incluido en la función Calculo1() es el siguiente:
n1='Derivada['+f+','+orden+']'
Cal.set('evalua',n1)
A la hora de generar la cadena de caracteres n1 se ha utilizado los valores de f y orden que están vinculados a los dos controles que se muestran en la escena para modificar, respectivametne, la expresión de la función y el orden de la derivada.
La página calculos.html, que está asociada al espacio Cal, recibe entonces el mensaje y ejecuta el código asociado al evento 'evalua' tras lo cual devuelve a la escena Descartes el resultado en una cadena de caracteres que siempre tiene por nombre vCalculado.
Todo este proceso es totalmente transparente al autor de la escena que puede utilizar el valor de la variable vCalculado de la misma forma que cualquier otra variable creada en la propia escena. Así, si por ejemplo se quiere representar la función derivada obtenida tras ejecutar Calculo1(), bastaría con:
- Evaluar la cadena de caracteres que se ha devuelto con el valor de la derivada: f1=_Eval_(vCalculado)
- Definir una función fun1(x)=f1 para poder crear un objeto gráfico de tipo ecuación cuya expresión sea: y=fun1(x)
Se puede practicar con la escena descargándola del siguiente enlace: Ejemplo1_CAS-JS.zip
El último fin de semana de Febrero se celebró en la Facultad de Ciencias de la Universidad de Cantabria, las VII Jornadas de Enseñanza de las Matemáticas en Cantabria (JEMC) organizadas cada dos cursos por la Sociedad Matemática de Profesores de Cantabria (SMPC). Las JEMC contaron con la asistencia de más de 150 profesores de Matemáticas de todos los niveles educativos: Infantil, Primaria, Secundaria y Universitaria.
Se puede acceder al resumen de las Jornadas en este enlace.
Desde la RED Descartes, Elena Álvarez, presentó el taller titulado "Descartes y Geogebra: una relación de conveniencia" en el que mostró ejemplos de los últimos proyectos promovidos por la Red Descartes para los diferentes niveles educativos y presentó las últimas novedades que proporciona la herramienta Descartes.
Entre estas novedades se enseñó la posibilidad de incluir audios y vídeos interactivos y la capacidad de establecer una comunicación de Descartes con Geogebra. Se exploró algunas de las posibilidades didácticas de esta comunicación a través de varios ejemplos mostrando que el nivel de diálogo que se puede conseguir entre Descartes y Geogebra facilita la construcción de objetos educativos con un alto nivel de interactividad, siendo el procedimiento totalmente transparente para el estudiante que lo utilice.
En próximos artículos se describrirá en detalle algunos de los ejemplos que se expusieron en este taller.
Este mes vamos a ver la unidad de 3ºESO correspondiente a "Figuras planas. Propiedades métricas":
En este video hemos tratado los siguientes apartados:
1.Ángulos en la circunferencia
Ángulo central y ángulo inscrito
2.Semejanza
Figuras semejantes
Semejanza de triángulos. Criterios
3.Triángulos rectángulos
El teorema de Pitágoras
Aplicaciones del T. de Pitágoras
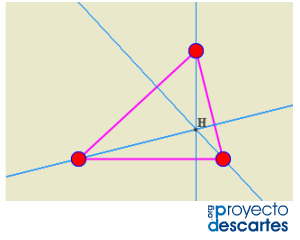
4.Lugares geométricos
Definición y ejemplos
Más lugares geométricos: Cónicas
5.Aplicaciones
Áreas de figuras planas
Este mes vamos a comentar una unidad de 1ºESO correspondiente a Múltiplos y divisores
en este video hemos tratado estos apartados:
1.Múltiplos y divisores
Múltiplos de un número
La división exacta
Divisores de un número
Criterios de divisibilidad
2.Números primos
Números primos y compuestos
Obtención de números primos
Descomposición factorial
3.m.c.m. y m.c.d.
El mínimo común múltiplo
Obtención del m.c.m.
El máximo común divisor
Obtención del m.c.d.
4.Aplicaciones
Problemas de divisibilidad
Este mes vamos a ver una unidad de estadística de 3ºESO:
Los contenidos del tema tratado son:
1.Hacer estadística
Necesidad.
Población y muestra
Variables
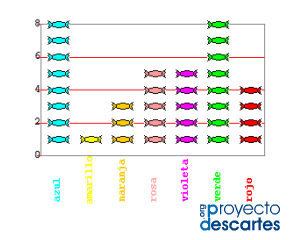
2.Recuento y gráficos
Recuento de datos
Gráficos
Agrupación de datos en intervalos
3.Medidas de centralización
y posición
Media
Moda
Cuartiles y mediana
4.Medidas de dispersión
Rango y desviación media
Desviación típica
Coeficiente de variación
Por Ángel Cabezudo Bueno – 24 de noviembre de 2014
Sixto Romero Sánchez es profesor del Departamento de Matemáticas en la Escuela Técnica Superior de Ingeniería de la Universidad de Huelva, 
con 39 años a su espalda como investigador y docente es catedrático en el área de Matemática aplicada.
Responsable en esta universidad del grupo de investigación “Modelización matemática, redes y multimedia”, actualmente trabaja en lo que se denomina Tratamiento Digital de Imágenes con importantes aplicaciones en Arqueología, Geología, Medicina, Biología, etc… y en la obtención de modelos para determinación y predicción de datos.
Desde hace años dedica su tiempo a la innovación docente aplicada a la mejora y enseñanza de las Matemáticas siendo en la actualidad Presidente de la Sociedad Andaluza de Educación Matemática Thales y Vicepresidente a nivel internacional de The Commission for the Study and Improvement of Mathematics Teaching (CIEAEM). Además preside la Academia Iberoamericana de La Rábida desde 2007, que se centra en el estudio de cualquier tema histórico, literario, artístico, científico o técnico, relacionado con la cultura y la sociedad andaluzas, así como en la interrelación entre éstas y la cultura y la sociedad iberoamericanas.
Desde aquí agradecemos a Sixto que entre tantos compromisos como tiene nos haya hecho un hueco y nos permita conocer a través de su palabra y con más detalle acerca de Sociedad Andaluza de Educación Matemática (SAEM) Thales.
Gracias en mi nombre y en el de todos los compañeros que formamos Red Educativa Digital Descartes.
La entrevista paso a paso:
- ¿Cómo nació la SAEM Thales y cuáles son sus fines societarios? 3:21
- ¿Quién puede pertenecer a SAEM Thales y qué pasos tiene que dar para ello? 6:16
- SAEM es un organismo de iniciativa privada que cuenta con sus propios recursos técnicos y humanos, no obstante, ¿cuenta también con recursos externos, fruto de la relación con otras instituciones y entidades, públicas o privadas, para llevar a cabo algunas de sus propuestas? Detállanos, en la medida de lo posible, este conjunto total de recursos. 7:30
- Sabemos que el ámbito en el que actúa SAEM Thales no es sólo el andaluz, también participa en un contexto nacional e internacional en los procesos de enseñanza y aprendizaje. Danos cuenta de algunas de estas participaciones. 9:45
- Una de las acciones de la SAEM Thales es la de divulgación y popularización de las matemáticas. ¿Cómo lo lleva a cabo y en este sentido, cual es la característica que le distingue de otros medios? y también, ¿Qué papel juega en todo esto el Centro de Documentación Thales? 12:25
- ¿Qué opinas de la RED Descartes, sobre sus acciones y recursos educativos y también de su herramienta de desarrollo Descartes? 15:10
- Desde la sociedad SAEM Thales se promueve GeoGebra ¿no cabría promover también otras herramientas, entre ellas Descartes? 16:43
- Muchos socios andaluces de RED Descartes son socios de SAEM Thales ¿Crees que sería conveniente establecer una colaboración entre ambas asociaciones? En caso afirmativo ¿cómo consideras que podría plasmarse esa colaboración? 17:50
- Como profesor universitario y dada tu amplia experiencia y conocimiento en el uso de las TIC ¿nos podrás decir cómo se están usando en las aulas de la Universidad? ¿No deberían también incluirse las TIC en las pruebas de acceso a la misma? 19:05
- Para terminar, ¿hay algo de interés que no hayamos recogido en esta entrevista y que a tu juicio conviene añadir o matizar mejor? 22:22
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
