Mostrando artículos por etiqueta: bachillerato
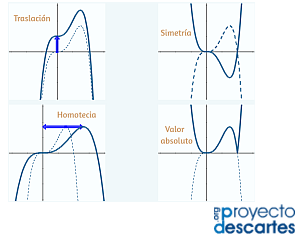
Título: Transformaciones de funciones
Sección: Miscelánea
Bloque: Cálculo
Unidad: Operaciones con funciones
Nivel/Edad: Bachillerato y Universidad (17 años o más)
Idioma: Castellano
Autor: José R. Galo Sánchez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
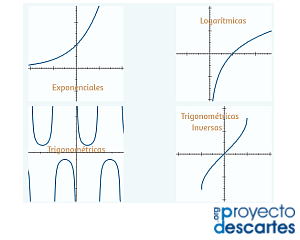
Título: Funciones trascendentes
Sección: Miscelánea
Bloque: Cálculo
Unidad: Funciones elementales
Nivel/Edad: Bachillerato y Universidad (17 años o más)
Idioma: Castellano
Autor: José R. Galo Sánchez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Título: Análisis Matemático para Bachillerato
Sección: iCartesiLibri
Bloque: Análisis Matemático
Unidad: Funciones, límites, derivación e integración
Nivel/Edad: 2º Bachillerato y Universidad (17 años o más)
Idioma: Castellano
Autores:
José R. Galo Sánchez y María José García Cebrian
ISBN: 978-958-52963-7-4
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Dibujando a Descartes
Sección: iCartesiLibri
Bloque: Geometría
Unidad: Geometría analítica plana
Nivel/Edad: Universidad (18 años o más)
Idioma: Castellano
Autor: Pedro Roses Amat
ISBN: 978-958-52963-4-3
![]() Haz clic aquí para ver una versión en pdf
Haz clic aquí para ver una versión en pdf
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Unas gotas de astrofísica
Sección: Ingeniería y Tecnología
Bloque: Ciencias básicas
Unidad: Física general - Astrofísica
Nivel/Edad: Bachillerato/Universidad (17 años o más)
Idioma: Castellano
Autor: José Luis San Emeterio Peña
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Ingeniería y Tecnología en
https://proyectodescartes.org/ingenieria/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Cálculo vectorial Parte II
Sección: iCartesiLibri
Bloque: Análisis matemático
Unidad: Cálculo vectorial
Nivel/Edad: Universidad (18 años o más)
Idioma: Castellano
Autores: Juan Guillermo Rivera Berrío, y Elena Esperanza Álvarez Sáiz
ISBN: 978-958-52963-1-2
![]() Haz clic aquí para ver una versión en pdf
Haz clic aquí para ver una versión en pdf
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Para este nuevo curso académico 2020 – 2021 el 'Proyecto Descartes' ofrece una amplia cantidad de objetos informáticos, dinámicos e interactivos de ayuda a la enseñanza y al aprendizaje de los contenidos curriculares de las diferentes asignaturas de Bachillerato.
Una de las características de la #REDDescartes es la continua atención a todo lo relacionado con las nuevas tecnologías y la educación de ahí que esté analizando ininterrumpidamente nuevas posibilidades didácticas en este ámbito. La mayor parte de los materiales didácticos de #REDDescartes lleva implícitas técnicas de autoformación y autoevaluación.
El interés actual que tiene para los usuarios del Proyecto Descartes queda perfectamente resumido en los siguientes enlaces: enlace 1 y enlace 2. Señalamos la particularidad de que en el último mes de Agosto se han servido más dos millones cien mil páginas.
El Proyecto Descartes ha creado recursos interactivos para PC, tablet y smartphone en las áreas de: Matemáticas, Lengua, Ciencias Naturales, Física y Química, Biología, Inglés, Francés, Artes Plásticas, Tecnología, Geografía, etc. Ver:
https://proyectodescartes.org/indexweb.php
En la página enlazada anteriormente se muestran todos los recursos disponibles hasta el momento del acceso. Se observa que los relativos a Bachillerato se encuentran en los subproyectos:
En algunos subproyectos no se menciona que contengan material para bachillerato pero los hemos añadido por considerar que parte de los recursos de dichos subproyectos son aplicables a la etapa.
Hemos hecho notar que la disponibilidad de materiales está actualizada hasta el momento del acceso debido a que, en la actualidad, el proceso de creación de nuevos recursos está experimentando un crecimiento extraordinario tanto en cantidad como en calidad y diversidad, lo que hace aconsejable revisar con cierta frecuencia el contenido de la página. En la actualidad se está adaptando el 'Proyecto Prometeo', abundante en contenidos con lo que el aporte de nuevo material es contínuo.
Si bien los libros del subproyecto iCartesiLibri son creaciones dinámicas e interactivas pensadas para usarse tal cual están, al igual que los recursos del resto de los subproyectos, es de señalar la posibilidad de adaptar fácilmente los contenidos de dichos recursos a las necesidades propias o a las características del aula, especialmente las Misceláneas que con un mínimo de cambios pueden convertirse en una herramienta propia que satisfaga nuestros criterios educativos y de aprendizaje. Todo lo que necesitamos para realizar los cambios en los recursos es el 'Editor Descartes' herramienta (editor) intuitiva y de fácil uso.
Una vez que se ha visto la estructura de un recurso y se ha hecho uso de él se intuye la facilidad para la creación de uno parecido para lo cual disponemos de tres libros interactivos en el subproyecto iCartesiLibri, 'Formación en DescartesJS', que detallan todas las funcionalidades y procedimientos del editor Descartes y también está disponible una documentación exhaustiva en línea.
Cada subproyecto y cada recurso del mismo disponen de la documentación necesaria para que fácilmente identifiquemos sus objetivos y las indicaciones necesarias para su uso.
Estamos hablando de los recursos digitales que podemos encontrar en el Proyecto Descartes y de planificación de un curso escolar en estado de pandemia donde es importante disponer de un método de trabajo que pueda facilitar la formación de alumnos cuando se dificulta o incluso se suprime la enseñanza presencial. Recomiendo el informe de la experiencia de nuestro compañero José Antonio Salgueiro, hábil usuario de las técnicas de comunicación, cuando en el curso pasado se vio obligado a cerrar su aula e interrumpir la enseñanza presencial con un grupo de alumnos. El resultado de su experiencia bien puede servir de inspiración al docente o al menos tenerlo en cuenta al hacer su propia planificación.
En su reciente artículo titulado "Evaluación, durante el estado de alarma, de la práctica docente a distancia con un modelo sin videoconferencia" nos dice
"En primer lugar, dejaremos constancia de que este artículo no se fundamenta en ningún trabajo de investigación educativa ni en una experimentación didáctica previamente planificada y diseñada con unos objetivos concretos, sino que pretende difundir entre el claustro virtual una experiencia surgida de la improvisación y compartir los recursos generados con la práctica docente a distancia y sin videoconferencia en la materia de Matemáticas-II del Bachillerato de Ciencias con el alumnado del IES Bajo Guadalquivir de Lebrija, por si fuera de utilidad para otros compañeros y compañeras."
Ildefonso Fernández Trujillo. 2020
Título: Crecimiento exponencial
Sección: Prometeo
Bloque: Análisis
Unidad: Sucesiones y progresiones
Nivel/Edad: Bachillerato y Universidad (17 años en adelante)
Idioma: Castellano
Redacción y programación: Juan José Rivaud
Diseño gráfico: Lyssette Calapiz Estrella
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Prometeo en https://proyectodescartes.org/Prometeo/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: La sucesión de Fibonacci
Sección: Prometeo
Bloque: Análisis
Unidad: Sucesiones y progresiones
Nivel/Edad: Bachillerato y Universidad (17 años en adelante)
Idioma: Castellano
Redacción y programación: Alejandro Radillo Díaz
Diseño gráfico: Lyssette Calapiz Estrella
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Prometeo en https://proyectodescartes.org/Prometeo/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Huerto de manzanas
Sección: Prometeo
Bloque: Aritmética
Unidad: Números y operaciones
Nivel/Edad: Bachillerato y Universidad (17 años en adelante)
Idioma: Castellano
Redacción y programación: Óscar Escamilla González
Diseño gráfico: Lyssette Calapiz Estrella
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Prometeo en https://proyectodescartes.org/Prometeo/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)




















 CONTACTO
CONTACTO
