Pedro Roses Amat
Fondo Editorial Pascual Bravo
Barcelona
2020
Título de la obra: Dibujando a Descartes
Primera edición mayo 2020
Autor: Pedro Roses Amat
rosesamat.pedro@gmail.com
Lo más curioso, es que todos aquellos que estudian seriamente esta Ciencia, caen en una especie de pasión. Verdaderamente, lo que más placer proporciona no es el saber, sino el estudiar; no es la posesión, sino la conquista; no es el estar aquí, sino el llegar allá.
Johann Carl Friedrich Gauss (1777-1855)
Diseño del libro: Juan Guillermo Rivera Berrío
Diseño de portada y carátulas: Teresa Roses Amat
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos:
DescartesJS y
Geogebra.org
Recursos GeoGebra con la colaboración de Bernat Ancochea Millet
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Núcleo del libro interactivo: julio 2022
2020 Bajo licencia Creative commons, Atribución - NoComercial - Compartir Igual 4.0 Internacional (CC BY-NC-SA 4.0)
Creative Commons Attribution License 4.0.Durante la Guerra de los Treinta Años, el 11 de noviembre de 1619, un soldado del ejercito de Maximiliano de Baviera, tuvo un sueño: “el espíritu de la verdad me reveló el acceso al tesoro de la naturaleza y a poseer los verdaderos fundamentos de todas las ciencias”. El soldado creía que las ideas, cuando son claras y precisas, también son ciertas y confió en su sueño. Escribió un libro, no muy largo, porque todo lo que se sabia en la época cabía en pocas páginas.
Probablemente en las mismas fechas de noviembre, 400 años después, he leído el libro. Encontré en Internet la versión facsímil de la edición de 1634. También una versión editada por la fundación Gutenberg que publica libros cuyos derechos de autor han caducado.
Al final de su libro, el soldado escribe:
¡En eso estamos! La Covid19 me ha regalado el tiempo para recrear con GeoGebra las figuras que ilustran el texto original. A vosotros “el placer de descubrirlas”.
El Renacimiento es un periodo histórico (siglos XV-XVI) de transición entre el mundo medieval y el mundo moderno, muy reconocible desde nuestra perspectiva porque coincide con una gran explosión del arte y de la arquitectura. En el terreno científico las ideas renacentistas se expresan para evolucionar la ciencia tradicional, basada en la autoridad de los clásicos y de la Biblia, en ciencia basada en la observación y la experimentación.
Donde mejor se manifiesta esta evolución de la ciencia es en el debate astronómico, porque las nuevas observaciones ponen en duda el modelo del Universo, que situaba a la tierra en un lugar privilegiado según el relato de la Biblia, cuando Yahvé detiene el sol a petición de Josué:
Este pasaje es interpretado literalmente justificando la creencia en una Tierra inmóvil y un Sol en movimiento.
Es evidente que el movimiento aparente de los planetas se puede describir tomando como referencia el punto de vista del observador, pero Copérnico se da cuenta que el modelo se simplifica mucho si se considera al Sol en el centro del sistema. Las ideas de Copérnico no se publican hasta 1543, año de su muerte.
Tycho Brahe desde su observatorio en la isla danesa de Hven recopila datos sobre las trayectorias planetarias de forma sistemática y con una precisión muy superior a la disponible en la época. A su muerte en 1601, Kepler tiene acceso a sus observaciones y en base a ellas calcula las órbitas de los planetas.
Después de varios intentos de ajustar los datos a órbitas circulares, describe el movimiento de los planetas en orbitas elípticas, calculando la velocidad de desplazamiento a lo largo de ellas y su periodo, el tiempo que tardan en completar una órbita, en función de su lejanía al Sol. Son las tres leyes de Kepler de 1609.
Galileo (1564-1642), defiende las ideas de Kepler y busca su confirmación mediante observaciones astronómicas adicionales. Utiliza telescopios que él mismo construye y perfecciona. Gracias a la mejora en la resolución de sus instrumentos hace observaciones que no hubieran sido posibles anteriormente.
La más decisiva, el descubrimiento de cuatro satélites de Júpiter, que evidencian que la Luna no es el único astro en orbitar un planeta y por lo tanto que no todos los astros giran alrededor de la tierra.
Al observar la Vía Láctea pudo ver estrellas no visibles a simple vista y comprobar que los planetas aumentan su tamaño con el telescopio y las estrellas no lo hacen. La explicación es bien sencilla, las estrellas están mucho mas distantes de lo que se podía suponer. Con esta observación, aumentó los limites del universo mas allá de la octava bóveda celeste donde, en teoría, se sostienen las estrellas.
En febrero de 1616, el Santo Oficio condena las teorías heliocéntricas como «una insensatez, un absurdo en filosofía y formalmente herética» y ruega a Galileo que exponga su tesis presentándolas como una hipótesis y no como un hecho comprobado.
En 1632, Galileo, publica en Florencia su celebre “Diálogo sobre los principales sistemas del mundo”, (Dialogo sopra i due massimi sistemi del mondo), contraviniendo las instrucciones del tribunal que le prohibía defender sus ideas.
A través de un debate entre sus personajes, defiende la superioridad del sistema heliocéntrico de Copérnico frente al geocentrismo medieval, al que ridiculiza. La estratagema de presentar sus ideas como un “dialogo” no funciona. Galileo es juzgado y amenazado de tortura si no se retracta. A pesar de hacerlo, es condenado a cadena perpetua y el Papa conmuta la pena por arresto domiciliario que se mantuvo hasta su muerte.
La sentencia eclesiástica no pudo oscurecer el papel de Galileo en la construcción de la moderna visión del Universo.
Sus descubrimientos tendrán una trascendencia decisiva en la ciencia y en la filosofía, al poner de manifiesto que el universo es más complejo y más extenso de lo que se había imaginado hasta entonces. Las teorías cosmológicas vigentes desde la época de Aristóteles se desmoronaron.
Observar la realidad y construir a partir de ella hemos visto que era en su época una idea peligrosa, porque dejaba fuera de juego a los que decidían cómo debía funcionar el mundo en base a criterios de autoridad y negaban las evidencias para no cuestionar el orden establecido.
Además de sus extraordinarios resultados como astrónomo, la importancia de Galileo está en la introducción del método experimental en la investigación científica por lo que se le considera fundador de la ciencia moderna.
Sus investigaciones siguieron una metodología precisa, basada en la observación de los hechos, la realización de experimentos, y la descripción de su comportamiento. La secuencia es por tanto: observación, experimentación y después la formulación de las leyes que describen el fenómeno observado.
Sus trabajos se centran principalmente en lo que hoy llamamos mecánica, el estudio del movimiento de los sólidos. Para formular las leyes de la naturaleza necesitamos mediciones para cuantificar los fenómenos a describir.
Para hacer medidas precisas, Galileo construye un plano inclinado por el que deja rodar una bola y consigue comprobar que, partiendo del reposo, el espacio recorrido es proporcional al cuadrado del tiempo transcurrido.
Pero, la experimentación de Galileo es también “ideal”, fruto de la reflexión sobre la experiencia. En el caso de la caída libre, por la observación, constata la diferente velocidad de caída de los objetos según el medio en el que se produce, aire, agua… Luego… en una situación ideal, suprimida esta influencia, los cuerpos caen a la misma velocidad. El experimento mas famoso de la física, dejando caer objetos desde lo alto de la torre inclinada de Pisa, podemos estar seguros de que nunca se llevo a cabo, porque experimentar es también reflexionar sobre las observaciones.
Este proceder, que combina la experimentación directa y la “ideal” se convierte en general a partir de entonces en la física, donde los comportamientos se definen en condiciones ideales. Choque instantáneo, rozamiento cero, elasticidad perfecta… condiciones ideales para obtener las leyes del comportamiento, limpias del ruido de la realidad.
Para Galileo, la naturaleza se rige por leyes universales y su comportamiento es regular y necesario.
No se puede ser mas claro y convincente, las matemáticas son el lenguaje con el que Dios ha ordenado el Universo.
Los modelos matemáticos son una “descripción” de la realidad, no son una justificación de su causalidad física. La ciencia antigua, se siente insatisfecha por la descripción matemática. Hemos pasado de las explicaciones “filosóficas” del tipo,
a la descripción cuantitativa de las observaciones,
Este cambio de enfoque es el que define la ciencia moderna, cuyos modelos de la realidad han conseguido cuantificar con éxito los fenómenos físicos, sin atender a preguntas mas profundas de “porqué, las cosas son como son”.
En sentido inverso, la necesidad de desarrollar modelos de utilidad practica para la navegación, para el cálculo de trayectorias, medida del tiempo etc.… es el motor de la innovación matemática. La ciencia necesita de las matemáticas y el progreso requiere que también en el dominio matemático se produzcan avances significativos.
El Discurso del método publicado por Descartes en 1637, (Discours de la méthode pour bien conduire la raison, et chercher la vérité dans les sciences) es una de las primeras obras de la filosofía moderna y se sitúa en el contexto que hemos definido antes de la transición a la edad moderna. Es un libro de una ambición singular porque rebasa el planteamiento filosófico y Descartes intenta desarrollar la aplicación practica de sus ideas, en tres apéndices, “La Géométrie”, “la Dioptrique” y “les Météores”.
Descartes propone para la filosofía, para el estudio de la naturaleza y para la física, el método de las matemáticas que consiste, según él, en seguir unas reglas claras.
En definitiva desde nuestro punto de vista sus propuestas son de lo mas sensatas, es difícil de entender que en su época causaran revuelo. Pero la traducción de sus ideas a principios filosóficos representan un cataclismo en la filosofía occidental dominada por los escolásticos, de tradición aristotélica.
El punto de partida de cualquier construcción filosófica, para excluir cualquier duda de acuerdo con el primer principio, es “cogito ergo sum”, "pienso luego existo". Es superior la certeza de las ideas que la que podemos depositar en la realidad. Para Descartes la confianza en las observaciones es engañosa. Los hechos que provienen de la experimentación solo pueden conducir al engaño.
Su posicionamiento a favor de la prioridad del pensamiento le obliga a demostrar la existencia de Dios y del mundo, a los que no acepta como punto de partida. Descartes, devoto cristiano, lo resuelve mediante un ingenioso razonamiento, que entronca con la tradición cristiana de San Agustín, seguidor de Platón y por tanto fiel al mundo de la ideas, depositarias de la perfección y que nosotros solo vemos como un reflejo en las “paredes de la caverna” del mundo real.
Los esfuerzos de Descartes para conciliar sus ideas con la fe oficial de la Iglesia, por el miedo de ser juzgado como Galileo, no sirvieron de mucho pues, a su muerte, sus libros fueron prohibidos.
Las ideas de Descartes están en el origen de las corrientes filosóficas “idealistas” que defienden la prioridad de las ideas sobre la experiencia de los sentidos y a las matemáticas como ideas divinas que se aplican al mundo real.
En relación a la experimentación, su posición es opuesta a la sostenida por la corriente filosófica “empirista” que se desarrolla principalmente en Inglaterra y que sostiene las tesis que hemos expuesto al hablar de Galileo.
El Discurso del método fue, en sus sucesivas reediciones, publicado sin sus apéndices que tuvieron un éxito desigual. “La Dioptrique” sobre la reflexión y refracción de la luz y “les Meteores” sobre el medio natural, fueron rápidamente superados por el avance de la ciencia empírica y olvidados. El dedicado a la Geometría adquirió vida independiente y se convirtió pronto, en uno de los libros mas influyentes de las matemáticas.
“La Géométrie” es la aplicación del método científico cartesiano a las matemáticas. El sujeto escogido es la geometría clásica, que para Descartes es un ejemplo de los métodos antiguos que había que renovar.
Las etapas centrales del método cartesiano, que hemos citado antes son:
La primera etapa se corresponde con lo que los matemáticos de la época llamaban “análisis” y la segunda con lo que entendían como “síntesis”.
Descartes divide el análisis para la Geometría en dos pasos:
A partir de aquí hay que efectuar la síntesis y para ello utilizamos un lenguaje simbólico que nos permite detallar la relación entre los datos y las incógnitas y expresarla en ecuaciones. El álgebra es el lenguaje escogido para expresar esta síntesis y Descartes necesita perfeccionarlo para que sea útil a este fin. Confía en “mecanizar el razonamiento” y definir un lenguaje matemático universal.
Nos quedan las ultimas fases del proceso:
Como estamos planteando problemas geométricos, la solución será también geométrica. El álgebra es el instrumento intermediario que permite manipular los datos obtenidos de la geometría y obtener la solución que deberá traducirse nuevamente en una figura geométrica.
Las ecuaciones algebraicas son “el esqueleto” de la síntesis que deja a descubierto como se ha obtenido la solución. Este detalle es esencial porque define la nueva geometría. Descartes critica a los geómetras clásicos precisamente por exponer sus resultados ocultando el proceso de síntesis. Los clásicos construyen caso a caso y las soluciones aparecen por la intuición o la genialidad del geómetra que no revela sus “trucos”. La nueva geometría no obliga a esfuerzos de la imaginación sino a aplicar fórmulas mecánicamente.
El “Método” de Descartes es revolucionario porque establece un procedimiento o método de validez general para todos los problemas y continua siendo valido hoy en día. Hoy, la síntesis ya no se expresa solo con las cuatro operaciones básicas del álgebra disponibles en la época. Se han incorporado nuevos operadores, de manera que las expresiones del lenguaje simbólico se han hecho mas complejas y se han convertido en nuestra manera mas natural de razonar matemáticamente.
“La Géométrie” establece la relación entre la construcción de figuras geométricas y sus ecuaciones algebraicas y el éxito en este empeño ha difuminado el limite entre ambas materias, geometría y álgebra, y el resultado se ha visto tradicionalmente como una colaboración al mismo nivel.
Efectivamente, asistimos al nacimiento de la Geometría algebraica, fusión de dos ramas de las matemáticas, pero no podemos perder de vista que, detrás de ello, Descartes establece la supremacía del análisis y en consecuencia el álgebra pasara a ser la disciplina matemática principal.
La geometría algebraica es el primer fruto de “La Géométrie” pero su influencia llega mucho mas lejos formulando una nueva manera de hacer matemáticas.
Desde nuestro punto de vista “La Géométrie” tiene un encanto especial, porque va desarrollando sus ideas planteando y resolviendo ejercicios sencillos, apoyándose en mas de treinta figuras que son necesarias para seguir el texto. Nuestra propuesta, es hacer una lectura de “la Géométrie” siguiendo la estructura original de la exposición cartesiana en lo que llama LIBROS y dar vida al texto a través de la reconstrucción de las figuras que lo ilustran. Hemos intentado en la mayor parte reproducir fielmente el original, manteniendo el mismo numero de referencia, aunque en algunos casos hemos adaptado las figuras a las convenciones aceptadas hoy universalmente, como el sentido creciente de los ejes de coordenadas hacia arriba y hacia la derecha, y la incorporación de los semiejes negativos ausentes en “La Géométrie”.
Las citas de descartes se refieren, salvo que se diga lo contrario, a “La Géométrie” y se identifican por el numero de página de la edición Gutenberg en la que se encuentran. En las referencias bibliográficas, se puede encontrar el texto original en francés y alguna traducción al español.
La suma y su inversa, la resta, la multiplicación y la división, la exponencial, como un caso particular de multiplicación y la extracción de raíces, son las operaciones del álgebra. Descartes demuestra que estas operaciones pueden efectuarse y son equivalentes a construcciones geométricas.
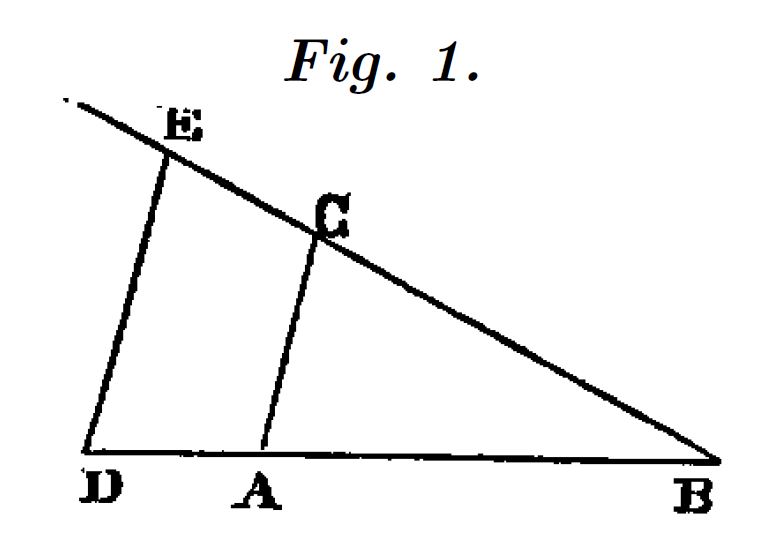 Las cantidades se representan por líneas según su magnitud. La suma de dos magnitudes es evidente, situando los dos segmentos en prolongación sobre una recta. Para la multiplicación utiliza el teorema de Tales.
Las cantidades se representan por líneas según su magnitud. La suma de dos magnitudes es evidente, situando los dos segmentos en prolongación sobre una recta. Para la multiplicación utiliza el teorema de Tales.
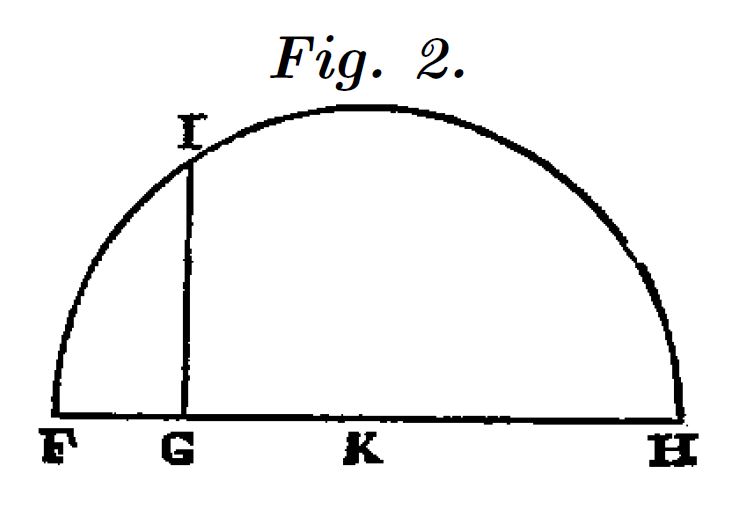 La obtención de la raíz cuadrada es el problema clásico de la cuadratura del rectángulo, que se resuelve obteniendo la media proporcional entre una magnitud y la unidad. Para las raíces de grado superior en el LIBRO SEGUNDO, Descartes desarrolla lo que llama proporciones continuas para obtener las raíces sucesivas de una magnitud.
La obtención de la raíz cuadrada es el problema clásico de la cuadratura del rectángulo, que se resuelve obteniendo la media proporcional entre una magnitud y la unidad. Para las raíces de grado superior en el LIBRO SEGUNDO, Descartes desarrolla lo que llama proporciones continuas para obtener las raíces sucesivas de una magnitud.
Una vez establecida la correspondencia entre las operaciones algebraicas y su construcción geométrica Descartes se ocupa de la notación.
Descartes establece un sistema de notación completando la propuesta de François VièteLa obra de Viète "In Artem Analyticam Isagoge" está inspirada profundamente en la obra de Diofanto y Pappus. En ella Viète fundamenta los principios y las reglas del cálculo algebraico literal. que es el primero en intentar establecer una forma normalizada para las ecuaciones algebraicas.
Descartes mejora su propuesta e introduce para las operaciones símbolos abstractos semejantes a los actuales, salvo para el signo “igual”, para el que utiliza “$\infin$”.
A cada segmento se le asigna, como nombre o identificador, una letra minúscula si se trata de una magnitud conocida y una letra del final del abecedario $(x, y, z)$ si es desconocida.
En el álgebra geométrica clásica, multiplicando una magnitud por otra se obtiene un área (un cuadrado en el caso de dos magnitudes iguales) y en el caso de tres obtenemos un volumen (un cubo en el caso de tres magnitudes iguales). Para Descartes las sucesivas potencias de una magnitud son a su vez magnitudes de la misma naturaleza. De esta manera se reciben en la geometría potencias de orden superior a tres que carecían de sentido para los clásicos y se abandona el principio de homogeneidad, que obligaba a tratar separadamente las magnitudes según fueran líneas, superficies o volúmenes. Para Descartes todas las magnitudes son de la misma naturaleza y se expresan según la longitud del segmento que las representa. Este criterio es un punto esencial de ruptura con la tradición del álgebra geométrica clásica y con Viète.
Como resultado de las aportaciones de Descartes, los textos de “la Géométrie” son fácilmente legibles por un lector moderno.
A cada segmento se le asigna una magnitud, por comparación con la unidad de medida definida para cada ocasión. Esta premisa es frontalmente contraria a la geometría clásica que no aceptaba identificar la longitud de las líneas con números. Esta oposición tenia su origen en el descubrimiento de que algunas magnitudes eran “inconmensurables”, no eran divisibles por ninguna unidad de medida, o lo que es lo mismo, que no pueden expresarse como una fracción de números enteros.
El descubrimiento de los “inconmensurables” esta ligado al problema número uno de la geometría clásica, la cuadratura del círculo, siendo $\pi$ el primer número identificado como tal.
Otro ejemplo sencillo es $\sqrt{2}$ que es la longitud de la diagonal de un cuadrado de lado $1$ o $\sqrt{3}$ que es la diagonal del cubo de lado $1$. Todos estos números podían obtenerse gráficamente con regla y compás, la diagonal del cuadrado o del cubo, incluso el numero áureo, pero no se les podía asignar una magnitud, un numero, lo que establecía la superioridad de la geometría sobre el álgebra.
Descartes ignora este problema al asignar a “todos” lo segmentos una magnitud, lo que implica aceptar la existencia de los “inconmensurables” como números. En la imagen hoy corriente, según la cual suponemos todos los números ordenados sobre una recta de menor a mayor, a estos números les corresponde un punto. Los “inconmensurables” no son un corte o discontinuidad de la recta real. Descartes no se detiene en este problema, pero acierta pasándolo por alto y aceptando lo que unos años mas tarde serán los números “irracionales” de infinitas números decimales.
La notación simbólica que asigna letras a las magnitudes, conocidas o desconocidas, facilita que estos números intervengan en las ecuaciones en igualdad de condiciones con el resto de los números. Descartes interpreta, de forma un tanto contradictoria, que este tipo de ecuaciones,
en las que intervienen inconmensurables, derivan en una falta de exactitud, como veremos al hablar mas adelante de la clasificación de las curvas.
Consecuente con su criterio de correspondencia entre números y segmentos, Descartes rechaza los números negativos, por la imposibilidad de imaginar longitudes, áreas o volúmenes negativos. No se puede hacer intervenir en las construcciones geométricas segmentos de magnitud negativa.
En consecuencia, $a-b$ es diferente a $a+b$, puesto que solo considera valores de $a$ y $b$ positivos y las dos expresiones se corresponden con dos construcciones geométricas diferentes, suma y resta, a tratar separadamente (si aceptamos números negativos, $a+b$, puede ser $a+(-b)$ y según las reglas del álgebra se convierte en $a-b$). Para Descartes las raíces negativas de una ecuación algebraica son “raíces falsas”.
Para resolver cualquier problema, debemos considerarlo como resuelto y dibujarlo, identificando cada segmento con una letra según sea conocido o desconocido.
El conocimiento del problema que hemos obtenido mediante la fase de análisis, o nuestra intuición, nos deben llevar a expresar las relaciones que hay entre los diferentes segmentos, conocidos y desconocidos. Para Descartes:
En el caso de que tengamos solo una magnitud desconocida el problema consistirá en resolver una ecuación de una sola variable. Si el problema nos lleva a obtener “$n$” segmentos desconocidos, obtendremos tantas ecuaciones como variables desconocidas, es decir un sistema de “$n$” ecuaciones, con “$n$” incógnitas.
Los problemas planos, construibles mediante rectas y circunferencias dan lugar a ecuaciones algebraicas de segundo grado. Esta afirmación, que hoy sabemos es cierta, se acepta por Descartes sin demostración.
Descartes establece una relación entre el nivel de un problema, problema construible con regla y compás, la construcción que resulta al plantear el problema, formada exclusivamente por rectas y circunferencias, y el grado de la ecuación que relaciona las incógnitas y que debemos resolver para obtener la solución. Según esta lógica, la resolución gráfica de las ecuaciones de segundo grado se puede obtener mediante la intersección de una circunferencia con una recta.
Descartes propone dos construcciones diferentes según el signo del termino independiente de la ecuación, ya que los coeficientes, $b$ y $c$ son siempre positivos.
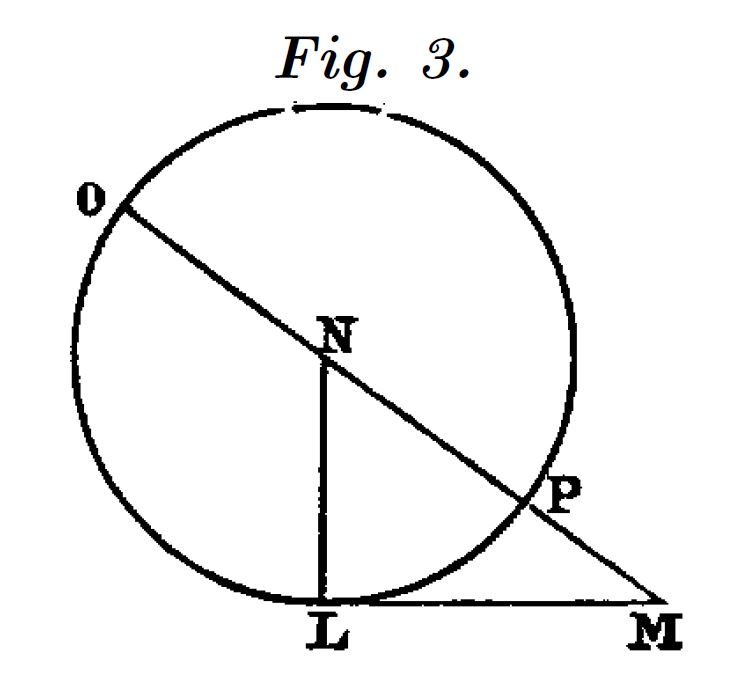
En el caso $x^2-bx-c^2=0$ (figura 3), solo obtiene una raíz, puesto que la segunda es siempre negativa o “falsa” y la ignora.
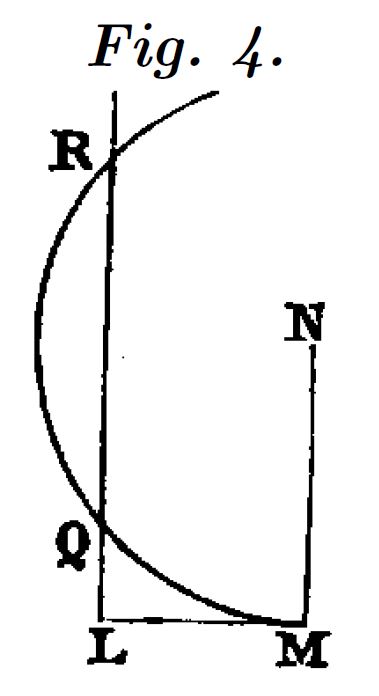
En el caso de $x^2-bx+c^2=0$ (figura 4), podemos comprobar los casos en los que obtenemos dos raíces reales o por el contrario no se obtiene ninguna por ser el discriminante negativo.
Desde una perspectiva actual podemos mejorar la solución de Descartes con un nuevo dibujo, con el que obtenemos las raíces por la intersección de una circunferencia con la recta $y=0$, en una propuesta de resolución gráfica de validez para coeficientes de cualquier signo.
 Descartes aplica su método para resolver el problema planteado en el año 340 por Pappus, (Papo de Alejandría 290-350) , que no había sido resuelto hasta la fecha. Este problema consiste en hallar el lugar geométrico de los puntos del plano cuya distancia a cuatro rectas dadas cumpla la condición de que el producto de la distancia a dos de ellas sea igual al producto de las otras dos.
Descartes aplica su método para resolver el problema planteado en el año 340 por Pappus, (Papo de Alejandría 290-350) , que no había sido resuelto hasta la fecha. Este problema consiste en hallar el lugar geométrico de los puntos del plano cuya distancia a cuatro rectas dadas cumpla la condición de que el producto de la distancia a dos de ellas sea igual al producto de las otras dos.
El interés en resolver este problema es demostrar la utilidad del álgebra y la potencia de su “método” para obtener soluciones a los problemas planteados por la geometría. Aparece en el LIBRO PRIMERO de “La Géométrie” pero es en si mismo un avance y un resumen del conjunto de las ideas de Descartes. Resuelto el problema para cuatro rectas, retomara el problema en el LIBRO SEGUNDO para el caso de mas de cuatro rectas, hasta declarar finalmente con orgullo la solución general del problema.
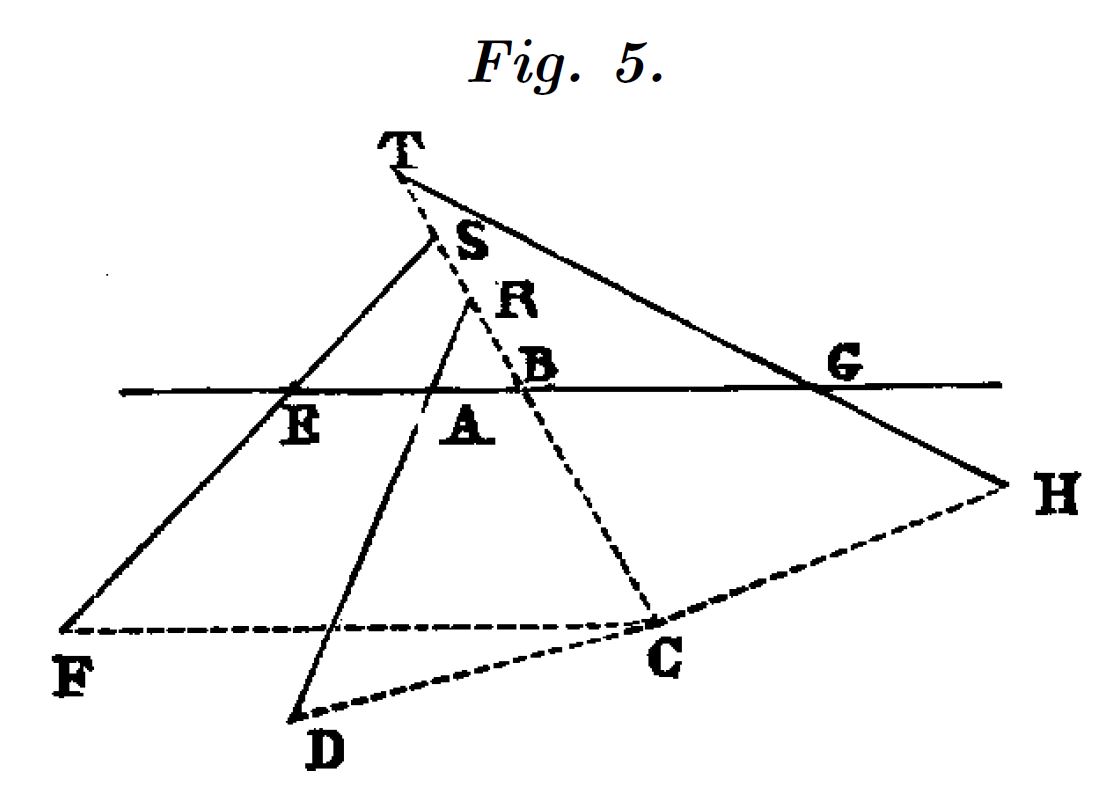
La aplicación del “método” es clara, en primer lugar supone dibujada la solución, con tres rectas arbitrariamente trazadas que cortan a una cuarta horizontal. Desde un punto cualquiera $C$, traza rectas de diferente pendiente que cortan a las cuatro definidas. Sobre estas rectas medimos las distancias de $C$ a cada una de las cuatro rectas.
La primera parte de la resolución consiste en definir las ecuaciones que definen estas distancias en función de las coordenadas del punto $C$, para obtener la ecuación de la curva a la que pertenecen todos los puntos que cumplen la condición establecida en el enunciado del problema:
Para situar el punto $C$ en relación a las rectas dibujadas, Descartes define un sistema de coordenadas. La recta horizontal hace de eje de las “$X$”, a partir del punto de intersección de una de las tres rectas restantes con ella (punto $A$). La recta, que desde $C$ nos define la distancia al eje “$X$”, queda establecida como eje “$Y$”, creciente en sentido descendente, contrariamente a como hoy estamos acostumbrados a verlo. En definitiva utiliza un sistema de coordenadas oblicuas. (ver figura 5).
En nuestro caso, para dibujar el problema nos mantendremos fieles al sistema de coordenadas ortogonales habitual, para obtener ecuaciones que sean directamente interpretables por GeoGebra.
Recordemos que la solución de un problema no depende del sistema de coordenadas elegido, aunque las ecuaciones referidas a uno y otro sistema sean diferentes. Cada una de ellas debe ser interpretada de acuerdo a las coordenadas a las que se refiere.
Seguiremos, de todos modos, la misma estrategia de Descartes para obtener las distancias $CF$, $CK$, $CD$, y $CH$ que necesitamos. Para ello, basta observar los tres triángulos que forman:
Cada uno de estos triángulos conserva sus proporciones, cualquiera que sea la posición del punto $C$. Planteamos las ecuaciones que nos definen las distancias que requerimos, una vez que quedan establecidas las pendientes de las rectas $A$, $E$ y $G$ sobre las que se construye el problema, que llamamos $m1$, $m2$ y $m3$ y los parámetros $p1$, $p2$, $p3$ y $p4$ que se obtienen estableciendo la proporción entre los lados de cada uno de los triángulos antes citados.
Por tanto, una vez dibujado el problema y definidos los valores que nos “fijan” la posición de todas las rectas, solo nos quedan como incógnitas las 4 distancias a las rectas, que tenemos que expresar en función de las coordenadas, $x$ e $y$, del punto $C$.
Definición de las rectas que intervienen: El punto $A$, naranja, es fijo y el origen de coordenadas. El punto $H$, verde, y $E$ , azul, pueden moverse sobre el eje $X$.
La pendiente de las rectas principales y de las rectas trazadas desde $C$ puede modificarse moviendo el punto de su color en los relojes de control.
Suponemos un punto $C$ situado aleatoriamente en el plano, hacemos los cálculos y obtenemos el valor del producto de las distancias que como es natural no cumple con la igualdad propuesta.
cálculo de las distancias. En el dibujo podemos ver como calcular la distancia de $C$ a cada recta, mediante el triángulo formado por cada una de ellas con la recta vertical que pasa por $C$. Activando las casillas $CF$, $CD$, $CH$, $CK$ visualizamos cada triángulo y la ecuación de su distancia.
Obtenidas las distancias sustituimos las ecuaciones obtenidas en la condición.
$$CF × CK=CD × CH$$Podemos comprobar que el punto $C$, cumple con la condición al situarse sobre el lugar geométrico calculado.
Cálculo de las distancias de un punto $C$ a las rectas
Llamamos “$x$” a la coordenada sobre el eje $X$ a partir de $A$. Llamamos “$y$” a la distancia $CB$.
Nuestro objetivo es calcular: $CF$, $CD$ y $CH$ que son las distancias de $C$ a las rectas, $E$, $A$, $G$ y $CK$, que es la distancia a la recta horizontal y que obtenemos fácilmente a partir de la "$y$" de $C$.
Para $CF$, sabemos que $SB = (x-x_E) m_2$ siendo $m_2$ la pendiente de la recta $E$.
$SC$ es:
$$SC=\big((x-x_E) m_2\big) -y$$$CF$ resulta:
$$CF=\big((x-x_E)m_2-y\big)p_2$$Siendo $p_2$ la proporción entre los lados $FC$ y $CS$ del triángulo $SCF$.
De la misma manera, $CD$ resulta:
$$CD=(x m_1-y)p_1$$Siendo $m_1$ la pendiente de $A$ y $p_1$ la proporción entre los lados $CD$ y $CR$ del triángulo $RCD$.
Siguiendo el mismos procedimiento para $CH$, en el triángulo $TCH$, tenemos:
$$CH=\big((x-x_G)m_3-y\big)p_3$$Por ultimo $CK$ se obtiene directamente multiplicando $y$ por $m_4$ que es la proporción entre los lados $CK$ y $CB$ del triángulo $BCK$.
$$CK=m_4 \; y$$Obtención del lugar geométrico
El lugar geométrico viene definido por la igualdad del producto de las distancias:
$$CF \times CK = CD \times CH$$Multiplicando las expresiones obtenidas:
$$\big[((x-x_E)m_2-y)p_2\big] \big[m_4y\big]=\big[((x-x_G)m_3-y)p_1\big]\big[((x-x_G)m_3-y)p_3\big]$$Efectuando las operaciones obtenemos una ecuación de segundo grado en $x$ e $y$.
$$(p_2 m_4+p_1p_3) y^2+(x_G m_3p_3p_1+x_E m_2p_2 m_4) y \\– (m_2p_2 m_4+m_3p_1p_3+m_1p_1p_3) xy \\– (x_G m_1p_1p_3m_3)x +(m_1p_1m_3p_3)x^2=0$$Los coeficientes de esta ecuación dependen de las pendientes de las tres rectas definidas, de la pendiente de las rectas sobre las que se miden las distancias y de las coordenadas de los puntos de corte de las rectas $G$ y $E$. Todas estas cifras son conocidas al definir el problema.
Para el manejo de esta ecuación podemos sustituir las cantidades incluidas en los paréntesis por un solo coeficiente, de manera que la expresión resulta:
$$my^2+oy-nxy-ex+ux^2=0$$siendo:
$m=(p_2 m_4+p_1p_3)\\ o=(x_G m_3p_3p_1+x_E m_2p_2 m_4)\\ n=(m_2p_2 m_4+m_3p_1p_3+m_1p_1p_3)\\ e=(x_G m_1p_1p_3m_3)\\ u=(m_1p_1m_3p_3)$Como hemos visto la ecuación de la distancia del punto $C$ a cada curva es de primer grado. La solución, en la que se iguala el producto de dos de ellas con el de las otras dos, es una ecuación de segundo grado, que según el valor de sus coeficientes puede ser una elipse, una hipérbola o una parábola.
Nada impide generalizar el problema a mas rectas, siguiendo el mismo procedimiento de cálculo de las distancias. El grado de la ecuación del lugar geométrico se incrementa según el numero de factores que intervienen.
Para Apolonio, el problema no tenia solución para mas de seis rectas, al alcanzarse una ecuación de tercer grado, lo que correspondía a un volumen. Para mas rectas el problema se consideraba irresoluble (era absurdo para la geometría considerar mas de tres dimensiones en el espacio). Descartes demuestra que, si abandonamos el criterio de homogeneidad de las magnitudes, para la resolución del problema con $n$ rectas se obtiene una ecuación de $\frac{n}{2}$ grados si $n$ es par, y $\frac{n-1}{2}$ para $n$ impar.
Hasta aquí llega Descartes en el PRIMER LIBRO. Antes de continuar necesita justificar que las ecuaciones de cualquier grado representan curvas y que cada una de ellas es interpretable como un lugar geométrico en el plano. A este propósito dedica el SEGUNDO LIBRO.
Para la geometría clásica las curvas se describen de dos maneras, por el lugar geométrico que las define o por el procedimiento a utilizar para dibujarlas. Por ejemplo una circunferencia es el lugar geométrico de los puntos que distan de un punto una cantidad constante, llamada radio. La circunferencia se dibuja con un compás.
Según estos criterios, las curvas se clasificaban en planas, las que podían dibujarse con regla y compás y solidas las que se obtenían de las secciones de un cono por un plano, es decir la elipse, la parábola y la hipérbola. Las que no cumplían estos criterios se llamaban curvas mecánicas, que se llamaban así por estar asociadas generalmente a algún tipo de movimiento. En este grupo se incluyen curvas muy diversas, como es el caso de las espirales o, las que están asociadas a la longitud del arco de círculo, como las cicloides.
Descartes define un criterio de clasificación de las curvas diferente. Todas las curvas se definen por el movimiento de un punto sobre el plano. La diferencia entre unos casos y otros viene dada por la exactitud con la que puede ser definido ese movimiento.
No hay motivo para excluir de la geometría las curvas mas complejas si pueden imaginarse descritas por un movimiento continuo o de varios movimientos sucesivos siempre que cada uno de ellos venga determinado por los precedentes y nos permita un conocimiento exacto de su medida.
Propone también, abandonar las limitaciones de la geometría clásica sobre las herramientas para obtener su dibujo:
La superación de la regla y el compás lleva a Descartes a crear nuevas herramientas de dibujo, que son evidentemente “ideales” como lo eran la regla y el compás clásicos, para definir de forma precisa y exacta cada uno de los puntos de una curva.
Descartes supone que las curvas generadas mediante mecanismos articulados son todas ellas algebraicas, pero no lo demostró. La demostración se debe a Alfred Bray Kempre, en 1876.
El primer mecanismo que crea es el de la figura 7, que es un compás con un conjunto de barras articuladas dispuestas de forma que definen dos series de triángulos rectángulos semejantes que permiten establecer entre sus lados medias proporcionales continuas, es decir para cualquier magnitud y para todas las potencias enteras de esa magnitud.
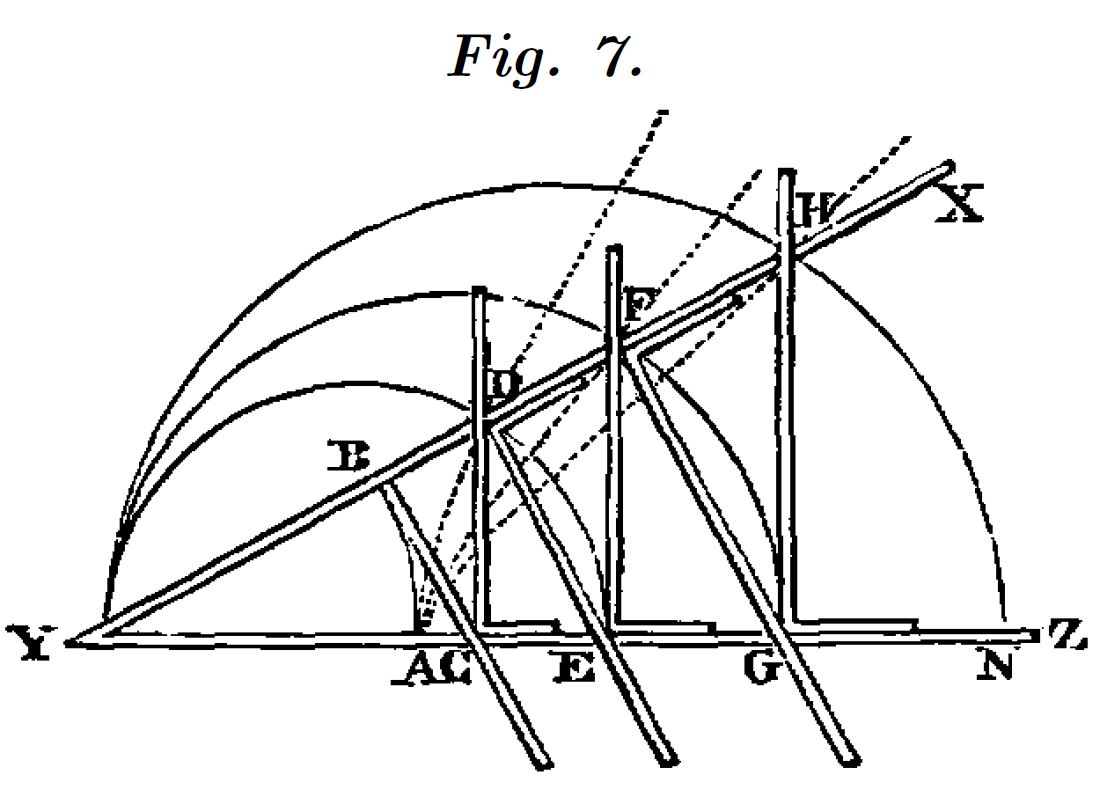
Este compás se conoce como “mesolabio” de Descartes y va a servirle para exponer su propuesta de clasificación de las curvas en diferentes géneros según el grado de su ecuación.
El nombre del compás, se debe a la máquina construida por Eratóstenes (276 ac-194 ac) para el cálculo de raíces cúbicas.
El deslizador $b$ nos permite visualizar el lugar geométrico de los puntos sobre $YH$ al mover $B$. El grado de la ecuación de esta curva se incrementa al elegir puntos mas alejados de $B$, sobre $YH$. El mesolabio transforma el movimiento de $B$ sobre una circunferencia en nuevas curvas de grado superior a dos.
Obtención de medias proporcionales
Como primera observación comprobamos que los triángulos rectángulos con hipotenusa en $YG$ y $YH$ son semejantes con lo que:
$${YB\over YC} = {YC\over YD} = {YD\over YE} = {YE\over YF} = {YF\over YG} = {YG\over YH}$$Si $YB = 1$, de la primera igualdad se deduce:
$$YC^2 = YD \qquad\ YC=\sqrt{YD}$$Sustituyendo en la segunda igualdad $YD$ por $YC^2$:
$$YE=YC^3 ;\qquad\ YC=\sqrt[3]{YE}$$El mismo proceso en la tercera igualdad, sustituyendo $YD$ y $YE$ por su valor:
$${YC^2\over YC^3} = {YC^3\over YF}$$ $$YC=\sqrt[4]{YF}$$Así, sucesivamente el mesolabio nos permite el cálculo de todas las proporciones, lo que en el lenguaje de la época consiste en la obtención de medias proporcionales continuas.
Obtención de las ecuaciones de las curvas trazadas por el mesolabio.
Curva descrita por el punto D
$$\textcolor{red}{{YB\over YC}={YC\over YD}}={YD\over YE}={YE\over YF}={YF\over YG}={YG\over YH}$$$YB=\;a,\quad YC=\;x,\quad CD=\;y,\quad YD=\;z$
$$\textcolor{red}{{z\over x} = {x\over a}}$$ $$ z = {x^2 \over a} $$Tenemos además que,
$$z^2=x^2+y^2$$Sustituyendo en esta ecuación $z$,
$$x^4=a^2(x^2+y^2)$$Obtención de la ecuación de la curva descrita por $F$:
$$\textcolor{green}{{YB\over YC}}=\textcolor{red}{{YC\over YD}}=\textcolor{blue}{{YD\over YE}= {YE\over YF}}={YF\over YG}={YG\over YH}$$$YB=\;a,\quad YE=\; x,\quad EF=\; y,\quad YF=\; z$
Sustituyendo estos valores en la igualdad azul,
$$\textcolor{blue}{{YD\over x} = {x\over z}}$$ $$\textcolor{blue}{YD} = {x^2\over z}$$También tenemos la segunda igualdad:
$$\textcolor{red}{{YC\over YD}} = \textcolor{blue}{{YD\over x}}$$ $$\textcolor{red}{YC} = {x^4\over z^2}\;{1\over x} = {x^3\over z^2}$$ $$\textcolor{red}{{YC\over YD}} = \textcolor{green}{ {a\over YC}}$$Sustituyendo $YC$ e $YD$ por su valor obtenemos,
$$z=\sqrt [3]{x^4\over a}$$Sustituyendo en:
$$z^2= x^2+y^2$$ $$x^8=a^2(x^2+y^2)^3$$Para el punto $n$: Generalizando el procedimiento anterior obtenemos la ecuación general de las curvas descritas por los puntos del mesolabio.
$$x^{4n}=a^2(x^2+y^2)^{2n-1}$$Cuando a una expresión algebraica se le añade una segunda variable, obtenemos una curva como lugar geométrico de los puntos cuyas referencias a dos rectas predefinidas cumplen con esa expresión. La magnitud de esas “referencias” son las coordenadas del punto. En definitiva una curva plana queda descrita por una ecuación algebraica de dos variables, con independencia del grado con el que figuren sus variables.
Hoy llamamos “coordenadas cartesianas” a los sistemas de referencia basados en ejes ortogonales, aunque Descartes no impone este requisito a las rectas de referencia y utiliza en cada caso el que considera mas adecuado. La dirección para las coordenadas crecientes tampoco es en todos los casos hacia la derecha y hacia arriba como estamos acostumbrados a ver hoy.
Las coordenadas son siempre positivas y por la tanto no existe el tramo negativo de los ejes de coordenadas.
Salvando estos detalles, la principal diferencia entre la propuesta de Descartes y nuestra interpretación de un sistema de coordenadas es que Descartes utiliza como referencia rectas que forman parte de la construcción del problema (el dibujo del problema resuelto).
Nota: al redibujar las figuras de Descartes hemos definido los ejes de coordenadas tal como es usual hoy en día. En la mayor parte de sus figuras Descartes utiliza el eje vertical en sentido creciente hacia abajo, a partir de un punto origen arbitrario. El eje horizontal también es positivo hacia la izquierda. Al no aceptar valores negativos de las coordenadas sus dibujos se limitan al cuadrante con ambas coordenadas positivas.
En la interpretación actual, los ejes de coordenadas mantienen una existencia independiente del dibujo y se sobreponen a él.
La adopción de un sistema de ejes ortogonales como referencia se impuso rápidamente. En las obras de Newton aparecen los ejes $X$ e $Y$ en mayúsculas, tal como los conocemos hoy, con su parte positiva y negativa a partir del punto de cruce de ambos que recibe el nombre de origen de coordenadas. Los sistemas de referencia se multiplicaron, de manera que Newton llego a identificar 7 maneras de referenciar un punto en el plano. Coordenadas oblicuas, diferentes tipos de coordenadas polares e incluso sistemas basados en la distancia a dos puntos fijos en el plano.
Pero finalmente el sistema de referencia por excelencia se basa en ejes ortogonales, y en reconocimiento a Descartes, las coordenadas y las ecuaciones referidas a ellas se denominan Cartesianas.
Admitir en geometría las curvas algebraicas supone la entrada en el dominio matemático de una gran variedad de curvas junto a las curvas planas y solidas de la geometría clásica.
A pesar de ello quedan fuera las curvas mecánicas, espirales y cicloides, porque Descartes no encuentra la manera de definir de forma precisa y exacta sus puntos. Esta “expulsión” no implica su desinterés por estas curvas, es simplemente el reflejo de la insuficiente maduración de los problemas asociados a los “inconmensurables”, generalmente el numero $π$, involucrado en la definición de magnitudes angulares y longitudes de arco. En la época no están definidas lo que hoy son funciones trigonométricas. Seno y coseno eran simplemente tablas de proporciones entre el arco, la flecha y la cuerda del ángulo central de una circunferencia y por lo tanto sus valores eran aproximados.
Para las curvas aceptables, Descartes define su “género”, según sea el grado de la ecuación que las define y propone una clasificación basada en este criterio, identificando la complejidad de una curva con el grado de su expresión algebraica.
Las ecuaciones de primer y segundo grado son resolubles con regla y compás como hemos visto en el LIBRO PRIMERO, son los problemas planos y pertenecen al primer género.
Descartes sabe que la resolución de ecuaciones de cuarto grado se puede conseguir mediante su reducción a una de tercer grado. Por este motivo agrupa las curvas de tercer y cuarto grado en un único género.
Generaliza esta posibilidad de reducción en un grado para las ecuaciones de cualquier grado, lo cual no es cierto, y decide clasificar las curvas en géneros sucesivos, agrupando en el mismo género las que se describen por ecuaciones en grados de dos en dos.
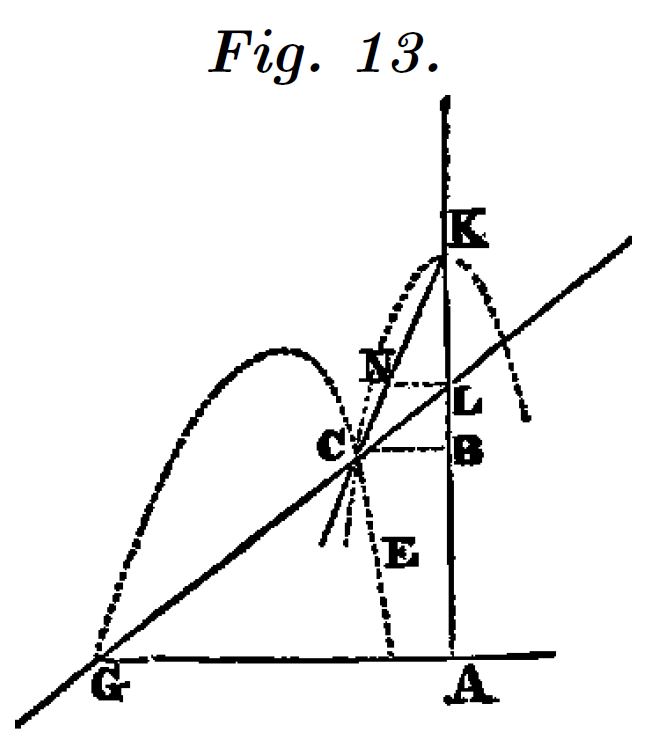 Descartes quiere demostrar que podemos construir una curva de cualquiera de los géneros definidos mediante su segundo compás, que consiste en una sencilla regla que se mueve alrededor de un punto fijo y que obtiene una curva a partir de otra, que le sirve de plantilla, y que se desplaza verticalmente según el movimiento del compás. La curva resultante es superior en un grado a la original.
Descartes quiere demostrar que podemos construir una curva de cualquiera de los géneros definidos mediante su segundo compás, que consiste en una sencilla regla que se mueve alrededor de un punto fijo y que obtiene una curva a partir de otra, que le sirve de plantilla, y que se desplaza verticalmente según el movimiento del compás. La curva resultante es superior en un grado a la original.
Este compás se conoce como hiperbológrafo porque Descartes lo aplica a una recta y obtiene una hipérbola. Se abre así un camino para generar curvas de cualquier grado de forma mecánica
El deslizador $a$ controla el movimiento de la recta trazadora.
El deslizador $b$ ajusta la distancia $KL$ entre la curva plantilla y el punto $L$ de intersección con la recta trazadora. Podemos seleccionar la curva de plantilla que nos interese.
El tercer deslizador que aparece al seleccionar una plantilla es un parámetro que modifica la ecuación de la curva base, recta, parábola ó circunferencia.
Trazando sobre una recta
Buscamos la intersección de la rectas
$$\textcolor{green}{y=ax}$$ $$\textcolor{red}{y-y_K=n(x-x_A)}$$Sabiendo que: $\textcolor{blue}{y_K=ax_A+b}$
Sustituyendo resulta:
$$\textcolor{red}{y-\textcolor{blue}{\bigg(\textcolor{green}{{y\over x}}\bigg)x_A+b }=n(x-x_A)}$$ $$y(x-x_A)=nx(x-x_A)-bx$$De segundo grado en $x$.
Trazando sobre una parabola
Para el caso de la parábola obtenemos la intersección de la recta, $(\dfrac{y}{x})=a,$ con la parabola, $-(y-y_K)=w(x_A-x)^2$, y sabemos que:
$$y_K=ax_A+b$$Sustituyendo en la ecuación de la parábola $y_K$ y $a$ por sus valores obtenemos la ecuación de la curva trazada por el compás que resulta ser de tercer grado.
El hiperbológrafo permite iterar el proceso, sustituyendo la curva plantilla por la generada en un proceso anterior para obtener curvas de mayor complejidad en cada paso. A partir de este instrumento básico muchos matemáticos posteriores propusieron diferentes mecanismos para el trazado de curvas, en un gran despliegue de imaginación y creatividad.
El dibujo de curvas no es una cuestión menor. Hasta que han estado disponibles medios de cálculo informáticos, el dibujo de las curvas era un proceso laborioso que requería tiempo y esfuerzo. La abolición por Descartes de la regla y el compás como único instrumento aceptable en geometría abre la puerta a numerosas aportaciones de mecanismos trazadores.
El primero en publicar este tipo de mecanismos trazadores fue el holandés Franz von Schooten el joven, que hemos mencionado anteriormente como traductor al latín de “La Géométrie”, el cual en su tratado “De organica conicarum sectionum in plano descriptione tractatus” publicado en 1675, presenta seis mecanismos para dibujar cónicas. Uno de los mas conocidos consiste en un rombo articulado que permite dibujar hipérbolas y elipses.
El rombo articulado $ABCD$ tiene fijo el punto $A$ y el punto $C$ se mueve en una circunferencia de radio $r$ centrada en otro punto fijo $O$, el punto de corte de la recta $OC$ con la diagonal del rombo $BD$ describe una cónica.
Esa cónica es:
una elipse si $r < OA$,
una hipérbola si $r > OA$
y degenera en un punto si $r = OA$.
Si $C$ describe una recta, $P$ describe una parábola.
A partir de la popularización de los mecanismos de Van Schooten, se han sucedido propuestas. Reproducimos aquí el mecanismo diseñado por Newton para trazar cónicas.
El video pertenece al canal de YouTube de F.J. Manzano que recomendamos visitar, donde se encuentra junto con otros 40 videos de diferentes mecanismos.
Para completar la resolución del problema de Pappus planteado en el LIBRO PRIMERO, es de singular interés para Descartes el dibujo de la curva que corresponde a la ecuación del lugar geométrico obtenido. Es el retorno al resultado geométrico, una vez obtenido el resultado algebraico, al resultado geométrico.
 La exposición de su procedimiento es bastante difícil de seguir por el sistema de coordenadas oblicuas que utiliza y la referencia continua a los signos de los términos de sus ecuaciones, al trabajar solo con valores positivos de los parámetros.
La exposición de su procedimiento es bastante difícil de seguir por el sistema de coordenadas oblicuas que utiliza y la referencia continua a los signos de los términos de sus ecuaciones, al trabajar solo con valores positivos de los parámetros.
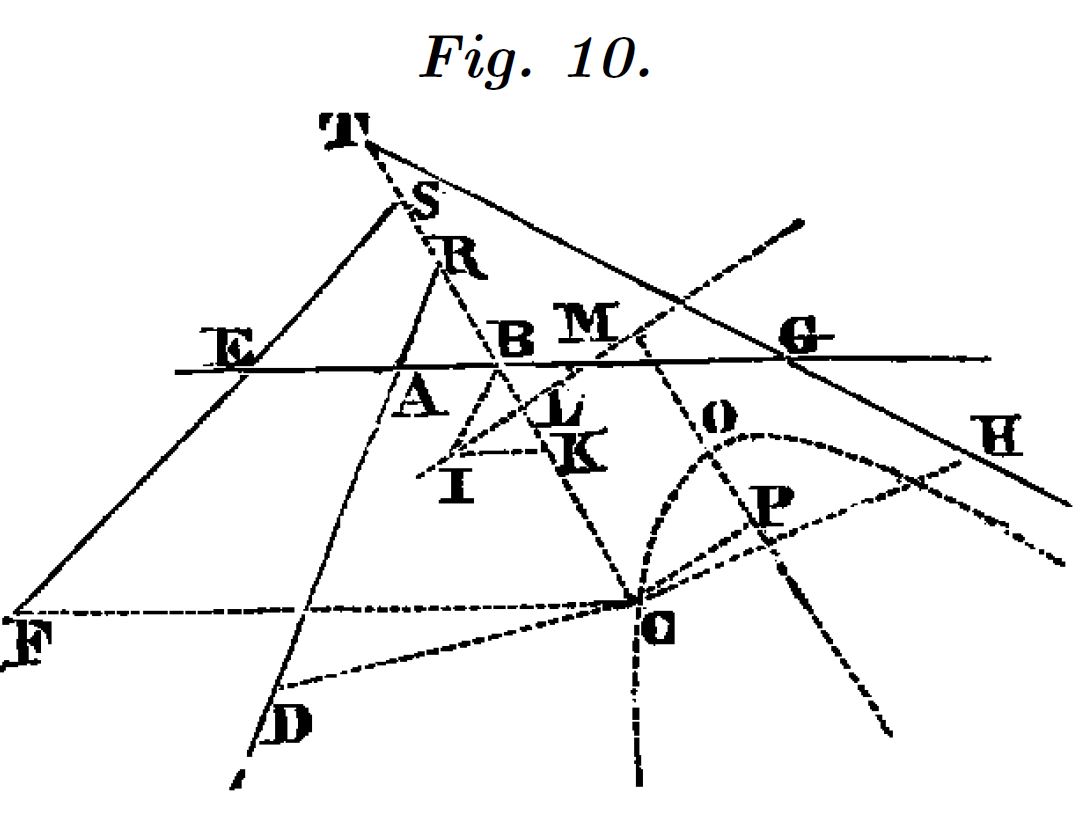
Toda su exposición no se apoya mas que en las figuras 9 y 10 escasamente esclarecedoras.
Para el dibujo del lugar geométrico, Descartes descompone su ecuación en la suma de una recta y una cónica.
Si reordenamos la ecuación que hemos obtenido en el apartado 3.1.3 referida a ejes ortogonales, obtenemos:
Para despejar la "$y$", aplicamos la fórmula de resolución de ecuaciones de segundo grado (ecuación en $y$, considerando la $x$ como un parámetro), obtenemos:
$$y={(nx-o)\over 2m}\pm {\sqrt{(o-nx)^2-m(ux^2-ex)}\over 2m}$$Esta ecuación podemos verla como la suma de una recta y de una cónica:
recta: $\qquad y=\Large {(nx-o)\over 2m}$
cónica: $\qquad 4m^2y^2=(o-nx)^2-m(ux^2-ex)$
$\qquad 4m^2y^2=o^2+(4me-no)x+(n^2-4mu)x^2$
Estas ecuaciones están referidas a coordenadas ortogonales, por lo que la cónica tiene siempre su eje vertical (eje “$Y$”) y se puede observar que la composición de recta y cónica, consiste en un giro centrado en el punto de intersección de ambos ejes con la línea recta con la que la componemos.
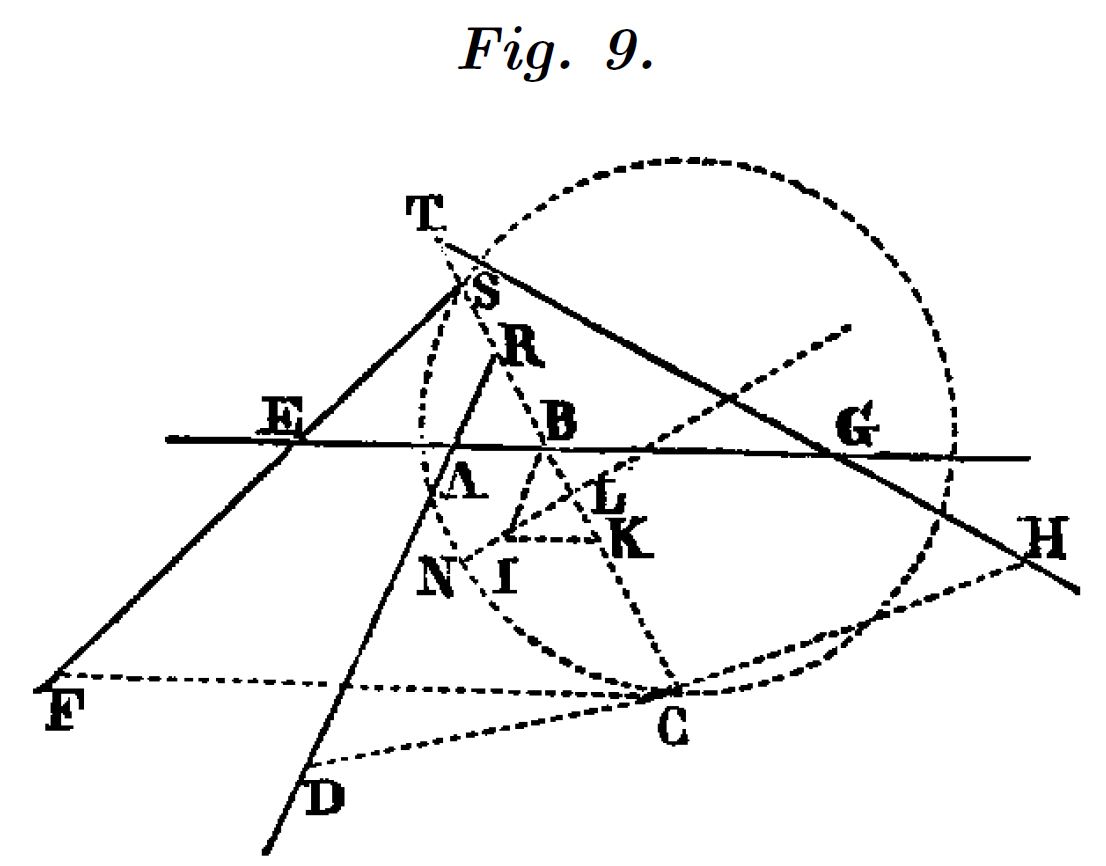 La figura 9 es el dibujo de un caso para cuatro rectas, con valores establecidos numéricamente, para las rectas y sus pendientes. Descartes dibuja este caso para comprobar las fórmulas obtenidas, con valores concretos de los parámetros. El resultado es una circunferencia.
La figura 9 es el dibujo de un caso para cuatro rectas, con valores establecidos numéricamente, para las rectas y sus pendientes. Descartes dibuja este caso para comprobar las fórmulas obtenidas, con valores concretos de los parámetros. El resultado es una circunferencia.
Datos el dibujo:
$$ AE =3,\; AG =5, \;AB = BR, \;BS ={1\over 2}BE,\;GB=BT, \\CD ={3\over 2}CR,\;CF=2CS, \;CH ={2\over 3}CT \;y\; ABR = 60º$$
Al inicio los dos puntos $B$ coinciden en $x=1$.
Para desplazar $C$, debemos mover $B$ y deslizar $C$ sobre la recta $CB$.
La recta $IB$ es la recta de composición, en este caso perpendicular al eje “$Y$” oblicuo (recta $BRST$).
La ecuación del lugar geométrico en coordenadas oblicuas es de ecuación:
$$y=1-{1\over2}+\sqrt{1+4x-{3x^2\over4}}$$Para materializar esta coordenada dibujamos el círculo de este radio, de centro en $B$, y obtenemos el punto buscado sobre la paralela a $BRST$ que pasa por $B$.
Observemos que la ecuación solo nos define un arco de la circunferencia en la zona donde la $x$ y la $y$ son positiva según la elección del sentido de los ejes de Descartes.
Situando $C$ sobre la circunferencia, comprobamos que se cumple la condición establecida para las distancias.
La definición de las rectas coincide aparentemente con las de la figura 10. Con la misma definición del problema para la figura 9 y 10 se obtienen diferentes resultados, lo que plantea dudas sobre la exactitud de la figura 10. Este es el único caso de este tipo que encontramos en “La Géométrie”, donde todas las figuras están dibujadas con mucha precisión.
Problema de Pappus para 5 rectas, 4 de ellas paralelas.
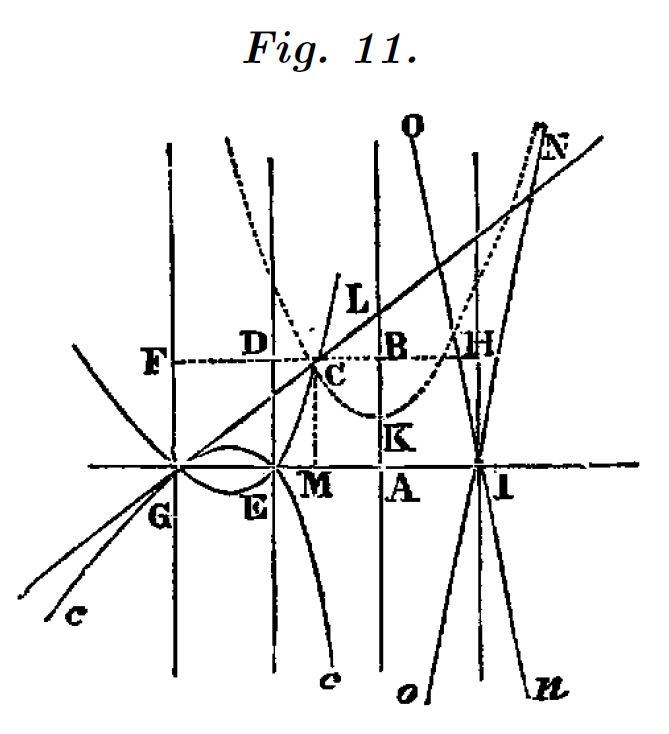
Descartes aborda el problema de Pappus para el caso de 4 rectas paralelas y una quinta perpendicular a ellas. Supone que las distancias se obtienen perpendicularmente a todas las rectas. Adicionalmente pone como condición que las rectas paralelas sean todas ellas equidistantes. La condición del lugar geométrico es:
$$\big(x(A)-x\big)a\times y=\big(x(G)-x\big)\big(x(E)-x\big)\big(x(I)-x\big)$$Que es una ecuación de tercer grado.
Para dibujar esta curva descartes recurre a su regla trazadora, deslizándola sobre una parábola como plantilla.
Con el deslizador modificamos las distancias $EA$ y $AI$.
El punto $C$ podemos moverlo libremente y observar que se cumple la condición de las distancias cuando esta sobre el lugar geométrico.
La cúbica de trazos es la simétrica de la solución, que también lo es si tomamos las distancias en valores absolutos.
Hemos resuelto el problema adicionalmente para el caso de 4 rectas tres de ellas paralelas.
Revisión de las soluciones obtenidas
Tal como hemos planteado nosotros las ecuaciones del problema, las distancias obtenidas algebraicamente pueden ser negativas.
Descartes no acepta distancias negativas, pero para nosotros el signo solo expresa el sentido de la medición de la distancia, siendo positiva cuando coincide con la dirección de coordenadas crecientes y negativa en el caso contrario.
El problema de Pappus se refiere evidentemente a distancias absolutas, por lo que la ecuación del lugar geométrico en nuestro caso debe plantearse en valores absolutos. Si lo hacemos así, obtenemos dos cónicas que satisfacen la ecuación.
Para Descartes ambas deberían ser igualmente validas, a pesar de que en ningún caso se refiere a la existencia de mas de una solución. Estamos ante las consecuencias de su tratamiento de las magnitudes negativas. En nuestro caso, mediante una única ecuación resolvemos dos casos que para Descartes son distintos.
Adicionalmente, es posible discutir el orden de los factores en la expresión del lugar geométrico, con lo que con cuatro curvas podemos obtener tres ecuaciones diferentes.
$$CF\times CK=CD\times CH$$ $$CD\times CK=CF\times CH$$ $$CH\times CK=CD\times CF$$Todas ellas tienen cabida en el enunciado del problema por Pappus y cada una de ellas tiene dos soluciones. Planteado de esta forma el número total de lugares geométricos para cuatro rectas es de seis.
Para las curvas algebraicas el dibujo punto a punto siempre es posible, calculando para cada $x$ el valor de la $y$ correspondiente. Para las curvas mecánicas, por ejemplo las espirales, esto no es posible para todos sus puntos, aunque si puede calcularse, de forma exacta, alguno de ellos.
Descartes deja claro que, son perfectamente aceptables las curvas que no podemos “construir" geométricamente y que solo podemos representar punto a punto. Este posicionamiento es inevitable, porque la construcción geométrica de curvas de grado superior no es factible.
A pesar de ello, no hay ejemplos en “La Géométrie” de curvas construidas punto a punto a partir de su ecuación.
Las únicas curvas de tercer grado que aparecen, están dibujadas a partir del hiperbológrafo, como hemos visto en la figura 11 y lo veremos en las figuras 31 y 32. También en la figura 9 se dibujan curvas de grado superior mediante el mesolabio.
Respecto de las construibles gráficamente:
La cuerda tensa es el instrumento para representar una distancia, por lo que aparece frecuentemente en el dibujo de lugares geométricos. Las distancias se traducen a una expresión algebraica aplicando el teorema de Pitágoras, por lo que su aceptación como instrumento de dibujo no plantea problemas.
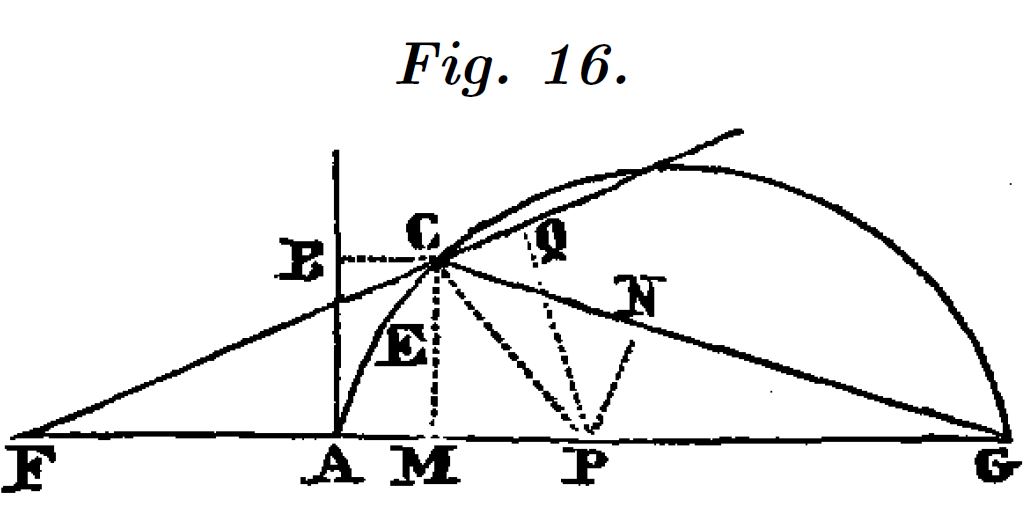
Descartes plantea trazar la perpendicular a una curva en un punto y obtener en ese punto un círculo tangente como la manera mas directa de resolver el problema de la tangente a una curva.
Este apartado, tiene una importancia capital, porque queda establecido uno de los principios básicos de la geometría algebraica, la relación entre las propiedades de la ecuación de una curva y las características geométricas de la curva representada.
El punto de partida es la obtención de la ecuación que represente la curva ($y=f(x)$ en verde), mediante su referencia a dos rectas cualesquiera del plano. Elegimos un punto $C$ de la curva para el que queremos obtener la perpendicular.
Sobre una de las rectas de referencia, que nosotros identificaremos como “eje $X$”, se elige un punto (punto $P$) desde el que se traza una circunferencia que pasa por el punto $C$. La ecuación de una circunferencia de centro en $P$ y radio $r$ es:
$$(x-x_p)^2+y^2=r^2$$Tenemos por lo tanto dos ecuaciones con dos incógnitas y podemos obtener una ecuación en $x$, que llamaremos $g(x)$.
Sustituyendo el valor de $y$ obtenido de la ecuación de la curva, en la ecuación de la circunferencia:
$$g(x) = \big(f(x)\big)^2 +(x- x_p)^2-r^2$$
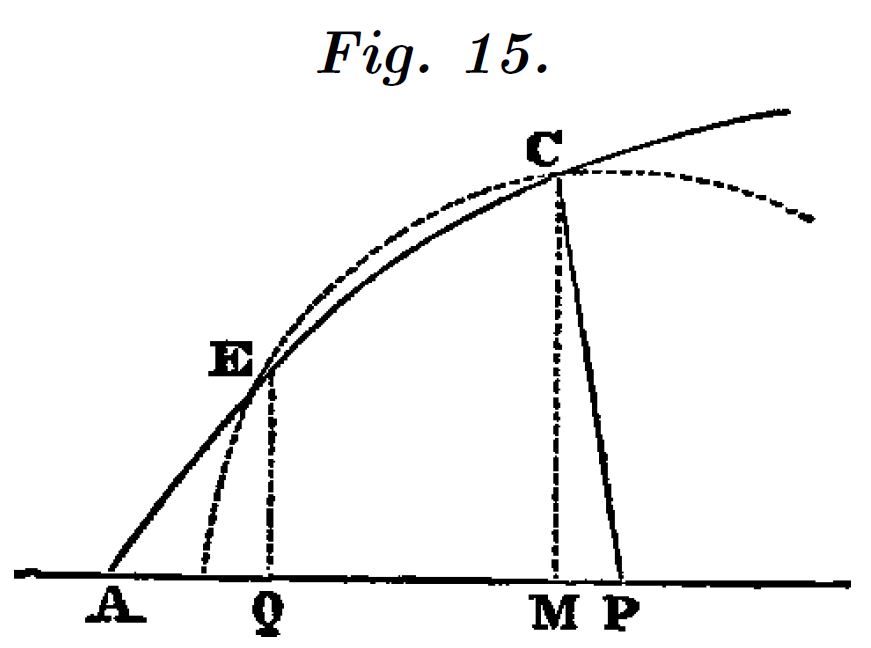 Puesto que $P$ lo hemos situado en un punto cualquiera sobre el eje $X$ no hemos acertado con el punto exacto, $A$, desde el que el círculo es tangente a la curva $y=f(x)$ en $C$. La ecuación $g(x)$ tiene por tanto dos raíces, $(x=x_Q\; y\; x=x_M)$, que nos identifican los puntos de intersección entre las dos curvas.
Puesto que $P$ lo hemos situado en un punto cualquiera sobre el eje $X$ no hemos acertado con el punto exacto, $A$, desde el que el círculo es tangente a la curva $y=f(x)$ en $C$. La ecuación $g(x)$ tiene por tanto dos raíces, $(x=x_Q\; y\; x=x_M)$, que nos identifican los puntos de intersección entre las dos curvas.
La intersección de curvas, que es un problema geométrico, se reconduce a la resolución de sistemas de ecuaciones, que es un problema algebraico.
Si $x_Q$ y $x_M$ son raíces de la expresión algebraica sabemos que es divisible por $(x-x_Q)$ y por $(x-x_M)$. Podemos descomponer $g(x)$ en un producto de polinomios de la forma:
$$g(x)=(x-x_Q)(x-x_M)\sum\big(b_{(n-2)}\;x^{(n-2)}\big)$$Si el centro de la circunferencia se sitúa en el punto $A$, los puntos $E$ y $C$ se confunden en uno y esta ecuación tiene una raíz doble en $M$. La expresión anterior es igual a:
$$g(x)= (x-x_M)^2 \sum\big(b_{(n-2)}\;x^{(n-2)}\big)$$Siendo $\sum\big(b_{(n-2)}\;x^{(n-2)}\big)$ un polinomio de grado ($n-2$), y "$n$" el grado de $g(x)$.
Para que los dos polinomios sean iguales deben de ser iguales los coeficiente de cada uno de sus términos en $x^n$, con los que obtenemos un sistema de $n+1$ ecuaciones con $n+1$ incógnitas, $(x_P,r,b_0,b_1,b_2)$.
Resolviendo este sistema obtenemos $x_P$ que es el valor que buscamos ya que $x_M = x_C$ por tanto un dato de partida.
El método de la circunferencia es novedoso porque resuelve el problema de la tangente a una curva únicamente con recursos algebraicos cincuenta años antes de que el cálculo infinitesimal aporte una solución general y mas directa al problema.
También vemos que se adelantan aquí, teoremas que se demostraran en el LIBRO TERCERO, como la divisibilidad de un polinomio por $(x-x_i)$ cuando $x_i$ es una de sus raíces y se hace uso el procedimiento de igualar los coeficientes de los términos del mismo grado para establecer la igualdad de dos polinomios.
Debemos establecer la igualdad:
$$\textcolor{blue}{[f(x)]^2}+\textcolor{green}{(x-x_P)^2-r^2}=\textcolor{red}{(x-x_M)^2(ax^2+bx+c)}$$Caso 1
En el caso de una parabola $y^2=2px$, la igualdad se convierte en:
$$\textcolor{blue}{2px}+\textcolor{green}{(x-x_P)^2-r^2}=\textcolor{red}{(x-x_M)^2}$$Igualando coeficientes obtenemos:
$$x_P=p+x_M$$Caso 2
En el caso de una parábola de ecuación $y = x^2$, la igualdad se convierte en:
$$\textcolor{blue}{x^4}+\textcolor{green}{(x-x_P)^2-r^2}=\textcolor{red}{(x-x_M)^2(ax^2+bx+c)}$$ $$\textcolor{blue}{x^4}+\textcolor{green}{x^2+x_P^2-2x_P\;x-r^2}=\textcolor{red}{x^2+x_M^2-2x_M\;x(ax^2+bx+c)}=$$ $$\textcolor{red}{ax^4-2ax_M\;x^3+bx^3+ax_M^2\;x^2-2bx_M\;x^2+cx^2\\+bx_M^2\;x-2cx_M\;x+cx_M^2}$$Igualando coeficientes tenemos:
$$\begin{aligned} x^4\quad &\rarr\textcolor{blue}{1}=\textcolor{red}{a}\\ x^3\quad &\rarr\textcolor{green}{0}=\textcolor{red}{2a\;x_M-b}\\ x^2\quad &\rarr\textcolor{green}{1}=\textcolor{red}{a\;x_M^2-2b\;x_M+c}\\ x\quad &\rarr\textcolor{green}{-2x_P}=\textcolor{red}{b\;x_M^2-2c\;x_M}\\ &\rarr\textcolor{green}{-r^2}=\textcolor{red}{c\;x_M^2}\end{aligned}$$Resolviendo las tres primeras ecuaciones obtenemos:
$1=a$
$b=2x_M$
$1=x_M^2-4\;x_M^2+c\;$ que nos da $\;c=1+3x_M^2$
Sustituyendo en la cuarta
$$-2x_P=2x_M^3-2(x_M+3x_M^3)$$ $$x_P=-x_M^3+(x_M+3x_M^3)=2x_M^3+x_M$$y obtenemos $x_P=2x^2+x$ en función de la $x$ del punto $C$ en el que queremos obtener la normal.
Buscamos la recta que corta perpendicularmente en el punto $B$ a la elipse de ecuación:
$$\textcolor{red}{{(x-a)^2\over a^2} +{y^2\over b^2} =1}$$El objetivo de la construcción es identificar el centro del círculo tangente a la elipse en ese punto. La elipse es una curva simétrica, por lo que sabemos que el centro del círculo estará en el eje de coordenadas.
$$\textcolor{blue}{h^2=y_B^2+(x_D-x_b)^2}$$Elegimos un punto cualquiera, $D$, sobre el eje $X$ y trazamos la circunferencia de centro $D$ que pasa por $B$. De ecuación:
$$(x-x_D)^2+y^2=h^2$$Sustituyendo $y^2$ en la ecuación de la elipse resulta,
$$\textcolor{red}{{(x-a)^2\over a^2}}+\textcolor{blue}{{h^2\over \textcolor{red}{b^2}} - {(x-x_D)^2\over \textcolor{red}{ b^2}}}=1$$Siendo $h$ el radio de la circunferencia y aplicando Pitágoras al triángulo $CBD$,
$$h^2=y_B^2+(x_D-x_B)^2$$Sustituyendo $h^2$ por su valor, y ordenando según el exponente de $x$, obtenemos una ecuación de segundo grado, $m x^2 + p x + q = 0$, cuyos coeficientes son:
$${1\over a^2} - {1 \over b^2}=m$$Las raíces de esta ecuación son los dos puntos de intersección de la elipse y la circunferencia.
Si $D$ fuese el centro de la circunferencia tangente, la ecuación tendría una raíz doble y por tanto podríamos escribirla en la forma,
$$(x-x_B)^2=0$$es decir:$\quad x^2+x_B^2-\textcolor{green}{2x_B}\;x=0$
Para que ambas ecuaciones sean iguales deben ser iguales los coeficientes de los términos del mismo grado, por lo que podemos igualar los coeficientes en $x$ de la dos ecuaciones:
$$\textcolor{green}{-2 x_B ={p\over m}} = {-2\over am} + {2x_D\over b^2 m}$$Con lo que obtenemos $x_D$, que es la abscisa del centro de la circunferencia ($J$) cuando es tangente a la elipse.
La obtención de la normal en un punto por el método del círculo es aplicable a cualquier curva pero, cuando el grado de la ecuación de la curva aumenta o no es posible obtener su ecuación explicita, despejar la $y$ de $f(x,y)=0$, para obtener $y=f(x)$, el método se complica considerablemente.
Para la concoide Descartes propone un método geométrico para obtener la normal en un punto, aceptando indirectamente las limitaciones de su método que en este caso es difícil de aplicar.
Tenemos que aclarar que el método del círculo solo nos identifica la recta perpendicular a la curva en un punto. Cualquier punto sobre esa recta permite dibujar un círculo tangente a la curva en $C$. El punto obtenido, sobre el eje $X$, no tiene respecto de cualquier otro, sobre la recta, una relevancia particular.
Con el ejemplo de la tangente a la concoide que Descartes resuelve gráficamente queda claramente resaltada esta observación, ya que el punto obtenido por el método grafico no esta obre el eje $X$ y ambos puntos coinciden sobre la recta normal en $C$.
Un óvalo es el lugar geométrico de los puntos para los cuales la suma o la diferencia de su distancia a dos puntos del plano, suman una cantidad constante y adicionalmente estas distancias están en una proporción establecida. Es decir, es el lugar geométrico de los puntos para los que se cumple:
$F$ y $Q$ son los focos del óvalo, $m$ y $a$ son números reales. Cuando $m=1$ el lugar geométrico es una elipse y si $P$ y $Q$ coinciden la elipse se convierte en una circunferencia.
El estudio de los óvalos en “La Géométrie” mas interesante desde el punto de vista de su relación con el conjunto de la obra que a la relevancia de su contenido. El interés de Descartes en estas curvas es consecuencia de su aplicación al estudio de la refracción y la reflexión de la luz que es el objeto de “La Dioptrique”. Es una prueba de la coherencia del conjunto del “Discurso del Método” y la ilustración de cómo las matemáticas se aplican a ramas especificas de la ciencia y la algebraización de la geometría es esencial en esta función.
Descartes, divide los óvalos en cuatro géneros según los diferentes procedimientos geométricos de construcción que utiliza. En segundo lugar dedica un notable esfuerzo para obtener sus perpendiculares por el método general del círculo tangente.
En tercer lugar demuestra las propiedades de los óvalos cuando sus proporciones coinciden con los coeficientes de la ley de la refracción que el matemático holandés Willebrord Snell van Royen (1580-1625) había establecido unos años antes.
Finalmente añadimos un apartado sobre la definición de las ecuaciones algebraicas del óvalo que no pertenece a “La Géométrie” pero que complementan la exposición sobre ellos.
Hemos visto la definición de los óvalos como el lugar geométrico para el que se cumple:
$F$ y $Q$ son los focos del óvalo, $m$ y $a$ son números reales. Para dibujar un óvalo situamos sobre una recta los dos polos $F$ y $G$. Definimos un tercer punto $A$, sobre la misma recta, como el punto de intersección del óvalo con la recta $FG$.
Conocido $m$, podemos obtener $a$, puesto que la ecuación del óvalo debe cumplirse en $A$ que es un punto del óvalo. Así pues:
Siendo las distancias $FA$ y $GA$ conocidas
Descartes clasifica los óvalos en $4$ “géneros” según la posición relativa de $A$ respecto de los polos.
Óvalos del primer y segundo género
Para estos óvalos el punto $A$ se sitúa entre los polos $F$ y $G$. Definido $m$ calculamos $a$. El primer y segundo género se diferencian en el signo de la ecuación.
Óvalos de tercer y cuarto género
El punto $A$ se sitúa fuera del segmento $FH$ (para estos óvalos el polo $G$ lo nombramos como $H$). Para estos óvalos definimos $m$ según la proporción de las distancias $AF$ y $AH$. Se diferencian, como en el caso anterior, en el signo de la ecuación.
Con la casilla “ver óvalo completo” visualizamos la ecuación algebraica del óvalo completo correspondiente. Las ecuaciones del óvalo completo se verán mas adelante en el apartado 2.2.9.
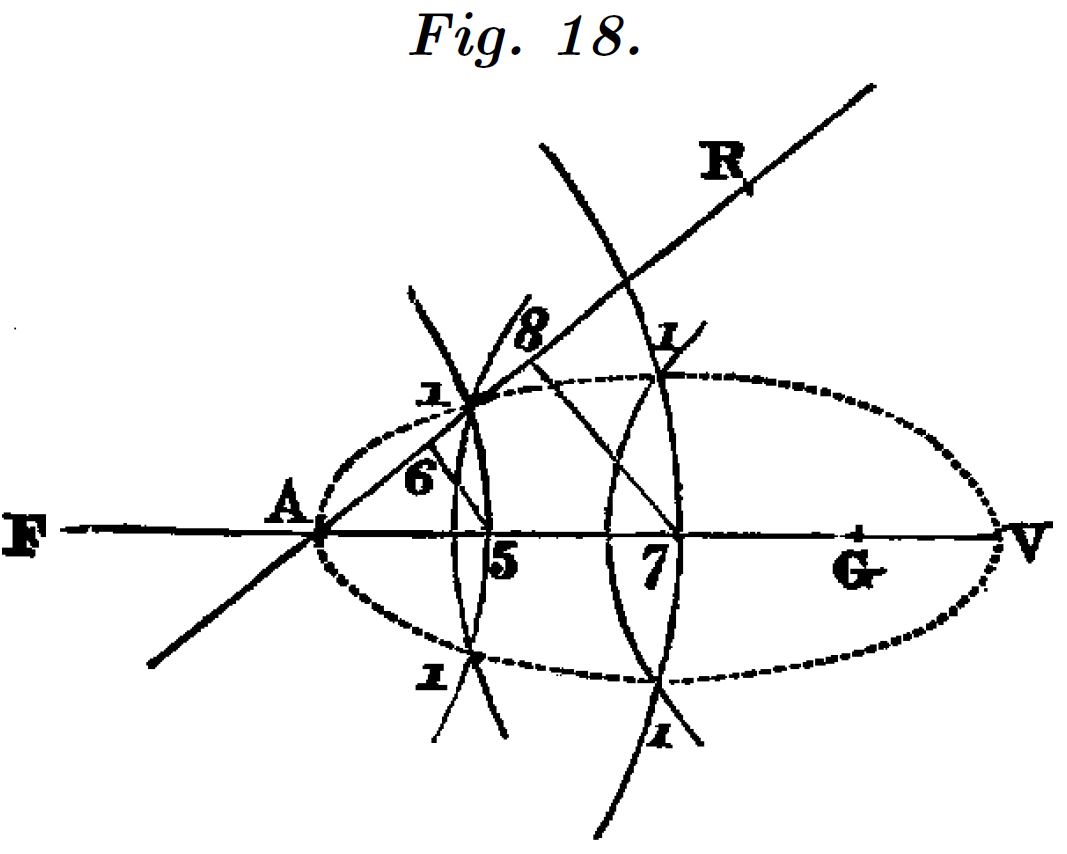
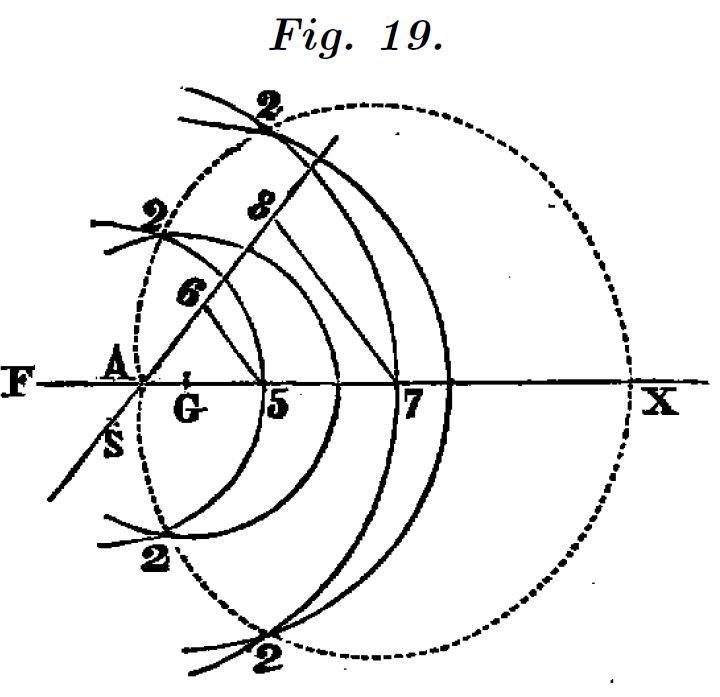
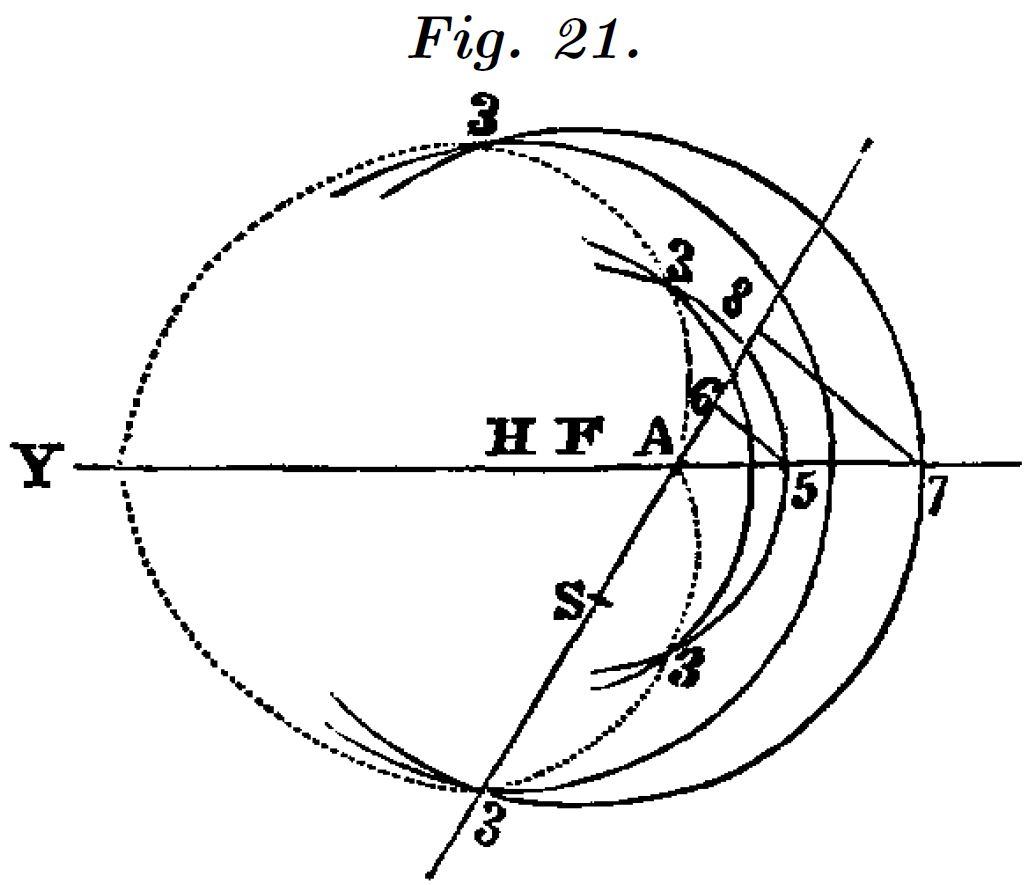
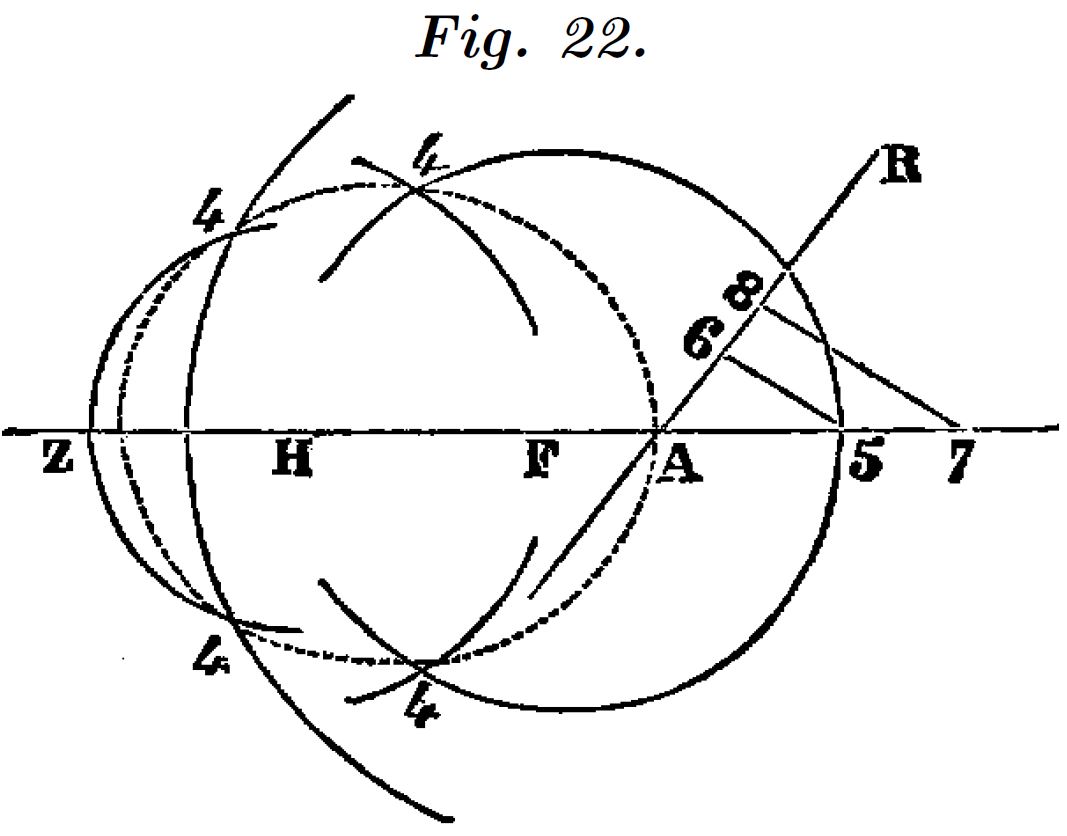
Para los 4 casos el polo $F$ lo situamos en el origen de coordenadas. Los radios de los círculos de centro $F$ y $G$ ($H$) nos definen las distancias a los polos y su intersección los puntos del óvalo.
Descartes utiliza una recta auxiliar, que pasa por $A$, cuya pendiente determina la proporción entre los radios.
En nuestro caso, mediante el deslizador, obtenemos directamente todos los puntos del lugar geométrico.
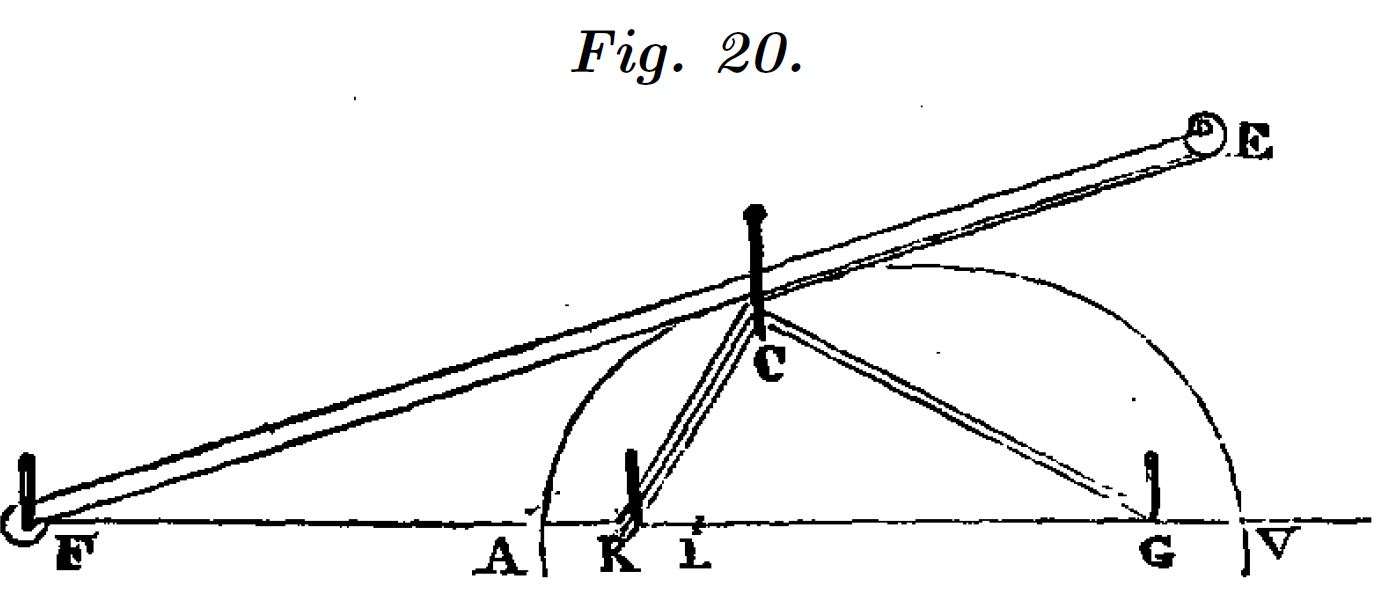
Descartes propone dibujar el óvalo de primer género de focos $F$ y $G$. El punto $A$ se sitúa en el punto medio de $FG$ y situando el punto $L$ definimos la proporción de los radios del óvalo.
Dibujamos el óvalo moviendo la regla $FE$. La cuerda esta sujeta al punto $K$, en el punto medio de $AL$, en $G$, y en el extremo $E$ de la regla. Su recorrido es $DCKCG$ de manera que en el tramo $KC$ la cuerda es doble.
La elección del punto $A$ en la mediatriz de $FG$ y de $K$ en la mediatriz de $AL$, es condición necesaria para que la longitud del hilo se mantenga constante mientras movemos la regla. Esta longitud debe ajustarse según la elección de las proporciones del óvalo. Por este motivo mostramos el cálculo de la longitud total de la cuerda.
Ecuación del óvalo
En primer lugar debemos obtener una ecuación del óvalo referida a los ejes de coordenadas que nos convengan.
Sobre una recta, que será nuestro eje $X$, situamos los focos del óvalo ($F$ y $G$) y un punto ($A$), del segmento $FG$ por donde queremos que pase el óvalo. Definimos:
$GA =b\quad y\quad FA = c$
Queremos obtener la normal del óvalo en el punto $C$. Para definir este punto vamos a referirlo al eje $X$ trazando la perpendicular al eje $X$, obteniendo el punto $M$.
Como segundo eje de coordenadas tomaremos la recta $FC$, que llamaremos eje $Z$.
El origen de distancias en el eje $X$ lo tomamos en el punto $A$ y llamamos $x$ a la distancia $MA$, de manera que tenemos:
$$MA = x,\quad MG = b - x,\quad MF = x + c$$El origen de distancias en el eje $Z$ lo situamos en el punto $E$, siendo $FE=FA=c$.
La relación de las distancias de $C$ a $F$ y $G$ en el óvalo es constante y la fijamos en $m= e/d$ y podemos decir que,
$$CF = FA + z = c + z \\ GC =GA – m z = b – m z$$Siendo $z$, el exceso de $CF$ y $GC$ sobre las distancias $FA$ y $GA$ que definen la proporción base del óvalo. Por Pitágoras podemos poner $CM$ del triángulo $GMC$ en función de la hipotenusa y del otro cateto:
$$CM^2=(b-mz)^2-(b-x)^2=\textcolor{red}{m^2z^2-2bmz+2bx-x^2}$$Y del mismo modo para el triángulo $FCM$:
$$CM^2=(z+x)^2-(x+c)^2=\textcolor{blue}{z^2+2cz-2cx-x^2}\tag{$1$}$$Igualando las dos ecuaciones obtenemos.
$$\textcolor{red}{m^2z^2-2bmz+2bx-x^2}=\textcolor{blue}{z^2+2cz-2cx-x^2}$$despejando $x$
$$(m^2-1)z^2-2bmz-2cz=-(2c+2b)x$$ $$x=\textcolor{orange}{{(1-m^2)z^2+2bmz+2cz\over(2c+2b)}\tag{$2$}}$$Que es la ecuación del óvalo referida a los ejes $X$ y $Z$.
Descartes ha obtenido una ecuación de segundo grado en $z$ para el óvalo en base a una elección de coordenadas acertada. Es en el único lugar de la “Géométrie” donde da una ecuación algebraica para el óvalo.
En la figura podemos mover los puntos $A$ y $G$ sobre la recta $X$ y seleccionar un valor para $m$, la magnitud que define la proporción de las distancias a los focos.
Para dibujar el lugar geométrico definido par la ecuación $(2)$ Trazamos desde $F$ la circunferencia de radio $c+z$, y con el valor de $z$ obtenemos la $x$ del punto $C$. Moviendo el deslizador de $z$ obtenemos el lugar geométrico buscado.
Si observamos con atención, la posición del punto $C$ se obtiene en función de su distancia a $F$ y trazando la perpendicular al eje $X$ en $M$. Es por la tanto un sistema de referencia mixto, donde el punto se sitúa en el plano por su abscisa ($x+c$) y su distancia ($c+z$) a un punto fijo ($F$). Es un ejemplo de la flexibilidad con la que Descartes utiliza las coordenadas para definir unívocamente los punto de una curva en el plano.
Ecuación de la circunferencia de centro $P$
Si suponemos conocer el punto $P$, para el que $PC$ es perpendicular al óvalo, podemos definir su posición por:
$$PC=s\\ PA=v$$Con lo que $PM=v-x$ y la circunferencia de centro en $P$,
$$PM^2+CM^2=s^2$$sustituyendo $PM^2$:
$$\textcolor{green}{CM^2}=\textcolor{red}{s^2-(v^2-2vx+x^2)\tag{$3$}}$$Siendo $s^2$ el radio de la circunferencia de centro $P$ que pasa por $C$.
Intersección de la circunferencia $(3)$ y el óvalo
Para obtener la intersección de las dos curvas vamos a sustituir los valores de $x$ en función de $z$ obtenidos en $(2)$ en la ecuación de la circunferencia $(3)$. Tenemos que conseguir que esta ecuación quede únicamente en función de $z$, por lo que previamente también deberemos obtener $CM^2$ a partir de la ecuación $(1)$ sustituyendo la $x$ por el valor obtenido para la ecuación del óvalo $(2)$:
$$\textcolor{green}{CM^2}=\textcolor{blue}{z^2+2cz-2c}\textcolor{orange}{{[(1-m^2)z^2+2bmz+2cz]\over(2c+2b)}}-\textcolor{blue}{x^2}$$Y efectuando operaciones:
$$\textcolor{green}{CM^2}={\big[(z^2+2cz)(c+b)+cm^2z^2-cz2-2c^2z-2cbmz\big]\over(c+b)}-x^2$$$$\textcolor{green}{CM^2={(cm^2z^2+bz^2-2cbmz+2cbz)\over(c+b)}-x^2}$$
Sustituyendo el valor obtenido de $CM^2$ en $(3)$ obtenemos:
$$\textcolor{green}{{(cm^2z^2+bz^2-2cbmz+2cbz)\over(c+b)}}=\textcolor{red}{s^2-v^2+2vx}$$Ha desaparecido el termino en $x^2$ con lo que solo queda sustituir nuevamente $x$ por su valor,
$$\textcolor{green}{{(cm^2z^2+bz^2-2cbmz+2cbz)\over(c+b)}}=$$ $$\textcolor{red}{s^2-v^2+2v}\textcolor{orange}{{[((1-m^2)z^2+2bmz+2cz)]\over(2c+2b)}}$$que podemos simplificar como,
$$\textcolor{green}{cm^2z^2+bz^2 - 2cbmz+ 2cb z = \\(c+b)}\textcolor{red}{s^2} \textcolor{green}{-(c+b)}\textcolor{red}{v^2+v}\textcolor{orange}{[(1-m^2) z^2+2bmz+2cz]}$$ $$cm^2z^2+bz^2 - 2cbmz+ 2cb z - \\cs^2+cv^2-bs^2+bv^2-vz^2+m^2z^2v-2bmvz-2cvz=0$$ $$\textcolor{green}{(b+cm^2-v+mv^2)}z^2+\textcolor{red}{(-2cbm+2cb-2bmv-2cv)}z-\textcolor{blue}{\\cs^2+cv^2-bs^2+bv^2}=0$$dividiendo por el coeficiente de $z^2$
$$z^2+{(-2cbm+2cb-2bmv-2cv)z-cs^2+cv2-bs^2+bv^2\over(b+cm^2-v+m^2v)}=0$$Que es la ecuación que buscamos.
Raíces dobles de la ecuación $(4)$
Si esta ecuación en $z$ tiene dos raíces iguales es de la forma:
$$(z-z_1)^2=0$$ $$z^2+z_12-2z_1z = 0$$El termino en $z$ es por lo tanto $-2z_1$, que toma el valor $-2z$ para el punto $C$.
Igualando los coeficientes en $z$, para que las dos raíces sean iguales,
$$\textcolor{green}{{(-2cbm+2cb-2bmv-2cv)}\over \textcolor{red}{(b+cm^2-v+mv^2)}}= \textcolor{red}{-2z}$$despejando $v$ y dividiendo por $2$,
$$\textcolor{green}{(-cbm+cb-bm}v-\textcolor{green}{c}v)=\textcolor{red}{-cm^2z-bz-zm^2}v+\textcolor{red}{z}v$$ $$(\textcolor{green}{-bm-c}\textcolor{red}{+zm^2-z})v=\textcolor{red}{-cm^2z-bz}+\textcolor{green}{cbm-cb}$$ $$v={\textcolor{red}{cm^2z+bz}\textcolor{green}{-cbm+cb}\over(\textcolor{green}{bm+c}\textcolor{red}{-zm^2+z})}$$que es la distancia $AB$, con lo que hemos resuelto el problema obteniendo las coordenadas del centro del círculo tangente al óvalo buscado.
Consideramos el óvalo como el límite entre dos medios de diferente naturaleza. Según la naturaleza de ambos medios, tendremos una relación, definida por la ley de Snell, entre los ángulos con la normal a la superficie de los rayos incidentes y refractados. Se trata de demostrar que podemos definir un óvalo de proporciones adecuadas para que los rayos que provienen de un foco del óvalo ($F$) se desvían para pasar exactamente por el otro foco ($G$).

Trazando las perpendiculares de $P$ a $GC$ y a la tangente en $C$, quedan definidos los segmentos $PQ$ y $PN$. Observamos que
$\displaystyle {PQ \over PC}=sen(\beta)$ y $\displaystyle {PN \over PC}=sen (\alpha)$
por lo que inmediato podemos deducir que $${PQ \over PN} ={sen(\beta) \over sen(\alpha)}$$
Tenemos que demostrar que esta razón es igual a $m$ (proporción con la que hemos construido el óvalo) y es la misma para cualquier punto $O$ de la superficie del óvalo.
Las ecuaciones que hemos definido al calcular la normal en un punto son:
$b=AG$ y $c=AF$
Por la elección de coordenadas $z$ sobre la tangente sabemos que:
$$CF = c+ z$$y la distancia de $C$ al otro foco es $CG = b- m\; z$
Hemos obtenido el punto $P$ en función de $z$ al calcular la perpendicular al óvalo en $O$:
$$AP={(cm^2z+bz-cbm+cb)\over(bm+c-zm^2+z)}$$
A partir de aquí podemos observar que $PQF$ es semejante a $CMF$ luego:
$${CF\over CM}={FP\over PQ}\\ {(FP\times CM)\over CF} = PQ$$Del mismo modo para los triángulos $PNG$ y $CMF$ resulta:
$${(GP\times CM)\over CG} = PN$$Eliminando $CM$, que multiplica ambas fracciones, tenemos:
$${FP\over CF}=PQ \;\;y\;\; {GP\over CG}=PN$$Multiplicando ambas fracciones por $CF \times CG$ y simplificando tenemos:
$${FQ = FP \times CG}\\ {PN = GP \times CF}$$y tenemos que demostrar que $\Large {PQ \over PN} = {(FP \times CG)\over (GP \times CF)} = m$
Solo nos queda sustituir estos valores por los que conocemos por las ecuaciones del óvalo :
$$ FP= c+\bigg[{(cm^2z+bz-cbm+cb)\over(bm+c-zm^2+z)}\bigg]$$ $$ GC = b-mz$$$FP \times GC=$
$$cb+b\bigg[\small{(cm^2z+bz-cbm+cb)\over(bm+c-zm^2+z)}\bigg]-cmz-mz\bigg[\small{(cm^2z+bz-cbm+cb)\over(bm+c-zm^2+z)}\bigg]$$y para $GP$ y $CF$ tenemos:
$$GP=b-AP=b-\bigg[\small{(cm^2z+bz-cbm+cb)\over(bm+c-zm^2+z)}\bigg]\\ CF=c+z$$ $GP \times CF=$ $$cb+zb-c\bigg[\small{(cm^2z+bz-cbm+cb)\over(bm+c-zm^2+z)}\bigg]-z\bigg[\small{(cm^2z+bz-cbm+cb)\over(bm+c-zm^2+z)}\bigg]$$Efectuando las operaciones obtenemos los numeradores:
$FP\times GC=$Y comprobamos que efectivamente la segunda expresión es igual a la primera multiplicada por $m$. Queda demostrada la propiedad de los óvalos en relación a la refracción de la luz.
Hemos visto que un óvalo se define por la relación de distancias de un punto $S$ a dos puntos $P$ y $Q$ tales que se cumple la relación:
$$d(F, S) \pm m d(Q, S ) = r$$Siendo $m$ y $r$ números reales.
Supongamos que las coordenadas de $F$ y $Q$ sean: $F = (0,0)$ y $Q = (c, 0)$.
Trazamos desde $F$ y $Q$ las circunferencias que pasan por el punto $S$.
La ecuación de la circunferencia de centro $P$ y que pasa por $S$ es:
$$x^2+y^2= d(F,S)^2$$La ecuación de la circunferencia de centro $Q$ y que pasa por $S$ es:
$$(x-c)^2+y^2= d(Q,S)^2$$Sustituyendo en la relación que define el óvalo tenemos:
$$\sqrt{(x^2+y^2)}+ m \sqrt{(x-c)^2+y^2}=r$$pasando una raíz a cada lado del signo igual y elevando al cuadrado,
$$r-\sqrt{(x^2+y^2)}= m \sqrt{(x-c)^2+y^2}$$ $$r^2+x^2+y^2-2r\sqrt{(x^2+y^2)}=m^2(x^2+c^2-2xc+y^2)$$ordenando los términos,
$$r^2+x^2+y^2-m^2(x^2+c^2-2xc+y^2)=2r\sqrt{(x^2+y^2)}$$y elevando nuevamente al cuadrado
$$\big((1-m^2)(x^2+y^2)+r^2+2m^2cx-m^2c^2\big)^2=4r^2(x^2y^2)$$Al haber elevado al cuadrado dos veces para eliminar las raíces, la ecuación obtenida es de grado cuarto y podemos ver que, si cambiamos $m$ por $–m$ ó $r$ por $–r$ la ecuación no se altera, ya que ambos parámetros están elevados al cuadrado.
La ecuación describe en realidad el lugar geométrico de los puntos,
$$d(F, S) \pm m d(Q, S ) = \pm r$$y su gráfica consiste en dos óvalos anidados.
Generalizamos la ecuación del óvalo expresándola en función de tres parámetros y haciendo intervenir la distancia entre focos:
$$\pm a\;d(F,Q)= b \;d(F,S) \pm c\;d(Q,S)$$Esta ecuación se suele llamar del óvalo completo.
La equivalencia entre esta expresión y la anterior:
$$d(F, S) \pm m \; d(Q,S) = \pm r$$Es simple, dividiendo por $b$ obtenemos:
$$r={\large a\over b}\; d(FQ)$$ $$m={\large c\over b} $$Podemos relacionar esta ecuación con los óvalos clasificados según su “género” por Descartes.
Haciendo $b=1$
para $c > a$ obtenemos óvalos de primer y segundo género.
para $c < a$ obtenemos óvalos de tercer y cuarto género.
Al final del libro segundo, Descartes hace una proyección de su método para las curvas en el espacio. Para cumplir con su criterio de definición exacta, propone utilizar dos planos perpendiculares entre si y proyectar los puntos de la curva tridimensional perpendicularmente a cada uno de los planos, obteniendo dos representaciones de la curva, una en cada uno de los planos de referencia. Cada proyección, que es una curva plana, puede definirse mediante una ecuación referida a la recta intersección de los dos planos, tal como hemos visto en apartados anteriores.
Obtenemos por tanto dos ecuaciones que determinan unívocamente las curvas proyectadas y en base a ellas podemos trazar la curva en el espacio. Si llamamos $z$ al eje común a los dos planos, las curvas proyectadas serán $y=f(z)$, $x=g(z)$.
Este enfoque de la representación de curvas en el espacio tiene el inconveniente de que, en el caso de que en la ecuación de las curvas proyectadas resulte mas de un valor de $x$ o de $y$ para un determinado valor de $z$, el resultado es indeterminado.
La generalización de Euler es mas acorde con los planteamientos actuales.
La ecuación mas sencilla de primer grado, $ax+by+cz+d=0$, representa un plano, que queda establecido como lugar geométrico de todos los puntos cuyas coordenadas cumplen con la ecuación.
A partir de aquí, podemos empezar a reconstruir en tres dimensiones lo que ya conocemos en el plano, de manera que con ecuaciones de segundo grado, nos aparecerán cilindros, conos, hiperboloides, paraboloides etc. … y cada una de estas superficies responderá a una ecuación en tres variables que establece su relación con un sistema de tres ejes de coordenadas.
Hemos visto en el LIBRO PRIMERO la resolución gráfica de ecuaciones de segundo grado cuya solución algebraica era conocida desde la antigüedad. El LIBRO TERCERO trata de la resolución de ecuaciones de una variable, de grado tres y cuatro mediante procedimiento algebraico y el estudio de su resolución gráfica, en continuidad con lo expuesto en el LIBRO PRIMERO.
Gran parte del contenido del LIBRO TERCERO no es original. Podemos decir que es una recopilación y sistematización de los conocimientos de la época, lo que explica que este libro sea el menos valorado de “La Géométrie”.
Para las ecuaciones de tercer grado ya existe la experiencia de los matemáticos renacentistas italianos que dio lugar a lo que se conoce como fórmula de Cardano. Para las ecuaciones de cuarto grado, Descartes presenta un método de resolución propio, mediante su reducción a una de tercer grado.
Las ecuaciones de una cantidad desconocida, pueden tener tantas raíces como dimensiones de esa cantidad, lo que llamamos normalmente grado de la ecuación. Esta afirmación queda sin demostrar, pero se justifica observando como mediante la multiplicación de ecuaciones con una sola raíz, del tipo $(x-a)=0$ y $(x-b)=0$, obtenemos una ecuación de segundo grado cuyas raíces son precisamente $a$ y $b$.
Aplicando el razonamiento a la inversa, Descartes enuncia el teorema del factor, que dice que una ecuación es divisible por $x-a$, solo si $a$ es una raíz de la ecuación y obtiene mediante la división por $x-a$ una nueva ecuación, un grado inferior a la primera.
Las raíces negativas son raíces “falsas” y relaciona el numero de raíces verdaderas y falsas según la alternancia de los signo $+$ y $–$ en la ecuación ordenada según los grados de la variable.
También afirma que las raíces, verdaderas o falsas, pueden ser imaginarias. Afirmación que no es mas que una manifestación de la imposibilidad de explicar adecuadamente su significado.
Los conocimientos necesarios de álgebra básica tardaran casi dos siglos en ser superados. Hay que esperar hasta la introducción de los números imaginarios por Gauss.
El grafico ilustra las diferentes posibilidades que se dan para las ecuaciones cuarticas.Seleccionando la opción “ecuación de la parábola $A$”.
Movemos los puntos $E$ y $F$ a nuestro criterio y obtenemos las rectas que pasan por esos puntos $\quad b_1(x-x_B)=0\; y\; b_2(x-x_F)=0$
Multiplicado ambas ecuaciones obtenemos una parábola, en trazo rojo, como resultado. Esta parábola pasa por $E$ y $F$ que son raíces de la ecuación. Podemos observar que moviendo los puntos $E$ y $F$ a lo largo del eje $x$ y modificando los valores de los parámetros, siempre obtendremos una parábola que corta al eje $x$ en esos dos puntos $y$ en el caso mas extremo solo es tangente en un punto. En ese caso decimos que tenemos una raíz doble.
Seleccionando la opción “Ecuación de parábola $B$” , podemos mover la parábola desplazando su vértice $B$. Si la parábola corta al eje $X$ estamos en el mismo caso de la parábola $A$. Si desplazamos el vértice para que la parábola no corte al eje $X$ estamos en el caso de una ecuación irreductible, con raíces imaginarias.
Podemos comprobar que del producto de dos parábolas $A$ y $B$ resulta una ecuación de cuarto grado. El numero de raíces de la ecuación depende de la posición de las parábolas respecto al eje $x$. Como hemos visto antes estas parábolas pueden descomponerse o no en productos de rectas y por lo tanto una ecuación cuádrica tiene dos o cuatro raíces reales según sea el caso.
Según la regla del factor, si un polinomio es divisible por $(x-a)$, al efectuar la división obtenemos un polinomio un grado inferior y además confirmamos que $a$ es una raíz de la ecuación $y=P(x)$, es decir se cumple que $P(a)=0$.
Si repetimos esta operación sucesivamente, reduciremos la ecuación de grado hasta obtener un polinomio no divisible, no reducible.
Los polinomios de grado impar, siempre tienen al menos una raíz real. Esta es una afirmación que se puede comprobar porque para valores de la variable negativos crecientes el polinomio tendera a $-\infin$ y para los valores positivos crecerá hacia $+\infin$, por lo que para algún valor intermedio de la variable la ecuación será igual a cero y por lo tanto cortara el eje $x$.
Si partimos de un polinomio de grado tres y el resultado no es reducible, podemos asegurar que el resultado es de grado $2$ y que no tiene raíces reales, no corta el eje $x$ en ningún punto. Es una ecuación de segundo grado cuyo discriminante, $b^2-4ac$, es negativo. Las raíces en el caso de discriminante negativo son las raíces que llamamos imaginarias. Esas ecuaciones representan parábolas que no cortan el eje $x$.
Multiplicando estas parábolas irreducibles podemos obtener polinomios de grado par como producto de parábolas sin raíces reales y por tanto con $2n$ raíces imaginarias.
Alternativamente, si podemos obtener la división tantas veces como grado tiene el polinomio, podemos afirmar que el polinomio tiene $n$ raíces reales.
Podemos resumir diciendo que siempre existirá un numero par de raíces imaginarias y el los polinomios de grado impar siempre existirá una raíz real.
La forma general de una ecuación de cuarto grado es:
$$ax^4+bx^3+cx^2+dx+e=0$$Que podemos suponer de la forma dividiendo por $a$.
$$x^4+bx^3+cx^2+dx+e=0$$Partimos de esta ecuación con coeficiente de $x^4=1$ para detallar el método de resolución que se puede seguir paso a paso en la figura adjunta.
Paso 1:
Seleccionar los coeficientes , $b$, $c$, $d$ y $e$ de la ecuación a resolver.
Paso 2:
Con el cambio de variable $x=z-{\Large b\over 4}$ obtenemos una ecuación en $z$ sin el termino $z^3$.
$$z^4+(c-{3b^2\over8})z^2+(d-{bc\over2}+{b^3\over8})z+(e-{bd\over4}+{b^2c\over16}-{3b^4\over256})=0$$ $$q=(c-{3b^2\over8})$$ $$r=(d-{bc\over2}+{b^3\over8})$$ $$s=(e-{bd\over4}+{b^2c\over16}-{3b^4\over256})$$Resulta:
$$z^4+qz^2+rz+s=0$$Obtenemos una ecuación de cuarto grado sin termino en $z^3$ y de coeficientes $q$, $r$ y $s$.
Como era previsible por el cambio de variable efectuado, la gráfica de la ecuación es la misma desplazada según el eje $X$ en $\Large b\over4$.
Paso 3:
Una ecuación de cuarto grado de este tipo la podemos expresar como producto de dos ecuaciones cuadráticas.
$$z^2+kz+l=0 \\ \text{y} \\ z^2-kz+m=0$$Que multiplicadas nos dan:
$$z^4+((l+m)-k^2)z^2+(l-m)kz+ml=0$$Igualando los coeficientes de igual grado de la ecuación en $z$ obtenemos:
$$q=(l+m)-k^2$$ $$r=(l-m)k$$ $$s=lm$$Paso 4:
Tenemos que resolver este sistema de tres ecuaciones con tres incógnitas. Despejando $l$ y $m$ en las dos primeras y sustituyendo en la tercera obtenemos:
$$k^6+2qk^4+(q^2-4s)k^2-r^2=0$$que es una ecuación de grado 6 en $k$, con coeficientes de la variable $k$ conocidos, ya que $q$, $r$ y $s$ los hemos obtenido anteriormente. Esta ecuación se transforma en una cúbica si hacemos $t = k^2$.
Visualizamos la ecuación cúbica en $t$,
$$t^3+2qt^2+(q^2-4s)t-r^2=0$$Para resolver esta ecuación cúbica recurrimos a la fórmula de Cardano, para lo cual necesitamos transformar la ecuación en otra sin el termino en $t^2$, con el cambio de variable $t = t - \Large{q\over3}$, lo que podemos ver como un desplazamiento de la gráfica en $\Large {q\over3}$.
Conocida una raíz del polinomio en $t$, deshacemos los cambios de variable hechos y obtenemos $k$, y resolvemos el sistema ecuaciones anterior,
$$q=(l+m)-k^2$$ $$r=(l-m)k$$ $$s=lm$$Obtenemos $m$ y $l$, que son los coeficientes de las dos ecuaciones que necesitamos para descomponer la ecuación de cuarto grado en el producto de dos ecuaciones de segundo grado, de las que sabemos como obtener sus raíces.
Este paso es el punto débil del método, porque veremos mas adelante, al hablar de las ecuaciones de tercer grado, que la fórmula de Cardano no detecta raíces reales del polinomio en algunos casos. En la figura que ilustra el método, obtenemos la raíz “gráficamente” para seguir adelante en estos casos y aparece un aviso en rojo de “Discriminante negativo”.
Paso 5:
Visualizamos las dos parábolas obtenidas que multiplicadas nos dan la ecuación en $z$ a resolver. Visualizamos que efectivamente esto es así activando el botón.
Los puntos donde estas parábolas cortan el eje $X$ podemos comprobar en el grafico que corresponden a raíces de la ecuación en $z$. Una ecuación de cuarto grado puede tener 2 o 4 raíces reales que coinciden con las de las parábolas, que pueden tener 2 o ninguna.
Paso 6:
Obtener las raíces de las parábolas y deshacer el cambio de variable inicial, para obtener las raíces de la ecuación de partida.
Hemos visto cómo la resolución de las ecuaciones de cuarto grado, por el método de reducción depende, en un paso intermedio, de la resolución de una ecuación de tercer grado. Las ecuaciones de tercer grado podemos expresarlas de forma general como:
$$x^3+qx+r=0$$Haciendo $s=0$ en la ecuación de cuarto grado y dividiendo por $x$, obtenemos la ecuación de tercer con las mismas letras para los coeficientes que en la ecuación de cuarto grado.
El álgebra clásica trata la ecuación según el signo de sus coeficientes, ya que para ellos $q$ y $r$ son siempre positivos. Se distingue así entre:
$$x^3=-qx-r$$ $$x^3=\;qx-r$$ $$x^3=\;qx+r$$En el problema de la trisección del ángulo, se obtiene una ecuación del segundo tipo, $x^3 = 3x – r$, siendo $r$ la cuerda el ángulo a trisecar y $x$ la cuerda del ángulo que buscamos.
El tercer caso es el que resulta en la obtención de dos medias proporcionales entre $a$ y $b$, con $q=0$ y cuya raíz $x$ cumple la relación,
$$x^3=a^2 b$$Esta ecuación cúbica aparece en el problema de la duplicación del cubo.
$$x^3=r$$La fórmula para obtener algebraicamente las raíces de una ecuación de tercer grado se debe a Cardano y publicada en 1545, casi un siglo anterior a Descartes.
Para la ecuación cúbica:
$$x^3+qx+r=0$$La expresión de las raíces es :
$$x=\bigg({-q\over2}+\sqrt{({q^2\over4}+{r^3\over27})}\bigg)^{\large{1\over3}} + \bigg({-q\over2}-\sqrt{({q^2\over4}+{r^3\over27})}\bigg)^{\large{1\over3}}$$Como en el caso de las ecuaciones de segundo grado, la expresión bajo la raíz cuadrada se llama discriminante, que en este caso es:
$$\bigg({q^2\over4}+{r^3\over27}\bigg)$$Para discriminante positivo, obtenemos una solución, y en el caso de discriminante negativo la fórmula fracasa.
En la siguiente figura analizamos la gráfica de la función cúbica y sus raíces en función del discriminante.
Modificando los valores de $a$ y $b$, podemos ver el número de raíces reales de la ecuación.
Representamos con una recta horizontal el valor del discriminante. Podemos observar que con discriminante positivo la curva solo corta al eje $x$ en un punto, es decir, solo existe una raíz que la fórmula de Cardano nos identifica perfectamente.
Con discriminante negativo, la fórmula no da resultado pero podemos ver que la curva corta el eje $x$ en tres ocasiones, es decir tiene tres raíces reales no detectadas. Es por lo tanto una situación diferente al de las ecuaciones de segundo grado, donde el discriminante negativo delata raíces “imaginarias”. La fórmula de Cardano no nos identifica ninguna raíz en el caso de discriminante negativo, a pesar de existir tres raíces reales.
Vista la dificultad para resolver algebraicamente las ecuaciones de cuarto grado, Descartes plantea un método grafico.
Además de obtener las raíces de la ecuación, la construcción geométrica también tiene la finalidad de demostrar que las ecuaciones de este tipo se corresponden con construcciones geométricas, como es el caso de las ecuaciones de segundo grado. Es decir hay una correspondencia entre las curvas de segundo género que resuelven problemas sólidos y sus ecuaciones algebraicas y estas también representan lugares geométricos construibles de forma precisa y exacta.
Si para las ecuaciones de segundo grado la solución consiste en resolver la intersección de una recta con una circunferencia, para las ecuaciones de cuarto grado la resolución gráfica consiste en obtener la intersección de una circunferencia con la parábola $y=x^2$. Esta construcción nos dará cuatro puntos de intersección en el caso de que todas las raíces sean reales y no dará puntos de corte en el caso de que existan raíces imaginarias.
Si resolvemos el sistema de ecuaciones formado por la parábola $y=x^2$ y la circunferencia de centro en el punto $(a,b)$ y radio $d$, obtenemos:
$$y=x^2$$ $$(x-a)^2+(y-b)^2=d^2$$desarrollando la ecuación de la circunferencia y sustituyendo $y$ por $x^2$ obtenemos:
$$x^2+(1-2b)x^2-2ax+(a^2+b^2-d^2)=0$$Igualando los coeficientes con la ecuación de cuarto grado a resolver:
$$x^4+px^2+qx+r=0$$obtenemos:
$$p=(1-2b)$$ $$q=-2a$$ $$r=a^2+b^2-d^2$$Ecuaciones que nos permiten deducir $a$, $b$ y $d$ en función de los coeficientes de la ecuación a resolver.
El centro de la circunferencia será:
$$a={-q\over2}$$ $$b={(1-p)\over2}$$y su radio:
$$d^2=r+({q\over2})^2+({(1-p)\over2})^2$$Esta es la construcción que propone Descartes y que explica de manera bastante confusa pero que como vemos, no tiene misterio.
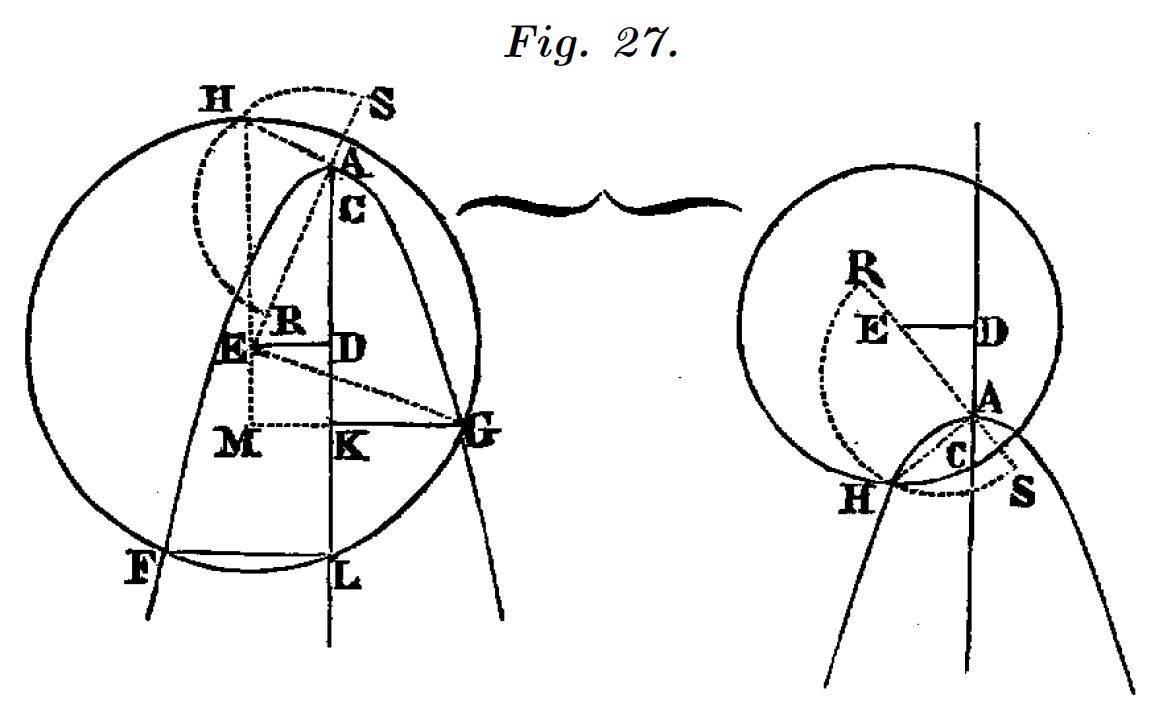
La resolución gráfica de las ecuaciones se obtiene por la intersección de una circunferencia y una parábola.
El dibujo es la figura 27 de “La Géométrie”, considerando la dirección creciente de los ejes en el sentido habitual, hacia la derecha y hacia arriba, a partir del origen de coordenadas en el punto $O=(0,0)$.
La parábola es $y=x^2$
Esta circunferencia debe pasar por el punto $G$ que se construye según el valor de $r$ sobre la perpendicular a la recta $OC$ que pasa por $O$.
Las raíces obtenidas corresponden a la ecuación cuartica con los coeficientes $p$, $q$, $r$ de signo contrario al tomado para la construcción.
Si hacemos $r=0$, la ecuación se reduce a una de tercer grado, de la que podemos obtener las raíces con la misma construcción. En este caso el círculo pasa por el origen de coordenadas.
En el caso de $r$ negativo la resolución gráfica se resuelve según la figura siguiente.
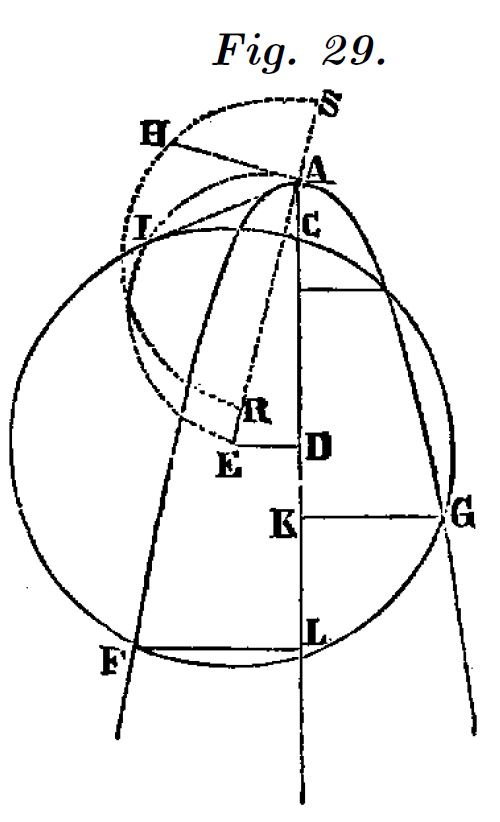
La resolución gráfica de las ecuaciones de tercer grado puede obtenerse por el mismo procedimiento que hemos visto para las cuárticas, pero la vamos a presentar con la resolución de los problemas clásicos en las que aparecen.
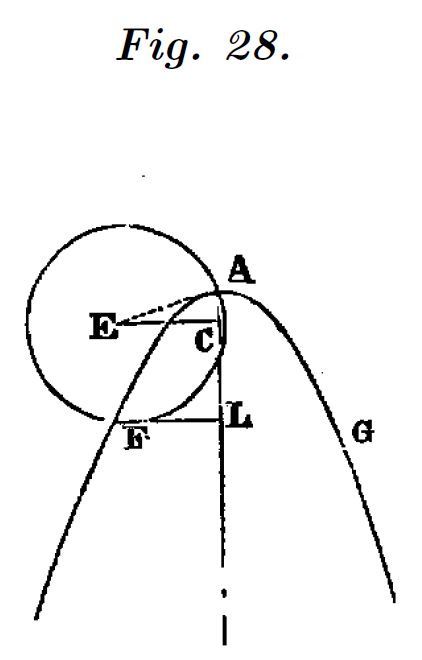
En primer lugar las ecuaciones ligada a la duplicación del cubo, del tipo $x^3 - q = 0$, y que también se presenta en la obtención de medias proporcionales continuas. (Ya las hemos visto planteadas cuando hemos hablado de los compases).
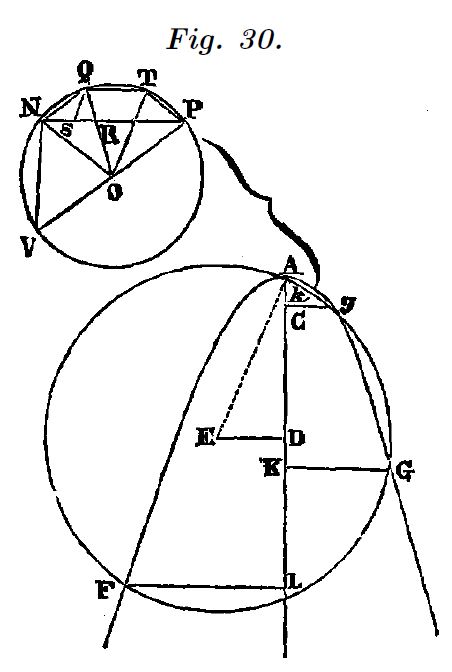
En segundo lugar abordamos la trisección de un ángulo que también nos lleva a resolver una ecuación de tercer grado, del tipo: $x^3-3x+q=0$
Planteamos dos medias proporcionales de $a$ y $b$:
$$\dfrac{a}{x}=\cfrac{x}{\cfrac{(x^2)}{a}}=\cfrac{\cfrac {(x^2)}{a}}{\cfrac{(x^3)}{(a^2)}}$$Identificando $\cfrac{(x^3)}{(a^2)} =\;b$, podemos deducir, multiplicando en cruz la primera y la ultima fracción, $x^3=a^2 b$
Esta ecuación la podemos resolver por el método grafico para ecuaciones de tercer grado sin termino en $p$.
La solución es $x=DB$ y obviamente $AD=x^2$, al estar el punto $B$ sobre la parábola $y=x^2$. Para $a=1$, tenemos que $DB^3 =\;b$.
Además de las soluciones de Descartes, añadimos la solución gráfica de Fermat que utiliza una parábola y una hipérbola en su construcción, para confirmar que pueden imaginarse diferentes construcciones geométricas para resolver el problema, pero que todas ellas consisten necesariamente en plantear la intersección de curvas de segundo grado.
El ángulo $QNP$ es igual al ángulo $NOQ$. El primero abarca un arco doble que el segundo pero tiene su vértice sobre la circunferencia. Los triángulos coloreados con semejantes. $NR$, $SF$ y $IP$ son iguales a $NP$, luego $NP=3NQ - SR$. Si $NQ$ es igual a $z$, al plantear las medias proporcionales, resulta que $RS =z^3$.
La trisección nos lleva a resolver $z^3=3z-q$ siendo $q$ la cuerda del ángulo a trisecar. La construcción del cálculo grafico de las raíces de una ecuación de tercer grado nos da la solución.
Finalmente, incluimos también la resolución gráfica aportada por Fermat para las ecuaciones del tipo, $x^3+b x^2-b a^2=0$, mediante la intersección de la parábola, $y=x^2+bx$ y la hipérbola, $xy=a^2$.
Para ecuaciones de tercer grado del tipo, $x^3+b x^2-ba2=0$, Fermat obtiene su solución gráfica mediante la intersección de la parábola,
$$by=x^2+bx$$y la hipérbola: $xy=a^2$ lo que podemos comprobar fácilmente, sustituyendo el valor de $y$ obtenido de la parábola en la ecuación de la hipérbola, comprobando que obtenemos la ecuación de tercer grado a resolver.
Para las ecuaciones de grado superior a cuatro no existe una fórmula para su resolución mediante un número finito de sumas, restas, multiplicaciones, divisiones y extracciones de raíces. Esto también se cumple para las ecuaciones de mayor grado. La demostración de que las ecuaciones de quinto grado en adelante no son resolubles mediante una fórmula general, es el teorema de Abel Ruffini de 1824, por lo tanto en la época de Descartes se desconocía esta imposibilidad.
Algunas ecuaciones particulares son resolubles si son factorizables. (Por ejemplo $x^5 − x^4 − x + 1 = 0$, se puede escribir como $(x^2 + 1) (x + 1) (x -1)^2 = 0).$
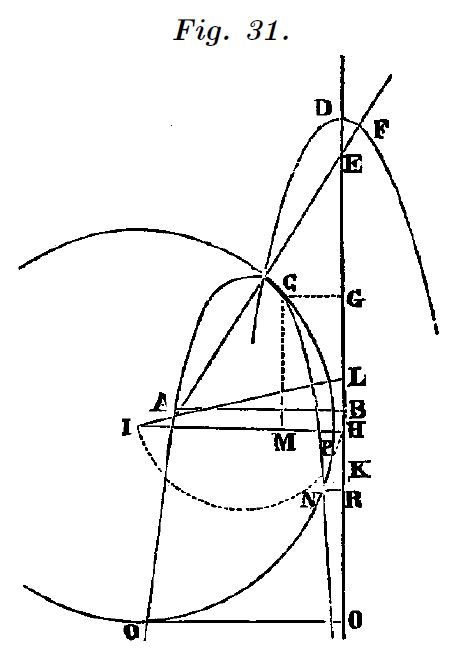 Para las ecuaciones de sexto grado polinómicas, del tipo $ax^6 + bx^5 + cx^4 + dx^3 + ex^2 + fx + g = 0$, Descartes propone un método de resolución grafico, que en general da resultados correctos, salvo con algunas combinaciones de coeficientes en particular. Si la resolución de ecuaciones de cuarto grado se conseguía mediante la intersección de una circunferencia y una parábola, en este caso Descartes sustituye la parábola $y=x^2$ por una curva de tercer grado obtenida, mediante el hiperbológrafo de la figura 8 del libro segundo, a partir de una parábola.
Para las ecuaciones de sexto grado polinómicas, del tipo $ax^6 + bx^5 + cx^4 + dx^3 + ex^2 + fx + g = 0$, Descartes propone un método de resolución grafico, que en general da resultados correctos, salvo con algunas combinaciones de coeficientes en particular. Si la resolución de ecuaciones de cuarto grado se conseguía mediante la intersección de una circunferencia y una parábola, en este caso Descartes sustituye la parábola $y=x^2$ por una curva de tercer grado obtenida, mediante el hiperbológrafo de la figura 8 del libro segundo, a partir de una parábola.
En primer lugar, obtenemos en la segunda pantalla gráfica la curva que nos servirá para la resolución. En este caso la opción ha sido conservar la parábola invertida como en el dibujo original, como ya hemos hecho en la figura 8. La distancia $ED$ viene definida por el parámetro:
$$d={-t\over2no}$$y el coeficiente de la parábola es $\frac{1}{n}$ siendo
$$n=\sqrt{({-t\over o}+q-{p^2\over4})}$$
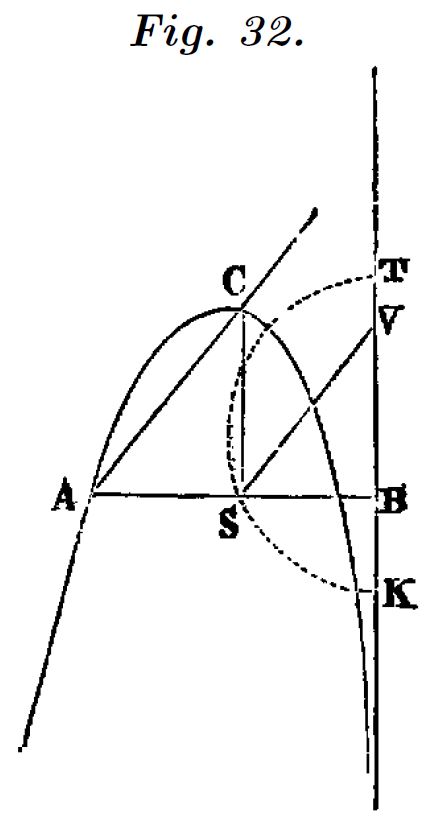 Descartes no obtiene el lugar geométrico completo, pues omite el tramo negativo del eje $x$. Aporta un sistema de construcción de la curva alternativo, que hemos llamado “método círculo” y que también completa la curva del hiperbológrafo en un tramo del eje $y$ negativo.
Descartes no obtiene el lugar geométrico completo, pues omite el tramo negativo del eje $x$. Aporta un sistema de construcción de la curva alternativo, que hemos llamado “método círculo” y que también completa la curva del hiperbológrafo en un tramo del eje $y$ negativo.
Dibujada la curva base pasamos a la siguiente pantalla gráfica en la que mantenemos la curva obtenida en azul.
Definimos los siguientes parámetros para simplificar el tratamiento de los 6 coeficientes de la ecuación.
$$o=\sqrt{u}$$ $$d={-t\over 2no}$$El punto $I$ es $(e, b-d)$
El punto $L$ es $(0, b)$
El punto $H$ es $(0, b-d)$
El radio de la circunferencia es $\sqrt{(e^2+d2)}$
Y su centro esta en el punto $({\Large{e\over 2}}$, ${\Large{d\over 2}}+b-d)$
La resolución gráfica de ecuaciones es complicada de construir y además no nos aporta en ningún caso una solución algebraica exacta.
Para la resolución de ecuaciones, Descartes podría haber acudido a métodos de aproximación, que ya eran conocidos por Vieta y con tradición histórica, pero en ningún momento en “La Géométrie” habla del procedimiento de exhaución, mediante el que los clásicos planteaban aproximaciones sucesivas a los problemas no resolubles de forma exacta (por ejemplo el cálculo de $\pi$).
El objetivo de Descartes al plantear la resolución gráfica de las ecuaciones hay que entenderla en su empeño de demostrar la equivalencia geométrica de cualquier expresión algebraica.
En “La Géométrie” Descartes ha puesto las bases para una nueva geometría, con apellido de algebraica, por la asociación de las construcciones geométricas a las operaciones aritméticas, pero que también podemos llamar analítica por el método empleado para el planteamiento de los problemas aunque este apellido se reserva actualmente para la geometría que incorpora el cálculo infinitesimal. Dos elementos son clave para el éxito del método científico aplicado. Por un lado la mejora del lenguaje simbólico del álgebra y por otro la introducción de los sistemas de referencia que permite establecer las ecuaciones entre magnitudes conocidas y desconocidas del problema geométrico. Al resolver el problema de las normales, Descartes demuestra la intima relación entre las propiedades de las curvas y de las ecuaciones que las definen.
Podríamos suponer que esta demostración de la equivalencia, tendría como consecuencia la perdida de utilidad de una de las dos aproximaciones. Una de las dos sobra, es innecesaria y puede ser sustituida por la otra. Los hechos y la historia que se sigue a “La Géométrie” desmiente esa perdida de protagonismo de cualquiera de los dos enfoques. Bien al contrario, establecer la relación entre una aproximación y otra ha enriquecido la comprensión de los problemas y ha estimulado avances imposibles sin el apoyo mutuo.
Pensemos cómo, hoy en día, están estrechamente vinculadas ambas aproximaciones. Pensemos, por ejemplo, en un programa de dibujo para el diseño de arquitectura o en GeoGebra que utilizamos para las figuras de este libro. Para nuestro ordenador el tratamiento de las imágenes que nos presenta es evidentemente numérico, pero nuestra interacción con el programa, es estrictamente geométrico. Introduciremos instrucciones como: “dibuja la recta que pase por estos dos puntos”, el programa hará sus cálculos y nos presentara el dibujo de su resultado. El conjunto de la funcionalidad es un continuo ir y venir de la geometría al álgebra.
Pero además de la importancia de las aportaciones cartesianas en si mismas, podemos ver que la fusión de álgebra y geometría a la que Descartes contribuyó de forma decisiva, posibilitó en los años inmediatamente posteriores, el descubrimiento y desarrollo del cálculo infinitesimal.
Fermat utiliza el álgebra para la aritmetización del método de exhaución griego, introduciendo el concepto de magnitud infinitesimal, lo que le convierte en un adelantado en el desarrollo del cálculo. Fermat aplica los infinitesimales al problema de la tangente y obtiene la solución para el caso de las potencias de $x$ ($y = a x^n$) y también el área contenida bajo las mismas curvas. Son las primeras derivadas e integrales de la historia.
El cálculo infinitesimal se desarrolla como una obra colectiva durante el siglo XVII hasta que Newton y Leibniz establecen sólidamente sus principios como una nueva rama de la matemática. El cálculo consolida el concepto de función al que se incorporan las funciones trigonométricas, la exponencial y la logarítmica y aporta la solución al problema de los “inconmensurables” que serán números “irracionales”, números reales de infinitas cifras decimales.
La geometría algebraica y analítica son llevadas a su edad madura por Euler con la idea de que “mejor que de nuestro juicio, debemos fiarnos del cálculo algebraico”, lo que supone implícitamente un reconocimiento a Descartes como iniciador de su línea de trabajo. Euler es el sistematizador de los avances de su siglo y en sus textos encontramos la geometría analítica tal como la conocemos hoy además de su generalización a tres dimensiones.
“La Géométrie” amplia el campo de las curvas aceptables matemáticamente a todas las que pueden expresarse algebraicamente. Hemos visto como para Descartes, cualquier construcción geométrica es traducible a una ecuación algebraica.
Fermat afirmaba la misma premisa en sentido contrario, “toda expresión algebraica que implica dos variables, representa una curva, lugar geométrico de los puntos del plano cuyas coordenadas satisfacen la ecuación”. Fermat recorre el camino en sentido contrario, la creación de curvas a partir de su ecuación y abre el camino a otras muchas a partir de la manipulación de sus ecuaciones.
Nos centraremos en dos manipulaciones sencillas de las ecuaciones algebraicas de las curvas.
En primer lugar, veremos cómo agrupar las curvas en familias, mediante la inclusión en la ecuación de la curva de un parámetro, cuyo valor es fijo para cada curva de la familia, pero que al variar nos va definiendo las diferentes curvas que pertenecen a la familia.
También veremos en que consiste un “cambio de variables”. Mediante un “cambio de variables” podemos girar una curva, trasladarla ó deformarla, estirando o encogiendo su gráfica en una dirección. Un cambio de variable supone el cambio del sistema de referencia utilizado. Una misma curva puede representarse mediante muchas ecuaciones, aunque estas transformaciones pueden no afectar a su “dibujo”.
Vamos a pasar revista a un catalogo de curvas señalando en cada caso su construcción geométrica y la ecuación algebraica que la define, en coordenadas Cartesianas. Una gran parte del catalogo son las curvas que Descartes cita expresamente en “La Géométrie” siguiendo su metodología de clasificación.
Las cisoides son curvas que se generan a partir de un punto, al que llamamos polo, trazando las rectas que pasan por ese punto y cortan a dos curvas dadas. La cisoide se obtiene como lugar geométrico del punto de esas rectas que dista del polo una distancia (suma, diferencia o semisuma de las distancia desde el polo a las dos curvas dadas), al girar la recta generatriz alrededor del polo.
La cisoide de Diocles se construye en base a una circunferencia que pasa por el punto elegido como polo y una recta tangente a esa circunferencia. La cisoide es el lugar geométrico de los puntos que distan del polo $A$ una distancia igual a la diferencia de la distancia a la recta y a la intersección de la circunferencia, sobre la recta generatriz.
Elegir la curva de la que queremos obtener la cisoide. Podemos mover el punto $A$ para obtener diferentes resultados.
Su procedimiento de construcción es el de una cisoide, a partir de una circunferencia de diámetro $a$ que pasa por el polo, en este caso el origen de coordenadas. Según el valor del parámetro $a$ la curva de Sluze coincide con algunas curvas definidas independientemente.
El nombre de esta curva se debe a Colin Maclaurin que estudio la curva en 1742. La particularidad de esta curva es que cualquier punto de su bucle nos permite dividir un ángulo dado en tres.
La trisectriz de Maclaurin es la cisoide de una circunferencia y una recta y se obtiene también como una de las curvas de Sluze
La cisoide trisectriz también puede relacionarse con el folio de descartes mediante un cambio de variable, para girar la curva 45 grados y que el bucle de ambas curvas adopte la misma forma. Esta transformación la podéis seguir en la figura dedicada al Folio de Descartes.
El folium de Descartes está relacionado con la trisectriz de Maclaurin por transformación afín. Para ver esto, comenzar con la ecuación
$$x^3+y^3=\;3a\;xy$$y cambiar las variables para encontrar la ecuación en un sistema de coordenadas girado 45 grados.
$$x=x_1+{y_1\over \sqrt2}$$ $$y=x_1-{y_1\over \sqrt2}$$Haciendo operaciones (volviendo a renombrar $x_1$ e $y_1$ por $x$ e $y$ una vez sustituidas) obtenemos:
$$2x^3-3ax^2+3xy^2+{3\over2}ay^2=0$$ $$x(2x^2+3y^2)=a\bigg(3x^2-{3\over2}y^2\bigg)$$Si estiramos la curva en la dirección del eje $y$, haciendo el cambio de variable $y$ por, $\sqrt {\large 2\over3}y_1$ , se convierte en:
$$2x(x^2+y^2)=a(3x^2-y^2)$$que es la ecuación de la trisectriz.
Una concoide es una variante de cisoide particular, cuando una de las curvas seleccionadas para su trazado, es una circunferencia centrada en el polo, es decir, la distancia a una de las dos curvas de la concoide es una magnitud fija.
Limaçon o caracol de Pascal, estudiado por Etienne Pascal (1588-1640), es la concoide de una circunferencia que pasa por el polo, obteniéndose una familia de curvas en función de la relación entre los radios de las circunferencias que la definen.
La ecuación cartesiana de la cardiode es:
$$(x^2+y^2+2ax)^2=4a^2(x^2+y^2)$$Podemos ver su gráfica en función del parámetro a moviendo el deslizador.
Una estrofoide es una curva engendrada, como las cisoides y concoides, a partir de un polo por el se trazan las rectas generatrices y de las distancias a una curva y a un punto fijo.
La figura nos permite dibujar la estrofoide de una circunferencia a partir de un polo ($B$) por el se trazan las rectas generatrices y de las distancias a una curva (circunferencia azul) y a un punto fijo ($A$).
En 1694 Bernoulli introdujo la lemniscata que es un caso particular de los óvalos de Jean Dominique Cassini (1.625-1.712).
Estas curvas son el lugar geométrico de los puntos cuyo producto de distancias a dos puntos o focos, es constante.
Esta curva fue estudiada por Pierre de Fermat en 1630, por Luigi Guido Grandi en 1703 y por Maria Gaetana Agnesi en 1748.
La ecuación para $a=1$ representa una de las primeras funciones desarrolladas en serie. La zona comprendida entre la curva y el eje $x$ es cuatro veces el área del círculo de diámetro $a$ con el que se construye la curva.
Los tridentes de Newton son curvas con una ecuación de la forma,
$$xy=ax^3+bx^2+cx+d$$con $a$ y $d$ no nulos.
Puede verse en el grafico la relación del tridente de Newton con la parábola de ecuación, $y=ax^2+bx+c$ y la hipérbola de ecuación, $xy=d$
Cuando dos curvas se aproximan de forma que su separación tiende a hacerse nula, se dice que son asintóticas.
Curva del diablo o mas correctamente del diábolo por su forma semejante al diábolo de los saltimbanquis.
La curva fue estudiada por Gabriel Cramer en su libro de 1750 “análisis de las líneas curvas algebraicas”.
También señalamos la curiosa forma que adopta la curva cuando su parámetro a vale $\frac{25}{24}$, que se asemeja al esquema de un motor eléctrico.
Hemos dicho que mediante un cambio de variables podemos modificar la ecuación de una curva para expresarla en relación a otro sistema de referencia, lo que es lo mismo que decir que la trasladamos, giramos ó deformamos respecto del sistema de referencia inicial. La ecuación que define una curva depende por tanto del sistema de referencia elegido, por lo que una buena elección de este puede simplificar las expresiones algebraicas y facilitar la resolución de los problemas.
La transformación mas elemental es la traslación, que desplaza una curva en una dirección del plano sin afectar a su forma y sus dimensiones. Lo hemos visto al utilizar un cambio de variable para eliminar el termino en $x^3$ de la ecuación cuartica y $x^2$ en la ecuación cúbica.
Una traslación se obtiene mediante el cambio de variable $x=x_1+t$, para una traslación según el eje $X$ ó $y=y_1+t$ para una traslación vertical según el eje $Y$.
Para aplicar un giro de los ejes de referencia el cambio de variable a ejecutar es:
$$x=x_1\cos\theta-y_1\sin\theta \;\;\;\; y=x_1\sin\theta-y_1\cos\theta$$Siendo $x$ e $y$ las coordenadas en el sistema actual y $x_1$ e $y_1$ las coordenadas en el sistema girado $θ$ grados.
Con un cambio de variables es posible deformar una curva en el sentido del eje $X$ o del eje $Y$. Si ambas deformaciones se hacen en la misma proporción tenemos un aumento de tamaño de la curva en sentido radial a partir del centro de coordenadas. Esta ampliación de las dimensiones de una curva, manteniendo sus proporciones, se llama Homotecia.
Una Homotecia se define a partir de un punto o polo, a partir del cual trazamos rectas, y obtenemos sus puntos de intersección con la curva, que desplazamos a lo largo de la recta aplicando una razón de proporcionalidad a su distancia al polo. El punto para efectuar una homotecia puede ser cualquier punto del plano, no solo el centro de coordenadas. Un ejemplo, que ilustra lo que decimos, lo hemos visto al transformar un folio de Descartes en una trisectriz de Mac Laurin.
La ecuación cartesiana de una curva plana es una ecuación de dos variables, en $x$ e $y$ en la que $x$ se interpreta normalmente como la variable independiente. Hemos visto también que es posible definir diferentes sistemas de coordenadas.
El sistema de coordenadas polares tiene un interés especial, por simplificar la ecuación de muchas curvas, entre ellas, las espirales. Las coordenadas polares definen la posición de un punto de la curva mediante su distancia a un punto de referencia que se llama polo y mediante el ángulo que forma la recta que une ese punto con el polo, respecto un eje de referencia. Normalmente la medición angular se establece con el mismo eje $X$ de las coordenadas cartesianas. Se puede establecer la convención de que tome valores $(0,2π)$ en sentido anti horario o en algunos casos de $(-π,π)$ en sentido horario.
La conversión de coordenadas polares a cartesianas es inmediata,
Para la conversión en sentido contrario tenemos que, $r=\sqrt{(x^2+y^2)}$.
Para obtener $θ$ se utiliza la función $\arctan \large {y\over x}$, cuyo resultado depende de la convención de signos elegida y del signo de $x$ e $y$.
Por ejemplo, para el caracol de Pascal, cuya ecuación en coordenadas cartesianas, hemos visto es:
$$(x^2+y^2+2ax)^2=4a^2(x^2+y^2)$$Puede expresarse en coordenadas polares como:
siendo $a$ el radio de la circunferencia y $h$ una constante.
Dos variables bastan para definir una curva plana, pero en algunos casos es difícil expresar la relación entre $x$ e $y$ en una sola ecuación y es mas sencillo desdoblar la ecuación de la curva en dos ecuaciones, incluyendo en el sistema una nueva variable que se llama parámetro (normalmente se utiliza para designar el parámetro la letra $t$). Pasamos por tanto, de una ecuación del tipo $f(x,y)=0$ a dos ecuaciones $y=f(t)$ y $x=g(t)$, que definen de forma separada cada una de las coordenadas de la curva.
Es fácil ver que para cada curva existen infinitas maneras de obtener una ecuación paramétrica. Las ecuaciones paramétricas ofrecen normalmente una representación mas sencilla de las curvas cicloides y sus variantes.
Hemos visto que Descartes es consciente de que existen curvas, conocidas desde antiguo, que no se pueden expresar analíticamente y abre para ellas un cajón de sastre al que llama curvas mecánicas y que quedan según su criterio fuera de la geometría. En particular cita la cuadratriz y la espiral de Arquímedes. Estas curvas se generan por la combinación de dos movimientos, con un movimiento giratorio y otro de traslación. Son por tanto la composición de dos movimientos independientes. Ambas son dibujables por puntos aunque no pueden serlo por compases o mecanismos articulados.
La cuadratriz no es construible con regla y compás y tampoco existe un sistema articulado capaz de dibujar esta curva mediante un movimiento continuo. Es posible dibujarla punto a punto procediendo a dividir sucesivamente el segmento $BD$ y $AD$. Si construimos el punto medio de la recta $BD$, podemos dividir el arco en dos partes iguales, después por los puntos medios de las dos cuerdas obtenidas repetir la división del arco sucesivamente (operaciones realizables con regla y compás). Dividiendo la recta $AD$ en segmentos que se correspondan con la fracción de arco $BKD$ obtenida, por ejemplo, el punto $H$ divide la recta $AD$ en su punto medio, igual que el punto $K$ divide el arco $BKD$ en dos mitades. La intersección de la recta paralela a $AB$ que pasa por $H$ y el radio $AK$ nos dan el punto $I$ de la cuadratriz. Repitiendo la división obtenemos $L$ y así sucesivamente podemos construir punto a punto la curva.
Esto es no es valido para el punto $X$, puesto que al disminuir el arco, la paralela a $AB$ y el radio son en ese punto paralelas, no pudiendo determinarse su intersección. En definitiva definir exactamente la abscisa del punto $X$ es el mismo problema que calcular la longitud del arco de circunferencia o de calcular $π$ por sucesivas aproximaciones. La cuadratriz resuelve el problema de la cuadratura del círculo solo aparentemente, como era de esperar.
La trisección del ángulo $BAF$ es trivial sin más que trisecar el segmento $AE$.
La curva mecánica que mas atención suscita en la época es la cicloide, que es la curva generada por el movimiento de un punto sobre un círculo que rueda sobre una recta. Ya era conocida por Hiparco en el siglo II a.C. Su nombre y definición se lo debemos a Galileo.
La cicloide y las curvas de su familia desarrolladas a partir del movimiento de uno o varios círculos, involucran en su definición magnitudes derivadas del arco de circunferencia y su ecuación requiere por tanto de expresiones trigonométricas que en la época eran perfectamente conocidas, pero interpretadas como tablas de valores y por lo tanto de valor no “exacto”.
El cálculo del área bajo la cicloide la obtiene Roberval en 1634 aplicando el principio de las áreas de Cavalieri.
En el dibujo es fácil ver que el área de la circunferencia generadora se corresponde al área comprendida entre la cicloide y la curva que hemos dibujado en rojo, que se obtiene por traslación del segmento infinitesimal del círculo.
En su construcción aparece por primera vez la curva del seno, cuando la circunferencia que rueda es de radio unidad, con valores en función del arco de circunferencia entre $0$ a $2π$. El cálculo del área bajo la cicloide incluye el cálculo del área bajo la curva del seno que es igual al doble de la circunferencia unidad.
Las epicicloide es el lugar geométrico de un punto de la circunferencia que rueda sin deslizar sobre otra circunferencia.
Para que la curva definida sea cerrada el cociente entre los radios de las dos circunferencias debe ser un numero racional. De este modo, completado un numero finito de revoluciones, la curva se cierra.
Para simplificar la figura hemos supuesto el radio de la circunferencia base igual a $1$ y hemos considerado el círculo que rueda en una fracción de la unidad.
Cuando los dos radios son iguales la figura resultante es una cardioide. Para $n=2$ la curva en forma de riñón se llama Nefroide.
La hipocicloide es el lugar geométrico de un punto de la circunferencia que rueda, sin deslizar, en el interior de otra.
Para el caso de $n=4$, obtenemos una curva llamada astroide ó hipocicloide de 4 vértices, de ecuación:
Un epitrocoide es en esencia la epicicloide de un punto que no esta situado sobre el perímetro de la circunferencia rodante, pero se nueve solidario con ella.
Las espirales son también curvas conocidas que tampoco tienen definición mediante ecuaciones algebraicas. Se definen por el movimiento de un punto que se desliza sobre una recta, según una ley predeterminada, cuando la recta gira alrededor de un polo.
La forma mas intuitiva de trazar una espiral es mediante un punto móvil sobre una semirrecta que gira alrededor del origen de coordenadas. La ecuación mas sencilla para la espiral es en coordenadas polares. La ecuación nos relaciona por un lado la distancia al origen del punto que traza la espiral, y el ángulo de la recta por la que se desliza.
Las espirales tienen dos ramas según el sentido de giro de la semirrecta trazadora.
La espiral mas conocida es la espiral de Arquímedes de ecuación:
$$r=a\theta$$Esta ecuación puede generalizarse obteniendo espirales de ecuación:
$$r^m=a\theta^m$$Para $m=2$ obtenemos la espiral de Fermat.
Para $m=-1$ la espiral hiperbólica.
Para $m=-2$ la curva llamada Lituus.
Jakob Bernoulli (1654-1705) estudio la espital equiangular y la llamó spira mirabilis (espiral admirable). Pidió que la curva fuese grabada en su lápida mortuoria con la frase en latín “Eadem mutata resurgo” (“Aunque transformado reaparezco”).
La ecuación de la espiral equiangular es: $\quad \large r=a\;e^\theta$
La tangente de esta espiral, en cualquier punto, forma un ángulo constante con su radio, de donde viene su nombre de “equiangular.
La ecuación de una espiral con ángulo dado es:
siendo $\cot\alpha ={\large 1\over \normalsize \tan\alpha}$
La espiral cuya $tan(α)$ es igual al numero áureo, $ψ$, tiene la propiedad de que los radios vectores de los puntos de corte con los ejes forman una sucesión de Fibonacci, y los rectángulos definidos son áureos.