En cada partido de este juego compiten dos equipos cuyos jugadores se distribuyen en tres líneas rotativas: delantera, media y defensa. Cada equipo recibirá 9 preguntas con 6 opciones de respuesta. En primer lugar la pregunta será formulada para la línea delantera, en caso de fallo pasará a la media, si no hay acierto deberá responder la línea de defensa que en caso de no acertar recibirá el equipo al que se ha formulado la pregunta recibirá un gol. Los equipos ganarán puntos por cada respuesta acertada, siendo mayor la ganancia cuanto antes se acierte la pregunta (mayor si se acierta en la delantera y menor en la defensa). Ganará el partido el equipo que menos goles reciba y más puntos consiga.
Pulsando sobre la imagen de la carátula se puede acceder directamente al juego.

Unidades didácticas de Matemáticas y Física y Química
Escrito por Montserrat Gelis BoschUnidades Didácticas es un proyecto de la RED Descartes que incluye un conjunto de unidades didácticas de Matemáticas y Física y Química elaboradas por profesores y profesoras a partir de su conocimiento y experiencia en el aula.
Cada una de estas unidades didácticas se refiere a una unidad temática o un conjunto de conceptos y habilidades como parte de un curso o plan de estudio, siguiendo los niveles y cursos del sistema educativo español. Estas unidades son independientes unas de otras, de esta forma el profesorado las puede seleccionar, reorganizar y adaptar a las necesidades de su alumnado.
Con la inclusión de escenas interactivas de Descartes se incentiva la reflexión, la conexión con conocimientos previos, la resolución de problemas y la aplicación práctica del conocimiento. Esto ayuda a los estudiantes a construir un entendimiento profundo que les permita aplicar lo aprendido en diferentes contextos, en lugar de simplemente memorizar información superficialmente.
En el siguiente vídeo se presenta este proyecto y se muestra el contenido de algunas de estas unidades.
Trabajo Fin de Grado. Estado del arte del aprendizaje basado en juegos educativos digitales y diseño e implementación de métodos estadísticos de validación aplicados a GBL
Escrito por Jesús Manuel Muñoz CalleEn febrero de 2024, se ha presentado el Trabajo Fin de Grado de Ingeniería en Telecomunicaciones por D. José Manuel Candilejo Egea, titulado "Estado del arte del aprendizaje basado en juegos educativos digitales y diseño e implementación de métodos estadísticos de validación aplicados a GBL". Dicho trabajo se enmarca dentro de los Proyectos Gamifica y AJDA y puede consultarse de forma completa en el siguiente enlace.
El objetivo de este proyecto ha sido diseñar un sistema de validación estadística de plataformas tecnológicas de GBL, con la intención de poder aplicarse de forma sencilla y obtener unos resultados útiles para la valoración de sistemas gamificados de educación en desarrollo o incluso decisiones de adquisición de productos relacionados.
Para ello el trabajo se divide en dos grandes bloques, el primero es un análisis sistemático de los proyectos que se han realizado en el campo de la gamificación, enfocada en entornos tecnológicos, especialmente aplicados a la educación. A partir de las conclusiones que se obtengan de este análisis del estado del arte, se propondrá un modelo de validación y se realizará una prueba de este, lo que dará lugar al segundo bloque del proyecto.
Se han buscado en las diferentes plataformas de publicaciones académicas artículos relacionados con experiencias empíricas con herramientas de gamificación digitales enfocadas en la educación. A través de términos relacionados se encontraron 1865 artículos que tras su lectura progresiva se fueron reduciendo hasta 100.
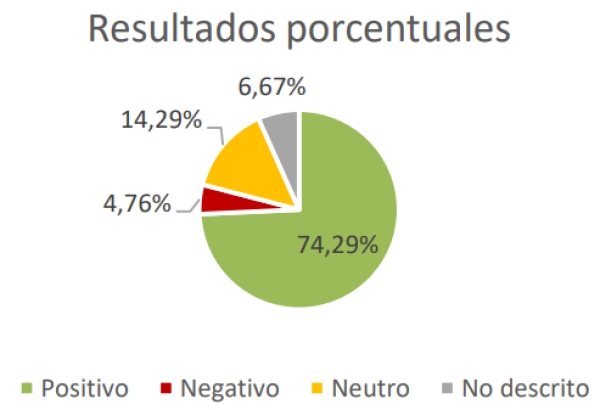
- Positivos: la experiencia habla concretamente de efectos positivos en uno o más de las dimensiones definidas anteriormente. Además, los otros campos no han sufrido alteraciones negativas, en todo caso, no varían con respecto al grupo de control o experiencias anteriores (permanecen neutros). Dentro de positivo, para añadir más granularidad se ha distinguido entre: ligeramente positivo, positivo y muy positivo.
- Neutros: no ha habido un incremento significativo en ninguno de los tres aspectos que se desean potenciar, tampoco ha habido efectos negativos.
- Negativos: algunos de los aspectos anteriores se han visto perjudicado por el experimento. Se ha distinguido, al igual que en los positivos entre: ligeramente negativo, negativo y muy negativo.
- No descrito: en el estudio no se especifica los resultados del experimento.
A. Bloque I
- La gamificación a través de plataformas digitales puede resultar beneficiosa si se aplica correctamente (74,9% de resultados positivos).
- 11 técnicas de gamificación distintas usadas, con resultados mayoritariamente positivos (siendo los quizzes la técnica con menor índice de éxito del 67,86%).
- La validación de los experimentos se realiza a través de métodos muy diversos, destacando entre ellos métodos que combinan distintos métodos, que se emplea en un 35% de los casos.
- La gamificación está considerablemente relacionada con las áreas de la educación, la telemática y las ciencias de la computación, el 70% de las revistas analizadas están dentro de este ámbito. • La metodología usada a la hora de gamificar tiene gran relevancia de cara a los resultados.
Sistemas de ecuaciones. Materiales ed@d
Escrito por Montserrat Gelis BoschEl Proyecto Ed@D ofrece una serie de herramientas y recursos digitales, diseñados para apoyar a profesores y estudiantes de secundaria en el proceso de enseñanza y aprendizaje de las Matemáticas, Ciencias de la Naturaleza y Física y Química. Estos recursos incluyen software educativo, actividades interactivas, materiales didácticos y tutoriales, entre otros.
La Red Descartes, a través del Proyecto Ed@D, busca fomentar una enseñanza más dinámica, participativa y accesible, aprovechando las posibilidades que ofrecen las TIC. Además, promueve el trabajo colaborativo entre docentes y el intercambio de experiencias y buenas prácticas en el ámbito de la educación en secundaria.
Para el desarrollo de los contenidos de cada unidad se tomó como referencia las competencias básicas y los contenidos mínimos establecidos para las asignaturas de Matemáticas, Ciencias de la Naturaleza y Física y Química.
Todos los materiales siguen un mismo diseño. Los contenidos de cada curso se dividen en unidades llamadas quincenas. La estructura de cada unidad es la siguiente:
Antes de empezar: Una primera página de introducción con los objetivos de la quincena y una introducción al tema.
Contenidos: En la parte central de cada capítulo se introducen las definiciones y conceptos y algún ejemplo interactivo para reforzar el contenido. También se propone un apartado de ejercicios con actividades resueltas que se abren en una ventana emergente.
Resumen: En este apartado se presenta un resumen de las definiciones y conceptos trabajados.
Ejercicios: Mediante un menú desplegable, se proponen diferentes tipos de actividades que el estudiante debe resolver en su cuaderno de trabajo. Con el botón solución se puede ver la solución desarrollada para comprobar si los cálculos realizados son correctos.
Autoevaluación: Se plantean diez ejercicios. Cuando el estudiante introduce la respuesta puede comprobar si es correcta o no. Si la respuesta no es correcta se ofrece el resultado correcto junto al desarrollo del ejercicio. Al finalizar la autoevaluación se puede observar el número de respuestas correctas.
Para enviar al tutor: En este apartado se proponen una serie de ejercicios para enviar al tutor. El estudiante debe introducir las respuestas e indicar sus datos y la dirección de correo electrónico del docente.
Para saber más: En este último apartado se presenta alguna actividad de ampliación, curiosidades o referencias históricas relacionadas con el tema tratado en la unidad.
En el siguiente vídeo se puede ver con detalle una quincena de este proyecto, se trata de la unidad Sistemas de ecuaciones para 3º de la ESO:
Más...
Jugando con las matemáticas. Día Internacional de las Matemáticas
Escrito por José Antonio Salgueiro GonzálezEn noviembre de 2019, la UNESCO proclamó el 14 de marzo de cada año como Día Internacional de las Matemáticas, con el fin de destacar el papel fundamental que desempeñan las ciencias matemáticas para hacer frente a los desafíos de nuestro tiempo en ámbitos como la inteligencia artificial, la salud, el cambio climático, la energía y el desarrollo sostenible y la mejora de la calidad de vida de la sociedad en general.
Para las personas que accedan por primera vez a esta información, debemos recordar que hemos venido celebrando desde hace años el conocido como "Día de π", una efemérides motivada por la forma de expresar la fecha diaria en el mundo anglosajón, es decir, 3/14, coincidiendo con las primeras cifras de este irracional número, considerado como una de las constantes matemáticas más importantes y conocidas.
"El tema de 2024, “Jugando con las matemáticas”, celebra los juegos matemáticos, puzzles y otras actividades lúdicas, pero también el “jugar” con las propias matemáticas, explorando, experimentando y descubriendo" (IMU).

Como el fin de RED Descartes es promover la renovación y cambio metodológico en los procesos de aprendizaje y enseñanza de las Matemáticas, y también en otras áreas de conocimiento, utilizando los recursos digitales interactivos generados con la herramienta de autor Descartes JS, hemos recopilado una humilde colección de objetos interactivos con los que, cualquier docente que no haya podido planificar este evento previamente para su aula, o cualquier alumno o alumna autodidacta, o en familia, puede participar desde un equipo tecnológico instalado en el aula o desde sus propios dispositivos móviles.
Puedes acceder sin más que pulsar sobre cada imagen y, en ciertos juegos, conviene leer la página de información.
| JUGANDO CON LAS MATEMÁTICAS DEL ... SUDOKU |
| JUGANDO CON LAS MATEMÁTICAS DE ... CAMUFLAR MONEDAS |
| JUGANDO CON LAS MATEMÁTICAS DE ... BUSCAR EL TESORO |
| JUGANDO CON LAS MATEMÁTICAS EN ... EL AULA |
| JUGANDO CON LAS MATEMÁTICAS CON ... OTROS RECURSOS |
Si no tienes suficiente con nuestra propuesta o buscas algo diferente, te recomendamos visitar los artículos de las ediciones anteriores:
- Día Internacional de las Matemáticas 2021
- Día Internacional de las Matemáticas 2022
- Día Internacional de las Matemáticas 2023
¡FELIZ DÍA INTERNACIONAL DE LAS MATEMÁTICAS!
Publicación del libro interactivo "Juegos didácticos. El Proyecto AJDA"
Escrito por Jesús Manuel Muñoz CalleTal y como anunciamos recientemente, en febrero de 2024 se ha publicado el libro interactivo titulado "Juegos didácticos. El Proyecto AJDA". Se puede acceder al mismo a través de las siguientes webs:
- Proyecto AJDA.
- Editorial iCartesiLibri de la Red Descartes.
- PubHTML5. Biblioteca de libros interactivos de la Red Descartes. (Estantería)
- Libros interactivos digitales. Universidad Autónoma de México (UNAM).
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)













 CONTACTO
CONTACTO
