Participantes de tres continentes en el curso para el diseño de libros interactivos
Escrito por José Antonio Salgueiro GonzálezLos avances tecnológicos y los recursos educativos abiertos han hecho posible que los profesionales de la enseñanza en el s. XXI puedan, con relativa facilidad, diseñar, crear, modificar, adaptar y compartir sus propios libros interactivos, con el contenido personalizado para las necesidades de su alumnado y la incorporación de las actividades validadas en el aula con las estrategias didácticas de su predilección.Y todo ello es factible con el modelo de libro interactivo de RED Descartes, cuya biblioteca supera ya los cien volúmenes, siendo de extrema importancia la formación del profesorado. Así, en ese sentido, ha comenzado la V Edición del curso para el "Diseño de Libros Interactivos", que se enmarca en el programa de Educación Abierta de nuestra red, con una alta inscripción que engloba a participantes procedentes de once países, 11, con docentes y profesionales de la educación que comprenden las etapas educativas de primaria, secundaria, bachillerato y universidad, así como una amplia gama de especialidades, alcanzando, por vez primera, el continente asiático.
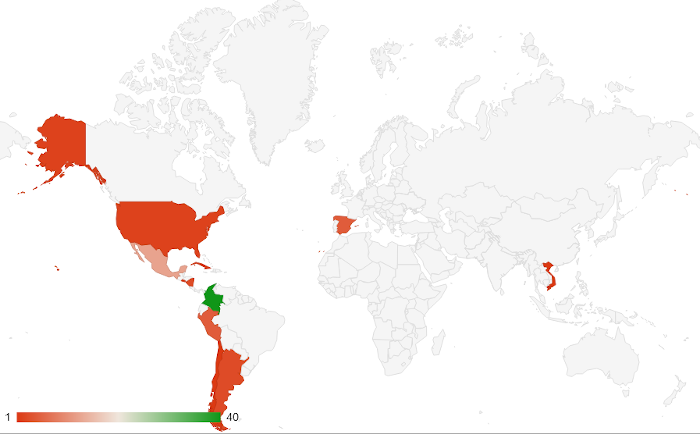
Compartimos el siguiente diagrama de sectores con el porcentaje de participación por países:
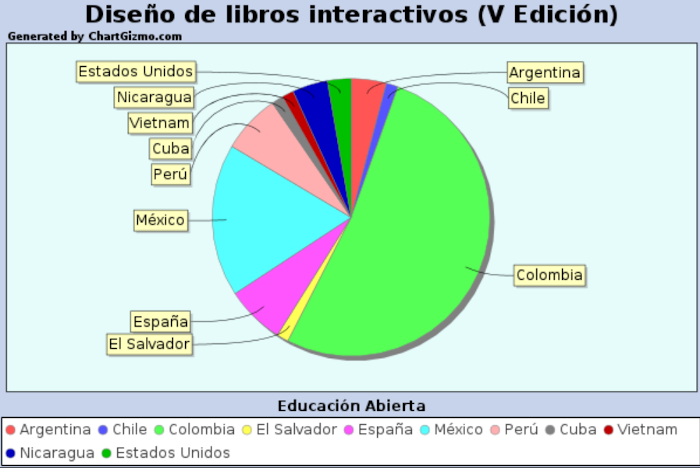
Las sesiones se imparten por videoconferencia, de 7 AM a 8 AM en el horario oficial de Colombia, de acuerdo al calendario previsto y contenidos a tratar, usando para ello la herramienta Meet de Google, para lo cuál, cada participante recibe, tanto en su calendario de Google como en el grupo de WhatsApp del curso, el enlace de acceso a la reunión, que será grabada para, posteriormente, compartirla por la herramienta de intercomunicación mencionada, el grupo de Google y en la página que enlazamos del portal de RED Descartes, en la que se recopilan todas las sesiones.
Ponemos a disposición de todas las personas interesadas la presentación de la primera sesión con las instrucciones y herramientas iniciales:
iCartesiLibri es un proyecto de la RED Descartes que engloba una serie de libros dinámicos interactivos agrupados en una gran diversidad de disciplinas. Este proyecto se encuentra en constante cambio y renovación, lanzando regularmente nuevas versiones con mejoras, correcciones de errores y características nuevas e incorporando nuevas publicaciones continuamente.
La educación con materiales interactivos ofrece numerosas ventajas, que pueden mejorar significativamente el proceso de aprendizaje.
Para el profesorado se ofrece un curso para el diseño de estos libros interactivos, dirigido a docentes de cualquier etapa educativa. En estos momentos está abierto el plazo de inscripción para la quinta edición del curso.
En este artículo se presenta el libro interactivo Fracciones que pertenece a este proyecto. En cada capítulo del libro se proponen actividades interactivas con corrección para practicar. En algunas escenas interactivas del apartado de operaciones con fracciones se proponen diferentes ejemplos y se muestran, paso a paso, los cálculos que deben realizarse. En otras escenas el alumnado debe ir completando cada paso del ejercicio hasta finalizar todos los cálculos.
En el siguiente vídeo se pueden ver con detalle algunas actividades de este libro y se muestra cómo insertar este material en un blog para su aplicación en el aula.
Curso "Edición de libros interactivos" de la RED Descartes (5ª edición en línea)
Escrito por José R. Galo Sánchez|
Diseño de libros interactivos |
Vídeos de la quinta edición en línea del curso "Edición de libros interactivos"
(se irán publicando a medida que se desarrollen las sesiones)
- Vídeo de la 1ª sesión (13 de octubre de 2023). Presentación de la 1ª sesión.
- Vídeo de la 2ª sesión (27 de octubre de 2023). Presentación de la 2ª sesión.
- Vídeo de la 3ª sesión (10 de noviembre de 2023). Presentación de la 3ª sesión.
- Vídeo de la 4ª sesión (24 de noviembre de 2023). Presentación de la 4ª sesión.
- Vídeo de la 5ª sesión (8 de diciembre de 2023). Presentación de la 5ª sesión.
- Vídeo de la 6ª sesión (19 de enero de 2024). Presentación de la 6ª sesión.
- Vídeo de la 7ª sesión (2 de febrero de 2024). Presentación de la 7ª sesión.
- Vídeo de la 8ª sesión, sesión final del curso (16 de febrero de 2024).
Experiencia de aula en el CGTD
Escrito por José Antonio Salgueiro González"El deporte gallego tiene en el Centro Gallego de Tecnificación Deportiva (CGTD) la instalación de referencia de su excelencia competitiva, una excelencia que contempla también, por supuesto, la formación académica de los deportistas con la finalidad de conseguir su formación integral. "(Literalmente extraído de la web del CGTD). Pues bien, en este contexto se desarrolla la experiencia de aula que comparte nuestra compañera María del Carmen Quireza Ramos, profesora de matemáticas en bachillerato con deportistas de alto rendimiento.
El curso 2020-2021 ha pasado a la historia como aquel en el que se tuvieron que tomar medidas extraordinarias para seguir con las enseñanzas en los colegios e institutos. En este caso, el alumnado del CGTD constituye una extensión del IES Sánchez Cantón de Pontevedra, y sus aulas no fueron suficientes para atenderlos con las restricciones de distancia de seguridad obligatorias para evitar al máximo contagios del COVID 19.

Por ello, la Conselleria de Deportes, de la que depende la preparación deportiva de estos alumnos, tuvo a bien ofrecer unos espacios en el edificio de oficinas, salas de charlas del CGTD, para impartir clase a los grupos de 2º Bachillerato de ambas modalidades, como podemos apreciar en el mapa del recinto deportivo y académico. A esta situación tan excepcional, hay que añadir que la falta de internet al principio de curso y los fallos que se dieron a lo largo del mismo hicieron el trabajo muy complicado, tanto para profesorado como alumnado, resultando un curso muy complicado para impartir las clases utilizando los materiales de Descartes, especialmente los libros interactivos, como viene siendo habitual.

Como el alumnado se veía en la necesidad de usar sus datos móviles en los espacios asignados, la profesora elaboró unas pequeñas presentaciones con captura de pantalla de los materiales teóricos contenidos en los libros interactivos para la enseñanza en el aula, y más tarde, el alumnado consolidaba su aprendizaje conectándose a los libros interactivos desde la red de la residencia. Lo mismo ocurría cuando iban a competiciones, a concentraciones o estaban confinados en sus casas.
Se han utilizado, fundamentalmente, los siguientes recursos educativos abiertos en formato libro interactivo:
- Integrando con Paco
- Análisis matemático para bachillerato (Página 49. Regla de L'Hôpital)(Página 32. Derivabilidad. Rectas tangente y normal)(Página 9. Cálculo de límites)
- Geometría analítica del espacio

Los test para detectar posibles contagios se llevaban a cabo aleatoriamente y con mucha frecuencia en las mismas instalaciones del CGTD, y cuando se detectaba algún positivo, no sólo se iban él o ella confinados, sino todos los compañeros de su equipo de entrenamientos.
Ese curso fue un reto tanto para el alumnado como para la profesora. Se vieron en la necesidad de ser mucho más autónomos para sacar la mayor parte de los contenidos adelante y enfrentarse a la prueba de acceso a la universidad. A pesar de las dificultades, los resultados fueron buenos. Lo que más les gustó de los materiales era el poder hacer muchos ejercicios con la retroalimentación de los mismos, las explicaciones muy claras y concisas, y lo que menos que tardase tanto tiempo en cargar el material en los dispositivos, pero eso ya dependía más de la red.

La experiencia de impartir las clases de matemáticas a alumnos de alto rendimiento deportivo ha sido muy enriquecedora, al tener que trabajar de una manera diferente, centrándonos en lo importante, preguntando de otra forma lo mismo para los múltiples exámenes que nos vemos obligados a realizar, pues casi nunca tienes al grupo completo en el aula. El trato con el alumno es mucho más cercano y entre ellos ves mucho apoyo tanto a nivel deportivo como académico.
Más...
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
Escrito por José Antonio Salgueiro GonzálezEl buen resultado obtenido en las ediciones anteriores y a demanda de usuarios y seguidores, realizamos una nueva convocatoria y abrimos el plazo de inscripción gratuita a la V Edición del Curso para el Diseño de Libros Interactivos de Aprendizaje, una acción formativa que permitirá desarrollar aún más tu competencia digital y elaborar tu programación digital de aula, organizando y secuenciando en un único soporte todos los recursos, actividades y tareas previstas para tu alumnado. Una acción que se enmarca en el programa de Educación Abierta desarrollado entre redes docentes de Colombia, México y España, fundamentalmente, aunque contamos con la participación de profesorado de otros países de habla hispana, portuguesa e inglesa. Este curso tiene como objetivo principal abordar la conceptualización y el diseño, desarrollo y experimentación de nuevos recursos educativos abiertos en formato libro del s. XXI y basados en la interactividad, que permitan poner de manifiesto que es posible dar una respuesta positiva y asequible a los retos educativos intrínsecos al paradigma educativo emergente.
Está dirigido a docentes de cualquier etapa educativa, infantil, primaria, educación secundaria obligatoria, bachillerato, formación profesional, enseñanzas de régimen especial y universidad, y de cualquier materia o especialidad, en activo o no, así como a profesionales vinculados a la educación o formación, utilizando una metodología activa, pues desde la primera sesión cada participante comenzará a diseñar y editar su proyecto de libro interactivo, recibiendo sesiones quincenales por videoconferencia, que serán grabadas y compartidas con todos los participantes y asesorados por docentes de las redes mencionadas.
El curso comienza el próximo día 13 de octubre y finaliza el 16 de febrero de 2024, impartiéndose las sesiones de 7 AM a 8 AM en el horario oficial de Colombia, de acuerdo al siguiente calendario previsto y contenidos a tratar:

Según las necesidades y proyectos de cada participante, el producto final podrá ser como los mostrados a continuación:
-
- Libro digital interactivo: artes visuales, ciencias computacionales, ciencias administrativas y económicas, ciencias agroindustriales, ciencias naturales, ciencias sociales y humanas, formación, matemáticas, física, química, ingeniería, lengua inglesa, literatura, textos institucionales...
- Revista digital interactiva
- Revista digital RED Descartes - 1
- Revista digital RED Descartes - 2
- Revista digital RED Descartes - 3
- Revista digital RED Descartes - 4
- Revista digital RED Descartes - 5
También puedes ampliar información en el artículo titulado "El libro interactivo al alcance de cualquier docente, etapa educativa y materia".
| ACCESO AL FORMULARIO DE INSCRIPCIÓN |
El plazo de inscripción estará abierto hasta el día 11 de octubre o hasta completar la oferta de plazas.
Recursos que utilizaremos:
Planifica el curso escolar 2023-2024 en la universidad con el Proyecto Descartes
Escrito por Elena Álvarez SáizLa Red Educativa Digital Descartes ofrece una serie de recursos digitales interactivos que pueden adaptarse y utilizarse en el contexto universitario para enriquecer la enseñanza y el aprendizaje en una variedad de disciplinas. Utilizar los recursos de la Red Educativa Digital Descartes ofrece numerosas ventajas para profesores y estudiantes en el ámbito educativo como pueden ser las siguientes:
- Acceso Gratuito: Los recursos disponibles en la Red Educativa Digital Descartes son gratuitos, lo que los hace accesibles para un amplio público sin ningún coste para los estudiantes y educadores.
- Variedad de Contenidos: La web ofrece una amplia gama de recursos que cubren una variedad de temas permitiendo encontrar recursos adecuados para muchas necesidades específicas.
- Interactividad: Los recursos digitales de la Red Descartes son interactivos, lo que significa que los estudiantes pueden participar activamente en actividades de aprendizaje. Esto ayuda a mejorar la retención y comprensión de conceptos.
- Visualización de Conceptos: Los recursos suelen incluir gráficos, animaciones y simulaciones que ayudan a visualizar conceptos abstractos. Esto es especialmente beneficioso para materias como matemáticas y ciencias.
- Retroalimentación: Muchos recursos proporcionan retroalimentación inmediata, lo que permite a los estudiantes evaluar su desempeño y corregir errores de manera efectiva.
- Personalización del Aprendizaje: Los recursos de la Red Descartes a menudo permiten la personalización, lo que significa que los profesores pueden adaptar el contenido para satisfacer las necesidades de sus estudiantes y adaptarlo a diferentes niveles de habilidad.
- Flexibilidad de Aprendizaje: Al estar disponibles en línea, los recursos de la Red brindan flexibilidad respecto a cuándo y dónde pueden acceder a ellos los estudiantes, lo que es particularmente útil para el aprendizaje a distancia y el aprendizaje autodirigido.
- Apoyo para la Enseñanza: Los profesores pueden utilizar estos recursos como herramientas complementarias en el aula, lo que enriquece la enseñanza y ofrece a los estudiantes una experiencia más dinámica.
- Comunidad Educativa: La Red Educativa Digital Descartes también puede servir como una comunidad donde profesores y estudiantes pueden compartir recursos y colaborar en proyectos educativos.
La siguiente escena interactiva muestra ejemplos de recursos digitales interactivos que se pueden utilizar en la universidad en distintas materias indicando alguna de las ventajas que supone la incorporación en el aula. Basta acercar el cursor a cada icono para obtener información y acceder al ejemplo pulsando sobre el botón Ver ejemplo.
Como se puede apreciar en los ejemplos anteriores, la Red Educativa Digital Descartes publica y mantiene gran cantidad de recursos interactivos tanto en matemáticas como en otras materias con los que enriquecer la enseñanza y el aprendizaje en asignaturas universitarias al proporcionar a los estudiantes experiencias prácticas y visuales que complementan la instrucción tradicional. Estos recursos ayudan a los estudiantes a comprender conceptos difíciles y a aplicar sus conocimientos en contextos reales. Dada la gran variedad de recursos educativos publicados se recomienda visitar los distintos subproyectos de la Red Digital Descartes para obtener información actualizada sobre cada uno de ellos. En la siguiente escena se muestran algunos de estos proyectos con las direcciones web de acceso a información específica sobre los objetivos y la clasificación de los materiales disponibles.
El inicio de un nuevo curso es la oportunidad perfecta para intentar crear experiencias que despierten la curiosidad y el interés de nuestros alumnos, esperamos que los recursos de la Red Educativa Digital Descartes contribuyan a ello. ¡Buen comienzo y desarrollo de curso 2023-2024!
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)







 CONTACTO
CONTACTO
