En cada partido de este juego compiten dos equipos cuyos jugadores se distribuyen en tres líneas rotativas: delantera, media y defensa. Cada equipo recibirá 9 preguntas con 6 opciones de respuesta. En primer lugar la pregunta será formulada para la línea delantera, en caso de fallo pasará a la media, si no hay acierto deberá responder la línea de defensa que en caso de no acertar recibirá el equipo al que se ha formulado la pregunta recibirá un gol. Los equipos ganarán puntos por cada respuesta acertada, siendo mayor la ganancia cuanto antes se acierte la pregunta (mayor si se acierta en la delantera y menor en la defensa). Ganará el partido el equipo que menos goles reciba y más puntos consiga.
Pulsando sobre la imagen de la carátula se puede acceder directamente al juego.

Un siglo informando, entreteniendo y educando. Día Mundial de la Radio 2024
Escrito por José Antonio Salgueiro GonzálezCon el lema «La Radio: Un siglo informando, entreteniendo y educando», el martes 13 de febrero se celebra el "Día Mundial de la Radio 2024", adoptado por la Asamblea General de las Naciones Unidas en 2012 como Día Internacional. Por ello, la UNESCO hace un llamamiento a las emisoras de radio y, desde nuestra humilde cadena Radio Descartes, hemos realizado una pequeña selección de pódcast para colaborar en esta nueva edición y mostrar una parte de aquello que la radio puede conseguir en una ONG del ámbito educativo, como es RED Descartes. Pues bien, la efemérides que celebramos en esta edición del DMR, destaca tres aspectos: la imborrable historia de la radio, el valor utilitario actual de la radio y el continuo valor democrático de la radio, y resulta que son tres los programas de pódcast en Radio Descartes.

Imagen generada por la IA Hotpot.
Este programa de la cadena cartesiana contiene pódcast sobre literatura específica de esta temática, como entrevistas a sus autores y dramatizaciones teatrales en versiones radiofónicas. Para esta ocasión compartimos "Operación estética exacta", dramatización de una obra de teatro de nuestra compañera Eva María Perdiguero Garzo, donde los personajes son elementos matemáticos. Al número 0,33333333... parece que no le van muy bien las cosas con esa estela infinita de treses. ¿Cómo conseguir transformarse en una fracción para eliminar esa inexactitud?
En esta historia se pretende mostrar al alumnado de secundaria la importancia de la relación entre fracción y decimal, y está interpretada por miembros de la RED Descartes de varios países, con motivo del taller básico de formación sobre edición de audios y vídeos para los socios de nuestra red.

Imagen generada por la IA Hotpot.
"El personaje misterioso" es un programa de Radio Descartes conducido por Eva Perdiguero y Ángel Cabezudo con el objetivo de dar a conocer un poco más de cerca la parte humana de los personajes matemáticos famosos a lo largo de la historia. Concretamente, tras la entrevista del invitado, que no se desvela, el escuchante debería conocer su nombre o bien tomar los datos que se aportan en la dramatización y tomarse un tiempo para averiguarlo consultando en la múltiple documentación que hoy día se encuentra disponible, principalmente en Internet o en libros divulgativos de Historia de las Matemáticas o de Matemáticos célebres, pasando a responder en un comentario del blog de nuestro portal. A la semana siguiente, se publica un puzle creado con Descartes JS que incluye imágenes alusivas, alegóricas o de efemérides que descubren al personaje, interpretado, en esta ocasión, por Ricardo Alonso Liarte, compañero y profesor de matemáticas del IES Salvador Victoria, Monreal Del Campo (Teruel). Ricardo dirige un programa sobre las matemáticas en la radio de Onda Cero Calamocha.

Imagen generada por la IA Hotpot.
En esta sección de nuestro canal de radio recogemos diversas entrevistas a docentes que nos describen sus experiencias de aula, personalidades que destacan en la educación matemática y, sobre todo, las producciones del alumnado participante en el proyecto "La radio ficción en el aula de Matemáticas", que tiene sus antecedentes en el personaje misterioso de Radio Descartes y que hemos tratado anteriormente.
Para la ocasión, hemos seleccionado la entrevista ficticia a la matemática francesa que se vió obligada a firmar sus descubrimientos bajo el pseudónimo de Monsieur Le Blanc, porque en su época las matemáticas "no eran cosas de mujeres". Por cierto, no te pierdas en la entrevista algunas propuestas de Sophie Germain para fomentar la vocación matemática en mujeres y niñas. Un producto de cultura digital realizado por María y Mireia, alumnas de 3º ESO del IES Bajo Guadalquivir de Lebrija, demostrando sus capacidades para comunicar, interpretar y transmitir emociones desde la cadena "Radio púrpura al cubo".
Con esta humilde aportación, RED Descartes colabora y rinde homenaje a la radio en su Día Mundial, recordando a nuestros usuarios y seguidores que pueden visitar y conocer todas las experiencias de Radio Descartes publicadas en nuestro portal o, bien directamente, en el canal de RED Descartes en iVoox.

Aprendizaje Basado en Juegos. "Crash por equipos"
Escrito por Jesús Manuel Muñoz Calle- Se formarán 4 equipos de tres jugadores cada uno, salvo un equipo que tendrá dos miembros (recordamos que el grupo de alumnos es de 11).
- Cada equipo dispondrá de un capitán. Los capitanes serán los participantes con calificaciones más altas en la prueba inicial.
- Como criterio para formar los equipos se ha realizado teniendo en cuentas que la calificación media de los grupos esté compensada.
- El alumnado ha recibido información clara y precisa de los contenidos sobre los que versarán las preguntas, mecánica del juego, evaluación, recompensas, etc.
- Se implementarán al menos dos sesiones completas utilizando metodología de Aprendizaje Basada en Juegos en el aula.
- La recompensa para los equipos ganadores será de 5 calificaciones positivas para cada uno de los miembros del equipo.
- Los equipos podrán entrenarse en conjunto para la preparación de la actividad y establecer las estrategias que seguirán.
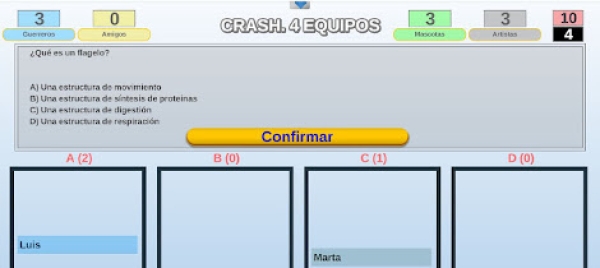
- Se formularán un máximo de 10 preguntas cuyos contenidos versarán sobre los temas objeto de la próxima prueba objetiva.
- Las preguntas dispondrán de 4 opciones de respuesta, siendo sólo una de ellas la opción correcta.
- Tras formularse cada cuestión, todos los alumnos, de forma independiente, deberán marcar mediante sus tarjetas de respuesta la opción elegida. Esto hará que los participantes se ubiquen en uno de los 4 contenedores existentes en el juego.
- Sobre cada uno de los 4 contenedores penden 4 "cajas fuertes gigantes". A aquellos participantes que se coloquen en un contenedor cuya opción de respuesta no sea correcta se les caerá encima una "caja fuerte gigante". En este caso los jugadores no recibirán ningún punto y, según se establezca inicialmente, podrán quedar eliminados.
- Los jugadores que se metan en el contenedor de respuesta correcta, conseguirán un punto para su equipo y continuarán jugando.
- En la configuración en la que no se eliminen los jugadores, ganará el juego el equipo que más puntos consiga tras formularse 10 preguntas. En la configuración con eliminación de jugadores, ganará el equipo que tras formularse las preguntas necesarias tenga jugadores no eliminados.
- Se jugaron un total de cinco partidas, tres con la configuración de jugadores eliminatorios y dos con no eliminatorios.
- La calificación media de la clase subió más de un punto respecto de la primera prueba.
- Varios alumnos obtuvieron calificación positiva, algunos de ellos con notas altas.
- Casi todos los alumnos mejoraron su calificación.
- La valoración global del alumnado de las actividades basadas en juegos superó los 9,5 puntos (en una escala de 0 a 10).
- Todo el alumnado manifestó un alto grado de satisfacción con este tipo de actividades y le gustaría que se realizaran más.
- El profesor también realizó un informe de evaluación de estas actividades, con resultados muy positivos. El desarrollo funcionó perfectamente en todos sus aspectos.
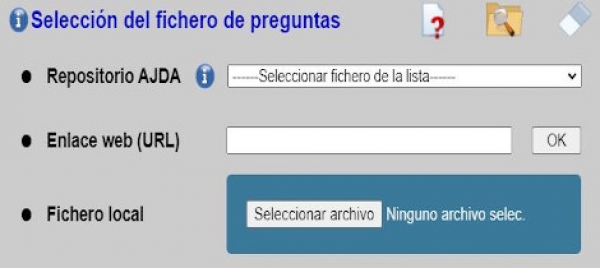
Otra de las mejoras significativas introducidas en el nuevo juego 10x10 es su menú inicial de configuración que se presenta nada más acceder al juego. Este menú consta de una o más páginas, las cuales vienen indicadas por las pestañas de su parte superior. En dichas pestañas, la primera hace alusión a los parámetros generales del juego y la segunda a la introducción de ficheros de preguntas.
- La primera es a través de un menú desplegable que permite seleccionar ficheros de preguntas disponibles el repositorio del Proyecto AJDA.
- La segunda es introduciendo la dirección URL en la que se encuentre un fichero de preguntas.
- La tercera es seleccionando un fichero ubicado en el equipo local del usuario, bien a través del explorador de archivos o bien arrastrando le fichero de preguntas seleccionado sobre esta zona.
Más...
La Radio y la Confianza. Día Mundial de la Radio 2022
Escrito por José Antonio Salgueiro GonzálezPor segundo año consecutivo, RED Descartes se suma y secunda la efemérides de este Día Internacional adoptado por la Asamblea General de las Naciones Unidas en 2012 que, declarado como "Día Mundial de la Radio", está dedicado a "La Radio y la Confianza" en su edición de 2022. De esta forma, acudimos al llamamiento de la UNESCO con algunas aportaciones. En primer lugar, se nos presenta una ocasión excelente para poner a disposición de la aldea global un nuevo recurso educativo abierto, en formato libro interactivo, que pasa a engrosar el catálogo de nuestra biblioteca cartesiana y que lleva por título, nada más y nada menos que, "La radio ficción en el aula. Uso educativo del pódcast".

En este libro se muestra uno de los usos educativos del pódcast, que se convierte en una estrategia didáctica relevante en el desarrollo de las competencias clave para el aprendizaje permanente a través de cualquiera de las ramas del saber o conocimiento que integran los diseños curriculares de secundaria, ya sean del ámbito científico, tecnológico, humanístico, artístico o deportivo.
En segundo lugar, siguiendo la línea de la edición anterior, compartimos una pequeña recopilación de audios de nuestra humilde cadena Radio Descartes, una cadena que dispone de tres programas de podcast, al igual que son tres los subtemas principales en que se divide esta nueva edición del Día Mundial de la Radio: confianza en el periodismo radiofónico, confianza y accesibilidad y confianza y viabilidad de las emisoras de radio.

El programa titulado obras matemáticas contiene podcast sobre literatura específica de esta temática, como entrevistas a sus autores y dramatizaciones teatrales en versiones radiofónicas. Para esta ocasión compartimos "Un robo descubierto. Dramatización", obra de nuestra compañera Eva María Perdiguero Garzo, donde los personajes son figuras matemáticas. A dos tercios le han robado el móvil, siendo su asaltante un famoso ladrón de la banda de las cuatro décimas. El detective PI se lanza a la búsqueda del ladrón.
En esta historia se pretende mostrar a los alumnos y alumnas de secundaria la importancia de la relación entre fracción y decimal, y está interpretada por miembros de la RED Descartes de varios países, con motivo del taller básico de formación sobre edición de audios y vídeos para los socios de nuestra red.

"El personaje misterioso" es un programa de Radio Descartes conducido por Eva Perdiguero y Ángel Cabezudo con el objetivo de dar a conocer un poco más de cerca la parte humana de los personajes matemáticos famosos a lo largo de la historia. Concretamente, tras la entrevista del invitado, que no se desvela, el escuchante debería conocer su nombre o bien tomar los datos que se aportan en la dramatización y tomarse un tiempo para averiguarlo consultando en la múltiple documentación que hoy día se encuentra disponible, principalmente en Internet o en libros divulgativos de Historia de las Matemáticas o de Matemáticos célebres, pasando a responder en un comentario del blog de nuestro portal. A la semana siguiente, se publica un puzle creado con Descartes JS que incluye imágenes alusivas, alegóricas o de efemérides que descubren al personaje.
Dado que nos encontramos en fecha próxima al "Día Internacional de la Mujer y la Niña en la Ciencia", otra efemérides que cuenta con la colaboración de RED Descartes, hemos seleccionado la entrevista realizada a un personaje femenino, y estamos convencidos de que conseguirás identificarla con rapidez.

En esta sección de nuestro canal de radio recogemos diversas entrevistas a docentes que nos describen sus experiencias de aula, personalidades que destacan en la educación matemática y, sobre todo, las producciones del alumnado participante en el proyecto "La radio ficción en el aula de Matemáticas", que tiene sus antecedentes en el personaje misterioso de Radio Descartes y que hemos tratado anteriormente.
Para la ocasión, hemos seleccionado la entrevista ficticia al gran matemático francés Évariste Galois, quien transmitió todos sus descubrimientos la noche antes de morir a la temprana edad de veinte años y que darían lugar a la Teoría de Grupos. Un producto de cultura digital realizado por Pablo García y Pablo Gutiérrez, alumnos de 3º ESO del IES Bajo Guadalquivir de Lebrija, con un peculiar recibimiento y bienvenida al programa y el lenguaje matemático verbal en el que se desenvuelven.
Con esta humilde aportación, RED Descartes colabora y rinde homenaje a la radio en su Día Mundial, recordando a nuestros usuarios y seguidores que pueden visitar y conocer todas las experiencias de Radio Descartes publicadas en nuestro portal o, bien directamente, en el canal de RED Descartes en iVoox.

“El Cazador. A la caza de los secretos de la Alquimia”
Escrito por Jesús Manuel Muñoz CalleUna cuestión fundamental a la hora de utilizar juegos didácticos es la forma de ponerlos en práctica. El diseño, la preparación previa, la contextualización, los recursos, etc, son aspectos fundamentales para su buen funcionamiento. Pero podemos ir un paso más allá, utilizando los juegos aplicando metodologías de gamificación, sumergiendo a los participantes en un entorno, mecánicas y dinámicas que potencian y enriquecen el proceso de una forma significativa. En este artículo vamos a tratar cómo hemos realizado una actividad gamificada utilizando los juegos del Proyecto AJDA y presentaremos un vídeo donde se muestra su resultado, su título es:
“El Cazador. A la caza de los secretos de la Alquimia”
- Primera fase. Cada jugador, recibirá durante un minuto preguntas por parte del presentador, y por cada acierto conseguirá 1.000 puntos.
- Segunda fase. Con los puntos conseguidos el participante se enfrentará en un duelo de preguntas individual al “cazador o cazadora” (oponente experto/a). El cazador hará una oferta de puntos por encima y otra por debajo de los conseguidos por el concursante, que según la propuesta elegida estará a cuatro, cinco o seis casillas de llegar a “casa”. A continuación empieza “La caza”, concursante y cazador recibirán preguntas que deberán responder de forma simultánea e independiente. Por cada acierto avanzarán una casilla. El objetivo del jugador es llegar a “casa” y el del cazador atraparlo antes. Cada uno de los cuatro jugadores realizará de forma individual las dos primeras fases, los participantes que sean “cazados” en la segunda fase serán eliminados y los que lleguen “a casa” sumarán al bote común del equipo los puntos ganados en la segunda fase y se enfrentarán al cazador en la “caza final”.
- Tercera fase (“caza final”). Durante dos minutos los jugadores no eliminados recibirán preguntas por parte del presentador. Cada una deberá ser respondida por un solo jugador, el que primero dé al pulsador (si responde otro la respuesta se considerará fallada). Cada acierto dará al equipo de jugadores una casilla de ventaja. Además el equipo partirá con una ventaja inicial de tantas casillas como jugadores haya clasificados. Después llega el turno del “cazador”, que durante dos minutos recibirá preguntas. Si el cazador falla una pregunta habrá rebote para el equipo de jugadores, que de forma conjunta podrá responder, y si acierta hará retroceder una casilla al “cazador”. El equipo de jugadores gana si el cazador no logra igualar las casillas de ventaja que los jugadores han conseguido y el premio se reparte a partes iguales entre los participantes no eliminados.
Una característica del concurso es que cada día el programa adquiere como hilo conductor una temática de forma que concursantes, cazador y presentador adquieren los papeles de la misma a lo largo del programa, y en nuestro caso es la Alquimia.
La puesta en práctica se llevó a cabo en el laboratorio de Física y Química, utilizando tres juegos didácticos del Proyecto AJDA, cada uno de los cuales se corresponde con una de las etapas del concurso, para los que se elaboraron en torno a 300 preguntas de Física y Química de Bachillerato,contando con los siguientes participantes:
- Alquimistas aprendices (Concursantes): Paracelso Morandine, Willian Bacon, Blas Trimigesto y Javier Avicena (alumnos de la asignatura de Física de 2º Bachillerato).
- Gran Maestra alquimista (Cazadora): Vanessa León (Profesora de Química).
- Amo del Calabozo (Narrador y presentador): Jesús Muñoz (Profesor de Física).
- Sauron (Cámara y testigo omnisciente): Marcos Rodríguez (Profesor de Biología).
- Pueblo medieval: Alumnos de Biología.
Los alquimistas aprendices obtendrán por cada 1.000 puntos conseguidos una insignia de la asignatura de Física de cualquiera de las tres evaluaciones. El resultado de la experiencia se muestra en la siguiente composición:
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)












 CONTACTO
CONTACTO
