Título de la obra:
Modelo ontogénico matemático del Nautilus
Autor:
JOSÉ R. GALO SÁNCHEZ
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-10368-02-6
Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-SinDerivadas 4.0 Internacional.
A Pablo y a Ana
Hace unos años, allá por 2016 (Galo et al., 2016)
en un rectángulo áureo que le venía excesivamente holgado o bien tan exageradamente pequeño que fracturaría sus frágiles paredes. Y ante tamaña discrepancia se han rebuscado otras proporciones en la que apareciera el número áureo $\phi = \frac{1+\sqrt{5}}{2}=1,618033...$, como puede ser $\sqrt{\phi}$, pero el Nautilus, sintiéndose incómodo al quedar suelto o constriñido, no pudiendo más nos confesó:
¡No!, ¡no soy áureo!
¡Soy cordobés!
.jpg)
|
.jpg)
|
|
Rectángulo áureo (tangente sólo en tres puntos). |
Rectángulo áureo (tangente sólo en tres puntos). |
.jpg)
|
.jpg)
|
|
Rectángulo $\sqrt{\phi}$ (tangente sólo en tres puntos). |
Rectángulo $\sqrt{\phi}$ (tangente sólo en tres puntos). |
|
|
| Rectángulo cordobés (tangente en cuatro puntos). | |
Ese grito desahogador nos permitió conformar el que denominamos "modelo matemático uniforme del Nautilus" en el que la sección sagital de la concha del Nautilus, desde su génesis hasta su madurez, crece siempre de igual forma. Una forma que Moseley (1838)
$$\varsigma=\frac{1}{\sqrt{2-\sqrt{2}}} = 1,306562... $$
Consecuentemente, en el primer capítulo de este libro se realiza una descripción del modelo uniforme y se detallan las ecuaciones que lo formalizan, mostrando en sintesis las características de este modelo:
..
Modelo matemático uniforme del Nautilus
No obstante, también en este primer capítulo, se echa una mirada al primer verticilo de la concha y se comprueba que lo que ahí nos refleja el modelo uniforme difiere bastante de lo que, biológicamente, se puede observar. No hay que caer en el pesimismo, pero salvo la espiral cordobesa que modela la pared ventral, que en esta etapa inicial sí se ajusta a la realidad, el resto de elementos (pared dorsal, sifúnculo, septos y número de estos) se muestran retadores y reacios a seguir esa uniformidad con la que, a espera de nuevas inspiraciones, nos habíamos conformado al no saber dar respuesta a las singularidades que ahí acontecen. Pero ¿acaso lo que sucede es algo que nos deba sorprender? La concha del Nautilus es el reflejo de la bitácora vital de este ser vivo y, en general, los seres vivos dentro de la homogeneidad de formas que mantienen durante su ciclo vital presentan ciertas particularidades en las etapas embrionaria, juvenil y adulta, por tanto, lo que será necesario e imprescindible es analizar, distinguir y describir su ontogenia y, para ello, la primera tarea que se aborda es la observación y aprendizaje sobre la ontogenia biológica para que podamos vislumbrar la esencia que encierra y así, quizás, poder llegar a la ontogenia matemática que la modele.
En el segundo capítulo es donde con ayuda de una escena interactiva abordamos esa tarea de análisis de la concha en el primer verticilo, detectando lo que hay que modelar —labio o pared dorsal, ombligo, ajuste del sifúnculo, distribución y amplitud de los septos y espiral de los polos de estos—, y cómo hacerlo. Para ello consideramos tres invariantes que se han de cumplir en todos los verticilos (constituyen la esencia del modelo global):
y modelando esos elementos específicos del primer verticilo, obtenemos que:
Pero, la singularidad más destacable en este verticilo inicial es la relativa a los septos y a las cámaras septales, que presentan un comportamiento bastante diferenciado respecto a lo que acontece en los siguientes verticilos, pues:
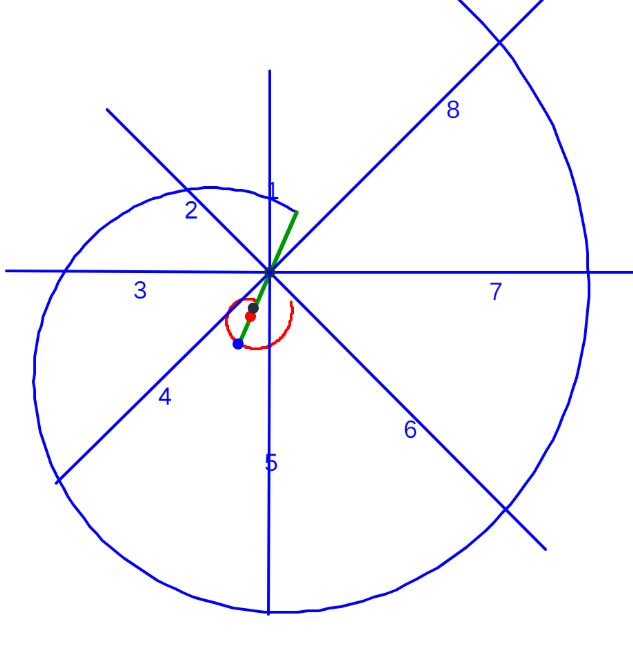
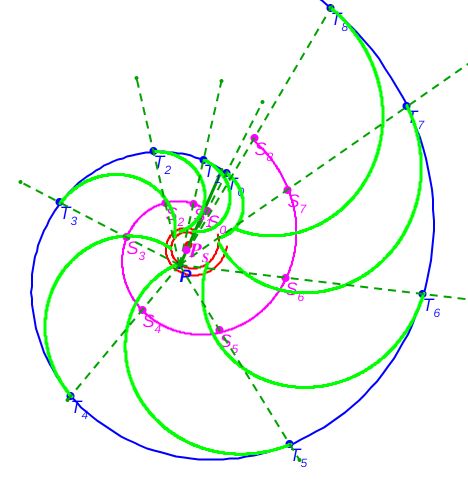
La idea que explica lo anterior es simple, como siempre, una vez que ha sido alumbrada. Y esa luz surgió inicialmente considerando dos circunferencias interiores no concéntricas y trasladando la situación, de manera similar, pero con dos espirales no copolares.
|
|
|
Esta dualidad ontogénica —compuesta por el fragmocono Segun Barroso-Barcenilla (2008)
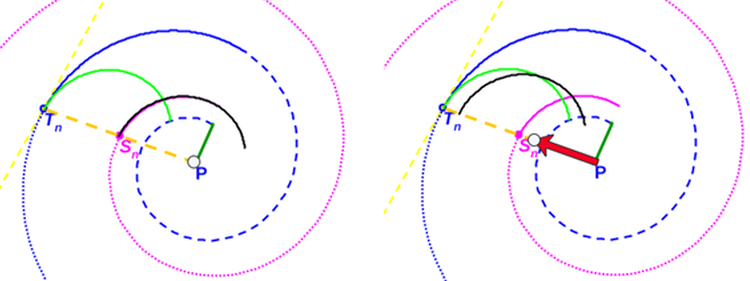
De nuevo, el Nautilus, mostrándose condescendiente nos desveló el secreto de sus septos, pues la tangencialidad se traduce en la necesidad de que para cada arco septal su polo $\color{magenta} S_n$ ha de estar alineado con el punto de tangencia $\color{blue} T_n$ y con el polo de la pared ventral $\color{blue} P$. Ello, conlleva un comportamiento diferenciado en cada una de las dos situaciones ya que, como podrá comprobar en ese
tercer capítulo, cada arco septal está escalado por el factor: $$a_n = \frac{\, \, \overline{\color{magenta} S_n \color{blue} T_n} \, \,}{\overline{\color{blue} P_v T_n}}$$
de manera que:
Por tanto, en este primer caso, todos los septos de estos verticilos tienen la misma amplitud angular, son arcos de la misma espiral (la de los polos de los septos), y no son más que una traslación de sendos arcos de ésta.
Por consiguiente, en este segundo caso, cada septo es un arco cordobés con diferente escala y amplitud angular, reflejando la realidad previamente observada en este primer verticilo.
Así pues, la no copolaridad de la espiral ventral y la espiral de los polos de los septos da explicación a esta variación ontogénica en el tamaño de los septos, manteniendo la forma cordobesa, y es la que provoca la variabilidad indicada en la volumetría de las cámaras septales que, como señalamos, es imprescindible para alcanzar rápidamente la flotabilidad neutra inicial. Y esta benevolente concesión nautiliana, al desnudarnos la esencia de sus septos, es la que también aporta de manera directa el conocimiento funcional matemático de los mismos, permitiéndonos el cálculo de datos cuantitativos descriptivos adicionales como, por ejemplo, que el apoyo de los septos con la pared dorsal no se produce de manera perpendicular y esto es la posible causa físico-biológica que explica la necesidad de construir las denominadas depresiones septales dorsales como refuerzo de ese apoyo no ortogonal.
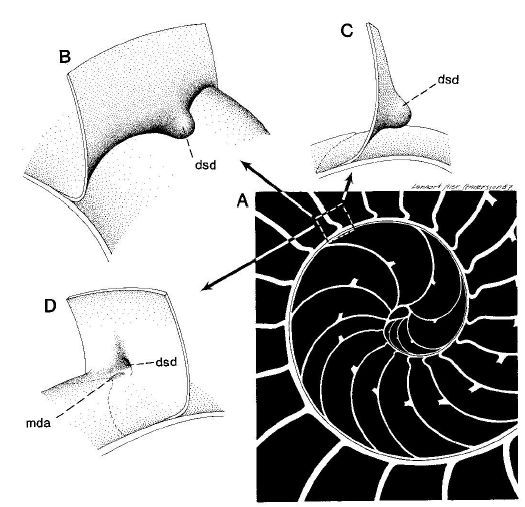
Una muestra más de cómo el análisis funcional y las abstractas ecuaciones que dan forma y gobiernan a los modelos de ese mundo virtual que es el matemático pueden aportar explicaciones en nuestra "realidad" existencial.
Pero el primer verticilo nos depara sorpresas adicionales, pues en él encontramos algunos sitios adicionales con un comportamiento singular y que requieren su análisis y encuadre matemático. Estos sitios singulares, que se analizan y modelan en el capítulo cuarto, son:
Este estudio completa el modelo matemático de ese primer verticilo:
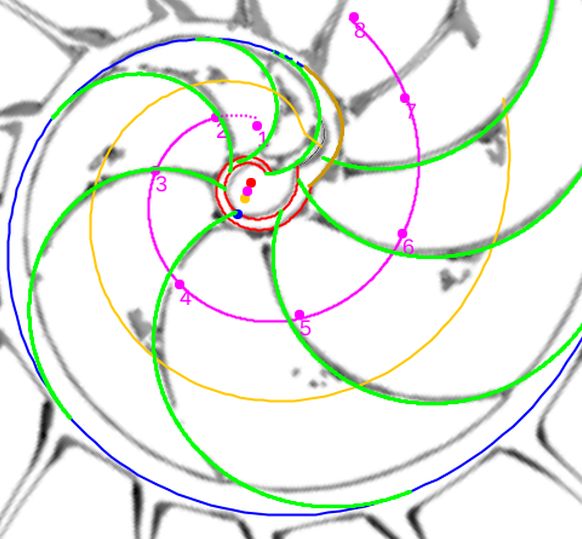
Llegado este momento y despúes de haber dedicado bastante tiempo a desentrañar los retos que el Nautilus nos ha ido marcando, y muy satisfecho de lo logrado, el capítulo quinto se centra en realizar una síntesis descriptiva de lo analizado y en abordar el montaje del "Modelo ontogénico matemático del Nautilus" reflejando el crecimiento del mismo en una presentación secuencial de lo que acontece, pero asíncrona, no temporalizada, ya que no he contado con los datos necesarios para que este modelo pudiera ser síncrono.
La conclusión o resumen final nos lleva a reafirmar el canon cordobés que se manifiesta en todos los niveles y etapas vitales del Nautilus y que las diferencias observadas en la ontogenia del mismo tienen su fundamento y causa al iniciar su crecimiento siguiendo patrones de espirales cordobesas con diferente polo y a partir del segundo verticilo confluir a un polo común.
Ahora, como lector y posible actor interactuante, ¡es su momento! Espero que quede satisfecho, pero no saciado ya que, aunque hemos trabajado sólo con la sección sagital de la concha, no podemos olvidar la naturaleza tridimensional de ésta y tendremos que dar una nueva oportunidad al Nautilus para que continúe susurrándonos sobre el rastro de su ser y de su crecimiento (Galo, 2024 b)
Córdoba (España), julio de 2024.
El Nautilus (), usualmente catalogado como un fósil viviente ―si bien Ward (1984)
Esta concha, al igual que el animal que la construye, ha sido ampliamente estudiada desde el punto de vista paleontológico, zoológico, biológico u ontogénico, pero también han puesto el foco en ella en el mundo artístico, el arquitectónico, el ingenieril, el físico-químico y, por supuesto, en el matemático —donde ha llegado a ser idealizada—, sin olvidar el contexto literario donde también se ha adentrado en lugares preminentes. Aupada como prototipo de belleza ha sido continuamente encajonada de manera forzada en el canon de belleza o proporcionalidad divina o áurea, a pesar de su resistencia y continuo grito de: ¡No!, ¡no soy áureo!
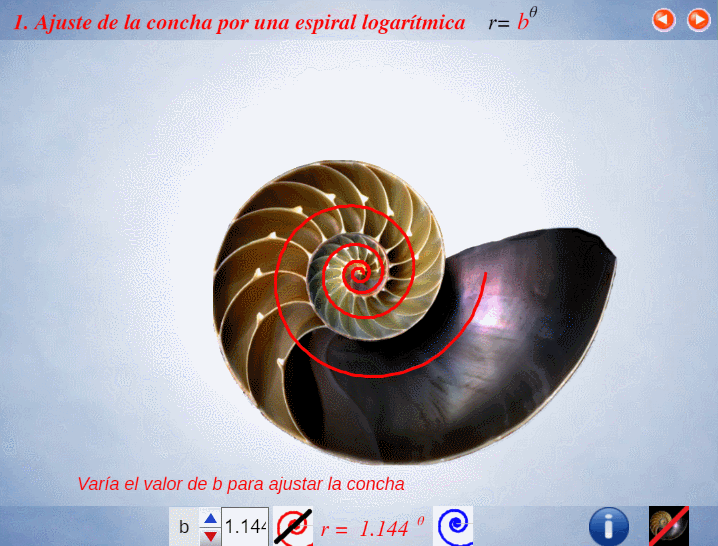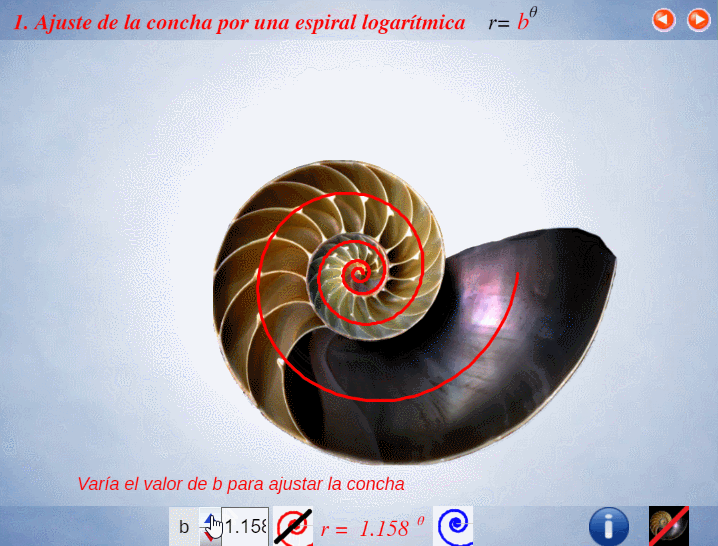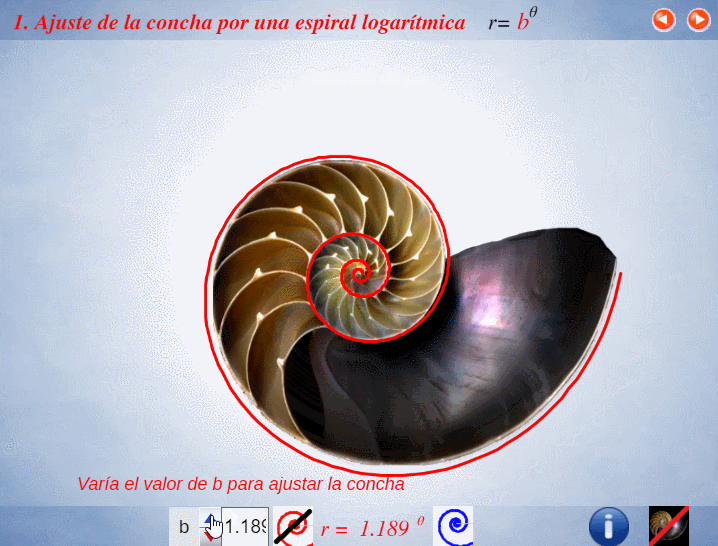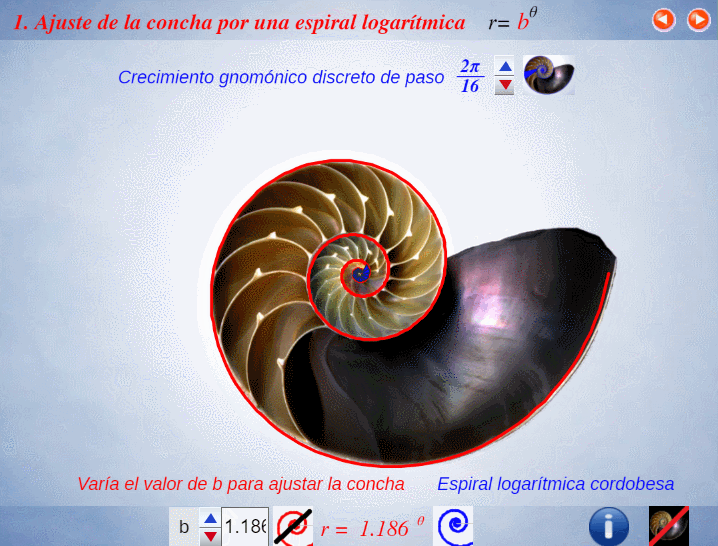
En el artículo "Sobre la forma y el crecimiento cordobés del Nautilus pompilius" (Galo, Cabezudo y Fernández, 2016)
Este hallazgo coyuntural que no deja de ser una mera coincidencia numérica, aunque para nosotros muy agradable, con la razón denominada cordobesa y que consecuentemente nos permite asociar su nombre al de Nautilus, hubiera quedado como una curiosidad anecdótica si no fuera porque ahí señalamos y detallamos que todo en el Nautilus se muestra cordobés ―sí, nosotros estuvimos silenciosos y atentos y le oímos decir:
“He vivido en un mundo áureo que me era ajeno, pero me habéis escuchado y ahora sí puedo cantar..."
|
|
|
|
¡Sí, soy cordobéEn Córdoba (España) la pronunciación de las eses a final de palabra suele ser muy débil y para los oídos no habituados a esa tonalidad, éstas quedan como omitidas.! porque además de que el perfil de mi concha sea una espiral logatítmica cordobesa:
Así pues, en el artículo citado (Galo et al., 2016)
Del libro "¡No!, ¡no soy áureo! ¡Soy cordobés! Firmado: Nautilus" (Galo, 2024)
En el instante de crecimiento de la concha correspondiente a un ángulo $\lambda $, el fragmocono es la región del plano: $$r=a \kappa^\theta \quad \text{con} \quad \begin{cases} \kappa^{-2 \pi} \le a \le 1 \\ \theta_0 \le \theta \le \lambda \end{cases} \tag{$1.1$}$$ donde $\kappa=1,185580...$ es la base de la espiralPor simplificación, el polo común de todas esas espirales se ha posicionado en el origen de coordenadas $O(0,0)$. $r=a \kappa^\theta$ que es cordobesa para cada valor de $a$, pues $\kappa=\varsigma^{\frac{2}{\pi}}$ y $\varsigma=\frac{1}{\sqrt{2-\sqrt{2}}}$ es el número cordobés.
El número de verticilos, hasta ese instante $\lambda$, viene dado por $\frac{\lambda-\theta_0}{2 \pi}$.
Así pues, todo puntoEn lo sucesivo, mediante el uso del subíndice $_F$ indicamos que ese valor depende del punto $\color{green} F$ que se considere. $\color{green}F (r_F, \theta_F) $ del fragmocono, el cual verifica que $\color{green} \theta_0 \le \theta_F \le \lambda$ y $\color{green} \kappa^{\theta_0-2 \pi} \le r_F \le \kappa^{\lambda}$, pertenece a una espiral cordobesa
$$\color{green} r_F=a_F \kappa^{\theta_F} \tag{$1.2$}$$ que denominaremos “longitudinal” (ver la espiral en color verde oscuro en la y pulsad los pulsadores inferiores "movimiento lateral" y "movimiento transversal" para desplazar el punto $\color{green} F$ en el fragmocono).
A su vez, ese punto $\color{green}F$ también pertenece a un arco de una espiral logarítmica cordobesa “transversal”Estos arcos bien son septos o bien son arcos interseptos semejantes. (ver la espiral en color rojo oscuro en la ). Su ecuación paramétricaDe la ecuación se deduce que todos estos arcos no son más que traslaciones de vector $\overrightarrow{OP_F}$ de arcos de la espiral logarítmica cordobesa de ecuación $r=d \, \kappa^\theta$.
es :
$$\color{IndianRed} \begin{cases} x_F
=P_{x_F}+d \, \kappa^{\varphi_F} cos({\varphi_F}) \\ y_F=P_{y_F}+d \, \kappa^{\varphi_F} sen({\varphi_F}) \end{cases} \quad {\varphi_F} \in [\alpha_F, \beta_F] \tag{$1.3$}$$
donde $d \simeq 0,5$ es independiente de $\color{green} F$ y $\color{IndianRed} P_F (P_{x_F}, P_{y_F})$ es su polo. La amplitud de este arco viene dada por el intervalo determinado por los ángulos $\color{IndianRed} \alpha_F$ y $\color{IndianRed} \beta_F$, ambos dependientes de $\color{green} F$, pero como consecuencia del crecimiento gnomónico se verifica que ésta es angularmente constante en todos esos arcos y en el modelo se tasaEn este libro veremos que este valor es mayor y justificaremos el porqué de ese cambio. que $\color{IndianRed} \beta_F - \alpha_F =\dfrac{5 \pi}{8}$, valor que coincide con el ángulo mayor del gnomon del triángulo cordobés.
También acontece que todos esos polos $\color{IndianRed} P_F$ de las espirales transversales son puntos de la espiral longitudinal, que denominamos espiral de los polos de los septos, cuya ecuación es:
$$\color{magenta} r=d \kappa^\theta \tag{$1.4$}$$
es decir,
$$\color{magenta} \begin{cases} P_{x_F}=d \, \kappa^{\theta_P} \, cos({\theta_P}) \\ P_{y_F}=d \, \kappa^{\theta_P} \, sen({\theta_P}) \end{cases} \tag{$1.5$}$$
Si $\color{magenta} P_F$ y $\color{magenta} P_{F'}$ son dos puntos de esa espiral de los polos que se diferencian un ángulo $\color{magenta} \Delta \theta_P$ entonces los arcos transversales asociados verifican que $$\color{IndianRed} \alpha_{F'} = \alpha_{F} + \color{magenta} \Delta \theta_P \tag{$1.6$}$$ y, por tanto, una traslación "longitudinal" en el fragmocono genera un traslación "transversal" en el arco septal asociadoEsto formaliza la traslación que se observa en la animación de la ..
Adicionalmente, tenemos que si $\color{magenta} \theta_P$ es el ángulo asociado a $\color{magenta} P_F$, entonces $\color{IndianRed} \alpha_{F}$ en (3) cumple queEl desfase angular $\frac{51 \pi}{64}$ está próximo a $\frac{3 \pi}{4}$ y haremos una revisión en el modelo ontogénico objeto de este libro: $$\color{IndianRed} \alpha_{F} = \color{magenta} \theta_P \color{black} - \frac{51 \pi}{64}. \tag{$1.7$}$$
El fragmocono está delimitado por:
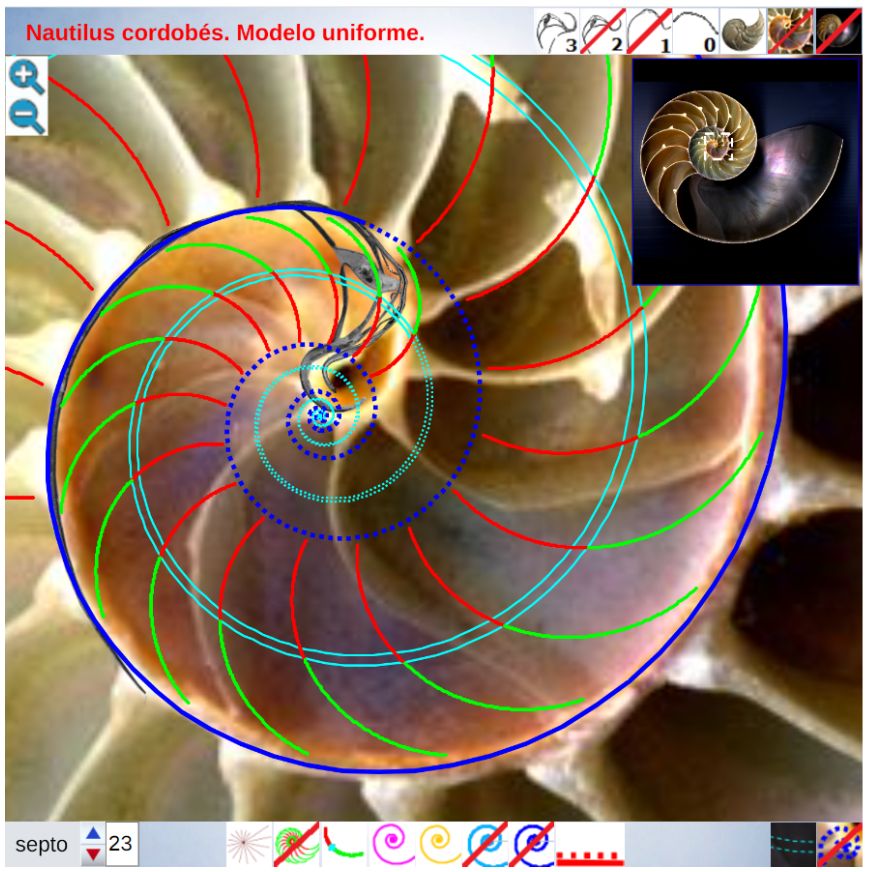
Y el sifúnculo es el eje del fragmocono (ver la espiral en color turquesa en la ):
$$\color{turquoise} r= \frac{1+\kappa^{-2 \pi}}{2}\kappa^{\theta} \quad 0 \lt \theta \le \lambda - \frac{3 \pi}{4} \tag{1.10}$$
El modelo matemático uniforme del Nautilus nos ha permitido aprender bastante sobre la idiosincrasia de la concha de este animal y el porqué de algunos aspectos de su forma, su causa y el efecto producido. No obstante, esto, no es más que un útil deseo purista matemático que se mostrará débil para cualquier detenido observador que aborde su confrontación con la realidad, pues somos conscientes por experiencia vital personal que en el desarrollo de un ser vivo acontecen diferentes fases o etapas que introducen matices distintivos dentro de una esencia identificadora que permanece. Por ejemplo, Ladman, Arnold y Mutvei (1989)
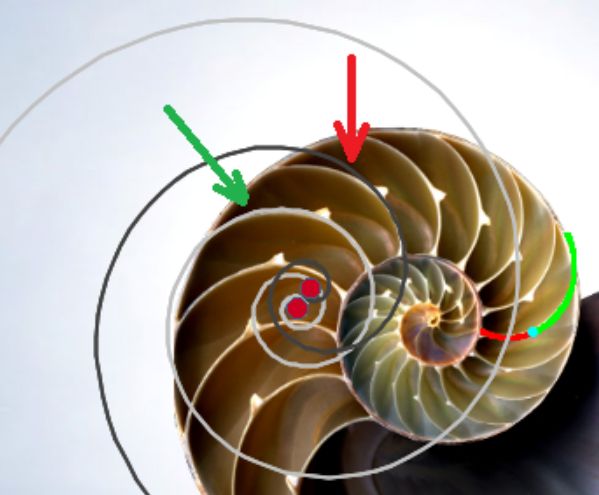
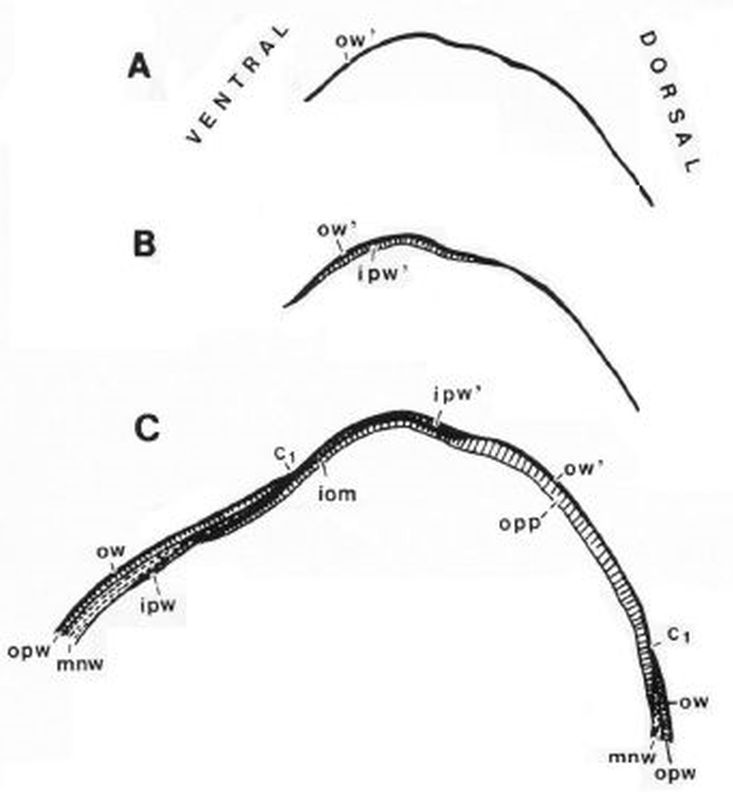
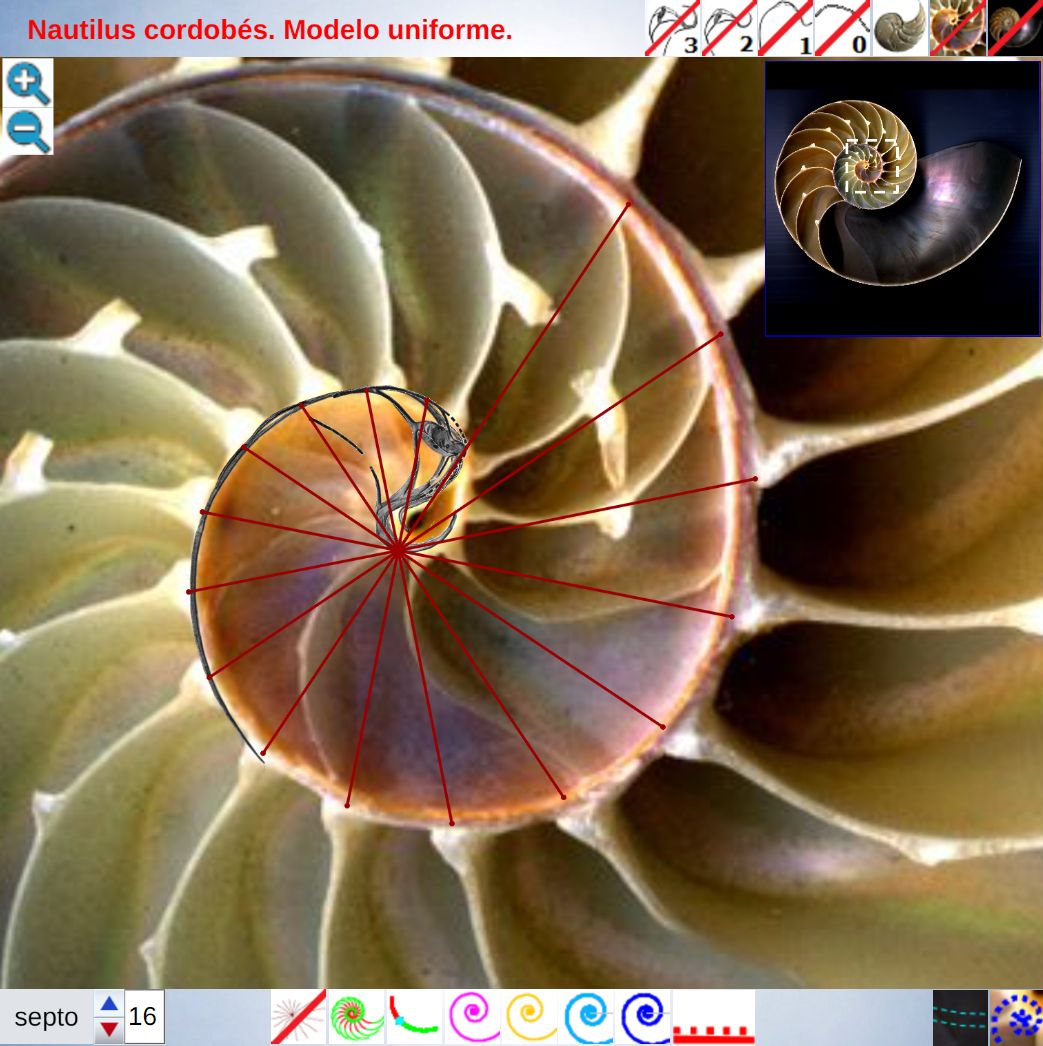
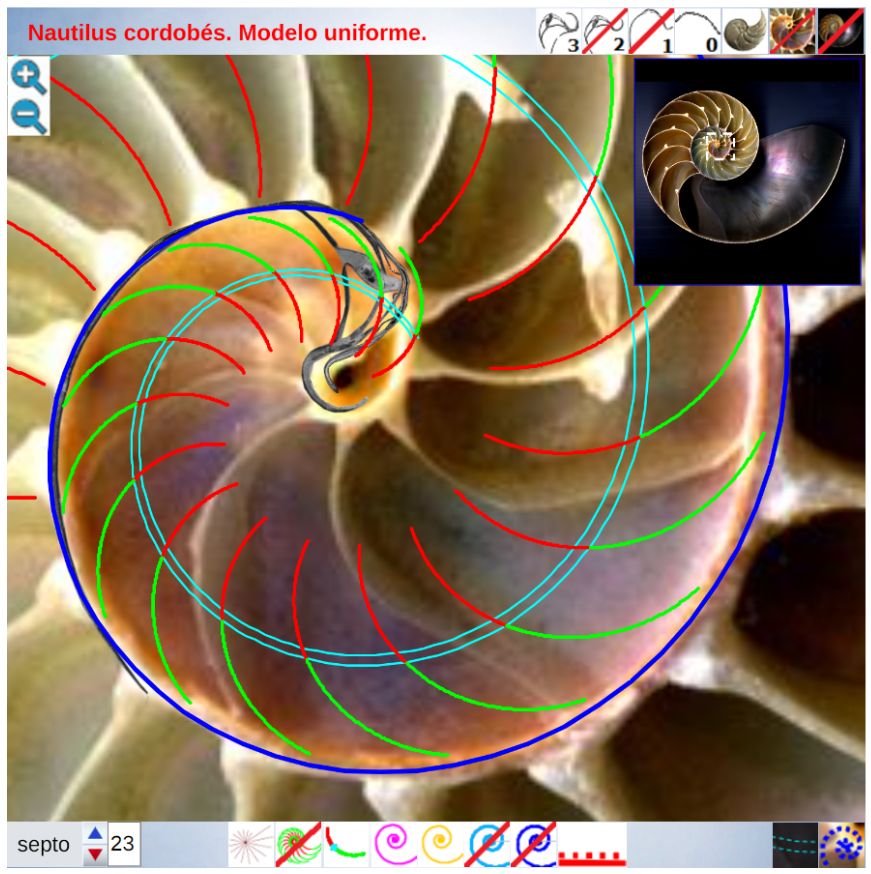
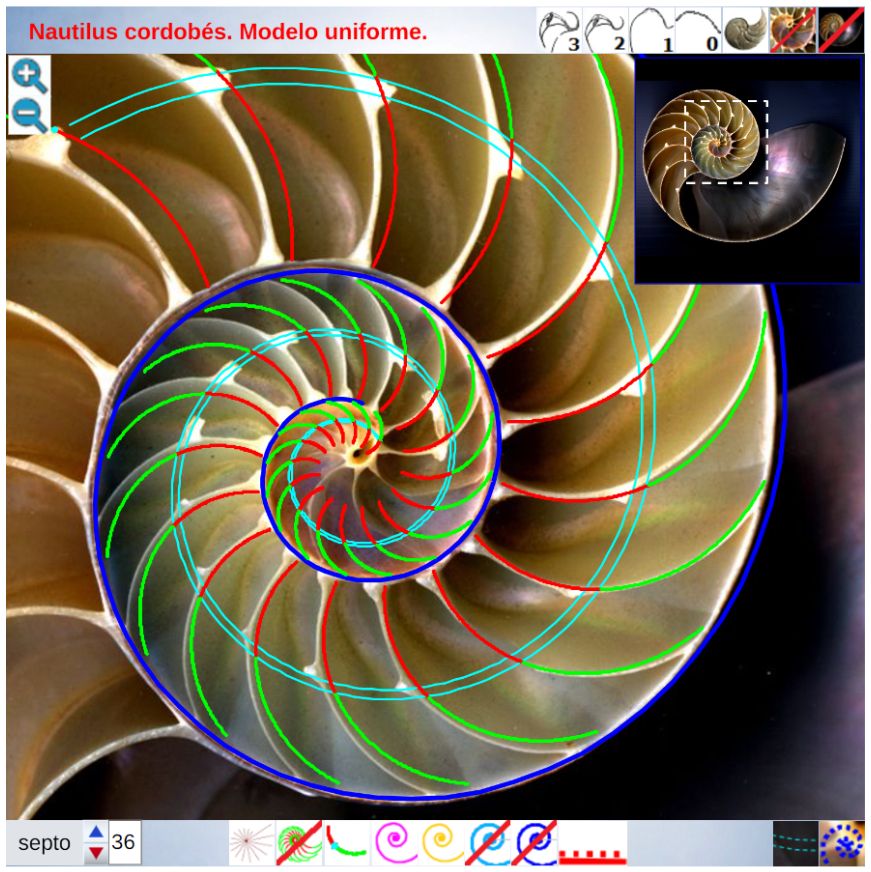
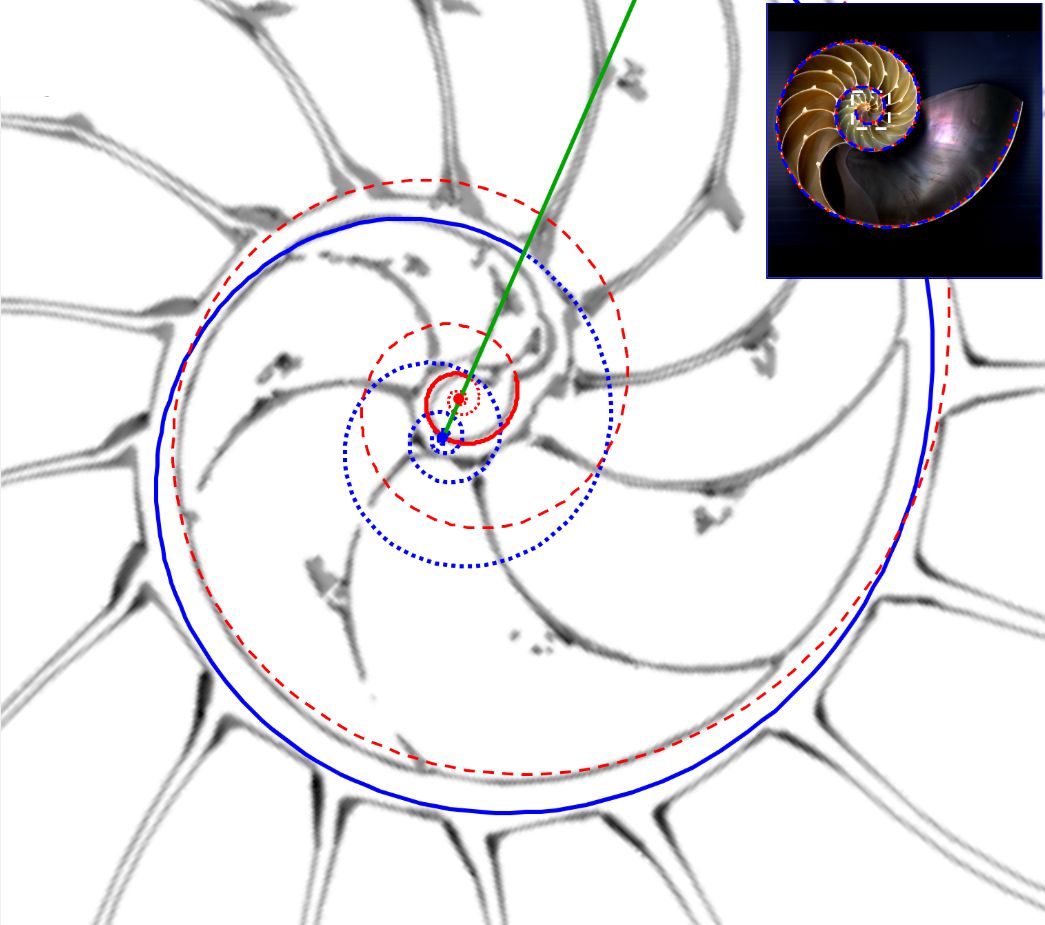
Una ilustración rápida de esos cambios, visible a primera vista, y por ende que muestra la no coincidencia con las presunciones asumidas en el modelo uniforme y que consecuentemente refleja alguna de sus limitaciones, podemos observarla en la donde en un simple recuento de cámaras por cada verticiloUn verticilo es una revolución de 360° en el crecimiento en espiral de la concha de un molusco. detectamos que hay ocho cámaras en la primera vuelta, dieciséis en la segunda y ocho en la tercera (pero con una cadencia de paso análoga al de la segunda), sin embargo en dicho modelo uniforme el valor de dieciséis es constante y, en particular, en la primera vuelta esto no concuerda con la realidad.
Es por ello, que en este libro lo que se persigue es abordar la ontogenia matemática del Nautilus, desde su periodo embrionario hasta la madurez y determinar cuál es el modelo matemático diferenciado en cada una de las etapas de crecimiento en correlación con los estudios biológicos micro y macroscópicos existentes. Y, de hecho, aquí veremos que se pueden diferenciar tres etapas que esencialmente se corresponden con cada uno de los tres verticilos que se contabilizan en la concha de un ejemplar adulto, tres etapas que encierran ciertas diferencias y matices dentro del citado modelo cordobés global. Todo, sin olvidar y teniendo siempre presente, siendo conscientes, que cuando atravesamos el canal que enlaza la discreta quecto-quetta realidadEste término lo construimos tomando como base el hecho de que, desde el año 2022, quecto y quetta son los prefijos del sistema internacional que marcan el rango de valores mínimo y máximo de nuestro mundo discreto, desde 10-30 a 1030. Realmente, en longitud, el orden de magnitud de aquello que es físicamente apreciable o medible en nuestro entorno se ubica actualmente en el rango determinado por el intervalo [10-35 1026] metros, es decir desde la longitud de Planck al tamaño del universo observable. , en la que vivimos, con la idealizada continuidad del mundo matemático siempre surgen interferencias (“aliasing”) que trataremos de mitigar y/o detallar, aunque hay que asumirlas.
La referencia zoológica de la que partiremos es: “Anatomy of living Nautilus: Reevaluation of primitiveness and comparison with Coleoidea” de Sasaki, Shigeno y Tanabe (2010)
También tendremos como referencia los cortes paralelos al plano sagital y los correspondientes a los planos transversales que realizó González-Restrepo (2019)
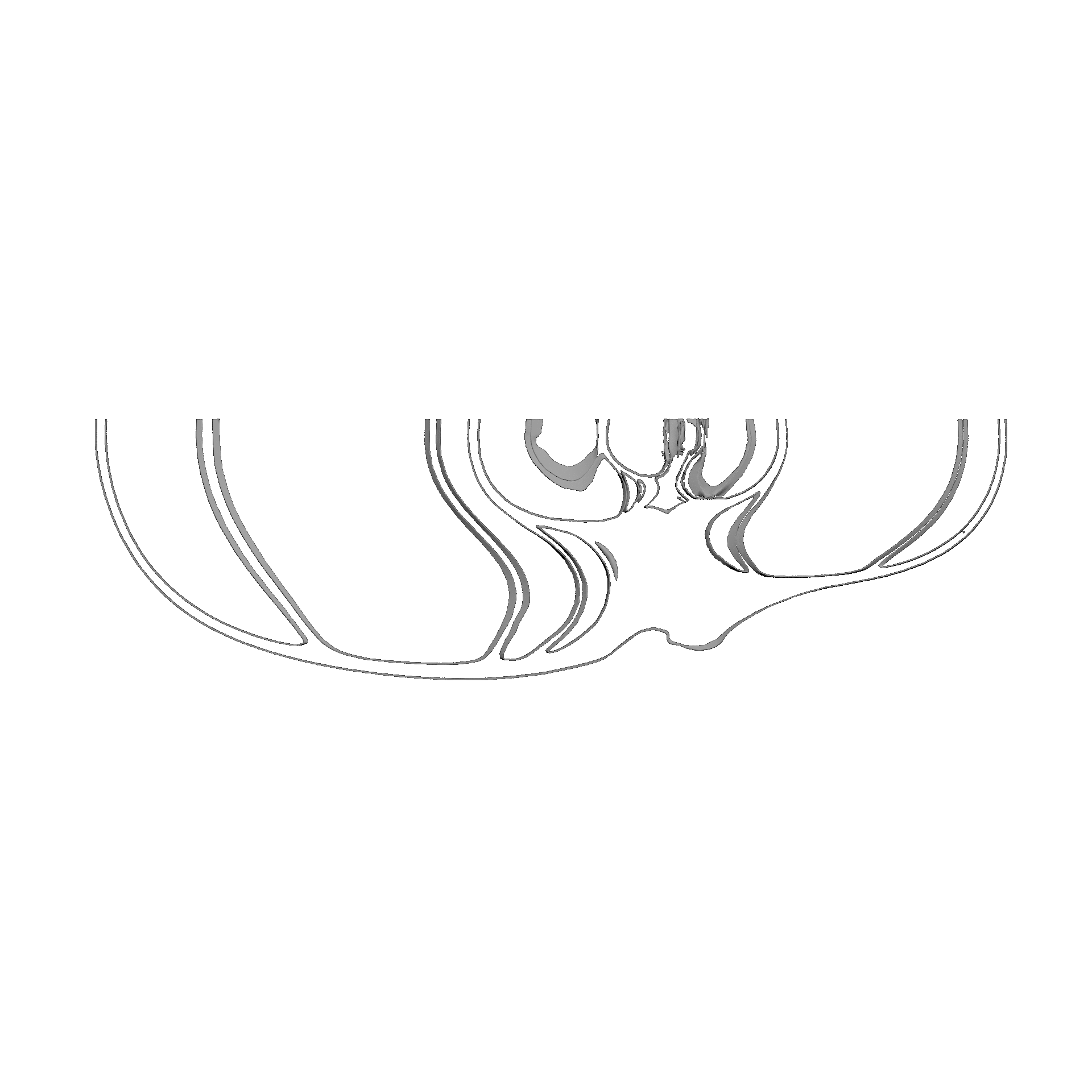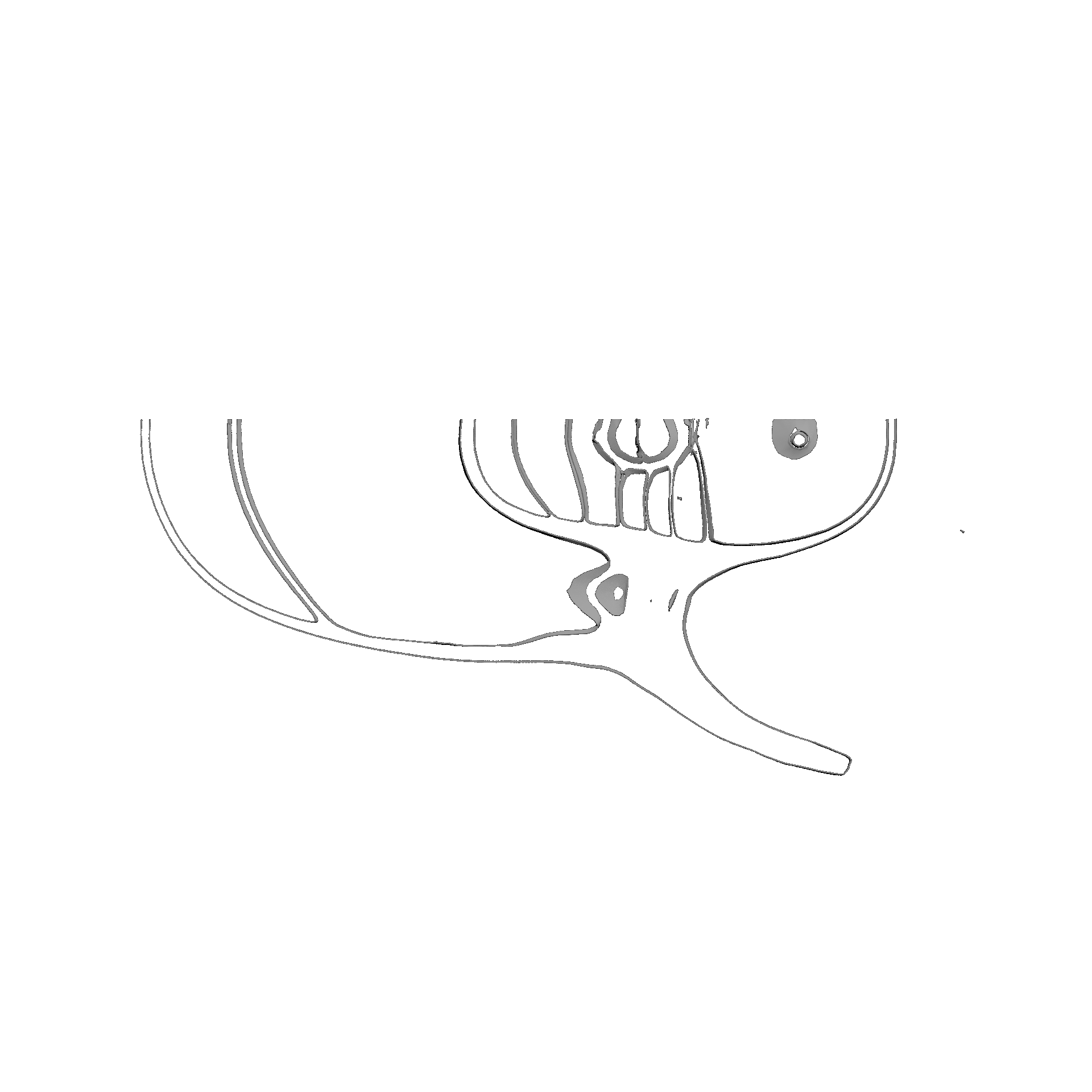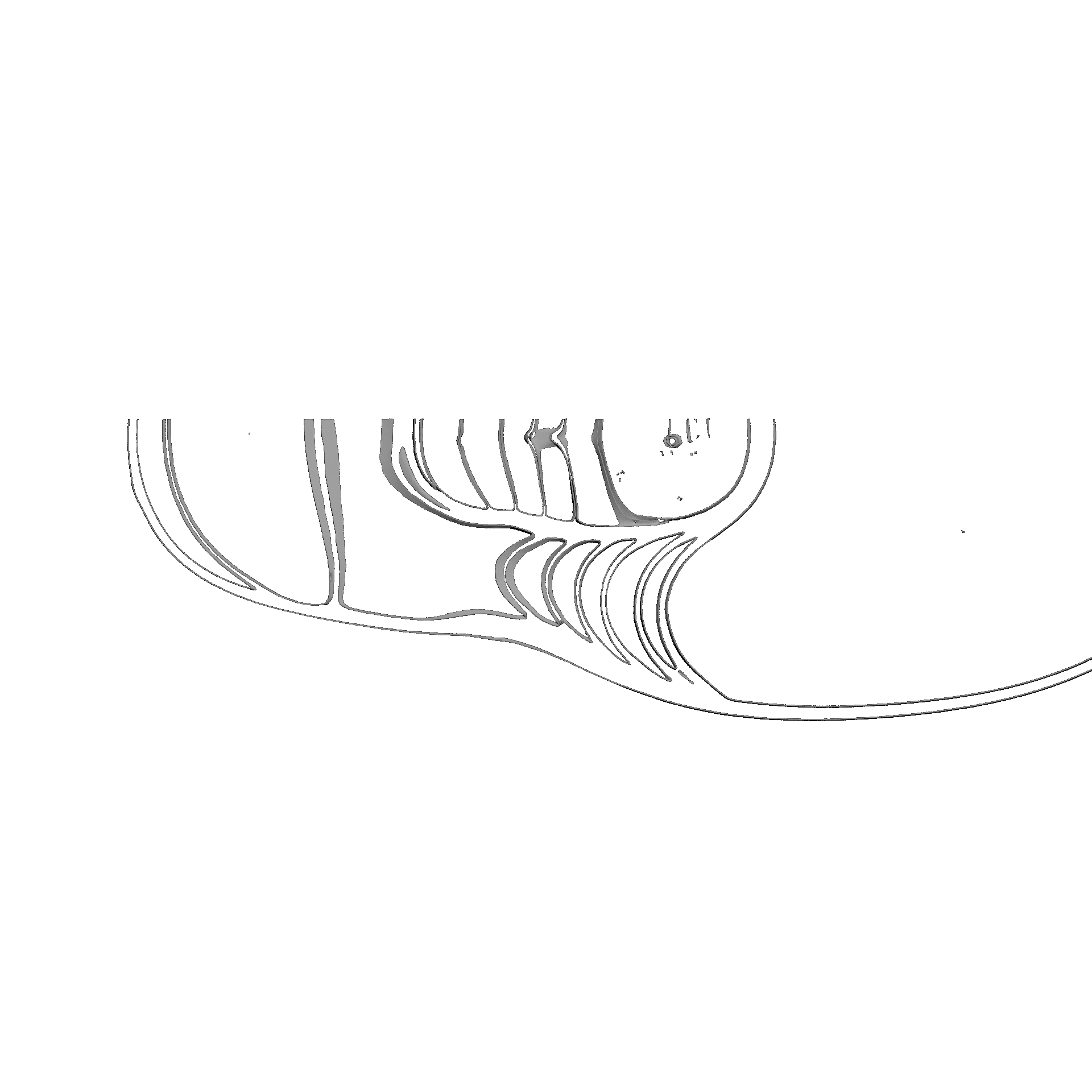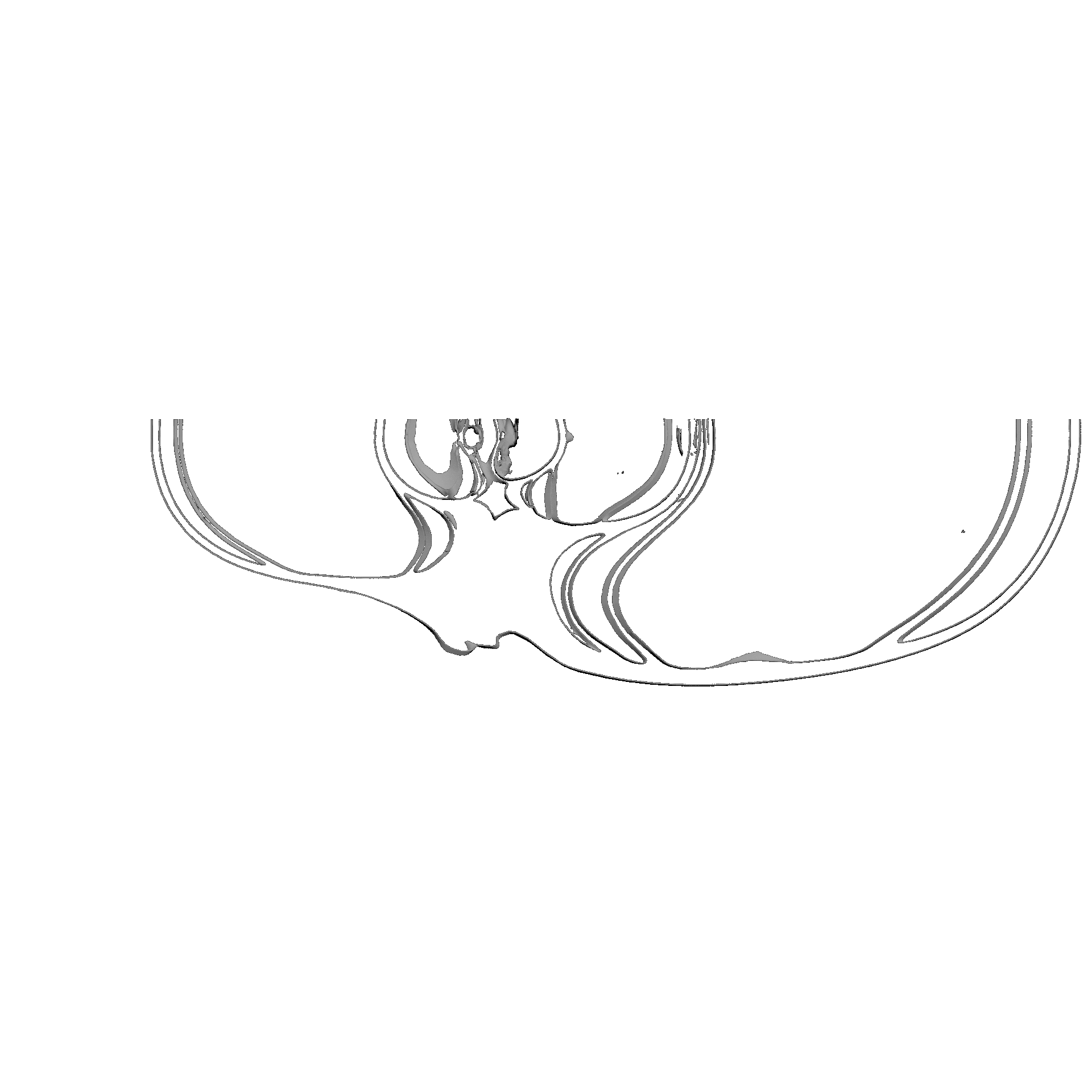
En su primer verticilo, la concha del Nautilus tiene un crecimiento diferenciado del que acontece en el segundo y tercero. Su esencia, implícita y explicitamente, es siempre cordobesa, pero de partida el número de cámaras en ese primer verticilo son ocho y consecuentemente con paso $\frac{\pi}{4}$ entre ellas, frente a las diecisés y paso $\frac{\pi}{8}$ del segundo, paso que también ocurre en el tercero aunque en la última o útilmas cámaras puede presentarse menor. ¿Qué acontece en la ontogenia del Nautilus que sea la causa productora de esa distinción? En este segundo capítulo nos adentraremos en la biología de este animal, o más precisamente en el rastro calcáreo que deja y que conforma su concha, para tratar de dar respuesta matemática a esta pregunta. Procedamos a iniciar y a adentrarnos en la ontogenia del Nautilus y desde ahí trascender a su ontogenia matemática.
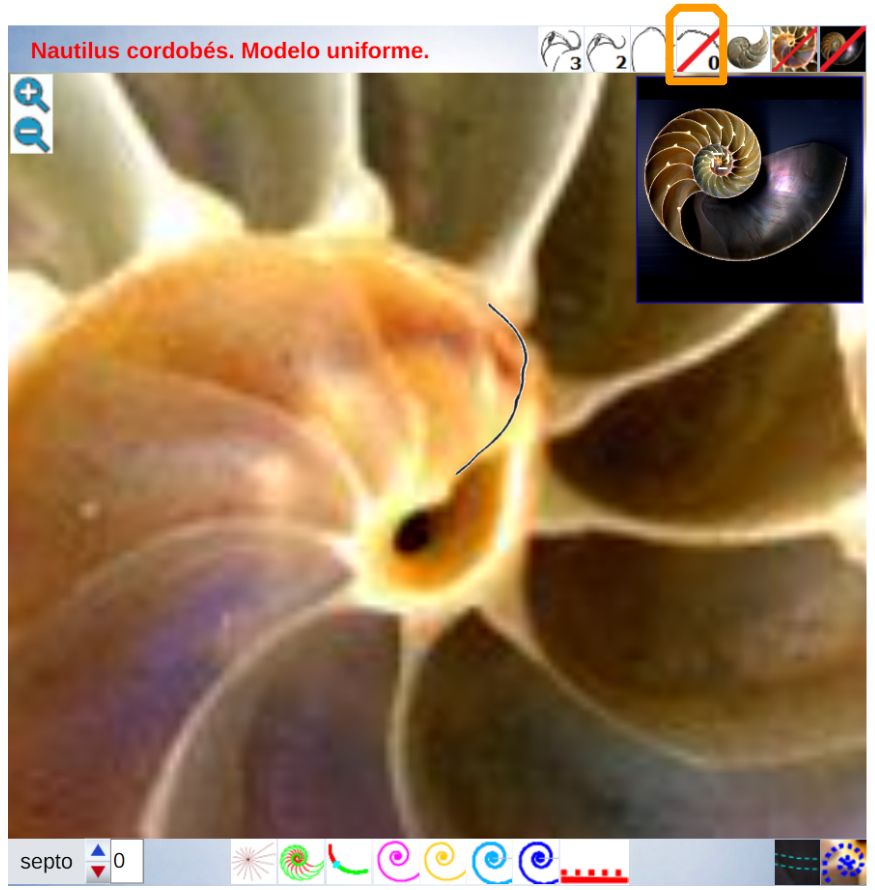
A primera vista la concha embrionaria del Nautilus (), en su periodo pre-cameral, aparenta una forma similar a la concha de una lapa (MolluscaBase eds., 2024
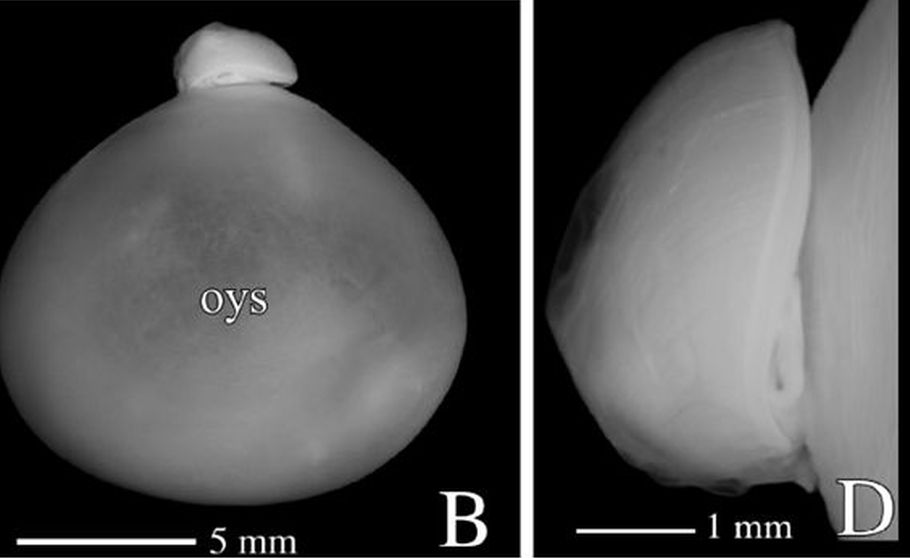
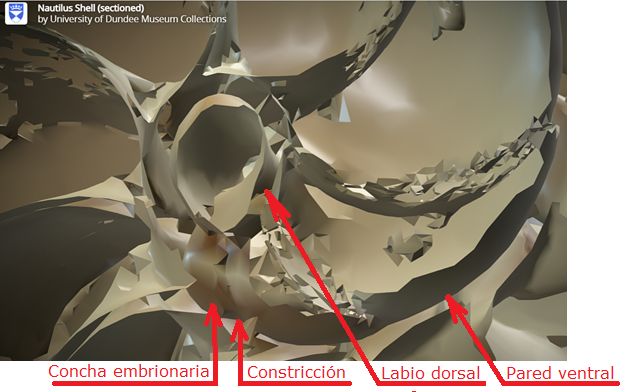
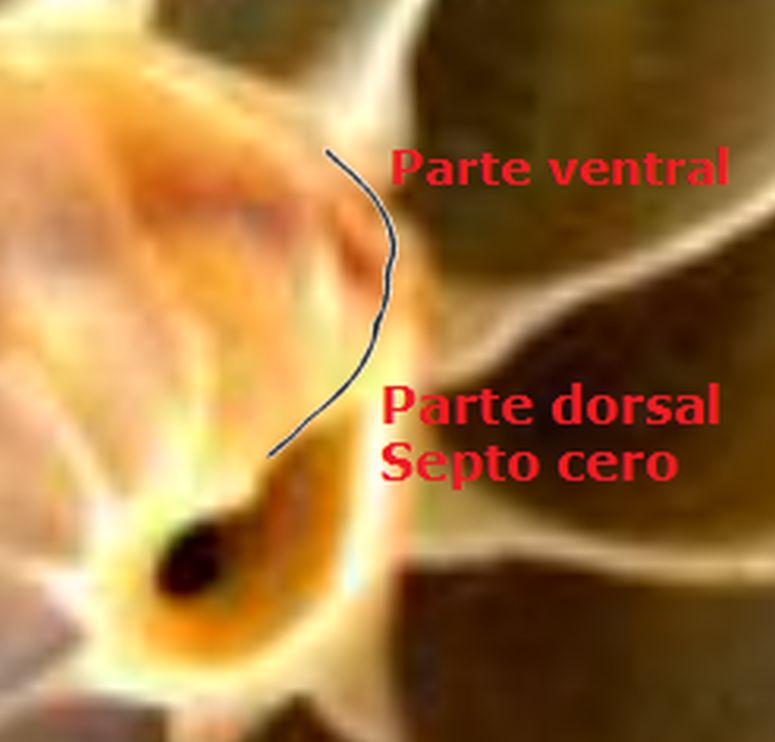
Si no se produjera ese cambio de concavidad en la parte dorsal, irremediablemente la concha se cerraría al intersecar consigo misma. Cuando al crecer, el labio llega a confluir con la parte dorsal inicial de la concha se produce la formación del espacio umbilical u ombligo (), momento en el que se completa el primer verticilo y, consecuentemente, la parte ventral inicial de la concha pasa ahora a ser interior a la misma y comienza a actuar como nueva parte dorsal de la cámara habitacional en el segundo verticilo.
Así pues, el perfil de la concha embrionaria preseptal del Nautilus () puede simplificarse o sintetizarse en dos líneas curvas: la que delimita la parte dorsal y la correspondiente a la ventral. Esta simplificación nos recuerda y hace pensar en la conjunción entre la espiral longitudinal y la transversal observada en el análisis resumen realizado en el capítulo primero. Y esa perspectiva se refleja claramente en la sección de dicha concha embrionaria correspondiente a esa fase preseptal () donde la parte dorsal embrionaria bien podremos catalogarla como el septo cero o inicial (Mutvei & Doguzhaeva, 1997
En la discusión que realizan en su artículo, Landman et al. (1989)
Con la base y los detalles aportados hasta ahora, nos surge el interrogante acerca de: ¿qué acontece con nuestro modelo cordobés uniforme del Nautilus
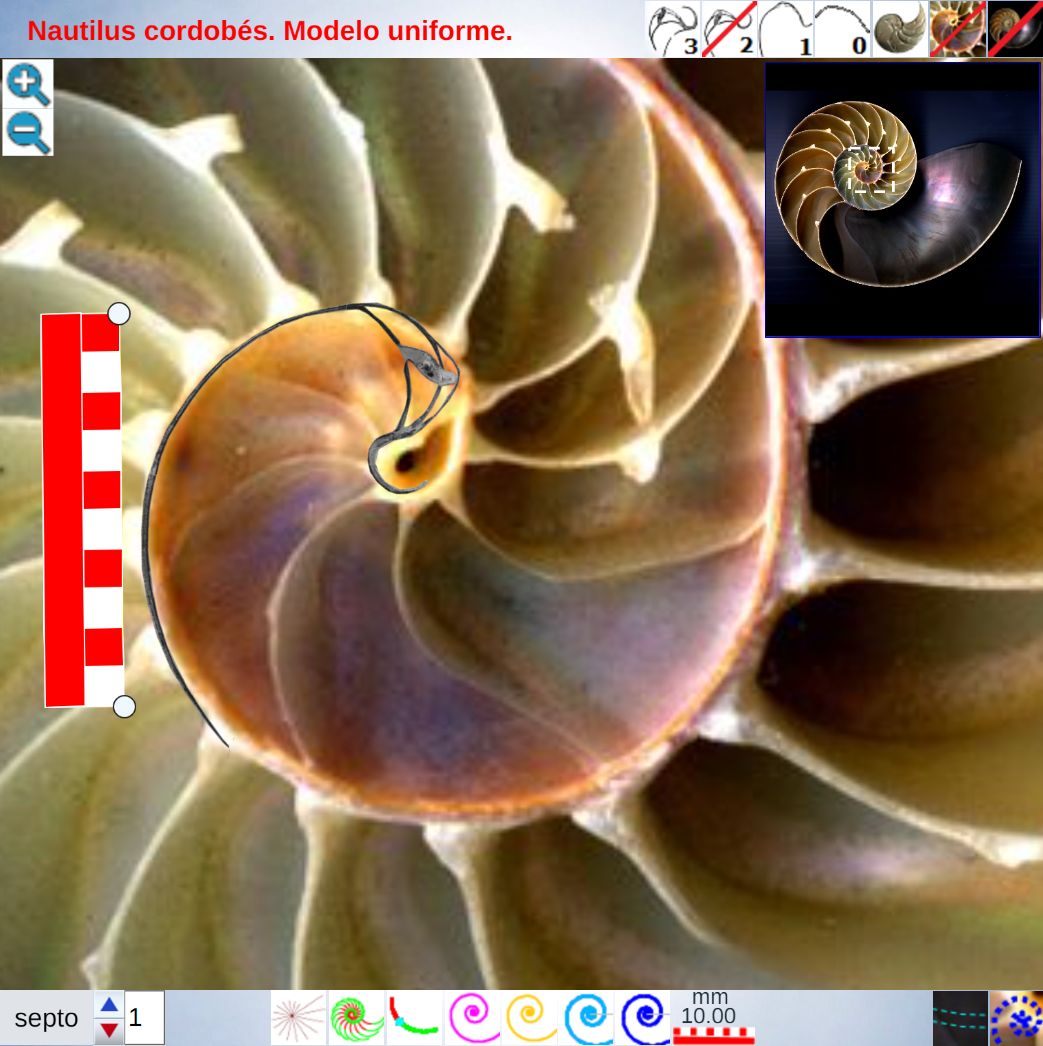
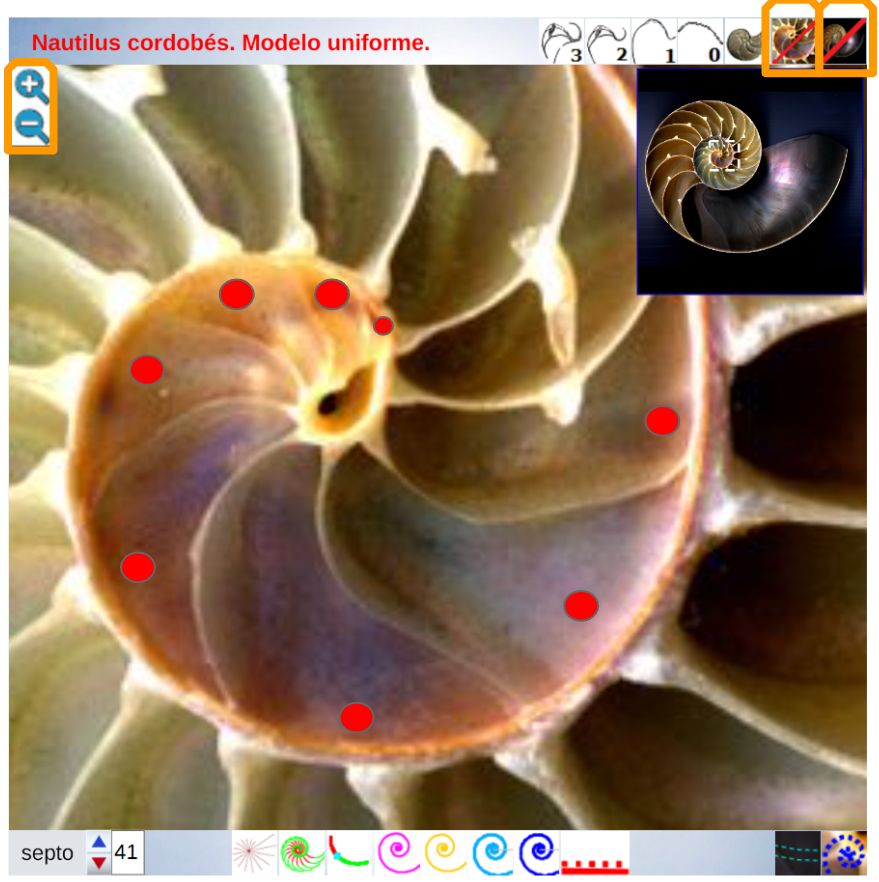
Para poder adentrarnos en este análisis y contraste, podemos aglutinar todo lo indicado en un recurso interactivo (ver la ) que nos permita tener una visión solapada comparativa y que ayude en la conceptualización de lo que acontece, es decir, partir de una agrupación de instantáneas para lograr extraer un continuo descriptivo matemático. Es obvio, de nuevo es necesario indicarlo aunque pueda ser reiterativo, que la superposición de las fotos anteriores mostrará variaciones, algunas debido a que proceden de diferentes ejemplares y especies de Nautilus, otras serán consecuencia de la variabilidad que intrínsecamente acontece en todo espécimen o individuo concreto dentro de las características comunes e identificadoras que comparten y que definen a esa especie; o quizás que estén generadas por posibles desviaciones angulares al realizar los cortes sobre la concha para obtener su sección o perfil. En definitiva, errores comunes e implícitos en cualquier estudio y que aquí, adicionalmente, se ven magnificados gracias a la amplificación visual que nos aporta la técnica.
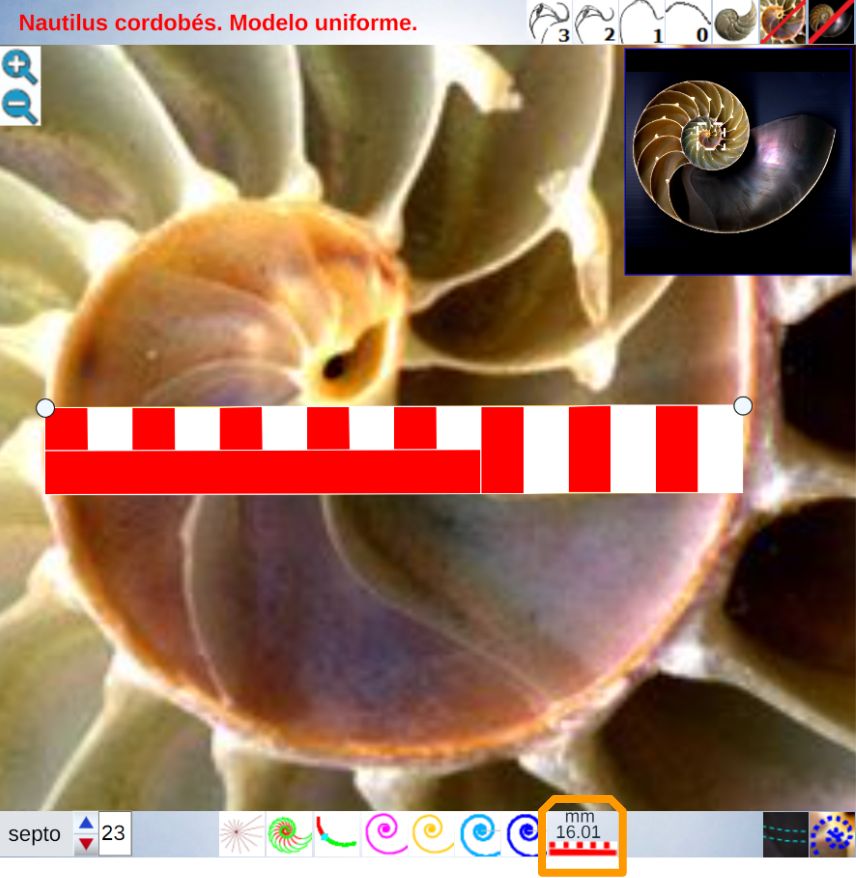
No obstante si alguien tiene un empeño cuantificador especial, en esa escena puede verificar ―con la regla interactiva que se dispone― que nos adentramos en variaciones en el entorno de la décima de milímetro. Estos son detalles con los que se ha de convivir y que han de ponderarse en su justa magnitud para lograr esa visión global y poder encuadrarse en la perspectiva de búsqueda de un modelo o patrón conceptual y, así, lograr encontrarlo.
El lector de este libro puede convertirse en actor al interactuar con la anterior y confrontar en primera persona el modelo uniforme con la biología nautiliana. Para ello, cuenta con los botones que escribiremos a continuación y también si posa el ratón sobre alguno emergerá un breve mensaje descriptivo de su función.
En el objeto interactivo podemos distinguir tres zonas:
En base a la ayuda portada por la herramienta interativa anterior se puede contrastar el modelo uniforme con las imágenes del Nautilus que reflejan la ontogenia del mismo y en la siguiente presentación se refleja la reflexión realizada en base a esa comparativa, la cual puede usarse también como guía a reproducir en la .
Presentación con Google Slides, Versión en pdf y versión en PowerPoint.
En la barra de herramientas inferior puede gestionar manualmente el paso de las diapositivas.
En las once primeras diapositivas se hace una síntesis del modelo uniforme, el cual ya lo hemos descrito en el primer capítulo. De ellas lo más ostensible y/o novedoso que hemos de destacar es:
|
|
|
|
|
En las restantes diapositivas profundizamos en las deficiencias del modelo y anotaremos los aspectos sobre los que es necesario abordar un nuevo estudio para tratar de modelarlos.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
La ontogenia nautiliana en este primer verticilo se muestra retadora y es evidente la necesidad de un nuevo modelo matemático que:
Por ello, adentrémonos en la ontogenia matemática del Nautilus.
La esencia del Nautilus es ostensiblemente cordobesa, pero al analizar su ontogenia biológica hemos detectado un comportamiento diferente en cada uno de los tres verticilos que pueden contabilizarse en la concha de todo animal adulto. Esta diferencia es especialmente manifiesta y significativa en el primero de ellos. Así pues, tendremos que ponernos nuestras gafas matemáticas para tratar de localizar la causa y así, poder mejorar el modelo matemático uniforme que previamente habíamos compartido, es decir, hemos de adentramos plenamente en la ontogenia matemática del Nautilus. Y para lograr modelarla tendremos que apoyarnos en la ontogenia biológica detectando en ésta los diferentes detalles y particularidades que determinan las características esenciales en cada momento y etapa, y habrá que concretar cada una de ellas para su adecuada traslación al modelo matemático final.
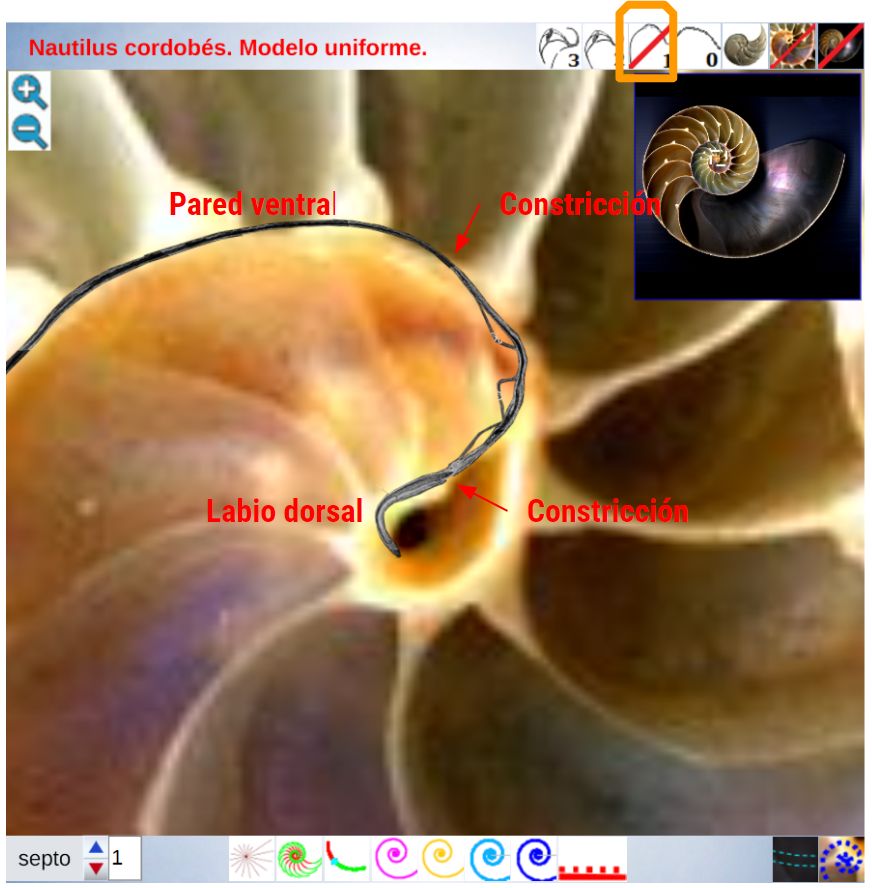
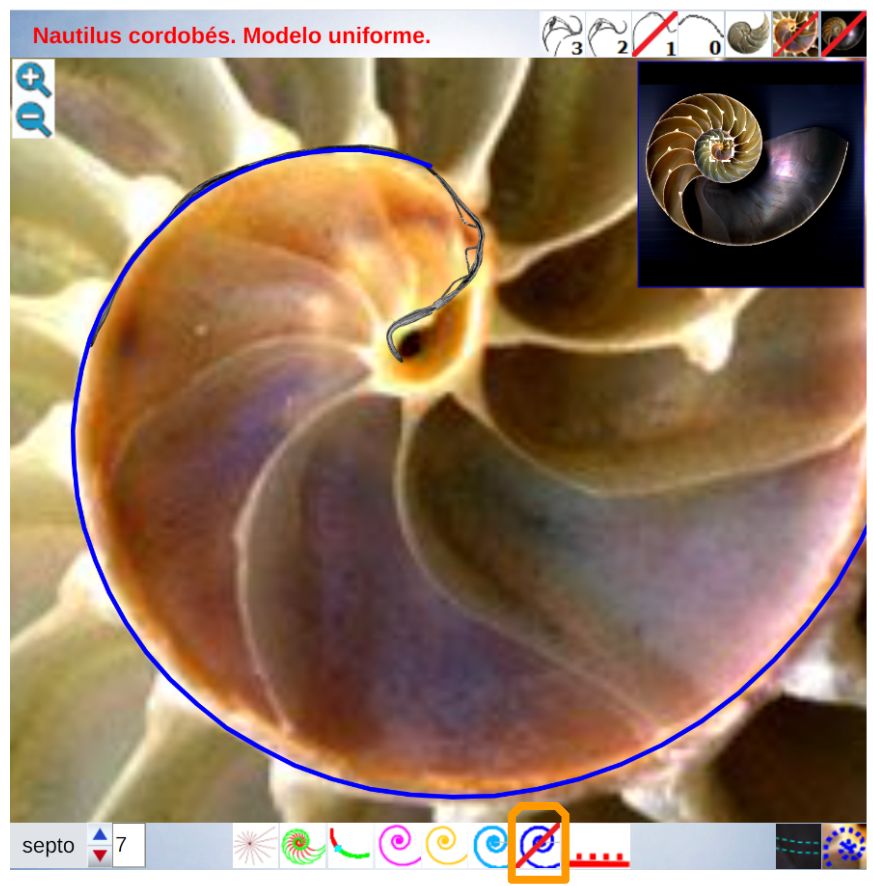
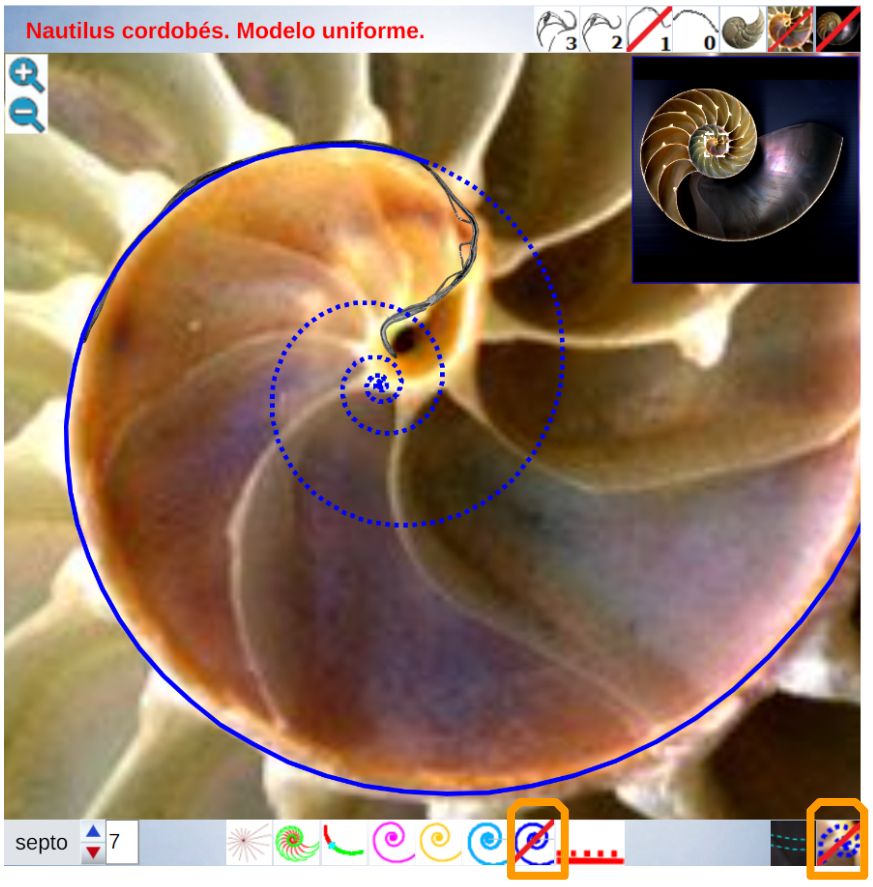
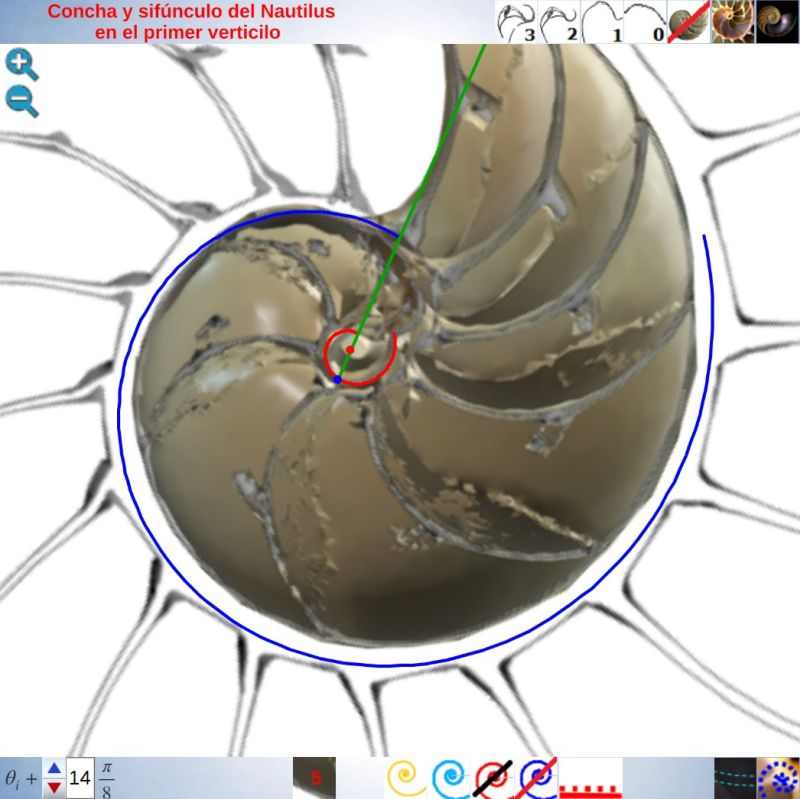
La constricción de la cicatriz, coincidente con la intersección de la concha embrionaria con el primer septo, es la que marca el inicio del patrón de crecimiento correspondiente a la sección de la concha ventral. A partir de la imagen correspondiente a la fase del primer septo () podemos observar claramente la curvatura de la parte ventral y verificar cómo ésta se ajusta a una espiral cordobesa, ajuste que permanece durante toda la vida del animal (). Por tanto, ésta es una característica intrínseca y permanente, un primer invariante, en toda la ontogenia del Nautilus desde el periodo embrionario septal a la madurez:
La pared ventral de la concha del Nautilus es una espiral cordobesa.
En la observación de la concha embrionaria inicial (imagen A de la ) ya indicamos que su perfil queda modelado por dos curvas, lo cual da pie y nos recuerda a un invariante citado en el modelo uniforme () que se mantendrá en el modelo revisado:
Todo punto de la concha o interior es la intersección de dos espirales cordobesas, una longitudinal tipo a la del perfil de la concha, pero con un factor de escala, y otra transversal tipo septal.
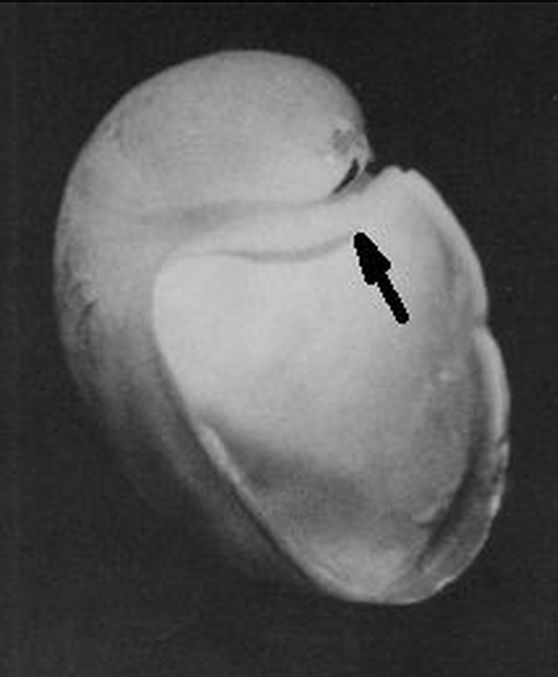
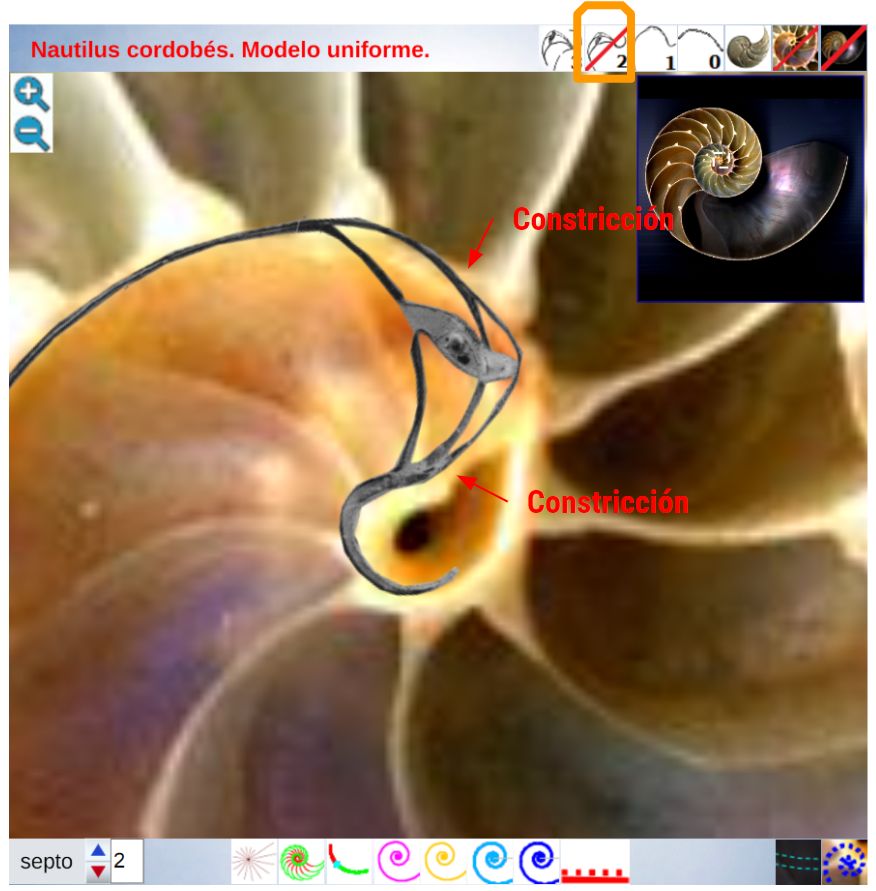
En las imágenes de la , la y la puede intuirse que las paredes septales confluyen con la pared ventral de la concha tangencialmente, lo cual a priori parece lógico que acontezca para que el cuerpo del animal pueda asentarse de manera uniforme
en la zona de unión de ambas paredes. Eso se visualiza claramente a nivel microscópico (), donde en la parte apical (parte izquierda en esa imagen) también puede observarse un cemento de unión entre ambas paredes que a nivel macroscópico difumina esta tangencialidad y puede inducir a interpretar inadecuadamente la forma en que ambas capas confluyen. Esta tangencialidad se da en toda la ontogenia del Nautilus, tercer invariante, y necesitamos destacarla y fijarla porque es básica para el modelo matemático buscado.
Los septos son tangenciales con la pared ventral
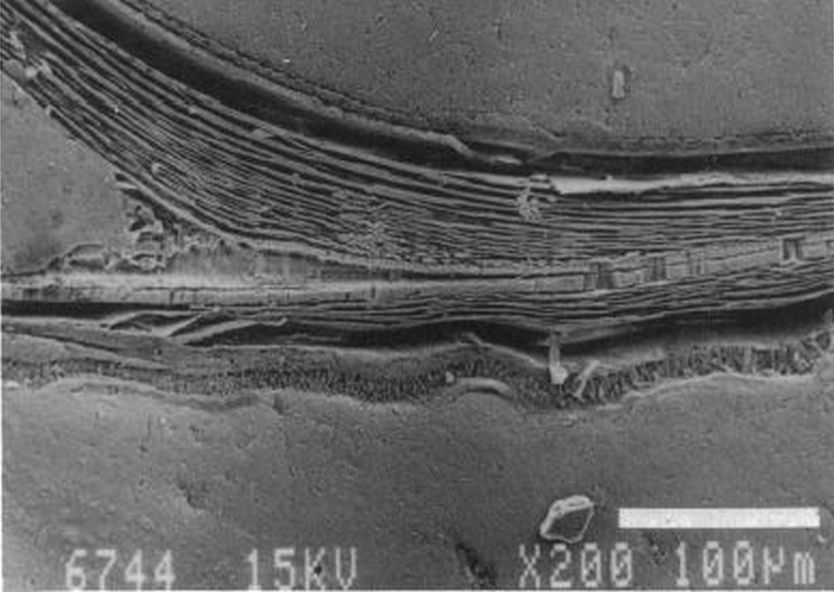
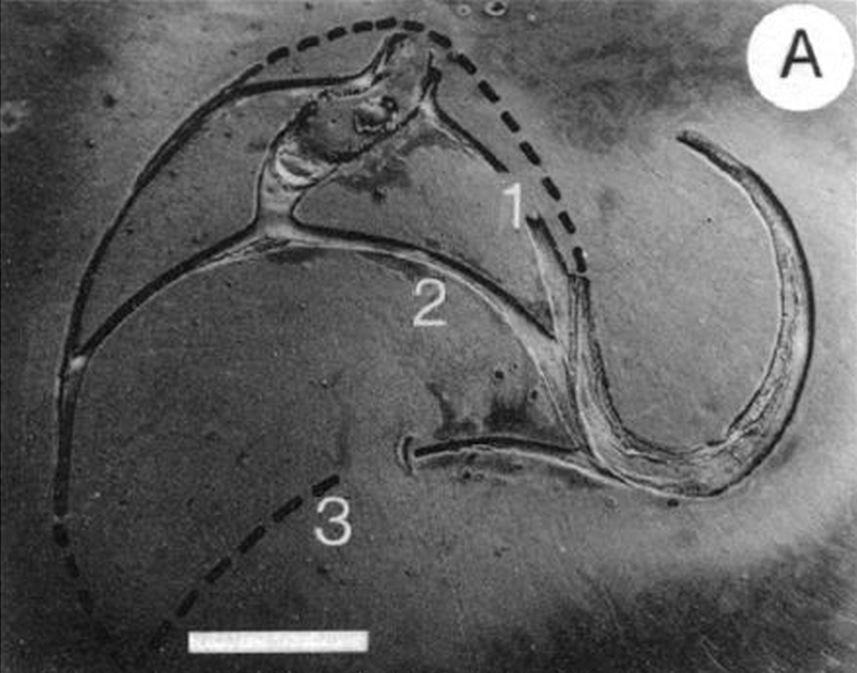
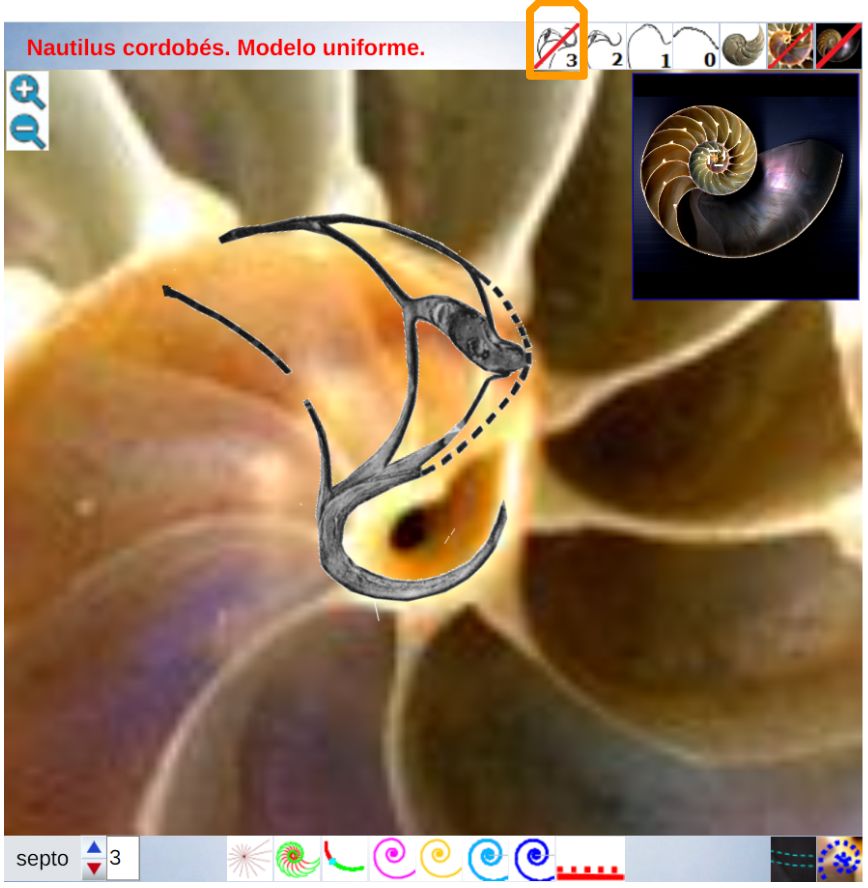
La modelación de la incidencia de los septos con la pared dorsal requiere un análisis detallado ya que presenta variaciones destacables en cada verticilo y, por tanto, habrá que localizar la causa de las mismas. Así pues, observando la unión de los dos primeros septos con dicha pared dorsal () podemos constatar que aquí no acontece, no se reproduce, la indicada tangencialidad ventral y se detecta cemento de unión en la parte apical (en esta imagen ubicada a la derecha) y en la adoral (izquierda).
Matemáticamente, si partimos de que la forma del septo sigue una determinada curva prefijada (en el modelo global uniforme indicamos, mostramos y asumimos que es un arco de espiral) y considerando la tangencialidad indicada de éste con la pared ventral, entonces se concluye que la incidencia que acontece con la pared dorsal viene dada, está preestablecida, es forzada y tiene que asentarse según el ángulo que corresponda en cada momento, y quizás ello es lo que constructivamente obliga a que la unión se tenga que reforzar para obtener una consistencia adecuada (de ahí el cemento indicado).
Algebraicamente, detectada la forma de la pared dorsal, la determinación del ángulo y punto de incidencia quedan reducidos a intersecar la ecuación del septo con la de la pared dorsal, y eso es lo que haremos en su momento y en cada una de las fases del crecimiento, las cuales hemos asociado a cada verticilo.
Adicionalmente, dado que la parte dorsal de la concha es diferente en el primer verticilo (lo analizaremos posteriormente en un apartado específico), la amplitud del arco del septo parece ser variable y, si es así, tendrá que acortarse o alargarse hasta encontrar el punto de apoyo necesario para el cierre de cada cámara. Acorde con ello, el ángulo de incidencia observado parece ser diferente en los septos del primer verticilo (observar detenidamente la , imagen A). En esa misma figura se observa que en el segundo verticilo, en el área dorsal media (mda), son ostensibles las depresiones septales dorsales (dsd), ver detalle de su forma en las imágenes B, C y D, y éstas se vuelven menos notables en el tercer verticilo. La ontogenia biológica parece mostrarse esquiva con la matemática o simplemente gusta de marcarnos retos adicionales sobre los que dilucidar.
Como indicamos con antelación (ver la ) es en la constricción dorsal, que es también el punto de incidencia del primer septo, donde el perfil de la concha en su parte dorsal cambia su concavidad y adopta la misma que la pared ventral, si no fuera así, la cavidad se cerraría. Y al confluir la pared dorsal de este primer verticilo con la concha embrionaria preseptal es como se forma el ombligo.
A priori, no es fácil poder modelar con certeza la forma que adopta este labio dorsal dado que su recorrido es inferior a una vuelta y, consecuentemente, las referencias sobre las que apoyarse puede que no sean suficientes. Lo que sí puede observarse es un posible crecimiento en espiral, es esperable que sea así ¿verdad?, y además que ésta sea una espiral geométrica para que el crecimiento sea gnomónico; por tanto, planteamos y establecemos esta hipótesis.
Adicionalmente, por uniformidad, consideraremos que el tipo de crecimiento sea también cordobés ya que la pared dorsal en el segundo y tercer verticilo tiene esa forma (las paredes dorsales en estos verticilos eran previamente, en la vuelta anterior, sendas paredes ventrales ) y es lógico que ésta se mantenga en el primero o mejor dicho que ésa sea la tendencia original que continúa posteriormente. Es esperable y lógico que la curvatura del dorso del animal se mantenga en toda su existencia. Bajo esa consideración, lo que sí es obvio (observar la ) que:
¡Vaya! Ya lo había adelantado literariamente antes, pero ahora ¡se me hizo irresistible mostrarles gráficamente, en esta , la causa o germen que permitirá comprender mejor al Nautilus! Bien sabe quien se dedica a investigar que no puede ocultarse la satisfacción cuando en el interior de nuestra mente surge la inspiración ¡Ajá! que sublimó Martin Gardner y la que llevó a Arquimedes a correr desnudo, insconcientemente, a la par que gritaba ¡Eureka! a sus paisanos de Siracusa. Y salvando las distancias y comparaciones, estaba deseoso de que lo vieran. Pero esa inspiración inicial, que esporádicamente regalan las musas generalmente sólo a quien está trabajando, no es más que la piedra angular que asienta y modula la futura estructura global, pero habrá que seguir construyendo sobre ella en base a nuevas inspiraciones y deducciones lógicas. Así pues, hemos de asentar esa piedra base y aplicar todos los detalles detectados, analizados y descritos en la particular revisión que hemos realizado de la ontogenia biologica del Nautilus, para así llegar con paso firme a nuestro objetivo que es poder comunicarles lo que sotto voce nos cuenta el Nautilus acerca de su ser y crecer, y poder hacerle de traductor al lenguaje que muchos catalogan como el criptográfico o secreto de la Naturaleza: el matemático.
Ahora sí, llegó el momento esperado, o al menos anunciado, de formular detalladamente la "Ontogenia matemática del Nautilus". Gracias por ser pacientes, considero que se verán gratificados por haber llegado aquí y por continuar conmigo.
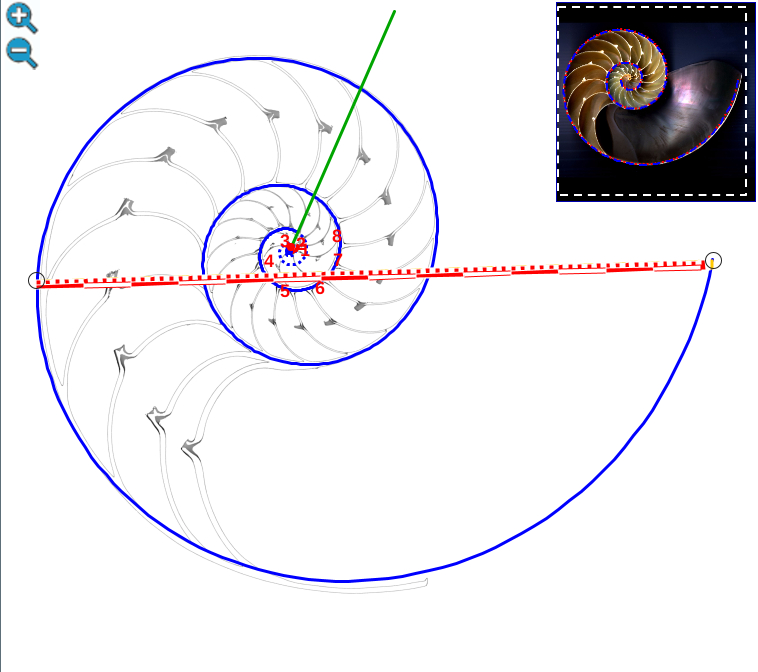
Para realizar el análisis matemático en este primer verticilo utilizaremos el siguiente recurso interactivo (). Puede interactuar libremente con él y si posiciona el ratón sobre los botones tendrá una breve información sobre su efecto o acción. También puede consultar las instrucciones.
Para mostrar la modelización del labio dorsal y el primer verticilo hemos elegido la concha digitalizada por el Museo de D’Arcy Thompson en la Universidad de Dundee () y, en particular, los datos tridimensionales aportados por dicho museo correspondientes a esa digitalización y los cortes parasagitales y transversales o radiales realizados por González-Restrepo (2019)
fuente gráfica el corte con los septos del primer verticilo y con los restos del canal sifuncular es más visible que los que pueden observarse en la concha que hemos utilizado, hasta ahora, como soporte de referencia () para mostrar el modelo uniforme y las propiedades observadas. Aquí se puede ver que los septos del primer verticilo están incompletos y consecuentemente tampoco se visualiza el rastro del canal del sifúnculo, por tanto, no es posible modelar lo que no es visible. Esta es la razón de cambiar la referencia gráfica que utilizamos como muestra.
|
|
|
|
|
Partamos de que la espiral logarítmica cordobesa que modela la pared ventral (representada en color azul en la y en sucesivas imágenes) viene dada en coordenadas polares por:
$$\color{blue} r=\kappa^\theta \quad \theta \in [\theta_i, \theta_f] \tag{2.1}$$
o en coordenadas cartesianas en función del parámetro $\theta$:
$$\color{blue} \begin{cases} x=\kappa^{\theta} cos(\theta) \\ y=\kappa^{\theta} sen(\theta) \end{cases} \quad \theta \in [\theta_i, \theta_f] \tag{$2.2$}$$ es decir, que ubicamos su polo en el origen de coordenadas. Adicionalmente denotaremos el ángulo inicial de la espiral como $\color{blue} \theta_i$, y como $\color{blue} \theta_f$ el ángulo final correspondiente a la boca de la concha.
Fijada la pared ventral y polo de la misma y con la orientación dada a la imagen de la concha tomada como referencia, tenemos que entonces el polo de la espiral cordobesa que aproxima al labio dorsal se situaría en $\color{red} D(0,035, 0,080)$ y su ecuación paramétrica sería:
$$\color{red} \begin{cases} x=D_x + a \, \kappa^{\theta} cos(\theta) \\ y=D_y + a \, \kappa^{\theta} sen(\theta) \end{cases} \quad \theta \in [\theta_i, \theta_i+\frac{7\pi}{4}] \tag{$2.3$}$$
Donde el coeficiente $\color{red} \, a \,$ verificaría que $\color{red} \, 0,10 \le a \le 0,13$.
En la se puede observar la pared ventral y el labio dorsal representados para $ \theta_i \le \theta \le \theta_i+\frac{7\pi}{4} \,$ y también reproducirlo en la .
De los valores posibles el que teóricamente podría ser más certero se correspondería con:
$$\color{red} a=\kappa^{-4 \pi} = 0,1177... \tag{$2.4$}$$
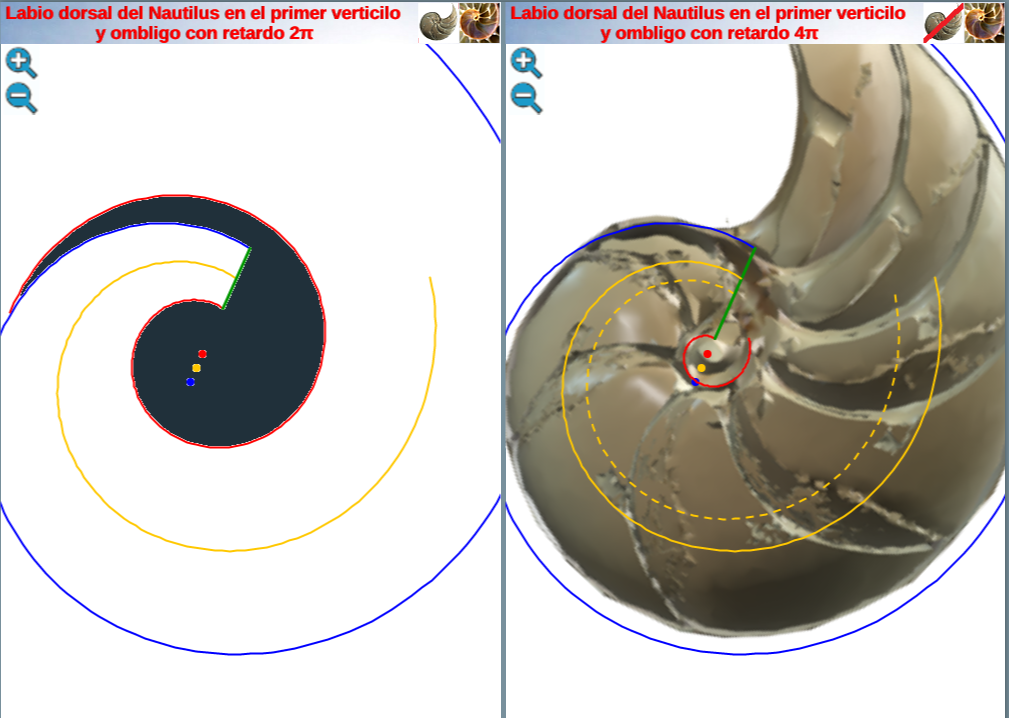
que matemáticamente representaría que el labio dorsal tiene un retraso de dos vueltas (un ángulo de retardo de $4 \pi$) respecto a la pared ventral inicial. Sería de esperar que el retraso fuera de $2 \pi$, dado que ésta es la relación que acontece en los siguientes verticilos cuando la que antes era pared ventral pasa a ser la nueva pared dorsal en la siguiente vuelta (de ahí lo de $2 \pi$), pero lo esperado no es siempre lo encontrado.
Geométricamente, si el labio dorsal en el primer verticilo tuviera sólo el retardo de $2\pi$ se generaría un ombligo de mayor tamaño al que se observa en la concha del Nautilus. Esto, representaría al animal un esfuerzo constructivo mayor, pues tendría que cubrir una superficie más amplia (en este caso más longitud dado que estamos trabajando con la sección) ya que este labio dorsal bordearía a la concha embrionaria. En la , espacio izquierdo, puede verse cuál sería la forma del labio dorsal, ombligo (superficie en color negro en ese espacio) y concha ventral en el supuesto de un retardo de $2\pi$ y en el espacio derecho el caso de retardo $4\pi$. Entre las dos alternativas la correspondiente a $4\pi$ parece la más eficiente. Podrían plantearse retardos que no tuvieran que ser múltiplos de $2\pi$, pero de partida ello no se observa como biológicamente adecuado, pues
estaría considerándose que la parte dorsal del cuerpo del animal tendría un crecimiento descompensado, al menos en algún instante o periodo temporal, respecto a la ventral. Pudiera acontecer, pero el deslizamiento que realiza a lo largo del fragmocono al crecer, inspira más una situación más regular. Si en el periodo evolutivo acontecido en la larga historia de este animal han ocurrido retardos de otro tipo, al menos parece que la selección natural ha conducido al retardo de $4\pi$ que hemos detectado y que consideramos en nuestro modelo del primer verticilo.
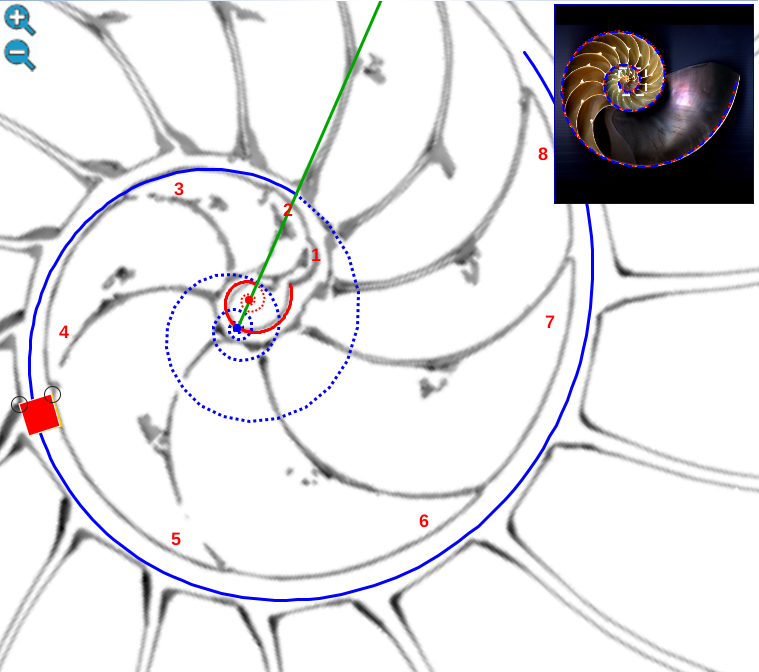
Ambas espirales comparten el mismo eje polar inicial (en ese color verde está pintado en la escena), es decir, el eje inicial de cada una de ellas está incluido en la semirrecta que pasa por el polo ventral y por el polo dorsal. Adicionalmente, esta semirrecta interseca a la concha en la constricción dorsal y la ventral que son los puntos de intersección y tangencia, respectivamente, del primer septo con la pared dorsal y la ventral de dicha concha. Esto cuadra con la ontogenia biológica descrita antes y matemáticamente aporta también una pauta común de crecimiento al compartir ambas espirales el mismo parámetro angular. El ángulo inicial común para ambas espirales indicamos que lo denotaríamos como $\color{red} \theta_i$ y entonces el recorrido total de la espiral dorsal termina en $\color{red} \theta_i+\frac{7\pi}{4}$.
|
|
|
|
|
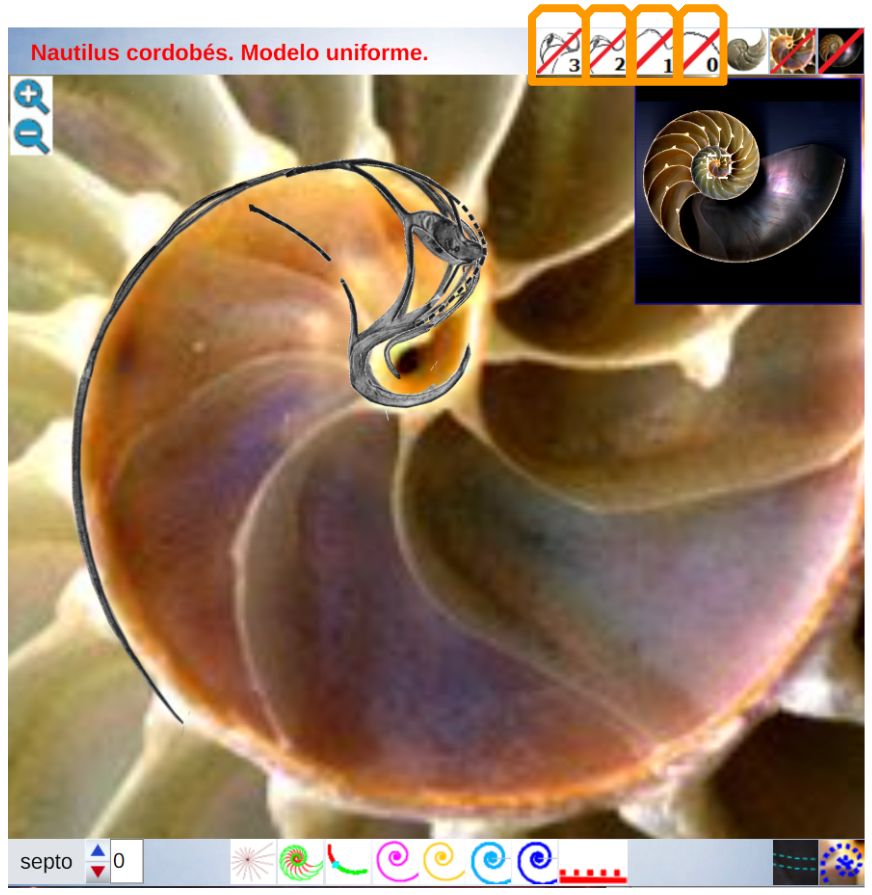
La pequeña variación existente entre los polos de ambas espirales (aproximadamente un milímetro) conduce a que el labio dorsal no finalice su recorrido siendo tangente a la concha embrionaria preseptal, sino que este labio incide e interseca a dicha concha primigenia cuando se cierra el primer verticilo y se genera el ombligo.
Consecuentemente, el enlace con la parte ventral inicial no es suave, sino que se produce a través del séptimo y octavo septo. Son estos últimos septos del primer verticilo los que al apoyarse en la concha primigenia se adaptan para dar continuidad con la pared ventral inicial. Más tarde abordaremos un estudio específico de la transición del primer al segundo verticilo. El hecho de que no se produzca la tangencialidad entre la pared ventral inicial y la finalización del labio dorsal refuerza y muestra la necesidad de considerar la existencia de dos polos diferenciados en el modelo teórico y, también, que no se pueda atribuir esta diferencia a un error en la precisión del ajuste gráfico realizadoDe nuevo, hemos de recordar que el paso de la quecto-quetta realidad al modelo teórico requiere de la consideración de cierta tolerancia, pero que hay que saber distinguirla de la existencia de una diferencia que provoque cambios en el modelo. Si la toma en consideración de esa tolerancia no cambia el modelo podremos aceptarla y admitirla, pero habrá que evitarla cuando se provoque un cambio en él. Así pues, en este caso es obligado considerar que los polos son diferentes. Por el contrario, por ejemplo, en las espirales que hemos considerado para ajustar el perfil del labio dorsal y de la pared ventral, en especial ésta, podría aducirse que necesitarían una mejora en su ajuste a la imagen de la concha en ese primer verticilo, pero realmente no es necesario ya que tal y como se ha considerado es suficientemente adecuado para determinar el modelo global que caracteriza al genus Nautilus. Esto ya lo mostramos en la , y lo detallamos ahora, pues al observar el ajuste de la pared ventral (espiral azul) en el primer verticilo y su ajuste global en la toda la concha, se marca de manera evidente que la tolerancia considerada es admisible para determinar el modelo a nivel tanto local como global (el grosor de la pared es inferior a un mm, lo puede medir en la escena, y el ejemplar considerado tiene unos 143 mm en su etapa adulta ( y ) . Sin embargo, si modificásemos la posición del polo de la pared dorsal, es decir, ignorásemos la pequeña distancia que existe entre ambos polos obtendríamos variaciones no admisibles a nivel local, es decir, cambiaría el modelo y no se ajustaría a la ontogenia del Nautilus.. Ver detalle del modelo a nivel local en la y a nivel global en la .
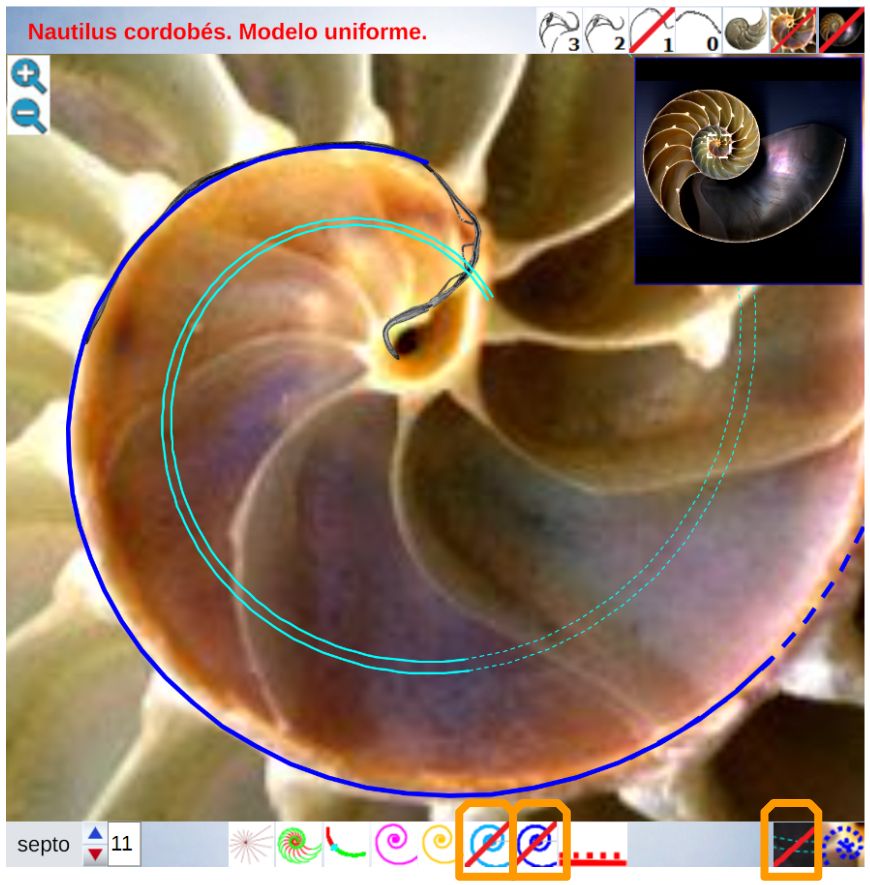
En nuestro primigenio modelo uniforme detectamos que el canal sifuncular actuaba como el eje del fragmocono, es decir, que es equidistante de la pared ventral y dorsal. En este supuesto uniforme
ambas paredes describen sendas espirales cordobesas con igual polo, de manera que si la ecuación en coordenadas polares de la primera es $\color{blue} r=\kappa^\theta$, la de la segunda sería $\color{red} r=\kappa^{-2\pi} \kappa^\theta = 0,3431... \kappa^\theta$ (realmente es la misma espiral, pero la segunda con un ángulo de retardo de $2\pi$ o coeficiente 0,3431...) y, entonces, el sifúnculo tiene de ecuación:
$$\color{DeepSkyBlue} r=b \, \kappa^\theta \tag{2.5}$$
donde $\color{DeepSkyBlue} b$ toma el valor medio de los respectivos coeficientes $\color{blue} 1$ y $\color{red} \kappa^{-2\pi}$ de las espirales anteriores, es decir,
$$\color{DeepSkyBlue} b=\frac{\kappa^{-2\pi}+1}{2}=\frac{0,3431...+1}{2}=0,6715... \tag{2.6}$$
lo que se corresponde con una espiral cordobesa con un ángulo de retardo de $\frac{-3\pi}{4}$. Pero, ya comprobamos que el ajuste anterior es adecuado en el segundo y tercer verticilo, pero no así para el primero (). No obstante, ahora sí, estamos en condiciones de determinar cómo queda modelado el sifúnculo en esta primera vuelta.
El fragmocono en el primer verticilo está delimitado por dos espirales cordobesas cuyas ecuaciones son (2.2) y (2.3), ambas con un ángulo polar común, pero con distinto polo. Si consideramos que el sifúnculo en este verticilo tiene un comportamiento similar a los dos posteriores, entonces éste sería el eje de ese fragmocono y, para determinarlo, procedamos a determinar el lugar geométrico de los puntos del plano que equidistan de ambas y obtendremos que viene determinado por la ecuación:
$$\color{gold} \begin{cases} x=\frac{D_x}{2} + \frac{\kappa^{-4\pi}+1}{2} \, \kappa^{\theta} cos(\theta) \\ y=\frac{D_y}{2} + \frac{\kappa^{-4\pi}+1}{2} \, \kappa^{\theta} sen(\theta) \end{cases} \quad \theta \in [\theta_i, \theta_f] \tag{$2.7$}$$
que se corresponde con una espiral cordobesa, cuyo polo $\color{gold} S(0,0175, 0,0400)$ es el punto medio de segmento determinado por el polo de la pared dorsal $\color{red} D(D_x, D_y)$ y el de la ventral $\color{blue} (0, 0)$, y su coeficiente es la media aritmética de los coeficientes respectivos: En general puede comprobarse que dadas dos espirales logarítmicas con igual base, con el mismo ángulo polar y con diferentes polos; si se halla el lugar geométrico de los puntos de plano obtenidos mediante una combinación lineal de las mismas se obtiene que es una espiral logarítmica del mismo tipo, es decir, de igual base y ángulo polar, y con polo la combinación lineal de los polos y coeficiente la combinación de los coeficientes.
$$\color{gold} \frac{\kappa^{-4\pi}+1}{2}= \frac{0,1177...+1}{2}=0,5588... \tag{2.8}$$
Al representar gráficamente la espiral (2.7) con el coeficiente (2.8) observamos que realmente no modela adecuadamente a dicho sifúnculo en ese verticilo (ver en la imagen derecha de la la línea discontinua en color naranja o interactuar en la ).
La ecuación de la espiral que se ajusta al sifúnculo es la siguiente:
$$\color{gold} \begin{cases} x=\frac{D_x}{2} + \frac{\kappa^{-2\pi}+1}{2} \, \kappa^{\theta} cos(\theta) \\ y=\frac{D_y}{2} + \frac{\kappa^{-2\pi}+1}{2} \, \kappa^{\theta} sen(\theta) \end{cases} \quad \theta \in [\theta_i, \theta_f] \tag{$2.9$}$$
donde
$$\color{gold} \frac{\kappa^{-2\pi}+1}{2}= \frac{0,3431...+1}{2}=0,6715... \tag{2.10}$$
y se corresponde con el eje del fragmocono, pero en el caso de que el labio dorsal tuviera sólo un retardo de $2\pi$ (ver imagen izquierda en la o interactuar en la ). Ese coeficiente o retardo en el sifúnculo es el mismo que acontece en el segundo y tercer verticilo, pero aquí el polo es diferente. En la podemos ver una comparativa de la espiral sifuncular determinada aquí (en color naranja) y la del sifúnculo en el modelo uniforme en (turquesa).
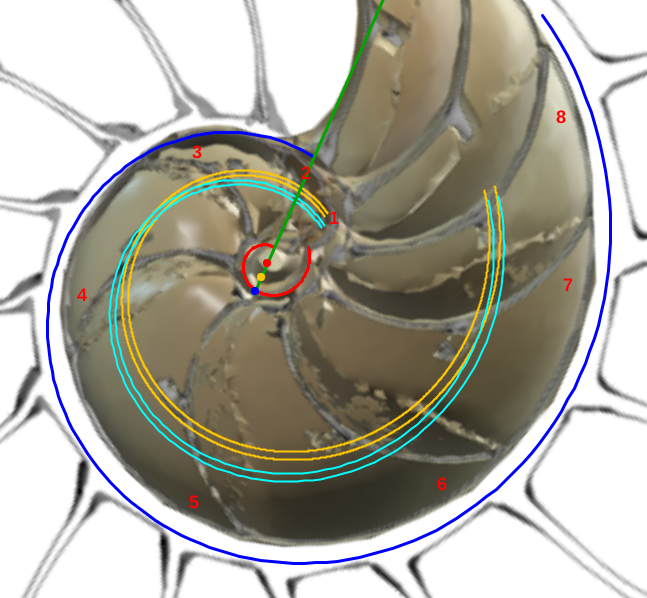
Así pues, la causa de que el sifúnculo tenga un comportamiento diferenciado en el primer verticilo se centra en el hecho de que el labio dorsal y la pared ventral tienen diferente polo. La explicación de cuál es la causa de su desviación respecto al eje del fragmocono queda abierta...
Pienso que hemos dado un gran paso en la comprensión y explicación de la ontogenia matemática del Nautilus. En ella, sigue imperando su carácter netamente cordobés, introduciendo bonitos matices matemáticos que explican los matices biológicos observados. Pero D. Antonio Machado nos indicó que se hace camino al andar y para ello, después del primer paso dado, han de llegar otros y en nuestro estudio, ahora, tendremos que centrarnos especialmente con las paredes septales y, ¿por qué no?, quizás tratar de localizar cuál es el germen de la esencia cordobesa de este entrañable, al menos para mí, animalito.
Continuemos nuestra andadura procediendo a revisar y a analizar los septos y las cámaras septales en la primera etapa de la ontogenia del Nautilus y busquemos caracterizar las particularidades que, de manera evidente, se muestran en el primer verticilo. Ya indicamos con una simple, pero atenta mirada, que en esa primera vuelta se observa que hay un número menor de cámaras que las que se contabilizan en la segunda y tercera, que se visualiza una amplitud angular de las mismas que se muestra como no uniforme, que se intuye un tamaño o capacidad volumétrica diversa con unas cámaras pequeñas y otras grandes con un crecimiento quizás no gnomónico e incluso en algunos casos decreciendo. Muchos detalles en los que aquí profundizaremos y sobre los que desvelamos y aportamos explicaciones y posibles causas que lo ocasionan, siempre desde una perspectiva y visión matemática, pero con soporte y con referencias biológicas.
Para el análisis de los septos en el primer verticilo nuestra referencia inicial ha de situarse en el modelo uniforme (Galo, 2024)
Los $n$ septosEn el modelo uniforme tenemos 16 septos en el primer verticilo, 16 en el segundo y 8 en el tercero, en todos ellos con una amplitud constante de $\frac{\pi}{8}$., $0 \le n \le 40$, tienen una ecuación común donde varía el polo $P_n(P_{n_x},P_{n_y})$ y el ángulo $\alpha_n$, pero todos con una amplitud constante $\frac{5\pi}{8}$:
$$\color{Lime} \begin{cases} x
=P_{n_x}+d \, \kappa^{\varphi} cos({\varphi}) \\ y=P_{n_y}+d \, \kappa^{\varphi} sen({\varphi}) \end{cases} \quad {\varphi} \in [\alpha_n, \alpha_n+\frac{5\pi}{8}] \tag{$2.11$}$$
en ellosEl valor de $d$ se aproxima al valor intermedio entre el coeficiente de la espiral dorsal $\kappa^{-2\pi}$ y el del sifúnculo $\frac{\kappa^{-2\pi}+1}{2}$, es decir $\frac{\kappa^{-2\pi}+\frac{\kappa^{-2\pi}+1}{2}}{2}=0,507359...$ y, por tanto, la espiral de los polos de los septos sería la intermedia entre la dorsal y el sifúnculo. $d \simeq 0,5$ y el polo $P_n$ de cada espiral está en la espiral cordobesa
$$\color{magenta} r=d \kappa^\theta \tag{$2.12$}$$
siendo
$$\color{magenta} \begin{cases} P_{n_x}=d \, \kappa^{\theta_n} \, cos({\theta_n}) \\ P_{n_y}=d \, \kappa^{\theta_n} \, sen({\theta_n}) \end{cases} \tag{$2.13$}$$
donde
$$\color{magenta} \theta_n=\theta_i+n \frac{\pi}{8} \tag{$2.14$}$$
para un ángulo inicial $\color{magenta} \theta_i$, que marca el comienzo de la construcción, y $$\color{Lime} \alpha_n=\color{magenta} \theta_n \color{black} -\frac{51\pi}{64} \tag{$2.15$}$$
Lo antes descrito ha de ser la base primordial sobre la que tenemos que apoyarnos para tratar de canalizar ese análisis y para poder focalizar adecuadamente la búsqueda y para lograr recopilar cuáles son los datos más certeros que nos conduzcan a la compresión del comportamiento y también a su modelación. O al menos a esta última, pues aun teniendo el modelo no siempre es factible saber la causa o posicionarse tajantemente en ella.
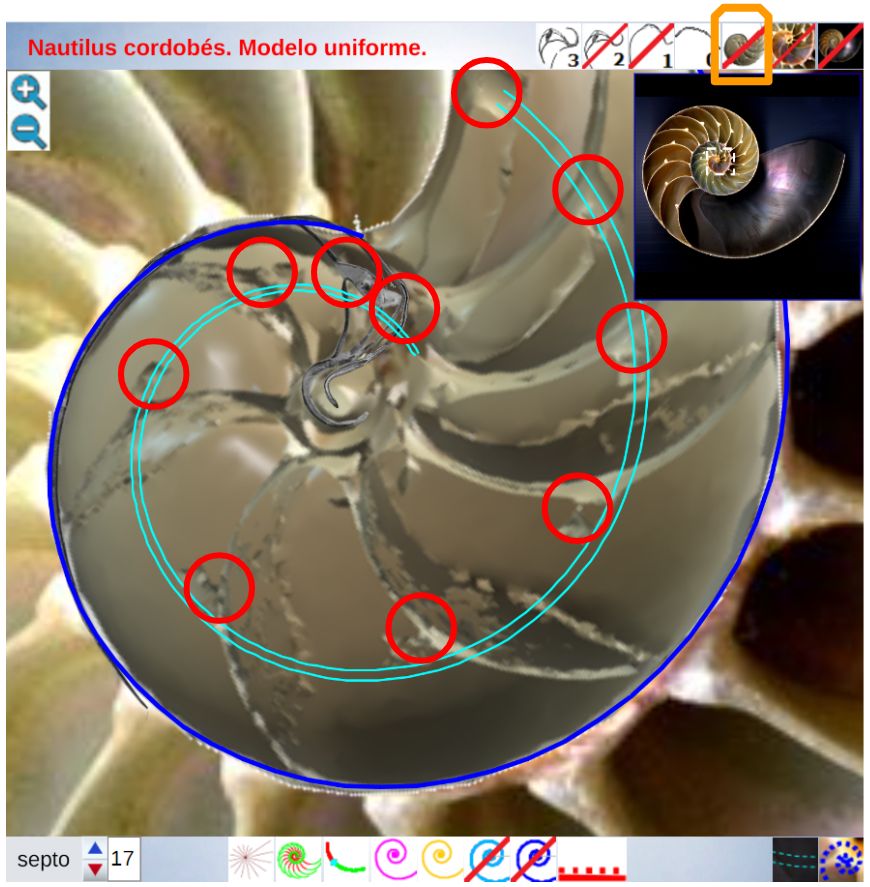
Si observamos las cámaras septales del primer verticilo es evidente, basta recordar el recuento que ya hicimos en la , que el número de éstas son ocho y ello se correspondería con una amplitud angular media de $\frac{2\pi}{8}=\frac{\pi}{4}$. No obstante, a primera vista o aparentemente, parece más que esa amplitud se manifiesta como variable y que no es obvio fijarla a priori. Esa cantidad de cámaras es inferior a las existentes en el segundo verticilo en el que son dieciséis con una amplitud constante de $\frac{2\pi}{16}=\frac{\pi}{8}$ y también a las del tercero donde hay un número variable, según el ejemplar y nivel de madurez, pero manteniendo también esa amplitud de $\frac{\pi}{8}$.
¿Por qué el número de cámaras es menor en el primer verticilo? Ilustrémonos en el devenir de esta etapa inicial del Nautilus acudiendo a algunas referencias descriptivas biológicas y acompañémoslas de unas primeras reflexiones matemáticas personales:
en el resto de las cámaras septales de ese verticilo la distancia entre septos es sólo algo superior. En el supuesto de considerar dieciséis cámaras estaríamos hablando de un espacio medio de $0,285$ mm… al Nautilus no le salen las cuentas, ni le trae cuentaDesde el punto de vista causal podríamos apuntar que el hecho de que el espacio disponible sea pequeño es precisamente lo que conduce a ese menor número de cámaras septales. El Nautilus, para construir un nuevo septo ha de desplazarse hacia adelante en su cámara habitacional, necesita un espacio interseptal mínimo, y ese espacio es el que adquiere para cumplir su objetivo natural de crecer y, si es posible, hacerlo gnomónicamente para mantener sus proporciones, su forma. Su preocupación o necesidad es la de avanzar para crecer, ocupando un nuevo espacio, y deja la contabilidad para otros o más precisamente para nosotros. elaborar tanto septo, más si consideramos adicionalmente lo que detallamos a continuación.
material calcáreo a utilizar ―dato que de nuevo incide y aporta cierto porqué relativo al menor número de septos― y que lo que se use ha de ser compensado por el empuje ocasionado por el volumen de líquido septal que se desaloje, es decir, ha de estar equilibrado con el volumen que alcancen las cavidades septales. Así pues, dado que el Nautilus inicialmente no flota y después sí, se deduce que debe haber una variabilidad volumétrica en las primeras cámaras y que este posible hecho puede ir también relacionado con la amplitud angular interseptos que parece ser variable, según indicamos con antelación.
Es necesario y procede analizar esta capacidad de las cámaras, pero en este estudio bidimensional acudiremos sólo al cálculo de la superficie ocupada por las secciones de las cámaras y analizaremos su variación. No obstante, avancemos sin precipitación, que progresivamente van apareciendo diversas facetas y es necesario asentar estas ideas con un material de apoyo adecuado y procede darle el necesario sustento matemático.
Ya hemos indicado, e incluso reiterado, que las dieciséis cámaras del segundo verticilo conducen a una amplitud angular entre cámaras de $\frac{\pi}{8}$, la cual se mantiene para los septos de tercer verticilo, y que las ocho del primero llevan a una amplitud de $\frac{\pi}{4}$. Si consideramos el retardo de la espiral dorsal respecto a la ventral en el segundo y tercer verticilo que es de $2\pi$, al efectuar el cociente $\frac{2\pi}{16}=\frac{\pi}{8}$ obtenemos el valor numérico antes indicado, pero si aplicamos igual proporción en el primer verticilo ¿qué ocurre? El retardo entre el labio dorsal y la pared ventral en este caso es de $4\pi$ y resulta que $\frac{4\pi}{16}=\frac{\pi}{4}$, es decir, un paso entre septos de $\frac{\pi}{4}$, paso que casualmente conduciría a los ocho septos observados en ese verticilo Al igual que acontecía con el eje del fragmocono, el retardo diferente entre pared dorsal y ventral, $4\pi$ vs. $2\pi$, vuelve a aparecer ahora ligado a las cámaras septales..
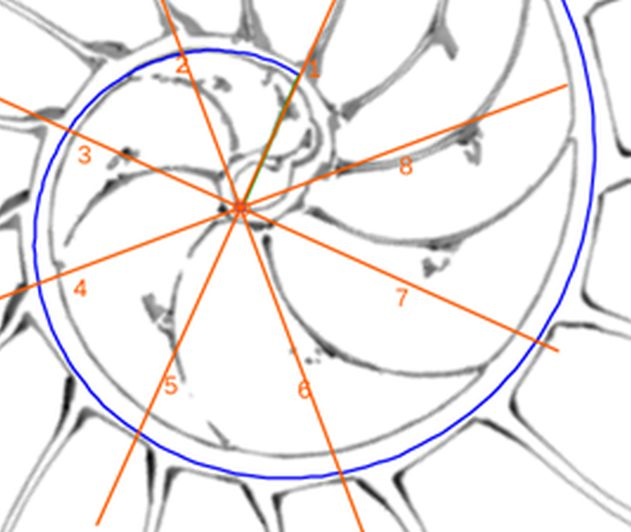
Sí, parece como si estuviéramos enfrascados en el reiterado y recurrente dilema de ¿qué fue antes: el huevo o la gallina?, pero más bien sería una estrategia de observación múltiple, desde puntos de vista opuestos o diferentes, buscando la generación de algún destello que, al menos, difumine un poquito las sombras platónicas en las que toda investigación siempre anda envuelta. Para tratar de provocar la necesaria chispa detonadora vamos a usar la . En el espacio izquierdo de esta escena contamos con herramientas auxiliares que nos permiten analizar la distribución que pueda acaecer en la amplitud septal. Con ellas hemos obtenido las imágenes mostradas desde la hasta la , que sintetizan el análisis que detallamos a continuación:
voluntad sin más que desplazar el centro o punto de intersección de ellos y, también, se pueden girar con el pulsador situado a la derecha de ese botón. Con esta herramienta podemos tratar de localizar, si existe, el punto de vista desde el que los apoyos de los septos sobre el labio dorsal y ventral se observen con la esperada o deseada distribución uniforme de paso $\frac{\pi}{4}$. Esta búsqueda viene impuesta por el hecho que desde el polo de la espiral ventral no se cumple esa relación (ver ) ni para los apoyos dorsales, ni para los ventrales; y si consideramos esos radios con centro el polo del labio dorsal los apoyos dorsales (ver ) puede considerarse quedan próximos a esa distribución, pero no ocurre así con los ventrales. Le invitamos a realizar sus pruebas e indagaciones usando dicha escena interactiva.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
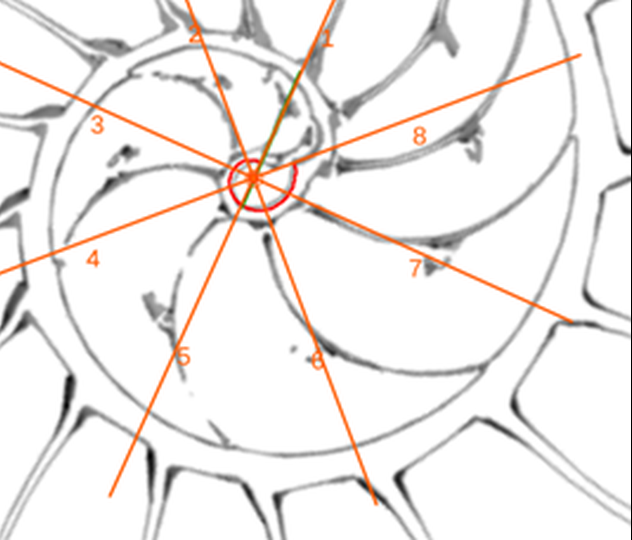
Adicionalmente, si mostramos conjuntamente el polo dorsal $\color{red} P_d$ y el ventral $\color{blue} P_v$ junto a los respectivos centros dorsal $\color{red} C_d$ y ventral $\color{blue} C_v$ (ver la ), se observa que la mediatriz del segmento $ \color{red}\overline{P_d C_d}$ coincide con la del segmento $ \color{blue}\overline{P_v C_v}$, es decir, que hay un punto $C$ que es centro de simetría de esas dos parejas de puntos.
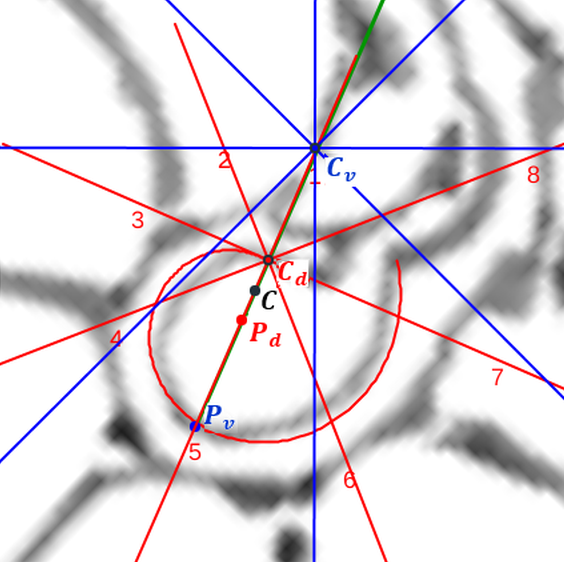
Ahora sí, podemos visualizar por qué las cámaras septales aparentan a primera vista una amplitud no uniforme y también por qué las superficies de las secciones de las cámaras se muestran tan diferentes. De nuevo, ya lo detectamos con el sifúnculo, la no coincidencia entre el polo dorsal y ventral que ahora se refleja (reflejo en sentido estricto dada la simetría detectada) en la existencia de dos centros no coincidentes da explicación matemática a esa diferente distribución de cámaras septales en este primer verticilo.
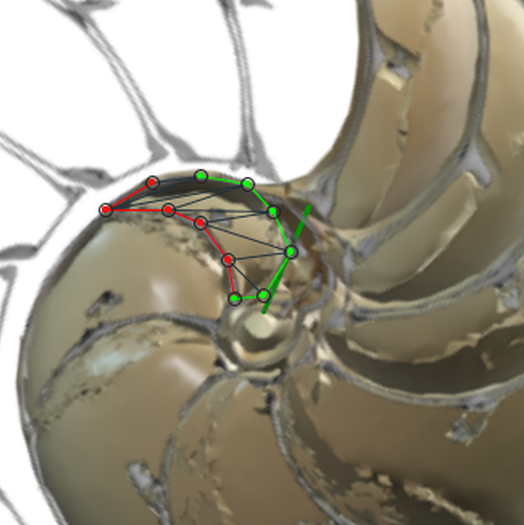
Para analizar el crecimiento de las cámaras y así tratar de detectar los aspectos alométricosLa alometría son los cambios de dimensión relativa de unas partes corporales en relación a los cambios que acontecen en el tamaño total. Y en particular, la alometría en el crecimiento detecta qué partes de un cuerpo o ente tienen un comportamiento diferenciado. que aquí acontecen, hemos construido una herramienta auxiliar que nos permite calcular el área de cada una de las secciones de esas cámaras (ver el espacio de la derecha en la y ver la y la ). Mediante la concanetación de triángulos se puede ajustar la superficie deseada y se facilita de manera automática su área a la escala real del Nautilus.
|
|
|
|
|
En la tabla incluida en la se refleja la medición realizada con dicha escena interactiva. La columna "Cámara" se corresponde con la numeración de las mismas, "Nautilus 1" recoge las áreas de las secciones del Nautilus Dundee y "Nautilus 2" las del otro ejemplar. El primero cuenta con treinta y tres cámaras y el segundo treinta y dos (en los gráficos comparativos no consideraremos la cámara 33). Las
columnas "$\sqrt{pc_1}$" y "$\sqrt{pc_2}$" reflejan respectivamente la raíz cuadrada de las proporciones entre las cámaras $pc = \frac{A_{n+1}}{A_n}, 1 \le n \le 31$ para cada uno de los ejemplares.
| Cámara | Nautilus 1 | Nautilus 2 | $\sqrt{pc_1}$ | $\sqrt{pc_2}$ |
|---|---|---|---|---|
| 1 | 1,72 | 0,75 | ||
| 2 | 5,82 | 3,10 | 1,839 | 2,033 |
| 3 | 12,92 | 6,65 | 1,490 | 1,465 |
| 4 | 22,00 | 13,02 | 1,305 | 1,399 |
| 5 | 28,59 | 18,85 | 1,140 | 1,203 |
| 6 | 30,24 | 31,60 | 1,028 | 1,295 |
| 7 | 31,24 | 32,22 | 0,867 | 1,010 |
| 8 | 23,35 | 24,96 | 0,945 | 0,880 |
| 9 | 24,38 | 24,46 | 1,096 | 0,990 |
| 10 | 30,68 | 31,88 | 1,122 | 1,142 |
| 11 | 30,13 | 35,25 | 0,991 | 1,052 |
| 12 | 37,41 | 39,19 | 1,114 | 1,054 |
| 13 | 43,59 | 51,17 | 1,079 | 1,143 |
| 14 | 46,52 | 53,71 | 1,033 | 1,025 |
| 15 | 60,19 | 56,40 | 1,137 | 1,025 |
| 16 | 60,26 | 63,36 | 1,001 | 1,060 |
| 17 | 70,21 | 67,97 | 1,079 | 1,036 |
| 18 | 86,81 | 81,07 | 1,112 | 1,092 |
| 19 | 91,61 | 94,61 | 1,027 | 1,080 |
| 20 | 105,61 | 110,02 | 1,074 | 1,078 |
| 21 | 118,35 | 112,36 | 1,059 | 1,011 |
| 22 | 143,88 | 138,63 | 1,103 | 1,111 |
| 23 | 166,65 | 145,73 | 1,076 | 1,025 |
| 24 | 188,53 | 174,74 | 1,064 | 1,095 |
| 25 | 215,37 | 211,64 | 1,069 | 1,101 |
| 26 | 251,96 | 228,15 | 1,082 | 1,038 |
| 27 | 286,89 | 276,36 | 1,067 | 1,101 |
| 28 | 334,66 | 317,02 | 1,080 | 1,071 |
| 29 | 370,82 | 368,22 | 1,053 | 1,078 |
| 30 | 468,01 | 432,54 | 1,123 | 1,084 |
| 31 | 466,53 | 508,39 | 0,998 | 1,084 |
| 32 | 481,31 | 578,76 | 1,016 | 1,067 |
| 33 | 300,14 | 0,790 |
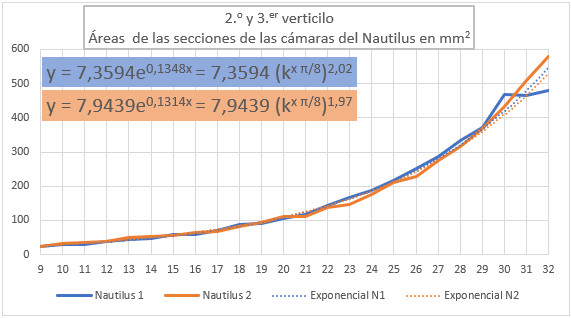
Dado que el crecimiento angular teórico de la pared ventral en el segundo y tercer verticilo es $\frac{\pi}{8}$, sin más que aplicar la expresión (2.16) que nos da la longitud de un arco de una espiral, en este caso cordobesa, se verifican la proporciones: $$\frac{l_{n+1}}{l_n}=\kappa^{\frac{\pi}{8}} \tag{2.17}$$ $$\frac{l_{n+1}-l_n}{l_n-l_{n-1}}=\kappa^{\frac{\pi}{8}} \tag{2.18}$$ donde $l_n$ es la longitud de la pared ventral hasta la cámara $n$ y, por tanto, $l_{n+1}-l_n$ es el incremento ventral que ocurre en la cámara $n+1$. Consecuentemente es de esperar que en esos verticilos la proporción entre las áreas de las cámaras sea: $$\frac{A_{n+1}}{A_n}=(\kappa^{\frac{\pi}{8}})^2 \tag{2.19}$$ Y en el primer verticilo también sería de esperar la obtención de relaciones análogas en base al crecimiento angular de $\frac{\pi}{4}$, pero quizás con matices diferenciados pues centros angulares y polos en este verticilo son distintos y ya estamos acostumbrándonos a la diferenciada ontogenia de esta etapa.
En la y la se han representado las áreas de las secciones de las cámaras mediante una poligonal y a su vez se ha determinado la línea de tendencia mediante un ajuste exponencial. En la primera de esas dos gráficas se han considerado todas las cámaras y en la segunda las correspondientes al segundo y tercer verticilo, como hemos señalado el objetivo es detectar posibles variaciones entre la primera etapa de crecimiento y las posteriores. En el primer caso la proporción entre las áreas de cada dos cámaras consecutivas es un poquito superior al valor teórico esperado indicado en (2.19), pues el exponente en ambos casos es algo
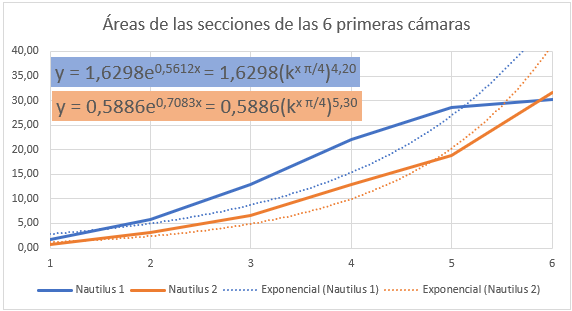
superior a dos. Esto está provocado por el crecimiento diferenciado que acontece en el primer verticilo, ya que si consideramos la proporción citada sólo en las cámaras del segundo y tercero (figura 37) entonces sí se está en el entorno cuadrático que caracteriza a ese valor teórico.
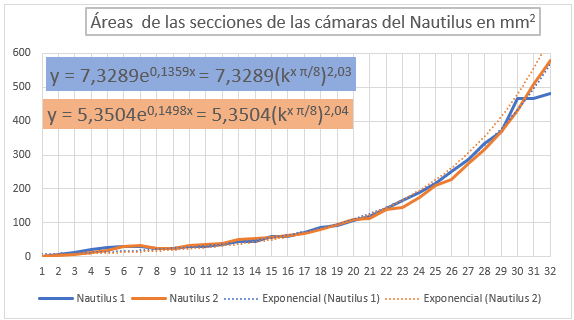
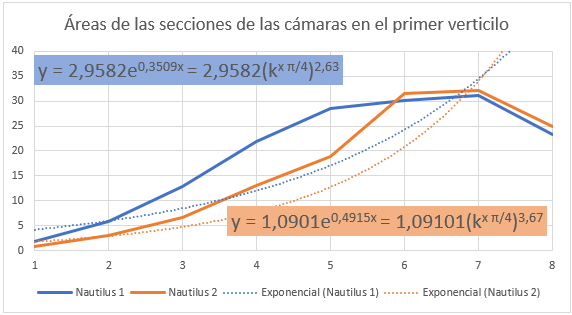
En la se refleja ese comportamiento diferenciado del primer verticilo y en especial la disminución que acontece en la octava cámara. Si realizamos un ajuste exponencial en este caso el valor esperado sería: $$\frac{A_{n+1}}{A_n}=(\kappa^{\frac{\pi}{4}})^2 \tag{2.20}$$ al ser el paso angular $\frac{\pi}{4}$, pero podemos observar en el ajuste que el valor es superior, e incluso si descartamos la octava cámara () el exponente es aún mayor, superior a cuatro.
Pero en este primer verticilo el ajuste más certero sería el logarítmico (ver la ) ya que inicialmente en este verticilo el Nautilus ha de conseguir la flotabilidad mediante un crecimiento rápido, es decir, con cámaras amplias y conseguida ésta cierta estabilización, retomando el crecimiento a partir de la cámara novena, pero en este caso ya de tipo exponencial.
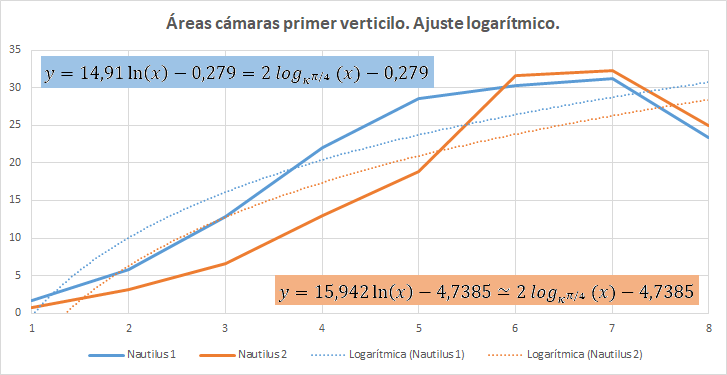
En el ajuste logarítmico del primer verticilo la relación obtenida entre las cámaras es: $$A_{n+1}-A_n=2 \, log_{k^{\frac{\pi}{4}}}(\frac{n+1}{n}) \tag{2.21}$$
Para poder tratar de comprender y explicar lo que acontece será necesario adentrarnos en otra tarea que está intrísecamente relacionada con ésta ya que cada cámara queda determinadas por dos septos y un arco de la pared ventral y otro de la dorsal. Por tanto, como ya adelantamos, necesitamos profundizar en los septos, en particular en su amplitud y en especial en el primer verticilo, y también cómo se intersecan estos con la paredes de la concha. Sobre la forma de los mismos sabemos que son arcos de espirales cordobesas. Así pues, ¡adentrémonos!... pero será en un nuevo capítulo.
En el modelo uniforme del Nautilus (Galo, 2024)
Siguiendo lo indicado en los capítulos anteriores de este libro, en particular en lo relativo a la modelación de la pared dorsal y ventral de la sección sagital de la concha, partimos de una base o fundamento primordial que es el que justifica y explica el distinto comportamiento de los septos entre el primer verticilo y los siguientes. En el primero, ambas paredes se corresponden con arcos de dos espirales cordobesas que tienen diferente polo; sin embargo, en el segundo y en el tercer verticilo las espirales de ambas paredes son copolares, tienen el mismo polo, siendo realmente arcos de una única espiral con un retardo angular entre ambas de $2\pi$. Así pues, dado que la complejidad es mayor en el primer verticilo vamos a proceder en orden cronológico inverso y analizaremos en primer lugar el segundo y tercer verticilo y posteriormente el primero.
La pared ventral en el segundo y tercer verticilo viene dada por:
$$\color{blue} \begin{cases} x=\kappa^{\theta} cos(\theta) \\ y=\kappa^{\theta} sen(\theta) \end{cases} \quad \theta \in [\theta_i+2 \pi, \theta_f] \tag{$3.1$}$$
donde $\color{blue} \theta_i$ es el ángulo que marca el inicio del fragmocono y $\color{blue} \theta_f$ la terminación de la misma delimitando la boca de la concha.
En el mismo instanteAl no tener una referencia temporal del crecimiento del Nautilus, sólo podemos señalar un mismo instante vital teórico mediante el uso de una amplitud angular común. De esta manera establecemos momentos, atemporales, en la que se han de dar coincidencias vitales. En este caso, para un valor fijado de $\theta$, conocemos el punto de la pared ventral y el punto de la pared dorsal que están relacionados entre sí. angular vital $\theta$, la pared dorsal sería:
$$\color{red} \begin{cases} x=\kappa^{-2\pi}\kappa^{\theta} cos(\theta) \\ y=\kappa^{-2\pi}\kappa^{\theta} sen(\theta) \end{cases} \quad \theta \in [\theta_i+2 \pi, \theta_f] \tag{$3.2$}$$
La espiral que contiene a los polos de los septos es:
$$\color{Magenta} \begin{cases} x=e \, \kappa^{\alpha} cos(\alpha) \\ y=e \, \kappa^{\alpha} sen(\alpha) \end{cases} \quad \alpha \in [\theta_i+2 \pi, \theta_f] \tag{$3.3$}$$
donde $\color{Magenta} e$ es un factor de escala o de retardo en la espiral cordobesaEn estos verticilos, en el modelo uniforme se detectó que $\color{Magenta} e \simeq 0,5$, que es un valor próximo al valor medio del factor correspondiente al sifúnculo y al del de la pared dorsal.
Y cada septo es un arco de una espiral cordobesa:
$$\color{lime} \begin{cases} x= \color{magenta}S_{n_x}\color{lime}+ d \, \kappa^{\rho} cos(\rho) \\ y=\color{magenta}S_{n_y}\color{lime}+ d \, \kappa^{\rho} sen(\rho) \end{cases} \quad \rho \in [\theta_{p_n}, \theta_{p_n}+\Delta \theta_{p_n}] \tag{$3.4$}$$
donde $\color{lime} [\theta_{p_n}, \theta_{p_n}+\Delta \theta_{p_n}]$ determina la amplitud angular del arco de esa espiral que comprende el septo $\color{lime} n$-ésimo; $\color{lime} \rho$ determina unívocamente cada uno de los puntos de dicho septo, pero todos ellos se corresponden con un mismo instante vital
Para conocer el proceso de formación de las cámaras de los nautilos podemos acudir a lo estudiado y analizado por Ward, Greenwald y Magnier (1981)
1. Formación de una cresta mural en la posición que ocupará el nuevo septo. Esta cresta es una delgada banda anular interna de carbonato cálcico.
2. Desplazamiento hacia delante del manto septal para ubicarse a la altura de la cresta mural y ajustarse a ella. Inicio del proceso de calcificación del nuevo septo. También el sifúnculo comienza a calcificar un anillo de conexión en el interior de la nueva cámara uniendo el septo anterior y el nuevo. Durante esta fase la nueva cámara está llena de líquido cameral (Ward, 1979)
3. Vaciado del líquido de la nueva cámara, que se inicia cuando el nuevo tabique ha alcanzado de un tercio a dos tercios de su espesor final. Este vaciado se denomina acoplado pues el líquido está en contacto con el anillo de conexión sifuncular. En esta fase el tabique septal sigue construyéndose, engrosándose, finalizando este proceso cuando el volumen del líquido vaciado es aproximadamente el 50% y ya no está en contacto con el anillo sifuncular, momento en el que se pasa a un proceso de vaciado desacoplado y comienza la formación de una nueva cresta mural y, consecuentemente, un nuevo ciclo.
Durante el ciclo de formación de una cámara, el crecimiento de la concha exterior parece ser que es continuo, pero hay una correlación inversa entre el porcentaje de líquido que se ha vaciado en la última cámara construida y la amplitud angular de la cámara habitacional. A medida que la cámara septal está más vacía la cámara habitacional es mayor y viceversa. Esta relación logra mantener la flotabilidad ya que cuando la nueva cámara está más llena de líquido el peso de la concha en la zona habitacional es menor y a medida que decrementa el líquido aumenta la amplitud de la zona habitacional. El inicio de cada cámara representa un punto crítico para la flotabilidad global, pero esto se compensa con el vaciado desacoplado que sigue aconteciendo en las cámaras anteriores.
, $\color{lime} d$ es un factor de
escala o de retardo a determinar en el modelo; y $\color{magenta} S_n(S_{n_x},S_{n_y})$ es el polo de la espiral que incluye a ese arco septal n-ésimo y que perteneciendo a la espiral (3.3) quedará determinado por cierto valor $\color{magenta} \alpha_n$.
La aplicación en el modelo del que hemos denominado tercer invariante (tangencialidad entre la pared ventral y las paredes de los septos) nos puede llevar a determinar los parámetros antes citados. De partida:
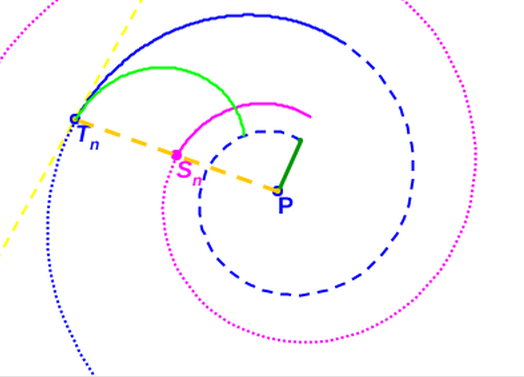
Y dado que
$$\overline{{\color{magenta}S_n} {\color{blue}T_n}}=\overline{P {\color{blue}T_n}}-\overline{P {\color{magenta}S_n}} \tag{3.8}$$
de las relaciones anteriores, (3.5) a (3.7), obtenemos que:
$$ d \, \kappa^\rho=(1-e) \, \kappa^\theta. \tag{3.9}$$
Expresando en (3.9) $d=d' \, \kappa^{\theta-\rho}$, es decir, considerando que $\rho$ es un ángulo de retardo, tenemos:
$$d' \, \kappa^\theta=(1-e) \, \kappa^\theta. \tag{3.10}$$
Y de ahí
$$d'=(1-e). \tag{3.11}$$
En Galo et al. (2016)
Centrémonos ahora en la determinación de la intersección de los arcos de los septos con la pared dorsal y la amplitud de estos.
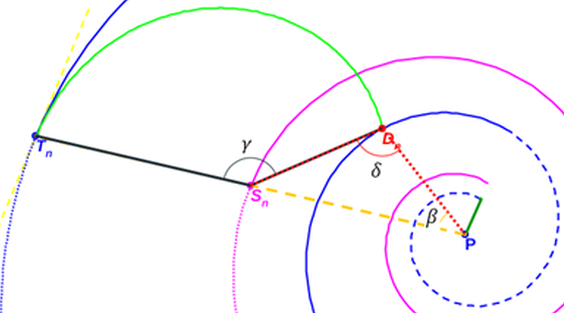
Para el septo $n$-ésimo, según la denominación de los ángulos reflejados en la y fijado el valor de $e = 0,5$, por (3.6) tenemos que: $$\overline{P {\color{magenta}S_n}}=0,5 \, \kappa^\theta. \tag{3.12}$$
El punto $\color{red}D_n$, intersección de ese septo con la pared dorsal, por pertenecer a ella y según (3.2) verifica que:
$$\overline{P {\color{red}D_n}}= \kappa^{\theta-2\pi-\beta} \tag{3.13}$$
y, a su vez, por pertenecer al arco del septo:
$$\overline{{\color{magenta}S_n} {\color{red}D_n}}=0,5 \, \kappa^{\theta-\gamma}. \tag{3.14}$$
A partir de (3.16) y (3.20) tenemos un sistema de dos ecuaciones que nos relaciona al ángulo $\gamma$ (amplitud del arco del septo), con el $\beta$ (retardo del punto de intersección dorsal del septo ${\color{red}D_n}$, respecto al punto de intersección ventral ${\color{blue}T_n}$). Este sistema puede reescribirse como:
$$ \begin{cases} \beta=-2\pi-log_\kappa(\frac{\sqrt{\kappa^{-2\gamma}+2\kappa^{-\gamma} cos \, \gamma +1} }{2}) \\ \beta=arcos(\frac{1+\kappa^{-\gamma} cos \, \gamma}{\sqrt{\kappa^{-2\gamma}+2\kappa^{-\gamma} cos \, \gamma +1}}) \end{cases} \tag{$3.21$}$$
Es decir,
$-2\pi-log_\kappa(\frac{\sqrt{\kappa^{-2\gamma}+2\kappa^{-\gamma} cos \, \gamma +1} }{2})$
$$
=
arcos(\frac{1+\kappa^{-\gamma} cos \, \gamma}{\sqrt{\kappa^{-2\gamma}+2\kappa^{-\gamma} cos \, \gamma +1}}) \tag{3.22}
$$
La resolución numérica de la ecuación (3.22) ―puede observarse en la , donde la gráfica en azul se corresponde con la función en la variable $\gamma$, definida por la expresión del miembro de la izquierda en (3.22) con $0 \le \gamma \le \pi$― nos permite determinar:
$\widehat{{\color{blue}T_n} {\color{magenta}S_n} {\color{red}D_n}}=\gamma=2,5090...$ radianes $\simeq 143,76º$.
$\widehat{{\color{blue}T_n} P {\color{red}D_n}}=\beta=0,6831...$ radianes $\simeq 39,14º$.
$\widehat{P {\color{red}D_n} {\color{magenta}S_n}} = \delta=1.8258...$ radianes $\simeq 104,62º$.
Apoyándonos en que en una espiral cordobesa el ángulo que forma el radio vector con la recta tangente es de $80,32º$ tenemos que (ver el detalle en la ) el ángulo que forma la recta tangente a la pared dorsal en ${\color{red}D_n}$ con la recta tangente al septo en ese mismo punto es de $75,38º$, es decir el septo no interseca a la pared dorsal perpendicularmente, si no formando con respecto a esa perpendicular un ángulo de $14,62º.$ Eso concuerda con lo indicado por Mutvei & Doguzhaeva (1997)
Este comportamiento teórico es el mismo tanto en el segundo como en el tercer verticilo, pues en ambos casos la pared dorsal y ventral comparten el mismo polo. En el tercer verticilo, esa depresión dorsal parece ser menos notable, al menos aparentemente, si bien sí pueden visualizarse o intuirse (interactuar por ejemplo con la digitalización del Nautilus del Museo Dundee incluida en el ―. Matemáticamente no hay diferencia entre esos dos verticilos.
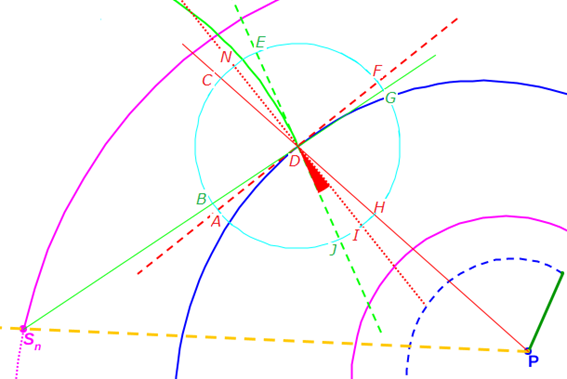
Así pues, en estos dos verticilos los arcos de los septos tienen por ecuación (3.4), la cual de acuerdo con lo antes analizado quedaría concretada como:
$$\color{lime} \begin{cases} x= \color{magenta}S_{n_x}\color{lime}+ d \, \kappa^{\rho} cos(\rho) \\ y=\color{magenta}S_{n_y}\color{lime}+ d \, \kappa^{\rho} sen(\rho) \end{cases} \quad \rho \in [\alpha_n -\gamma, \alpha_n] \tag{3.23}$$
donde
La introducción de la tangencialidad entre la pared ventral y los septos nos ha permitido lograr la modelación matemática de la sección sagital del Nautilus en el segundo y tercer verticilo y acentuar el caracter cordobés de sus elementos. En la , podemos observar e interactuar con este modelo.
El camino seguido en el análisis anterior nos puede servir de guía para abordar el estudio de los septos en ese primer verticilo que es tan especial. Especial por ser la pared dorsal y la ventral espirales cordobesas con distinto polo y, como veremos, por ser ésta la causa esencial de esas cámaras diferentes y esos septos variables. Un estudio que considero es interesante y matemáticamente bonito. La miel que le dejo en los labios podrá saborearla a continuación.
Después de haber modelizado los septos en el segundo y tercer verticilio bajo el invariante de tangencialidad, nos adentramos en la modelización de los septos en el primer verticilo. Esta primera fase de crecimiento ya hemos visto que se muestra diversa y con apariencia poco regular, cambiante (menor número de cámaras septales, ocho frente a las dieciséis de la etapa juvenil y adulta, con secciones y amplitudes que cambian como necesidad biológica para alcanzar la flotabilidad) y, ahora, ha llegado el momento de mostrar el modelo matemático que da explicación a esta etapa e introduce la regularidad esperada que parecía no acaecer, pero que queda al descubierto bajo la perspectiva matemática. De nuevo, el hecho de
que intervengan dos espirales con diferente polo, en este caso la espiral de la pared ventral y la espiral de los polos de los septos, conduce a proporciones variables entre los radios vectores y consecuentemente a que se formen septos con factores de escala variables. Ello nos conduce y permite determinar las ecuaciones de los septos, los puntos de tangencia con la pared ventral y los de intersección con la pared dorsal (para ello, nos encontraremos con la necesidad de introducir un grosor en el modelo matemático de esa pared, que es lo que físicamente acontece).
Completaremos el contenido de este análisis agrupando y relacionando entre sí diferentes puntos que se han ido detectando en este análisis. Unos que denominamos notables, porque matemáticamente son los que establecen el modelo matemático y dan explicación causal al mismo, y que son polos de diferentes espirales. Y otros que catalogaremos como destacables, posible fuente de inspiración matemática futura, y que son centros desde los que algunos objetos se observan con perspectiva angular constante.
En el primer verticilo la pared ventral es el arco de la espiral cordobesaDe acuerdo con la orientación con la que hemos presentado la concha del Nautilus en las escenas interactivas y, por tanto, la del eje inicial, el ángulo $\theta_i=-5,12$. Este valor lo necesitaremos en cálculos auxiliares posteriores. :
$$\color{blue} \begin{cases} x=\kappa^{\theta} cos(\theta) \\ y=\kappa^{\theta} sen(\theta) \end{cases} \quad \theta \in [\theta_i, \theta_i+2 \pi] \tag{$3.25$}$$
Y, como ya indicamos, en el mismo instante vital $\theta$ la pared dorsal es el arco de otra espiral cordobesa:
$$\color{red} \begin{cases} x=D_x+a \, \kappa^{\theta} cos(\theta) \\ y=D_y+ a \, \kappa^{\theta} sen(\theta) \end{cases} \quad \theta \in [\theta_i, \theta_i+\frac{7 \pi}{4}] \tag{$3.26$}$$
con $\color{red} P_D(D_x,D_y)=(0,035, 0,080)$ y $\color{red} a=\kappa^{-4 \pi}$.
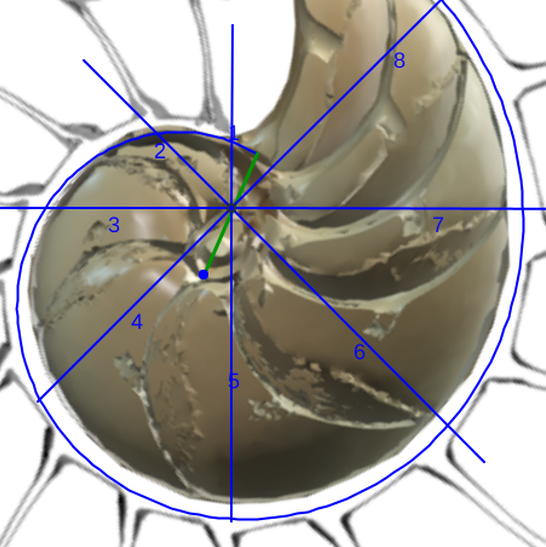
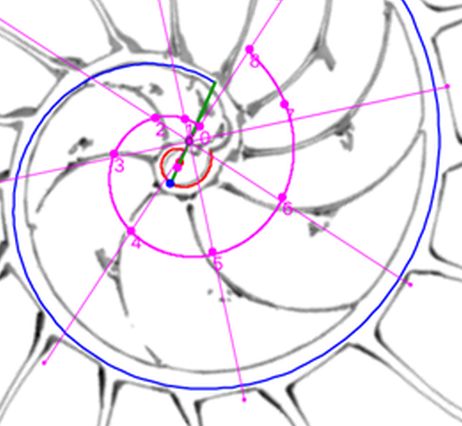
Para modelar los arcos de los septos en este verticilo, busquemos inicialmente cuales serían sus polos $\color{magenta} S_n (S_{n_x},S_{n_y})$ y, para ello, podemos utilizar la , donde activando el botón cuya imagen es una espiral en color negro 
disponemos de una espiral cordobesa que podemos desplazar cambiando su polo, así como escalarla adecuadamente para que se adapte a cada uno de esos septos. Su uso nos permite tabular las coordenadas de sus polos y verificar, en una primera aproximación, que cada septo tiene un factor de escala (o ángulo de retardo) diferente.
Los valores obtenidos están reflejados en la tabla de la .
|
Polo septo n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
$\color{magenta} S_{n_x}$ |
0,110 |
0,056 |
-0,057 |
-0,212 |
-0,150 |
0,160 |
0,425 |
0,430 |
0,300 |
|
$\color{magenta} S_{n_y}$ |
0,217 |
0,246 |
0,250 |
0,111 |
-0,180 |
-0,260 |
-0,050 |
0,300 |
0,510 |
|
|
Factor escala en el septo n |
|
|
|
|
|
|
|
|
|
|
Y usando de nuevo la espiral auxiliar de color negro, comprobamos que los polos $\color{magenta} S_n$ son puntos de la espiral cordobesa:
$$\color{magenta} \begin{cases} x=0,0263+0,4331\kappa^{\alpha} cos(\alpha) \\ y=0,0600+0,4331\kappa^{\alpha} sen(\alpha) \end{cases} \quad \alpha \in [\theta_i, \theta_i+2 \pi] \tag{$3.27$}$$
Podemos verlo en la pulsando el botón 
de la espiral magenta.
En esta espiral de los polos de los septos observamos que:
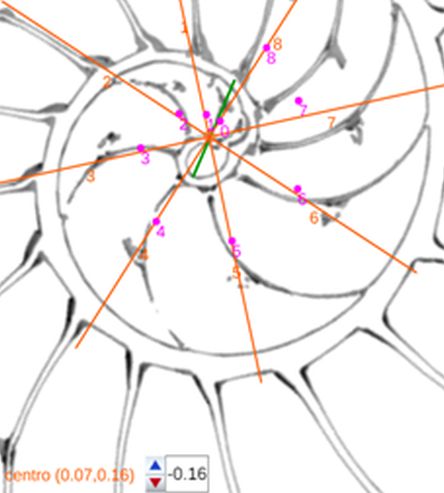
La determinación de este punto puede hacerse usando un haz de rectas de paso $\frac{\pi}{4}$ que podamos posicionar con un control gráfico y a su vez girarlo con otro control. Esta herramienta la tenemos disponible pulsando el botón 
en la . Al hacerlo vemos un haz de rectas que puede desplazarse desplazando su centro y girarse con un pulsador que cambia el ángulo de giro con una medición relativa al eje polar. En este caso cuando ese centro está posicionado en $\color{magenta} C_s$ y el giro relativo es $-0.16$ es cuando aproximadamente se ajusta mejor, siendo el polo séptimo $\color{magenta} S_7$ el que queda más desajustado (ver ).). ¿Tiene esa posición una razón especial, un porqué especial?|
Perspectiva desde la que el paso angular entre los polos de los septos en el primer verticilo es constante
. |
|
|
|
|
|
|
Así pues, la base constructiva que estamos siguiendo para la determinación del modelo nos marca que éste puede obtenerse mediante un procedimiento inverso al realizado en la experimentación y simulación anterior, es decir:
Para modelar los arcos de los septos en este primer verticilo acudamos de nuevo al principio de tangencialidad entre los septos y la pared ventral que ya aplicamos en el segundo y tercer verticilo (ver ) e igualmente a lo allí analizado, los puntos de tangencia $\color{blue} T_n$
comunes a ambas curvas, han de estar alineados con el polo ventral $\color{blue} P_v$ y con los polos de los septos $\color{magenta} S_n$. Así pues, para determinar cada punto $\color{blue} T_n$, intersequemos cada una de las semirrectas que contienen a los segmentos $\overline{\color{blue} P_v \color{magenta} S_n}$ con la espiral (3.25) y, para ello, nos basta hallar el paso angular $\varepsilon_n$ existente entre cada polo septal y el semieje polar $\overline{\color{blue} P_v \color{red} P_D}$ ya que con él obtenemos para $0 \le n \le 8 $ las coordenadas de
$$\color{blue} T_n(\kappa^{\theta_i + \varepsilon_n} \, cos(\theta_i + \varepsilon_n), \kappa^{\theta_i + \varepsilon_n} \, sen(\theta_i + \varepsilon_n)) \tag{3.28}$$
Estos puntos están representados en la y pueden verse en la pulsando el botón 
.
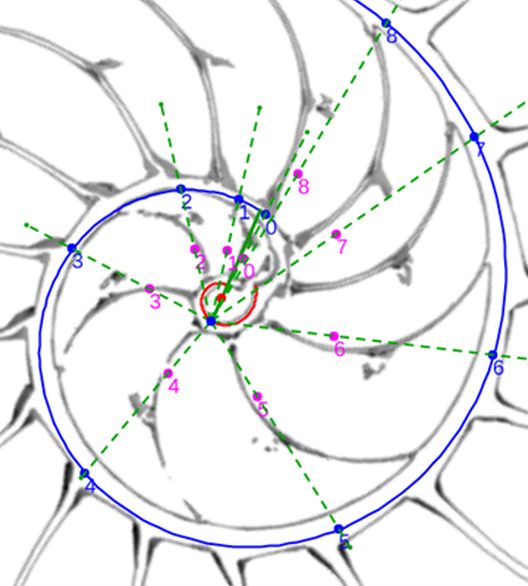
Para calcular los ángulos $\varepsilon_n, 0 \le n \le 8$, determinamos primero $\varepsilon_0 = \widehat{\color{red} P_D \color{blue} P_V \color{magenta} S_0} = -0,06=-3º$ y los ángulos $\eta_n = \widehat{ \color{magenta} S_n \color{blue} P_V \color{magenta} S_{n+1}} $ para $ 0 \le n \le 7$ que son los ángulos formados por las líneas discontinuas pintadas en color verde en la . Conocidos estos, tenemos $\varepsilon_n=\varepsilon_{n-1}+\eta_n$, $0 \le n \le 8$. Los valores de los ángulos citados están reflejados en la tabla de la .
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
$\eta_n $ |
0,25 |
0,45 |
0,86 |
1,36 |
1,25 |
0,90 |
0,73 |
0,43 |
|
|
14° |
26° |
49° |
78° |
72° |
52° |
42° |
25° |
|
|
|
$\varepsilon_n$ |
-0,06 |
0,19 |
0,64 |
1,50 |
2,86 |
4,11 |
5,01 |
5,74 |
6,17 |
|
-3° |
11° |
37° |
86° |
164° |
236° |
288° |
330° |
355° |
Adicionalmente, si incidimos en la búsqueda del paso angular de $\frac{\pi}{4}$, podemos emparejar esos puntos $\overline{\color{blue} T_0 T_4}$, $\overline{\color{blue} T_1 T_5}$ $\overline{\color{blue} T_2 T_6}$, $\overline{\color{blue} T_3 T_7}$ y $\overline{\color{blue} T_4 T_8}$ y ver qué acontece con su intersección. En la imagen de la , puede observarse que salvando el segmento $\overline{\color{blue} T_3 T_7}$ (ya observamos que $\color{magenta} S_7$ quedaba algo desplazado respecto al paso teórico de $\frac{\pi}{4}$ y, consecuentemente esto se traslada a $\color{blue} T_7$), esos segmentos se intersecan en torno a un punto que vamos a denominar $\color{blue} C_v$. Con la herramienta auxiliar usada anteriormente, accesible desde el botón en la , podemos determinar aproximadamente sus coordenadas: $\color{blue} C_v(0,14, 0,32)$, ver la . Se verifica que $\overline{\color{blue} P_v C_v}=4 \overline{\color{blue} P_v \color{red} P_D} $.
En la disponemos del botón 
que permite ver el modelo obtenido, que está reflejado también en la .
|
Perspectiva desde la que el paso angular entre los puntos de tangencia ventrales en el primer verticilo es constante e igual a $\frac{\pi}{4}$
. |
|
|
|
|
|
|
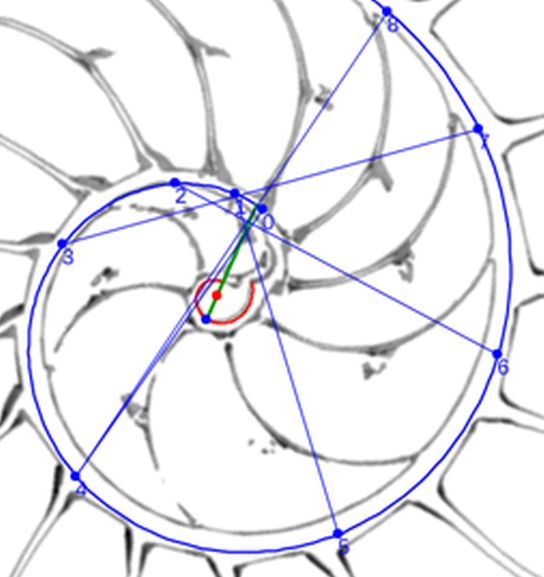
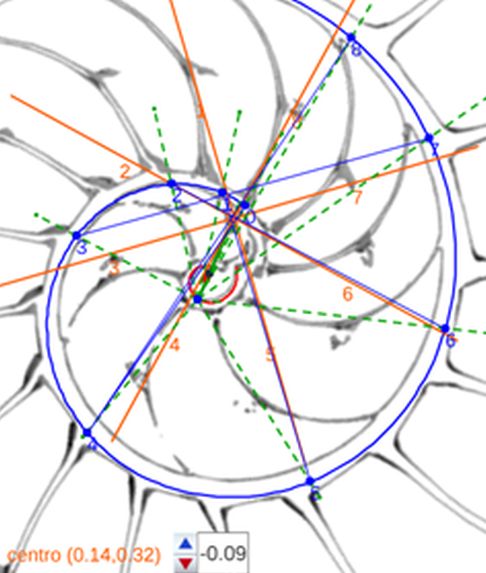
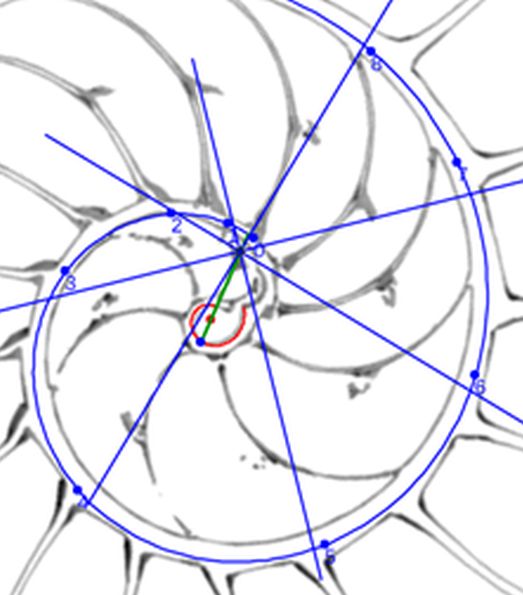
Conocidos los puntos de tangencia $\color{blue} T_n$ y los polos de los septos $\color{magenta} S_n$ procedamos a determinar la ecuación de cada uno de los arcos de los septos en este primer verticilo. En la tabla de la se refleja la proporción existente entre $\overline{\color{magenta} S_n \color{blue} T_n}$ y $\overline{\color{blue} P_v T_n}$ para $0 \le n \le 8$, es decir, entre el radio vector del arco del septo n-ésimo y el radio vector de la pared ventral, ambos en el punto de tangencia $\color{blue} T_n$ y el mismo ángulo $\color{blue} \theta_i +\varepsilon_n$. Así pues, $\overline{\color{magenta} S_n \color{blue} T_n}$ $=a_n \overline{\color{blue} P_v T_n}$ y, por tanto, $\overline{\color{magenta} S_n \color{blue} T_n}$ $=a_n \color{blue} \kappa^{\color{blue}\theta_i+ \varepsilon_n}$ y, consecuentemente, el arco de ese septo queda definido como:
$$ \begin{cases} \color{lime}x= \color{magenta}S_{n_x}\color{lime}+ a_n \, \kappa^{\sigma} cos(\sigma) \\ \color{lime} y=\color{magenta}S_{n_y}\color{lime}+ a_n \, \kappa^{\sigma} sen(\sigma) \end{cases} \quad \color{lime} \sigma \in [\color{blue}\theta_i+ \varepsilon_n-\color{lime} \lambda_n, \color{blue}\theta_i+ \varepsilon_n ] \tag{3.29}$$
donde $\color{lime} \lambda_n$ es el ángulo que determina la amplitud de ese arco y que tendremos que determinar.
|
$\color{blue} \theta_i=-5,12$ n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Podemos observar que los coeficientes obtenidos se corresponden con los factores de escala determinados experimentalmente en la tabla de la . Y aquí observamos que la causa de que las
cámaras y los septos del Nautilus sean diferentes en el primer verticilo es como consecuencia de que la espiral ventral y la espiral de los polos tienen diferente polo y, consecuentemente, cambia la razón de las distancias entre el polo ventral y los puntos de tangencia $\overline{\color{blue} P_v T_n}$ y la de cada uno de los polos de los septos con dicho punto de tangencia $\overline{\color{magenta} S_n \color{blue} T_n}$ ().
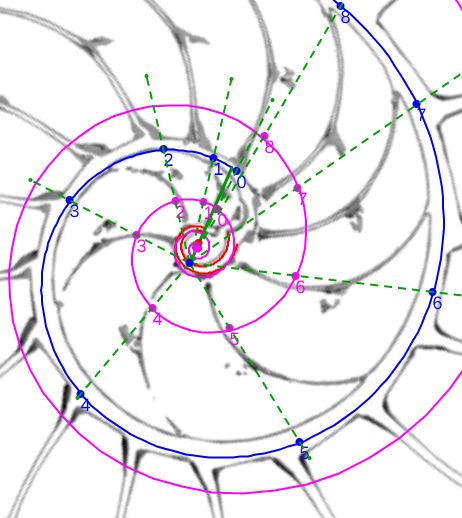
En la ecuación de los septos (3.29) el único parámetro por determinar para cada septo es su amplitud $\color{Lime} \lambda_n$ y para ello, dado que conocemos un extremo del arco del septo, que es el punto de tangencia $\color{blue} T_n$, podemos determinar el punto de intersección con la pared dorsal que vamos a denominar $\color{red} D_n$.
Igualando las coordenadas del punto común en (3.26) y (3.29) tenemos:
$$ \begin{cases} {\color{magenta}S_{n_x}} - {\color{red} D_x \color{lime}}+ a_n {\color{lime} \kappa^{\color{blue} \theta_i+\varepsilon_n \color{lime} - \lambda_n} \, cos({\color{blue} \theta_i+\varepsilon_n \color{lime} - \lambda_n} )}= \color{red} a \, \color{lime} \kappa^{\color{blue} \theta_i+\color{lime} \rho_n} cos({\color{blue} \theta_i+\color{lime} \rho_n}) \\ {\color{magenta}S_{n_y}\color{lime}} - {\color{red} D_y \color{lime}}+ a_n {\color{lime} \kappa^{\color{blue} \theta_i+\varepsilon_n \color{lime} - \lambda_n} \, sen({\color{blue} \theta_i+\varepsilon_n \color{lime} - \lambda_n} )} = \color{red} a \, \color{lime} \kappa^{\color{blue} \theta_i+\color{lime} \rho_n} sen({\color{blue} \theta_i+\color{lime} \rho_n}) \end{cases} \tag{3.30}$$
donde $\color{lime} \rho_n$ es el ángulo cuyo vértice es el polo dorsal $\color{red} P_D$, un lado el eje inicial y otro la semirrecta que une $\color{red} P_D$ con el punto de corte buscado $\color{red} D_n$ y $\color{red} a$ es el valor correspondiente a la pared dorsal que según lo hallado con anterioridad sería $\color{red} a = \kappa^{-4 \pi}$, pero que vamos a expresar de manera genérica como $\color{red} a = \kappa^{-\omega}$ porque posteriormente veremos que será necesario reproducir el cálculo con otro valor.
Elevando al cuadrado en ambas igualdades de (3.30), sumándolas y simplificando obtenemos que:
$${\color{red} \kappa^{-2 \omega} \, \kappa^{\color{blue} 2 \theta_i+\color{lime} 2 \rho_n}} = N({\color{lime} \lambda_n}) \tag{3.31}$$
Es decir,
$${\color{lime} \rho_n}= {\color{blue} \theta_i}+{\color{red} \omega} + log_\kappa \sqrt{N({\color{lime} \lambda_n})} \tag{3.32}$$
siendo
$$ \begin{aligned} N({\color{lime} \lambda_n}) &=({\color{magenta}S_{n_x}} - {\color{red} D_x \color{lime}}+ a_n {\color{lime} \kappa^{\color{blue} \theta_i+\varepsilon_n \color{lime} - \lambda_n} \, cos({\color{blue} \theta_i+\varepsilon_n \color{lime} - \lambda_n} )})^2 \\ &+ ({\color{magenta}S_{n_y}} - {\color{red} D_y \color{lime}}+ a_n {\color{lime} \kappa^{\color{blue} \theta_i+\varepsilon_n \color{lime} - \lambda_n} \, sen({\color{blue} \theta_i+\varepsilon_n \color{lime} - \lambda_n} )})^2 \end{aligned} \tag{3.33}$$
Luego la determinación de $\color{lime} \lambda_n$ y $\color{lime} \rho_n$ puede realizarse resolviendo el sistema:
$$ \begin{cases} {\color{magenta}S_{n_x}} - {\color{red} D_x \color{lime}}+ a_n {\color{lime} \kappa^{\color{blue} \theta_i+\varepsilon_n \color{lime} - \lambda_n} \, cos({\color{blue} \theta_i+\varepsilon_n \color{lime} - \lambda_n} )}= \color{red} \kappa^{-\omega} \, \color{lime} \kappa^{\color{blue} \theta_i+\color{lime} \rho_n} cos({\color{blue} \theta_i+\color{lime} \rho_n}) \\ {\color{lime} \rho_n}= {\color{blue} \theta_i}+{\color{red} \omega} + log_\kappa \sqrt{N({\color{lime} \lambda_n})} \end{cases} \tag{3.34}$$
La resolución numérica de (3.34) podemos realizarla usando la y, dado que puede haber más de una raíz, hemos de tener en consideración que la amplitud del septo tomará
aproximadamente valores en el intervalo $[\frac{\pi}{2},\pi]$ (pudiendo ser algo superior como veremos) y el ángulo en el intervalo $[-\frac{\pi}{2} , 2\pi]$.
Tomando ${\color{red} \omega} = {\color{red}4 \pi}$, que es el valor considerado para la pared dorsal, la resolución nos conduce a los valores representados en la tabla de la . En ella, no se ha considerado el septo octavo ya que su intersección no se produce con la pared dorsal, sino que lo hace con el septo cero, es decir, con la concha embrionaria. Adicionalmente, la intersección obtenida para el primer y segundo septo no es la adecuada (se ha puesto en color rojo solo a nivel informativo) ya que realmente ésta no ocurre para este valor ${\color{red} \omega} = {\color{red}4 \pi}$ (ver ), será necesario considerar cierto grosor en esa pared ―lo cual se corresponde con la situación real, aunque inicialmente lo omitamos en el mundo matemático― para que se produzca el corte esperado.
|
$\color{blue} \theta_i=-5,12$ n |
|
|
|
|
|
|
|
|
|
|
|
$\varepsilon_n$ |
-0,06 |
0,19 |
0,64 |
1,50 |
2,86 |
4,11 |
5,01 |
5,74 |
6,17 |
|
|
${\color{blue}\theta_i}+\varepsilon_n$ |
-5.18 |
-4,93 |
-4.48 |
-3,62 |
-2,26 |
-1,01 |
-0,11 |
0,62 |
1,05 |
|
|
|
||||||||||
|
Dorsal -4 π |
Resolución numérica del sistema (3.34) |
|||||||||
|
$\quad \color{lime}\lambda_n$ |
2,28 |
3,45 |
3,10 |
2,67 |
2,89 |
3,15 |
3,22 |
3,12 |
|
|
|
|
131° |
198° |
178° |
153° |
166° |
181° |
185° |
179° |
|
|
|
|
||||||||||
|
${\color{blue}\theta_i}+ \varepsilon_n - {\color{lime}\lambda_n} $ |
-7,46 |
-7,88 |
-7,38 |
-6,28 |
-5,15 |
-4,15 |
-3,33 |
-2,49 |
|
|
|
|
||||||||||
|
$\color{lime}\rho_n$ |
5,38 |
3,19 |
2,67 |
1,50 |
2,12 |
3,04 |
4,36 |
5,23 |
|
|
|
$\color{lime}\rho_n$ |
-51° |
183° |
153° |
86° |
121° |
175° |
250° |
300° |
|
|
|
|
||||||||||
|
$\color{red}D_{n_x}$ |
0,1544 |
0,0059 |
-0.0235 |
-0,0213 |
-0,0344 |
-0,0046 |
0,1110 |
0,1540 |
|
|
|
$\color{red}D_{n_y}$ |
0,1101 |
0,1597 |
0,1309 |
0,1097 |
0,0670 |
0,0070 |
0,0099 |
0,0938 |
|
|
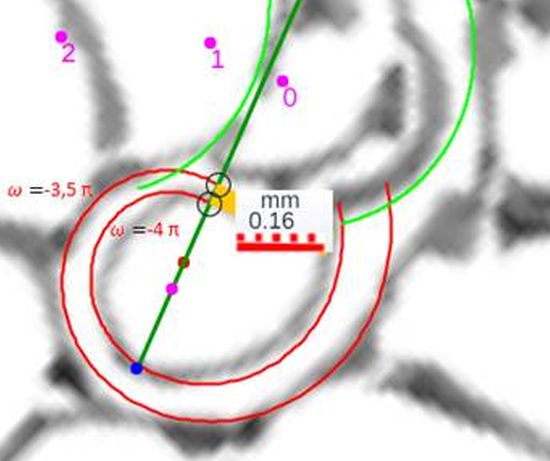
Utilizando la y, en concreto, la herramienta de medida de ángulos y las coordenadas del punto en que se posiciona el ratón pulsando clic (ver ) podemos verificar los resultados anteriores y aportar los valores correspondientes a los septos primero y segundo. Esos datos están reflejados en la .
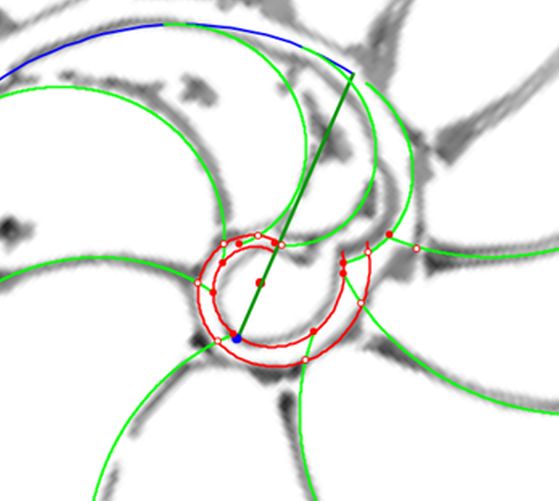
Si consideramos la espiral dorsal determinada con $\color{red}\omega= -3,5 \pi$, en la tabla de la está reflejados los datos obtenidos mediante la resolución del sistema (3.34) y manualmente en el caso del septo octavo. Puede observarse en la , la cual se ha obtenido con la .
|
$\color{blue} \theta_i=-5,12$ n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Dorsal $-4\pi$ |
|||||||||
|
$\color{lime}\lambda_n$ |
2,28 |
2,95 |
2,90 |
2,66 |
2,89 |
3,14 |
3,22 |
2,87 |
2,73 |
|
|
131° |
169° |
166° |
152° |
166° |
180° |
185° |
164° |
156° |
|
|
|||||||||
|
$\color{lime}\rho_n$ |
-0,91 |
0,05 |
0,91 |
1,52 |
2,16 |
3,05 |
4,38 |
5,24 |
|
|
|
-52° |
3° |
52° |
87° |
124° |
175° |
251° |
300° |
|
|
|
|||||||||
|
$\color{red}D_{n_x}$ |
0,1544 |
0,0539 |
0,0036 |
-0,0213 |
-0,0344 |
-0,0046 |
0,1110 |
0,1540 |
0,22 |
|
$\color{red}D_{n_y}$ |
0,1101 |
0,1389 |
0,1365 |
0,1097 |
0,0670 |
0,0070 |
0,0099 |
0,0938 |
0,15 |
|
$\color{blue} \theta_i=-5,12$ n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
$\varepsilon_n$ |
-0,06 |
0,19 |
0,64 |
1,50 |
2,86 |
4,11 |
5,01 |
5,74 |
6,17 |
|
${\color{blue} \theta_i}+\varepsilon_n$ |
-5.18 |
-4,93 |
-4.48 |
-3,62 |
-2,26 |
-1,01 |
-0,11 |
0,62 |
1,05 |
|
|
|
|
|
|
|
|
|
|
|
|
Dorsal $-3,5\pi$ |
|
||||||||
|
$\color{lime}\lambda_n$ |
1,96 |
2,84 |
2,66 |
2,53 |
2,80 |
3,07 |
3,09 |
2,98 |
2,84 |
|
|
112° |
163° |
152° |
145° |
160° |
176° |
177° |
171° |
163° |
|
|
|
|
|
|
|
|
|
|
|
|
${\color{blue} \theta_i}+\varepsilon_n-\color{lime}\lambda_n$ |
-7,14 |
-7,77 |
-7,14 |
-6,15 |
-5,06 |
-4,08 |
-3,20 |
-2,36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
$\color{lime}\rho_n$ |
5,39 |
-0.09 |
0,44 |
1,13 |
2,01 |
2,85 |
4,03 |
4,87 |
|
|
|
-51° |
-5° |
25° |
65° |
115° |
163° |
231° |
279° |
|
|
|
|
|
|
|
|
|
|
|
|
|
$\color{red}D_{n_x}$ |
0.1901 |
0.0653 |
0.0303 |
-0.0184 |
-0.0557 |
-0.0280 |
0.0987 |
0,1796 |
0,26 |
|
$\color{red}D_{n_y}$ |
0.1246 |
0.1357 |
0.1492 |
0.1369 |
0.0804 |
-0.0035 |
-0.0309 |
0,0515 |
0,13 |
Por otra parte, adicionalmente, usando la herramienta para la visualización del paso $\frac{\pi}{4}$ en la , podemos observar si las intersecciones de los septos con la pared dorsal desde algún punto siguen esa distribución:
|
|
|
|
|
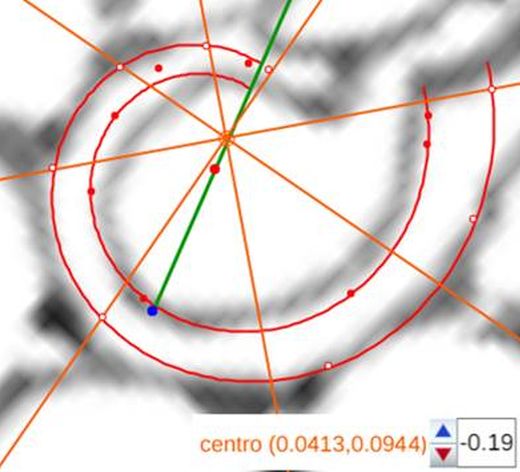
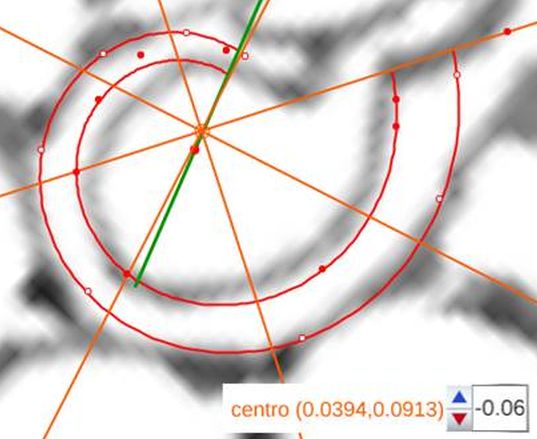
Y, también, podemos observar cuál es la perspectiva de paso $\frac{\pi}{4}$ para la intersección de los septos con el sifúnculo en este primer verticilo () donde desde el punto $\color{gold} C_{S_f}(0,105, 0,2400)$ y con un ángulo de desviación respecto al eje polar de $-0,06$ se hacen coincidir las intersecciones correspondientes a los septos segundo al séptimo.
A lo largo del análisis realizado hemos encontrado algunos puntos que podemos catalogar como puntos notables del Nautilus que son los que nos han permitido fundamentar y dar la explicación matemática a su ontogenia:
Y también hemos detectado, en la búsqueda de una regularidad en la irregularidad observable a primera vista, la posible existencia teórica de otros que podemos catalogar como puntos destacables, y que son los centros desde los que se observa un paso de $\frac{\pi}{4}$ entre puntos de análoga procedenciaEn una fase anterior de este estudio se realizó una primera aproximación de los valores de los centros y que aquí modificamos, la introducción de la tangencialidad de los septos y el cálculo de las intersecciones ventrales y dorsales ha permitido ubicar teóricamente mejor dichos centros.:
Unos y otros están reflejados en la y se ubican en el eje que hemos denominado polar, el cual marca el ángulo inicial común a todas las espirales cordobesas involucradas en el estudio y es el comienzo de la fase de crecimiento post embrionario.
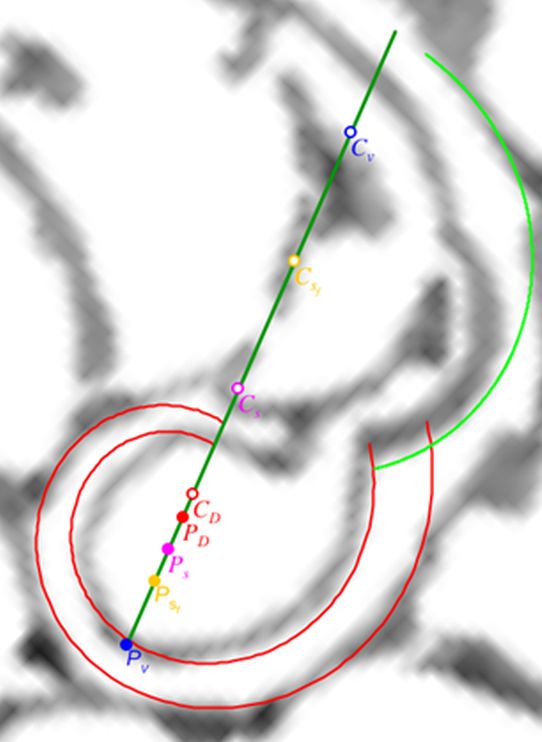
La relación existente entre los puntos notables ha quedado reflejada anteriormente y puede resumirse en:
Y la de estos puntos notables con los puntos destacables:
Relaciones, cuya causalidad queda abierta a futuras sinapsis neuronales de quienes profundicen en esta investigación.
En la el botón 
nos permite visualizar su localización y las relaciones, también puede observarse en la .
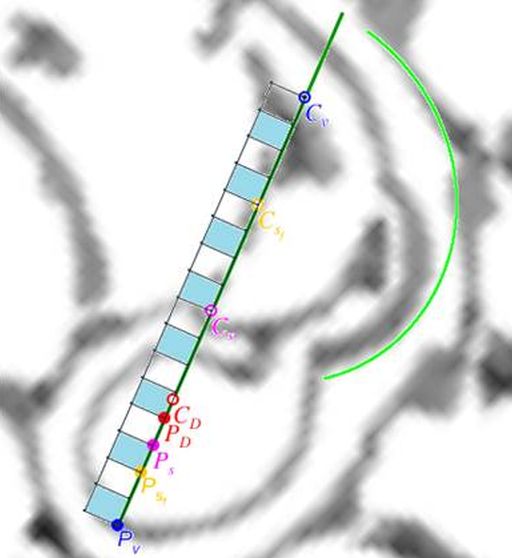
Adicionalmente a lo analizado hasta ahora, en el primer verticilo del Nautilus encontramos algunos sitios que podemos catalogar como singulares, pues se muestran como específicos respecto a su entorno o que, aparentemente, se salen de la uniformidad cordobesa que hemos ido detectando y desgranando en los capítulos anteriores sobre la "Ontogenia matemática del Nautilus". Pero, hasta en estas situaciones, la proporción cordobesa y la espiral cordobesa aparece sin más que rascar matemáticamente en la concha del Nautilus, por supuesto con gran mimo.
Esos sitios singulares son:
|
|
|
|
|
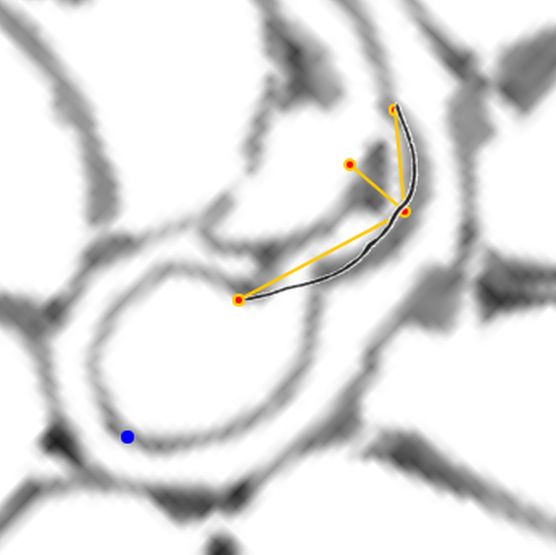
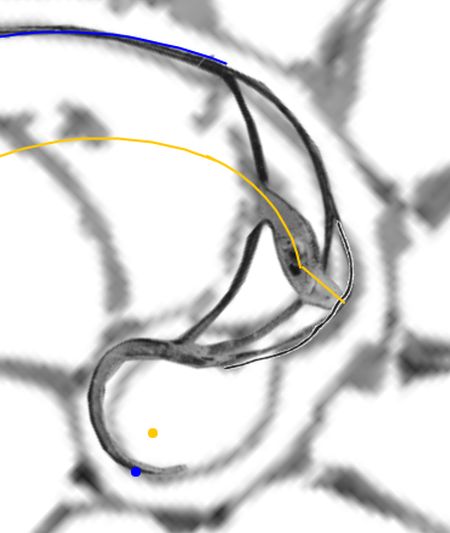
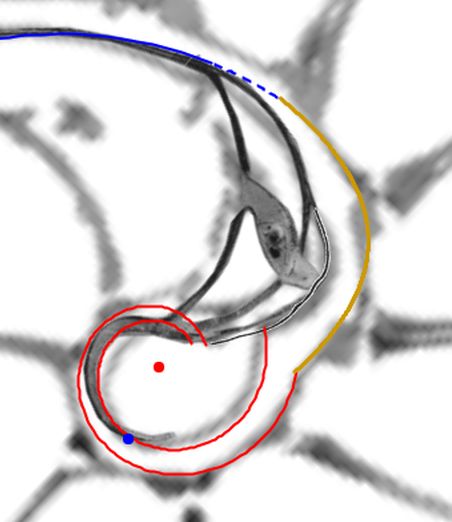
En este capítulo analizamos estas singularidades y encuadramos su modelado en el contexto cordobés del Nautilus. Para ello, acudimos y aplicamos el invariante enunciado desde el inicio y que reiteradamente hemos ido aplicando en toda la modelación:
"Todo punto interior a la concha o sobre ella se obtiene como la intersección de dos espirales cordobesas, una longitudinal similar a la ventral y otra transversal similar a la septal"
La es la que nos ha servido de base para efectuar el análisis de estos sitios singulares y en la podemos observar el modelo al que llegaremos.
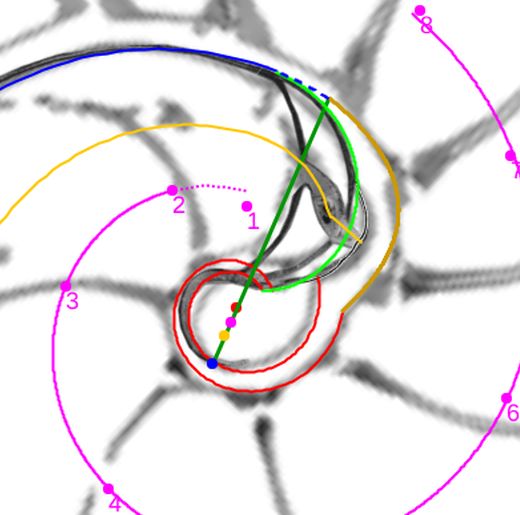
En nuestro planteamiento teórico, la concha embrionaria la hemos aproximado de manera análoga a los otros septos, es decir, como un arco de espiral cordobesa, asimilándola a un septo primigenio que hemos ordenado y enumerado como septo cero, pero es obvio que ese ajuste fue algo meramente coyuntural para salvar el desconocimiento de su forma exacta inicial y, por
ello, excluiremos ese septo del modelo final. En la (procedente de Tanabe and Uchiyama, 1997
En Galo et al. (2016)
Usando la , podemos contrastar el perfil de la concha embrionaria aportada por Tanabe, and Uchiyama 
, y mediante dos controles gráficos podemos posicionar ese gnomon, desplazarlo y escalarlo para
confrontarlo con ella (en el espacio izquierdo de esa escena se dibuja un paralelogramo para un ajuste mejor y en el derecho el ajuste final).
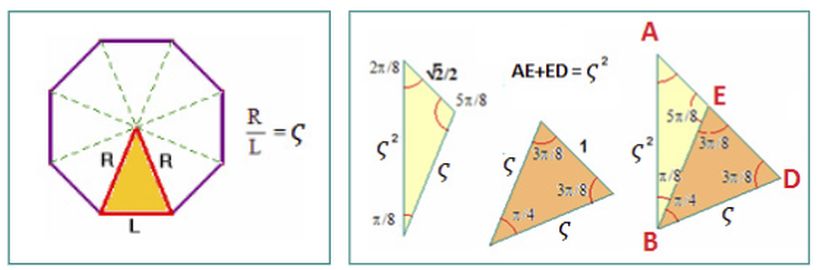
La concha embrionaria podemos ponerla visible pulsando el botón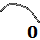 
. Cuando esos controles se posicionan en los puntos $P(0,0864,0,1063)$ y $Q(0,2155,0,1751)$ obtenemos la imagen reflejada en la . En ella: $P$ es la constricción dorsal,$Q$ se ubica en la cicatriz, $R(0,2078,0,2539)$ es la constricción ventral y $H(0,1723,0,2107)$ es el pie de la altura trazada desde $Q$.
Adicionalmente observamos que el segmento $\overline{P R}$ que une la constricción dorsal con la ventral se ubica en la semirrecta que pasa por el polo ventral $\color{blue} P_v$ y ésta forma un ángulo con el eje inicial de $-0,27$ radianes. Pero también nos encontramos con una nueva sorpresa, pues el segmento $\overline{P Q}$ está en la semirrecta que pasa por el polo dorsal $\color{red} P_D$, formando ésta un ángulo de $-0.69$ radianes con el eje inicial.
En las imágenes de la se refleja ese gnomon en una triple comparativa que se corresponde con las fases embrionaria, la del primer septo y la del segundo (éstas se obtienen pulsando los botones , 
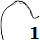y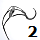 
en la ). Y ahora lo que se comprueba es que el sifúnculo en la primera cámara septal sigue la dirección de la altura $\overline{Q H}$ de este triángulo gnomon.
|
|
|
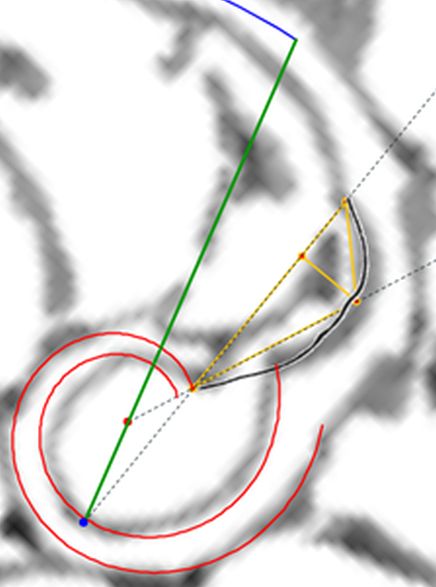
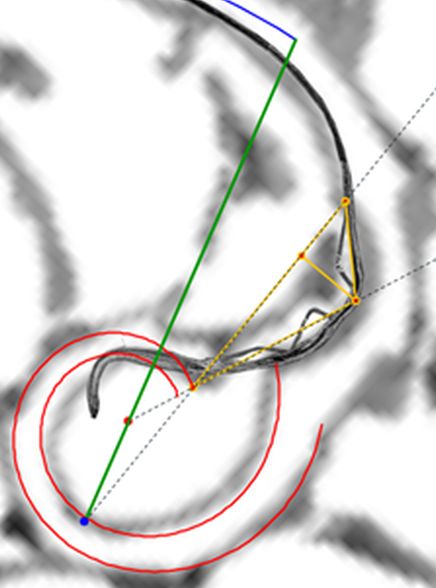
| A. Gnomón cordobés y concha embrionaria. | B. Gnomón cordobés y fase del primer septo. | C. Gnomón cordobés y fase del segundo septo. |
|
|
||
|
|
||
En el primer septo podemos distinguir dos fases: una correspondiente a la formación de la primera cámara septal al cerrar la concha embrionaria en la constricción dorsal $P$ y en la ventral $Q$, y otra en la que este septoPara ser más precisos, quizás deberíamos decir que es la concha embrionaria la que se extiende adoptando la misma forma que el primer septo. Biológicamente es distinguible por el tipo de sedimentos ―.C―, pero matemáticamente no es trascendente e identificamos ambas capas en una única línea. amplía su longitud hasta el primer punto de tangencia con la pared ventral $\color{blue}T_1$ (3.28). Ver la .
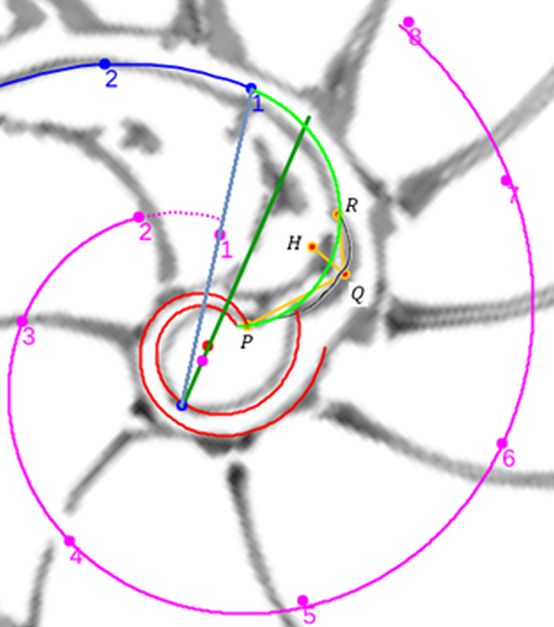
La imposición de que el primer septo pase por los puntos $P$ y $R$ y sea tangente en $\color{blue}T_1$, lo cual adicionalmente obliga a que el polo $\color{magenta} S_1$ de este septo esté incluido en el segmento $\overline{\color{blue} P_v T_1}$, nos fuerza a rectificar la posición que previamente habíamos considerado en (3.29) para $n=1$ o, más bien, a ubicarlo con más certeza y/o respaldo. Imponiendo estas condiciones determinamosSe tienen suficientes datos para hacerlo analíticamente y también de manera aproximada en la se dispone de la herramienta “espiral cordobesa”, accesible desde el botón 
. que la ecuación de este primer septo se ha de corresponder con:
$$ \begin{cases} {\color{lime}x= \color{magenta}0.0499 \color{lime}\, + \,} 0,4571 \, {\color{lime}\kappa^{\sigma} cos(\sigma)} \\ {\color{lime} y=\color{magenta} 0,2277\color{lime} \, + \,} 0,4571 \, {\color{lime} \kappa^{\sigma} sen(\sigma) } \end{cases} \quad \color{lime} \sigma \in [\color{blue}\theta_i-\color{lime} 2,42, \color{blue}\theta_i-\color{lime} 0,97 ] \tag{4.1}$$
donde el valor inferior en el intervalo $\color{lime} \rho = \color{blue}\theta_i \, \color{lime}- 2,42 = -7.54 \,$ es el argumento correspondiente a $P$, que es también el punto de inicio de la pared dorsal con ángulo de retardo $―3,5 \pi$, y para el valor superior $\color{lime} \rho = \color{blue}\theta_i \, \color{lime}- 0,97 = -6,09 \,$ tenemos $R$.
Hay que reseñar que el nuevo polo $\color{magenta}S_1 (0,0499,0.2277)$ obtenido para este septo ya no se ubica en la espiral de polos de los septos cuya ecuación es (3.27), sino que está trasladado respecto a ella. Pero como veremos a continuación, en la segunda cámara septal también acontece una traslación del sifúnculo al producirse una ampliación del fragmocono y, por tanto, esta aparente excepcionalidad hemos de encuadrarla en los cambios que acontecen en esta cámara que se muestra tan especial.
Cerrada la primera cámara con el arco de espiral descrito en (4.1), éste se prolonga hasta el punto $\color{blue} T_1$, es decir, $\color{lime} \rho$ en (4.1) va incrementando su valor en el intervalo $\color{lime}[-6,09,-4.93]$, y si consideramos también su intersección con la espiral dorsal con
ángulo de retardo $-4 \pi$, también $\color{lime} \rho$ decrementaría tomando valores en el intervalo $\color{lime} [-7.66,-7.54]$.
Para acotar el fragmocono correspondiente a la concha embrionaria determinemos analíticamente las espirales cordobesas que teniendo como polo el ventral $\color{blue} P_v$Parece coherente que en esta fase primigenia optemos por este tipo de espirales, pues el fragmocono en el segundo y tercer verticilo está delimitado por dos espirales cordobesas (realmente la misma) con ese polo $\color{blue} P_v$ común y en el primer verticilo interviene la espiral ventral que es de ese tipo y la espiral dorsal que tiene un polo diferente, pero ésta última se inicia en la segunda cámara. ―aquellas que son del tipo $\color{blue} r=a \, \kappa^\theta$―, pasan respectivamente por las constricciones dorsal y ventral ($P$ y $R$ en la y en la ):
Adicionalmente, ubiquemos también de análoga forma a $H$ y $Q$ ( y ) por su relación con el sifúnculo en la primera cámara septal, datos que usaremos posteriormente:
Y también al punto $\color{blue} T_1$, que además de punto de tangencia del septo es el inicio de la pared ventralEste es un nuevo detalle que precisamos aquí y, por tanto, en la ecuación de la pared ventral (2.1) o (2.2), dado que su trayectoria se inicia en $\color{blue} T_1$, entonces el intervalo donde toma valores $\color{blue} \theta$ es $\color{blue} [\theta_i+\varepsilon_1, \theta_f]$ con $\color{blue} \varepsilon_1 =0.19$ de acuerdo con lo reflejado en la tabla de la ., que está en la espiral en $\color{blue} r=\kappa^\theta$.
Con base en los datos anteriores, el fragmocono embrionario está acotado por las espirales $\color{FireBrick} r=\kappa^{-2\pi} \, \kappa^\theta$ y $\color{FireBrick} r=0,812 \, \kappa^\theta$ y al ir ampliándose el primer septo hacia $\color{blue} T_1$, va aumentando progresivamente su amplitud hasta quedar delimitado por la pared ventral $\color{FireBrick} r=\kappa^\theta$.
En las imagenes A y B de la puede observarse este cambio en el fragmocono y también pulsando el botón 
en la . En esas figuras, para reflejar la ampliación del fragmocono, se han tomado diez puntos ubicados en la parte ampliada de este primer septo, dibujados en color verde, y que están angularmente equiespaciados, es decir, que se corresponden con una partición uniforme del intervalo $\color{lime}[-6,09,-4.93]$ y en color marrón se han reflejado sendos arcos de espirales copolares, con polo $\color{blue} P_v$, y que pasan respectivamente por esos diez puntos. Se observa, que la distribución de esos arcos no es uniforme y, por tanto, que la ampliación del fragmocono acontece de manera no uniforme, crece más rápido inicialmente para estabilizarse después convergiendo a la espiral que será la pared ventral $\color{blue} r=\kappa^\theta$.
El incremento en la amplitud del fragmocono puede interpretarse que es un recurso o adaptación biológica mediante la que se aumenta sustancialmente la capacidad de la segunda cámara (en una relación cúbica, según las reglas de proporcionalidad) y de esta manera se contribuye significativamente a la consecución de la flotabilidad en fases posteriores.
|
|
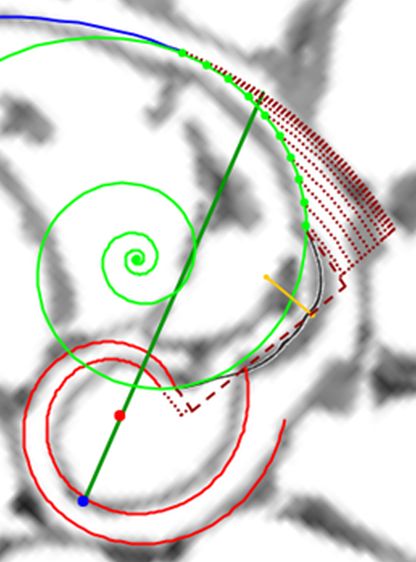
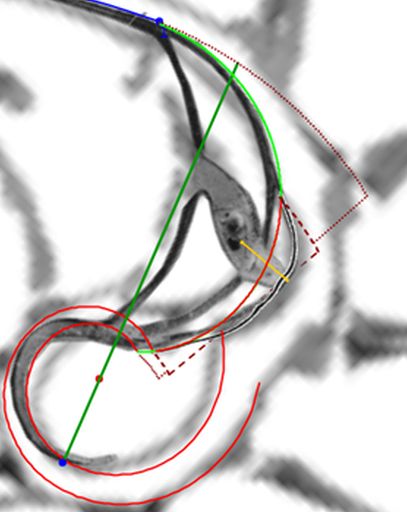
| A. Incremento de la amplitud del fragmocono en el primer septo. Detalle del crecimiento progresivo. | B. Comparación de la amplitud del fragmocono en la concha embrionaria y el primer septo ampliado. |
|
|
|
|
|
|
Observemos que el eje del fragmocono embrionario viene dado por la espiral: $$\color{FireBrick} {r=\frac{\kappa^{-2\pi}+0,8212}{2} \, \kappa^\theta=0,5820 \, \kappa^\theta} \tag{$4.2$}$$ que claramente difiere de la posición que ocupa la parte final del sifúnculo en esta primera cámara $\color{gold} r=0,6813 \, \kappa^\theta$, éste está desplazado respecto al eje y se encuentra más próximo a la pared ventral que a la dorsal. La asimetría de la concha embrionaria causa esa posición asimétrica del sifúnculo y este hecho es de gran interés
ya que si esa posición se mantiene en las cámaras posteriores, lo cual acontece según vimos en (2.7) y (2.8) y en la , entonces el sifúnculo está durante más tiempo en contacto directo con el líquido cameral y, por tanto, la fase de vaciado acoplado (Ward et al. 1981)
El coeficiente de valor $\color{gold}0,6813$ sí está próximo al coeficiente del sifúnculo que a partir de la tercera cámara es $\color{gold} \frac{1+\kappa^{-2\pi}}{2} \simeq 0,6715 \,$ y, éste sí coincide con el coeficiente del eje del fragmocono correspondiente al primer septo ampliado (el que está acotado entre $\color{FireBrick} r=\kappa^{-2\pi} \kappa^{\theta}$ y $\color{FireBrick} r= \kappa^{\theta}$), pero con la particularidad de que, en este primer verticilo, a partir del segundo septo, el polo del sifúnculo $\color{gold}P_{S_f}$ es diferente al ventral y, por ello, está trasladado respecto a dicho eje.
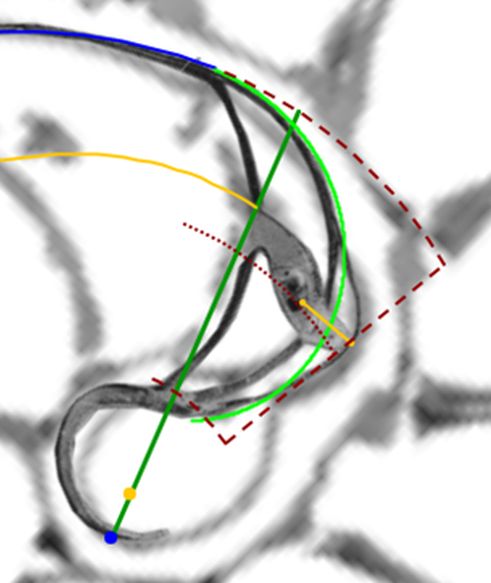
Ver detalle en la , donde el sifúnculo (en color naranja) a partir de la segunda cámara es la traslación del eje del fragmocono (línea marrón de puntos). Estos datos, junto al análisis que haremos en la próxima sección, nos permite explicar la causa de la desviación del sifúnculo en el primer verticilo respecto al eje del fragmocono, aspecto que había quedado abierto en la sección “El canal sifuncular en el primer verticilo”. El sifúnculo en el segundo y tercer verticilo, como ya vimos, sí coincide con el eje del fragmocono.
La variación en la amplitud del fragmocono en el inicio de la fase postembrionaria también va acompañada de una curiosa y, a priori, extraña y llamativa variación del sifúnculo en la segunda cámara septal, que bien acontece en su forma o bien ocurre en su posición (ver la y la ). Es obvio establecer una relación causal entre ambas situaciones y tratar de modelarlo matemáticamente. Un reto, pues este hecho acontece en un corto trayecto y se presenta como una singularidad respecto al comportamiento posterior ―el sifúnculo a partir del segundo septo es una espiral cordobesa que analizamos en (2.7) y (2.8)―. Planteando una analogía en lo que sería un comportamiento humano, en definitiva, un comportamiento animal, ¿qué haría usted, intuitivamente, si va avanzando por un pasillo que progresivamente va ensanchándose? Yo apuntaría a que su posición iría adaptándose al nuevo ancho manteniendo cierta correlación en la distancia a las paredes, es decir, si inicialmente ocupara la posición intermedia en el pasillo, tendería a mantener esa posición media, y si la posición inicial estuviera más cercana a una pared tendería a mantener una relación similar adaptativa al nuevo ancho encontrado, ¿opina igual?
|
|
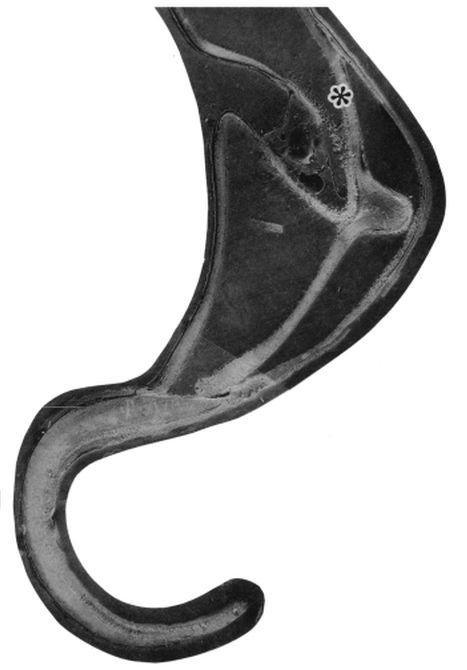
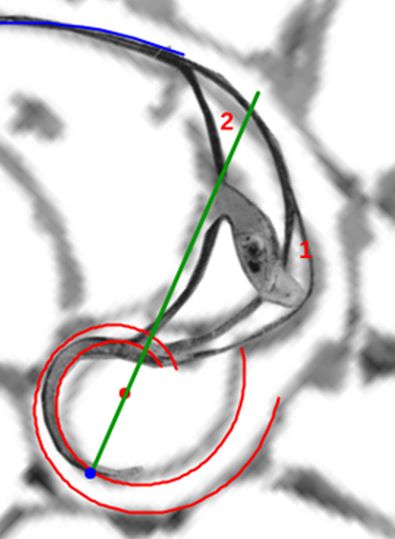
Consecuentemente, aquí establecemos que el incremento que acontece en la amplitud de la segunda cámara septal, respecto a la primera, es la causa del cambio sifuncular observado en esa segunda cámara. Y, desde el punto de vista matemático, entre la alternativa de cambio de forma del sifúnculo o cambio adaptativo a la nueva amplitud manteniendo la forma, optaremos por esta segunda opción aplicando la segunda invariante de nuestro modelo ―el sifúnculo es una espiral cordobesa―. Pero, a su vez, esta adaptación puede plantearse desde dos perspectivas: una mediante un cambio de escala (coeficiente variable con polo común al ventral, es decir, espiral cordobesa $\color{gold} r=a_t \, \kappa^\theta$ con $\color{gold} a_t$ variable en el tiempo $\color{gold} t$) u otra con coeficiente constante y traslación progresiva de la espiral mediante la correspondiente traslación de su polo.
Esta segunda opción puede ser la más plausible, ya que como hemos visto el sifúnculo en el primer verticilo y a partir de la segunda cámara tiene un polo común $\color{gold}P_{S_f}$ diferente del ventral. Así pues, inicialmente coincide su polo con el polo ventral $\color{blue}P_v$ y finalmente queda ubicado en $\color{gold}P_{S_f}$.
Para concretar analíticamente este modelo, quizás, sea conveniente realizar una retrospectiva rápida de lo analizado anteriormente en relación con el sifúnculo, en orden cronológico inverso al de crecimiento. Hemos visto que el sifúnculo:
En base a todo lo indicado, nuestra propuesta para modelar el sifúnculo en la segunda cámara septal establece que todos los puntos de este trozo sifuncular son puntos de la misma espiral cordobesa $\color{gold} r=\frac{1+\kappa^{-2 \pi}}{2} \, \kappa^\theta$, pero con un polo que va trasladándose en la dirección del eje polar y en el sentido de $\overrightarrow{\color{blue}P_v \color{red}P_D}$, en la misma proporción en la que se incrementa el fragmocono al ir ampliándose el primer septo, el polo inicial es el ventral $\color{blue}P_v$ y el final $\color{gold}P_{S_f}$. Formalicemos este modelo (ver y en la pulsando los botones y 
):
$$\color{gold} \begin{cases} x= b_a \kappa^{\theta_i} \, cos(\theta_i) + \frac{\kappa^{-2\pi}+1}{2} \, \kappa^{\theta} cos(\theta_a) \\ y=b_a \kappa^{\theta_i} \, sen(\theta_i) + \frac{\kappa^{-2\pi}+1}{2} \, \kappa^{\theta} sen(\theta_a) \end{cases} \tag{$4.3$}$$
donde $\color{gold} \theta_a= \theta_i+\chi_a$ y $\color{gold} \chi_a$ es el ángulo que forma el punto del primer septo correspondiente a $\color{FireBrick} r= a \,\kappa^\theta$ con el eje polar y
$${\color{gold} b_a}=\overline{\color{blue}P_v \color{gold} P_{S_f}} {\color{FireBrick} \frac{a-0,8212}{1-0,8212}} = 0,1044 \, {\color{FireBrick} \frac{a-0,8212}{1-0,8212}} \tag{$4.4$}$$
$\color{FireBrick} \frac{a-0,8212}{1-0,8212}$ es la proporción entre el incremento del fragmocono al pasar del límite del fragmocono $\color{FireBrick}r=0,8212 \kappa^\theta$ a $\color{FireBrick}r= a \, \kappa^\theta$ y la amplitud final que alcanza el fragmocono al quedar delimitado por las espirales $\color{FireBrick}r=0,8212 \kappa^\theta$ y $\color{FireBrick}r= \kappa^\theta$.
En la se han destacado con dos rombos azules el punto del septo para la espiral etiquetada como $\color{FireBrick}r= \kappa^\theta$ y su correspondiente del sifúnculo. Cada segmento en color magenta une una terna formada por polo del sifúnculo, punto de éste y punto del primer septo que son correspondientes entre sí.
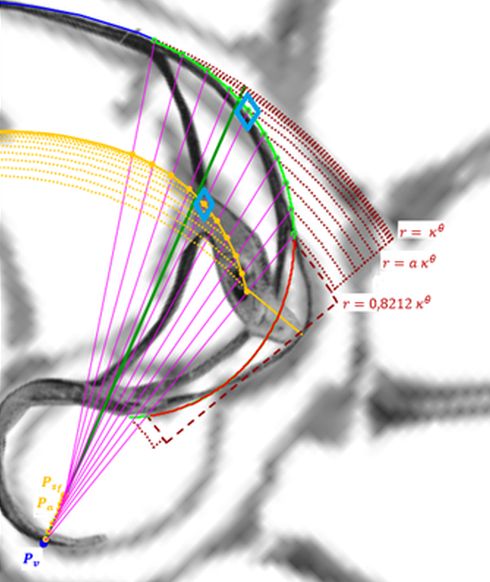
La fase de transición entre el primer y segundo verticilo recoge, a su vez, otra zona difícil de modelar (ver la región pintada en azul en la , realizada sobre el corte que González-Restrepo (2019)
|
|
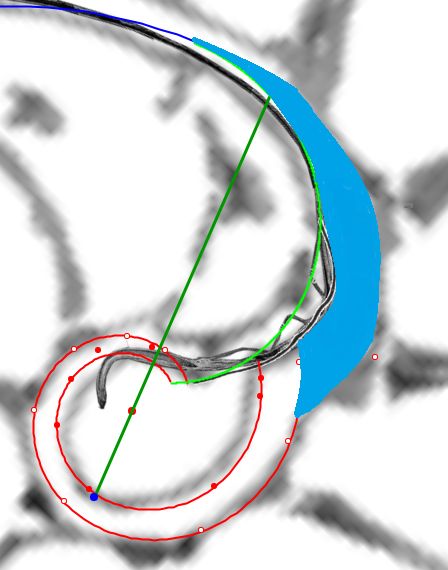
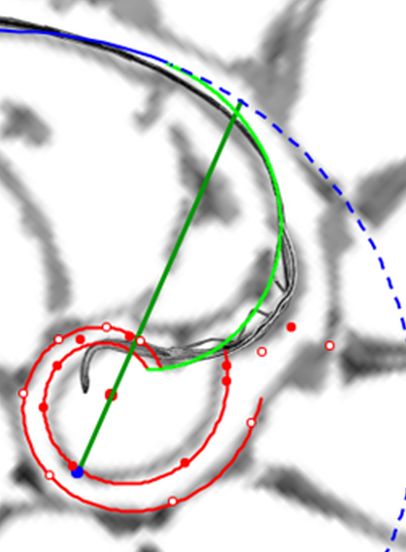
En una primera hipótesis puede pensarse inicialmente que la parte exterior de esa zona podría tener la forma de la espiral ventral inicial, pero en la se observa la gran diferencia existente. Y a
posteriori, después de ver esa imagen, es lógica esa diferencia, pues la situación real es que la pared dorsal es la que ha de adaptarse a la ventral y no al contrario.
Estamos hablando de un recorrido que, a la escala real de esa concha, representa un arco de unos tres o cuatro milímetros que afecta a los septos octavo, noveno y décimo (el undécimo se apoya ya sobre la pared ventral inicial) y comprende una amplitud angular aproximada de $\frac{3 \pi}{8}$ radianes. Un trayecto importante para la continuidad del crecimiento de nuestro Nautilus, que nosotros podemos interpretar inicialmente como un desajuste matemático ―de nuevo, adelanto que una visión ligera y apresurada puede llevarnos a equívocos―, pero que realmente no debe de suponer más que una pequeña incomodidad que ha de salvar este animal y que ésta ha de seguir un patrón continuo, como lo es su crecimiento. Trasladando de nuevo la situación a nuestro contexto humano, mediante otra analogía, ¿qué haríamos nosotros si nos encontramos con un estrechamiento o cambio en un pasillo en el que nos encontramos encajonados? La respuesta es obvia, modificamos levemente nuestro cuerpo, lo menos posible, encogiéndolo un poquito para adaptarnos a ese cambio y así poder sortear el obstáculo. Y es de suponer que eso es lo que hace nuestro Nautilus. Pero ¿cómo se realiza esa adaptación? La respuesta la podemos encontrar en el segundo invariante considerado en este modelo: “Todo punto interior a la concha o sobre ella se obtiene como la intersección de dos espirales, una longitudinal similar a la ventral y otra transversal similar a la septal". Así pues, la adaptación del Nautilus para sortear ese estrechamiento es un pequeño encogimiento corporal que libera el espacio necesario para una pequeña amplificación de la pared dorsal, es decir, que se pueda abordar un cambio de escala sin modificar su forma cordobesa y eso se traduce en puntos de una familia de espirales cordobesas con polo común ―ver la y la expresión funcional (4.5)―, el polo dorsal $\color{red}P_D$, y un factor de escala variable $\color{red} a(\mu)$.
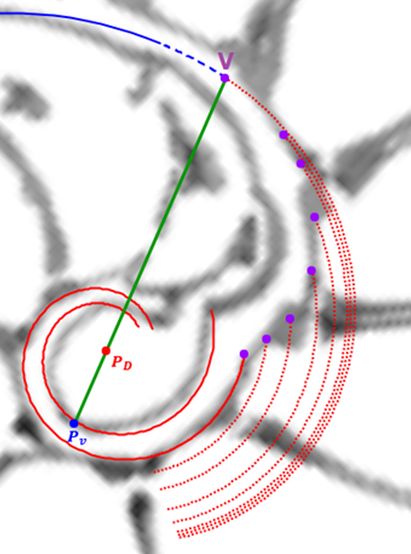
$$\color{red} \begin{cases} x=D_x + a(\mu) \, \kappa^{\theta} cos(\theta) \\ y=D_y + a(\mu) \, \kappa^{\theta} sen(\theta) \end{cases} \quad \theta \in [\theta_i, \theta_i+\mu], \mu \in [\frac{13}{8}\pi, 2 \pi]\tag{$4.5$}$$
El valor $\color{red} \frac{13}{8}\pi$ indicado en (4.5) es el valor observado para la espiral dorsal con factor de escala $\color{red} \kappa^{-3,5 \pi}$, es decir, $\color{red} a(\frac{13}{8}\pi)=\kappa^{-3,5 \pi}$ y la variación que introduce el factor de escala $\color{red}a(\mu)$ permite reflejar el modelo descrito e ir pasando desde la pared dorsal de partida con ese factor a aquella que ha de confluir con la pared ventral inicial para dar continuidad al crecimiento del Nautilus, es decir, la correspondiente a $\color{red}a(2 \pi)$. Estas dos espirales deben de ser tangentes porque es esperable un tránsito suave, regular, y efectivamente es así como acontece porque los tres puntos $\color{blue}P_v$, $\color{red}P_D$ y el que hemos denotado como $\color{DarkViolet}V$ en la son puntos del eje polar, están alineados, y consecuentemente siendo $\overline{\color{blue}P_v \color{DarkViolet}V}$ y$\overline{\color{red}P_D \color{DarkViolet}V}$ los radios polares de dos espirales cordobesas, comparten la misma recta tangente por ser equiangulares. Para hallar el factor de escala correspondiente a esta espiral de radio vector $\overline{\color{red}P_D \color{DarkViolet}V}$ partimos de la relación:
$$\overline{\color{blue}P_v \color{DarkViolet}V}=\overline{\color{blue}P_v \color{red}P_D}+\overline{\color{red}P_D \color{DarkViolet}V} \tag{$4.6$}$$
donde
$$\begin{cases} {\overline{\color{blue}P_v \color{DarkViolet}V}}= {\color{blue} \kappa^{\theta_i}}\\ {\overline{\color{blue}P_v \color{red}P_D}={\sqrt{\color{red} D_x^2 + D_y^2}}
= \color{red} 0,087321} \\{\overline{\color{red}P_D \color{DarkViolet}V}=\color{red} a(2\pi) \, \kappa^{\theta_i+2\pi}} \end{cases} \tag{$4.7$}$$
y, por tanto, en (4.5)
$$ {\color{red} a(2\pi)}={\color{red} \kappa^{-2 \pi}-0,087321 \kappa^{-\theta_i-2 \pi}}={\color{red} \kappa^{-2,44 \pi}} \tag{$4.8$}$$
Así pues,
$$ {\color{red} \kappa^{-3,5 \pi}}={\color{red} a(\frac{13}{8}\pi) \le a(\mu) \le a(2\pi)}={\color{red} \kappa^{-2,44 \pi}} \tag{$4.9$}$$
$\color{red}a(\mu)$ es una función creciente ya que la espiral se amplifica de manera continua para alcanzar la forma de la pared ventral inicial, y también podemos expresarla en función de ángulos de retardo $\color{red}r(\mu)$:
$$\color{red}a(\mu)=\kappa^{r(\mu) \pi} \quad \mu \in [\frac{13}{8}\pi, 2\pi], -3,5 \le r(\mu) \le -2,44 \tag{$4.10$}$$
En la se han representado algunas de las espirales de dicha familia (4.5), correspondientes a los valores angulares $\color{red} \mu$ y $\color{red} r(\mu)$ reflejados en la tabla de la . Esos valores se han obtenido usando la y abordando un ajuste de cada espiral al perfil de la concha que estamos modelando (usad el botón 
en esa escena).
| $\color{red}n$ | $\color{red}\mu=n \frac{\pi}{8}$ | $\color{red}r(\mu)$ | $\color{red}a(\mu)=\kappa^{r(\mu)\pi}$ |
|---|---|---|---|
| 13,00 | 5,10508806 | -3,50 | 0,15384652 |
| 13,25 | 5,20326283 | -3,25 | 0,17585424 |
| 13,50 | 5,30143760 | -3,00 | 0,20101016 |
| 14,00 | 5,49778714 | -2,75 | 0,22976463 |
| 14,50 | 5,69413668 | -2,60 | 0,24895582 |
| 15,00 | 5,89048623 | -2,50 | 0,26263243 |
| 15,30 | 6,00829595 | -2,47 | 0,26688009 |
| 16,00 | 6,28318531 | -2,44 | 0,27119644 |
Realmente la curva que describe la pared dorsal, en su transición del primer al segundo verticilo, está formada por los puntos extremos de cada una de esas espirales (ver los puntos morados dibujados en la ). Es decir,
$$\color{DarkViolet} D(\mu) \equiv \begin{cases} x= \color{red} D_x + a(\mu) \, \kappa^{\theta_i+\mu} cos(\theta_i+\mu) \\ y= \color{red}D_y + a(\mu) \, \kappa^{\theta_i+\mu} sen(\theta_i+\mu) \end{cases} \quad \text{con} \quad { \begin{matrix} \color{red} \mu \in [\frac{13}{8}\pi, 2 \pi] \\ \color{red} \kappa^{-3,5 \pi} \le a(\mu) \le {\color{red} \kappa^{-2,44 \pi}} \end{matrix}} \tag{$4.11$}$$
Y, ahora, la dificultad se centra en determinar cuál es la expresión analítica bien de $\color{red} a(\mu)$ o bien de $\color{red} r(\mu)$. Partiendo de los datos reflejados en la tabla de la se detecta que estos se ajustan con un coeficiente de determinación $R^2=0,9872$ a un polinomio de segundo grado $\color{orange} y=-1,0809 x^2 + 13,132 x -42,311$ ().
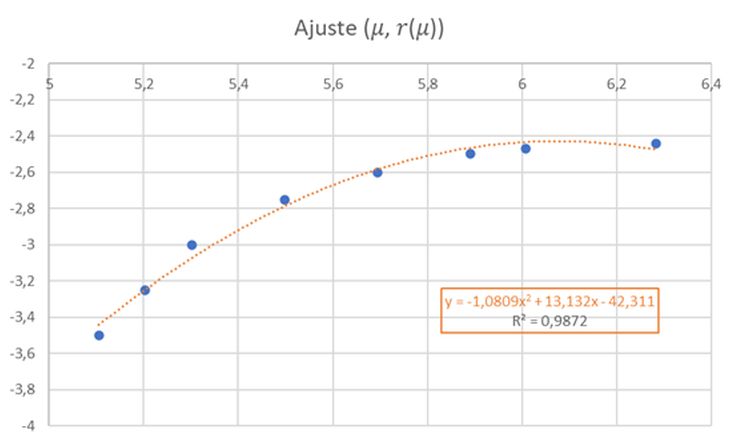
Consecuentemente podemos interpolar los valores de $\color{red} r(\mu)$ y calcular en (4.10) los puntos $\color{DarkViolet} D(\mu)$ que deseemos para modelar suficientemente la pared dorsal. Todo ello lo hemos reflejado en la tabla de la . Para los extremos de este ajuste consideraremos los valores teóricos obtenidos que dan continuidad a la pared septal previa a esta fase, es decir, $\color{red} r(13\frac{\pi}{8})=-3,50$ y la que es tangencial con la pared ventral inicial $\color{red} r(16\frac{\pi}{8})=-2,44$; esos valores están reflejados en esa tabla en color rojo.
| $\color{red}n$ | Ajuste $\color{red}\mu=n \frac{\pi}{8}$ |
$\color{red}r(\mu)$ | $\color{red}a(\mu)=\kappa^{r(\mu)\pi}$ | $\color{DarkViolet}D_x(\mu)$ | $\color{DarkViolet}D_x(\mu)$ |
|---|---|---|---|---|---|
| 13,00 | 5,10508806 | -3,441317352 -3,5 |
0,15875133 0,15384652 |
0.1932 0,1883 |
0.0769 0,0770 |
| 13,25 | 5,20326283 | -3,245978666 | 0,17623284 | 0,2131 | 0,0940 |
| 13,50 | 5,30143760 | -3,071476025 | 0,19347148 | 0,2313 | 0,1150 |
| 13,75 | 5,39961237 | -2,917809431 | 0,21004273 | 0,2468 | 0,1397 |
| 14,00 | 5,49778714 | -2,784978882 | 0,22550645 | 0,2588 | 0,1676 |
| 14,25 | 5,59596191 | -2,672984378 | 0,23942576 | 0,2662 | 0,1978 |
| 14,50 | 5,69413668 | -2,581825921 | 0,25138734 | 0,2683 | 0,2293 |
| 14,75 | 5,79231146 | -2,511503509 | 0,26102165 | 0,2647 | 0,2610 |
| 15,00 | 5,89048623 | 2,462017143 | 0,26802189 | 0,2551 | 0,2916 |
| 15,25 | 5,98866100 | -2,433366822 | 0,27216020 | 0,2398 | 0,3197 |
| 15,50 | 6,08683577 | -2,425552547 | 0,27329996 | 0,2191 | 0,3441 |
| 15,75 | 6,18501054 | -2,438574318 | 0,27140330 | 0,1939 | 0,3636 |
| 16,00 | 6,28318531 | -2,472432135 -2,44 |
0,26653318 0,27119644 |
0,1651 0,1674 |
0,3774 0,3826 |
El ajuste poligonal a partir de esos puntos $\color{DarkViolet} (D_x(\mu), D_x(\mu))$ está reflejado en la , y podemos tratar de verificar si siguen alguna trayectoria sencilla. Efectuando un ajuste por mínimos cuadrados se detecta que esa pared dorsal se ajusta, con un coeficiente de determinación $R^2=0,9894"$ a la parábola de ecuación: $$\color{DarkKhaki} x=-3,8329 y^2 + 1,6999096461 y + 0,07999021 \tag{4.12}$$ cuyo vértice es el punto $\color{DarkKhaki} V(0,26828946, 0,22164633) $ y su foco $\color{DarkKhaki} F(0,20306470, 0,22164633)$.
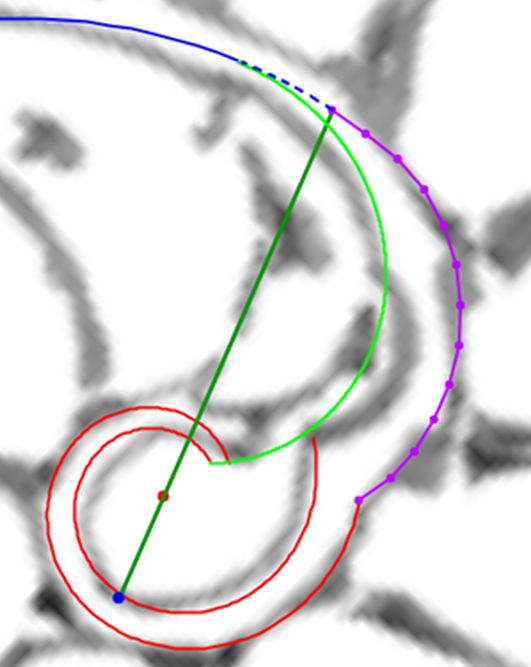
El ajuste teórico (4.12) está reflejado en la , y en la se muestra su superposición sobre el modelo y sobre la sección de la concha del Nautilus. Todo, también puede observarse en la pulsando el botón 
.
|
|
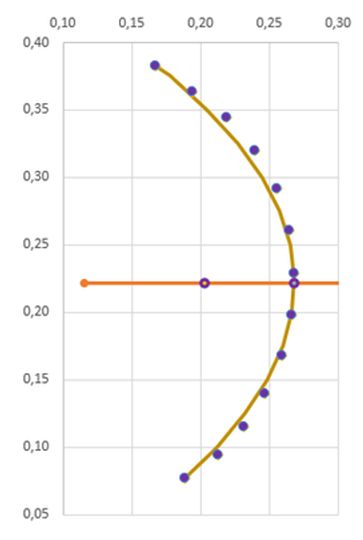
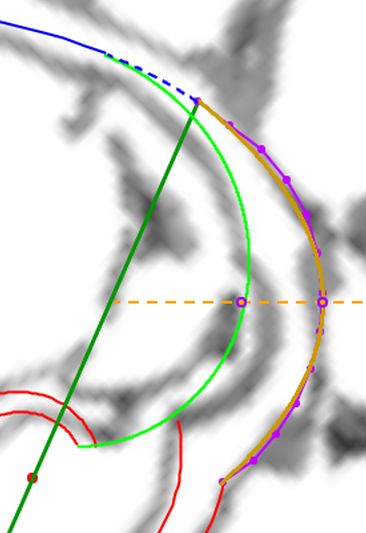
El tramo restante entre el punto final de esta parábola y el inicio de la pared ventral original es el arco de la espiral ventral $\color{blue} r=\kappa^\theta$ con $\color{blue} \theta \in [\theta_i, \theta_i+0,19]$.
Integrando todo lo analizado en este capítulo en relación a los sitios que hemos denominado singulares obtenemos el modelo que hemos reflejado en la e integrándolo con lo analizado con anterioridad obtenemos el modelo global del primer verticilo reflejado en la .
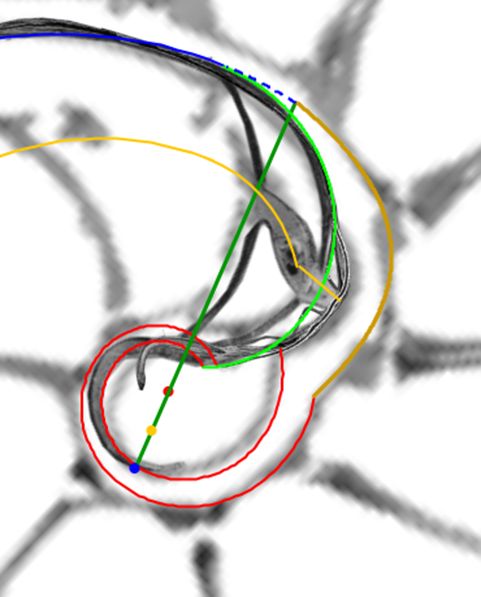
Llegados a este punto pienso que hemos logrado una modelación bastante completa de la sección sagital del Nautilus, si bien no seré yo quien excluya la posibilidad de que puedan surgir nuevas cuestiones, pues eso es lo que ha ido aconteciendo a lo largo de la investigación realizada y aquí expuesta. Pero, independientemente de que afloren nuevos aspectos o no, considero que para que los detalles no nos impidan o dificulten ver el modelo al que hemos llegado, es necesario completar este estudio adecuadamente y, por tanto, en el siguiente capítulo recopilaremos todo lo expuesto en una escena interactiva de Descartes y en una animación que muestre la
ontogenia matemática del Nautilus en un hilo temporal que recoja su crecimiento, si bien real y paradójicamente éste ha de ser atemporal porque en la literatura existente los datos relativos a los tiempos en el crecimiento de la concha son muy genéricos o yo no he logrado localizarlos.
Si bien el modelo uniforme del Nautilus, que sintetizamos en el capítulo primero de este libro (ver ) y que fue objeto de un encuadre contextual en el libro "¡No!, ¡no soy áureo! ¡Soy cordobés!
Para observar este modelo ontogénico, paso a paso y en detalle, podemos usar la de la página siguiente. Este recurso se presenta por defecto como una animación, pero puede pasar a modo manual sin más que pulsar el botón inferior izquierda, que está representado con la imagen de una mano, y usar el control etiquetado como "paso".
En el objeto interactivo podemos distinguir cuatro zonas:
donde se refleja por defecto el modelo teórico de paso interseptos $\frac{2\pi}{16}$, pero también se puede optar por el modelo $\frac{2\pi}{15}$ que se detecta en algunos ejemplaresEl paso radial interseptos en el segundo y tercer verticilo varía entre $\frac{2\pi}{15}$ y $\frac{2\pi}{16}$ según los ejemplares considerados y suele ser inferior en los últimos septos, en la etapa de madurez..
, que permiten ampliar o disminuir la zona que está representada.
o automático 
. Cuando está en automático a la derecha se dispone de un control de desacelaración o aceleración de la animación 
. Por defecto se inicia la escena con el control automático.
Selección del paso a mostrar en el espacio principal. Al cambiar su valor muestra una etapa o característica diferente, desde la concha embrionaria hasta el último septo. Cuando el control es automático este control está inhabilitado y ha de pasarse a control manual para poder usarlo.
Muestra u oculta el cuerpo del Nautilus. Es meramente una ubicación y tamaño aproximado, una simple referencia gráfica orientadora, sin valor biológico.
Fase de los tres septos.
Fase de los dos septos.
Fase del primer septo.
Concha embrionaria preseptal.
Sección de la concha del Nautilus con paso $\frac{2\pi}{15}$ (segundo y tercer verticilo).
Modelo de la concha del Nautilus con paso $\frac{2\pi}{15}$ (segundo y tercer verticilo).
Sección de la concha del Nautilus del "D'Arcy Thompson Zoology Museum (Museo Dundee) con paso $\frac{2\pi}{16}$ (segundo y tercer verticilo).
Modelo de la concha del Nautilus con paso $\frac{2\pi}{16}$ (segundo y tercer verticilo).
Primer verticilo del Nautilus del Museo Dundee.
Muestra u oculta la concha del Nautilus que se usa para ubicar cuál es la zona del modelo que se está visualizando en el espacio principal.
Como alternativa, puede consultar la siguiente presentación construida a partir de las imágenes de dicha , la cual está disponible en diferentes formatos (Google Slides, PowerPoint o pdf).
En la barra de herramientas inferior puede gestionar manualmente el paso de las diapositivas
y pulsando el icono ⋮ se tiene acceso a las notas del conferenciante.
Presentación con Google Slides. Versión en pdf y versión en PowerPoint.
En la siguiente presentación podemos hacer un recorrido en el que se ha sintetizado y descrito el modelo ontogénico construido.
En la barra de herramientas inferior puede gestionar manualmente el paso de las diapositivas
y pulsando el icono ⋮ se tiene acceso a las notas del conferenciante.
Presentación con Google Slides. Versión en pdf y versión en PowerPoint.
Omitiendo la parte descriptiva en la obtenemos la que refleja el modelo ontogénico en sí. Todos los botones y funcionalidades siguen siendo las mismas, salvo en el control "paso" que si se fija observará saltos, omisiones, en aquellos pasos descriptivos que se dejan de mostrar.
Y de manera análoga a la escena anterior tenemos como alternativa el uso de una presentación Google Slides, un pdf o una presentación en PowerPoint.
Finalmente ese modelo lo hemos recogido en la animación incluida en la , pero al no tener datos sobre la temporalización real del crecimiento del Nautilus hemos tenido que asignar el mismo tiempo a cada septo. Sirva ésta como colofón de la investigación realizada y que ha quedado detallada en este libro.
Pero el Nautilus no es un habitante de Planilandia, aunque hasta ahora nos hayamos limitado a tratarlo de esa manera, seccionándolo y restrigiendo su ser a un mero plano medio representativo de su concha. Así pues, siguiendo a Aristóteles que nos enseñó que "El todo es mayor que la suma de sus partes", es necesario y obligado que consideremos la tridimensionalidad de la concha del Nautilus, que la estudiemos y la analicemos. Para ello, una vez más, hemos de tratar de escuchar los nuevos susurros que éste nos quiera transmitir y que, a su vez, nuestros sentidos sean capaces de captar. Así, quizás podamos interpretar la matemática que implícita y explícitamente se manifiesta en su rastro calcáreo global. Sí, hemos de abordar ese salto espacial y lo haremos, pero sea algo paciente ya que éste será el contenido que podrá consultar en un tercer libro titulado "Modelo matemático tridimensional uniforme del Nautilus" (Galo, 2024-b)
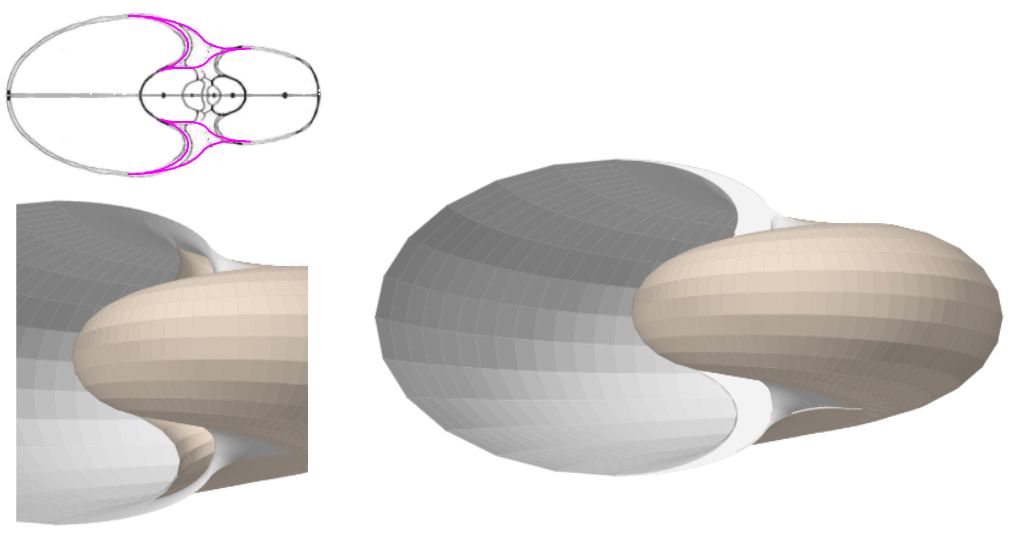
Imagen generada por la IA Designer de Microsoft
