Título de la obra:
Modelo matemático tridimensional uniforme del Nautilus
Autor:
JOSÉ R. GALO SÁNCHEZ
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-10368-10-1
A Conchi, mi mujer
y a Pablo, mi nieto
En mis primeros encuentros matemáticos con la concha del Nautilus, allá por el año 2014, a los que llegué de la mano de mis colegas Ángel Cabezudo e Ildefonso Fernández-Trujillo, no pude llegar a sentir que dedicaría tanto tiempo de análisis y estudio, dentro de la década que ya ha transcurrido desde entonces, a vislumbrar la sabiduría natural que encierra el rastro cálcareo de este animal y que se sublima en una belleza matemática de difícil parangón. El primer salto cualitativo que dimos se ubicó en la identificación de que su factor de crecimiento se corresponde con la proporción cordobesa, una mera anécdota que por sí no involucra ningún avance esencial, pero que servía para poner nombre a la proporción nautiliana que erróneamente, y a veces de manera sutilmente intencionada, se asocia a la proporción áurea. Esa casual coyuntura, sí que condujo a una visión más global, más valorable matemáticamente, al verificar que todo en la concha del Nautilus era cordobés, la pared ventral, la dorsal, el sifúnculo, los septos, la espiral en la se ubicaban los polos de esos septos. Todas estas propiedades nos permitieron conformar el modelo matemático cordobés de la sección sagital del Nautilus (Galo et al., 2016)
En ese contexto, el de la insignificante casualidad o coincidencia del detectado crecimiento cordobés del Nautilus y su empecinamiento en ser a todas luces cordobés, lo cual es obviamente agradable para alguien como yo cuyo gentilicio es también el de cordobés, me llevaba, me forzaba a abordar una confrontación entre proporciones, preguntarse sobre la vigencia o interés de unas sobre otras y, en particular, buscar el por qué una es la reina de ellas, la idealizada y magnificada proporción áurea que ahora resultaba que era denigrada por el Nautilus, o al menos no era su elegida. Mi invitación a impartir la conferencia inaugural del "24.º Encuentro de Geometría y sus aplicaciones", celebrado en junio de 2019 en Bogotá (Colombia), me llevó a enmarcar estas inquietudes y divulgarlas en dicho encuentro, confluyendo todo a la necesidad y obligación de configurar al Nautilus como referente del crecimiento gnomónico cordobés.
Para divulgar con detalle toda la información recabada, los recursos interactivos elaborados y las conclusiones obtenidas, pensé incluirlo en un libro interactivo que sirviera de referencia y que revindicara el verdadero marco matemático del Nautilus, quedando este aspecto claramente plasmado en su título: "¡No, no soy áureo! ¡Soy cordobés! Firmado: Nautilus" (Galo, 2024)
El segundo libro "Modelo ontogénico matemático del Nautilus" (Galo, 2024-b)
biológica del Nautilus requirió su tiempo investigador para extraer datos y generar información, a partir de la cual, y siempre tamizándola bajo el filtro matemático, nos condujeran a determinar la forma diferenciada según las fases de crecimiento y la compresión del porqué matemático de la misma. En 2021 y 2022 llegaron sucesivos avances y logros en este objetivo y fui divulgándolos en el blog de la Red Educativa Digital Descartes (RED Descartes). La sección de la concha embrionaria, asimétrica, permitía inscribir en ella el gnomón de un triángulo cordobés. La pared dorsal surgía, al igual que la ventral, como espiral cordobesa, pero ambas con polos diferentes lo que introducía una primera pauta diferenciadora respecto a la coincidencia que acontece en los verticilos restantes, dado que en estos la que antes era pared ventral pasa a ser la actual dorsal. El menor número de septos en la primera vuelta (ocho) surge como una imposibilidad física de acoger el número de dieciséis que construirá posteriormente, además de la masa adicional que supondría, y adicionalmente el tamaño de las cámaras es diferenciado por necesidades de alcanzar rápidamente la flotabilidad, lo cual logramos explicarlo matemáticamente como consecuencia de que la espiral ventral y la de los polos de los septos tampoco tenían el mismo polo. El sifúnculo también mantenía su forma cordobesa, pero con su polo diferenciado de los anteriores. La no copolaridad inicial daba sustento y explicación matemática al modelo ontogénico del Nautilus. Adicionalmente, a partir o en confluencia con estos avances, pude mejorar el modelo global en la parte uniforme del segundo y tercer verticilo, en especial, en lo relativo a los septos.
Lo realizado supuso un avance que considero hay que valorarlo como de gran interés, pues no tengo referencia de que este tema haya sido previamente tratado desde su perspectiva matemática y porque del análisis realizado se han obtenido conclusiones que dan explicación a las diferencias significativas que se observan en cada etapa y, en especial, en la embrionaria del primer verticilo donde acontecen hechos singulares difíciles de modelar y de comprender a priori.
Superado con holgura el reto anterior, el siguiente planteamiento necesariamente iba abocado a que fuera un salto dimensional que obviara la mirada plana en la que nos habíamos centrado en exclusiva hasta ahora y que asumiera la escondida tridimensionalidad del Nautilus. El tema del tercer libro, éste, como he indicado, se focalizaría en ese objetivo y, al igual que ya hicimos antes, procedería centrarse en el modelo uniforme. Y ello es lo que ahora tiene disponible, accesible, aquí entre sus dedos.
La investigación realizada se plasma en cinco bloques de contenido y una adenda. Iniciaremos la andadura abordando una revisión de artículos que se distribuyen en un amplio periodo de 200 años y que se adentran en el modelado tridimensional de las conchas, marcando pautas y caminos ingeniosos, de gran efectividad. A lo largo de esos años, se ha mostrado que todas las conchas existentes y las que matemáticamente podrían existir, pueden modelarse en base a cuatro parámetros: la forma de la sección de la concha o curva generatriz, el factor de amplificación de ésta, la posición respecto al eje de revolución y el ángulo apical o de desplazamiento para conchas turbinadas; parámetros que se plantean de esta forma o de otras equivalentes. En nuestro caso seleccioné y partí del modelo matemático planteado por Raup (1966)
Para la aplicación del modelo anterior al caso particular del Nautilus partíamos del factor de crecimiento cordobés característico de esta concha y, por tanto, la labor principal a llevar a cabo se centraba en la determinación de la curva generatriz que define la sección frontal del mismo. Y la representación de la misma la encontramos en el artículo
de Tanabe et al. (1985)
En el capítulo tercero nos centramos en la definición funcional de la curva generatriz e inicialmente realicé una aproximación mediante una curva de Bézier y, a partir de ella, aplicando el modelo adaptado de Raup, podemos ver una primera aproximación 3D de la deseada concha. Posteriormente, procedí a conjeturar cuál podría ser el modelo teórico de la misma obteniendo que es una concatenación de arcos elípticos, verificando así lo apuntado por Thompson (1917)
Pero la fase embrionaria de la concha queda inconclusa dado que no es posible aplicar una retroactividad en el crecimiento, ¡en tan escaso espacio surgen cambios tan drásticos que son difíciles de modelar! Para solventar el hueco inicial que queda en el modelo, se puede optar por una solución, al menos estética, de compromiso. En el capítulo cuarto se describe el criterio adoptado y se logra cerrar el vacío inicial en el modelo.
Inicialmente, el cierre del libro se aborda exponiendo cuáles son los puntos que han quedado abiertos en este análisis, especialmente la modelación matemática tridimensional de los septos que puede considerarse como el reto supremo. A mí, en este punto, la inspiración no me ha alcanzado y quedo deseoso de poder leer y ver, en algún momento, la solución aportada por otro u otros colegas. Con seguridad, la belleza sublime volverá a mostrarse cuando comprendamos la matemática que encierran.
El capítulo quinto finaliza con una síntesis del modelo matemático obtenido. Allí, nos paramos en la herramienta en la que hemos apoyado esta investigación, después, en el recurso interactivo principal desarrollado para obtener y mostrar el modelo final alcanzado y concluimos con la presentación del mismo plasmándolo en diferentes animaciones y presentaciones.
Se ha incluido una adenda que integra información complementaria a la descrita y citada en el libro. Se ha ubicado ahí con el ánimo de evitar la distracción del tema principal de discusión en aquellos apartados donde se referencia a este apéndice.
Concluyo, trasladando impresiones personales. Me siento alegre con el resultado obtenido, algo cansado por el largo trayecto recorrido, por el esfuerzo realizado, y muy contento de poder trasladar el conocimiento adquirido y el obtenido, a usted, atento lector de estas líneas, de estas páginas, de esta trilogía. La concha del Nautilus es un atractivo foco de estudio que libera comedidamente sus interioridades a quienes le prestan una curiosa atención, espero contribuir a que otros se sientan atraídos por los secretos que nos ha querido mostrar y por los que quedan por destapar.
Córdoba (España), diciembre de 2024.
La base literaria que podemos referenciar como primigenia en el modelado de las conchas se remonta a Aristóteles (384 a. C.- 322 a. C.) quien, según Sachs (1995)
«Hay ciertas cosas que cuando crecen no sufren alteración salvo en magnitud»
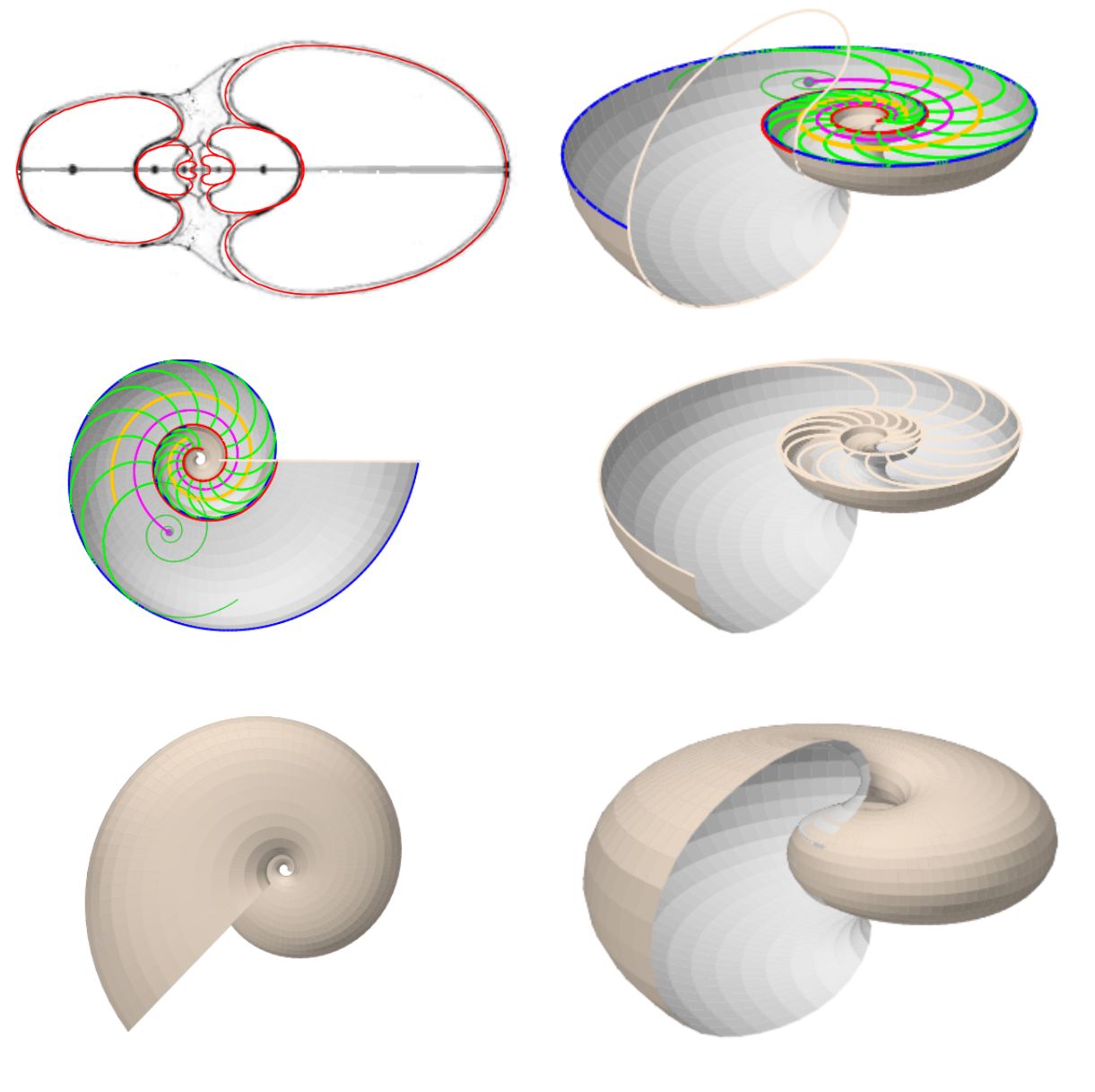
y definió el gnomon como toda figura cuya yuxtaposición a una dada produce otra que es semejante a la inicial. Este crecimiento autosemejante se produce en los seres vivos —la sección de la concha del Nautilus de la es un claro ejemplo del rastro dejado por ese tipo de crecimiento a nivel tridimensional—.

El crecimiento gnomónico aristotélico es habitual en la Naturaleza y puede observarse como un crecimiento continuo o como un crecimiento discreto —o de aparente crecimiento discreto, pues éste puede plantearse como instancias concretas del continuo—. Por ejemplo, observando las imágenes en la , podemos ver cómo las marcas en el fósil o las cámaras de flotación del Nautilus, o las hojas del cactus o las estrías en los cuernos marcan una pauta discreta, si bien nuestra mente construye, transmite y visualiza ese carácter discreto inmerso en una continuidad.
En el libro "¡No!, ¡no soy aureo! ¡Soy cordobés! Firmado: Nautilus" (Galo, 2024 cap. 2)

Pero la modelación en sí de las conchas —que obviamente no son seres vivos, pero sí son el reflejo o rastro vital del ser que las segrega— conllevará el paso de algunos siglos y podemos considerar como referente a Moseley (1801-1872) quien en su artículo de 1838
"The surface of any turbinated or discoid shell may be imagined to be generated by the revolution about a fixed axis (the axis of the shell) of the perimeter of a geometrical figure, which, remaining always geometrically similar to itself, increases continually its dimensions."Se puede imaginar que la superficie de cualquier concha helicoidal o discoidal es generada por la revolución alrededor de un eje fijo (el eje de la concha) del perímetro de una figura geométrica, la cual, permaneciendo siempre geométricamente similar a sí misma, incrementa de manera continua sus dimensiones.
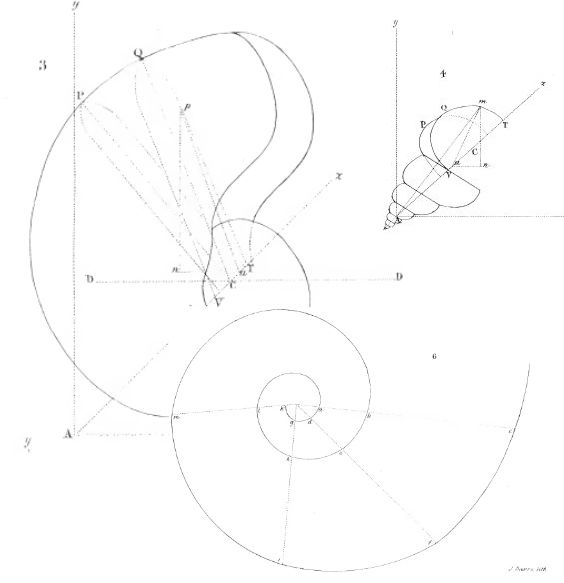
En su artículo, Moseley establece las bases para la modelación de las conchas discoidales y las helicoidales (ver la ), pues observa que las distancias entres sucesivas espiras, medidas sobre un mismo radio vector, están en progresión geométrica y consecuentemente la espiral es una espiral logarítmicaFue Descartes (1596-1950) quien se planteó la determinación de una curva que fuera equiangular, es decir, que en todo punto el ángulo que formara el radio vector con la recta tangente fuera siempre igual a un valor deseado, es decir, buscaba una generalización de lo que acontece en la circunferencia en la que la tangente en todo punto forma un ángulo de $90º$ con el radio. Su análisis y el de Josep Bernoulli (1654-1705) permitió determinar las propiedades de esta curva que llevaron a este último a denominarla como espiral maravillosa. Puede consultar al respecto en Galo (2024, pp. 142-151)
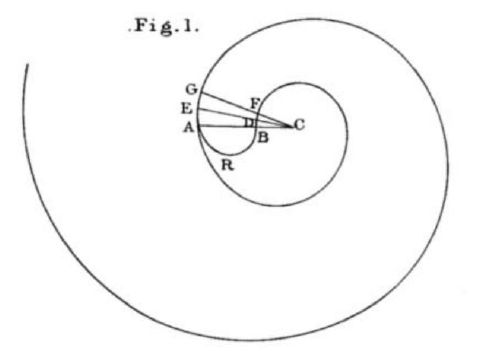
Desde un punto de vista más prágmatico, pero acorde con lo realizado por Moseley, Blake (1878)
Imágenes procedentes de Blake (1878)
|
|
|
|
Puede consultarse los términos que definen a los nautiloideos y ammnonoideos en Barroso-Barcenilla (2008) |
Blake, concluye que estos tres ángulos, junto con la ecuación del contorno de la concha obtenida como la traza de la misma al intersecarla con un plano que pasa por el polo, son suficientes por completo para determinar la forma de una concha cualquiera, siempre que el crecimiento sea uniforme. La traza indicada, obviamente, no tiene que coincidir con la forma de la abertura de la concha la cual ni siquiera tiene por qué ser plana.
Todos los resultados anteriores están incluidos también en una referencia que es básica e imprescindible para todo aquel interesado en esta temática. Nos referimos al libro de D'Arcy Thompson (1860-1948) "On growth and Form" del que tenemos diferentes ediciones en inglés: la inicial de 1917
De la extensa y detallada exposición que realiza, destaquemos que Thompson plantea la dualidad entre el crecimiento geométrico de la

de la espiral logarítmica y el crecimiento gnomónico aristotélico. Ciertamente ambos son como caras de una misma moneda, y todo es fruto de las múltiples propiedades intrínsecas de esta espiral maravillosa que se manifiesta como una ley de crecimiento matemático que modela a la ley física o dinámica que rige en esta especial forma de crecer. Una ley que se muestra cuando somos capaces de distinguir partes similares, con diferente antigüedad, que se han conformado mediante incrementos sucesivos y continuos que mantienen la forma, pero que amplifican su tamaño.
Y es que en el crecimiento de una concha no se puede concebir una ley más simple que la de ensancharse y alargarse manteniendo una misma proporción invariable; y esta ley, la más simple de todas, es la que la Naturaleza tiende a seguir. Esta autosemejanza, base en sí de las propiedades de la espiral logarítmica permite dar una definición de ella que no suele ser habitual (Whitworth, 1862)
Cualquier curva plana que parta de un punto fijo (que se llama polo) y tal que el arco intersecado entre este punto y cualquier otro de la curva sea siempre similar a sí mismo, se denomina espiral equiangular o logarítmica.
Y esa autosimilitud es la causa de la relación gnomónica antes indicada, pues:
Toda curva plana que procede de un punto fijo o polo, tal que cualquier sector delimitado por dos radios vectores es siempre un gnomon de toda la figura precedente, se llama espiral equiangular o logarítmica.
Que también puede plantearse de manera recíproca:
Si una estructura se construye añadiendo partes sucesivas semejantes y ubicadas de forma similar, a través de los puntos obtenidos se puede trazar una espiral logarítmica.
Que es lo que podemos observar en sendas construcciones reflejadas en la donde respectivamente se añade sucesivamente a un triángulo cualesquiera su gnomonEn la imagen, en particular, se ha reflejado el denominado triángulo sublime o triángulo áureo que es el triángulo isósceles cuyo ángulo desigual es de 36º y cuyo gnomon es un triángulo isósceles con ángulos iguales de 36º. Consecuentemente la espiral dibujada es la áurea., o a la diagonal de un cuadrado la de otro de lado doble, o a un hexágono regular se le superpone otro de lado doble.
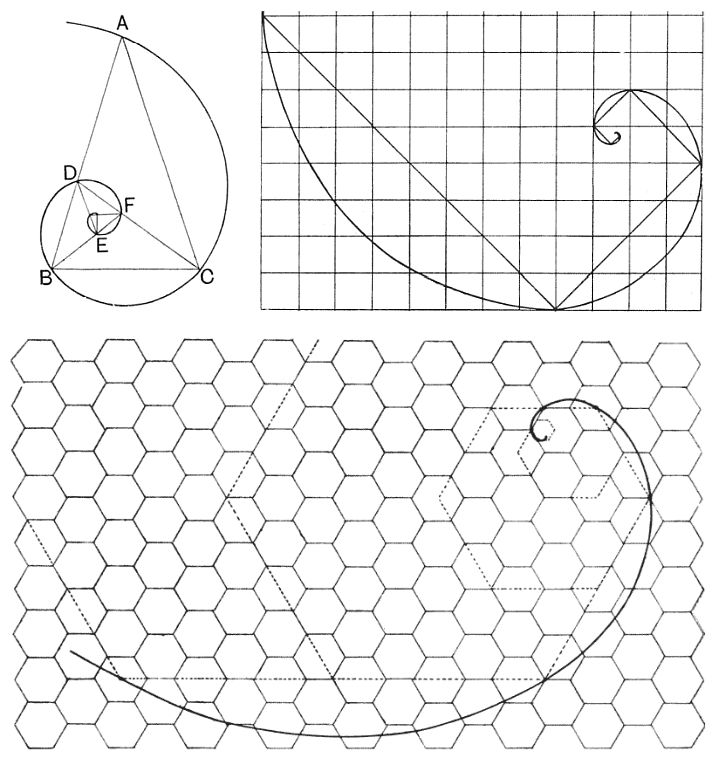
Thompson, en la p. 515 de la edición de 1917, afirma:
"Se sigue como corolario simple de este teorema de los gnomones que no debemos esperar encontrar la espiral logarítmica manifestarse en una estructura cuyas partes se producen simultáneamente, como por ejemplo en el borde de una hoja o entre las muchas curvas que forman el contorno de un pez. Sino que debemos buscarla más bien donde el organismo retiene información, y aún nos presenta a simple vista, las fases sucesivas del crecimiento anterior, las magnitudes sucesivas alcanzadas, los contornos sucesivos ocupados, a medida que el organismo o una parte de él perseguía el curso uniforme de su crecimiento, año tras año y día tras día. Y de esto se sigue fácilmente que es en las partes duras de los organismos, y no en las partes blandas, carnosas y en crecimiento activo, donde se encuentra característicamente esta espiral; no en los tejidos frescos y móviles cuya forma está limitada meramente por las fuerzas activas del momento; sino en cosas como la concha y el colmillo, el cuerno y la garra, donde el objeto está visiblemente compuesto de partes. En general, la espiral logarítmica es característica, no de los tejidos vivos, sino de los muertos. Y por la misma razón, siempre o casi siempre estará acompañada y adornada por un patrón formado por «líneas de crecimiento», el registro duradero de etapas anteriores y sucesivas de forma y magnitud."
Y apoyándonos en la equiangularidad se puede plantear de manera simple el crecimiento en espiral. Basta considerar que éste se produce formando un mismo ángulo constante respecto al punto anterior. Es la situación que usualmente se pone como imagen descriptiva cuando se dice que un hombre o un caballo, viajando por una gran pradera, es muy probable que, después de un largo día de viaje, se encuentre de nuevo cerca de su punto de partida. En este caso, algún pequeño e imperceptible sesgo, que podría ser causado por ejemplo por una pierna que es un poco más larga o más fuerte que la otra, desvía constantemente hacia un lado el movimiento hacia
adelante y lleva gradualmente al viajero de vuelta al punto de partida.
Pero para no extendernos excesivamente en lo mucho que nos expone y traslada Thompson respecto a la espiral logarítmica, derivamos al lector interesado a la lectura de su libro y también al nuestro (Galo, 2024; cap. 4 y pp. 220-227 de la adenda)
A nivel del crecimiento tridimensional y de su parametrización matemática no hay ninguna aportación diferente a los parámetros indicados por Moseley y Blake, es decir, la curva generatriz, el ángulo característico $\alpha$ de la espiral logarítmica, el ángulo $\lambda$ que marca la elevación de la helicoespiral y el ángulo de retardo $\beta$ que expresa el retraso en el crecimiento de la parte interior en comparación con la parte exterior de cada verticilo y, por lo tanto, mide hasta qué punto un verticilo se superpone o hasta qué punto está separado de otro.
Donde sí encontramos una aportación descriptiva novedosa, desde nuestro punto de vista o interés, es en la modelación de los septos (Thompson, 1917, pp. 578-587)
El contorno del tabique en el plano medio es una curva espiral idénticaDebe de entenderse que es semejante, es decir, la misma espiral logarítmica con diferente polo y con un ángulo de retardo o factor de escala. a la espiral logarítmica original.
Pero manifiesta la dificultad del modelado de la pared septal:
Si bien el contorno del tabique en la sección media es simple y fácil de determinar, la superficie curva del tabique en su totalidad es un asunto muy complicado, incluso en el Nautilus, que es uno de los casos reales más simples. Porque aunque la forma del tabique en la sección media es la de una espiral logarítmica, dado que su curvatura cambia constantemente, se sigue que, en secciones transversalesSecciones parasagitales, es decir, obtenidas por planos paralelos a la sección sagital o media. sucesivas, la superficie curva del tabique también cambia constantemente.
Esos cortes parasagitales podemos observarlos en la animación de la que se ha construido en base a los cortes que realizó González-Restrepo (2019)

En el caso del Nautilus, Thompson manifiesta que a pesar de esa dificultad puede ilustrarse la forma de estos septos:
Imaginemos una baraja de cartas en la que hemos recortado de cada carta un arco cóncavo similar a una espiral logarítmica, como la que vemos realmente en la sección media del tabique de un Nautilus. Luego, mientras mantenemos las cartas juntas, cuadradas, en la posición habitual del mazo, tenemos una superficie reglada simple, que en cualquier sección longitudinal tiene la forma de una espiral logarítmica, pero en cualquier sección transversal es una línea recta horizontal. Si cortamos o deslizamos las cartas una sobre otra, empujando las cartas del medio del mazo hacia adelante, por delante de las otras, hasta que un extremo del mazo sea una elipse convexa y el otro cóncava, los bordes cortados que se combinan para representar nuestro tabique formarán ahora una superficie curva de mucha mayor complejidad; y esto es parte, pero de ninguna manera toda la deformación que se produce por la forma de la sección del tubo en el Nautilus, dentro del cual debe estar el septo.
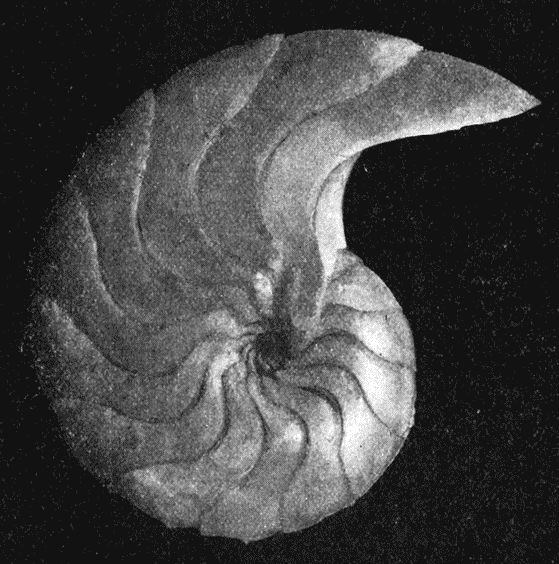
Imagen procedente de Thompson (1917) p. 582
Ciertamente no es fácil visualizar esta superficie que se muestra reacia a su modelación. En la podemos ver un molde de esos septos, pero lástima que el autor del mismo no mostrara uno de esos contornos aislado del resto. No obstante, sí podemos observar que el borde final de los septos ahí mostrados se asemeja al perfil adoral de la conchaadapertural (del lat. ad-, cerca de, y de abertura) o adoral. Cercano u orientado hacia la abertura de la concha [adapertural, adoral, orad].
Un siglo después de la referencia literaria y gráfica anterior, gracias a la tecnología actual de la tomografía por ordenador (ct-scan), se pueden obtener imágenes análogas —en este caso con la ventaja de ser un método no destructivo al dejar inalterable el ejemplar escaneado— que siendo procesadas con las aplicaciones informáticas adecuadas pueden generar reproducciones 3D y facilitar la medición y el cálculo de los parámetros de interés en la investigación, por ejemplo, calcular volúmenes relacionando el tamaño del vóxel, o píxel de volumen, y la densidad del cuerpo analizado. Ver la .
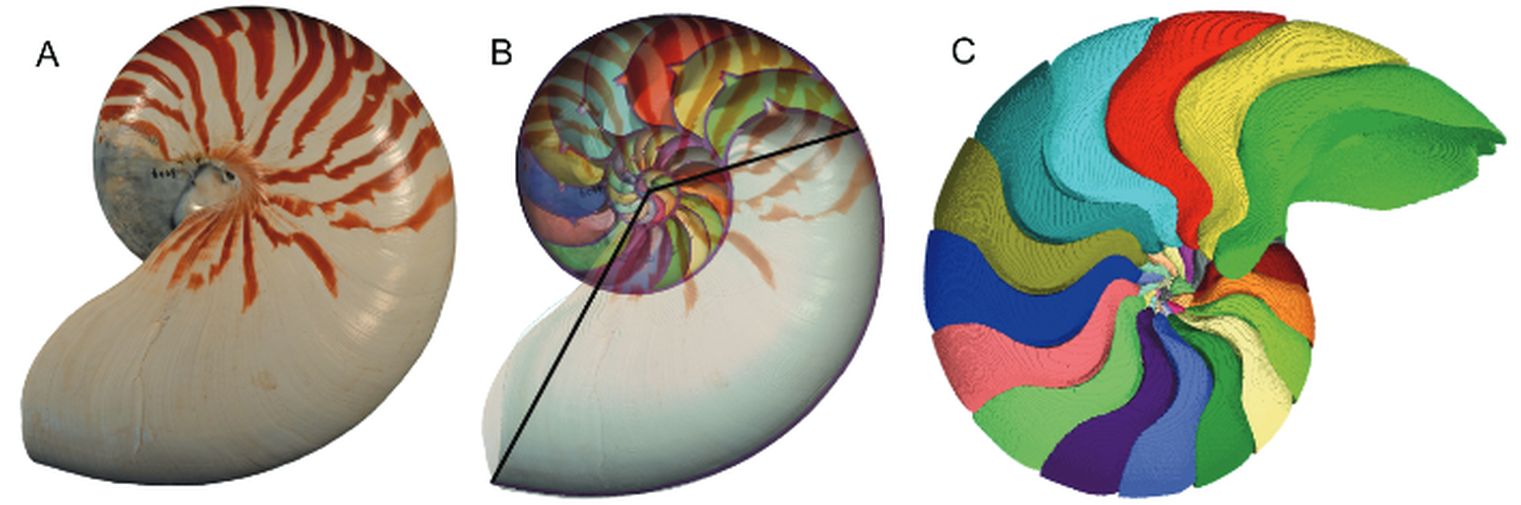
La imagen de la figura anterior también adolece de no mostrar de manera independiente una cámara septal para apreciar en detalle su forma. Pero podemos hacernos una primera idea observando la donde se nos muestra una imagen de esa cámara septal en una perspectiva dorsal/ventral y en otra lateral (Lemanis et al., 2016)
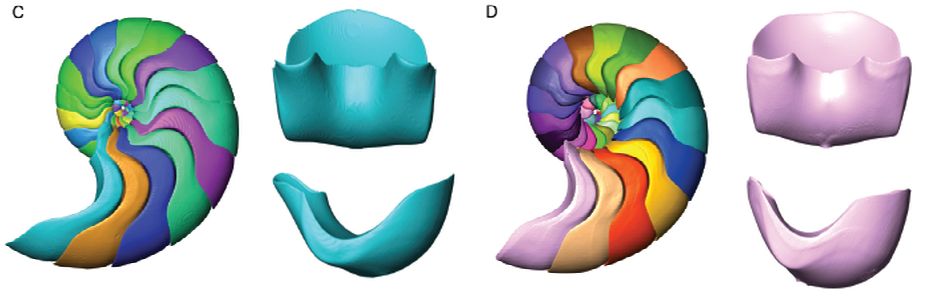
Finalmente, nuestro anhelo por ver esa imagen septal queda parcialmenteLa parcialidad indicada es porque, personalmente, hubiera quedado plenamente satisfecho si en lugar de esa imagen estática hubiéramos podido observar una dinámica similar a la del modelo 3D a partir de la que se ha obtenido. Pero claro, es un deseo de quien no tiene el conocimiento necesario para la manipulación de estas imágenes, ni los recursos que permitieran lograr ese objetivo y, por tanto, puede infravalorar su dificultad. alcanzado en el reciente artículo de Domokos et al. (2024)
datos del modelo 3D del "D’Arcy Thompson Zoology Museum" Esta digitalización
es la que ya enlacé en la de este libro y a partir de la cual González-Restrepo (2019)
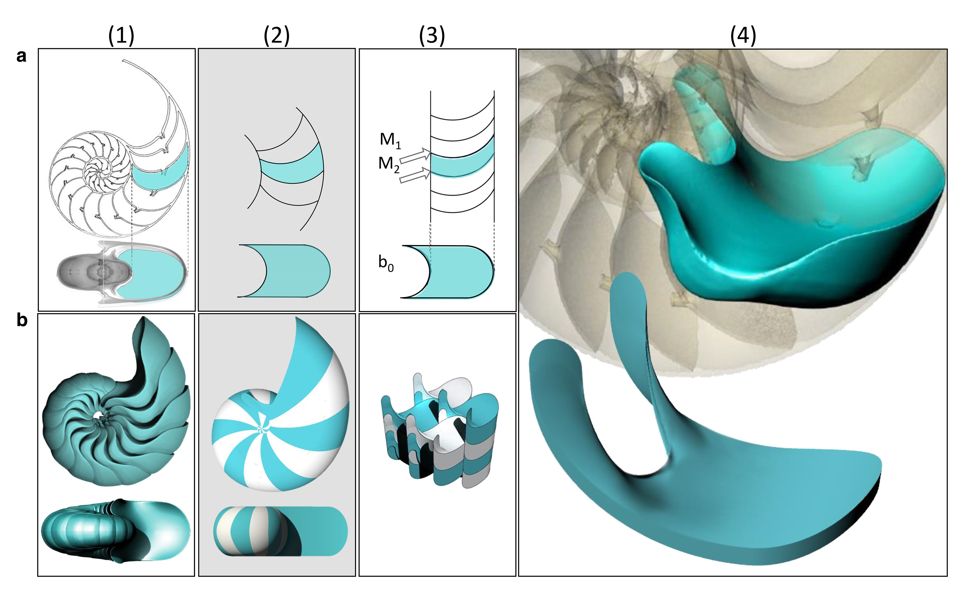
Domokos et al. indican que "la geometría 3D de la cámara no sólo es una buena aproximación de una celda blanda, sino que también es una buena aproximación de una celda monoédrica blanda que llena el espacio". Para la obtención de estas teselas suaves se basan en los modelos de Seilacher (1973
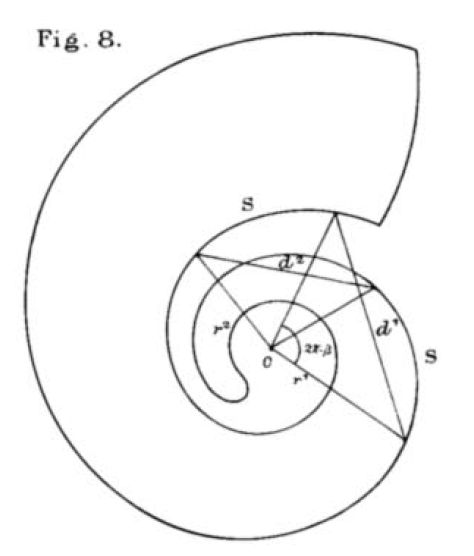
Estos estudios de las conchas de los ammonites y nautilodeos, que comprenden el análisis de las ornamentaciones y la forma de los septos, se aborda desde la perspectiva del crecimiento de las mismas y se fundamentan en los principios físicos que ahí intervienen. En la se esquematiza el modelo del globo en un cilindro que se ajusta a la modelación de los septos del Orthoceras y en la el cilindro considerado es de base elíptica que se ajusta a la modelación de los septos del Nautilus.
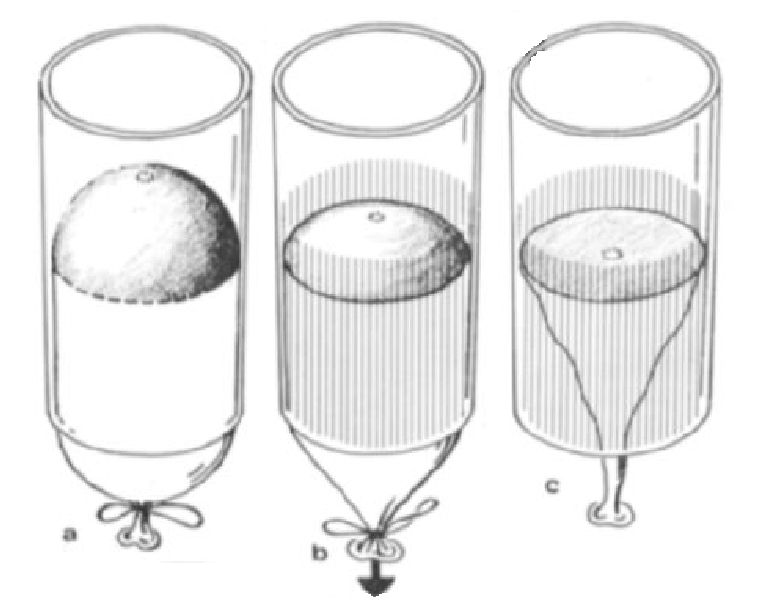
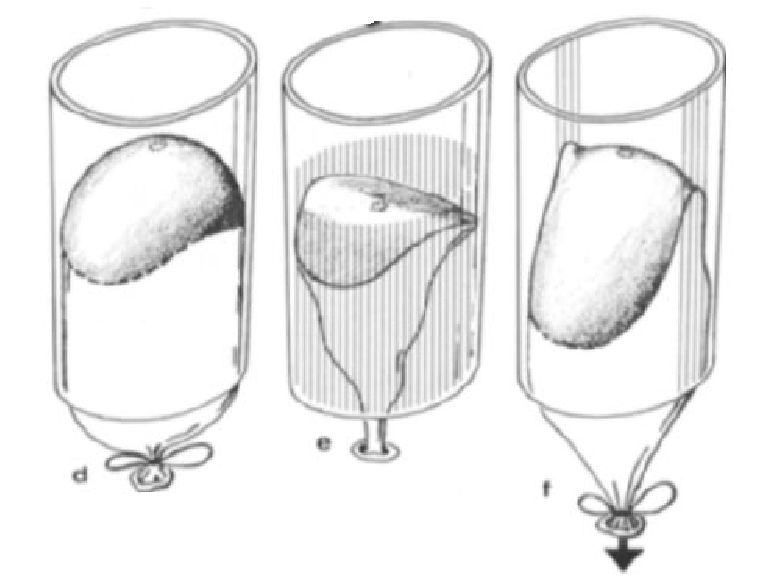
Si trasladamos este modelo a la cámara habitacional de un Nautilus, ya no nos parecerá extraño que se formen lóbulos en la parte lateral aplanada y también en la parte central donde está abollado por el verticilo anterior (ver la ).
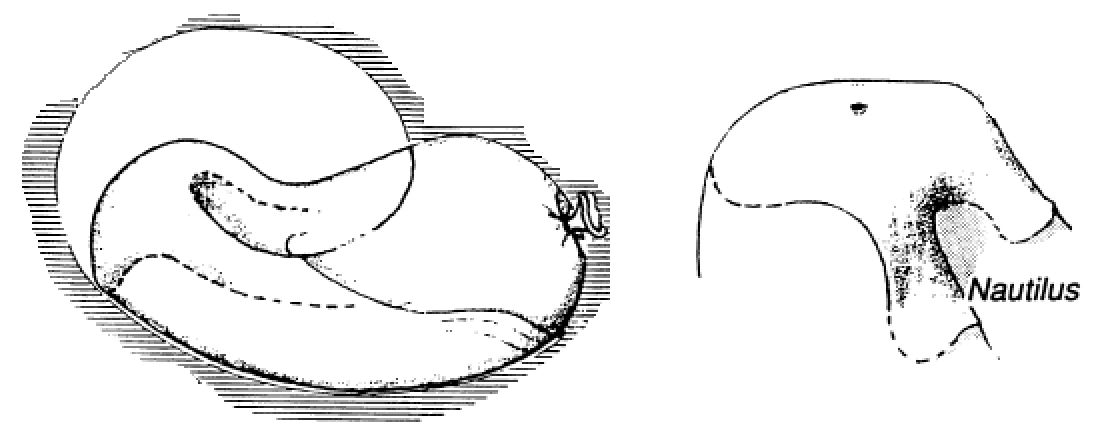
En la la imagen a refleja la forma que adopta el globo en el Nautilus cuando éste no está pegado y en b cuando se han pegado los lóbulos laterales. La c y la f muestran el septo del Nautilus en una vista lateral y semi frontal respectivamente. Para que el modelo b se aproxime a la forma real c es necesario tirar hacia atrás del globo.
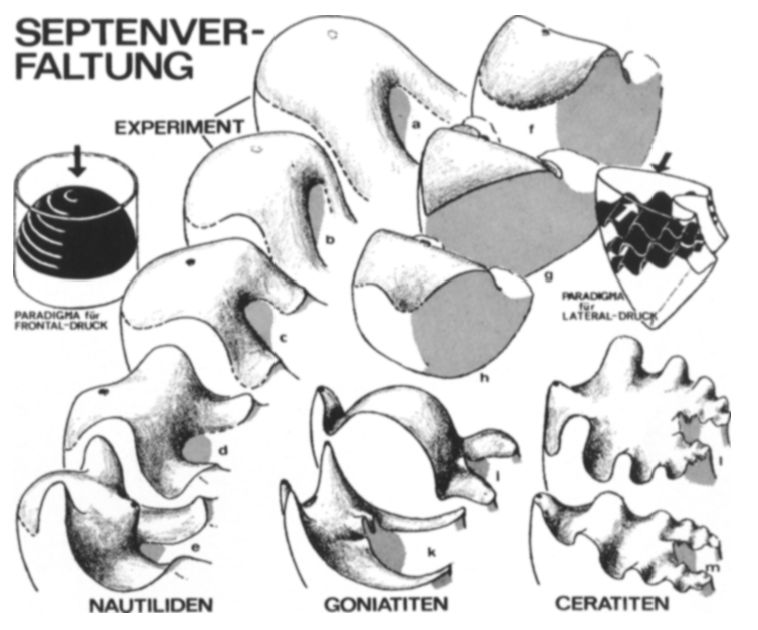
Aunque el modelo del globo se aproxima cualitativamente a la forma del septo no captura todas las características esenciales de la cámara del Nautilus, así pues, Seilacher, para describirlas también utilizó el modelo de papel (ver la ).
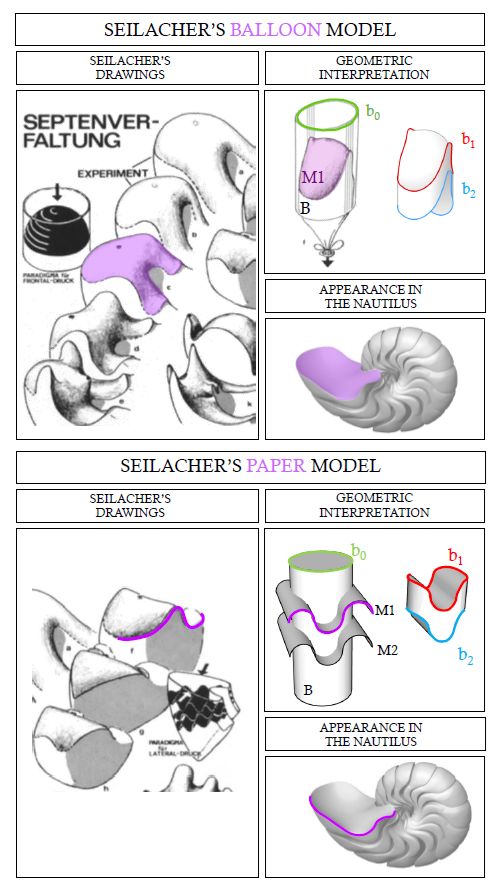
Todas estas investigaciones refuerzan lo ya indicado con antelación respecto a la dificultad de modelar los septos del Nautilus y, consecuentemente, la posibilidad de obtener la ecuación matemática de su superficie se presenta huidiza.
Raup en su artículo de 1961
Raup destaca el trabajo realizado por Thompson pues puso en evidencia que unos pocos parámetros son suficientes para modelar tanta complejidad, pero expone que esto que debería ser atractivo para zoólogos y paleontólos presenta ciertas dificultades prácticas a la hora de su medición, en particular para el ángulo apical y el de retardo, y también para el característico de la espiral en el caso de conchas helicoidades. Esta dificultad, indica, también se mantuvo en las publicaciones posteriores existentes que, realmente, no son más que extensiones de la de Thompson. Por ello, en su artículo buscó ofrecer un nuevo enfoque que fuera más pragmático.
La propuesta de Raup se centra también en cuatro parámetros, pero diferentes a los de Blake y Thompson:
Como ejemplo de aplicación considera la concha de Ecphora quadricostata (ver la ).
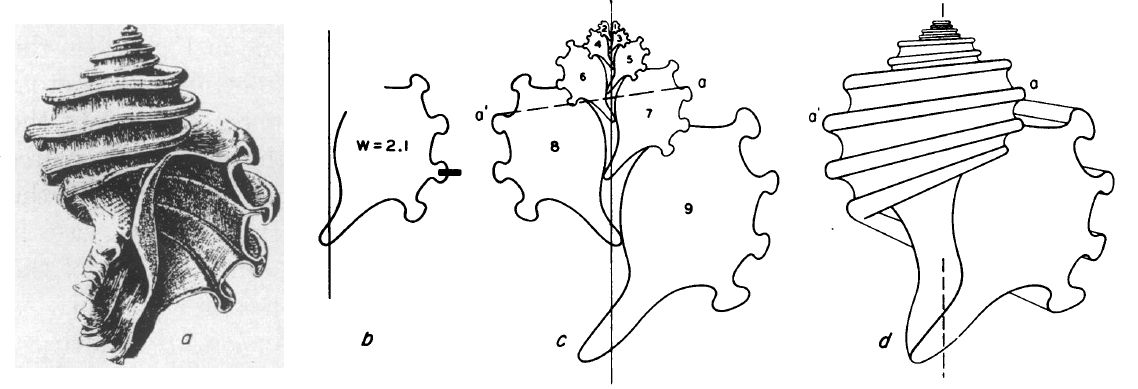
Imagen procedente de Raup (1961) p. 606
Según nos indica Raup, en la b:
La línea vertical es el eje de revolución. El contorno a la derecha de éste es la parte de la curva generatriz que se puede observar y se muestra su posición respecto al eje. La marca de verificación representa el punto de contacto con el verticilo siguiente (que sería la sutura) y, por lo tanto, indica la cantidad de superposición.
El factor de crecimientoEste factor $W$ se relaciona con el ángulo característico $\alpha$ de la espiral logarítmica por la igualdad $W=e^{2 \pi \, cotg \, \alpha}$, pero en la práctica $W$ es más fácil de calcular. ($W$) se muestra mediante un número que indica la relación entre la dimensión de un verticilo y la misma dimensión del verticilo anterior (las dos medidas están separadas por 360º de rotación). En este caso, la dimensión utilizada fue la distancia entre dos de las nervaduras prominentes en la curva generadora, pero se podría haber utilizado cualquier otra dimensión conveniente (en la mayoría de las especies, la distancia entre suturas sucesivas resulta ser la dimensión más favorable). Todas las características mostradas en esa b, excepto el valor de $W$, se obtuvieron con una cámara lúcida.
Los bocetos restantes en la muestran el procedimiento para reproducir la concha de Ecphora. Primero, se dibuja un eje de longitud arbitraria. A continuación, se dibujan réplicas de la curva generadora en diferentes tamaños utilizando el conjunto de lente y vidrio esmerilado (ground glass) de una cámara de fotos. El tamaño de la primera (la más pequeña) curva generadora es puramente arbitrario, y los tamaños de las copias sucesivas están determinados por el factor de crecimiento ($W$). El tamaño ($z$) de la curva generatriz está relacionado con el número de revoluciones ($y$) alrededor del eje de la siguiente manera: $z=W^y$. El tamaño de la curva generatriz que está en segundo lugar desde arriba en el lado derecho del eje (#3 en la c) es $W$ veces el tamaño de la curva generatriz anterior en el mismo lado (#1), #5 es $W$ multiplicado por #3, y así sucesivamente. Siguiendo la misma relación, una curva generatriz dada en el lado izquierdo del eje (#2, por ejemplo) es mayor que la anterior en el derecho (#1) por el factor $z=W^{\frac{1}{2}}$, es decir, lo correspondiente a media vuelta. $\sqrt{W}$.
Su descripción continúa:
El resultado de lo anterior (c) es esencialmente una sección transversal de Ecphora. Se puede construir fácilmente un dibujo en perspectiva (d) a partir de esta sección transversal conectando puntos similares (como $a$ y $a'$) en los contornos de las curvas generatrices que están separadas 180º.
Cabe destacar que la reconstrucción completa de la forma de gasterópodo ( c, d) sirve sólo para demostrar la validez del sistema. La b es suficiente para describir la concha de Ecphora.
Como podemos observar, el procedimiento es relativamente simple si bien, como Raup apunta, carente de elegancia matemática o más bien, yo apunto, de formulación de la misma.
En un nuevo artículo (Raup, 1962)
En posteriores artículos: Raup & Michelson (1965)
La formalización del modelo, ver la , se concreta en Raup (1966)
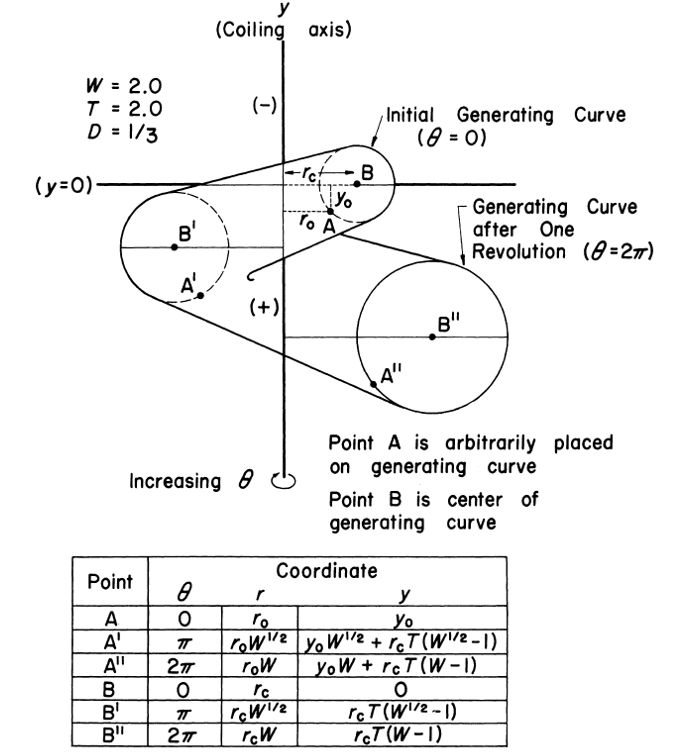
La curva generatriz se corresponde con una sección del cono helicoidal mediante un plano que contiene al eje $y$ y, en general, no se puede expresar matemáticamente de manera simple (en el ejemplo de la figura anterior se ha considerado una circunferencia, cuyo centro $B$ se ha ubicado en la recta $y=0$). Considerando un punto de esa curva generatriz cuyas coordenadas son $A(r_0, 0, y_0)$, las coordenadas de su transformado $A_\theta(r_\theta,\theta,y_\theta)$ obtenido después de realizar un giro de ángulo $\theta$, se expresan comoSegún hemos indicado, dado que $W=e^{2 \pi \, cotg \, \alpha}$, en (1) tenemos que $r_\theta=r_0 \, e^{\theta \, cotg \, \alpha}$, es decir, una espiral logarítmica de ángulo característico $\alpha$.: $$r_\theta=r_0 \, W^{\frac{\theta}{2 \pi}} \tag{1.1} $$ donde $W$ es el factor de crecimiento, e $y_\theta$ sería:
donde $T$ es la tasa de traslación definida como $\frac{dy}{dr}$ con respecto al centroPara una curva directriz cualquiera, diferente a una circunferencia, a priori, ese centro no estaría nitídamente determinado, pero realmente basta elegir un punto arbitrario $P$, de la curva o de su interior y su transformado $P''$ después de una vuelta y calcular el valor correspondiente de $T=\frac{dy}{dr}$, el cual queda fijado en (1.3) y, en esa expresión, $r_c=r_P$. $B$ de la curva generatriz y $r_c$ es el valor de su coordenada $r$.
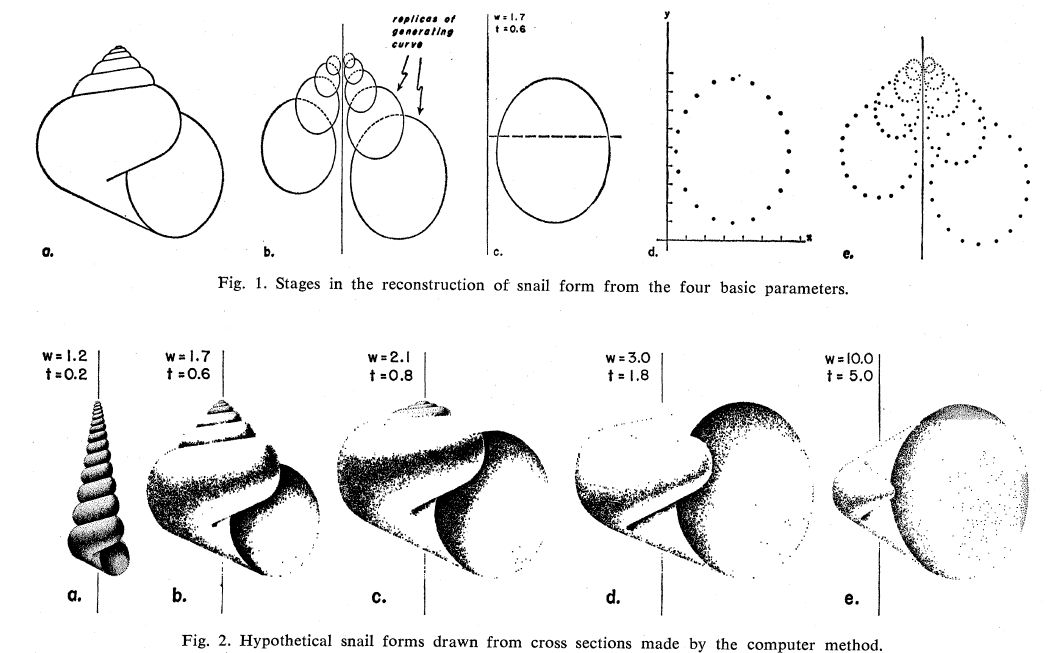
En la , para una curva generatriz dada, en este caso una circunferencia, podemos observar cómo influyen cada uno de los parámetros $W$, $D$ y $T$ cuando se fijan dos de ellos y se varía el tercero.
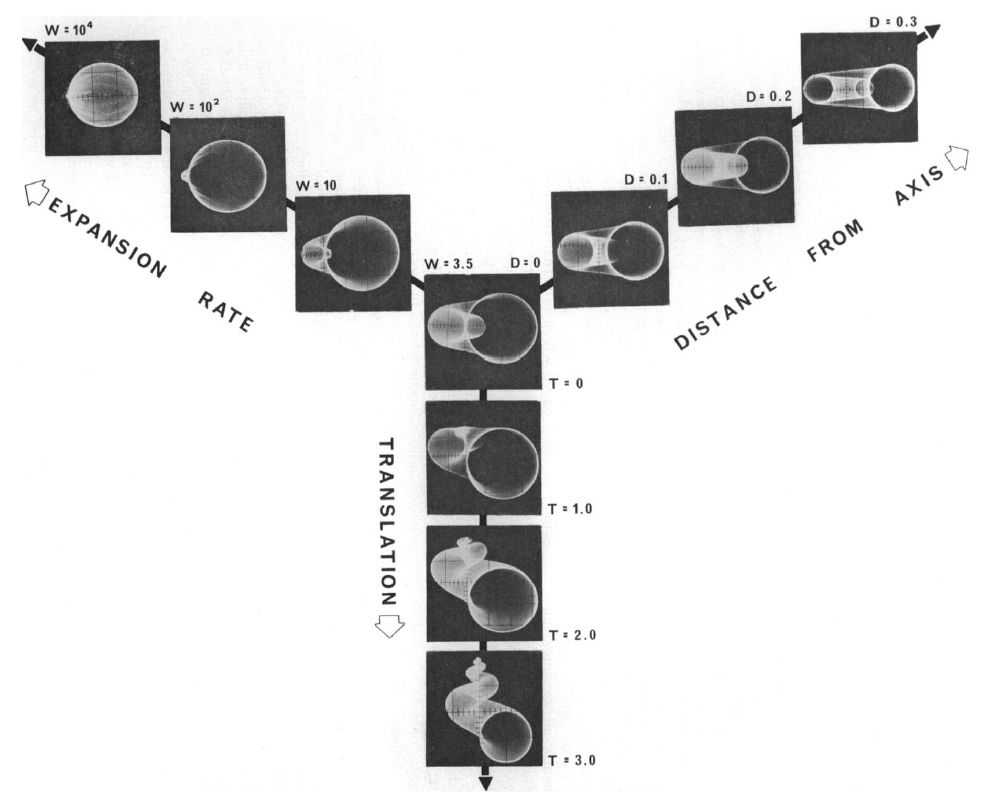
Siguiendo lo indicado por Raup, en esta figura podemos observar:
utiliza la superficie exterior del verticilo anterior. Sin embargo, a medida que disminuye el solapamiento la porción de la curva generadora que realmente deposita el organismo se hace cada vez mayor, hasta el caso extremo de que no haya superposición que es cuando deposita toda la curva geneneratriz.
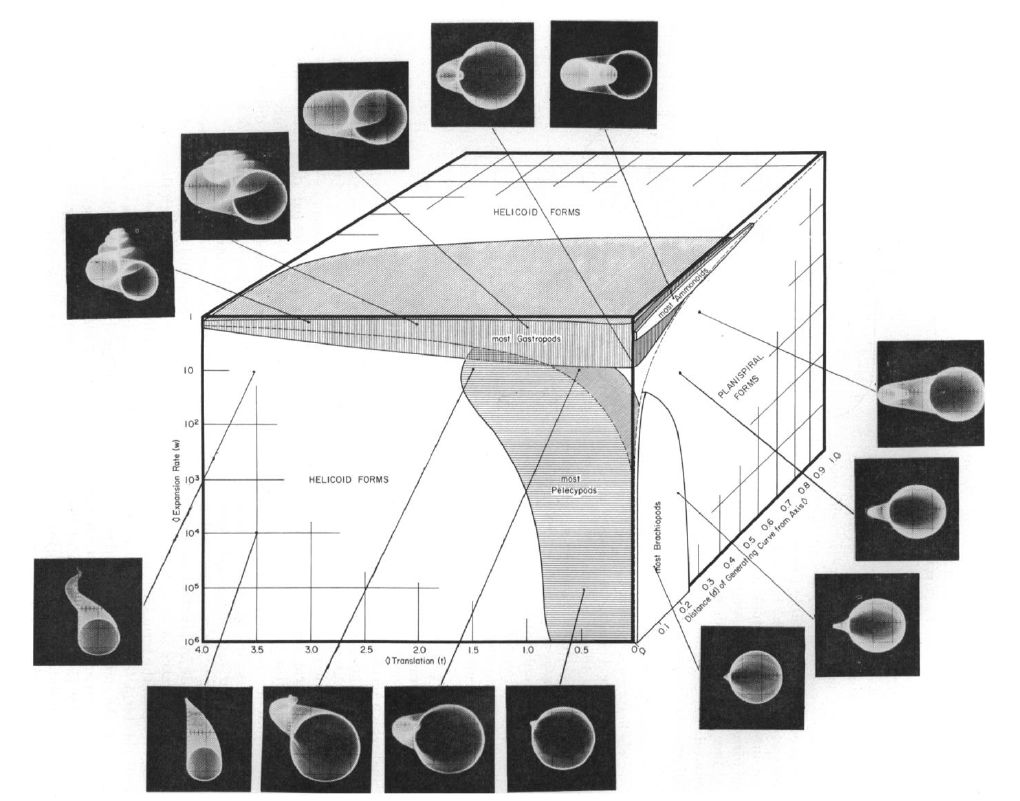
En la se representa el espacio tridimensional determinado por esos tres parámetros y se reflejan algunas muestras de conchas en él, manteniendo la circunferencia como curva generatriz. Todo el cubo se corresponde con formas estrictamente helicoidales, cuando $T>0$, y sólo en la cara lateral derecha es donde se ubican las conchas discoidales correspondientes a $T=0$, pero
obviamente puede considerarse como un caso particular de concha helicoidal. Dentro de esta cara lateral, según lo indicado antes, en la parte superior de la misma se ubican las conchas univalvas (valores pequeños de $W$ que generan caparazones enrollados que protegen las partes blandas del animal) y en la inferior las bivalvas, si bien se encuentran excepciones como las lapas en las que el factor de crecimiento es grande y la funcionalidad protectora es diferente al adherirse éstas a una superficie exterior.
El estudio particular de las conchas discoidales lo aborda Raup en su artículo "Geometric Analysis of Shell Coiling: Coiling in Ammonoids"
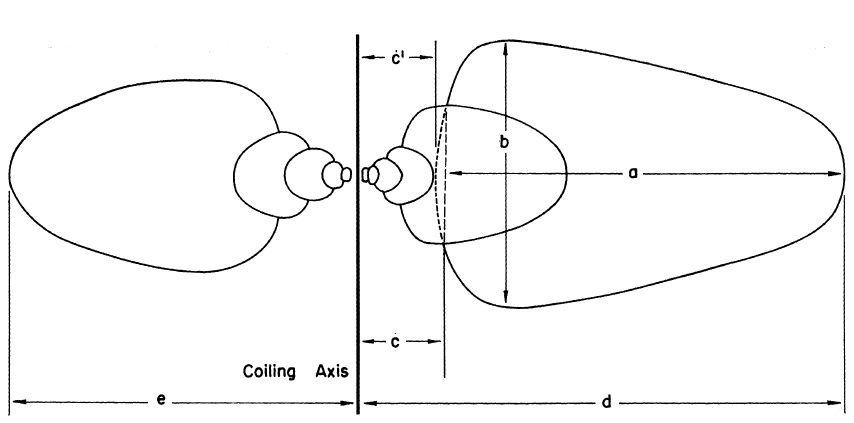
En la se reflejan las longitudes medidas para calcular los parámetros $W$, $D$ y $S$ y el diámetro de la concha. Aquí el parámetro $S$ (shape o forma) refleja las proporciones de la curva generatriz y no la forma de ésta en sí. Estas medidas se realizan mejor sobre una foto del ejemplar a medir, siempre que ésta esté correctamente orientada, y como $W$, $D$ y $S$ son proporciones no es necesario conocer la escala de la foto. Así pues, el uso de fotos o dibujos es útil para reproducir el estudio sin más que el plano de tal ilustración esté cerca de un plano que incluya al eje de giro o al plano sagital del ejemplar, es decir, el plano de simetría del mismoRaup afirma que: "Se puede demostrar, sin embargo, que se puede tolerar una distorsión y/o desorientación considerable de la ilustración sin alterar sustancialmente los valores calculados de las proporciones"..
Por otro lado, dado que son verticilos superpuestos o cuando lo sean, la consideración de la medida $c$ —distancia desde el eje de giro a la curva generatriz real— o de $c'$ —distancia desde el eje de giro a la curva generatriz teórica— no afecta sustancialmente al modelo geométrico al calcular $D$, pero sí surge un planteamiento biológico acerca de si el organismo esta genéticamente programado para generar toda la curva generatriz teórica (como curva cerrada) y deposita sólo la parte geométricamente posible (también controlado genéticamente), pues si es así un cambio evolutivo en $D$ no necesita ir acompañado de un cambio evolutivo en la curva generatriz. En la práctica, la medida que puede obtenerse es $c$, pues la forma teórica de la curva no deja de ser una estimación.
Con los artículos descritos contamos con información más que suficiente para avanzar en nuestro objetivo final y así lo haremos, pero para dejar un poco más completa la investigación de Raup y sus colegas citaremos dos artículos adicionales en los que poder profundizar o inspirarse:
Para modelar la concha tridimensional del Nautilus, de acuerdo a lo descrito en la sección anterior y, en particular, siguiendo el análisis realizado por Raup, necesitaremos determinar cada uno de los tres parámetros que están asociados a toda concha discoidal, es decir, cuál es su curva generatriz, qué distancia hay de ésta al eje de giro y cuál es el factor de crecimiento. Pero previamente procederemos a parametrizar el modelo e implantarlo en una escena interactiva y posteriormente lo particularizaremos con los datos del Nautilus.
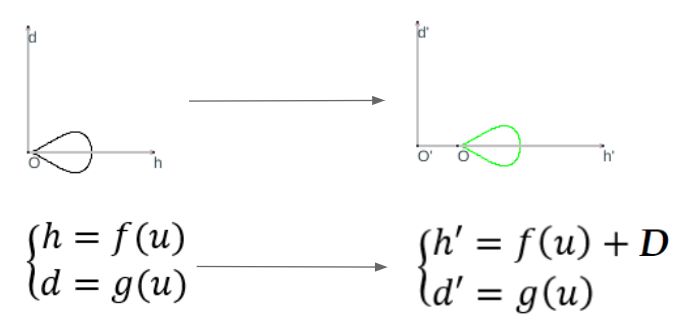
Según hemos indicado, la curva generatriz se puede obtener considerando cualquier sección plana de la concha, pero nosotros consideraremos la sección transversal obtenida al cortar por uno de los planos del haz de planos secantes generado por el eje de revolución, es decir, que tendremos una curva plana (ver la ) que expresaremos paramétricamente tomando como sistema de referencia uno ortogonal cartesiano $\{O, h, d\}$, donde el eje de ordenadas $d$ es paralelo y no necesariamente coincidente con el eje de giroLa forma de la curva es lo que aquí se persigue y su ubicación o posición respecto al eje de giro vendrá finalmente determinada por el segundo parámetro, la distancia al eje de giro, que permitirá ubicar esta curva en la posición correcta.:
$$\begin{cases} h=f(u) \\ d=g(u)\end{cases} \tag{$1.4$}$$
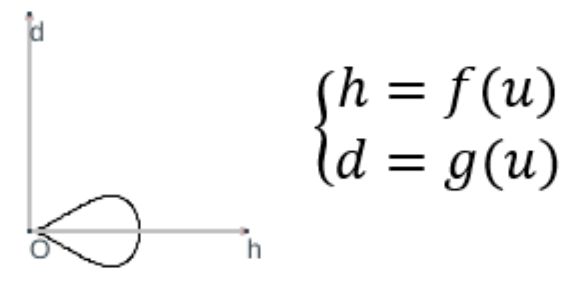
La distancia $D$ al eje de giro introduce una traslación en la sección tranversal (ver la ), un cambio del sistema de referencia a $\{O', h', d'\}$ en el que la curva generatriz tiene por ecuación:
$$\begin{cases} h'=f(u)+D \\ d'=g(u)\end{cases} \tag{$1.5$}$$
Si consideramos que el crecimiento es acorde con la espiral logarítmica de ecuación polarSi $\alpha$ es el ángulo característico de la espiral tenemos que $b=e^{cotg \, \alpha}$ —ver la p. 15 de este libro o bien p. 148 de Galo (2024)
Realizando esa amplificación (ver ), en el nuevo sistema de referencia $\{O'', h'', d''\}$ la curva generatriz tendrá por ecuación:
$$\begin{cases} h''=a \, b^V (f(u)+D) \\ d''=a \, b^V g(u)\end{cases} \tag{$1.7$}$$
donde $V$ representa el ángulo de giro en el crecimiento según la espiral logarítimica indicada.
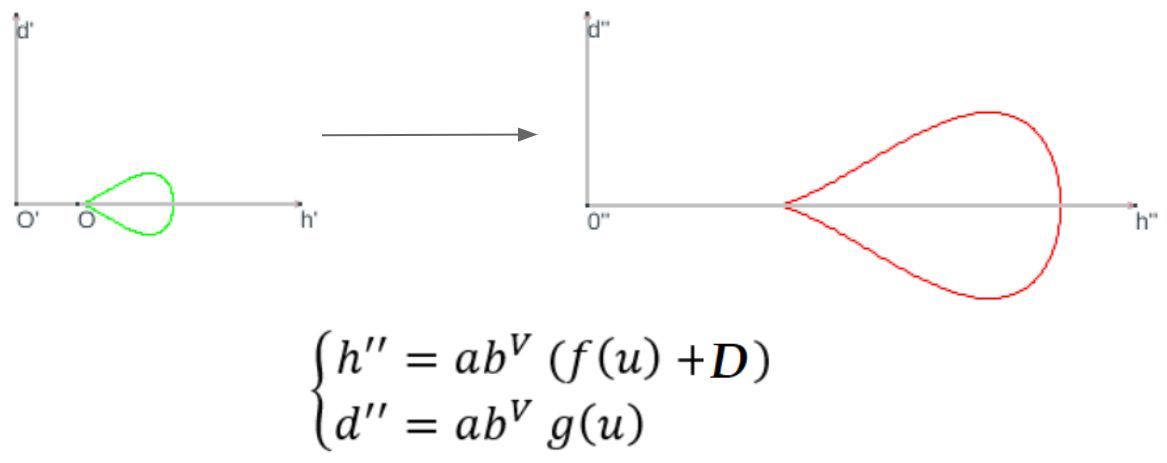
Finalmente para obtener las ecuaciones cartesianas de la transformación en el espacio tridimensional con sistema de referencia $\{O, x, y, z\}$, basta que ubiquemos la curva (1.7) en el plano cartesiano de ecuación:
$$sen V \, x - cos V \, y +0 \, z = 0 \tag{1.8}$$
es decir,
$$\begin{cases} x=h'' cos V \\ y=h'' sen V \\ z=d'' \end{cases} \tag{$1.9$}$$
de donde
$$\begin{cases} x=a \, b^V (f(u)+D) \, cos V \\ y=a \, b^V (f(u)+D) \, sen V \\ z=a \, b^V g(u) \end{cases} \tag{$1.10$}$$
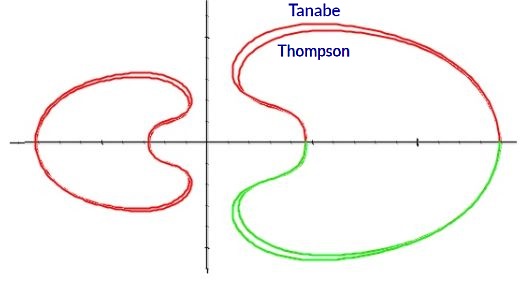
En la se ha representado en la imagen de la izquierda en color verde una curva generatriz correspondiente a una amplificación asociada al ángulo $V$ en (1.10) y en la de la derecha se representa ésta y la amplificación asociada al ángulo $V+ 2\pi$ en color rojo.
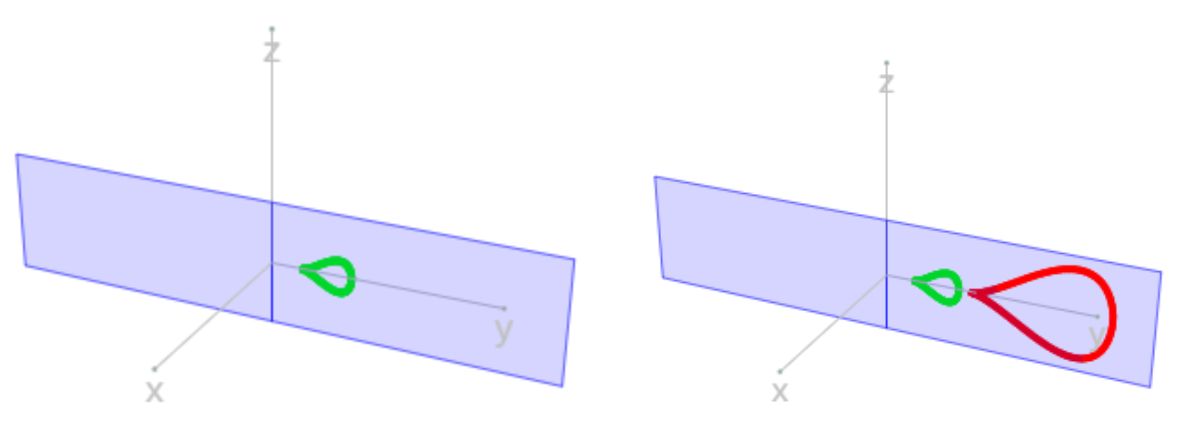
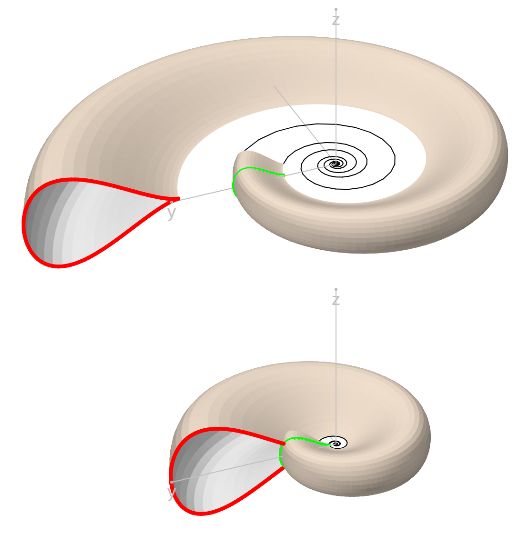
Variando el valor del parámetro $V$ obtenemos la superficie tridimensional asociada a la curva generatriz considerada en (1.5), siguiendo un crecimiento discoidal logarítmico de base $b$ y escalado por el factor $a$.
En la sección anterior hemos establecido el modelo de las conchas discoidales según la adaptación que hemos realizado del modelo de Raup, procede ahora su implementación y es lo realizado en la .
En la escena se distinguen tres espacios:
Al cambiar la distancia al eje pueden obtenerse conchas evolutas o involutas (). Ese efecto también se obtiene según el valor del factor de crecimiento y a su vez también depende de la forma de la sección frontal.
Adicionalmente se tienen tres controles ajenos al modelo de la concha y que sólo cambian la presentación visual de la gráfica tridimensional de la misma:
Para aplicar a la concha del Nautilus el modelo 3D, obtenido en el capítulo anterior, hemos de determinar los parámetros específicos que la configuran. El factor de crecimiento es ya bien conocido para nosotros, pues determinamos que sigue un crecimiento cordobés (Galo, 2024)
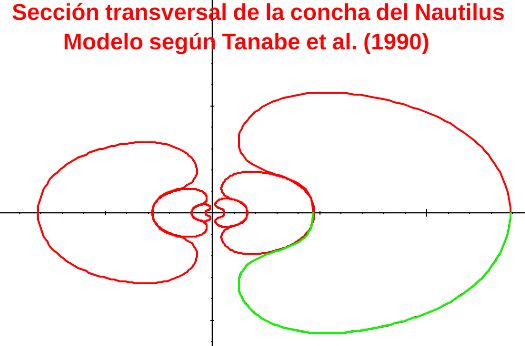
Para determinar la ecuación de la curva generatriz del Nautilus consideramos inicialmente la sección del Nautilus aportada por Tanabe et al. (1985)
Así pues, en las siguientes secciones procederemos a detallar la búsqueda de un tipo (holotipo) para la sección frontal del Nautilus y, a partir de él, determinar la curva generatriz del mismo.
En el artículo "Morphological Analysis of Nautilus pompilius" de Tanabe, Hayasaka y Tsukahara (Tanabe et al., 1985)
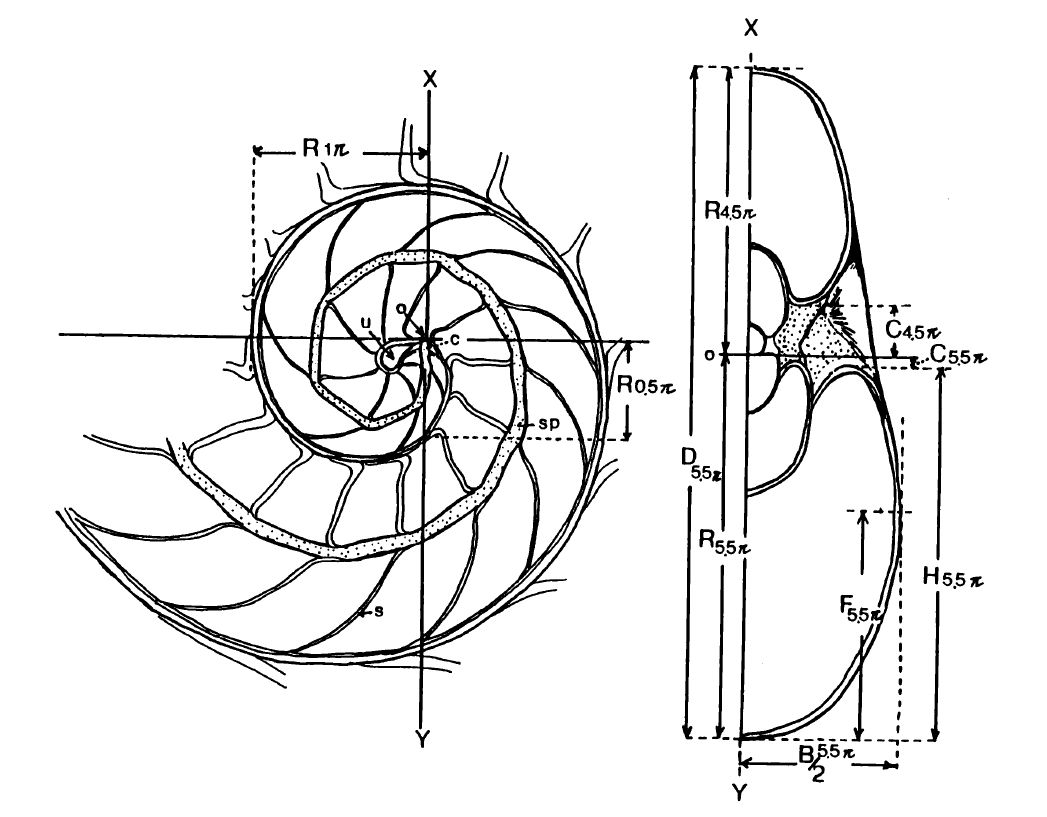
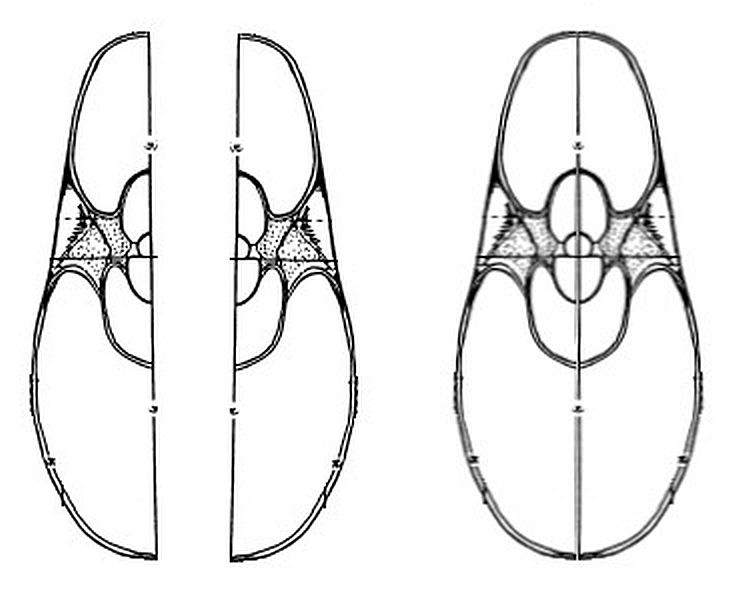
A partir de la imagen de la mitad de la sección frontal, editándola, podemos conformar la sección completa de la misma():
Sobre la concha seccionada sagitalmente (imagen izquierda de la ) estos autores proceden a medir el radio vector R en intervalos de $0,5 \pi$ radianes tomando como origen de coordenadas, del sistema de referencia considerado, el engarce inicial del sifúnculo en el punto apical de la conchaOtros autores han considerado como polo el centro del ombligo, pero estos aducen que realmente el ombligo no se genera hasta que se cierra el primer verticilo y, por tanto, consideran más apropiado que el origen sea el inicio del crecimiento de la concha. En Galo (2024-b, pp 70-79)
Posteriormente seccionan la concha frontalmente siguiendo la dirección del eje $XY$ dibujado en la citada imagen izquierda de la , obteniendo la imagen derecha reflejada en ella. Sobre la sección frontal, con un proyector de perfiles, proceden a medir en intervalos de $\pi$ radianes los siguientes parámetros : el diámetro de la concha (D), el ancho del verticilo (B) y la altura (H), la mitad de la
longitud del ombligo (C) y la posición del flanco (F) en la "mitad" de la sección transversal. Y a partir de estos datos calculan los cuatro parámetros propuestos por Raup (1966)
Los datos aportados por estos autores están accesibles en su artículo y los hemos registrado en una hoja de cálculo de "Google Sheets" a la que puede acceder en línea, o bien en local mediante una hoja de "Microsoft Excel" o a un pdf. Esta hoja de cálculo es un "libro" de seis hojas cuyo nombre y contenido es:
En la se han representado, en el plano sagital de la concha, los puntos aportados en la hoja del apartado (1) anterior, situándolos respecto a la concha nepiónica proporcionada por estos autores.
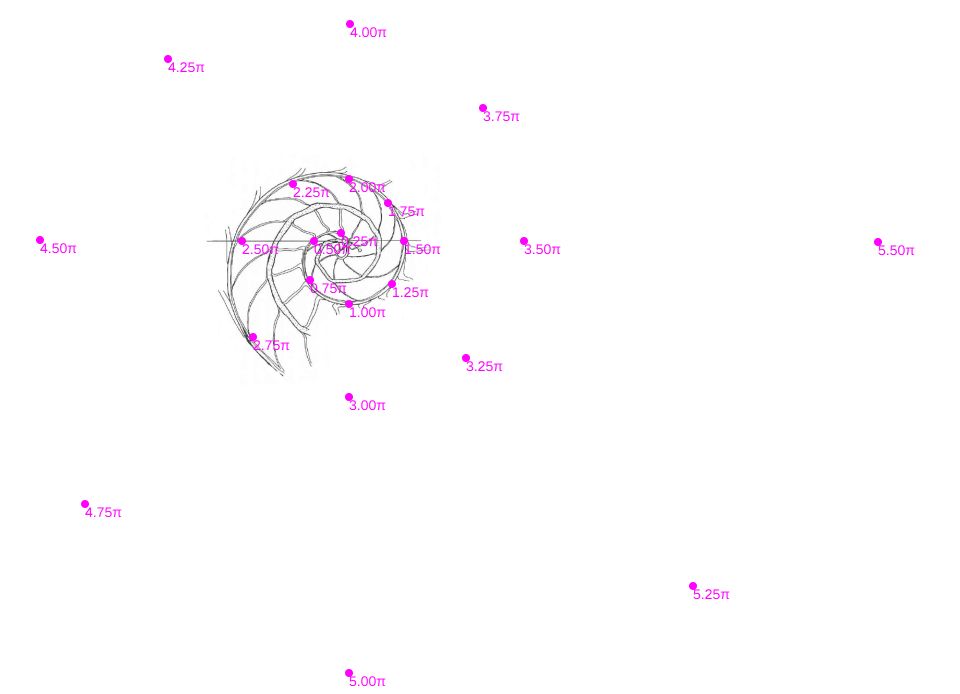
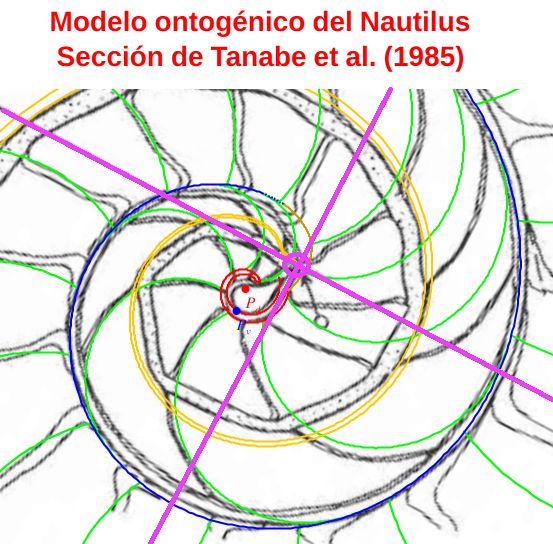
Si dibujamos la espiral cordobesa que determina el crecimiento de la sección sagital del Nautilus (Galo et al., 2016
Sin embargo, considerando el polo ventral indicado por Galo (2024-b)
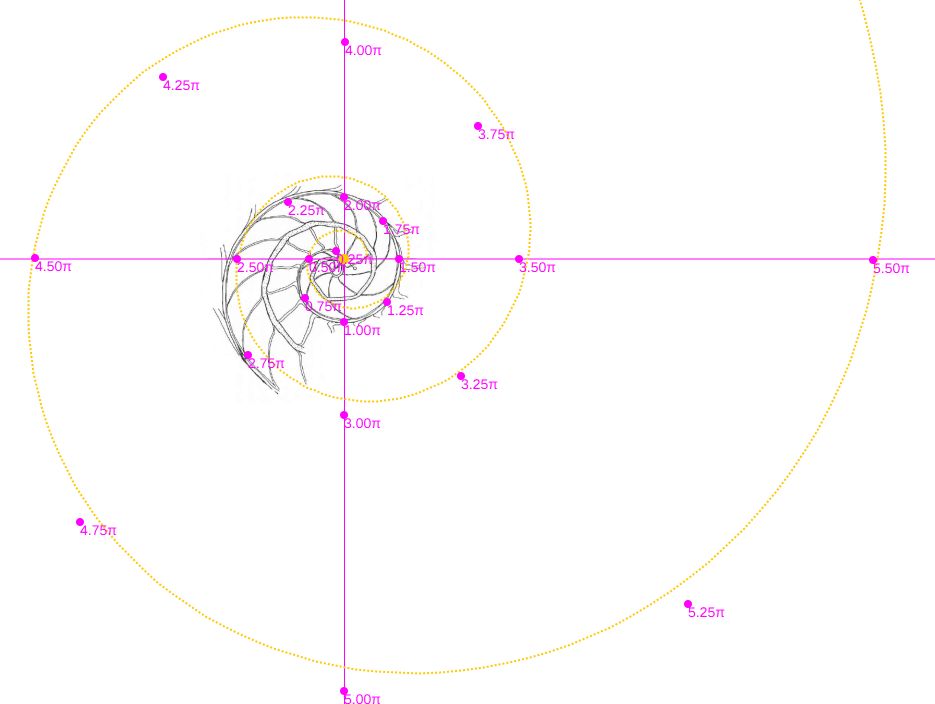
En la se observa cómo se ajusta adecuadamente a los datos de Tanabe et al. (1985).
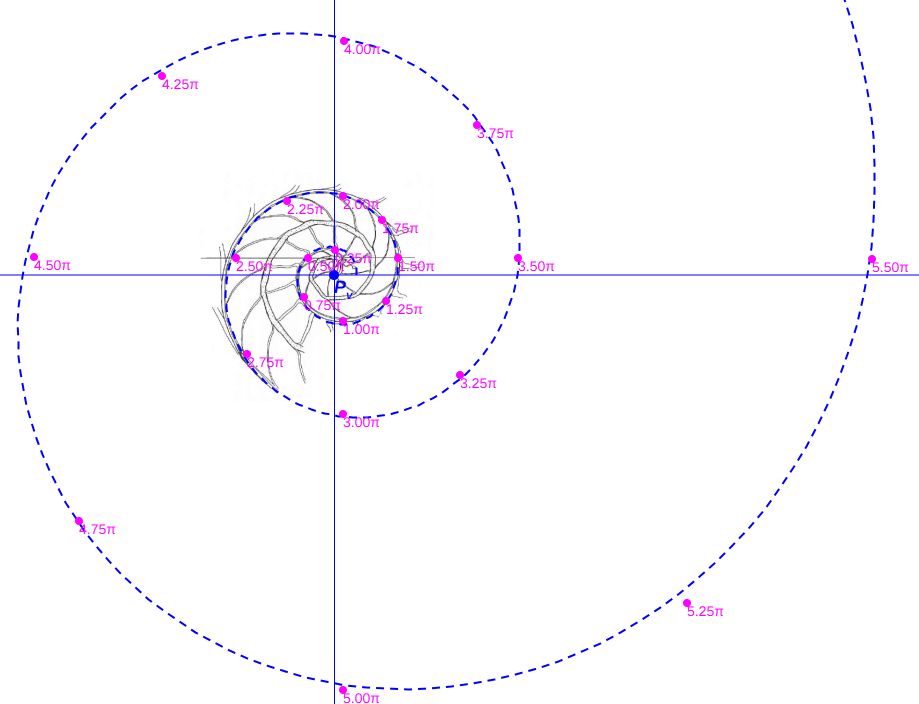
Comparando ambas espirales cordobesas (ver ) podemos concluir que el modelo de crecimiento cordobés con polo el indicado por Galo (2024-b), se ajusta a los datos aportados por Tanabe et al. (1985), reforzando lo indicado por Galo (2024
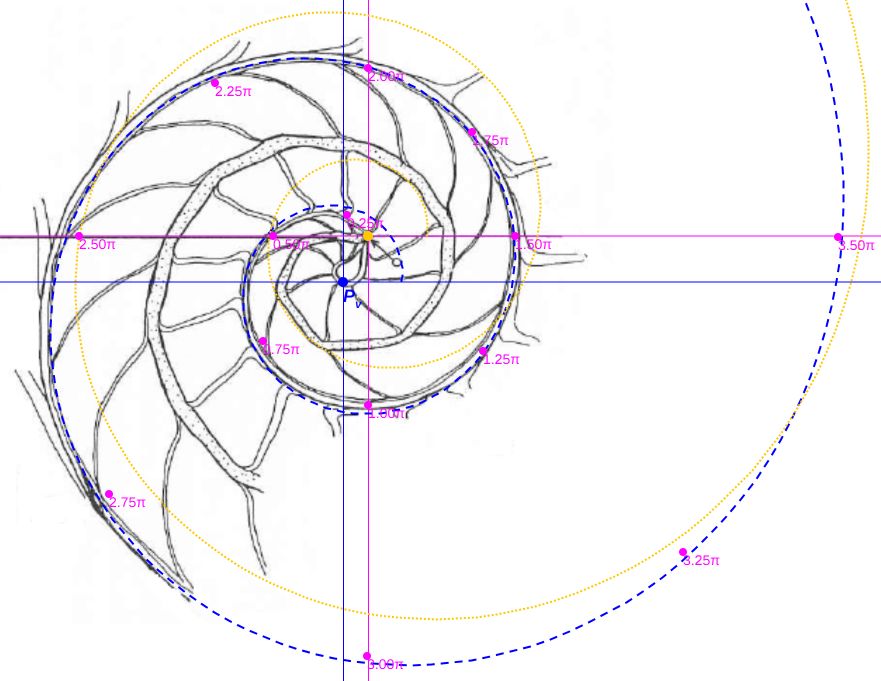
Consecuentemente, la búsqueda de la sección frontal del Nautilus quedaría terminada, pues podríamos considerar la reflejada en la imagen derecha de la como tipo para aplicarlo en el modelo 3D del mismo..., pero ¡nuestra sorpresa fue mayúscula! cuando al superponer esa sección con los datos considerados y con la espiral cordobesa (ver ) se mostró una diferencia notable entre ellos.
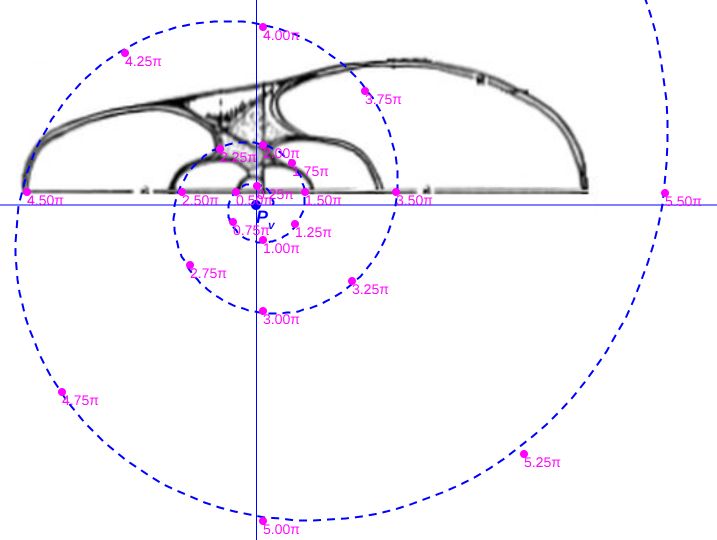
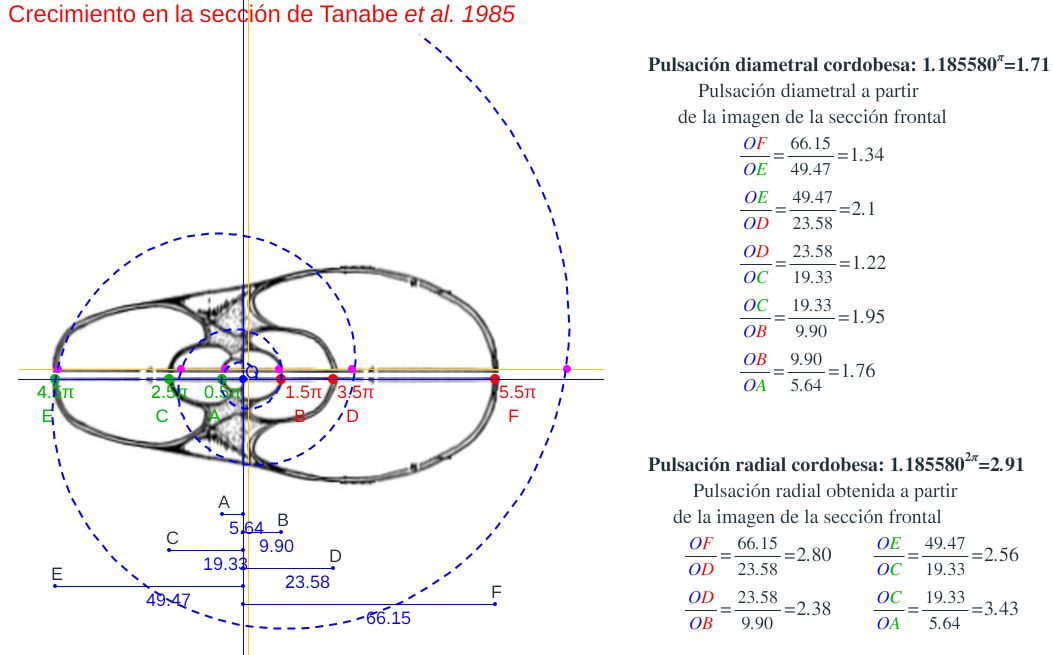
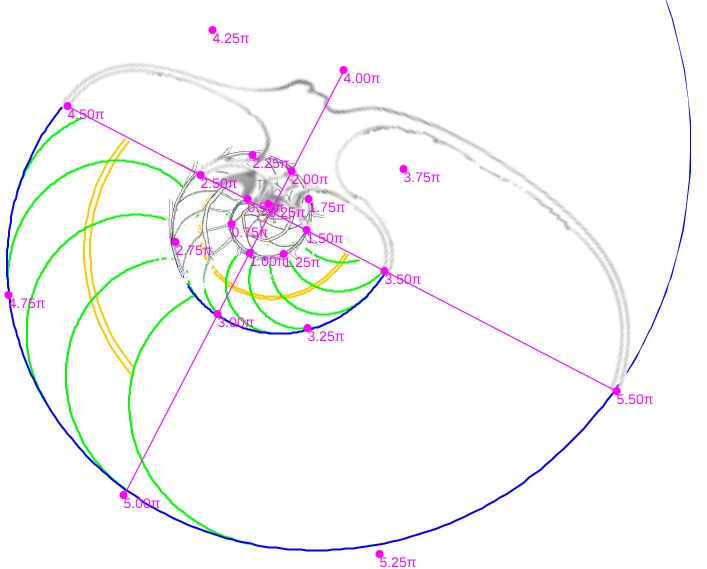
Es más, en la figura , en color azul, se refleja la espiral cordobesa que pasa por los puntos dados por Tanabe et al. (1985) para los ángulos $0,5\pi, 1,5\pi, 2,5\pi, 3,5\pi, 4,5\pi \text{ y } 5,5\pi$, dibujados de nuevo en color magenta, y que deberían de coincidir con las pulsaciones radiales de la sección frontal, pero claramente no lo hacen. Si obtenemos los puntos análogos a los anteriores pero a partir de la imagen de la seción frontal, etiquetados de A a E en esa imagen, vemos que esa espiral pasa por A, B y E, pero no pasa por los puntos C, D y F, es decir, hay una discrepancia entre los datos numéricos y la imagen de la sección frontal aportados por estos autores. Así pues, si esa imagen se correspondiera con la sección correcta obtendríamos que el factor de crecimiento diametral y radial no diferiría de sendas razones correspondientes al crecimiento
cordobés, pero según se refleja en las proporciones calculadas a la derecha de esa figura (sin más que considerar las medidas relativas de los radios vectores en esa imagen) y comparándolas con las pulsaciones diametrales y radiales téoricas esperadas, que son $b^{\pi}$ y $b^{2 \pi}$ respectivamente, la diferencia es evidente. El supuesto "tipo" que habíamos encontrado era obvio que quedó deformado en algún momento de la edición tipográfica de ese artículo (Tanabe et al., 1985) y ello nos forzaba a una nueva búsqueda.
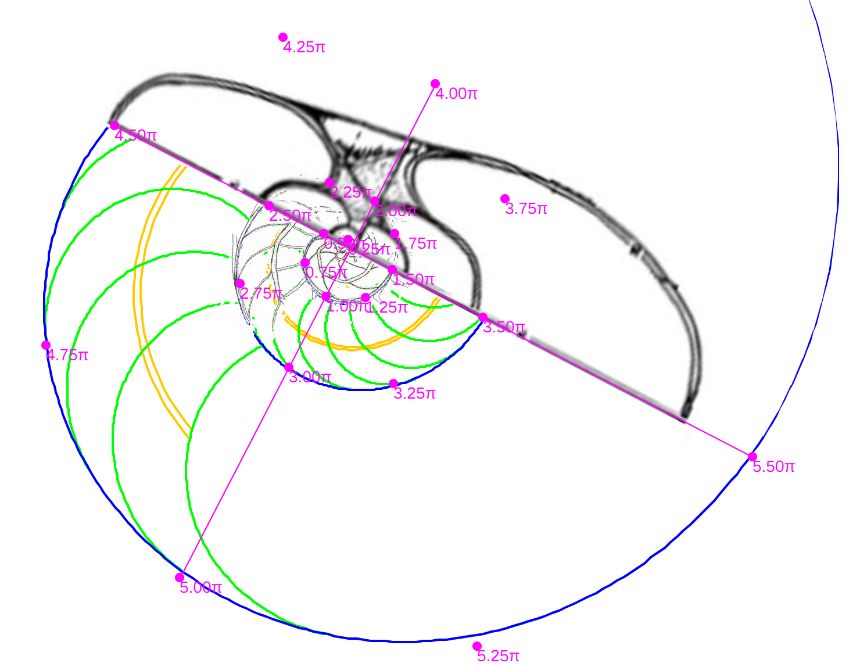
En la reflejamos la comparativa de esta sección frontal con el modelo ontogénico del Nautilus (Galo, 2024-b) pudiendo constatar la diferencia existente y, a su vez, cómo la sección sagital nepiónica sí se ajusta a lo previsto en la fase inicial de ese modelo.
Dado que los datos aportados en ese artículo coincidían y reforzaban el crecimiento cordobés, era obvio que dicha búsqueda podría encontrar respuesta en otros artículos de estos autores y, adelantamos, que afortunadamente así fue.
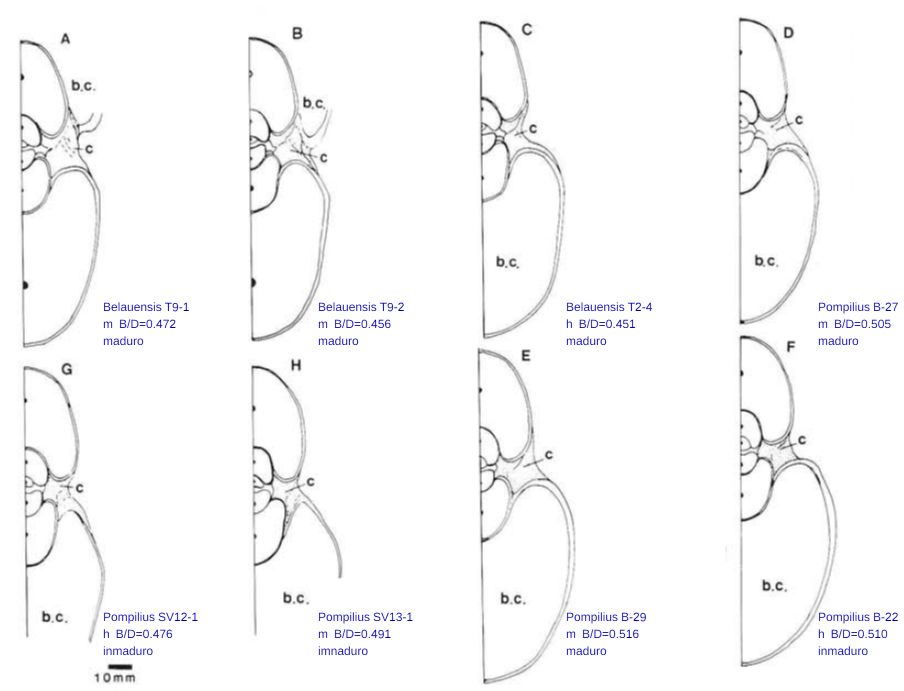
En el artículo "Comparative morphology of living Nautilus (Cephalopoda) from the Philippines, Fiji and Palau" de Tanabe, Tsukahara y Hayasaka de 1990
Todos los datos asociados a estos ejemplares y otros adicionales más pueden consultarse en las siguientes referencias:
De esos ocho ejemplares seleccionamos en concreto el etiquetado con la letra D por la razones que posteriormente indicaremos, pero previamente a ello era obvia la necesidad de verificar que dichas secciones se correspondieran con el modelo cordobés y evitar más sorpresas. En la se observa cómo, ahora sí, se ajusta al modelo teórico cordobés.
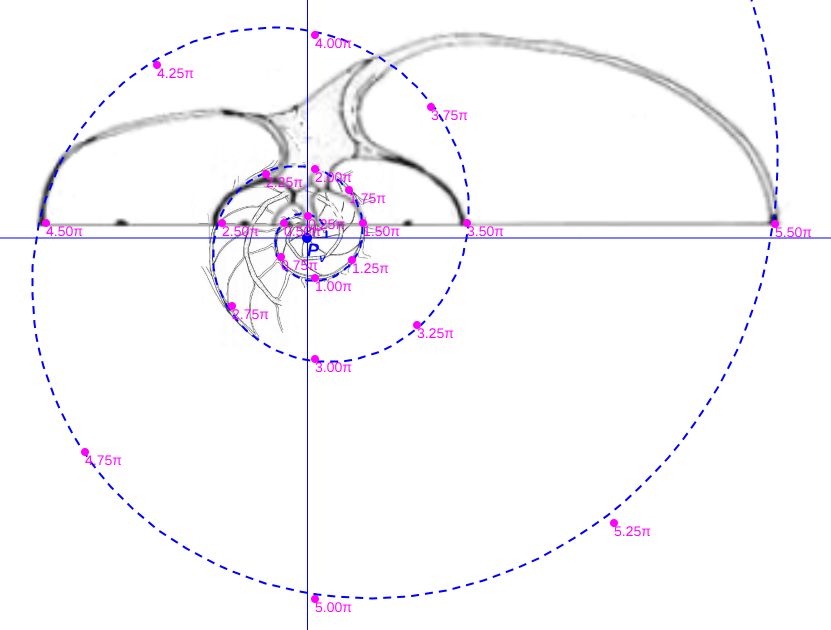
Calculando las proporciones relativas de las pulsaciones radiales y diametrales que acontecen en la imagen y comparándolas con las teóricas $b^\pi$ y $b^{2\pi}$ también se verifica el adecuado ajuste (ver la ).
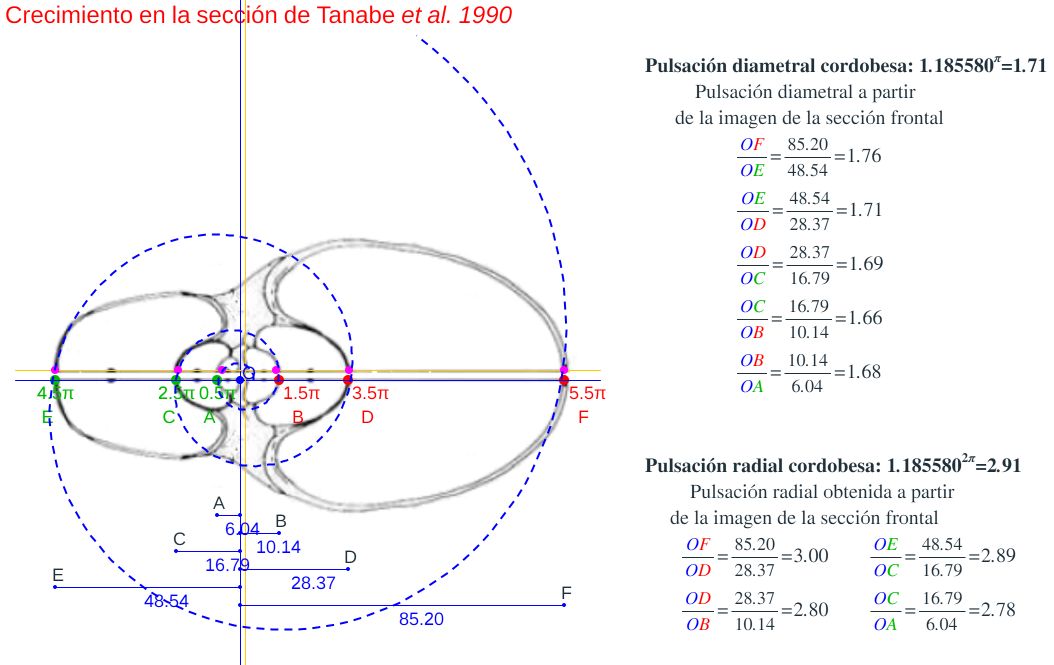
Y de similar manera en la realizamos la comparativa de esta sección con el modelo ontogénico de Galo (2024-b), comprobando que todo volvía a la normalidad esperada y que con esta nueva sección podríamos retomar y proseguir en la modelación tridimensional objeto de este estudio.
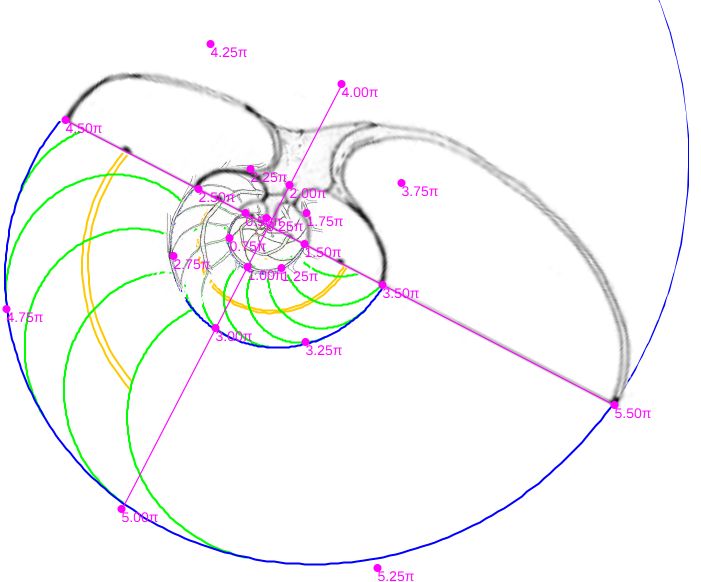
Aunque disponemos de la sección frontal canditata a considerarla como tipo, por cuestiones personalesGonzález-Restrepo obtuvo esta sección a petición mía y desde entonces esa sección ha sido un refrente en mi investigación del Nautilus. no podemos resistirnos a realizar una comparativa análoga con la sección frontal que González-Restrepo (2019)
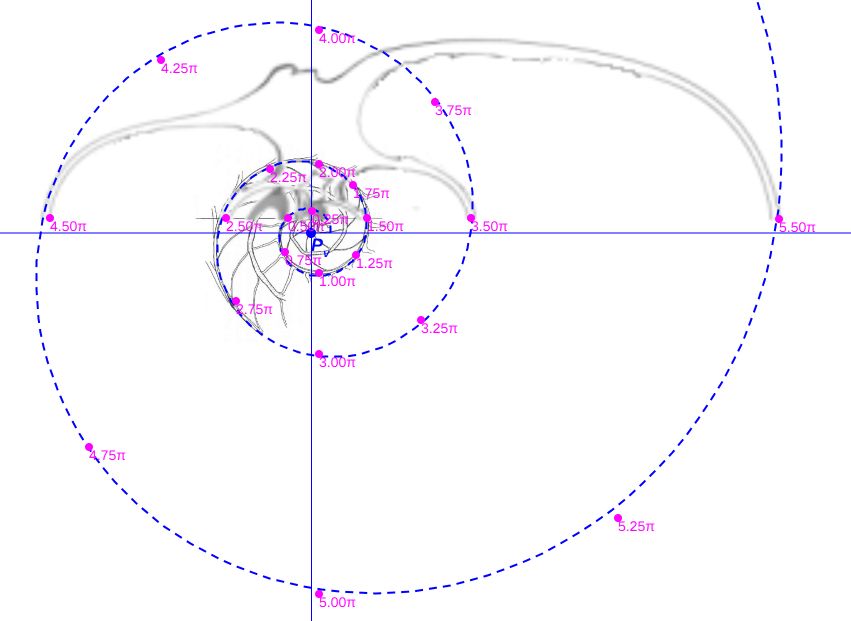
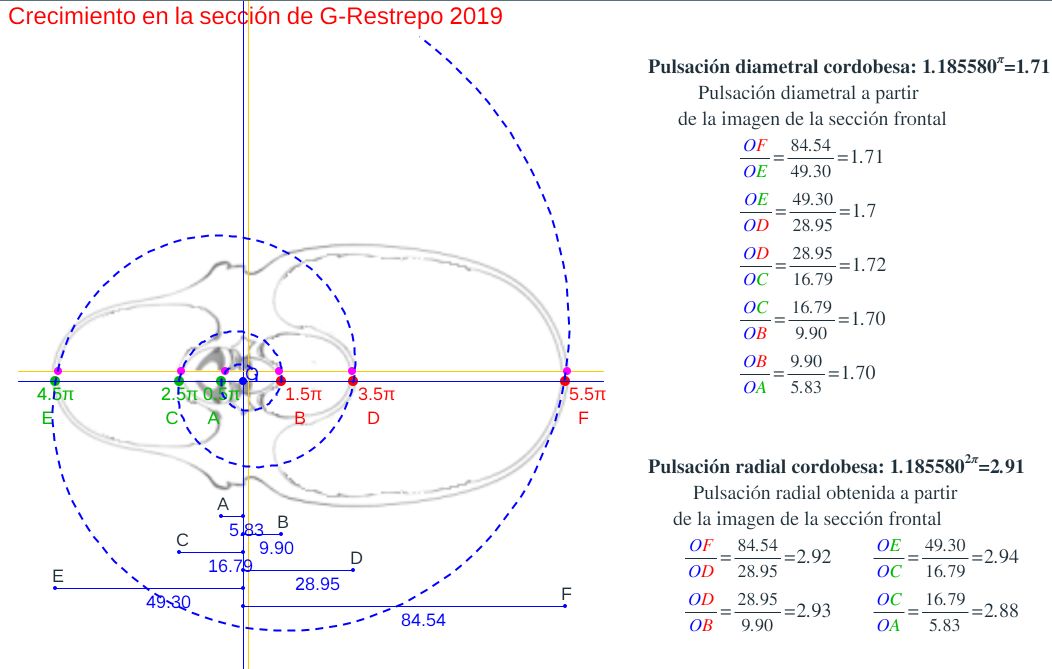
Verificada la concordancia de los datos métricos del Nautilus con diferentes secciones frontales del mismo y con el modelo cordobés, necesitamos proceder a elegir un tipo referencial que aporte la curva generatriz al modelo tridimensional. Si bien la predilección personal tendería a seleccionar el corte de González-Restrepo (2019), por idéntica razón la obviamos para que no fuera etiquetada como una mera razón subjetiva. En consecuencia, acudimos a las secciones reflejadas en la y tuvimos en consideración lo siguiente:

Por tanto, de los ejemplares D, E y F el candidato a elegir como tipo para el Nautilus pompilius sería el D por estar más cercano a la media indicada respecto a su sexo. La diferencia respecto a la media de machos es $0,505-0,4964 = 0,0086$, y con la media global $0,505-0,4938 = 0,0112$.
En base a lo anterior consideraremos como tipo de la sección del Nautilus a la etiquetada como D en la y que a partir de ahora identificaremos como tipo Tanabe (1990). Esta sección es con la que hemos trabajado anteriormente cuando cotejamos los datos numéricos de Tanabe et al. (1985) con la imagen de la sección frontal y con el modelo cordobés.
En el análisis abordado en las secciones anteriores de este capítulo para determinar la curva generatriz del Nautilus, hemos utilizado diferentes datos numéricos e imágenes que hemos confrontado con el modelo de crecimiento cordobés y el modelo ontogénico del mismo (Galo, 2024 y 2024b), estas comparativas se han realizado utilizando tres recursos interactivos desarrollados con la herramienta de autor "Descartes".
En la se aborda el crecimiento de las secciones frontales del Nautilus correspondientes a la imagen reflejada en el artículo de Tanabe et al. (1985), la de Tanabe et al. (1990) y la de González-Restrepo (2019), confrontando las mismas con los datos numéricos aportados por Tanabe et al. (1985).
La escena se inicia mostrando un espacio de portada que muestra un corte sagital de la concha nepiónica del Nautilus y están dibujados, en color magenta, los puntos correspondientes a los datos determinados por Tanabe et al. (1985) y aportados en ese artículo.
En el lateral izquierdo hay dos controles tipo botón con las imágenes de unas lupas y que permiten hacer zum en la representación gráfica de la escena.
En la parte inferior se incluyen varios controles:
En el espacio específico de datos, que se activa cuando se elige una opción en el menú de selección, podemos observar:
Un segundo recurso lo tenemos en la en el que confrontamos las secciones frontales antes analizadas con el modelo ontogénico uniforme nautiliano (Galo 2024b). La escena se inicia mostrando un espacio en el que se representa el modelo ontogénico del Nautilus, un corte sagital de la concha nepiónica del mismo y están dibujados, en color magenta los puntos correspondientes a los datos determinados y aportados por Tanabe et al. (1985).
En el lateral izquierdo hay dos controles tipo botón con las imágenes de unas lupas y que permiten hacer zum en la representación gráfica de la escena.
En la parte inferior se incluyen varios controles:
En la se muestran los ejemplares incluidos en el artículo de Tanabe et al. (1990) indicando los códigos identificadores aportados por los autores, el sexo y la proporción
entre el ancho del verticilo de la concha (B: whorl breadth) y el diametro (D: Shell diameter) de ella (B/D).
En la escena podemos distinguir dos zonas que hemos separado por una raya vertical.
En la parte inferior se dispone de dos controles tipo pulsador:
Establecido el Tipo que determina la sección frontal del Nautilus, lo natural es plantearse su modelación matemática obteniendo una curva que sirva como curva generatriz e incluyéndola en el modelo 3D, detallado en la sección 1.2 de este libro, obtener el modelo tridimensional del Nautilus asociado.
Para ello, procederemos inicialmente a una modelación aproximada mediante una curva de Bézier y posteriormente trataremos de hallar un modelo teórico que simplifique conceptualmente la forma de esta sección.
Las curvas de Bézier son curvas de ajuste polinómicas, pero se definen de manera que mitiguen los inconvenientes antes indicados. Son de amplio uso en el contexto del diseño asistido por ordenador porque la aplicación de transformaciones afines actúa sobre los coeficientes siguiendo la misma transformación. Todo esto es de gran utilidad en nuestro objetivo de aproximar la sección frontal por una curva suave a partir de algunos puntos de referencia, no necesariamente muchos como veremos.
En la se puede definir una nube de puntos y obtener la curva de Bézier correspondiente. También pueden observarse las propiedades de estas curvas y comprobar como son invariantes por transformaciones afines. En las indicaciones de esta escena pueden consultarse los controles de la escena y su funcionalidad.
Las curvas de Bézier se obtienen como combinaciones lineales de los denominados polinomios de Bernstein. En la podemos conocer cómo se definen estos polinominos y sus propiedades (consultad las indicaciones de esta escena).
En la escena hemos realizado una aproximación de la mitad de la sección frontal de Tanabe (1990) que es la que hemos considerado como Tipo.
El ajuste se ha obtenido aproximando el perfil en la última media vuelta mediante una curva de Bézier construida en base a una poligonal para la que han bastado nueve puntosEn esta escena se ha deshabilitado la posibilidad de modificar la poligonal de referencia para el ajuste, por tanto el lector/actor no puede cambiarla. Posteriormente se incluirá una escena en la que podrá realizar todas las modificaciones que desee y definir, ajustar y construir su propia concha.. Esta curva está reflejada en color verde en esa escena y en la , donde a su vez también se muestra el ajuste en los dos verticilos y medio anteriores (curvas en color magenta y turquesa), estas últimas curvas se han obtenido a partir de la anterior escalándola mediante la aplicación del correspondiente factor de crecimiento cordobés, es decir, $b^{-\pi}$, $b^{-2\pi}$,$b^{-3\pi}$, $b^{-4\pi}$ y $b^{-5\pi}$ con $b=1,185580...$ (consultar la sección 2.1). Esta imagen se obtiene pulsando sobre el botón etiquetado como "muestra crecimiento" en dicha escena.
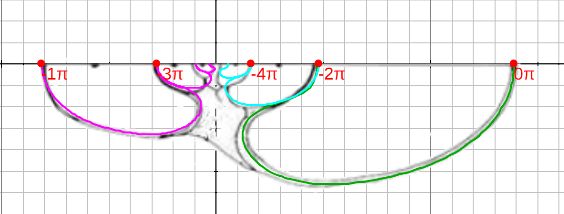
Hay que señalar que la curva de Bézier se ha construido de manera que la parte interior de ésta sea tangente con la exterior en los verticilos anteriores, que es lo que se observa de manera natural en la concha nautiliana cuando se superpone la pared dorsal de un verticilo sobre la pared ventral del verticilo anterior.
Por otro lado, también, hay que indicar que el ajuste que se obtiene al escalar la curva de Bézier de referencia y superponerla sobre la concha tipo es peor en el primer verticilo, si bien esto es lo esperado como consecuencia del crecimiento ontogénico y las diferencias que acontecen en esa primera etapa vital (Galo, 2024b)
El ajuste de la sección frontal Tipo de Tanabe (1990) está reflejado en la . En este modelo no se incluye el callo umbilical que será objeto de estudio posterior.
Determinada la curva generatriz, en este caso mediante el ajuste con la curva de Bézier, estamos en condiciones de poder mostrar un primer modelo tridimensional de la concha nautiliana aplicando lo indicado en el primer capítulo. Ello es lo que podemos observar en la (pulse sobre la imagen para acceder a ella, ya que por coste computacional no la hemos embebido en el libro).
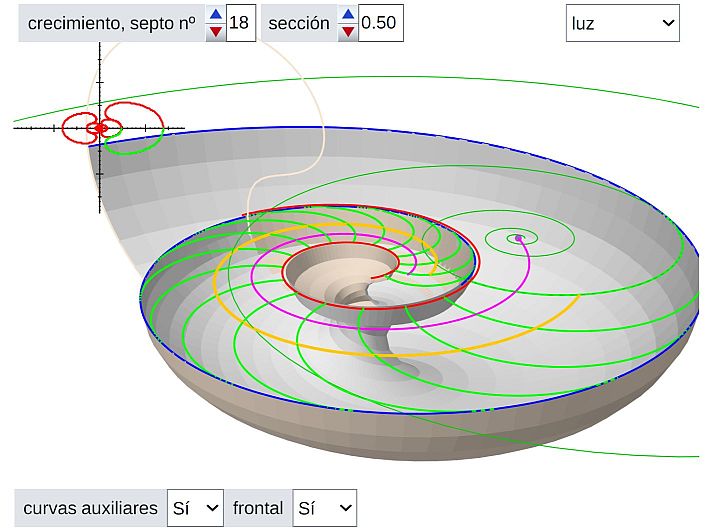
En esta escena no se representa la concha embrionaria por lo que se observa un hueco o vacío inicial que es el que ocuparía la misma. El usario dispone de varios controles:
De manera análoga podemos determinar la curva de ajuste para la sección realizada por González-Restrepo (2019). Es lo reflejado en la y en la , ambas obtenidas con la .
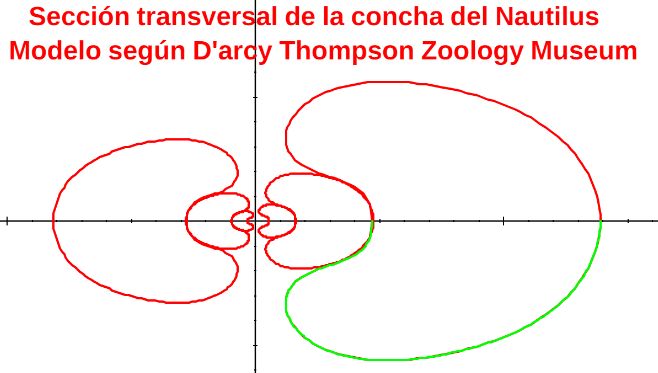
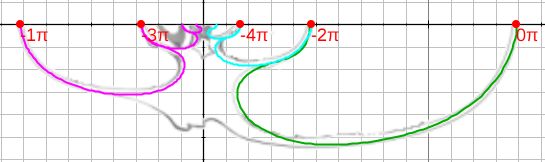
Y a partir de esa curva generatriz también obtenemos el modelo 3D asociado a esta sección de Thompson, que es el reflejado en la .
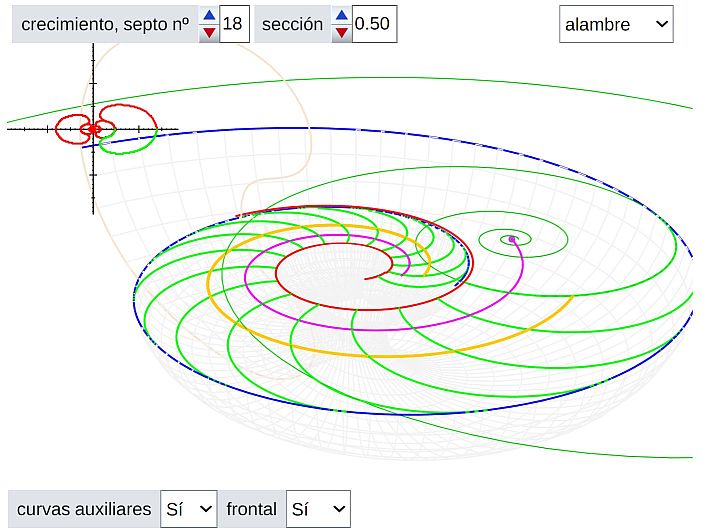
Pero, salvo que tenga un aguzado sentido de la vista, poca diferencia puede apreciarse a simple vista entre los modelos obtenidos para Tanabe y para Thompson (aunque basta el tipo de Tanabe, insisto, que el segundo lo abordo y reflejo por cuestión personal como ya indiqué con anterioridad). En parte, es lo esperado ¡¿verdad?!, si ambos son representativos de un mismo género taxonómico.
En la hemos superpuesto los ajustes anteriores por curva de Bézier y se observa que la curva correspondiente a Tanabe es la que contiene a la de Thompson. Consecuentemente la primera, con una proporciónRecordemos que esta proporción es entre el ancho del verticilo de la concha (B: whorl breadth) y el diametro (D: Shell diameter). Ver la . $\frac{B}{D} \simeq 0,5081$ Ver la en la sección 2.2, donde se reflejaba dicho valor y también que la media para el Nautilus pompilius es de $0,4938$., es algo más rechoncha que la segunda en la que se tiene que $\frac{B}{D} \simeq 0,4900$. Ambas proporciones, obviamente, no difieren de lo aportado en Hayasaka et al. (1982, p101)
En la siguiente sección mostraremos cómo hemos calculado estas proporciones usando la y la , que no son más que casos concretos de la que hemos incluido y descrito en la Adenda de este libro y que englobando todas las posibilidades también permite al usuario definir la curva generatriz que desee.
Como cierre del modelado realizado en base al ajuste de la sección frontal del Nautilus por una curva de Bézier, en la se ha reflejado el modelo 3D uniforme. Con posterioridad incluiremos el modelado del callo umbilicar y el de la concha embrionaria.
La modelación de la sección frontal se ha realizado siguiendo la curva que determina la parte correspondiente a la cámara habitacional y de manera que en cada verticilo (crecimiento correspondiente a un ángulo de $2 \pi$) la sección de una, sea tangencial a la otra. Pero, teóricamente, puede plantearse como un enrollamiento espiral que sea involuto, es decir, áquel en el que la curva que define la sección frontal en una vuelta se interseca con la del verticilo anterior.
Con las escenas interactivas antes utilizadas y en particular con la es fácil obtener respuesta a la pregunta ¿cuál puede plantearse como el modelo teórico de esa sección frontal? La respuesta es sencilla, pues la elipse se muestra como una alternativa evidente y así lo vamos a visualizar a continuación. Pero, en este punto, he de reseñar que esta posibilidad ya la calibramos Ángel Cabezudo Bueno, Ildefonso Fernández Trujillo y yo en los trabajos previos a nuestro artículo "Sobre la forma y crecimiento cordobés del Nautilus Pompilius" (2016)
Thompson (1917)
Obviamente las dimensiones indicadas son relativas a la escala considerada en dichas escenas interactivas, pero la excentricidad es independiente de esa escala, al igual que la proporción antes indicada entre el ancho del verticilo ($B$) y el diámetro ($D$) del mismo que para la sección de Tanabe es $\frac{B}{D} \simeq 0,5081$ y en el caso de la de Thompson es $\frac{B}{D} \simeq 0,4900$.
Observamos que la indicación de Thompson (1917), citada antes, es parcialmente acertada. Lo es en la forma elíptica de la curva generatriz, pero no en la porción de la curva que es necesaria para el ajuste de la sección de la concha nautiliana. El modelo teórico necesario es mucho más complejo, pues se necesitan reproducir los lóbulos dorsales y el callo umbilical. Éste último, en una primera simplificación, podría aproximarse con la misma elipse anterior, pero no es tan simple ya que la forma de ese callo incluye un cambio de concavidad que no acontece en un segmento elíptico.
Procede abordar un análisis detallado sobre el modelo teórico de la sección frontal del Nautilus y lo haremos usando la que hemos incluido en la Adenda de este libro, si bien en las secciones siguientes usaremos fragmentos concretos de la misma para focalizar la atención en cada uno de los aspectos abordados.
En el modelado procederemos a considerar por un lado el ombligo o callo umbilical y por otro la parte de la concha correspondiente a la zona habitacional. Ésta también requiere estudiarla dividiéndola en dos zonas: la ventral/dorsal y los salientes o lóbulos dorsales.
En el crecimiento discoidal involuto la pared ventral en un verticilo pasa a ser la pared dorsal en el siguiente, por ello titulamos este epígrafe como modelo de la pared ventral/dorsal.
En la puede optar bien por el tipo de Tanabe o el de Thompson y seleccionar alguna de las tres opciones que conducen al modelo de la concha ventral. El modelo correspondiente a cada opción se ha reflejado en la .
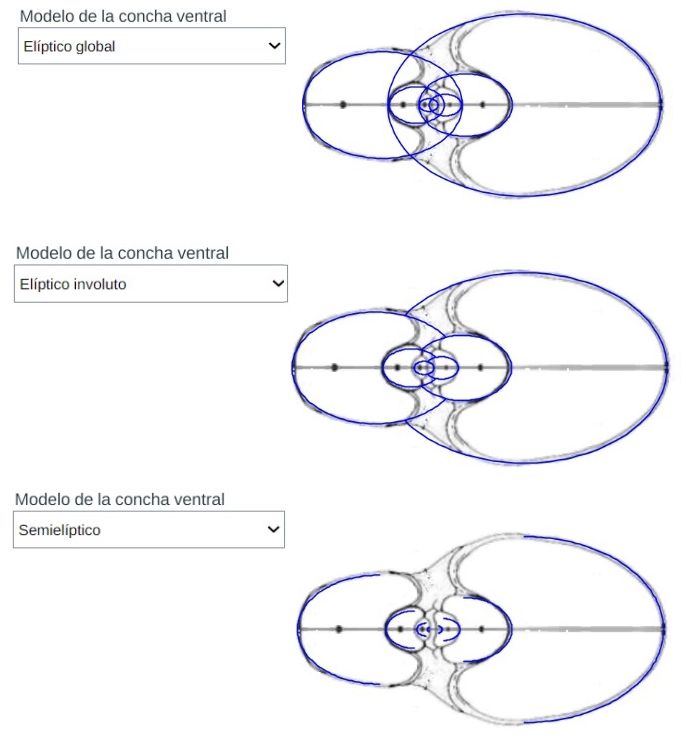
Centrándonos en los salientes o lóbulos dorsales es intuitivo observar que estos parecen seguir un esquema también elíptico. En la se dispone de un control con dos opciones que conducen a su modelación y también está reflejado en la :
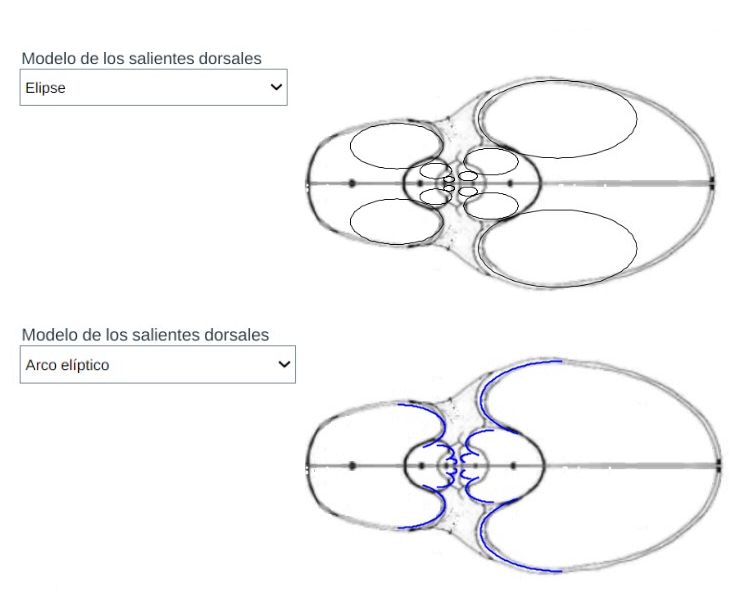
El modelo teórico de la concha habitacional del Nautilus se obtiene combinando el modelo de la pared ventral/dorsal con el de los salientes. Ello puede realizarlo en la y está reflejado en la , donde adicionalmente también se incluye el detalle de la tangencia entre el saliente dorsal y la pared dorsal. El punto de tangencia para la concha de Tanabe se corresponde con el ángulo de $217,16^\circ$ en el saliente superior y $-217,76^\circ$ para el inferior que fueron los valores que reflejamos en la sección anterior como límites del arco lobular, y para Thompson $216,70^\circ$ y $-216,70^\circ$.
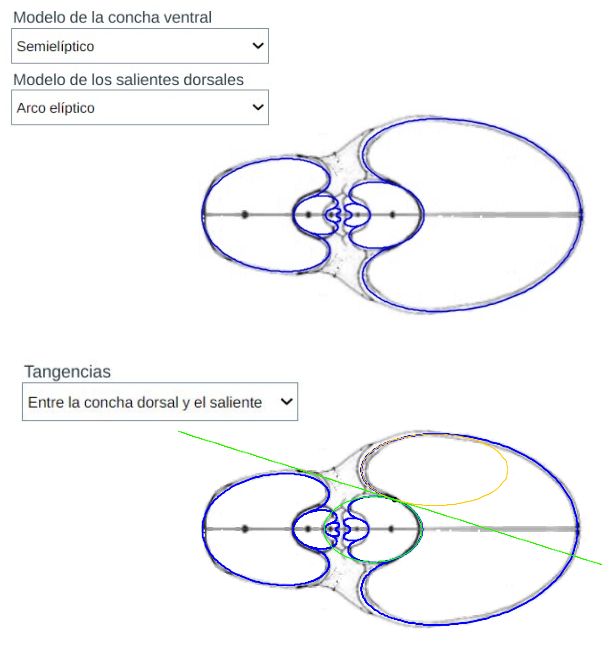
La curva que delimita esta cámara habitacional es una curva definida a trozos en la que intervienen cuatro arcos elípticos (ver la ), que a la escala considerada, se corresponden para la concha de Tanabe con:
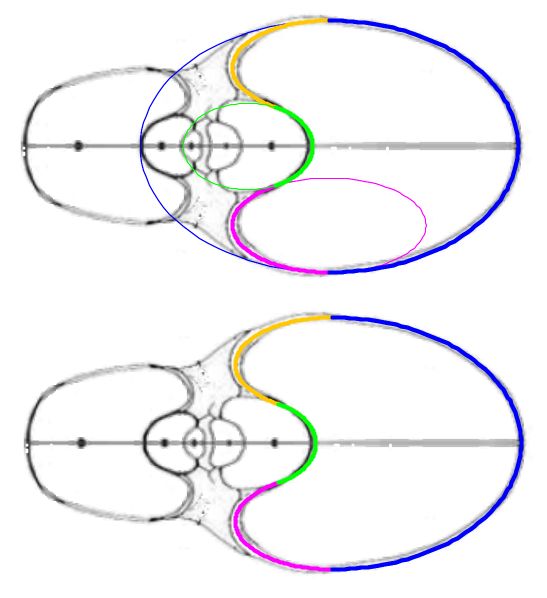
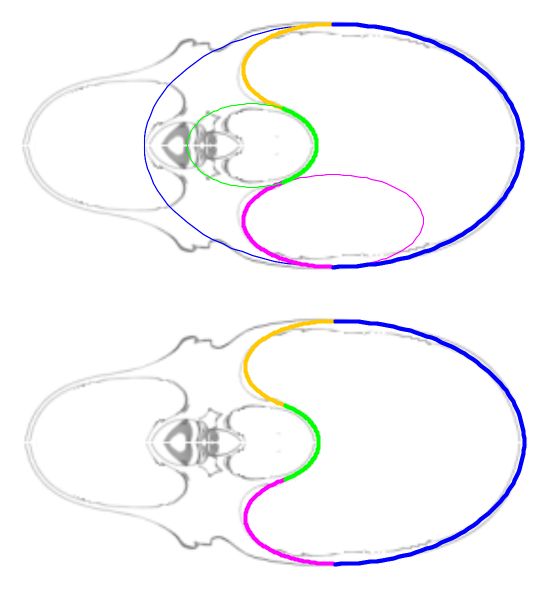
Y en el caso de Thompson la curva viene definida por los siguientes arcos elípticos, representados en la :
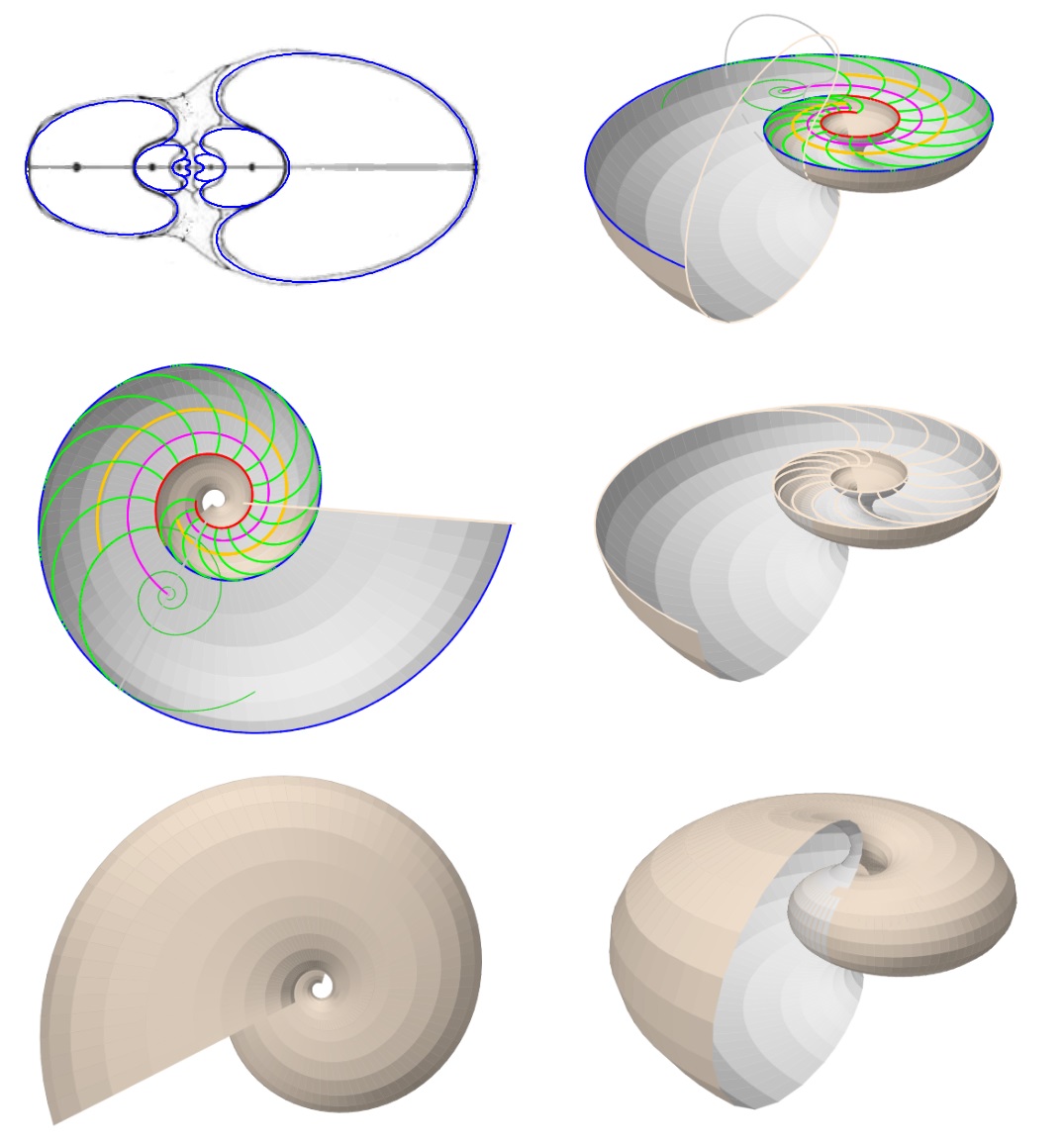
Teniendo en consideración el modelo teórico elíptico de la sección frontal del Nautilus, que hemos desarrollado anteriormente, podemos observar el modelo 3D correspondiente al aplicar el modelo de Raup que hemos adaptado para conchas discoidales. En la se ha reflejado ese modelo 3D uniforme. Esta imagen se ha obtenido con la incluida en la Adenda.
En el análisis del modelo teórico de la pared ventral/dorsal avanzamos un primer modelo del callo umbilical al considerar el modelo involuto, es decir, que el ombligo se formaría como una prolongación del arco elíptico ventral. No obstante, este modelo siendo sencillo no se ajusta al ombligo del Nautilus ya que en éste se produce un cambio de concavidad que no acontece en una elipse. Es necesario abordar otro posible modelo que recoja ese cambio y, dado el carácter elíptico observado y comprobado anteriormente, una plausible línea de investigación puede plantearse combinando dos arcos elípticos. En la se contempla esta alternativa y se refleja también en la .
En el control de la escena interactiva etiquetado como "Modelo del callo umbilical" tenemos tres opciones:
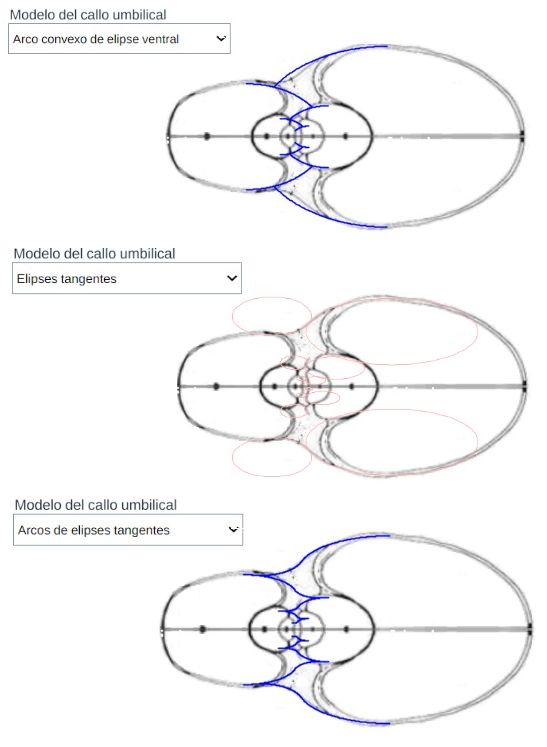
En la están dibujadas dichas elipses para la sección de la concha de Tanabe. Por un lado (con la escala considerada) tenemos:
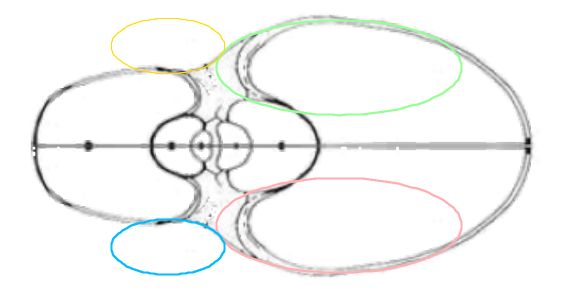
En la se ha reflejado el detalle de los arcos elípticos que conforman el callo umbilical de esta sección de Tanabe. Son los de color rojo y turquesa. También se han representado las elipses que determinan los salientes dorsales cuyas ecuaciones son:
siendo la segunda elipse la primera escalada por el factor de crecimiento cordobés del Nautilus $b^{-\pi}=1,185580...^{-\pi}$ y también es congruente con la naranja pero con centro en $(-0,32, 0,21)$.
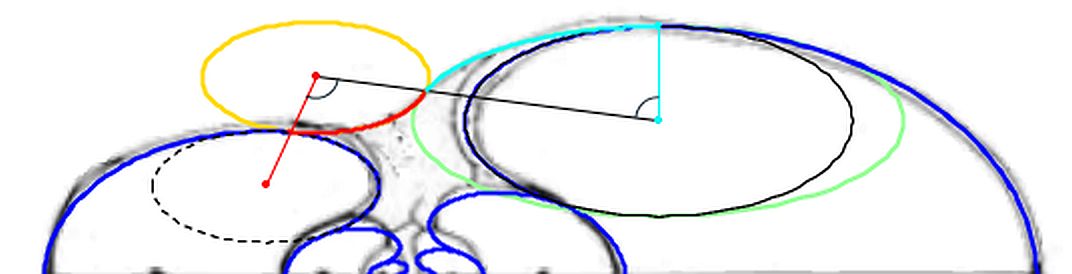
El arco rojo está delimitado por el segmento de igual color que une el centro de la elipse naranja y el de la elipse negra discontinua, y el segmento negro que une el centro de la elipse naranja con el de la la elipse negra continua. El ángulo que forman estos dos segmentos es aproximadamente $107^\circ$ y el intervalo del arco es $[-114,5^\circ,-7,5^\circ]$.
El arco turquesa está delimitado por el segmento anterior de color negro y el segmento turquesa que une el centro de la elipse negra continua (saliente dorsal) con el punto de tangencia de ésta con la pared ventral (arco derecho azul). Estos segmentos forman un ángulo de $82,5^\circ$, en el intervalo angular $[90^\circ,172,5^\circ]$.
Los dos arcos umbilicales son tangentes entre sí, estando el punto de tangencia en el segmento que une los centros de esos arcos elípticos. El turquesa es tangente con la pared ventral y con el saliente dorsal con los que tiene igual concavidad. El rojo es tangente con el saliente dorsal del semiverticilo anterior, teniendo diferente concavidad que éste y estando el punto de tangencia en el segmento rojo.
De manera análoga y con idéntica descripción, para la sección de Thompson (ver la ), tenemos las elipses que definen los arcos umbilicales:
a los salientes dorsales:
Y siendo la amplitud del ángulo formado por el segmento rojo y el negro de $106,83^{\circ}$ (intervalo angular del arco$[-113,5^\circ, -6,67^\circ]$), y el del negro con el turquesa de $83,33^{\circ}$ (intervalo angular del arco$[90^\circ, 173,33^\circ]$).

En la puede verse este detalle para ambas secciones:
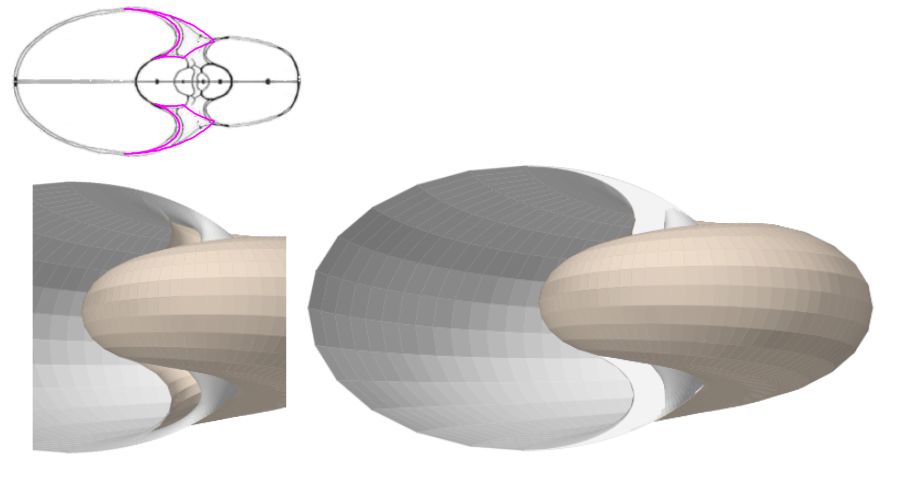
De nuevo podemos observar el modelo 3D del callo umbilical correspondiente sin más que partir del modelo teórico elíptico obtenido para la sección de dicho callo y aplicando el modelo de Raup adaptado. En la se ha reflejado ese modelo 3D uniforme tanto para el modelo involuto de arcos ventrales como para el de arcos elípticos con diferente concavidad. Esta imagen se ha obtenido con la incluida en la Adenda.
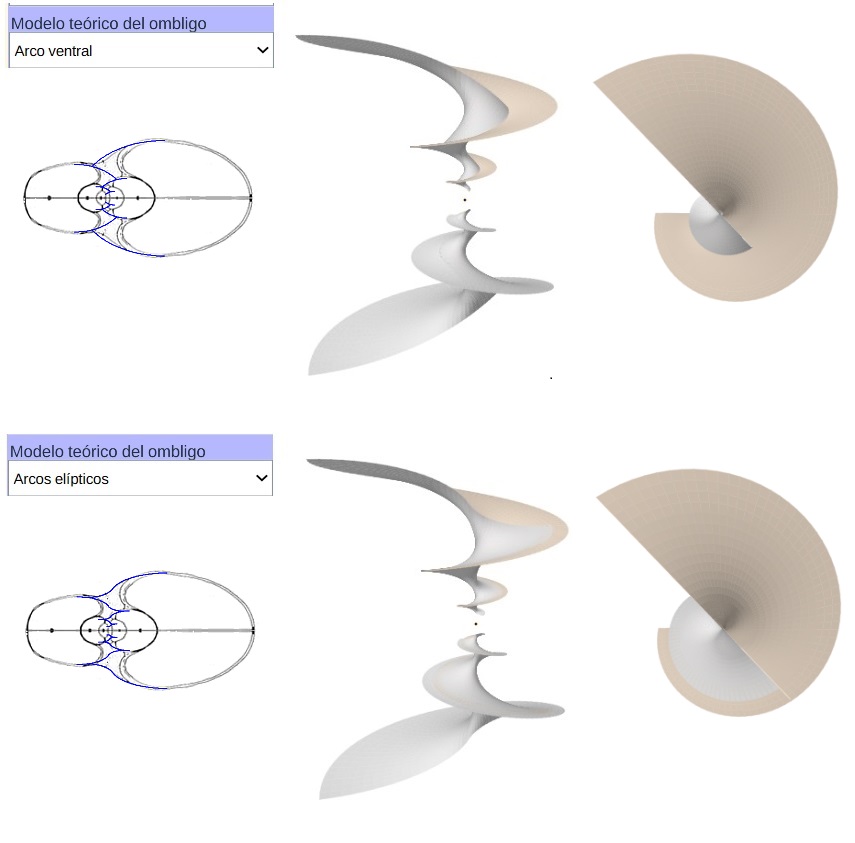
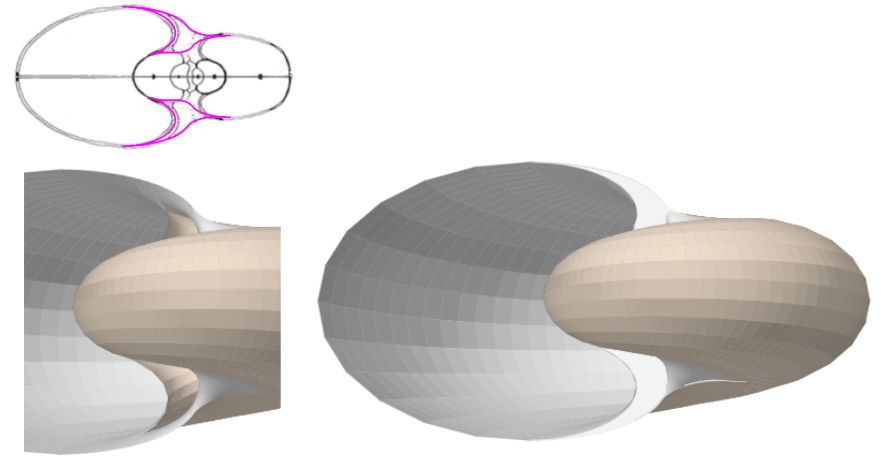
En la imagen anterior sólo se ha representado lo que es el callo exterior en sí, es decir, la superficie que cubre el espacio umbilical, la tapa del mismo. Si añadimos a él la superficie que describe el arco dorsal de la concha podemos visualizar la superficie lateral que determina el volumen ocupado por el callo umbilical (hemos dejado sin cubrir la parte final para poder vislumbrar su interior). Es lo reflejado en la . En color gris se refleja el interior y en beige el exterior (hay cierta intersección ficticia o solapamiento ocasionado por la representación gráfica en las zonas de tangencia).
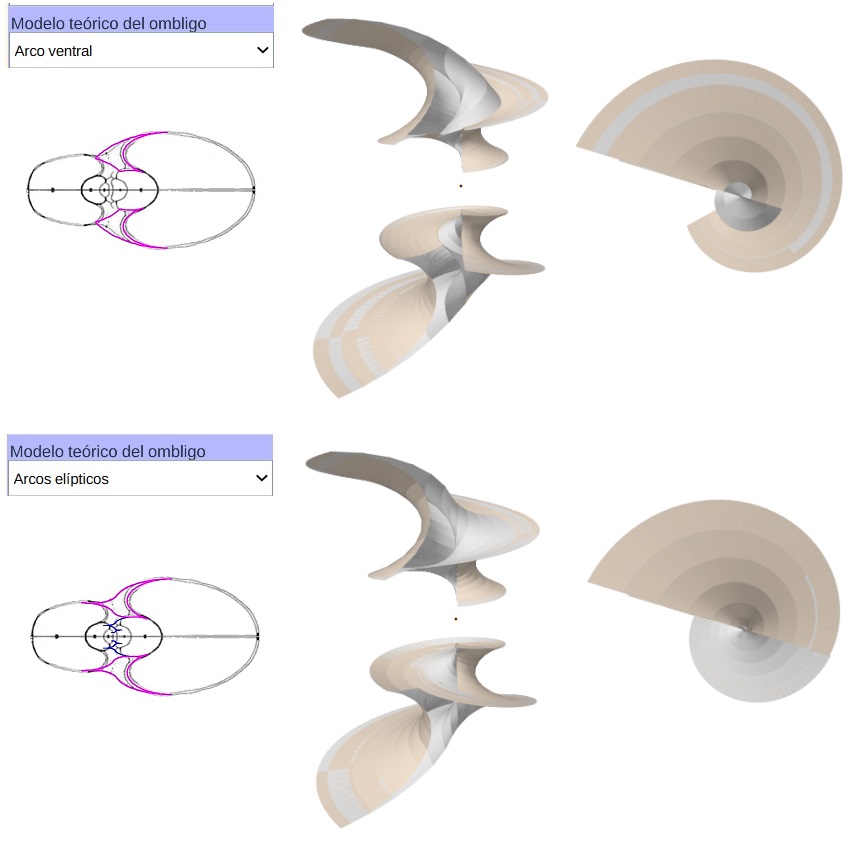
En la podemos observar las tangencias que acontecen entre los diferentes arcos elípticos que configuran el modelo teórico de la sección frontal. Además del control tipo menú que nos permite seleccionar bien la sección de Tanabe o la de Thompson, se dispone de otro con cuatro opciones:
y otros dos adicionales que permiten ocultar o mostrar el detalle de la tangencia seleccionada en el menú anterior y ocultar o mostrar el detalle de los arcos.
En la observamos como el arco elíptico que determina la concha ventral es tangente con el arco del saliente dorsal y a su vez con el del callo umbilical. El punto de tangencia se corresponde con el ángulo polar de $90^\circ$ en los tres arcos.
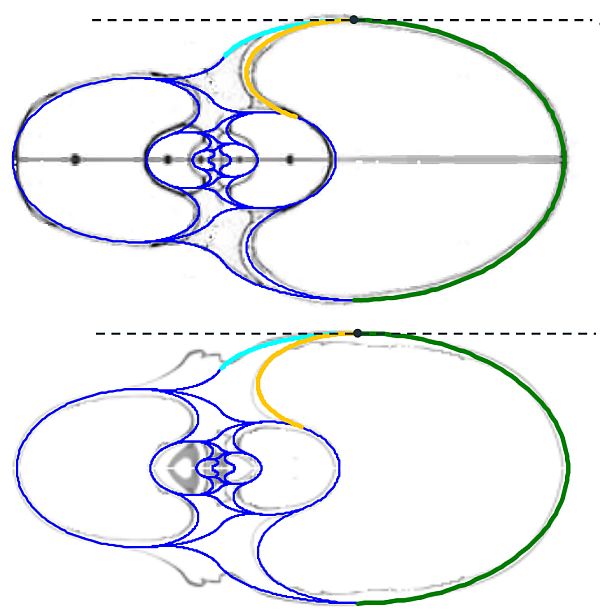
En la se observa cómo el saliente dorsal es tangente a la concha dorsal. Cuando en la se selecciona esta tangencia se activan dos controles, etiquetados como A y B, que permiten al usuario desplazarse por ambos arcos y observar la recta tangente correspondiente a la posición seleccionada (ver la ).
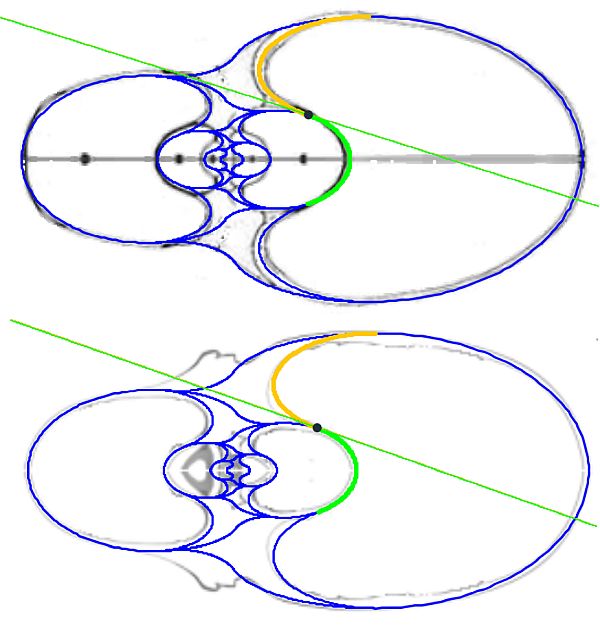
Como ya hemos indicado el punto de tangencia se corresponde para Tanabe con el ángulo polar $\color{gold}217,16^\circ$ en el saliente dorsal y $\color{lime}54,72^\circ$ en la concha dorsal y, analogamente para Thompson $\color{gold}216,70^\circ$ y $\color{lime} 49,59^\circ$.
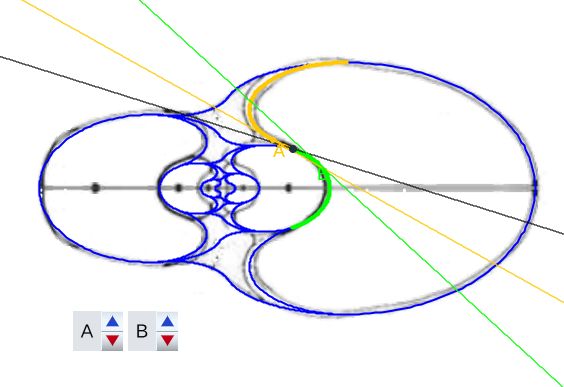
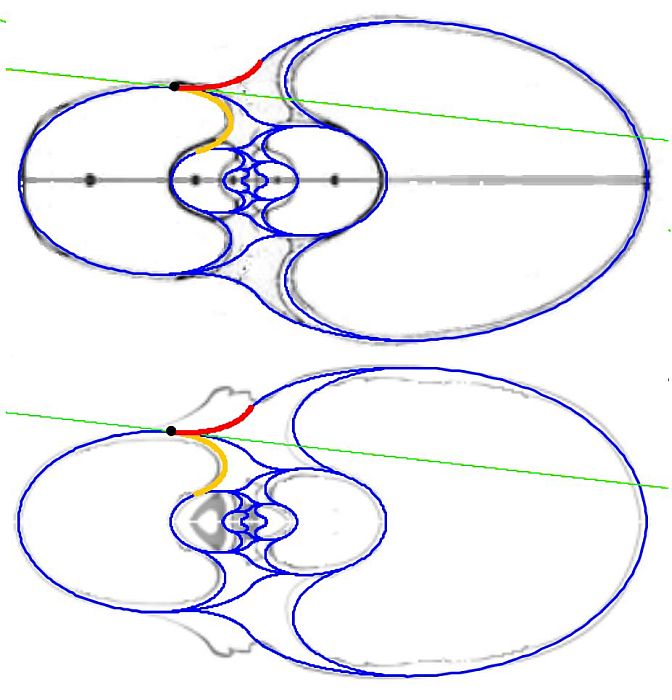
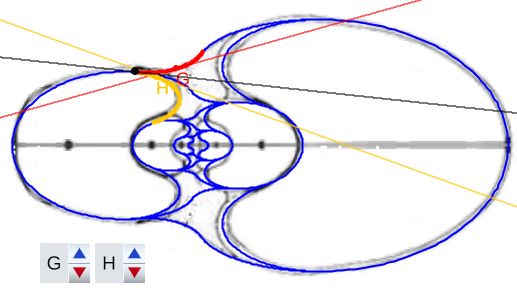
El callo umbilical es tangente también con el saliente dorsal correspondiente al semiverticilo anterior. El detalle de esta tangencia se refleja en la . En este caso, en la , se activan los controles etiquetados G y H que permiten desplazarse en sendos arcos y comparar las rectas tangentes en esos puntos ().
En este caso para Tanabe el ángulo polar correspondiente al punto de tangencia es $\color{red}-114,5^\circ$ y $\color{gold}65,5^\circ$ y para Thompson $\color{red}-113,5^\circ$ y $\color{gold}66,5^\circ$.
En la se muestra la recta tangente en el punto de inflexión del callo umbilical. El ángulo polar en el punto de tangencia se corresponde con $\color{red}-7,5^\circ$ y $\color{turquoise}172,5^\circ$ para Tanabe y $\color{red}-6,67^\circ$ y $\color{turquoise}173,33^\circ$ para Thompson.
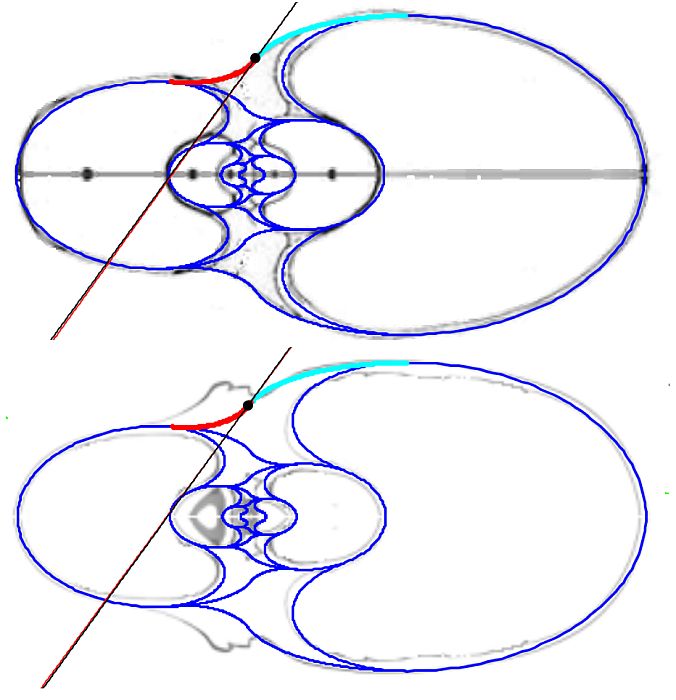
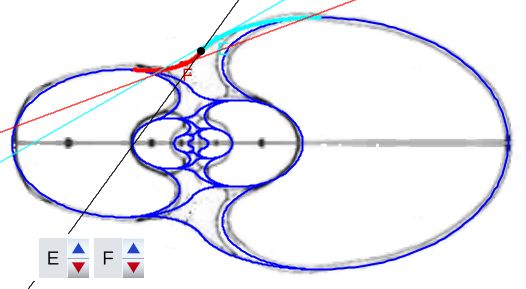
Al seleccionar la opción "Distinta convexidad en el ombligo" en la , se activan los controles etiquetados E y F que permiten el desplazamiento en sendos arcos y ver la rectas tangentes en esos puntos ().
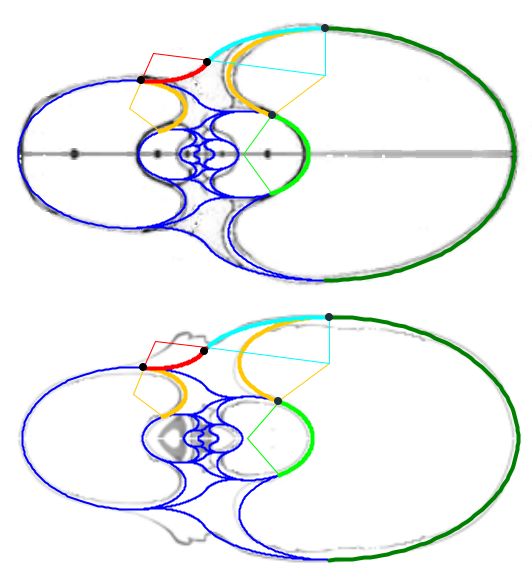
En la se han reflejado los puntos de tangencia de los diferentes arcos y la relación existente entre ellos y los centros de las elipses que determinan a dichos arcos. Esta gráfica se obtiene seleccionando en la la opción: "Muestra el detalle de los arcos".
Como síntesis y adelanto del modelo global, que detallaremos en el capítulo V, en la está reflejado el modelo elíptico 3D de la concha y el del ombligo con arco elíptico ventral.
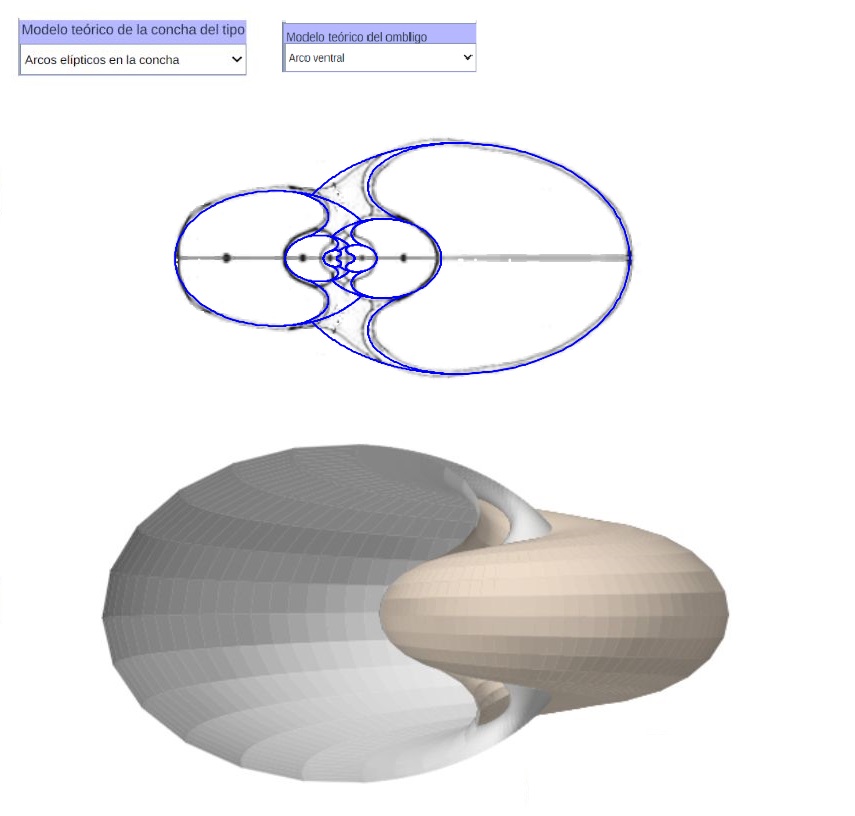
Y en la está reflejado el modelo elíptico 3D de la concha y el ombligo con arcos elípticos. Ambas imágenes se han obtenido con la incluida en la Adenda.
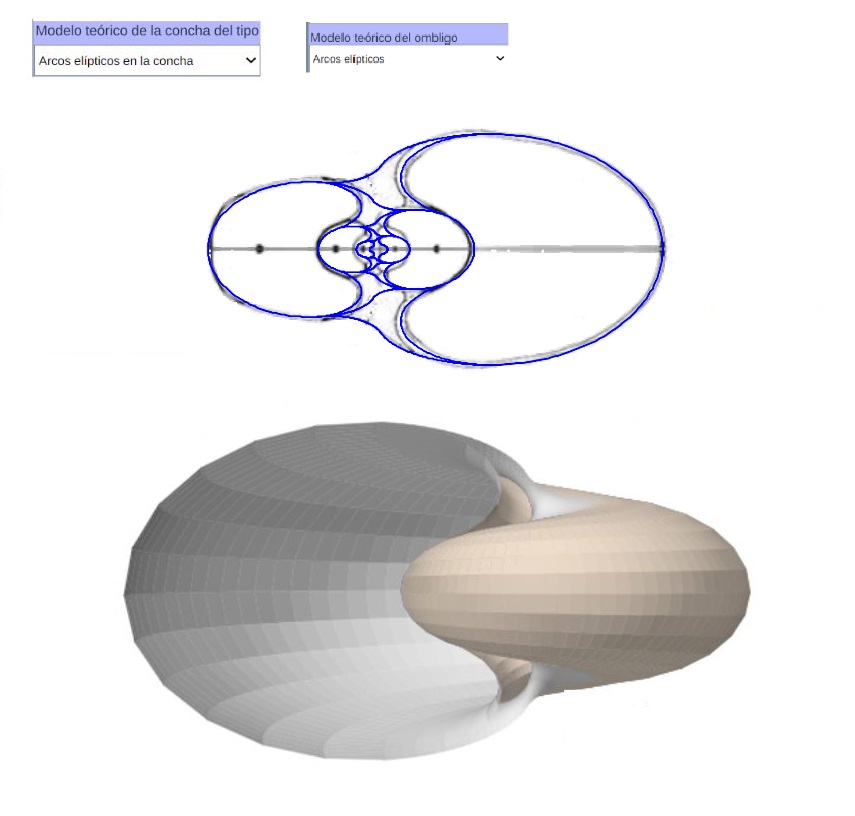
Si nos fijamos en las figuras anteriores veremos que el callo umbilical queda sin rellenar, observándose un hueco que permite ver la pared dorsal a través de él. Ello es como consecuencia de que el modelado 3D lo realizamos tomando como base la sección transversal de la concha y el perfil del callo umbilical. Para una imagen más realista es necesario rellenar ese vacío, es decir, hemos de modelar el callo en sí.
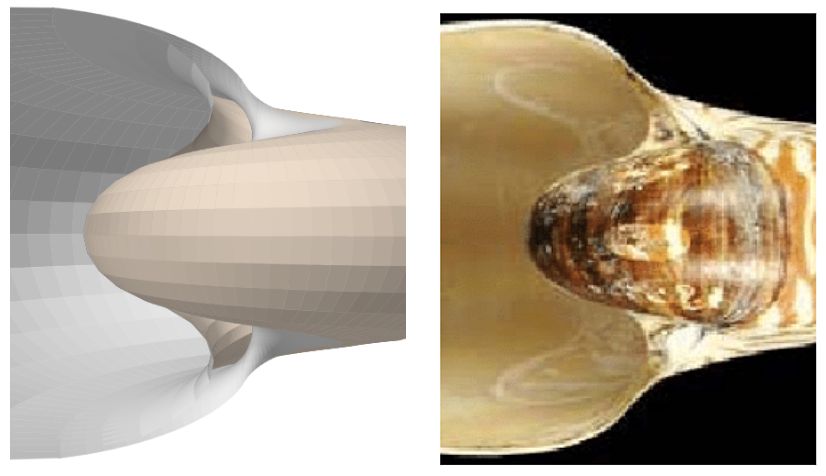
En la tenemos una comparativa del modelo 3D de la concha y del ombligo, obtenido con arcos elípticos, y la imagen de un ejemplar de Nautilus, observando en éste último cómo el ombligo está rellenado por el callo umbilical que según Barroso-Barcenilla (2008)
En la podemos ver, en color magenta la sección del callo umbilical en el caso del modelo del ombligo mediante arco ventral y también cómo ubicamos esta figura en el modelo 3D tapando el hueco indicado.
Finalmente y de manera análoga en la tenemos la representación de esa tapa en el caso del modelo del ombligo con arcos elípticos.
En el libro "Modelo ontogénico matemático del Nautilus" (Galo 2024b) 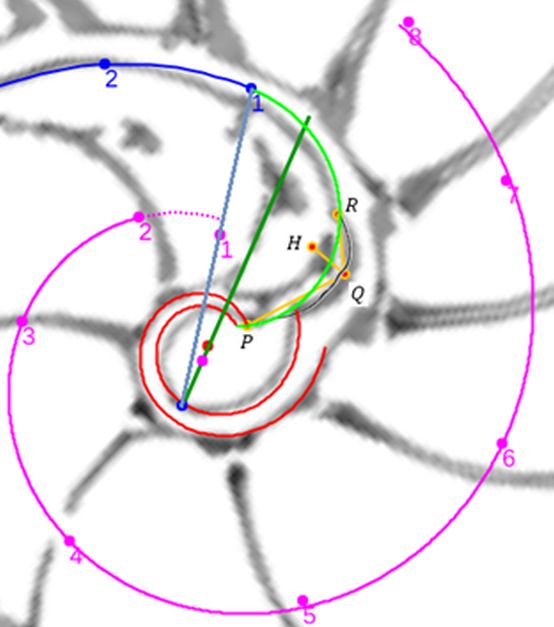
En color verde oscuro segmento $\overline{\color{blue}P_v \color{magenta}P_s \color{red}P_d}$ (polo ventral, polo de la espiral de los polos de los septos y polo dorsal).
En color azul grisáceo segmento $\overline{\color{blue}P_v \color{magenta}S_1 \color{blue}T_1}$ (polo ventral, polo del primer septo y primer punto de tangencia con la pared ventral).
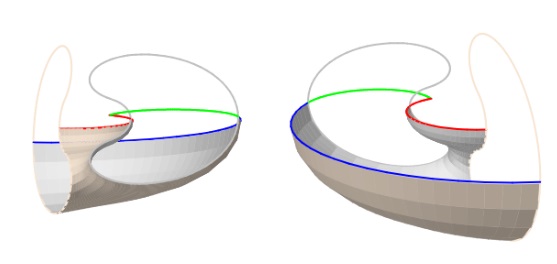
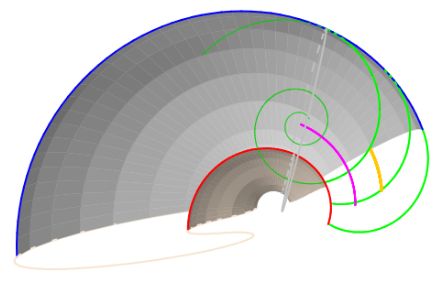
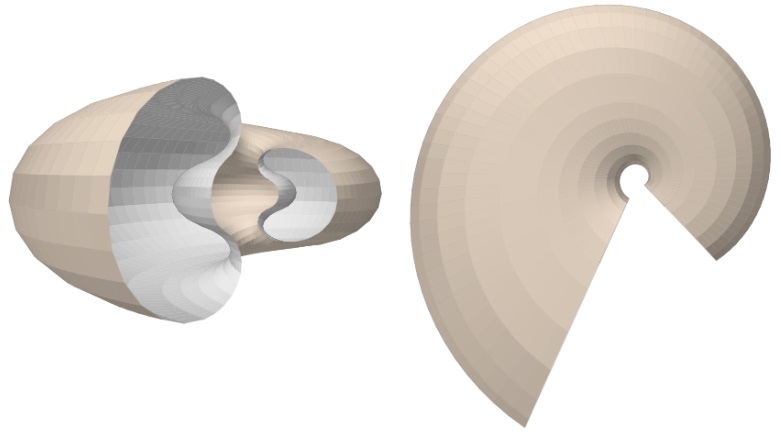
Así pues, el modelo 3D que generamos, en base a la sección frontal antes indicada, refleja el crecimiento de la concha a partir de un plano frontal que interseca a la primera y segunda cámara septal (ver la ) y, por tanto no contempla ni la concha embrionaria, ni la zona intermedia desde ésta hasta la sección indicada. Esto genera (ver la ) la irreal impresión de una instantánea generación espontánea y, a la vez, provoca desasosiego ante un extraño hueco inicial. Consecuentemente, en aplicación de un adecuado horror vacui que aplaque esa intranquilidad, procede tratar de cubrir ese espacio considerando la información biológica de la que disponemos y teniendo muy presente que estamos hablando de un espacio que se inscribe en un rectángulo de aproximadamente $1,70 \times 3,50 \, mm^2$ de tamaño real en la concha del Nautilus ().
Procedamos a recordar (Galo, 2024b)
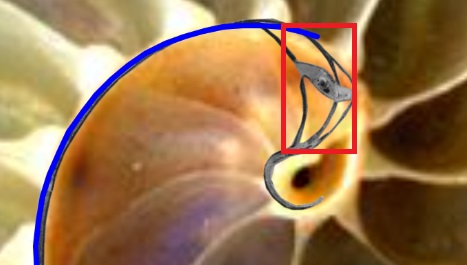
A primera vista la concha embrionaria del Nautilus (), en su periodo pre-cameral, aparenta una forma similar a la concha de una lapa (MolluscaBase eds., 2024
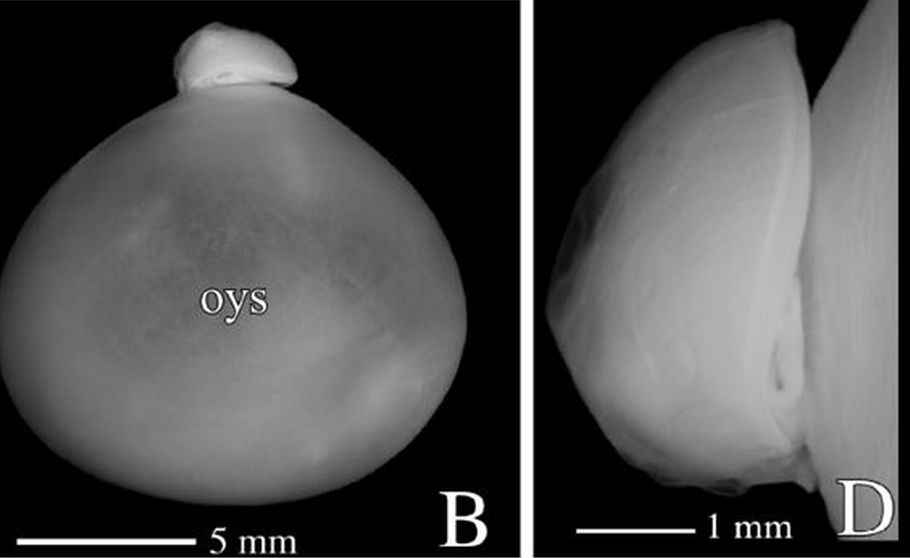


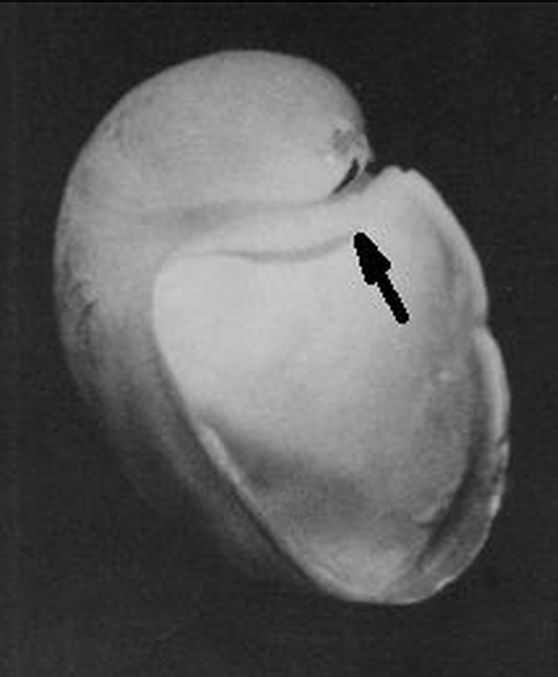
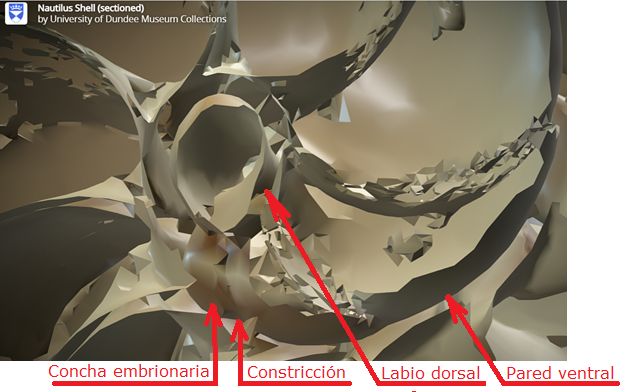


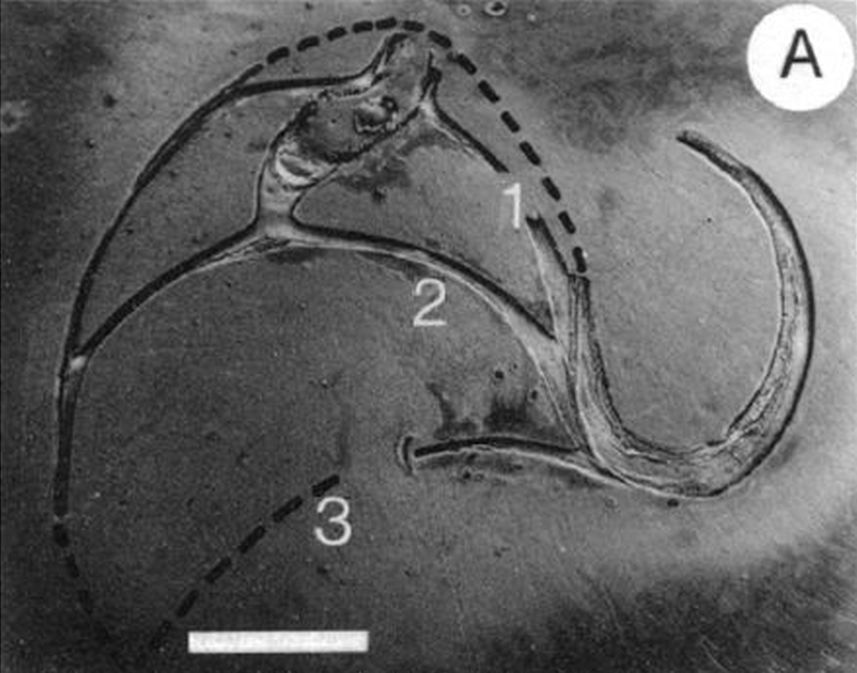
A pesar de disponer de la docta información sintetizada e ilustrada en la sección anterior, cuya fuente está refrendada por tan renombrados investigadores del Nautilus, nos encontramos que en tan escueto espacio acontecen muchos cambios ontogénicos que complican excesivamente el modelado matemático de la concha en esta etapa primigenia, tanto que, al menos para mí, no hay posibilidad de verificar la corrección o no del modelo que propondré a continuación y que consecuentemente voy a etiquetar como "una solución de compromiso". Una alternativa que nos permita cubrir el vacío antes señalado, al menos estéticamente y siempre evitando el provocar un descarrío significativo, y que comprenderá desde el primer septo al plano frontal que marca el inicio de la pared ventral. Con ello, cubriremos esa parte de la concha y lograremos cerrar el fragmocono nautiliano en la parte apical. Adicionalmente, de manera consciente, dejaremos sin dibujar la concha embrionaria pre-septal, si bien ésta sí que es más fácil de modelar teóricamente dada su forma cónica con pared lateral alabeada, con base elíptica y con eje desplazado que se asemeja a una lapa y con una sección sagital en la que se inscribe el gnomon de un triángulo cordobés, siendo dicho eje coincidente con su altura ().
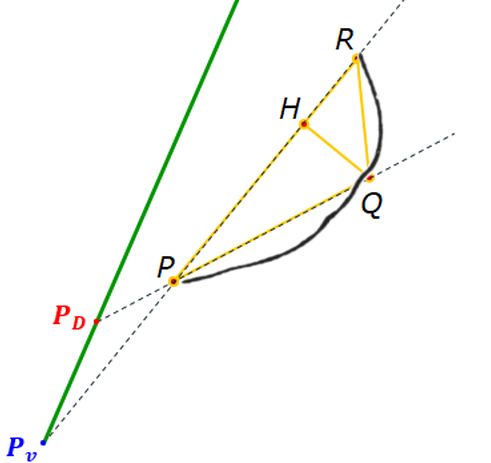
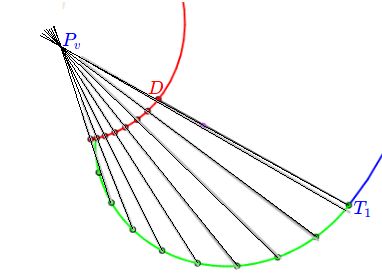
El criterio básico que hemos seguido para el cierre apical de la concha es mantener el perfil de la sección frontal del Nautilus, pero someterlo a una contracción más rápida a medida que nos aproximamos al ápice y, para ello, dado que la zona objeto de estudio es la determinada por el primer septo, por el arco inicial dorsal y por el eje que une el polo ventral $\color{blue}P_v$ y el primer punto de tangencia ventral $\color{blue}T_1$ (ver la ), primero hemos procedido a trazar segmentos con origen común el polo ventral y cuyo extremo son puntos del arco del primer septo. Estos segmentos intersecan al arco dorsal determinando segmentos interiores cuya longitud, comparándola con la de segmento $\overline{\color{red}D \color{blue}T_1}$ en la , nos sirve de factor de escala para contraer la sección frontal considerada como referencia en todo el modelo. En la podemos observar esas secciones frontales escaladas y la superficie de la concha que podemos generar con ellas, la cual tiene cierto parecido con la concha inicial del Nautilus (pero en un mero ejercicio estético al no contar con base documental al respecto).
Después del recorrido realizado en la literatura previa nautiliana, de lo alcanzado en nuestras investigaciones particulares que quedaron articuladas en los dos libros anteriores (Galo, 2024
No ha mucho que un entrañable colega y amigo —Josep Maria Navarro Canut— me dijo: "¡Lo que está dando de sí el Nautilus!" y ¡es verdad!, ello está aconteciendo así. Aquí, en particular, y en nuestro contexto vital en general, es evidente que es tan corto nuestro conocer y tan amplia nuestra necesidad de saber que cualquier detalle es un nuevo hito sobre el que investigar y aprender. Así pues,
¿hay algo más que modelar matemáticamente en el Nautilus?, ¿qué opinan? Mi respuesta es afirmativa. Yo trato de oír al Nautilus y, la realidad, es que no para de susurrar. Otra cuestión es que yo sepa escuchar e interpretar adecuadamente sus indicaciones, si bien les garantizo que empeño no deja de haber nunca en mí. ¿Qué aspectos quedan abiertos aún, por ahora?, lo que surja después llegará y lo trataremos en su momento.
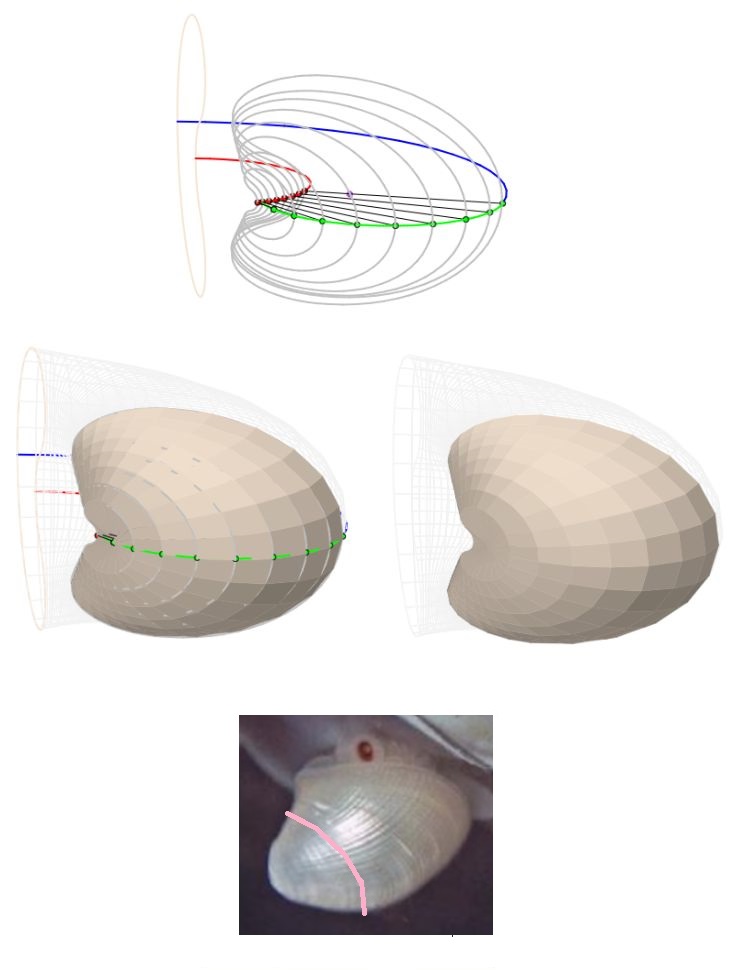
Si bien, para el modelado 3D se ha considerado la sección transversal de la concha, una sección que es plana, la abertura de ésta no coincide con esta sección, sino que presenta un perfil cóncavo-convexo (ver la ) desde las primeras etapas vitales ( y ).

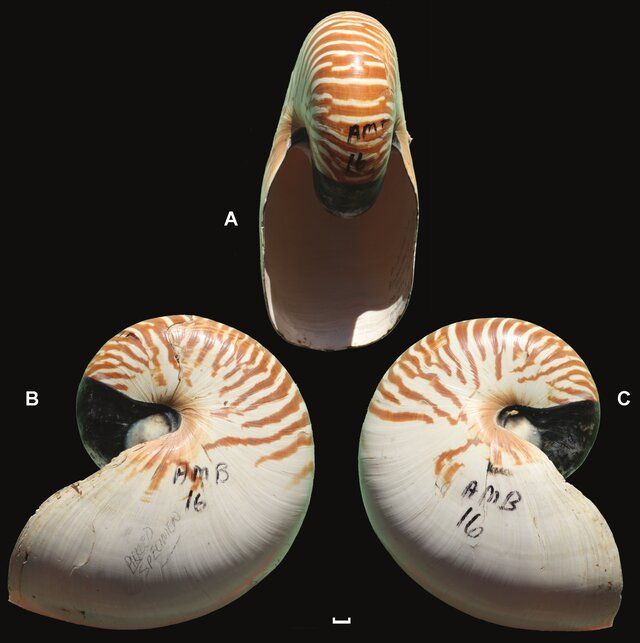
En la se refleja el neotipo del Nautilus pompilius propuesto por Nikolaeva et al. (2015)
Si en lugar de la sección plana, hubiéramos considerado determinar la curva 3D que determina el perfil de la abertura, ésta se podría haber utilizado para aplicar el modelo de Raup y generar la concha tridimensional. Ésta alternativa sería incluso más plausible pues modela la concha hasta el final de la parte adoral, pero tiene la desventaja de que si bien la sección frontal está ampliamente estudiada y referenciada, el perfil citado parece no estarlo.
Consecuentemente marcamos como un primer aspecto de interés, abierto a su análisis y estudio, la modelación del perfil tridimensional de la abertura de la concha. Y de manera colateral surge la necesidad de adaptar el modelo de Raup (epígrafes 1.1.5 y 1.1.6) para obtener la superficie de la concha a partir de una curva tridimensional. Surgen, como hemos indicado antes, nuevos eslabones que construir y enlazar adecuadamente.
Es bien conocido para nosotros (Galo et al., 2016)
En los epígrafes 1.1.3 y 1.1.4 nos detuvimos en analizar la información aportada por diferentes autores sobre qué superficie tridimensional es la que modela a las paredes septales, desde la fuente clásica de Thompson a otras más cercanas. En general, estas fuentes aportan obviamente información interesante, curiosa, pero ninguna aporta el modelo teórico septal, el modelo matemático que buscamos. Tanto a priori como a posteriori, nos encontramos con un problema complicado y difícil (ver la ).
En la podemos observar, y por el crecimiento gnomónico parece lógico lo que acontece una vez que se ha visto esa relación, que la curva que define el perfil de la intersección de los septos con la concha se asemeja al perfil de la abertura. Puede ser un avance sobre el que reflexionar, que refuerza la necesidad de abordar el modelado de la curva de abertura, pero insuficiente porque hay infinitas superficies con ese perfil ¿cómo es el diseño 3D de la superficie que teniendo como frontera dicho perfil, es la que modela el septo? Un nuevo reto, abierto a quienes quieran satisfacer su mente.


Finalmente, sin que signifique cerrar el camino a las inquietudes u observaciones de otros investigadores de este tema, tendríamos que retomar un camino similar al que realizamos al abordar el modelo ontogénico bidimensional (Galo, 2024b)

En particular, habría que analizar:
Para todo el análisis que hemos realizado, en éste y en los dos anteriores libros sobre la modelación del Nautilus (Galo, 2024
Y el contexto donde se ha desarrollado esta investigación ha sido dentro de la "Red Educativa Digital Descartes" (RED Descartes), una organización no gubernamental que agrupa a profesorado que evidencia su lema: "Trabajando altruistamente por la comunidad educativa de la aldea global" y que continúa avanzando en su proyecto educativo ( Proyecto Descartes) con recursos educativos interactivos desarrollados con la herramienta Descartes, proyecto que surge a la vez que la herramienta o, más bien la herramienta surgió por necesidad para llevar a cabo el proyecto, pero para qué entrar en intrascendentes discusiones bizantinas sobre "qué fue antes el huevo o la gallina", cuando lo importante es la labor realizada y los logros educativos alcanzados durante todo este periodo que sigue ampliándose.
Y, en particular, hay que agradecer el trabajo realizado por RED Descartes en la promoción de los libros, cómo no, interactivos que se inició con el subproyecto iCartesiLibri, con el que se marcaba su principal objetivo:
Todo el trabajo previo de modelación tridimensional de la concha del Nautilus se ha logrado usando los recursos interactivos enlazados y descritos en capítulos anteriores y finalmente hemos condensado ese modelado en la (descrita también en la Adenda) que nos sirve de recapitulación del modelo matemático uniforme de dicha concha. En ella, se disponen diferentes controles mediante los cuales podemos seleccionar el modelo teórico de la concha ventral, el de los salientes dorsales y el del callo umbilical y, de acuerdo con lo seleccionado, proceder a visualizar el correspodiente modelo 3D asociado. Ese modelo puede obtenerse tanto para la sección frontal correspondiente al tipo seleccionado (Tanabe 90) como a la de Thompson (2019).
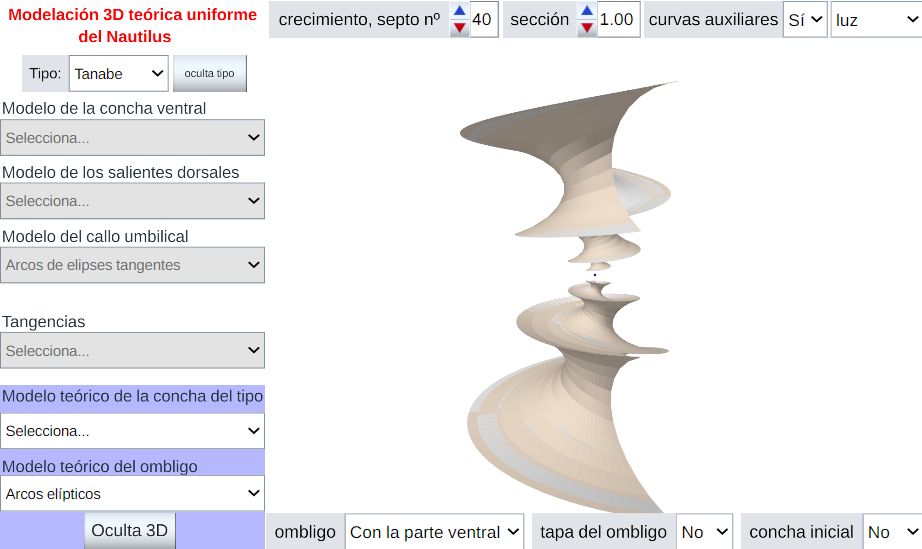
Hay que indicar que cuando se accede a la representación tridimensional la respuesta de la escena puede ser algo lenta dado
que se requiere un elevado cálculo computacional, obviamente dependiendo de los recursos del sistema informático que esté utilizando.
Como hemos indicado la sirve de síntesis de la modelación matemática tridimensional de la concha del Nautilus en la que hemos denominado modalidad uniforme, es decir, aquella en la que el crecimiento se considera sin cambios en los tres verticilos que se observan en los ejemplares adultos y, por tanto, obviándose los cambios ontogénicos que sabemos acontecen especialmente en el primer verticilo.
Dado que lo que caracteriza a este libro es su interactividad, nuestro consejo es que interactúe con la escena y sea usted quien construya dicho modelo. No obstante, siendo conscientes que ello requiere un tiempo del que no siempre se dispone, procederemos inicialmente a sintetizarlo en unas animaciones que complementaremos con algunas imágenes estáticas, junto a un par de presentaciones que pueda gestionar cómodamente.
En la tenemos la animación del modelo 3D uniforme de la concha, donde se han considerado los arcos elípticos tanto para la concha en sí como para el callo umbilical. Esta animación la realizamos en el año 2023 que fue cuando abordamos y fraguamos todo este análisis y que coincidió con el vigésimo quinto aniversario de la herramienta "Descartes" y de su proyecto homónimo antes citados. La refleja el modelo matemático final obtenido.
De manera análoga en la tenemos una animación que muestra el detalle del callo umbilical con arcos elípticos en el modelo de la concha antes considerado.




La muestra la superficie que cubre al callo umbilical considerando como modelo matemático el de arcos elípticos con distinta concavidad. En la se incluyen los arcos de la pared dorsal mostrando la superficie completa que da forma al al callo umbilical considerando en ambos el modelo matemático de arcos elípticos. Y finalmente en la se incorpora una tapa que oculta el espacio umbilical intermedio que se observa en la imagen anterior.


Finalmente en la y en la hemos reflejado algunas diapositivas que permitan poder ver rápidamente, y bajo el control del usuario/lector, algunas fases del modelo matemático obtenido para la concha y para el ombligo.
Llegados a este punto, alcanzados muchos de los objetivos que nos hemos ido planteando en el largo camino y el amplio tiempo que llevamos dialogando con el Nautilus, procede agradecer a los lectores de esta trilogía su interés y es de desear que hayan quedado, al menos, medianamente satisfechos y que su aprendizaje, al igual que el nuestro, haya sido positivo.
En la disponemos de una herramienta que nos permite modelar, mediante una curva de Bézier, la sección frontal del Nautilus y, en general, para aquellos que sepan "Descartes" poder ajustar cualquier otra sección. Consultad en las Indicaciones las diferentes posibilidades que se incluyen y su potencial.
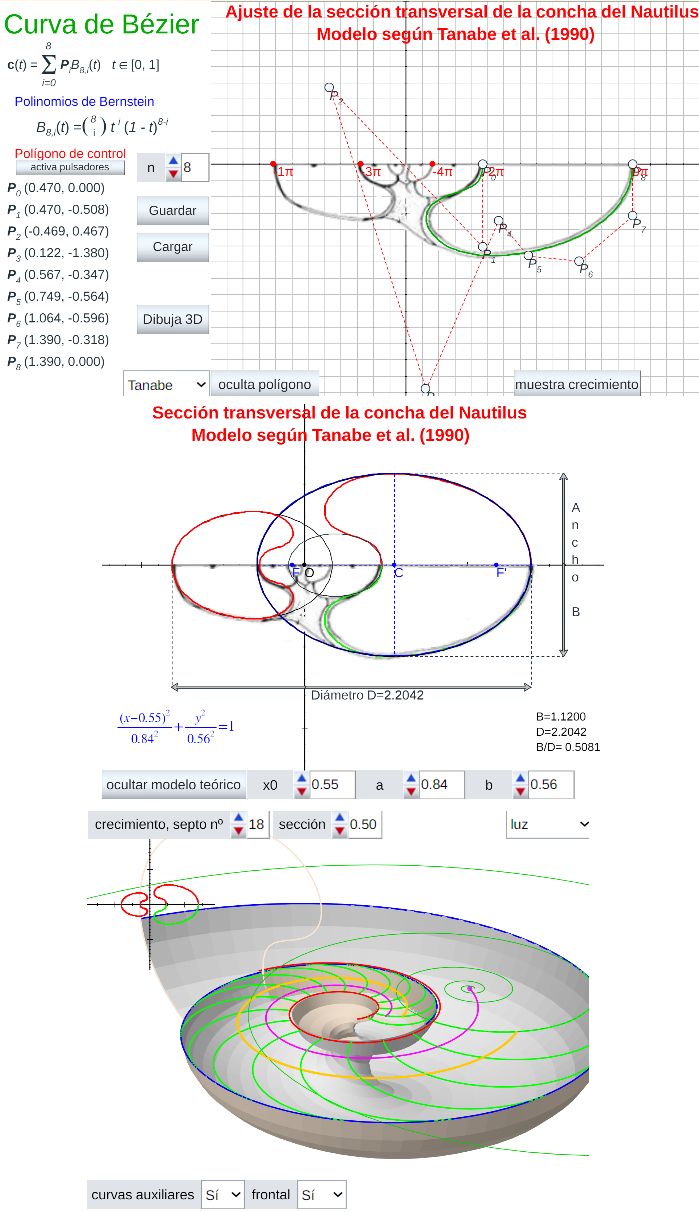
En la obtención del modelo teórico de la sección frontal del Nautilus hemos detectado que la concha ventral/dorsal, los salientes dorsales y el callo umbilical puede definirse usando arcos elípticos. Para poder definir estos arcos necesitamos indicar cuál es su amplitud angular y ésta, como veremos a continuación, depende de la parametrización que se considere de la elipse. Así pues, procede tratar de determinar qué parametrización puede ser la más conveniente, si hay alguna que cumpla ese objetivo.
La elipse de centro $(h,k)$ y semiejes $a$ y $b$, puede expresarse de diversas formas equivalentes, entre ellas:
Si consideramos la parametrización (6.2), sustituyendo en (6.3) obtenemos: $$ \begin{aligned} r &= \sqrt{(x-h)^2+(y-k)^2} \\ &= \sqrt{a^2 \text{cos}^2 \alpha+ b^2 \text{sen}^2 \alpha} \end{aligned} \tag{6.4} $$ y $$ \begin{aligned} \text{cos} \, \theta &= \displaystyle \frac{\vec{r} \cdot \vec{i}}{|\vec{r}| |\vec{i}|} \\ &= \frac{a }{\sqrt{a^2 \text{cos}^2 \alpha+ b^2 \text{sen}^2 \alpha}} \, \text{cos} \alpha \end{aligned} \tag{6.5} $$ De (6.5) se concluye que el ángulo $\alpha$ de la parametrización (6.2) no concuerda con el ángulo polar, salvo cuando $a = b$, es decir, cuando la elipse es una circunferencia. En el espacio de la izquierda de la puede observarse esta discrepancia.
La relación existente entre el parámetro $\alpha$ y el ángulo polar $\theta$ es: $$ \text{tg} \, \theta = \frac{b}{a} \text{tg} \, \alpha \tag {6.6}$$ coincidiendo ambos valores en $[0, 2 \pi)$ sólo para $0, \frac{\pi}{2}, \pi$ y $\frac{2 \pi}{3}$. Adicionalmente:
No obstante, hay una parametrización en la que el parámetro coincide con el ángulo polar y ésta es:
$$\left\{ \begin{array}{lcc} x = h + \displaystyle \frac{1}{\sqrt{\frac{\text{cos}^2 \theta}{a^2}+ \frac{\text{sen}^2 \theta}{b^2}} } \, \text{cos}(\theta) \\ y = k + \displaystyle \frac{1}{\sqrt{\frac{\text{cos}^2 \theta}{a^2}+ \frac{\text{sen}^2 \theta}{b^2}} } \, \text{sen}(\theta) \end{array} \right. \tag{6.7}$$
Fácilmente puede comprobarse que los puntos $(x, y)$ definidos de esa forma verifican la ecuación de la elipse (6.1) y que se cumple que $\theta = ángulo(\vec{r}, \vec{i})$.
En el espacio de la derecha de la puede observarse esta concordancia.
Consecuentemente todo arco de una elipse parametizada según (6.7) puede definirse si más que indicar el intervalo ángular y esto es lo que hemos realizado en la modelación de la sección frontal del Nautilus en el capítulo III.
La sirve de recapitulación del modelado tridimensional del Nautilus. En ella se disponen diferentes controles mediante los cuales podemos seleccionar el modelo teórico de la concha ventral, el de los salientes dorsales y el del callo umbilical y, de acuerdo con lo seleccionado, proceder a visualizar el correspodiente modelo 3D asociado. Ese modelo puede obtenerse tanto para la sección frontal correspondiente al tipo seleccionado (Tanabe 90) como a la de Thompson (2019).

Hay que indicar que cuando se accede a la representación tridimensional la respuesta de la escena puede ser algo lenta dado que se requiere un elevado cálculo computacional, obviamente dependiendo de los recursos del sistema informático que esté utilizando.
Al iniciar la escena se distinguen dos espacios:
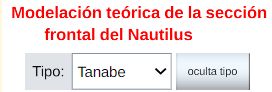
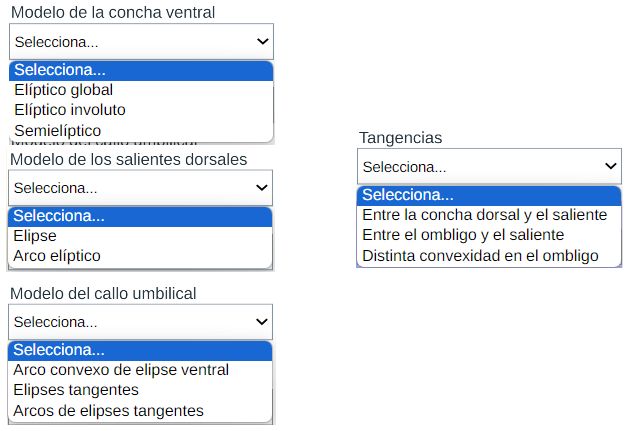
La investigación que hemos detallado en este libro fue realizada durante el año 2023 y, de ella, publicamos una síntesis de la misma en el blog de la "Red Educativa Digital Descartes" como felicitación de año nuevo de 2024 (ver la y el ubicado en la siguiente página).

En el se incluye un enlace a una presentación resumida de este modelo, que es la que incorporamos a continuación en diferentes formatos:
Presentación con Google Slides .
Versión en pdf y versión en Powerpoint.
En la barra de herramientas inferior puede gestionar manualmente el paso de las diapositivas
y pulsando el icono ⋮ se tiene acceso a las notas del conferenciante.
Imagen generada por la IA Designer de Microsoft