Mostrando artículos por etiqueta: bachillerato
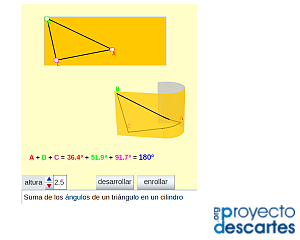
Título: Triángulos en la Geometría Euclídea
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría métrica tridimensional
Nivel/Edad: Bachillerato y Universidad (17 o más años)
Idioma: Castellano
Autor: José R. Galo Sánchez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
| |
|
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-ShareAlike 4.0 International
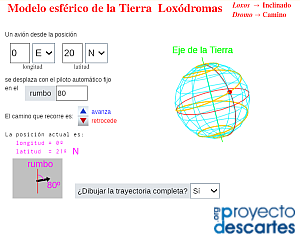
Título: Loxódromas en la esfera
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría métrica tridimensional
Nivel/Edad: Bachillerato y Universidad (17 o más años)
Idioma: Castellano
Autor: José R. Galo Sánchez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
| |
|
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-ShareAlike 4.0 International
Las Comunidades Autónomas de España han publicado ya las fechas y horarios para la realización de las pruebas para la Evaluación de Bachillerato para el Acceso a la Universidad (EBAU), que se celebrarán entre el 22 de junio y el 10 de julio en convocatoria ordinaria.
Para preparar dichas pruebas los estudiantes pueden encontrar, entre los diferentes Proyectos de la RED, muchas unidades con contenidos de los diferentes bloques del currículum de 2º de Bachillerato.
En el vídeo de esta semana se proponen una serie de unidades para estudiar y repasar los temas de Matemáticas del bloque de análisis pertenecientes al Proyecto Misceláneas. Se trata de unidades independientes, con ejercicios de continuidad y cálculo diferencial e integral. En cada unidad el estudiante selecciona el tipo de ejercicio que quiere realizar, lo resuelve en su cuaderno y puede comprobar la solución correcta que se muestra con detalle en la escena.
Estos ejercicios se pueden repetir cuantas veces se desee ya que cada vez se generan aleatoriamente distintas funciones, de tal modo que se convierten en un material idóneo para preparar las pruebas de Selectividad.
Las unidades seleccionadas son:
- Continuidad de una función en un punto
- Derivadas de funciones elementales
- Derivadas regla de la cadena
- Integración de funciones casi inmediatas
- Integrales por partes
- Área encerrada por dos curvas
- EVALUACIÓN de BACHILLERATO para el Acceso a la Universidad
Esta selección de unidades se puede presentar al alumnado mediante los correspondientes enlaces o formando parte de un curso virtual en caso de disponer de un blog, moodle o cualquier otro tipo de espacio web. En este vídeo se propone la presentación de dichas unidades en un curso moodle.
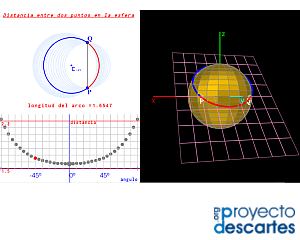
Título: Geodésicas en la esfera. Círculo máximo.
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría métrica tridimensional
Nivel/Edad: Bachillerato y Universidad (17 o más años)
Idioma: Castellano
Autor: José R. Galo Sánchez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
| |
|
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-ShareAlike 4.0 International
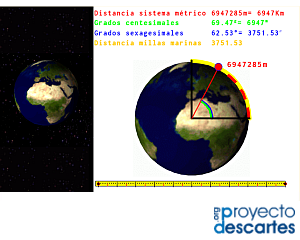
Título: El metro y el cuadrante del meridiano terrestre
Sección: Miscelánea
Bloque: Álgebra
Unidad: Unidades de medida
Nivel/Edad: Secundaria y Bachillerato (12 o más años)
Idioma: Castellano
Autor: José R. Galo Sánchez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
| |
|
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-ShareAlike 4.0 International
Los cilindros generalizados, los conos generalizados y las superficies tangenciales son los tres tipos de superficies regladas desarrollables. Todas ellas pueden obtenerse a partir de una curva directriz sobre la que desplazando una recta se genera la superficie, de ahí que a la recta se le denomine generatriz. En el caso de los cilindros todas las rectas tienen la misma dirección, en los conos todas pasan por un punto que es el vértice y en las superficies tangenciales son las rectas tangentes a la curva directriz. Todas ellas pueden parametrizarse como:
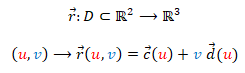
donde 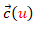 es la curva directriz y
es la curva directriz y 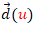 es la dirección de la generatriz. En el artículo "Superficies desarrollables con Descartes" detallé todos estos aspectos e indiqué que en las misceláneas allí compartidas la curva directriz que había considerado era plana y, por tanto, procedería abordar una extensión que contemplara que fuera tridimensional. También planteé abordar una miscelánea en la que se obtuvieran superficies tangenciales y el desarrollo plano de las mismas. Todo ello es lo que aquí presento.
es la dirección de la generatriz. En el artículo "Superficies desarrollables con Descartes" detallé todos estos aspectos e indiqué que en las misceláneas allí compartidas la curva directriz que había considerado era plana y, por tanto, procedería abordar una extensión que contemplara que fuera tridimensional. También planteé abordar una miscelánea en la que se obtuvieran superficies tangenciales y el desarrollo plano de las mismas. Todo ello es lo que aquí presento.
Cilindros y conos generalizados
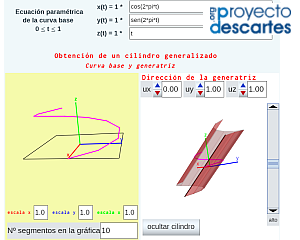
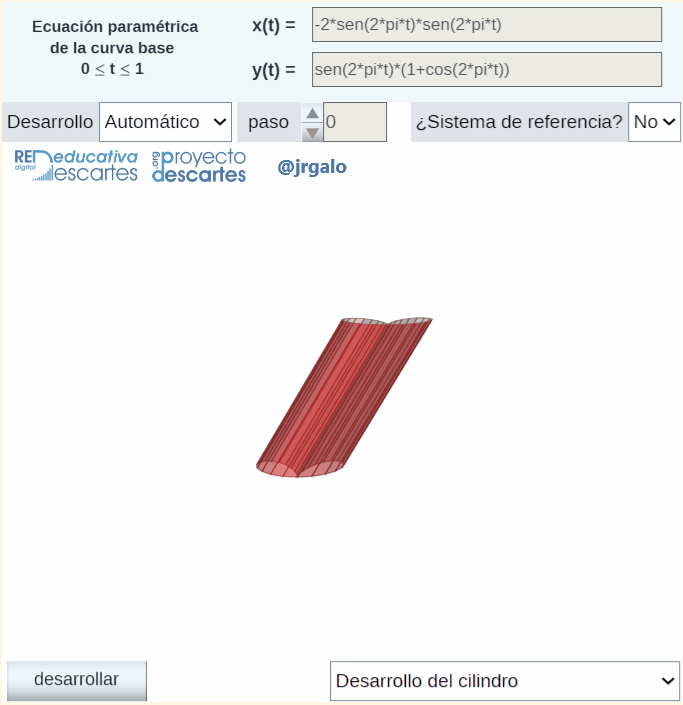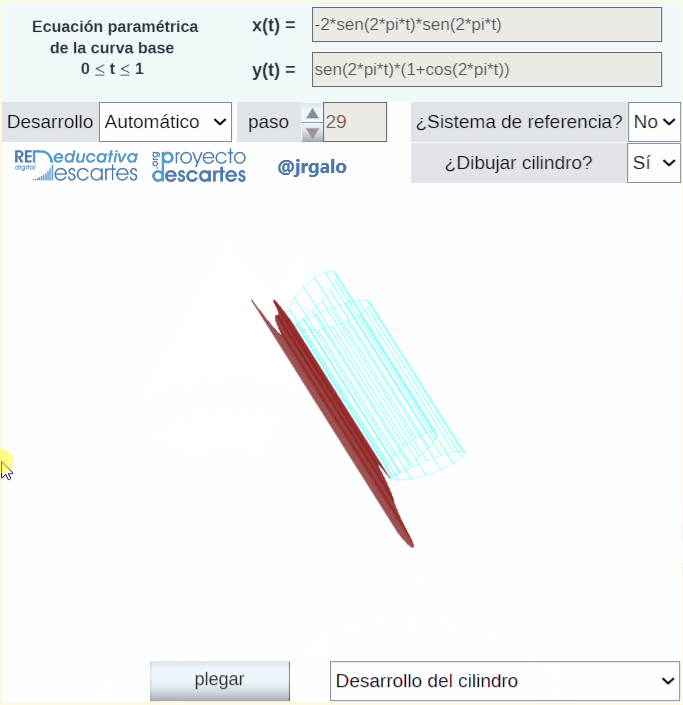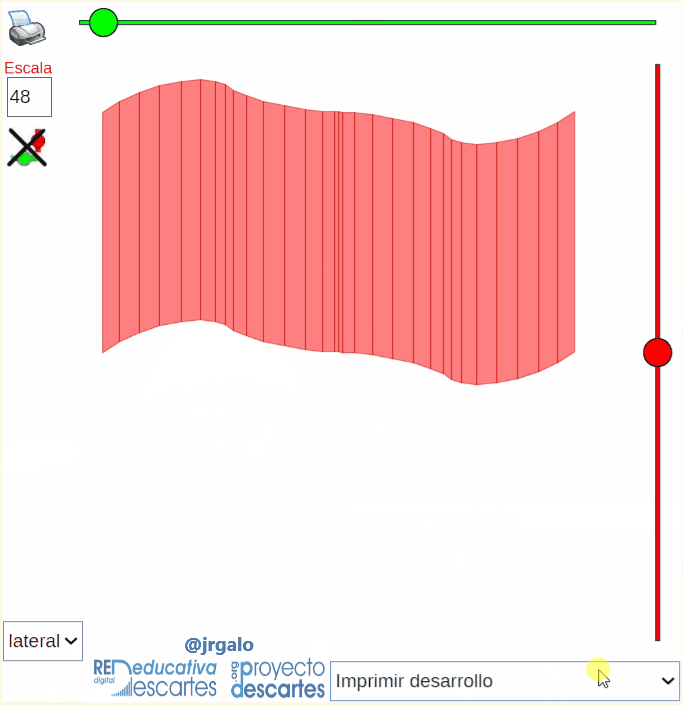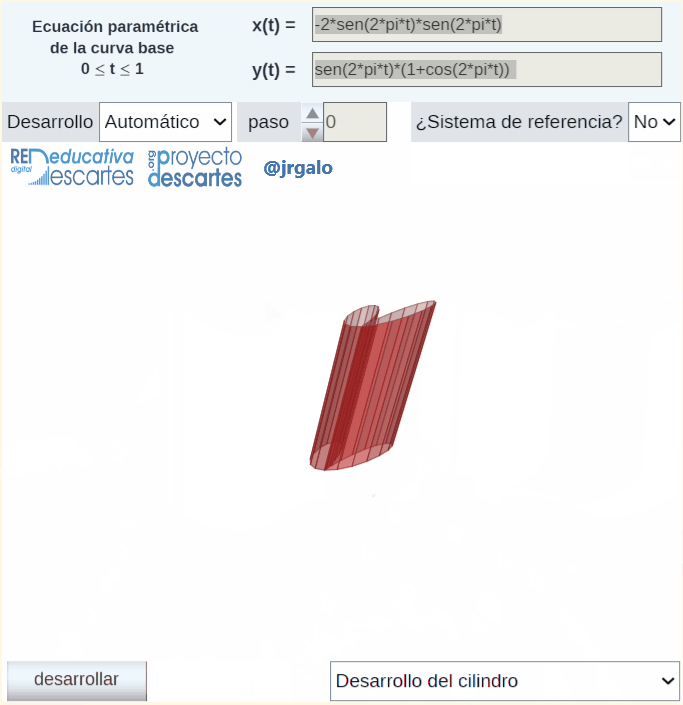
En la miscelánea "Construyo mis cilindros generalizados con curva base 3D" se abordan las superficies que pueden parametrizarse como 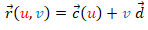 . El usuario define su curva directriz tridimensional
. El usuario define su curva directriz tridimensional 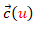 y la dirección de la generatriz que es constante y puede simular la generación del cilindro, obtener su desarrollo plano e imprimirlo si lo desea. En el caso en el que la curva directriz es plana, imprimiendo la base, se tiene una guía sobre la que proceder a la reproducción física del cilindro a partir del desarrollo impreso, pero en el caso de curva tridimensional no siempre será fácil esa construcción ya que no dispone de la reproducción física tridimensional de la curva directriz en la que poder apoyarse para poder plegar el desarrollo. Se requeriría abordar una impresión 3D de la directriz o bien construir la superficie lateral de un prisma cuya base inferior fuera plana y la superior siguiera el perfil de la curva directriz que serviría como soporte sobre el que apoyar y construir el cilindro. Ambas opciones son accesibles, pero no se contemplan en este recurso interactivo.
y la dirección de la generatriz que es constante y puede simular la generación del cilindro, obtener su desarrollo plano e imprimirlo si lo desea. En el caso en el que la curva directriz es plana, imprimiendo la base, se tiene una guía sobre la que proceder a la reproducción física del cilindro a partir del desarrollo impreso, pero en el caso de curva tridimensional no siempre será fácil esa construcción ya que no dispone de la reproducción física tridimensional de la curva directriz en la que poder apoyarse para poder plegar el desarrollo. Se requeriría abordar una impresión 3D de la directriz o bien construir la superficie lateral de un prisma cuya base inferior fuera plana y la superior siguiera el perfil de la curva directriz que serviría como soporte sobre el que apoyar y construir el cilindro. Ambas opciones son accesibles, pero no se contemplan en este recurso interactivo.
Pulsa sobre la imagen para acceder a la escena interactiva
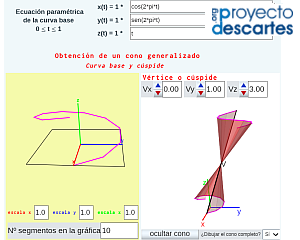
Con identica funcionalidad tenemos la miscelánea "Construyo mis conos generalizados con curva base 3D" correspondiente a la parametrización 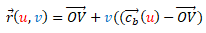 . En ella, definiendo la curva directriz tridimensional y el vértice se procede a generar el cono y a obtener su desarrollo plano. En este caso la reproducción material del cono, gracias a la referencia del vértice, puede ser más sencilla.
. En ella, definiendo la curva directriz tridimensional y el vértice se procede a generar el cono y a obtener su desarrollo plano. En este caso la reproducción material del cono, gracias a la referencia del vértice, puede ser más sencilla.
Pulsa sobre la imagen para acceder a la escena interactiva
El desarrollo de las dos escenas anteriores a partir de las escenas análogas de base plana no requirió mucho trabajo porque realmente estaban diseñadas para ello y practicamente lo que había era una restricción de la curva directriz estableciendo que la tercera componente fuera nula. El pimer objetivo planteado se alcanzó sin un coste excesivo.
Superficies tangenciales
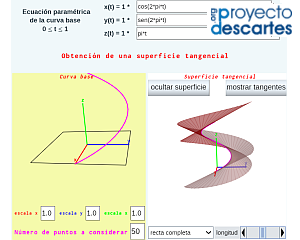
El segundo objetivo era desarrollar la miscelánea "Construyo mis superficies tangenciales" asociada a las parametrizaciones del tipo 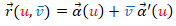 y en las que en cada punto de la curva directriz la generatriz sigue la dirección de la recta tangente a dicha directriz. He aquí la miscelánea:
y en las que en cada punto de la curva directriz la generatriz sigue la dirección de la recta tangente a dicha directriz. He aquí la miscelánea:
Pulsa sobre la imagen para acceder a la escena interactiva
En ella hay que detallar y aclarar algunas cuestiones:
- El usuario define la curva directriz y ésta, teóricamente, ha de ser diferenciable para que en todo punto esté definida la recta tangente que es la generatriz de la superficie.
- A nivel interno en la escena interactiva se trabaja a nivel discreto, es la realidad computacional. Por tanto, realmente, lo que se tiene es que la curva directriz es una poligonal y para segmentos de longitud pequeña la dirección de estos son buenas aproximaciones de la recta tangente. Consecuentemente en cada nodo de esa poligonal (punto de la curva directriz) se puede optar por considerar la dirección de la tangente bien por la del segmento anterior a ese nodo (que se corresponde con diferencias finitas regresivas) o la del segmento posterior (diferencias progresivas) o la media aritmética de ellas (diferencias centradas). En la escena se ha optado por considerar la tangente asociada a las diferencias regresivas
- En toda superficie tangencial los puntos singulares son los puntos de la curva directriz (arista de retroceso) que se corresponden con el valor del parámetro v = 0 y la superficie está formada por dos hojas (v < 0 y v > 0) —en la escena se ha indicado como semirrecta negativa y semirrecta positiva—.
- Para aproximar cada una de las hojas de la superficie, entre cada dos tangentes consecutivas de la poligonal aproximante citada se considera el ángulo plano que forman ambas (en la escena un triángulo). Obviamente a medida que se consideran más número de segmentos la aproximación es mejor. Ver las siguientes imágenes:
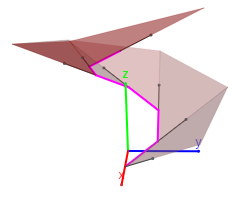 |
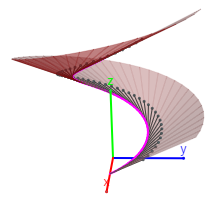 |
| Aproximación con seis segmentos | Aproximación con cincuenta segmentos |
- La aproximación indicada es similar a la que se efectúa en el caso de los cilindros que se aproximan por prismas y para los conos aproximados por pirámides. Y a partir de ésta la obtención dinámica del desarrollo plano y éste en sí es algo inmediato con la parafernalia técnica que habitualmente empleo.
En la animación siguiente se refleja parte de lo que puedes abordar y obtener con esta escena interactiva.
Pulsa sobre la imagen para ampliarla
Te invito a construir ¡tus superficies regladas desarrollables!
tanto de manera virtual como real.
Título: Construyo mis superficies tangenciales
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría tridimensional
Nivel/Edad: Bachillerato y universidad (17 o más años)
Idioma: Castellano
Autor: José R. Galo Sánchez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
| |
|
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-ShareAlike 4.0 International
Título: Construyo mis conos generalizados con curva base 3D
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría tridimensional
Nivel/Edad: Bachillerato y universidad (17 o más años)
Idioma: Castellano
Autor: José R. Galo Sánchez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
| |
|
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-ShareAlike 4.0 International
Título: Construyo mis cilindros generalizados con curva base 3D
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría tridimensional
Nivel/Edad: Bachillerato y universidad (17 o más años)
Idioma: Castellano
Autor: José R. Galo Sánchez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
| |
|
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-ShareAlike 4.0 International
En este artículo se describen y clasifican las superficies regladas desarrollables poniendo de manifiesto que éstas son cilindros, conos y superficies tangenciales. Y, mediante el uso de Descartes, se permite al usuario abordar la construcción virtual de "su" cilindro y cono personalizado, pero también se le da la posibilidad de convertirlo en un objeto tridimensional tangible sin más que proceder a la obtención automática de su desarrollo plano y, mediante su impresión en papel, proceder a su construcción.
Superficies regladas desarrollables
Una superficie es reglada si está constituida por una familia de rectas. Todas estas superficies se pueden parametrizar como:
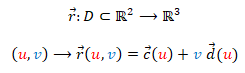 (1)
(1)
donde 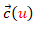 y
y 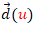 son curvas en el espacio tridimensional. La primera es la curva base o curva directriz y la segunda es el vector director de cada una de las rectas (generatriz). Efectivamente, fijado un valor del parámetro u puede observarse que la expresión obtenida es la ecuacion de una recta y, variando u, geométricamente lo que se puede interpretar es que se va recorriendo cada punto de la curva base
son curvas en el espacio tridimensional. La primera es la curva base o curva directriz y la segunda es el vector director de cada una de las rectas (generatriz). Efectivamente, fijado un valor del parámetro u puede observarse que la expresión obtenida es la ecuacion de una recta y, variando u, geométricamente lo que se puede interpretar es que se va recorriendo cada punto de la curva base 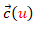 y por él pasa una recta cuya dirección viene dada por
y por él pasa una recta cuya dirección viene dada por 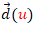 .
.
También puede expresarse de manera equivalente como:
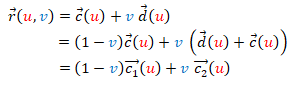 (2)
(2)
que algebraicamente representa, para cada valor de u, a una recta (o un segmento si consideramos 0 ≤ v ≤ 1), pero en este caso lo que se pone de manifiesto es que esa recta se apoya en un punto de la curva 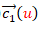 y en otro de la
y en otro de la 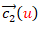 .
.
El ejemplo más simple de superficie reglada es un plano, pero entre otras, también lo son los cilindros, los conos, la banda de Moebius, el hiperboloide, etc.
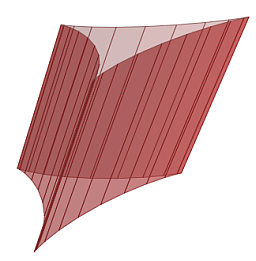 |
 |
| Cilindro generalizado | Cono generalizado |
 |
 |
| Banda de Möbius | Hiperboloide |
Una herramienta matemática que permite caracterizar la curvatura de cualquier superficie regular es la denominada curvatura de Gauss, y se verifica que dicha curvatura es invariante por isometrías. Todas las superficies regladas cumplen que su curvatura de Gauss es menor o igual que cero y, en particular, que la curvatura de Gauss de un plano es identicamente nula. En base a lo anterior, todas las superficies regladas que tienen curvatura cero son isométricas con el plano y son denominadas como superficies desarrollables ya que, consecuentemente, pueden construirse a partir de su desarrollo plano.
En la parametrización (1) la condición de curvatura nula equivale a que el denominado parámetro de distribución sea nulo, y éste viene dado por:
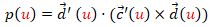 (3)
(3)
o en el caso de la parametrización (2) como:
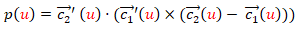 (4)
(4)
De (4) se observa que para que la superficie reglada sea desarrollable tiene que ocurrir que para todo u el vector tangente a la curva 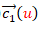 , el vector tangente a
, el vector tangente a 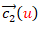 y el vector director de la recta que une a ambas curvas sean coplanarios al ser el producto mixto de los tres cero, o dicho de otra forma que el plano tangente es constante lo largo de cada recta generatriz.
y el vector director de la recta que une a ambas curvas sean coplanarios al ser el producto mixto de los tres cero, o dicho de otra forma que el plano tangente es constante lo largo de cada recta generatriz.
Pero un análisis más detenido de cuándo es identicamente nulo el parámetro de distribución nos puede permitir clasificar a las superficies desarrollables. Así en la expresión (3):
- Si
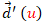 es identicamente nulo, entonces
es identicamente nulo, entonces 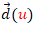 es un vector constante, es decir que todas las rectas tienen la misma dirección y la superficie es un cilindro generalizado de ecuación
es un vector constante, es decir que todas las rectas tienen la misma dirección y la superficie es un cilindro generalizado de ecuación 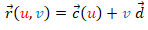 .
. - Si
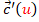 es idénticamente nulo, entonces
es idénticamente nulo, entonces 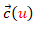 es el vector de posición de un punto V y la superficie desarrollable es un cono generalizado de vértice V, cuya ecuación sería
es el vector de posición de un punto V y la superficie desarrollable es un cono generalizado de vértice V, cuya ecuación sería 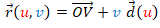 . También puede expresarse en función de una curva base como
. También puede expresarse en función de una curva base como 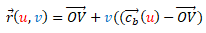 .
. - En cualquier otro caso se demuestra que es una superficie tangencial, que mediante un cambio de parámetro se puede expresar como
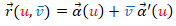 .
.
- Si
Superficies desarrollables con Descartes
En el proyecto "El metro: patrón inexacto para medir exactamente", que en el año 2004 contó con una ayuda de la Junta de Andalucía (España) para la elaboración de materiales y recursos educativos digitales, desarrollamos con Descartes en su versión Java algunos objetos educativos interactivos sobre conos y cilindros generalizados incluyendo la posibilidad de obtener su desarrollo plano. En este año 2020 hemos procedido a adaptarlos a DescartesJS y a mejorar sus posibilidades, en particular en lo relativo a forma de obtener ese desarrollo plano, a incluir la posibilidad de su impresión y consecuentemente a la posibilidad de su reproducción tangible tridimensional. Estos recursos actualizados están publicados en el subproyecto "misceláneas" de la RED Descartes y los enlazamos a continuación aquí en dos triadas de imágenes que respectivamente se corresponden con cilindros y conos generalizados.
En la primera triada correspondiente a los cilindros tenemos:
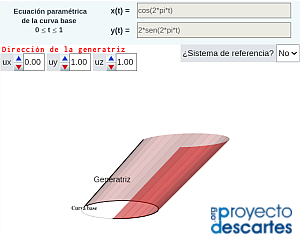
- "Cilindro generalizado" donde se muestra la construcción de un cilindro tomando como curva base una elipse y en la que podemos cambiar la dirección de la recta generatriz. La escena permite reproducir la generación del cilindro mediante desplazamiento de la generatriz sobre la curva base; simular y obtener el desarrollo plano; imprimir dicho desarrollo y el de las bases del cilindro. Adicionalmente, dado el contexto en el que se desarrolló originalmente esta escena —el metro—, se puede obtener un sistema de referencia basado en meridianos y paralelos.
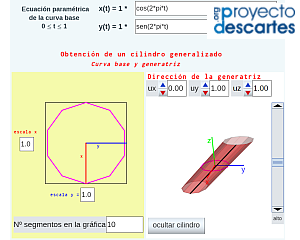
- "Ejemplos de cilindros generalizados" donde se puede elegir diferentes curvas base (circunferencia, elipse, parábola, rama de hipérbola, segmento, cardiode, deltoide, bifolium, astroide, bicircular) y reproducir las acciones indicadas en la escena anterior.
- "Construyo mis cilindros" que como indica el título permite al usuario definir la curva base en coordenadas paramétricas y la dirección de la generatriz que desee y con ellas construir su cilindro generalizado. De nuevo puede realizar de manera virtual interactiva las acciones ya indicadas, pero también procediendo a la impresión del desarrollo pasar a disponer de la versión tangible de "su" cilindro. Para cada curva base cambiando el número de segmentos que se desean considerar en la representación se obtienen diferentes cilindros, para simular el caso continuo basta seleccionar un número de segmentos suficientemente elevado.
 |
 |
 |
| Cilindro generalizado | Ejemplos de cilindros generalizados | Construyo mis cilindros |
De manera análoga en la triada correspondiente a los conos generalizados tenemos:
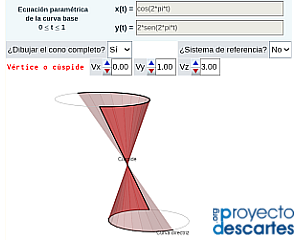
- "Cono generalizado" en el que se muestra la construcción de un cono tomando como curva base una elipse y en la que podemos cambiar su vértice. La escena interactiva permite reproducir la generación del cono mediante desplazamiento de la generatriz sobre la curva base; visualizar el cono completo; simular y obtener el desarrollo plano; imprimir dicho desarrollo y el de la base del cono. Adicionalmente, dado el contexto en el que se desarrolló originalmente esta escena —el metro—, se puede obtener un sistema de referencia basado en meridianos y paralelos.
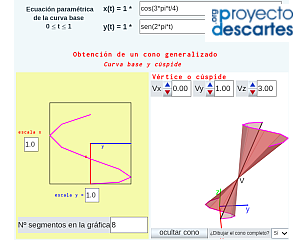
- "Ejemplos de conos generalizados" donde se puede elegir diferentes curvas base (las mismas que en el caso de los cilindros) y reproducir las acciones indicadas en la escena anterior.
- "Construyo mis conos" que permite al usuario definir la curva base y el vértice y construir su cono generalizado tanto virtual como tangible..
 |
 |
 |
| Cono generalizado | Ejemplos de conos generalizados | Construyo mis conos |
En estos objetos interactivos se ha considerado que la curva base es una curva plana, así pues, he de ponerme la tarea de incorporar la tridimensionalidad de la curva base y presentarlo en un próximo artículo en este blog. Y, adicionalmente, este trabajo debería incoporar el caso de superficies tangenciales que implictamente, a priori, entraña cierta dificultad si se deja libertad de definición al usuario, pero sobre ello ya hablaremos.
Finalizo reseñando que para la obtención automática y animada del desarrollo plano del cilindro y el cono se aplica la rotación de Rodrigues descrita en un artículo anterior de este blog. Lo que se hace es plantearlo como el desarrollo plano de un prisma o una pirámide que se ajuste suficientemente al cilindro o cono dado. En la animación siguiente se refleja el desarrollo plano de un cilindro generalizado en el que su base es la curva denominada bifolium.
Pulsa sobre la imagen para ampliarla
Bibliografía
Lucas, E. (2017). Superficies regladas [Trabajo fin de grado]. Universidad de Murcia.
Rosado, E (2010). Superficies regladas [Apuntes docentes]. Universidad Politécnica Madrid.