Este mes vamos a ver una unidad de 4ºESO sobre los números reales:
En el vídeo hemos tratado los siguientes temas:
1.Números racionales e irracionales
Decimales periódicos
Fracción generatriz
Números racionales
Números irracionales
Números reales
2.Calculando con números reales
Aproximaciones
Medida de errores
Notación científica
3.La recta real
Ordenación de los números reales
Valor absoluto
Intervalos
¿Estás buscando actividades para los más pequeños?
En el recurso que hoy presentamos, encontrarás actividades de recuento que te permitirán introducir los números de forma lúdica y motivadora. Se trata del objeto digital interactivo Recuento de objetos perteneciente al Proyecto Canals, un recurso con escenas para iniciar y ejercitar el recuento, incluye sonido y es adecuado para parvulario y primer curso de primaria.
Los recursos interactivos del Proyecto Canals están formados por actividades de matemáticas adecuadas para infantil, primaria y primero de la ESO y han sido desarrollados en base a los materiales elaborados por la profesora Maria Antònia Canals.
Añadimos el recurso en nuestra aula virtual moodle
Aunque desde la página del objeto digital podemos acceder directamente a las actividades a través de un hiperenlace, en este caso vamos a descargar el archivo comprimido para subirlo a nuestra aula virtual moodle.
|
Los materiales interactivos de la Red Educativa Digital Descartes están compuestos por una o varias escenas contenidas en páginas html enlazadas. En las páginas de los diferentes proyectos encontramos para cada objeto un archivo comprimido con todos los documentos, imágenes y recursos necesarios para el correcto funcionamiento de la actividad. |
|
Para iniciar la actividad en nuestro curso moodle deberemos proceder de la siguiente manera:
- Descargar la carpeta comprimida desde la página del objeto
- Activar el modo edición en nuestro curso moodle y seleccionar el recurso archivo
- Subir la carpeta comprimida
- Descomprimir y abrir la carpeta
- Seleccionar el documento index.html como archivo principal
En el siguiente vídeo puedes ver con detalle todo el proceso:
EDAD 4º ESO Opc. A Funciones y gráficas
Escrito por Alfonso Saura EspínEste mes vamos a tratar una unidad sobre funciones y gráficas correspondiente a 4º de la ESO:
En el video hemos tratado los siguientes apartados:
1. Funciones
Concepto
Tablas y gráficas
Dominio y recorrido
2. Propiedades
Continuidad
Simetrías
Periodicidad
Tendencia
3. Monotonía
Tasa de variación media
Crecimiento y decrecimiento
Máximos y mínimos
Audios y Vídeos Interactivos con Descartes
Continuación de la práctica (2)
Los contenidos de la Documentación técnica de la herramienta de autoría DescartesJS son dinámicos debido a la permanente labor de mantenimiento y actualización del código fuente de la librería descartes-min.js por parte de los responsables de la Red Digital Descartes de México, España y Colombia. Hay épocas en las que este dinamismo es vertiginoso tal y como ocurre actualmente. Por eso comenzamos esta nueva entrada del Blog recomendando la visita a dicha documentación mediante el enlace del título y también de este otro que llevan, respectivamente, a la información sobre el uso de vídeos interactivos, tanto en local como en línea y a la información sobre cómo comunicar las escenas con el HTML y viceversa.
Continuando con la práctica, recordamos que ya hemos definido en los espacios: E1, E2 y E3, los gráficos (textos) necesarios para dirigir y complementar el flujo de la actividad. Ahora, siguiendo el paso 7 crearemos los dos controles, tipo botón, para manipular el vídeo ya que los propios del mismo están enmascarados.
Abrimos la opción de menú Controles y procedemos como muestra el vídeo siguiente.
Recordamos que la expresión '\n' que aparece en el vídeo puede interpretarse como un salto de línea y permite introducir una nueva instrucción.
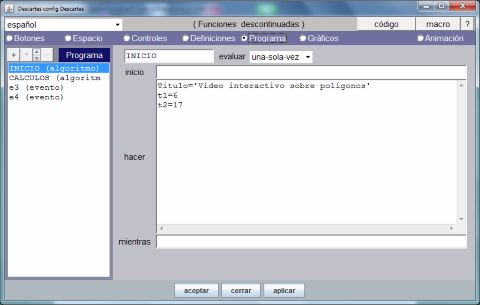
El paso 8 consite en definir, en la opción de menú Programa, dos eventos para controlar la reproducción del vídeo mediante el manejo de la animación tal y como se explica detalladamente en la documentación.
Después de seguir las instrucciones, la opción de menú Programa debe tener el aspecto que muestra el gráfico siguiente.
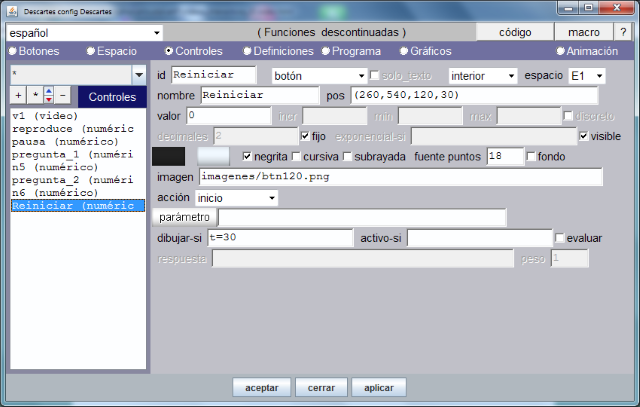
A continuación, siguiendo las indicaciones del paso 9, volvemos a seleccionar la opción de menú Controles para definir en los espacios E1 y E3 los botones, cuadros de texto y controles de tipo menú que son el soporte de la interactividad de la escena tal y como se muestra en el documento videos_interactivos.pdf enlazado al principio del artículo.
El gráfico siguiente muestra cómo debe quedar la opción de menú Controles después de completar el paso anterior.
En próximas entradas se completará la práctica y continuaremos analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
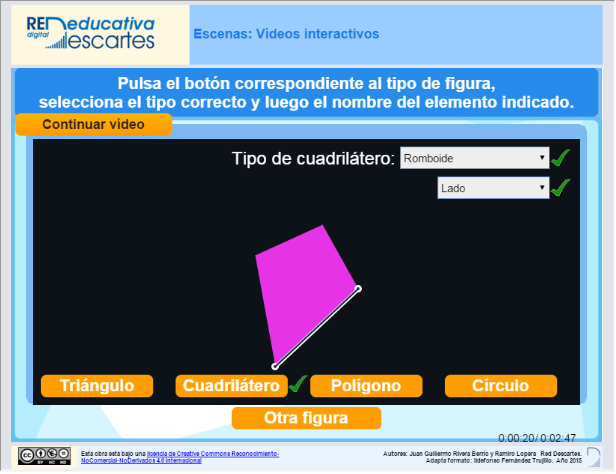
El siguiente gráfico es un enlace a un ejemplo de la implementación de vídeos interactivos dentro de una escena DescartesJS. Este ejemplo, realizado por Juan Guillermo Rivera Berrío y que es una propuesta para evaluación de la viabilidad del proyecto y su potencial formativo y que aún está en fase de prueba, ha sido posible gracias a la colaboración de la Red Descartes de Colombia (Juan Gmo. Rivera y Ramiro Lopera) y de España (José R. Galo).
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Más...
Una actividad de funciones en nuestro blog. Código de la escena
Escrito por Montserrat Gelis BoschHoy presentamos un vídeo en el cual se indican los pasos a realizar para embeber una actividad interactiva de la Red Educativa Digital Descartes en nuestro blog, a partir del código de la escena.
En vídeos anteriores hemos visto cómo embeber actividades de la Red Descartes en nuestro blog utilizando el código iframe:
<iframe style='width: ..px; height: ..px;' src='dirección web de la página'></iframe>
En el cual deberemos escribir las dimensiones y la dirección web de la página de la actividad.
Pero en algunos casos es posible que deseemos embeber solamente la escena con la actividad y no toda la página. En este caso deberemos utilizar el código que genera la escena.
Para copiar dicho código procederemos de la siguiente forma:
- Elegimos la actividad que queremos embeber, en este caso hemos seleccionado una escena del tema 1 de la unidad Funciones y Gráficas para 4º de la ESO del Proyecto ED@D. para 4º de la ESO del Proyecto ED@D.
- Situamos el ratón sobre la escena y pulsamos el botón derecho.
- Se abre una ventana auxiliar, activamos el botón config que nos da acceso al código y lo copiamos.
Una vez copiado el código, activaremos la edición en html de la página de nuestro blog y lo pegaremos. Deberemos comprobar que contiene el parámetro docBase (para las imágenes y recursos auxiliares) y la línea de código del script de llamada al intérprete.
Una opción interesante que nos permite Blogger es la posibilidad de alojar el script en la plantilla de nuestro blog, lo cual nos ahorra tener que estar pendientes de su inclusión en los códigos y además agilizará la activación de las escenas.
Activaremos la edición de la plantilla de nuestro blog y situaremos, en la cabecera, entre <head> y </head>, la línea de código:
<script type='text/javascript' src='http://arquimedes.matem.unam.mx/Descartes5/lib/descartes-min.js'></script>
Veamos ahora el siguiente vídeo en el cual se muestra el proceso a seguir, paso a paso:
Este mes vamos a ver una unidad de estadística de 3ºESO:
Los contenidos del tema tratado son:
1.Hacer estadística
Necesidad.
Población y muestra
Variables
2.Recuento y gráficos
Recuento de datos
Gráficos
Agrupación de datos en intervalos
3.Medidas de centralización
y posición
Media
Moda
Cuartiles y mediana
4.Medidas de dispersión
Rango y desviación media
Desviación típica
Coeficiente de variación
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)



 CONTACTO
CONTACTO
