Mostrando artículos por etiqueta: vídeos
Título: Desarrollo de la comunicación audiovisual en secundaria
Sección: iCartesiLibri
Bloque: Formación
Unidad: Formación en comunicación audiovisual
Nivel/Edad: Secundaria, Bachillerato y Universidad (14 años o más)
Idioma: Castellano
Autores: José Antonio Salgueiro González
ISBN 978-84-10368-08-8
![]() Haz clic aquí para ver una versión en pdf
Haz clic aquí para ver una versión en pdf
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Mucho Teatro ha sido el nombre de un proyecto educativo que durante unos años fue llevado a efecto en el I.E.S. Blas Infante de Córdoba (España). El libro ofrece a aquellos que todavía estén inmersos en el maravilloso mundo del teatro en las aulas, las obras que el autor escribió para tantos grupos de alumnos y de profesores. Pues bien, Paco Torres, su autor, ha tenido la gentileza de acceder a nuestra propuesta de presentación de este libro interactivo, de y para instituto, mediante el siguiente vídeo que compartimos en este artículo.
Con objeto de facilitar la accesibilidad, o para aquellas personas que necesiten visualizarlo en silencio, hemos incorporado subtítulos en lengua castellana, así que te recordamos que, posiblemente, tengas que activarlos desde la barra del reproductor de Youtube.
- Acceso directo al recurso para su visualización en línea.
- Acceso a la versión PDF con enlaces a los interactivos de su interior.
- Descargar el recurso en archivo comprimido para su visualización en local, aunque necesitarás conexión solamente para los multimedias embebidos.
- Doña Juana Tenorio
- Luces de pandemia
- La casa de Bernardo Amanecer
- Historia de un ascensor
Un año más, desde RED Descartes queremos aportar nuestros recursos y colaboración para celebrar la efemérides del "Día Internacional de la Mujer y la Niña en la Ciencia", a la vez que animamos a programar y desarrollar actividades en el aula con nuestro alumnado para cumplir con los objetivos establecidos:
- Visibilizar el trabajo de las mujeres que se dedican a las áreas STEM (Science, Technology, Engineering and Mathematics), creando así referentes femeninos para la infancia que puedan contribuir a la elección de estas áreas como carreras profesionales.
- Conocer los diferentes factores que afectan a la situación actual de la mujer en las áreas STEM para fomentar prácticas que conduzcan a su eliminación y alcanzar la igualdad de género en el ámbito científico.

| JUEGO DIDÁCTICO SOBRE GRANDES CIENTÍFICAS |
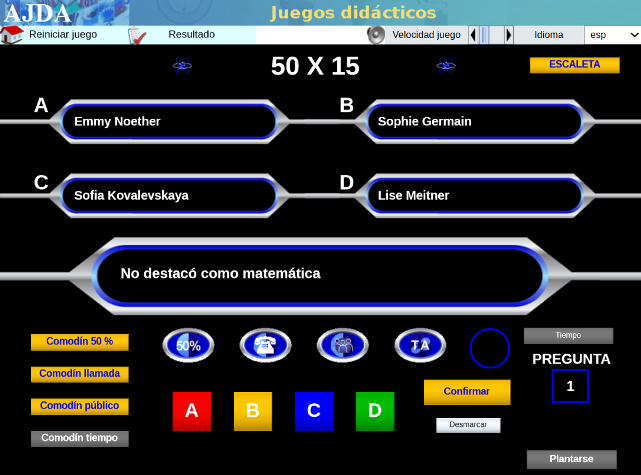
El juego es una de las estrategias didácticas de gran valor que motiva a nuestro alumnado y que se potencia con las tecnologías de la información y la comunicación. Así que os dejamos el que ha creado nuestro compañero Jesús M. Muñoz Calle, del proyecto Aplicación de Juegos Didácticos en el Aula, para difundir algunos de los decubrimientos y avances científicos gracias a la mujer, con algunas capturas de pantalla por si fueran necesarias. Es idóneo para organizar una pequeña competición en el aula proyectado desde la pizarra digital interactiva.
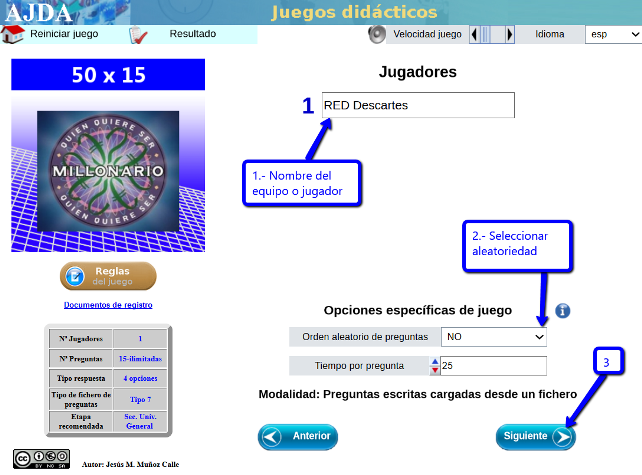
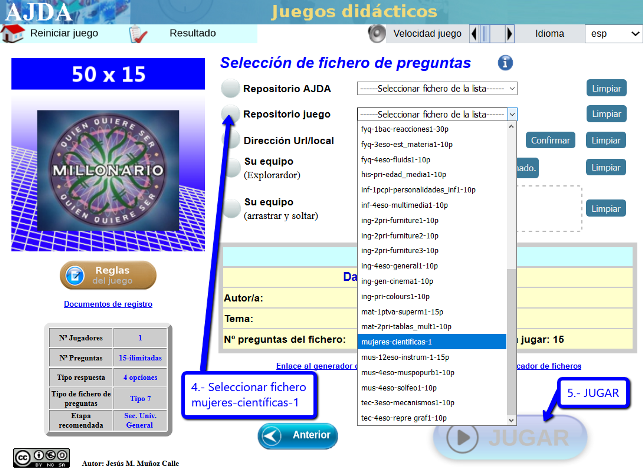
| LA MUJER EN LA CIENCIA |
"El personaje misterioso" es un programa de Radio Descartes conducido por Eva Perdiguero y Ángel Cabezudo con el objetivo de dar a conocer un poco más de cerca la parte humana de los personajes matemáticos famosos a lo largo de la historia. Concretamente, tras la entrevista del invitado, que no se desvela, el escuchante debería conocer su nombre o bien tomar los datos que se aportan en la dramatización y tomarse un tiempo para averiguarlo consultando en la múltiple documentación que hoy día se encuentra disponible, principalmente en Internet o en libros divulgativos de Historia de las Matemáticas o de Matemáticos célebres, pasando a responder en un comentario del blog de nuestro portal. Pues bien, de este proyecto hemos seleccionado las siguientes entrevistas a grandes matemáticas de la historia, cuyas voces son interpretadas por científicas del ámbito educativo. Así, aportamos los siguientes recursos:
- Entrevista a Hipatia de Alejandría, interpretada por Eva Mª. Perdiguero Garzo, profesora de matemáticas.
- Entrevista a Sofía Kovalévskaya, interpretada por Marta Macho Stadler, matemática y divulgadora científica.
- Entrevista a Emmy Noether, interpretada por Elena Vázquez Abal, matemática y divulgadora científica.
- Entrevista a Ada Lovelace, interpretada por Montse Gelis Bosch, profesora de matemáticas.
- Entrevista a María Gaetana Agnesi, interpretada por Elena Ramírez Ezquerro, profesora de matemáticas.
Para descubrir al personaje misterioso, se publica un puzle creado con Descartes JS que incluye imágenes alusivas, alegóricas o de efemérides que descubren al personaje:
- Puzle dedicado a Hipatia de Alejandría
- Puzle dedicado a Sofía Kovalévskaya
- Puzle dedicado a Emmy Noether
- Puzle dedicado a Ada Lovelace
- Puzle dedicado a María Gaetana Agnesi
| CONTRIBUCIONES DE ALUMNAS A LA CIENCIA |
Son varios los proyectos difundidos desde el portal de RED Descartes donde las alumnas son protagonistas y divulgadoras de la ciencia, especialmente de la matemática. Así, hemos seleccionado con motivo del día 11 de febrero las siguientes contribuciones y aportaciones de alumnas a la ciencia, clasificadas por etapa educativa, con objeto de que puedan usarse en las pizarras digitales de las aulas, en los espacios virtuales de aprendizaje, abrir debates y plantear la actividad que cada docente determine.
| CIENTÍFICAS EN INFANTIL Y PRIMARIA |
- Color y cantidad. Pensamos juntos para resolver una situación
- Significado de perímetro
- Experiencia de pensamiento autónomo en resolver un problema. Alumna de 3 años
- Ángulo recto para construir un metro cuadrado en papel
- Alumnas de cuarto de primaria en la investigación y aprendizaje de capacidades y su expresión en lenguaje matemático
| CIENTÍFICAS EN SECUNDARIA |
- Antonia y Maite nos enseñan la aplicación de la maqueta en la semejanza de figuras
- Ángela y Cristina nos muestran la utilidad de la maqueta en el aprendizaje de la semejanza
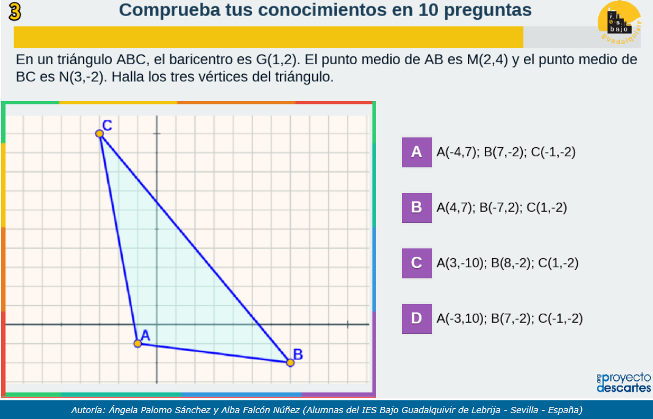
- Alba y Ángela nos enseñan a discutir y resolver sistemas de ecuaciones con Descartes y herramientas tecnológicas
- Natalia y Celeste comunican y comparten ideas matemáticas con Descartes
- Carmen, divulga la simplificación de fracciones algebraicas y la suma de las mismas
- Rocío, divulga la resolución de una unidad liberada de PISA
- Virginia, María y Laura, divulgan una técnica de resolución de problemas
- María del Castillo e Irene, divulgan las operaciones con fracciones algebraicas
- María y Claudia entrevistan a Sofía Kovalévskaya, con su matrimonio de conveniencia para poder estudiar matemáticas.
- Mireia y María entrevistan y divulgan la obra de Sophie Germain, la primera mujer en acceder a la Academia de Ciencias de París.
- Antonia y Maite entrevistan y divulgan la vida y obra de Ada Lovelace, con su reflexión sobre la mujer en la ciencia y el techo de cristal.
- Clara, Ángela y Cristina, entrevistan y divulgan la vida y obra de Mary Cartwright, a quien conocí gracias a mis alumnas.
- María y Julia, entrevistan y divulgan la vida y obra de Mary Somerville, conocida como "La Reina de las ciencias del siglo XIX".
- Ángela y Alejandro, entrevistan y divulgan la vida y obra de Euclides
| CIENTÍFICAS EN BACHILLERATO |
- María, divulga la resolución de triángulos rectángulos
- Claudia y María, divulgan la simplificación de expresiones trigonométricas de cociente
- Margarita y María, divulgan la simplificación de expresiones trigonométricas de cociente
- Ángela y Alba, ponen a prueba tus conocimientos de Matemáticas-1
- Laura y Ángela, ponen a prueba tus conocimientos de Matemáticas-1
- Zuleima y Raquel, ponen a prueba tus conocimientos de Matemáticas-1
- Ana y Virginia, ponen a prueba tus conocimientos de Matemáticas-1
- María y Alba, ponen a prueba tus conocimientos de Matemáticas-1
- Lucía e Ismael, ponen a prueba tus conocimientos de Matemáticas-1
- Ángela y Laura y ponen a prueba tus conocimientos de Matemáticas-2
- Joana y Ana ponen a prueba tus conocimientos de Matemáticas-2
- Aurora, Alba, Ángela y Teresa recrean la importancia de la seguridad al desarrollar experiencias en el laboratorio
- Carmen, Joana, Beatriz y Ángela muestran, de forma desenfada, las normas en el laboratorio de Química.
| CIENTÍFICAS EN LA UNIVERSIDAD |
- Sofía, Marcos y Juan Luis nos enseñan a calcular el volumen de un cono por integrales triples.
- Daniela, Beatriz y Jonathan nos muestran algunas aplicaciones de las coordenadas esféricas.
- Tania y Samuel nos enseñan a cambiar de coordenadas cartesianas a polares y cilíndricas.
- Lucía y Alicia nos presentan el cálculo de áreas de figuras planas utilizando integrales dobles.
- Daniela, Beatriz y Jonathan calculan el aforo de un recinto para conciertos.
- Lucía y Alicia nos explican cómo calcular el volumen del Atomium de Bruselas.
- Almudena y Clara nos enseñan a calcular el gradiente de un campo escalar y el uso correcto del operador nabla.
- Clara y Almudena nos muestran el rotacional y la divergencia de un campo vectorial.
- Tania y Samuel nos presentan la resolución de ecuaciones diferenciales con variables separables.
- Andrea y Andrés nos enseñan la función delta de Dirac, sus propiedades y algunas aplicaciones.
Coincidiendo con el 8º aniversario de RED Descartes, y con el objetivo de actualizar algunas de nuestras producciones audiovisuales, hemos decidido editar y compartir con todos nuestros usuarios y seguidores el siguiente vídeo, que hemos denominado ¿Por qué me gusta Descartes?, donde socios y miembros de la RED Descartes de cinco países responden escuetamente a la pregunta formulada aportando su personal valoración, además de poner rostro y voz a nuestra red con una representación de la misma. Una red docente bien conectada que, con sólidos pilares asentados entre Colombia, España y México, se va extendiendo a otros países de lenguas hispana y portuguesa.
Desde Brasil, Colombia, Costa Rica, España y México, podemos conocer las valoraciones de diferentes perfiles o roles en RED Descartes, como desarrollador y documentalista de la herramienta de autor Descartes JS y del código para la edición y diseño de libros interactivos, autores y creadores de recursos educativos abiertos con Descartes JS y sus libros interactivos, coordinadores y formadores del programa de Educación Abierta, traductor de los recursos a portugués de Brasil y docentes de primaria, secundaria obligatoria, bachillerato y universidad de distintas especialidades.
Quiero aprovechar la efemérides para recordar la trayectoria profesional del profesorado de RED Descartes quien, además de una dilatada experiencia docente, fue pionero en la investigación sobre la incorporación generalizada de las TIC en el aula durante el año 2005, dio lugar a una de las primeras redes docentes oficiales en España, se formó, generó recursos y colaboró en la implantación del programa Escuela 2.0 hasta evolucionar y coordinar la red de Buenas PrácTICas 2.0. Prácticamente, la totalidad de sus miembros han desempeñado o desempeñan funciones directivas en sus respectivos centros de destino, poseen gran experiencia en la coordinación de proyectos de colaboración escolar, tanto en el marco de eTwinning como en el eliminado Programa ARCE, de agrupaciones o redes de centros educativos de distintas comunidades autónomas. Además, han desempeñado funciones de tutorización o coordinación de cursos de formación en línea de INTEF y de sus administraciones autonómicas respectivas y, hoy en día, constituidos como organización no gubernamental, ponen todos sus conocimientos y empeño en trabajar de forma altruista para y por la comunidad educativa de la aldea global, lema de RED Descartes.

"En la actualidad, las mujeres y niñas encuentran barreras de muchos tipos, a veces muy sutiles, que dificultan su presencia en la ciencia. El 15 de diciembre de 2015, la Asamblea General de las Naciones Unidas proclamó el 11 de febrero Día Internacional de la Mujer y la Niña en la Ciencia, invitando a que se organizaran actividades de educación y sensibilización pública que ayudaran a lograr una mayor participación y progreso de las mujeres y las niñas en la ciencia. Así, en septiembre de 2016, un grupo de personas del ámbito científico, de forma completamente voluntaria y sin ánimo de lucro, lanzan la Iniciativa 11 de Febrero, con el objetivo de llenar las agendas de actividades que conmemoren el Día Internacional de la Mujer y la Niña en la Ciencia, que ayuden a visibilizar el trabajo de las científicas, a crear roles femeninos en los ámbitos de la ciencia y la tecnología y que promuevan prácticas que favorezcan la igualdad de género en el ámbito científico-tecnológico".
El párrafo ha sido extraído literalmente del sitio web 11 de febrero, donde puedes encontrar toda la información relativa a esta importante fecha, a la que, un año más, RED Descartes se suma animando a celebrar dicha efemérides, programando y realizando actividades en las aulas y aportando los recursos y experiencias disponibles en nuestros dominios.

Desde RED Descartes se difunde la enorme labor desarrollada, a lo largo de la historia, por la mujer en la ciencia, y muy especialmente en las ciencias matemáticas, físicas y químicas. Además, promovemos en nuestras aulas y divulgamos la ciencia que realizan nuestras alumnas, de cualquier etapa educativa, desde los diversos proyectos que abordamos y que compartimos en este artículo para apoyar los objetivos del 11 de febrero.
| LA MUJER EN LA CIENCIA |
"El personaje misterioso" es un programa de Radio Descartes conducido por Eva Perdiguero y Ángel Cabezudo con el objetivo de dar a conocer un poco más de cerca la parte humana de los personajes matemáticos famosos a lo largo de la historia. Concretamente, tras la entrevista del invitado, que no se desvela, el escuchante debería conocer su nombre o bien tomar los datos que se aportan en la dramatización y tomarse un tiempo para averiguarlo consultando en la múltiple documentación que hoy día se encuentra disponible, principalmente en Internet o en libros divulgativos de Historia de las Matemáticas o de Matemáticos célebres, pasando a responder en un comentario del blog de nuestro portal. Pues bien, de este proyecto hemos seleccionado las siguientes entrevistas a grandes matemáticas de la historia, cuyas voces son interpretadas por científicas del ámbito educativo. Así, aportamos los siguientes recursos:
- Entrevista a Hipatia de Alejandría, interpretada por Eva Mª. Perdiguero Garzo, profesora de matemáticas.
- Entrevista a Sofía Kovalévskaya, interpretada por Marta Macho Stadler, matemática y divulgadora científica.
- Entrevista a Emmy Noether, interpretada por Elena Vázquez Abal, matemática y divulgadora científica.
- Entrevista a Ada Lovelace, interpretada por Montse Gelis Bosch, profesora de matemáticas.
- Entrevista a María Gaetana Agnesi, interpretada por Elena Ramírez Ezquerro, profesora de matemáticas.
Para descubrir al personaje misterioso, se publica un puzle creado con Descartes JS que incluye imágenes alusivas, alegóricas o de efemérides que descubren al personaje:
- Puzle dedicado a Hipatia de Alejandría
- Puzle dedicado a Sofía Kovalévskaya
- Puzle dedicado a Emmy Noether
- Puzle dedicado a Ada Lovelace
- Puzle dedicado a María Gaetana Agnesi
| CONTRIBUCIONES DE ALUMNAS A LA CIENCIA |
Son varios los proyectos difundidos desde el portal de RED Descartes donde las alumnas son protagonistas y divulgadoras de la ciencia, especialmente de la matemática. Así, hemos seleccionado con motivo del día 11 de febrero las siguientes contribuciones y aportaciones de alumnas a la ciencia, clasificadas por etapa educativa, con objeto de que puedan usarse en las pizarras digitales de las aulas, en los espacios virtuales de aprendizaje, abrir debates y plantear la actividad que cada docente determine.
| CIENTÍFICAS EN INFANTIL Y PRIMARIA |
- Color y cantidad. Pensamos juntos para resolver una situación
- Significado de perímetro
- Experiencia de pensamiento autónomo en resolver un problema. Alumna de 3 años
- Ángulo recto para construir un metro cuadrado en papel
- Alumnas de cuarto de primaria en la investigación y aprendizaje de capacidades y su expresión en lenguaje matemático
| CIENTÍFICAS EN SECUNDARIA |
- Antonia y Maite nos enseñan la aplicación de la maqueta en la semejanza de figuras
- Ángela y Cristina nos muestran la utilidad de la maqueta en el aprendizaje de la semejanza
- Alba y Ángela nos enseñan a discutir y resolver sistemas de ecuaciones con Descartes y herramientas tecnológicas
- Natalia y Celeste comunican y comparten ideas matemáticas con Descartes
- Carmen, divulga la simplificación de fracciones algebraicas y la suma de las mismas
- Rocío, divulga la resolución de una unidad liberada de PISA
- Virginia, María y Laura, divulgan una técnica de resolución de problemas
- María del Castillo e Irene, divulgan las operaciones con fracciones algebraicas
- María y Claudia entrevistan a Sofía Kovalévskaya, con su matrimonio de conveniencia para poder estudiar matemáticas.
- Mireia y María entrevistan y divulgan la obra de Sophie Germain, la primera mujer en acceder a la Academia de Ciencias de París.
- Antonia y Maite entrevistan y divulgan la vida y obra de Ada Lovelace, con su reflexión sobre la mujer en la ciencia y el techo de cristal.
- Clara, Ángela y Cristina, entrevistan y divulgan la vida y obra de Mary Cartwright, a quien conocí gracias a mis alumnas.
- María y Julia, entrevistan y divulgan la vida y obra de Mary Somerville, conocida como "La Reina de las ciencias del siglo XIX".
- Ángela y Alejandro, entrevistan y divulgan la vida y obra de Euclides
| CIENTÍFICAS EN BACHILLERATO |
- María, divulga la resolución de triángulos rectángulos
- Claudia y María, divulgan la simplificación de expresiones trigonométricas de cociente
- Margarita y María, divulgan la simplificación de expresiones trigonométricas de cociente
- Ángela y Alba, ponen a prueba tus conocimientos de Matemáticas-1
- Laura y Ángela, ponen a prueba tus conocimientos de Matemáticas-1
- Zuleima y Raquel, ponen a prueba tus conocimientos de Matemáticas-1
- Ana y Virginia, ponen a prueba tus conocimientos de Matemáticas-1
- María y Alba, ponen a prueba tus conocimientos de Matemáticas-1
- Lucía e Ismael, ponen a prueba tus conocimientos de Matemáticas-1
- Ángela y Laura y ponen a prueba tus conocimientos de Matemáticas-2
- Joana y Ana ponen a prueba tus conocimientos de Matemáticas-2
- Aurora, Alba, Ángela y Teresa recrean la importancia de la seguridad al desarrollar experiencias en el laboratorio
- Carmen, Joana, Beatriz y Ángela muestran, de forma desenfada, las normas en el laboratorio de Química.
| CIENTÍFICAS EN LA UNIVERSIDAD |
- Sofía, Marcos y Juan Luis nos enseñan a calcular el volumen de un cono por integrales triples.
- Daniela, Beatriz y Jonathan nos muestran algunas aplicaciones de las coordenadas esféricas.
- Tania y Samuel nos enseñan a cambiar de coordenadas cartesianas a polares y cilíndricas.
- Lucía y Alicia nos presentan el cálculo de áreas de figuras planas utilizando integrales dobles.
- Daniela, Beatriz y Jonathan calculan el aforo de un recinto para conciertos.
- Lucía y Alicia nos explican cómo calcular el volumen del Atomium de Bruselas.
- Almudena y Clara nos enseñan a calcular el gradiente de un campo escalar y el uso correcto del operador nabla.
- Clara y Almudena nos muestran el rotacional y la divergencia de un campo vectorial.
- Tania y Samuel nos presentan la resolución de ecuaciones diferenciales con variables separables.
- Andrea y Andrés nos enseñan la función delta de Dirac, sus propiedades y algunas aplicaciones.
| JUEGO DIDÁCTICO SOBRE GRANDES CIENTÍFICAS |
El juego es una de las estrategias didácticas de gran valor que motiva a nuestro alumnado y que se potencia con las tecnologías de la información y la comunicación. Así que os dejamos el que ha creado nuestro compañero Jesús M. Muñoz Calle, del proyecto Aplicación de Juegos Didácticos en el Aula, para difundir algunos de los decubrimientos y avances científicos gracias a la mujer, con algunas capturas de pantalla por si fueran necesarias.


Los recursos multimedia de esta propuesta de actividades para celebrar el Día Internacional de la Mujer y la Niña en la Ciencia, han sido seleccionados de los siguientes proyectos liderados por miembros de RED Descartes:
- El personaje misterioso, un programa de Radio Descartes.
- Procesos metodológicos y estrategias didácticas de éxito en Infantil y Primaria.
- Modelos didácticos para Primaria.
- Desarrollo de la comunicación audiovisual a través de las matemáticas con Descartes
- La radio ficción en el aula de matemáticas.
- El alumnado como generador de contenido multimedia con Descartes JS.
- Matemáticas a un clic. Aprendizaje móvil a través de microcontenidos.
- Aplicación de Juegos Didácticos en el Aula.
Título: Juego memoriza vídeos de YouTube
Sección: Plantillas
Bloque: Herramientas de edición
Unidad: Juegos
Idioma: Castellano
Autor: Juan Guillermo Rivera Berrío
![]() Haz clic aquí para ver las instrucciones
Haz clic aquí para ver las instrucciones
![]() Haz clic en la imagen para abrir una muestra de este recurso
Haz clic en la imagen para abrir una muestra de este recurso
Puedes encontrar todas las plantillas en
https://proyectodescartes.org/plantillas/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Con motivo de la Jornada 50yTICo, celebrada en septiembre en el hiperaula de la Facultad de Educación de la Universidad Complutense de Madrid, y que difundimos desde nuestro portal con "Una crónica de la Jornada 50yTICo", se generó un importante movimiento de información desde el claustro virtual en Twitter con el hashtag #50yTICo, y tuve la ocasión de acceder al artículo titulado "Sobre TIC, Web 2.0 y cultura digital en educación" publicado en 2017 por José Luis Cabello, a quien tengo la fortuna de conocer personalmente y aprovecho para enviar un cordial saludo. Pues bien, este artículo me ha motivado para reflexionar y compartir experiencias sobre la creación de contenidos por parte del alumnado, uno de los aspectos adecuados para el desarrollo de su competencia digital, y todo ello integrado desde la materia de mi especialidad. Aunque quizás no dispongamos de un plan específico de integración de la competencia digital en matemáticas, entre los contenidos del bloque uno, denominado "Procesos, métodos y actitudes en Matemáticas", tanto en la ESO como el Bachillerato, se contempla la utilización de medios tecnológicos en el proceso de aprendizaje para la elaboración de informes y documentos sobre los procesos llevados a cabo y los resultados y conclusiones obtenidos. A su vez, en los criterios de evaluación para este bloque aparece utilizar las tecnologías de la información y la comunicación de modo habitual en el proceso de aprendizaje, buscando, analizando y seleccionando información relevante en Internet o en otras fuentes, elaborando documentos propios, haciendo exposiciones y argumentaciones de los mismos y compartiendo éstos en entornos apropiados para facilitar la interacción. Pero más específicos aún son los estándares de aprendizaje evaluables, donde se recoge:
- 12.1. Elabora documentos digitales propios (texto, presentación, imagen, video, sonido,…), como resultado del proceso de búsqueda, análisis y selección de información relevante, con la herramienta tecnológica adecuada, y los comparte para su discusión o difusión.
Ahora bien, ¿cómo idear estrategias didácticas y diseñar actividades de aula para aplicar estos criterios de evaluación junto a sus correspondientes estándares de aprendizaje? Peor aún, ¿cómo hacerlo en el aula de un centro que no dispone de equipamiento? Parece ser que a la primera pregunta debemos responder con creatividad e imaginación docentes y compartiendo y divulgando experiencias. Sin embargo, para la segunda se propone en el artículo mencionado el denominado BYOD, que se refiere a Bring Your Own Device, es decir, que cada alumno o alumna traiga su propio dispositivo al aula, lo que viene a ser el Programa Escuela 2.0 pero con las familias encargadas de sufragar los dispositivos. Así que todo ello viene a ratificar mis manifestaciones en algún que otro tuit cuando difundo el lema de que "No existe otro camino que el de la Escuela 2.0".
Pero no creas que aquí terminan todos los obstáculos para cumplir con lo que se te exige como docente, porque todavía puede ocurrir que tu centro, en el ámbito de su autonomía, decida prohibir el uso de dispositivos móviles amparándose en que uno o dos alumnos han hecho un mal uso de los mismos. Por cierto, al momento de redactar este artículo, cierta comunidad autónoma anuncia que "impedirá de forma explícita la utilización de teléfonos y otros dispositivos electrónicos en los periodos lectivos, «salvo en aquellos casos que esté expresamente previsto en el proyecto educativo y siempre con fines didácticos»". Me pregunto si se llegarán a prohibir algún día el uso del compás, la tijera o el cúter en el aula por tratarse de armas blancas.
Recomiendo la difusión del "Decálogo del buen uso de la tecnología móvil en el aula", elaborado por el grupo de trabajo sobre el buen uso de los dispositivos móviles en el aula, en el marco de la Jornada 50yTICo.
Para finalizar esta pequeña reflexión, ¿cómo podemos desarrollar las competencias clave sin equipamiento de aula y sin BYOD?
Comparto aquí una propuesta basada en varios proyectos que vengo desarrollando desde hace algunos años, que son perfectamente extrapolables a otras materias y especialidades, donde el alumnado utiliza sus propios dispositivos móviles fuera del aula.
| DESARROLLO DE LA COMUNICACIÓN AUDIOVISUAL |
Se trata de un proyecto que llevo a cabo con el alumnado de 4º ESO y cuyos orígenes se encuentran en el artículo del mimo nombre, es decir, "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes", habiendo publicado hasta el momento varias producciones con distinta temática en cada edición, así tenemos "Matemáticas para todos con Descartes", dedicado a fracciones algebraicas, "Los alumnos pueden aprender divirtiéndose y generando contenido inédito", dedicado a ecuaciones y sistemas lineales, "Aprendemos a resolver problemas con Descartes y Wiris", dedicado a la búsqueda de un modelo matemático para la resolución de un problema o el compartido en este artículo, dedicado a la maqueta como instrumento para entender la semejanza de figuras.
| LA RADIO FICCIÓN EN EL AULA |
Se trata de un proyecto que llevo a cabo con el alumnado de 3º ESO y cuyos orígenes se encuentran en el artículo del mimo nombre, es decir, "La radio ficción en el aula de Matemáticas", habiendo publicado hasta el momento varias producciones como "Sophie Germain: la primera mujer en acceder a la Academia de Ciencias de París", "Ada Lovelace, la mujer en la ciencia y el techo de cristal", "Évariste Galois visto e interpretado por alumnos de 3º ESO", "Alumnas de 3º ESO entrevistan a Mary Somerville" o la entrevista a Leonardo de Pisa, conocido como Fibonacci, compartida en este artículo.
| EL ALUMNADO COMO GENERADOR DE CONTENIDO CON DESCARTES JS |
Se trata de un proyecto que llevo a cabo con el alumnado de 1º Bachillerato y cuyos orígenes se encuentran en el artículo del mimo nombre, es decir, "El alumnado como generador de contenido multimedia con Descartes JS", que cuenta con otra experiencia de año distinto titulada "¿Sabes que tu alumnado puede generar fácilmente contenido multimedia con Descartes JS?" y que ampliamos en este artículo con producciones del curso 2018/2019.
Autoevaluación - 9, generada por el equipo Émilie du Châtelet
Autoevaluación - 10, generada por el equipo Sofia Kovalévskaya
Autoevaluación - 11, generada por el equipo Carl Friedrich Gauss
Quiero felicitar a todos mis alumnos y alumnas que, año tras año, son capaces de superar los retos que les planteo, con su creatividad e imaginación, utilizando sus propias herramientas tecnológicas en sus domicilios y sin la intervención del profesor, mostrando sus capacidades ocultas y demostrando que son plenamente competentes para trabajar de forma colaborativa y en la distancia. Asimismo, mi gratitud a sus familias por autorizar la publicación y difusión de estas producciones digitales, conscientes de que repercuten notablemente en la formación de sus hijos e hijas.
La maqueta como estrategia en el aprendizaje de la semejanza de figuras es una iniciativa del Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija, realizada con el alumnado de 4º ESO durante el curso escolar 2018/2019 desde la materia de Matemáticas Orientadas a las Enseñanzas Académicas, basada en la experiencia para el "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes", con objeto de fomentar en nuestros alumnos y alumnas el aprendizaje de las técnicas necesarias del lenguaje cinematográfico y audiovisual, a la vez que proporcionarles una formación básica que les permita, de forma autónoma, generar y producir sus propios contenidos audiovisuales o multimedia en esta materia, a la vez que compartir y comunicar los mismos en entornos apropiados.
Durante el primer trimestre habíamos trabajado en el aula los aspectos correspondientes a la semejanza de figuras usando la unidad interactiva del mismo nombre, es decir, "Semejanzas", con su cuaderno de trabajo asociado y, como colofón, procedimos a la construcción de la maqueta y a poner en práctica todo lo aprendido para garantizar su consolidación. Además, es aconsejable el uso de materiales manipulativos para que el alumnado aprenda haciendo, construyendo y “tocando las matemáticas”.Pues bien, una vez construida la maqueta y determinada la escala, se aplican los conceptos de semejanza para obtener, al menos, el ángulo de inclinación, el área de la base y el volumen de la torre real, situada en Plaza de Castilla de la capital.


Quiero felicitar públicamente a Maite y Antonia, Antonia y Maite que, constituídas en el equipo Ada Lovelace, a quien entrevistaron el curso pasado dentro del proyecto "La radio ficción en el aula de matemáticas", han conseguido un producto final de calidad, demostrando con la incorporación de las tomas falsas la compatibilidad entre aprendizaje y diversión en esta etapa final de la ESO.
Muchas gracias también a sus familias por apoyar la iniciativa autorizando las grabaciones y su difusión por las redes sociales, lo que obviamente repercute en una mejora de la formación de sus hijos e hijas como ciudadanos y ciudadanas del s. XXI y en su preparación para la siguiente etapa educativa.
He reservado el mes de carnaval por antonomasia para compartir otra experiencia de aula realizada con mi alumnado de 4º de Educación Secundaria Obligatoria del IES Bajo Guadalquivir de Lebrija, en la materia Matemáticas Orientadas a las Enseñanzas Académicas, durante el curso escolar 2017/2018, dando continuidad al proyecto "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes", que puse en marcha hace ya cuatro años con el alumnado de 1º de Bachillerato, unos vanguardistas que inspiraron a sus sucesores. En el artículo enlazado pueden encontrarse los orígenes, objetivos, fundamentación de este proyecto, referencia normativa y los detalles con las distintas fases que deben ir superando los alumnos y alumnas, de forma completamente autónoma, con trabajo colaborativo y sin la intervención del profesor.
Cada año procuro elegir una temática diferente, correspondiendo esta edición a la discusión y resolución de sistemas de ecuaciones lineales, habiendo publicado anteriormente los artículos "Desarrollamos nuestra comunicación audiovisual y nos convertimos en divulgadoras matemáticas", "¿Son incompatibles el aprendizaje y la diversión en el segundo ciclo de la ESO?" y "Alumnas comunicando y compartiendo ideas matemáticas con Descartes".
A pesar del tiempo transcurrido y del número de alumnos y alumnas participantes en la experiencia, no dejan de sorprenderme con su creatividad e imaginación, pues todos los vídeos son completamente diferentes, así como la diversidad en el uso de editores de vídeo y sus estrategias de dirección y realización para desarrollar su comunicación audiovisual a través de las matemáticas, contenidos incorporados en el bloque de “Procesos, métodos y actitudes en Matemáticas”, que debe desarrollarse de modo transversal y simultáneamente al resto de bloques, constituyendo el hilo conductor de la asignatura. Un bloque que se articula sobre procesos básicos e imprescindibles en el quehacer matemático: la resolución de problemas, proyectos de investigación matemática, la matematización y modelización, las actitudes adecuadas para desarrollar el trabajo científico y la utilización de medios tecnológicos, proporcionando, además, una formación competencial.
La organización y planificación de la experiencia se coordina desde el aula virtual Moodle de RED Descartes, que dispone de acceso a invitados. Además, los ejemplos que aparecen en el vídeo han sido seleccionados de la unidad interactiva dedicada a "Ecuaciones y sistemas" de Proyecto Descartes.
Quiero felicitar públicamente a Fernando y José Antonio, José Antonio y Fernando que, constituídos en el equipo Augustin Louis Cauchy, en homenaje a este prolífico matemático francés, han conseguido un producto final de calidad con el que nos enseñan a discutir y resolver sistemas 2x2 por los métodos algebraicos conocidos y usando herramientas tecnológicas. Pero además, con su creatividad, imaginación, humor y dominio de la edición de vídeo, abren un nuevo horizonte al proyecto con la posibilidad de la caracterización en personajes matemáticos.
Mi agradecimiento, como es habitual, a sus familias por autorizar la difusión de este audiovisual en portales educativos y redes sociales.
Primera píldora invernal para compartir otra experiencia de aula realizada con mi alumnado de 4º de Educación Secundaria Obligatoria del IES Bajo Guadalquivir de Lebrija, en la materia Matemáticas Orientadas a las Enseñanzas Académicas, durante el curso escolar 2017/2018, dando continuidad al proyecto "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes", que puse en marcha hace ya cuatro años con el alumnado de 1º de Bachillerato, unos vanguardistas que inspiraron a sus sucesores. En el artículo enlazado pueden encontrarse los orígenes, objetivos, fundamentación de este proyecto, referencia normativa y los detalles con las distintas fases que deben ir superando los alumnos y alumnas, de forma completamente autónoma, con trabajo colaborativo y sin la intervención del profesor.
Cada año procuro elegir una temática diferente, correspondiendo esta edición a la discusión y resolución de sistemas de ecuaciones lineales, habiendo publicado anteriormente los artículos "Desarrollamos nuestra comunicación audiovisual y nos convertimos en divulgadoras matemáticas" y "¿Son incompatibles el aprendizaje y la diversión en el segundo ciclo de la ESO?".
A pesar del tiempo transcurrido y del número de alumnos y alumnas participantes en la experiencia, no dejan de sorprenderme con su creatividad e imaginación, pues todos los vídeos son completamente diferentes, así como la diversidad en el uso de editores de vídeo y sus estrategias de dirección y realización para desarrollar su comunicación audiovisual a través de las matemáticas, contenidos incorporados en el bloque de “Procesos, métodos y actitudes en Matemáticas”, que debe desarrollarse de modo transversal y simultáneamente al resto de bloques, constituyendo el hilo conductor de la asignatura. Un bloque que se articula sobre procesos básicos e imprescindibles en el quehacer matemático: la resolución de problemas, proyectos de investigación matemática, la matematización y modelización, las actitudes adecuadas para desarrollar el trabajo científico y la utilización de medios tecnológicos, proporcionando, además, una formación competencial.
La organización y planificación de la experiencia se coordina desde el aula virtual Moodle de RED Descartes, que dispone de acceso a invitados.
Quiero felicitar públicamente a Natalia y Celeste, Celeste y Natalia que, constituídas en el equipo María Gaetana Agnesi, en homenaje a esta gran matemática italiana, han conseguido un producto final de calidad con el que nos enseñan a discutir y resolver sistemas 2x2 por los métodos algebraicos conocidos y usando herramientas tecnológicas. Por cierto, en el momento de redactar este artículo, Natalia y Celeste se encuentran ya cursando el primer curso de bachillerato en la modalidad de ciencias sociales.
Mi agradecimiento, como es habitual, a sus familias por autorizar la difusión de este audiovisual en portales educativos y redes sociales.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)













 CONTACTO
CONTACTO
