Mostrando artículos por etiqueta: lugar geométrico
Título: Puntos en movimiento I
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Todos los niveles/Todas las edades
Idioma: Castellano
Autoría: Rita Jiménez Igea
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Misceláneas. Lugares geométricos. Cuadraturas V. La cuadratura del círculo II.
Son varios los grandes matemáticos que han conseguido, por uno u otro camino, la cuadratura del círculo. Hemos analizado, en este blog, algunas de las formas en que dicha cuadratura se ha logrado, fundamentalmente las relacionadas con lugares geométricos que de una u otra manera consiguen determinar un segmento relacionado con el número π.
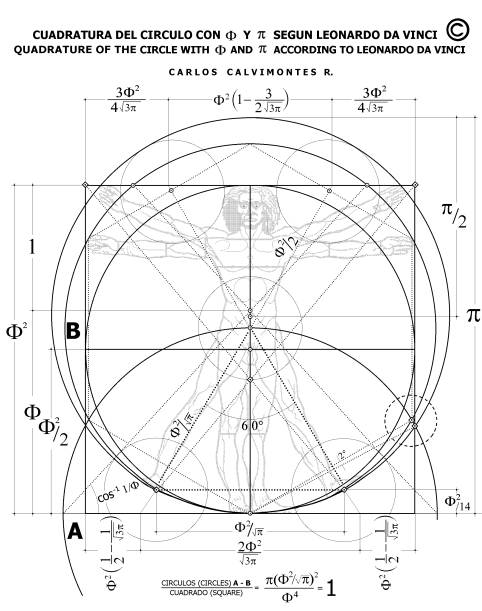
Dentro de la particularidad que nos ocupa: la cuadratura del círculo, también hemos podido apreciar el indudable valor de algunos de los procedimientos mecánicos (técnicos) que diferentes artistas, arquitectos y científicos interesados en el tema han elaborado. En este sentido enlazamos a continuación con el interesante trabajo del profesor Carlos Calvimontes Rojas sobre la cuadratura del círculo donde muestra una selecta documentación relacionada con el tema y basada en la desarrollada por Leonardo Da Vinci y Vitrubio, con la verificación de la aportación gráfica de la misma con el programa de diseño arquitectónico Autocad.
Recomendamos la lectura completa del documento así como el análisis de su bibliografía.
Volvemos a enlazar con el blog de Miguel Ángel Morales Medina, en esta ocasión lo hacemos al artículo sobre la cuadratriz.
A continuación exponemos varias escenas interactivas elaboradas con DescartesJS y el programa GeoGebra que muestran la cuadratura del círculo utilizando los lugares geométricos aportados por Hípias (Dinostrato) y Arquímedes.
- Cuadratura del círculo I: Con la ayuda de la animación y siguiendo las instrucciones encontramos la media proporcional que depende de π y de r y que nos permite hallar el cuadrado con el mismo área que el círculo dado.
Escena desarrollada con DescartesJS. - Cuadratura del círculo II: La siguiente escena, creada también con el editor DescartesJS muestra la generación de la espiral de Arquímedes y la determinación de un segmento de longitud (raíz cuadrada de π) · r con dicha espiral.
A continuación exponemos las mismas escenas anteriores pero en esta ocasión elaboradas con el programa GeoGebra. Las escenas son especialmente sencillas por si se desean tomar como referencia para ampliar con contenido propio.
En primer lugar se muestra la cuadratura del círculo con la cuadratriz de Dinostrato y a continuación la cuadratura del círculo con la espiral de Arquímedes.
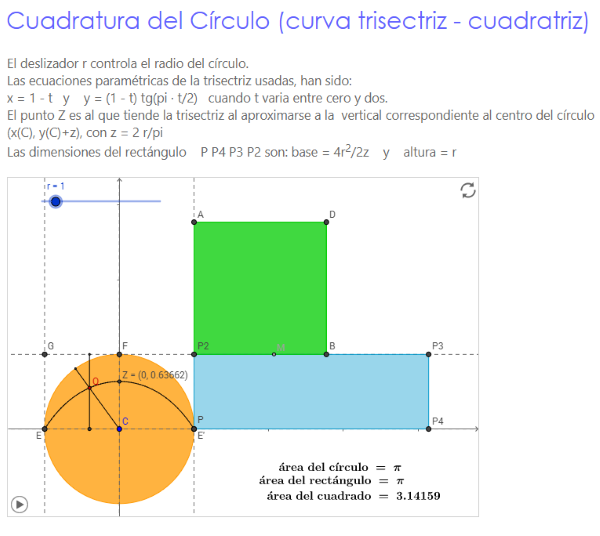
cuadratura del círculo (Dinostrato)
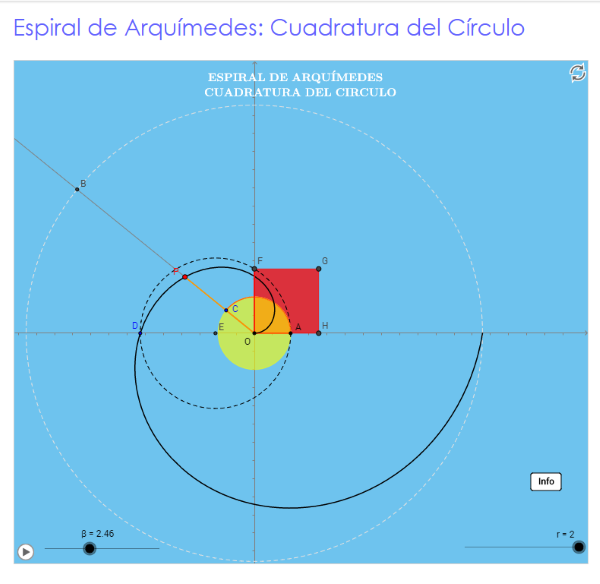
cuadratura del círculo (Arquímedes)
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra la deducción, paso a paso, de la generación del lugar geométrico Trisectriz - Cuadratriz de Hípias - Dinostrato.
Continuando con la creación de la miscelánea "Las Espirales" sugerimos completar su elaboración extrayendo el contenido relacionado con las cuadraturas estudiadas para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos. Cuadraturas"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La cuadratura del círculo: Historia de una obsesión.
XIV Programa de Promoción de la Cultura Científica y Tecnológica.
Rev. Real Acad. Ci. Exact. Fis. Nat. (Esp) Vol. 105, Nº 2 (2012), 241-258
Fernando Bombal - Cuadraturas
Prof. Esteban Rubén Hurtado Cruz. Facultad de Ciencias UNAM. Cálculo Diferencial e Integral II - Páginas en GeoGebra de Vicente Martín Torres López
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2018
Misceláneas. Lugares geométricos. Cuadraturas V. La cuadratura del círculo.
Como prólogo a un breve estudio sobre la cuadratura del círculo, hemos analizado la manera de cuadrar algunos polígonos y hecho una breve reflexión sobre los teselados. En particular se ha visto, entre otros asuntos, el método general de cuadrar los polígonos regulares y referente a las teselaciones se ha mostrado, entre otras, la manera de teselar un triángulo cordobés con una sucesión de triángulos cordobeses.
Dentro del tema que nos ocupa: los Lugares geométricos también, en su día, estudiamos las Trisectrices de Hipias y Nicomedes y en otros artículos se han expuesto misceláneas y escenas que desarrollan la espiral de Arquímedes y la cuadratriz de Dinostrato; no obstante en la presente entrada volvemos a insistir en el estudio de las primeras curvas mecánicas o lugares geométricos creados por estos autores por su evidente interés y para animar a la conversión en misceláneas de las escenas que aún no lo son.
Anteriormente hemos enlazado el extraordinario trabajo del profesor Fernando Bombal sobre la cuadratura del círculo, volvemos a hacerlo y en el leemos:
Recomendamos la lectura completa del documento así como el análisis de su extensa bibliografía.
También en entradas anteriores hemos enlazado con el blog de Miguel Ángel Morales Medina, en esta ocasión lo hacemos al básico pero minucioso artículo sobre la cuadratura del círculo: ¿Quién dijo que la cuadratura del círculo era imposible?.
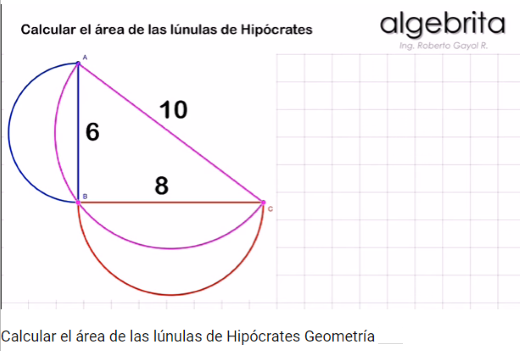
A continuación y también como prolegómeno al estudio de la cuadratura del círculo enlazamos con dos pequeños trabajos sobre la cuadratura de las lúnulas: el primero de ellos creado con DescartesJS y el segundo con el programa GeoGebra.
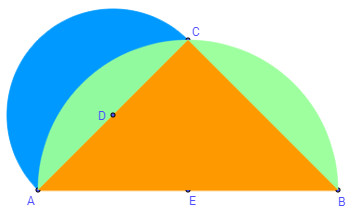
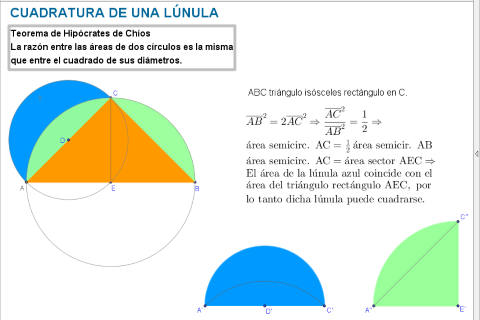
- Cuadratura de una lúnula I: Con la ayuda de dos semicírculos creamos una lúnula y aplicando el teorema de Hipócrates de Chios encontramos, según se muestra en la siguiente escena interactiva, un triángulo de igual área que dicha lúnula. Cuadrando el triángulo obtenemos la cuadratura de la lúnula.
Escena desarrollada con DescartesJS.
- Cuadratura de una lúnula II: actuando de forma análoga a como hemos hecho en la escena anterior obtenemos la cuadratura de una lúnula con el programa GeoGebra
Las escenas que se exponen a continuación son recreaciones de otras ya expuestas en este blog y tienen como objetivo refrescar la memoria sobre las curvas mecánicas mencionadas anteriormente.
Todos los trabajos dejan, para quien tenga interés en el tema, una buena cantidad de opciones de ampliación y mejora.
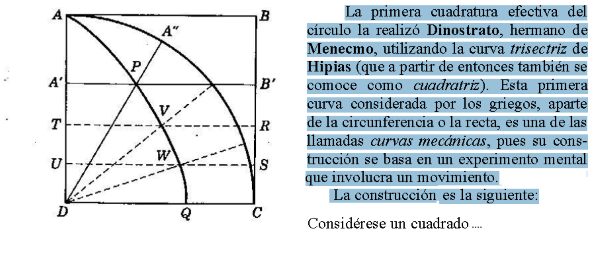
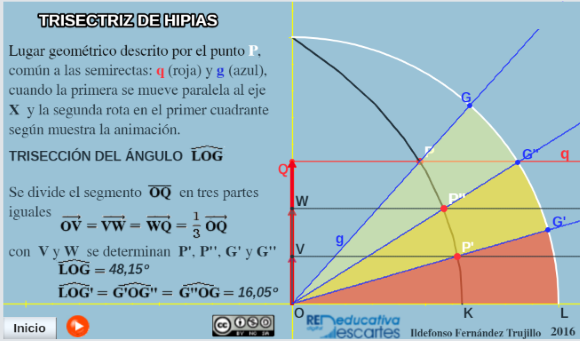
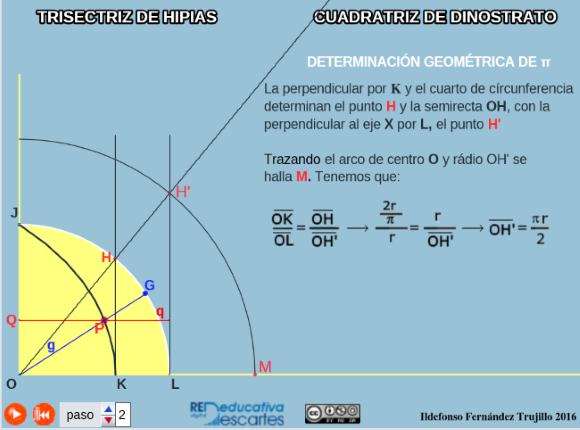
La trisectriz de Hípias
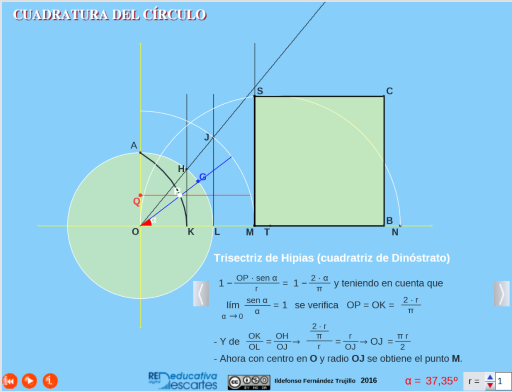
La trisectriz - cuadratriz de Hípias - Dinostrato
En la siguiente escena se determina un segmento relacionado directamente con el número π utilizando la trisectriz - cuadratriz de Hípias - Dinostrato
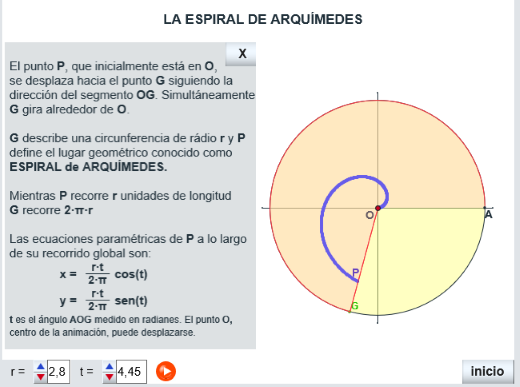
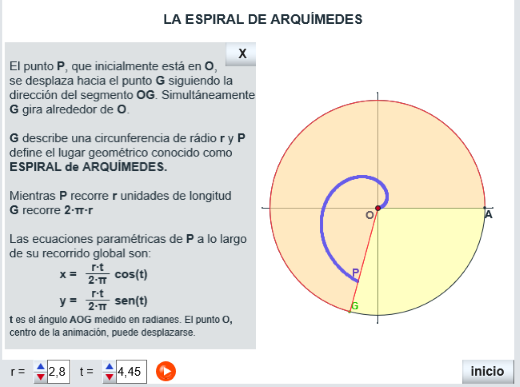
Las siguientes utilidades muestran: la primera, además de las ecuaciones paramétricas de la espiral, la manera como se genera el lugar geométrico conocido como espiral de Arquímedes y la otra la determinación de un segmento de longitud raiz cuadrada de π, en esta ocasión mediante la mencionada espiral de Arquímedes y la ecuación cartesiana de dicho lugar geométrico.
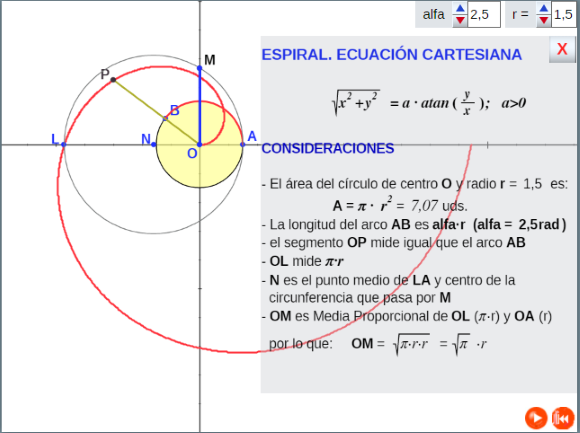
deducción de raiz de π con la espiral de Arquímedes
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra la deducción, paso a paso, del área de las lúnulas de Hipócrates.
,Continuando con la creación de la miscelánea "Las Espirales" sugerimos completar su elaboración extrayendo el contenido relacionado con las cuadraturas estudiadas para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos. Cuadraturas"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La cuadratura del círculo: Historia de una obsesión.
XIV Programa de Promoción de la Cultura Científica y Tecnológica.
Rev. Real Acad. Ci. Exact. Fis. Nat. (Esp) Vol. 105, Nº 2 (2012), 241-258
Fernando Bombal - Cuadraturas
Prof. Esteban Rubén Hurtado Cruz. Facultad de Ciencias UNAM. Cálculo Diferencial e Integral II - Páginas en GeoGebra de Vicente Martín Torres López
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
CUADRATURAS IV.
La cantidad de patrones de teselado, por lo tanto la cantidad de teselados, es infinita e inagotable. También lo es la cantidad de no teselados. Los alarifes que hicieron posible la habitación de retiro de la reina y sus alrededores, en la alhambra de Granada, hicieron realmente, poesía geométrica viva, dinámica, sensorial, placentera, evocativa…
Hacemos hincapié en el estudio de los patrones más elementales del grupo de los básicos con objeto de analizar como una sutil variación en la forma o el color produce efectos anímicos y visuales muy diferentes y así facilitar el proceso de análisis y creación de las teselaciones más complejas.
Además de nuevos enlaces volvemos a mostrar, por su interés, algunos de los ya expuestos en entradas anteriores:
Para quien considere necesaria una inmersión en los conceptos básicos relacionados con las teselaciones hemos preparado los siguientes contenidos:
La imagen anterior enlaza con una unidad que, en su día, desarrolló el profesor Ángel Aguirre Pérez y que he comenzado a adaptar a DescartesJS debido a que sus objetivos son similares a los que nos proponemos en este artículo y por tanto nos introduce en el tema de la forma clásica y básica.
Consideramos, por tanto, que el estudio se centra en el problema clásico de la cuadratura del círculo y que nos acercamos a él haciendo, primero, la cuadratura de algunos polígonos regulares y no regulares. No debe olvidarse la idea de círculo como límite, cuando el número de lados tiende a infinito, de los polígonos regulares.
Dentro del amplio grupo de trabajos relacionados con el tema destacamos, además de los que se muestran en la bibliografía, los que se enlazan a continuación.
- teselado del plano y del espacio
Wikipedia - "Teselas de Escher y otras consideraciones sobre las teselaciones y movimientos en el plano.
Autora: María José Sánchez Quevedo. - Matemáticas mágicas, ingeniosas y... muy serias.
Autora: Therese Eveilleau. - Amplio estudio del plano.
Blog. Vaios Autores - Estudio de los frisos, cenefas y celosías.
Autora: Ángela Núñez Castaín
Tomando como base, fundamentalmente, la documentación anterior hemos elaborado, con DescartesJS, las escenas que se exponen a continuación. Queremos notar que en dichos trabajos se hace uso de gran parte de los conceptos elementales de Geometría del Currículo para ESO y Bachillerato.
Todos los trabajos dejan, para quien tenga interés en el tema, una buena cantidad de opciones de ampliación y mejora.
A poco que se observen los trabjos de teselción expuestos o enlazados se evidencia que en cada uno de ellos se reproduce un patrón. Existe un amplio grupo de patrones y entre los más elementales están los conocidos como 'tipo mitad del cuadrado' que son los que se obtienen descomponiendo el cuadrado en dos o más partes diferenciadas, en nuestro caso, por el color, de manera que ambas formas tengan igual área. A continuación se exponen varios ejemplos de estos patrones que aclaran el concepto.
- Estudio de los patrones y sus teselaciones correspondientes tipo "mitad del cuadrado".
Mitad del cuadrado I. - Mitad del cuadrado II.
- Mitad del cuadrado III.
Este patrón ya ha sido expuesto en entradas anteriores, en la actual enlazamos con un ejemplo de las teselaciones a que da lugar. - Mitad del cuadrado IV.
- Mitad del cuadrado V.
A continuación exponemos los trabajos que desarrollan la cuadratura del pentágono regular, tanto con DescartesJS como con GeoGebra.
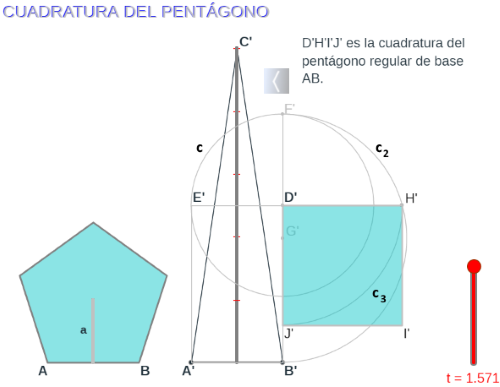
- Cuadratura de un pentágono regular de lado AB. La miscelánea Pentágono regular: Cuadratura. Método clásico detalla más explícitamente la misma escena.
Recordamos que:
- La circunferencia c tiene de centro el punto D' y radio A'B'.
- El arco c2 tiene de centro el punto G' (punto medio de B'F') y radio G'B'.
- El arco c3 tiene de centro el punto D' y radio D'H'.
- La misma cuadratura realizada con el programa GeoGebra
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra la creación, paso a paso, de una tesela reutilizando un "cede (CD)".

Interesante manualidad sobre teselación.
Continuando con la creación de la miscelánea "Las Espirales" sugerimos completar su elaboración extrayendo el contenido relacionado con las cuadraturas estudiadss para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos. Cuadraturas"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
Una forma lúdica de teselar es resolver un rompecabezas, esto es un ejercicio para ejercitar la memoria visual y otras habilidades por lo que proponemos, temporalmente, un amplio grupo de puzles para su resolución, uso y disfrute.

Juegos para entrenar la memoria visual.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La cuadratura del círculo: Historia de una obsesión.
XIV Programa de Promoción de la Cultura Científica y Tecnológica.
Rev. Real Acad. Ci. Exact. Fis. Nat. (Esp) Vol. 105, Nº 2 (2012), 241-258
Fernando Bombal - Cuadraturas
Prof. Esteban Rubén Hurtado Cruz. Facultad de Ciencias UNAM. Cálculo Diferencial e Integral II - Páginas en GeoGebra de Vicente Martín Torres López
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
CUADRATURAS III.
Los problemas clásicos de la geometría griega son, por activa o por pasiva, fuente inagotable de inspiración. En esta ocasión el estudio de los lugares geométricos nos llevó a sus orígenes por ende a Hípias, Dinostrato, Arquímedes... e inevitablemente a la cuadratura dinámica del círculo, esto es, a la cuadratura de cualquier polígono regular; o no, con cualquier número de lados. Resultando que, aparentemente, en la base de este proceso está el cuadrado. Motivo por el cual decidimos estudiar este polígono. Ahora bien, al intentar analizar el cuadrado este, en sí mismo, parece desaparecer mostrando como en su interior subyacen infinidad de polígonos: triángulos, cuadrados, rectángulos, trapecios, rombos… y una infinidad de otras formas inexistentes, virtuales, cuya proyección a la realidad tangible proporcionan, probablemente, los objetos y formas más útiles, en todos los sentidos, para el ser humano. Puede comprobarse como el trazo de unas pocas líneas en un cuadrado y a continuación al realizar el teselado del plano con el mismo, aparecen, de manera dinámica, formas que son el resultado de la composición de una traslación y/o de un giro; u otros, y como la visión de conjunto, a veces un palíndromo geométrico bidimensional, sugiere formas, sensaciones y conceptos cambiantes. Este procedimiento constructivo es el que los siguientes enlaces y escenas interactivas pretenden analizar aún cuando sea basándonos en los conceptos teóricos básicos y en los efectos visuales elementales que intervienen en el proceso.
La imagen siguiente está vinculada a la miscelánea que recoge un resumen de las ideas visuales expuestas a lo largo de esta entrada.
Para quien considere necesaria una inmersión en los conceptos básicos relacionados con las teselaciones hemos preparado los siguientes contenidos:
La imagen anterior enlaza con una unidad que, en su día, desarrolló el profesor Ángel Aguirre Pérez y que he comenzado a adaptar a DescartesJS debido a que sus objetivos son similares a los que nos proponemos en este artículo y por tanto nos introduce en el tema de la forma clásica y básica.
Consideramos, por tanto, que el estudio se centra en el problema clásico de la cuadratura del círculo y que nos acercamos a él haciendo, primero, la cuadratura de algunos polígonos regulares y no regulares. No debe olvidarse la idea de círculo como límite, cuando el número de lados tiende a infinito, de los polígonos regulares.
Dentro del amplio grupo de trabajos relacionados con el tema destacamos, además de los que se muestran en la bibliografía, los que se enlazan a continuación.
- Rellenado mínimo del plano y del espacio
Autor:

cubo de colores (origen de la imagen) - "Teselas de Escher y otras consideraciones sobre las teselaciones y movimientos en el plano.
Autora: María José Sánchez Quevedo. - Matemáticas mágicas, ingeniosas y... muy serias.
Autora: Therese Eveilleau. - Amplio estudio del plano.
Blog. Varios Autores - Estudio de los frisos, cenefas y celosías.
Autora: Ángela Núñez Castaín
Tomando como base, fundamentalmente, la documentación anterior hemos elaborado, con DescartesJS, las escenas que se exponen a continuación. Queremos notar que en dichos trabajos se hace uso de gran parte de los conceptos elementales de Geometría del Currículo para ESO y Bachillerato.
Todos los trabajos dejan, para quien tenga interés en el tema, una buena cantidad de opciones de ampliación y mejora.
A poco que se observen los trabjos de teselación expuestos o enlazados se evidencia que en cada uno de ellos se reproduce un patrón. Existe un amplio grupo de patrones y entre los más elementales están los conocidos como 'tipo mitad del cuadrado' que son los que se obtienen descomponiendo el cuadrado en dos o más partes diferenciadas, en nuestro caso, por el color, de manera que ambas formas tengan igual área. A continuación se exponen varios ejemplos de estos patrones que aclaran el concepto.
- Estudio de los patrones y sus teselaciones correspondientes tipo "mitad del cuadrado".
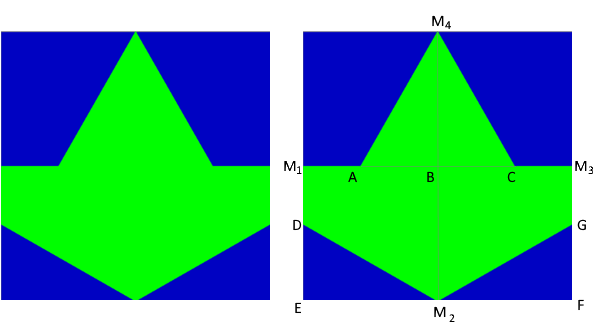
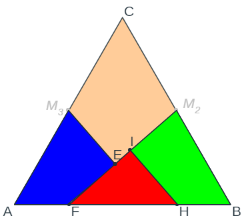
Mitad del cuadrado I.
El gráfico muestra que, por construcción, los triángulos ABM4, BCM4, DEM2 y M2FG son iguales por lo tanto el área de la parte azul es igual al área de la parte verde ya que los puntos: M1, M2, M3 y M4 son los puntos medios de los lados del cuadrado. - Mitad del cuadrado II.
- Mitad del cuadrado III.
- Mitad del cuadrado IV.
- Mitad del cuadrado V.
Debido a la extensión de la entrada las escenas que desarrollan la cuadratura del pentágono regular, tanto con DescartesJS como con GeoGebra, y otras relacionadas con el tema serán expuestas próximamente.
En esta ocasión, en la sección de vídeo, hemos elegido la tercera parte de la colección que muestra la deducción, paso a paso, de la cuadratura del círculo usando el número de oro.
Continuando con la creación de la miscelánea "Las Espirales" sugerimos completar su elaboración extrayendo el contenido relacionado con los lugares geométricos (cuadraturas) estudiados para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos. Cuadraturas."; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Una forma lúdica de teselar es resolver un rompecabezas, esto es un ejercicio para ejercitar la memoria visual y otras habilidades mentales por lo que proponemos, temporalmente, un amplio grupo de puzles para su resolución, uso y disfrute.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- La Mitad del cuadrado. De José Antonio Mora Sánchez: aproximación al estudio de las teselaciones.
- CUADRATURAS. De Ildefonso Fernández Trujillo: aproximación al estudio de las cuadraturas.
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La cuadratura del círculo: Historia de una obsesión.
XIV Programa de Promoción de la Cultura Científica y Tecnológica.
Rev. Real Acad. Ci. Exact. Fis. Nat. (Esp) Vol. 105, Nº 2 (2012), 241-258
Fernando Bombal - Cuadraturas
Prof. Esteban Rubén Hurtado Cruz. Facultad de Ciencias UNAM. Cálculo Diferencial e Integral II - Páginas en GeoGebra de Vicente Martín Torres López
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
CUADRATURAS II
Adentrarse en el estudio de los lugares geométricos, las cuadraturas, las teselaciones y las particiones de un polígono en otros más pequeños con la intención de teselar, en general el espacio plano, y en particular otros polígonos de diferente forma es estar, literalmente, predispuesto a perderse dentro de la espiral del tiempo en un ir y venir por las manifestaciones más sobresalientes de las diferentes culturas y épocas. Esta es la razón por la que en esta entrada vamos a continuar la aproximación al conocimiento genérico de los ll.gg. analizando algunos aspectos de las Cuadraturas, asuntos estos tan íntimamente ligados que, a veces, es difícil discernir cuál es la causa y cuál el efecto.
Recordamos que el estudio de las cuadraturas, los ll.gg. y la descomposición de un polígono en otros más pequeños que lo recubren completamente con objeto de, con ellos, recubrir otro polígono diferente, están ligados, también, al estudio de las teselaciones.
Aprovechamos la oportunidad para señalar el aspecto popular, lúdico, espiritual, económico, agrario y funcional que la Geometría clásica, la Cosmología, la Astronomía y en general el conocimiento ha tenido en las poblaciones cultas.
Consideramos, por tanto, que el estudio se centra en el problema clásico de la cuadratura del círculo y que nos vamos a aproximar a él haciendo, primero, la cuadratura de algunos polígonos regulares y no regulares. No debe olvidarse la idea de círculo como límite, cuando el número de lados tiende a infinito, de los polígonos regulares.
Dentro del amplio grupo de trabajos relacionados con el tema destacamos, además de los que se muestran en la bibliografía, los que se enlazan a continuación.
- Teselaciones
- Mosaico de Escher
Autor: Enrique Martínez Arcos. Adaptación a DescartesJS: Mª José García Cebrian. Publicado por: Ángel Cabezudo Bueno - Salamandra de Escher
Fernándo Pavez Peñaloza. - Descubierto un nuevo pentágono que tesela el plano
Tomando como base, fundamentalmente, la documentación anterior hemos elaborado, con DescartesJS, las escenas que se exponen a continuación. Queremos notar que en dichos trabajos se hace uso de gran parte de los conceptos elementales de Geometría del Currículo para ESO y Bachillerato.
Todos los trabajos dejan, para quien tenga interés en el tema, una buena cantidad de opciones de ampliación y mejora.
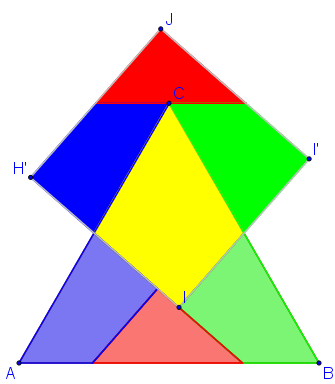
- Estudio de la Cuadratura y Teselación de un Triángulo Equilátero.
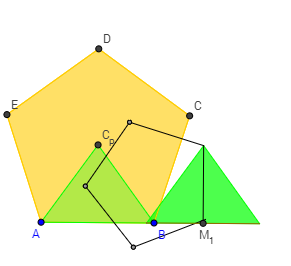
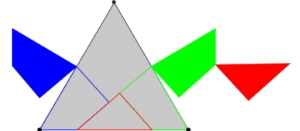
Supongamos que el triángulo equilátero ABC (ver la siguiente figura), se descompone en los polígonos: AFEM3, FHI, IHBM2 y EM2CM3.
Con los polígonos anteriores podemos formar muchas figuras, además del triángulo equilátero ABC, según coloquemos los polígonos en el plano. Una de las maneras de situar los polígonos es la que muestra la escena que enlaza la imagen anterior. En dicha escena: activando el botón anima o pulsando en el control alfa se observa como se recolocan los polígonos para formar el rectángulo EE2E3E4, visible cuando alfa = 3.14, que evidentemente es un cuadrado con el mismo área que el triángulo equilátero ABC.
Con la misma intención y con objeto de practicar con las animaciones y diferentes formas de lograr un objetivo se ha creado la escena que enlaza la imagen siguiente.
Analizadas las dos escenas anteriores, conviene pulsar el botón ver aux. o aux, vamos a elaborar una nueva escena para obtener infinitas teselaciones del triángulo equilátero ABC y con dichas teselaciones recubrir un rectángulo y/o un cuadrado.
En esencia la escena es la misma que las anteriores pero simplificada en extremo. Hemos procedido de la siguiente manera:
- dibujamos el triángulo equilátero ABC: A(0,0), B(6,0) y C(3, 6·sen(60º)).
- particionamos el lado horizontal de la siguiente forma:
- segmento AD controlado por el pulsador t
- segmento DE de longitud igual a la mitad del lado AB
- segmento EB tal que AD+EB=DE
- situamos los puntos medios de los lados AC y BC, M3 y M2.
- unimos, mediante una recta, uno de esos puntos medios con el punto más alejado de él entre D y E
- desde el otro punto medio y desde el punto intermedio de la partición que no se ha usado se trazan segmentos perpendiculares a la recta anterior.
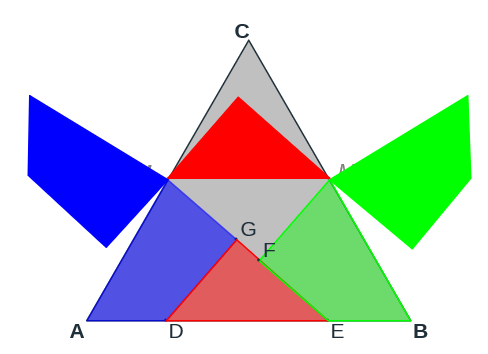
- así se obtienen (por ejemplo) los polígonos: ADGM3, DEG, FEBM2 y FM2CM3 que teselan al triángulo. (ver escena enlazada con la imagen anterior)
- en la escena mencionada al pulsar el botón anima o llevar el pulsador ang a 3.14, se construye el rectángulo FF2F3F4 de igual área que el triángulo ABC y que cuando t vale 0.97 es un cuadrado.
- por lo tanto para cada valor de t tenemos una teselación diferente y para ciertos valores, además, la cuadratura.
- debe indicarse que la construcción está aproximada a las centésimas y que para cualquier otro grado de precisión habría que reajustar los valores.
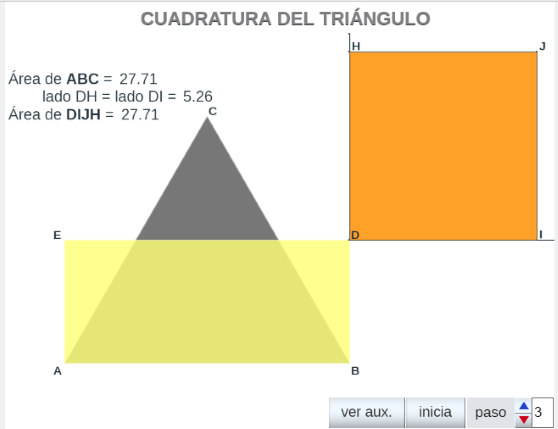
- Cuadratura estándar de un triángulo. El método estándar de cuadrar un triángulo consiste en hallar el rectángulo con la misma área que él y a continuación cuadrar dicho rectángulo como muestra la escena que enlaza la siguiente imagen.
Construcción de la escena:
- paso 0
- Representamos el triángulo, en esta ocasión equilátero, ABC y los puntos médios de los lados: AC y BC.
- paso 1
- El rectángulo ABDE, obviamente, tiene la misma superficie que el triángulo ABC.
- El botón comprobar muestra una animación que evidencia la afirmación anterior.
- paso 2
- Prolongamos los lados BD y ED como apoyo a la construcción.
- Con centro en D y radio DB se traza la circunferencia que junto a la extensión del lado ED definen el punto F.
- Se determina G, punto medio del segmento EF.
- Con centro en G y radio EG se traza la circunferencia que en su intersección con la prolongación de BD determina el punto H.
- En la escena (paso 2) se observa que el segmento DH es medía geométrica de ED y DF, pero DF = BD, por lo tanto AB·BD = DH2.
- Construimos el cuadrado DIJH.
- paso 3
- SABC=SABDE=SDIJH
- paso 0
Enlazamos a continuación otros ejemplos relacionados con el cuadrado y su partición en dos partes iguales o en dos/tres partes de forma que el área de una de las partes es siempre igual a la mitad de la superficie del cuadrado.
Escena 1

Partición dinámica del cuadrado en dos/tres partes.
Escena 2

Partición dinámica del cuadrado en dos partes iguales
Las escenas anteriores muestran la intima relación del cuadrado con el triángulo, el rectángulo y los trapecios para conformar teselas de indudable belleza.
Notamos que las utilidades mostradas son fácilmente adaptables y admiten las modificaciones y/o ampliaciones que se consideren convenientes para los propósitos particulares de uso.
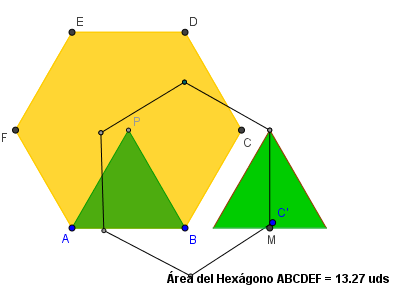
Las siguientes imágenes enlazan con pequeñas herramientas realizadas con el programa GeoGebra en las que se recrean los procesos de generación de la Cuadratura del Hexágono, por el método estándar o clásico y la descomposición de un triángulo equilátero de infinitas formas diferentes en cuatro polígonos para teselar rectángulos e incluso el cuadrado .
La siguiente imagen es el vínculo a la utilidad que muestra la generación de la Cuadratura del Hexágono por el método estándar.
Cuadratura del Hexágono. Método clásico.
Descomposición de un triángulo equilátero.
La siguiente utilidad es copia de la ya analizada anteriormente.
También, en esta introducción elemental al estudio de las cuadraturas, puede ser de interés el estudio de este otro trabajo sobre la cuadratura de un triángulo cualquiera.
Proponemos el análisis de las utilidades anteriores, su modificación y mejora con objeto de lograr un profundo conocimiento de ambas plataformas y así potenciar la inclusión del cálculo simbólico en escenas DescartesJS de forma eficaz.
Esta vez en la sección de vídeo hemos elegido la segunda parte de la colección que muestra la deducción, paso a paso, de la cuadratura del círculo usando el número de oro.
Continuando con la creación de la miscelánea "Las Espirales sugerimos completar su elaboración extrayendo el contenido relacionado con los lugares geométricos estudiados para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografia:
- La Mitad del cuadrado. De José Antonio Mora Sánchez: aproximación al estudio de las teselaciones.
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La cuadratura del círculo: Historia de una obsesión.
XIV Programa de Promoción de la Cultura Científica y Tecnológica.
Rev. Real Acad. Ci. Exact. Fis. Nat. (Esp) Vol. 105, Nº 2 (2012), 241-258
Fernando Bombal - Cuadraturas
Prof. Esteban Rubén Hurtado Cruz. Facultad de Ciencias UNAM. Cálculo Diferencial e Integral II - Páginas en GeoGebra de Vicente Martín Torres López
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
CUADRATURAS.
Adentrarse en el estudio de los lugares geométricos es estar, literalmente, predispuesto a perderse dentro de la espiral del tiempo en un ir y venir por las expresiones artísticas, religiosas, estructurales y técnicas de las diferentes culturas y épocas. Los conceptos, fundamentalmente los geométricos, físicos y filosóficos aparentan una evolución-involución atractiva y armónica que fascina. Esta es la razón por la que en esta entrada vamos a continuar la aproximación al conocimiento genérico de los ll.gg. analizando algunos aspectos de las Cuadraturas, asuntos estos tan íntimamente ligados que, a veces, es difícil discernir cuál es la causa y cuál el efecto.
Recordamos que el estudio de las cuadraturas, los ll.gg. y la descomposición de un polígono en otros más pequeños que lo recubren completamente con objeto de, con ellos, recubrir otro polígono diferente, están ligados, también, al estudio de las teselaciones.
Aprovechamos la oportunidad para señalar el aspecto popular, lúdico, espiritual y funcional que la Geometría clásica, la Cosmología, la Astronomía y en general el conocimiento ha tenido en las poblaciones cultas.
Consideramos, por tanto, que el estudio se centra en el problema clásico de la cuadratura del círculo y que nos vamos a aproximar a él haciendo, primero, la cuadratura de algunos polígonos regulares y no regulares. No debe olvidarse la idea de círculo como límite, cuando el número de lados tiende a infinito, de los polígonos regulares.
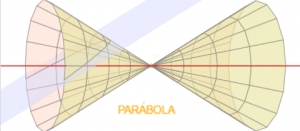
Las cónicas como lugares geométricos: La Parábola.
Dentro del estudio de los lugares geométricos tienen un especial interés los relativos a las cónicas por motivos muy diversos, fundamentalmente geométricos, físicos y filosóficos. Esta es la razón por la que en esta entrada vamos a continuar la aproximación a su conocimiento genérico analizando algunos aspectos de la Parábola considerada como lugar geométrico. Aprovechamos la oportunidad para señalar el aspecto popular, lúdico y funcional que la Geometría clásica ha tenido en las poblaciones cultas: el cucurucho con sus múltiples aplicaciones, los niños y niñas jugando con el aro, la peonza, el yoyo...
Consideramos, por tanto, que el estudio se centra en los ll.gg. generados por puntos que se mueven en el plano de forma que la razón (excentricidad) entre sus distancias a un punto fijo (foco) y a una recta (directriz) se mantiene constante.
Dentro del amplio grupo de trabajos relacionados con el tema destacamos, además de los que se muestran en la bibliografía, los que se enlazan a continuación.
- La Parábola como lugar geométrico.
- Generación de la Parábola como lugar geométrico.
Trabajo muy detallado de la creación del l.g. Ignacio Larrosa Cañestro (Grupo XeoDin)
Tomando como base, fundamentalmente, la documentación anterior hemos elaborado, con DescartesJS, las escenas que se exponen a continuación. Queremos notar que en dichos trabajos se hace uso de gran parte de los conceptos elementales de Geometría del Curriculum para ESO y Bachillerato.
Ambos trabajos dejan, para quien tenga interés en el tema, una buena cantidad de opciones de ampliación y mejora.
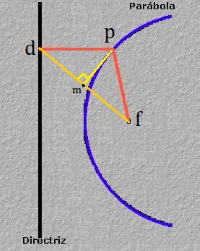
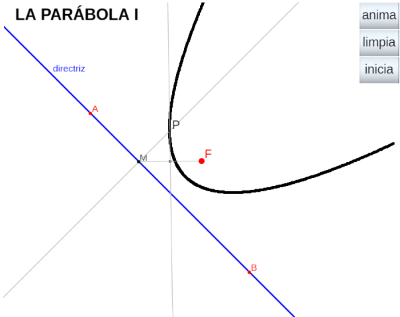
- Estudio de la PARÁBOLA I. La parábola como l.g. generado por el método, basado en la definición, del triángulo isósceles.
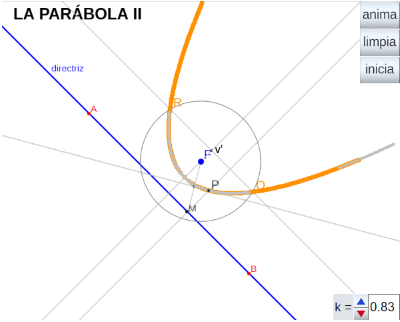
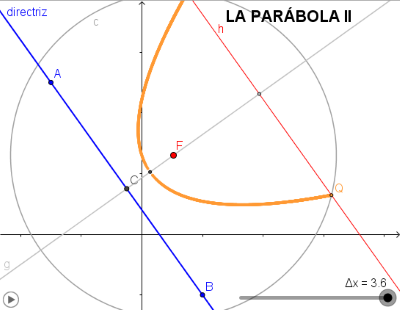
A partir de una recta d (directriz) y de un punto F (foco) consideramos que un punto del plano, P, pertenece a la parábola (F,d) si la distancia de P a M (ver imagen) es igual a la distancia de P a F. Esto es, el triángulo PMF es isósceles y por lo tanto la altura de dicho triángulo trazada desde P corta al lado FM en su punto medio. O bien que la intersección de la perpendicular a la directriz por un punto M de la misma con la perpendicular por el punto medio de FM es un punto de la parábola. Haciendo que M recorra la directriz obtendremos la parábola (F,d). - Estudio de la PARÁBOLA II. En esta ocasión se considera la parábola como el l.g. generado por los puntos, Q y R, intersección de la circunferencia c(F,r) con la paralela a la directriz por el vértice cuando el vértice, como punto virtual v', se desplaza por el eje focal desde su posición original hasta el infinito alejandose de la directriz (ver la animación completa), el radio de la circunferencia, r es igual a la distancia del vértice virtual v' a la directriz.
Es trivial comprobar que los puntos Q y R siempre son puntos de la parábola.
Se ha construido el l.g. por este segundo método sobre la construcción anterior por motivos didácticos.
En la primera escena el botón anima y en la segunda el pulsador k y el botón anima, generan el l.g. (parábola).
Continuamos animando a conocer el editor DescartesJS. Volvemos a exponer la adaptación a DescartesJS de la Unidad realizada por el profesor Antonio Caro Merchante debido a su relación con los conceptos en estudio.
Como en anteriores ocasiones notamos que las utilidades mostradas son fácilmente adaptables y admiten las modificaciones y/o ampliaciones que se consideren convenientes para los propósitos particulares de uso.
Las siguientes imágenes enlazan con pequeñas herramientas realizadas con el programa GeoGebra en las que se recrean los procesos de generación de la Parábola, primero por el método del triángulo isósceles y a continuación por el método clásico de la intersección de recta y circunferencia.
La Parábola. Método I.
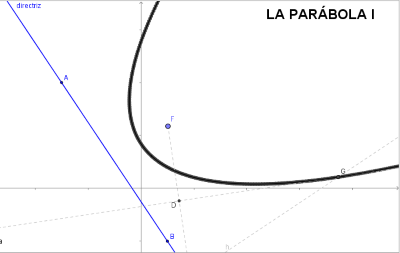
hoja de trabajo de la parábola (I)
La siguiente imagen es el vínculo a la utilidad que muestra la generación del l.g. por el segundo método, intersección de paralela a la directriz con la circunferencia de centro el foco y radio variable..
La Parábola. Método II.
Proponemos el análisis de las utilidades anteriores, su modificación y mejora con objeto de lograr un profundo conocimiento de ambas plataformas y así potenciar la inclusión del cálculo simbólico en escenas DescartesJS de forma eficaz.
Esta vez en la sección de vídeo hemos elegido uno que muestra la deducción, paso a paso, de la ecuación del lugar geométrico que define a una curva cónica.
Las Cónicas como lugares geométricos
Continuando con la creación de la miscelánea "Las Espirales sugerimos completar su elaboración extrayendo el contenido relacionado con los lugares geométricos estudiados para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
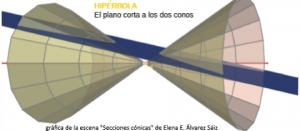
Lugares geométricos: La Hipérbola.
Dentro del estudio de los lugares geométricos tienen un especial interés los relativos a las cónicas por motivos muy diversos y no únicamente cronológicos; si no que también filosóficos, mercantilísticos y geométricos y en esta entrada vamos a continuar la aproximación a su conocimiento genérico analizando algunos aspectos de la Hipérbola considerada como lugar geométrico. Aprovechamos la oportunidad para señalar el aspecto popular, lúdico y funcional que la Geometría clásica ha ejercido sobre las poblaciones cultas: el cono como cucurucho para envolver desde tiempos ancestrales, los niños y niñas jugando con el aro y el yoyo...
Consideramos, por tanto, que el estudio se centra en los ll.gg. generados por puntos que se mueven en el plano de forma que la razón (excentricidad) entre sus distancias a un punto fijo (foco) y a una recta (directriz) se mantiene constante.
Dentro del amplio grupo de trabajos relacionados con el tema destacamos, además de los que se muestran en la bibliografía, los que se enlazan a continuación.
- La Hipérbola como lugar geométrico. MB (M. Banasik)
- Construcción de la hipérbola como lugar geométrico, a partir de un circulo y un punto exterior al círculo. La hipérbola que se genera tiene como focos el centro del círculo y el punto exterior al círculo. DORIS ÁLVAREZ QUINTERO
Tomando como base, fundamentalmente, la documentación anterior hemos elaborado, con DescartesJS, las escenas que se exponen a continuación. Queremos notar que en dichos trabajos se hace uso de gran parte de los conceptos elementales de Geometría del Curriculum para ESO y Bachillerato.
Ambos trabajos dejan, para quien tenga interés en el tema, una buena cantidad de opciones de ampliación y mejora.
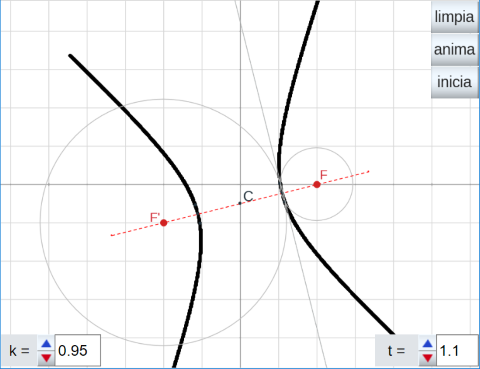
- Estudio de la HIPÉRBOLA I. La hipérbola como l.g. generado, la mitad del mismo, por los puntos de intersección de dos circunferencias: una con centro en el foco F y radio k y otra de centro el foco F' y radio r dependiente del pulsador k, de forma que cuando un radio aumenta el otro también. La otra mitad de la hipérbola se genera intercambiando los radios.
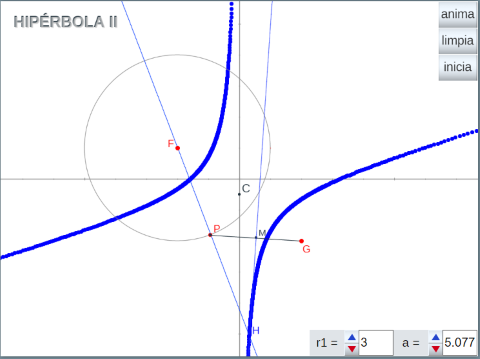
- Estudio de la HIPÉRBOLA II. En esta ocasión se considera la hipérbola como el l.g. generado por un punto, H cuando un punto P gira alrededor de la circunferencia de centro uno de los focos y radio cualquiera r1. El punto H se obtiene de la siguiente forma:
- Los puntos F y G son dos puntos libres que van a ser los focos de la hipérbola.
- Se traza la recta que une el centro de la circunferencia, punto F (uno de los focos), con el punto P.
- Se une el punto P con el otro foco, punto G.
- Se halla el punto medio del segmento PG, punto M y por él se traza la perpendicular al segmento.
- La intersección de las dos rectas trazadas es el punto H.
En ambas escenas los pulsadores k y a o el botón anima, generan el l.g. (hipérbola).
Continuamos animando a conocer el editor DescartesJS. Exponemos, en esta ocasión, la adaptación a DescartesJS de una Unidad realizada por el profesor Antonio Caro Merchante
Como en anteriores ocasiones notamos que las utilidades mostradas son fácilmente adaptables y admiten las modificaciones y/o ampliaciones que se consideren convenientes para los propósitos particulares de uso.
Las siguientes imágenes enlazan con pequeñas herramientas realizadas con el programa GeoGebra en las que se recrean los procesos de generación de la Hipérbola, primero como el l.g. creado por los dos puntos intersección de las circunferencias con centro en los focos y radios variables y en segundo lugar el l.g. generado por un punto cuando otro se desplaza por una circunferencia.
La Hipérbola. Método I.
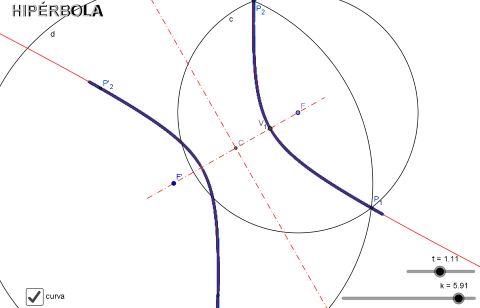
hoja de trabajo de la hipérbola (I)
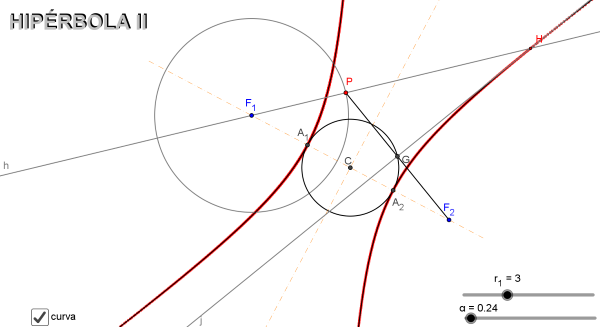
La siguiente imagen es el vínculo a la utilidad que muestra la generación del l.g. por el segundo método.
La Hipérbola. Método II.
Proponemos el análisis de las utilidades anteriores, su modificación y mejora con objeto de lograr un profundo conocimiento de ambas plataformas y así potenciar la inclusión del cálculo simbólico en escenas DescartesJS de forma eficaz.
Esta vez en la sección de vídeo hemos elegido uno que muestra la creación, paso a paso, del lugar geométrico que define a la hipérbola.
Las Cónicas como lugares geométricos
Continuando con la creación de la miscelánea "Las Espirales sugerimos completar su elaboración extrayendo el contenido relacionado con los lugares geométricos estudiados para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
Lugares geométricos: Las Cónicas.
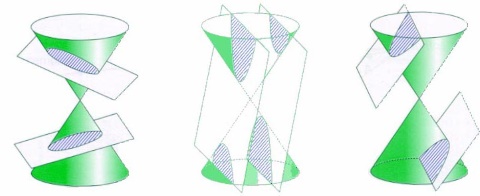
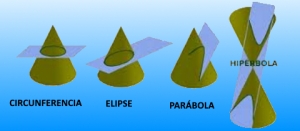
Continuamos con el estudio de los lugares geométricos y en esta entrada vamos a desarrollar una aproximación al conocimiento genérico de las curvas Cónicas no degenaradas, esto es: de la circunferencia, la Elipse, la Parábola y la Hipérbola consideradas como lugares geométricos. Curvas estas resultantes del trabajo de observación y posterior interpretación geométrica de la relación entre el ser humano y la naturaleza, por parte de los sabios griegos clásicos. En esta ocasión estudiaron la incidencia, en el cono de la visión ocular, de las ondas visibles, con objeto de establecer los principios teóricos del conocimiento de las formas y los colores.
Es de interés recordar que estas curvas están entre las primeras que fueron estudiadas y descritas.
Consideramos, por tanto, que el estudio se centra en los ll.gg. generados por puntos que se mueven en el plano de forma que la razón (excentricidad) entre sus distancias a un punto fijo (foco) y a una recta (directriz) se mantiene constante.
Dentro del amplio grupo de trabajos relacionados con el tema destacamos los que se enlazan a continuación.
- Estudio de las CÓNICAS. Trabajo realizado por M. Teresa Pérez y Oscar Arratia. Universidad de Valladolid.
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas.
- CÓNICAS, del profesor Antonio Caro Merchante. Tanto la unidad didáctica como la miscelánea que sobre este tema creó en su día el profesor Caro Merchante están en fase de adaptación al nuevo editor DescartesJS; no obstante avanzamos algunos resultados, aún provisionales, por el interés didáctico y posibilidad de uso del material en clase para consolidar conceptos y sobre todo como ayuda a la realización de ejercicios sobre cónicas: ecuaciones, tangencias, clasificación,.....
Tomando como base, fundamentalmente, la documentación anterior hemos elaborado o adaptado, con DescartesJS, las misceláneas que se exponen a continuación. Queremos notar la intención didáctica de dichos trabajos en los que se condensan una buena cantidad de los conceptos elementales de Geometría del Curriculum.
- Los trabajos dejan, para quien tenga interés en el tema o desee trabajar la precisión en clase, el ajuste fino de algunas variables controladas con pulsadores.
- Las siguientes posibles mejoras de la utilidad:
- convertir los pulsadores en animaciones.
- mostrar la ecuación de la elipse en algunas de sus formas
- ampliar la generación del l.g. al caso en el que el eje mayor de la elipse sea el vertical
- .................
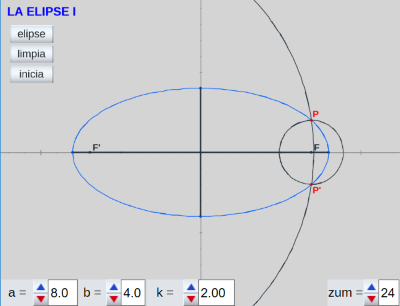
- Estudio de la ELIPSE I. La elipse como l.g. generado por los puntos, P y P', de intersección de dos circunferencias una con centro en el foco F y otra en el F' ambas con radios dependientes del pulsador k de forma que cuando un radio aumenta el otro disminuye.
Tanto en esta como en la siguiente miscelánea el pulsador k controla la generación del l.g.
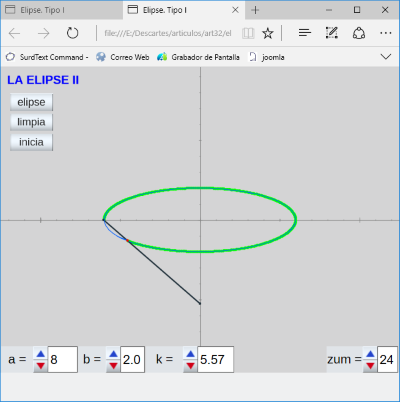
- Estudio de la ELIPSE II. En esta ocasión se considera la elipse como el l.g. generado por un punto de un segmento, distinto de los extremos, cuando dicho segmento desliza sin separarse por dos rectas perpendiculares tal como se muestra a continuación.
-
A continuación exponemos la adaptación a DescartesJS de la miscelánea realizada por el profesor Antonio Caro Merchante como ilustración de la contundencia didáctica del uso interactivo de una utilidad simple, que muestra de forma palpable un único concepto, como la enlazada a continuación.
propiedad de los puntos de la elipseLas miceláneas siguientes, que abordan algunas situaciones de tangencia, son también consecuencia directa del trabajo del profesor Caro Merchante.
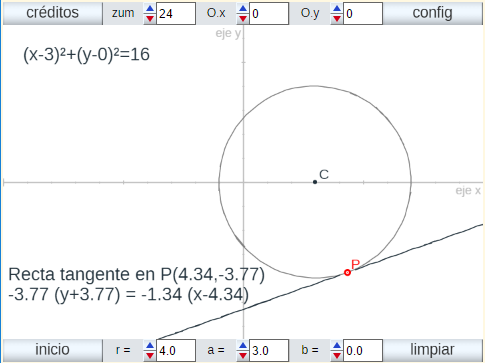
- Estudio de la ecuación de la tangente a una circunferencia por uno de sus puntos.
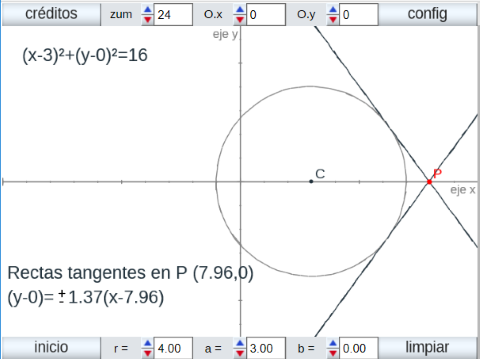
- Estudio de las ecuaciones de las tangentes a una circunferencia desde un punto exterior.
Como en anteriores ocasiones notamos que las utilidades mostradas son fácilmente adaptables y admiten las modificaciones y/o ampliaciones que se consideren convenientes para los propósitos particulares de uso.
Las siguientes imágenes enlazan con pequeñas herramientas realizadas con el programa GeoGebra en las que se recrean los procesos de generación de la Elipse, primero como el l.g. creado por los dos puntos intersección de las circunferencias con centro en los focos y radios variables y en segundo lugar el l.g. generado por un punto de un segmento cuando dicho segmento se desliza por dos rectas perpendiculares.
La Elipse. Método I.
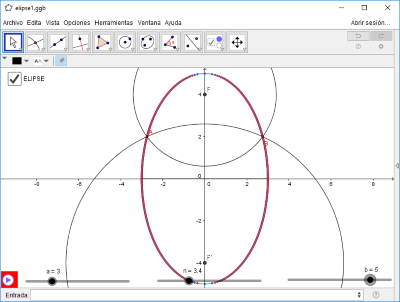
hoja de trabajo de la Elipse (I)
La siguiente imagen es el vínculo a la utilidad que muestra la generación del l.g. por el segundo método.
La elipse. Método II.
Proponemos el análisis de las utilidades anteriores, su modificación y mejora con objeto de lograr un profundo conocimiento de ambas plataformas y así potenciar la inclusión del cálculo simbólico en escenas DescartesJS de forma eficaz.
Esta vez en la sección de vídeo hemos elegido uno que muestra la deducción, paso a paso, de la ecuación del lugar geométrico que define a una curva cónica.
Las Cónicas como lugares geométricos
Continuando con la creación de la miscelánea "Las Espirales" sugerimos completar su elaboración extrayendo el contenido relacionado con los lugares geométricos estudiados para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- "Secciones cónicas" de la profesora: Elena E. Álvarez Sáiz.
- " Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- " Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)




























 CONTACTO
CONTACTO
