Proyecto ASIPISA

Objetivos

El objetivo básico inicial que se pretende con este proyecto se podría describir como la elaboración de una herramienta o colección temática, centrada por un lado en el área de conocimiento de Matemáticas del Proyecto PISA y por otro el de Lectura, Ciencias y Resolución de Problemas, que proporcione una ayuda sistemática interactiva para ese proyecto internacional, permitiendo el aprendizaje significativo de las competencias contempladas en él mediante el entrenamiento y adaptación a los contenidos, procedimientos y situaciones que allí se contemplan.

Esta herramienta se concibe como un conjunto de objetos de aprendizaje, independientes, basados en las unidades y preguntas liberadas por la OCDE entre las utilizadas en el PISA 2000, prueba piloto de 2002 y PISA 2003 (dónde el área principal fue las Matemáticas). Pero estas preguntas, pensadas para pruebas con lápiz y papel, tienen un carácter estático, una presentación inamovible que impide su reutilización en la preparación del alumnado, pues conocido el planteamiento de una pregunta y su respuesta, ésta, fácilmente puede ser recordada por dicho estudiante, teniendo que catalogarse por tanto como no utilizable para él. Así pues, el valor añadido que se introduce y persigue en este proyecto ASIPISA se centra en introducir aleatoriedad en los enunciados, en los planteamientos, en los esquemas, en los gráficos, en los textos, etc., es decir, en todos los elementos u objetos que componen una unidad PISA. De esta manera la unidad adquiere una estructura dinámica que soporta un mismo conjunto de competencias, pero éstas son presentadas formalmente de diferente forma en cada activación del objeto de aprendizaje. Consecuentemente cada unidad o pregunta PISA, desarrollada de esta forma, es reutilizable por un mismo alumno como medio de aprendizaje y entrenamiento, tantas veces como desee. Es de reseñar que el número de posibilidades o ejercicios diferentes que pueden plantearse con un mismo esquema o unidad crece exponencialmente en función del número de elementos aleatorios considerados, por lo que la diversidad y potencialidad es muy elevada.

Una unidad PISA está compuesta por una o más preguntas relacionadas a través un tema o exposición común, pero no necesariamente cubren ni los mismos contenidos, ni requieren los mismos procedimientos, ni persiguen la evaluación de las mismas competencias.
 

Ejemplo de introducción de aleatoriedad en una unidad PISA

Como ejemplo de dinamización de una unidad PISA consideremos la denominada “Caramelos de colores” correspondiente al PISA 2003. A esta pregunta le correspondió un porcentaje de aciertos del 50,2% en el ámbito de la OCDE y del 42,1% en España.

CARAMELOS DE COLORES

La madre de Roberto le deja coger un caramelo de una bolsa. Él no puede ver los caramelos. El número de caramelos de cada color que hay en la bolsa se muestra en el siguiente gráfico:

Cuál es la probabilidad de que Roberto coja un caramelo rojo?

A. 10%
B. 20%
C. 25%
D. 50%

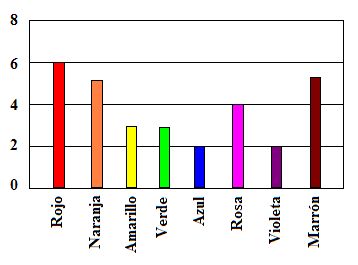
Para este ejemplo de unidad PISA podríamos plantear diferentes elementos en los que se podrían incluir valores aleatorios, permitiendo consecuentemente que el mismo ejercicio adquiera un análisis diferenciado en cada instancia, aunque las destrezas y competencias se mantienen, al igual que la dificultad, o bien ésta puede variarse si se desea.

 

En el gráfico:

Cambio del rango de valores admisible. En la figura aparece de 0 a 8 (entero). Puede pasar a un rango aleatorio dentro de un intervalo o valor máximo. En este caso esta ampliación puede aumentar la dificultad pues las frecuencias absolutas de cada color pueden aumentar y requerir un cálculo con cantidades mayores.

Cambio de las frecuencias absolutas correspondientes a cada color.

Permutación de colores.

Cambio del número total de colores considerado.

Cambio del tipo de gráfico de frecuencias (histogramas, poligonales, pictogramas).

Permutación de los ejes.

En la respuesta el cambio de datos iniciales obliga a una elaboración interna de la contestación correcta y de las otras tres incorrectas, todas obviamente determinadas y en función de los datos generados aleatoriamente. Puede cambiarse, por ejemplo, el color sobre el que se pregunta entre los previamente considerados. Adicionalmente la respuesta correcta se presentará también de manera aleatoria en cada una de las posiciones posibles (de A a D).
Un nivel adicional de aleatoriedad se establece en el cambio de los elementos no conceptuales del enunciado, por ejemplo cambio de caramelos por canicas o sobres o piezas de un puzle, cambio del parentesco: madre por padre, abuelo, hermano, etc., cambio de nombre: Roberto: Antonio, Juan, etc.

Así pues otra instancia aleatoria de la misma pregunta podría adoptar, de manera automática, esta presentación:

CANICAS DE COLORES

El padre de Luis le deja coger una canica de una bolsa. Él no puede ver las canicas. El número de canicas de cada color que hay en la bolsa se muestra en el siguiente gráfico.

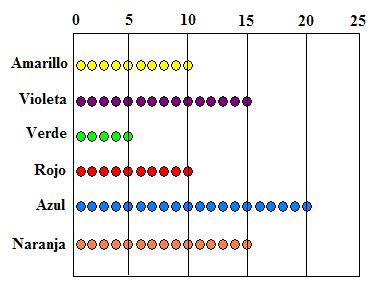
¿Cuál es la probabilidad de que Luis coja una canica violeta?

A. 40%
B. 10%
C. 35%
D. 20%

Podemos observar como en el enunciado se han cambiado los elementos no conceptuales como parentesco, nombre, objeto, tipo de gráfico, rango de valores, valores de cada color, colores, número de colores, e igualmente en la respuesta se pregunta por un color diferente, a la vez que se ajusta la respuesta correcta y las tres alternativas erróneas, ubicando estas aleatoriamente y por tanto no coincidiendo necesariamente con el valor y la posición de una instancia anterior de la misma pregunta.

Tipos de preguntas en las unidades PISA.

Según el tipo de contenidos, competencias y grupos o variables de proceso (ver apartado d) y e) de este proyecto) los instrumentos de evaluación de PISA contemplan cinco tipos de preguntas o ejercicios:

Ejercicios de respuesta breve. En los que la respuesta es una cantidad o palabra fija que requiere en general un proceso poco elaborado.

Ejercicios de elección múltiple. En los que hay que señalar o elegir una respuesta y sólo una de un conjunto de respuestas posibles.

Ejercicios de elección múltiple compleja. En los que hay que elegir más de una respuesta posible entre un conjunto de ellas.

Ejercicios de respuesta construida cerrada. En los que la respuesta requiere un proceso de elaboración para obtener la respuesta correcta que en general es breve y única.

Ejercicios de respuesta construida abierta. Análogos al caso anterior, pero la respuesta puede requerir una explicación detallada o indicaciones sobre el proceso realizado.

La actuación que hay que contemplar ha de ser diferenciada según el tipo de respuesta, seleccionando y empleando aquellos recursos que se adapten mejor a cada tipo para su corrección automática o para su registro y posterior corrección manual si fuese necesario.

Las respuestas a los cuatro primeros tipos permiten una corrección automática ya que al ser de tipo cerrado permiten comparar la respuesta proporcionada por el estudiante y confrontar su corrección con la respuesta correcta generada internamente en el objeto de aprendizaje.

El tratamiento de las respuestas de último tipo requieren en cada caso un estudio más detallado. Se contempla el registro o seguimiento de los procesos y de los avances realizados por cada alumno, pero éstos se realizarán con herramientas externas. Este elemento potencia las posibilidades del proyecto aquí detallado, pero no es objeto directo del mismo.

Concreción de objetivos

Y llegado este punto podemos descender al nivel de mayor concreción e indicar los objetivos establecidos en el desarrollo de este proyecto. El producto final obtenido es una colección temática interactiva o repositorio compuesto por objetos de aprendizaje cuyos contenidos se enmarcarán dentro del tema central del proyecto “ASIPISA en el área de Matemáticas y ASIPISA en Lengua, Ciencias y Resolución de Problemas”.