Mostrando artículos por etiqueta: comunicación
La dimensión histórica, social y cultural de las matemáticas debe programarse de manera cuidada y coordinada para ayudar a la comprensión de los conceptos a través de la perspectiva histórica, así como para contrastar las situaciones sociales de otros tiempos y culturas con la realidad actual, conociendo de manera más humana a los personajes y sus aportaciones, visibilizando las circunstancias personales de mujeres matemáticas y las dificultades que han tenido para acceder a la educación y a la ciencia. Resulta idóneo el uso de Internet y de las herramientas educativas existentes, de vídeos y películas sobre la vida y obra de los personajes matemáticos para lo que es de gran ayuda la pizarra digital, o el tradicional trabajo monográfico que ahora puede crear nuestro alumnado de forma colaborativa haciendo uso de los documentos compartidos. También podemos ir más allá, pues resulta sumamente enriquecedor para la formación competencial crear de forma colaborativa una línea del tiempo con la secuenciación cronológica de descubrimientos matemáticos. Además, debemos enseñar a nuestro alumnado a generar contenido matemático inédito y desarrollar la comunicación audiovisual desde las matemáticas con la creación de un audio o vídeo o poniendo voz a los personajes célebres de ambos géneros, organizando una cadena de radio matemática o un canal de televisión que entreviste de forma ficticia a dichos personajes.

El párrafo anterior están literalmente extraído de la Orden de 14 de julio de 2016, por la que se desarrolla el currículo correspondiente a la Educación Secundaria Obligatoria en la Comunidad Autónoma de Andalucía, se regulan determinados aspectos de la atención a la diversidad y se establece la ordenación de la evaluación del proceso de aprendizaje del alumnado, que es la que conozco como docente en activo, pero estoy convencido de que las orientaciones y estrategias metodológicas aportadas serán de gran similitud con las ofrecidas por otras comunidades autónomas en el ámbito de sus competencias.
Comparto un nuevo producto final generado por mis alumnas de 3º ESO desde la materia de Matemáticas Orientadas a las Enseñanzas Académicas, dentro del proyecto "La radio ficción en el aula de Matemáticas", desarrollado en el curso 2018/2019 e iniciado durante el curso escolar 2015/2016 por el Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija. En el artículo enlazado pueden encontrarse los orígenes, objetivos, fundamentación de este proyecto, referencia normativa y los detalles con las distintas fases que deben ir superando los alumnos y alumnas, de forma completamente autónoma, con trabajo colaborativo y sin la intervención del profesor.
En esta ocasión, la cadena "Radio púrpura al cubo" entrevista a la matemática que se vió obligada a firmar sus descubrimientos bajo el pseudónimo de Monsieur Le Blanc, porque en su época las matemáticas "no eran cosas de mujeres". Por cierto, no te pierdas en la entrevista algunas propuestas de Sophie Germain para fomentar la vocación matemática en mujeres y niñas. Tampoco debemos ignorar que, por razones de género, fue la gran "olvidada" en la relación nominal publicada en la Torre Eiffel de los científicos e ingenieros franceses que realizaron aportaciones y contribuciones, como nos recuerda Marta Macho en "Cuaderno de Cultura Científica".
Enlace a la entrevista en nuestro canal de iVoox
Quiero felicitar públicamente a mis alumnas María y Mireia, o Mireia y María, por la gran calidad del producto conseguido, por el trabajo desempeñado en la fase de documentación, por superar todos los aspectos técnicos para generar el archivo de audio y por sus capacidades para comunicar, interpretar y transmitir emociones, así como trasladar mi gratitud a sus familias, por su colaboración autorizando la difusión de las voces de sus hijas, conscientes de la repercusión en la mejora de sus procesos formativos para la sociedad del s. XXI.
La fase final del proyecto consiste en realizar un breve análisis de la experiencia que lleve a la reflexión sobre lo aprendido, describiendo todos los detalles, desde la planificación, redacción del guion, grabación del audio, lugar elegido, recursos usados, obstáculos encontrados y cómo se han afrontado y las conclusiones finales.
Enlace al análisis de la experiencia en nuestro canal de iVoox
A lo largo de este proyecto, que no deja de proporcionarme satisfacciones, se han publicado los siguientes artículos:
- La radio ficción en el aula de Matemáticas, que incorpora la entrevista ficticia al ilustre y prolífico matemático Leonhard Euler.
- Entrevistamos a Euclides en 3º ESO, para dar a conocer la vida y obra del autor de los Elementos.
- Alumnas de 3º ESO entrevistan a Mary Somerville.
- Évariste Galois visto e interpretado por alumnos de 3º ESO
- Conocí a Mary Cartwright gracias a mis alumnas. ¿Y tú?
- Ada Lovelace, la mujer en la ciencia y el techo de cristal.
También puedes conocer los antecedentes de la iniciativa consultando el artículo titulado "La ficción de Radio Descartes en el programa Boulevard de Radio Euskadi".
He reservado el mes de carnaval por antonomasia para compartir otra experiencia de aula realizada con mi alumnado de 4º de Educación Secundaria Obligatoria del IES Bajo Guadalquivir de Lebrija, en la materia Matemáticas Orientadas a las Enseñanzas Académicas, durante el curso escolar 2017/2018, dando continuidad al proyecto "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes", que puse en marcha hace ya cuatro años con el alumnado de 1º de Bachillerato, unos vanguardistas que inspiraron a sus sucesores. En el artículo enlazado pueden encontrarse los orígenes, objetivos, fundamentación de este proyecto, referencia normativa y los detalles con las distintas fases que deben ir superando los alumnos y alumnas, de forma completamente autónoma, con trabajo colaborativo y sin la intervención del profesor.
Cada año procuro elegir una temática diferente, correspondiendo esta edición a la discusión y resolución de sistemas de ecuaciones lineales, habiendo publicado anteriormente los artículos "Desarrollamos nuestra comunicación audiovisual y nos convertimos en divulgadoras matemáticas", "¿Son incompatibles el aprendizaje y la diversión en el segundo ciclo de la ESO?" y "Alumnas comunicando y compartiendo ideas matemáticas con Descartes".
A pesar del tiempo transcurrido y del número de alumnos y alumnas participantes en la experiencia, no dejan de sorprenderme con su creatividad e imaginación, pues todos los vídeos son completamente diferentes, así como la diversidad en el uso de editores de vídeo y sus estrategias de dirección y realización para desarrollar su comunicación audiovisual a través de las matemáticas, contenidos incorporados en el bloque de “Procesos, métodos y actitudes en Matemáticas”, que debe desarrollarse de modo transversal y simultáneamente al resto de bloques, constituyendo el hilo conductor de la asignatura. Un bloque que se articula sobre procesos básicos e imprescindibles en el quehacer matemático: la resolución de problemas, proyectos de investigación matemática, la matematización y modelización, las actitudes adecuadas para desarrollar el trabajo científico y la utilización de medios tecnológicos, proporcionando, además, una formación competencial.
La organización y planificación de la experiencia se coordina desde el aula virtual Moodle de RED Descartes, que dispone de acceso a invitados. Además, los ejemplos que aparecen en el vídeo han sido seleccionados de la unidad interactiva dedicada a "Ecuaciones y sistemas" de Proyecto Descartes.
Quiero felicitar públicamente a Fernando y José Antonio, José Antonio y Fernando que, constituídos en el equipo Augustin Louis Cauchy, en homenaje a este prolífico matemático francés, han conseguido un producto final de calidad con el que nos enseñan a discutir y resolver sistemas 2x2 por los métodos algebraicos conocidos y usando herramientas tecnológicas. Pero además, con su creatividad, imaginación, humor y dominio de la edición de vídeo, abren un nuevo horizonte al proyecto con la posibilidad de la caracterización en personajes matemáticos.
Mi agradecimiento, como es habitual, a sus familias por autorizar la difusión de este audiovisual en portales educativos y redes sociales.
Primera píldora invernal para compartir otra experiencia de aula realizada con mi alumnado de 4º de Educación Secundaria Obligatoria del IES Bajo Guadalquivir de Lebrija, en la materia Matemáticas Orientadas a las Enseñanzas Académicas, durante el curso escolar 2017/2018, dando continuidad al proyecto "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes", que puse en marcha hace ya cuatro años con el alumnado de 1º de Bachillerato, unos vanguardistas que inspiraron a sus sucesores. En el artículo enlazado pueden encontrarse los orígenes, objetivos, fundamentación de este proyecto, referencia normativa y los detalles con las distintas fases que deben ir superando los alumnos y alumnas, de forma completamente autónoma, con trabajo colaborativo y sin la intervención del profesor.
Cada año procuro elegir una temática diferente, correspondiendo esta edición a la discusión y resolución de sistemas de ecuaciones lineales, habiendo publicado anteriormente los artículos "Desarrollamos nuestra comunicación audiovisual y nos convertimos en divulgadoras matemáticas" y "¿Son incompatibles el aprendizaje y la diversión en el segundo ciclo de la ESO?".
A pesar del tiempo transcurrido y del número de alumnos y alumnas participantes en la experiencia, no dejan de sorprenderme con su creatividad e imaginación, pues todos los vídeos son completamente diferentes, así como la diversidad en el uso de editores de vídeo y sus estrategias de dirección y realización para desarrollar su comunicación audiovisual a través de las matemáticas, contenidos incorporados en el bloque de “Procesos, métodos y actitudes en Matemáticas”, que debe desarrollarse de modo transversal y simultáneamente al resto de bloques, constituyendo el hilo conductor de la asignatura. Un bloque que se articula sobre procesos básicos e imprescindibles en el quehacer matemático: la resolución de problemas, proyectos de investigación matemática, la matematización y modelización, las actitudes adecuadas para desarrollar el trabajo científico y la utilización de medios tecnológicos, proporcionando, además, una formación competencial.
La organización y planificación de la experiencia se coordina desde el aula virtual Moodle de RED Descartes, que dispone de acceso a invitados.
Quiero felicitar públicamente a Natalia y Celeste, Celeste y Natalia que, constituídas en el equipo María Gaetana Agnesi, en homenaje a esta gran matemática italiana, han conseguido un producto final de calidad con el que nos enseñan a discutir y resolver sistemas 2x2 por los métodos algebraicos conocidos y usando herramientas tecnológicas. Por cierto, en el momento de redactar este artículo, Natalia y Celeste se encuentran ya cursando el primer curso de bachillerato en la modalidad de ciencias sociales.
Mi agradecimiento, como es habitual, a sus familias por autorizar la difusión de este audiovisual en portales educativos y redes sociales.
Nueva píldora veraniega para compartir otra experiencia de aula realizada con mi alumnado de 4º de Educación Secundaria Obligatoria del IES Bajo Guadalquivir de Lebrija, en la materia Matemáticas Orientadas a las Enseñanzas Académicas, durante el curso escolar 2017/2018, dando continuidad al proyecto "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes", que puse en marcha hace ya cuatro años con el alumnado de 1º de Bachillerato, unos vanguardistas que inspiraron a sus sucesores. En el artículo enlazado pueden encontrarse los orígenes, objetivos, fundamentación de este proyecto, referencia normativa y los detalles con las distintas fases que deben ir superando los alumnos y alumnas, de forma completamente autónoma, con trabajo colaborativo y sin la intervención del profesor.
Cada año procuro elegir una temática diferente, correspondiendo esta edición a la discusión y resolución de sistemas de ecuaciones lineales, habiendo publicado ya un artículo anterior titulado "Desarrollamos nuestra comunicación audiovisual y nos convertimos en divulgadoras matemáticas". A pesar del tiempo transcurrido y del número de alumnos y alumnas participantes en la experiencia, no dejan de sorprenderme con su creatividad e imaginación, pues todos los vídeos son completamente diferentes, así como la diversidad en el uso de editores de vídeo y sus estrategias de dirección y realización.
Quiero felicitar públicamente a Rubén y Antonio, Antonio y Rubén que, constituídos en el equipo Lobachevski, en homenaje a este matemático ruso, han conseguido un producto final de calidad, demostrando con la incorporación de las tomas falsas la compatibilidad entre aprendizaje y diversión en esta etapa final de la ESO. Además, han tenido la deferencia de compartir con todos nosotros los preparativos de su estudio de grabación.
Mi agradecimiento, como es habitual, a sus familias por autorizar la difusión de este audiovisual en portales educativos y redes sociales.
Durante los dos cursos académicos en los que vengo desarrollando el proyecto "La radio ficción en el aula de Matemáticas", con mi alumnado de 3º ESO en el IES Bajo Guadalquivir de Lebrija, no he dejado de sorprenderme por su creatividad, imaginación, capacidades ocultas y habilidades para superar retos y obstáculos tecnológicos. En el artículo enlazado pueden encontrarse los orígenes, objetivos, fundamentación de este proyecto, referencia normativa y los detalles con las distintas fases que deben ir superando los alumnos y alumnas, de forma completamente autónoma, con trabajo colaborativo y sin la intervención del profesor.
Pues bien, en este sencillo y escueto artículo veraniego deseo compartir todo lo que he aprendido de mis alumnas Clara, Ángela y Cristina, que me han presentado aspectos relevantes de la vida y obra de una matemática británica completamente desconocida para mí, dejando constancia pública de cómo los docentes podemos aprender de los discentes.
A lo largo de este proyecto, que no deja de proporcionarme satisfacciones, se han publicado los siguientes artículos:
- La radio ficción en el aula de Matemáticas, que incorpora la entrevista ficticia al ilustre y prolífico matemático Leonhard Euler.
- Entrevistamos a Euclides en 3º ESO, para dar a conocer la vida y obra del autor de los Elementos.
- Alumnas de 3º ESO entrevistan a Mary Somerville.
- Évariste Galois visto e interpretado por alumnos de 3º ESO
También puedes conocer los antecedentes de la iniciativa consultando el artículo titulado "La ficción de Radio Descartes en el programa Boulevard de Radio Euskadi".
En Educación Secundaria Obligatoria, sin perjuicio de su tratamiento específico en algunas de las materias de cada etapa, la comprensión lectora, la expresión oral y escrita, la comunicación audiovisual, las Tecnologías de la Información y la Comunicación, el emprendimiento y la educación cívica y constitucional se trabajarán en todas las materias.
Además, la materia de Matemáticas Orientadas a las Enseñanzas Académicas se distribuye a lo largo de tercero y cuarto de Educación Secundaria Obligatoria en cinco bloques que no son independientes entre sí : Procesos, métodos y actitudes en Matemáticas, Números y Álgebra, Geometría, Funciones y, por último, Estadística y Probabilidad.
Entre los contenidos de este bloque se contempla la utilización de medios tecnológicos en el proceso de aprendizaje, entre otros para:
- la elaboración de informes y documentos sobre los procesos llevados a cabo y los resultados y conclusiones obtenidos.
- comunicar y compartir, en entornos apropiados, la información y las ideas matemáticas.
A su vez, en los criterios de evaluación para este bloque aparece emplear las herramientas tecnológicas adecuadas, de forma autónoma, realizando cálculos numéricos, algebraicos o estadísticos, haciendo representaciones gráficas, recreando situaciones matemáticas mediante simulaciones o analizando con sentido crítico situaciones diversas que ayuden a la comprensión de conceptos matemáticos o a la resolución de problemas. CMCT, CD, CAA.
También se dice utilizar las tecnologías de la información y la comunicación de modo habitual en el proceso de aprendizaje, buscando, analizando y seleccionando información relevante en Internet o en otras fuentes, elaborando documentos propios, haciendo exposiciones y argumentaciones de los mismos y compartiendo éstos en entornos apropiados para facilitar la interacción. CCL, CMCT, CD, CAA.
Más específicos aún son los estándares de aprendizaje evaluables, donde se recoge:
12.1. Elabora documentos digitales propios (texto, presentación, imagen, video, sonido,…), como resultado del proceso de búsqueda, análisis y selección de información relevante, con la herramienta tecnológica adecuada, y los comparte para su discusión o difusión.
12.2. Utiliza los recursos creados para apoyar la exposición oral de los contenidos trabajados en el aula.
12.3. Usa adecuadamente los medios tecnológicos para estructurar y mejorar su proceso de aprendizaje recogiendo la información de las actividades, analizando puntos fuertes y débiles de su proceso académico y estableciendo pautas de mejora.
| DESCRIPCIÓN DE LA EXPERIENCIA |
Esta iniciativa, desarrollada desde el Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija, durante el curso escolar 2017/2018 con un grupo de 4º ESO del área de Matemáticas Orientadas a las Enseñanzas Académicas, tienen su origen en el proyecto "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes", y se ha coordinado desde el aula virtual de Matemáticas, que tiene acceso para invitados, donde se fueron publicando, paulatinamente, las distintas fases con las correspondientes instrucciones para el alumnado. Así, con la pregunta ¿Qué tienes que hacer?, se decía que el reto a superar consiste en generar contenido audiovisual de Matemáticas. Concretamente, tienes que grabar un vídeo en el que se ejecute y explique la discusión y resolución de sistemas de ecuaciones lineales en sus tres casos: sistema compatible determinado, sistema compatible indeterminado y sistema incompatible.
En el vídeo deberá contemplarse perfectamente, y en este orden:
- Que los tres ejercicios se obtienen de la página del Proyecto Descartes.
- Que la discusión del sistema se realiza con el navegador de Google o con Photomath, como hemos hecho en clase.
- Que, para los casos en que sea un sistema compatible, el equipo lo resuelve por el método más adecuado.
- Que la solución coincide con la proporcionada por la página del Proyecto Descartes.
Para ello, estableceremos distintas etapas o fases.
| PRIMERA FASE |
La clase se organizará en equipos constituidos por dos personas, actuando una de ellas como coordinador o coordinadora del equipo que, además, deberá llevar el nombre de un personaje matemático, hombre o mujer.
Será el coordinador o coordinadora la persona encargada de entregar las tareas en las distintas fases y en los plazos establecidos.
| SEGUNDA FASE |
Comienza la fase de investigación y documentación, así que te propongo algunas sugerencias y te recomiendo espacios y recursos. Por ejemplo:
- Guía rápida para grabar en vídeo. ¡Muy bueno!
Necesitas un guion para tu película, con lo que vas a grabar y a decir, pudiendo alternar planos de lo que se visualiza en el ordenador, tableta o smartphone con planos de la ejecución técnica del ejercicio, es decir, el desarrollo con las fórmulas y operaciones. Puedes realizar los ejercicios en una pizarra, en un cuaderno o folio, con un software que lo permita, grabando en interior o en exterior y, por supuesto, todo lo que se te ocurra. Aquí es donde entra en juego tu creatividad e imaginación.
Recuerda que tú no eres el protagonista de la película, sino la resolución del ejercicio, por lo que no es necesario que aparezcas ni que se te vea.
En cualquier caso, se debe ver y oir cómo se elige el ejercicio desde el libro digital del Proyecto Descartes, comprobando después la solución en el mismo libro y usando, además, una de las dos herramientas tecnológicas que hemos aprendido en clase, es decir, Wiris Calc o Photomath, o incluso ambas.
Recuerda que publicaremos en internet el producto final, así que procura la mejor calidad de imagen y audio posibles.
El lenguaje matemático será primordial para las explicaciones, por eso, me enviaréis, desde el foro "Entrega del guion", el borrador del guion para que yo pueda revisarlo.
No puedes usar ni imágenes ni música con derechos de autor. Para estos casos, te recomiendo:
- Banco de imágenes y sonidos del INTEF.
- Imágenes con licencia Creative Commons, del mismo banco anterior o de Pixabay.
- Jamendo, descarga de música libre y gratis.
En cualquier caso, hay que citar en el vídeo el lugar de procedencia de las imágenes y audios usados.
Deberá aparecer en el vídeo, ya sea al final o al principio, el logotipo del IES Bajo Guadalquivir.
En cualquier caso, hay que dedicar una página de créditos para citar en el vídeo el lugar de procedencia de las imágenes y audios usados.
Si tienes alguna idea y no sabes cómo llevarla a efecto, puedes consultar en el foro del aula virtual denominado "Dudas sobre la segunda fase".
¡Es el momento de la CREATIVIDAD E IMAGINACIÓN!
| TERCERA FASE |
Para entregar el vídeo puedes usar un servicio gratuito para envío de archivos de gran tamaño. Si no conoces ninguno, te recomiendo WeTransfer.
Cuando la página te avise que se ha concluído la transferencia, me envías un mensaje por la plataforma para que me lo descargue. Así quedará constancia de haber entregado el vídeo en su plazo y me llegará un aviso a mi correo para que me descargue vuestra obra.
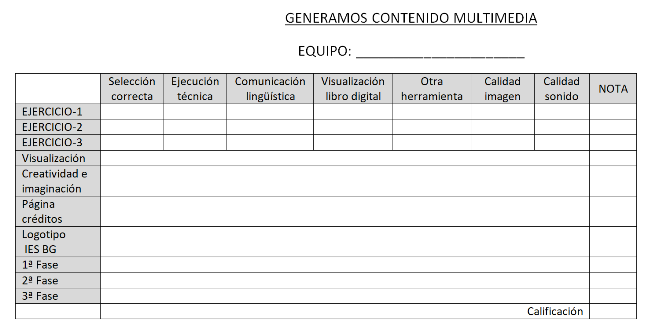
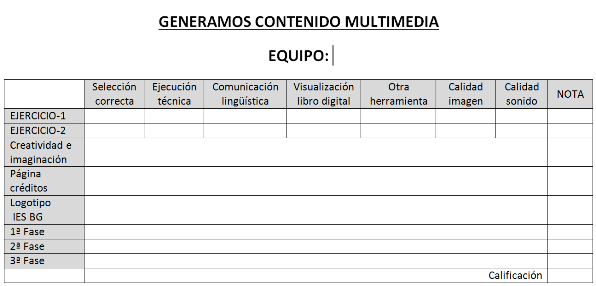
Para evaluar el producto final se tendrán en cuenta las siguientes variables:
La experiencia ha resultado sumamente satisfactoria y quiero felicitar desde el portal de RED Descartes al equipo Sofía Kovalevskaya por la calidad del producto final conseguido. ¡ENHORABUENA!, Ángela y Alba o Alba y Ángela.
Mi agradecimiento también a sus familias por autorizar la difusión de esta obra en entornos apropiados.
La dimensión histórica, social y cultural de las matemáticas debe programarse de manera cuidada y coordinada para ayudar a la comprensión de los conceptos a través de la perspectiva histórica, así como para contrastar las situaciones sociales de otros tiempos y culturas con la realidad actual, conociendo de manera más humana a los personajes y sus aportaciones, visibilizando las circunstancias personales de mujeres matemáticas y las dificultades que han tenido para acceder a la educación y a la ciencia. Resulta idóneo el uso de Internet y de las herramientas educativas existentes, de vídeos y películas sobre la vida y obra de los personajes matemáticos para lo que es de gran ayuda la pizarra digital, o el tradicional trabajo monográfico que ahora puede crear nuestro alumnado de forma colaborativa haciendo uso de los documentos compartidos. También podemos ir más allá, pues resulta sumamente enriquecedor para la formación competencial crear de forma colaborativa una línea del tiempo con la secuenciación cronológica de descubrimientos matemáticos. Además, debemos enseñar a nuestro alumnado a generar contenido matemático inédito y desarrollar la comunicación audiovisual desde las matemáticas con la creación de un audio o vídeo o poniendo voz a los personajes célebres de ambos géneros, organizando una cadena de radio matemática o un canal de televisión que entreviste de forma ficticia a dichos personajes.
El párrafo anterior están literalmente extraídos de la Orden de 14 de julio de 2016, por la que se desarrolla el currículo correspondiente a la Educación Secundaria Obligatoria en la Comunidad Autónoma de Andalucía, se regulan determinados aspectos de la atención a la diversidad y se establece la ordenación de la evaluación del proceso de aprendizaje del alumnado, que es la que conozco como docente en activo, pero estoy convencido de que las orientaciones y estrategias metodológicas aportadas serán de gran similitud con las ofrecidas por otras comunidades autónomas en el ámbito de sus competencias.
| ANTECEDENTES |
RED Descartes posee una gran experiencia, reconocida además, en la radio ficción en Matemáticas, gracias a su programa "El personaje misterioso" conducido por Eva Perdiguero y Ángel Cabezudo, con el objetivo de dar a conocer un poco más de cerca la parte humana de los personajes matemáticos famosos a lo largo de la historia. Pues bien, "La radio ficción en el aula de Matemáticas" es un proyecto del Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija con los mismos objetivos que los de Radio Descartes, pero entre discentes en vez de entre docentes, que empieza durante el curso escolar 2015/2016 con un grupo de alumnos de Matemáticas Orientadas a las Enseñanzas Académicas en 3º de ESO, es decir, con 14 y 15 años de edad, que se coordina desde el aula virtual y comprende las fases que se relacionan a continuación.
| ELECCIÓN DEL PERSONAJE MATEMÁTICO Y DIFUSIÓN EN TWITTER |
Cada equipo estará constituido libremente por dos personas que deberán elegir a un personaje matemático para entrevistar en un programa de radio, masculino o femenino garantizando la paridad en el aula, de modo que una persona ejerza de entrevistador y la otra represente al personaje seleccionado. Seguidamente, para información de todos y no repetir personajes, un miembro del equipo publicará un tuit con la composición del mismo, incluyendo el personaje seleccionado con una imagen y el hashtag del curso #MATES3BAJO.
| DOCUMENTACIÓN |
En la segunda fase, cada equipo realizará una búsqueda de información en internet sobre la vida y obra del personaje elegido para entrevistar.
Pueden ser documentos de texto, imágenes con información, presentaciones, infografías, vídeos, audios y cualquier multimedia, en general.
Es fundamental que la información provenga de fuentes fiables, así que se hará una selección de dos o tres recursos y se compartirán en el foro habilitado en el aula virtual las direcciones de cada uno de ellos.
Después, cuando el profesor aprueba los recursos seleccionados, se tendrán que difundir esas direcciones por Twitter con el hashtag del curso #MATES3BAJO.
| ELABORACIÓN DEL GUION |
Cada equipo tiene que elaborar un guion en un documento de texto con la entrevista completa y enviarla al profesor desde la tarea habilitada en el aula virtual, cuidando la expresión, el vocabulario y la escritura.
| INSTRUCCIONES PARA LA GRABACIÓN DE LA ENTREVISTA |
¡Ha llegado el momento! Recuerda que son fundamentales la creatividad e imaginación del equipo, así que, si no tienes experiencia anterior a la hora de protagonizar un programa de radio, te daré algunos consejos:
- Busca un espacio exento de ruidos, internos o externos, y evitarás sorpresas de última hora y pérdida de tiempo.
- Es muy importante ensayar algunas veces y vocalizar perfectamente, haciendo algunas pruebas hasta conseguir el efecto deseado.
- Es muy complicado grabar la entrevista de una sola vez, por ello aconsejamos grabarla por partes, según se estime oportuno.
- Conviene dejar grabando unos segundos de silencio después de cada intervención, lo que facilita la edición y montaje de la entrevista completa.
- Tenéis que hablar con tranquilidad y vocalizando lo mejor posible.
- El protagonista es el entrevistado, es decir, el personaje matemático, no el periodista. No obstante, ambos deben transmitir emociones al público, evitando usar un tono constante.
- Evitar apostillar las respuestas del entrevistado. Conforme el entrevistado va contestando, no debemos decir “ya”, “claro”.
- Como todo programa de radio, deberá contener una presentación, donde se explique el objetivo de la sesión, y una despedida, dando un pequeño resumen de lo tratado y agradeciendo, en nombre de la cadena, la presencia del entrevistado.
La mejor forma de conocer el producto final deseado es oir algunas entrevistas similares.
Encontrarás una docena de entrevistas a personajes matemáticos que te servirán de orientación, sin olvidar que están realizadas por docentes para docentes, mientras que las vuestras son de alumnos para alumnos, y se recomienda que no sobrepasen los cinco minutos de duración.
| EDICIÓN DEL AUDIO |
Una vez grabada la entrevista, te aconsejo hacer una copia de la misma y guardarla en una carpeta llamada copia de seguridad, para evitar posibles problemas, ya que ahora procede editar los distintos archivos para proceder a enriquecer el audio con las uniones correspondientes, incluyendo la presentación, despedida, sintonía del programa de radio, efectos sonoros, etc, para lo que es fundamental la creatividad e imaginación del equipo.
En ningún momento podrás incluir música o sonidos que tengan derechos de autor, es decir, copyright, debiendo usar recursos originales o que tengan licencias que lo permitan, como las Creative Commons. Así que, para ello, te recomiendo que uses el
Descárgate los archivos que sean de tu agrado en formato mp3, preferiblemente.
Abrimos en el aula virtual un foro denominado "Soporte técnico" para que, entre todos, planteemos las dificultades que encontremos y poder compartir soluciones conforme vayamos aprendiendo.
| ENTREGA DEL AUDIO |
Una vez finalizada la edición del audio con los efectos especiales y el equipo considere concluída la entrevista, deberá generar con el software empleado un archivo en formato mp3 para entregarlo desde la tarea habilitada en la plataforma, o bien usar un conversor para pasar su archivo al formato solicitado.
Pues bien, en el marco del proyecto "La radio ficción en el aula de Matemáticas", compartimos en este segundo artículo la entrevista realizada por dos alumnas de 3º ESO a Mary Somerville, conocida como "La Reina de las ciencias del siglo XIX".
Por cierto, he de reconocer ante los usuarios y seguidores de RED Descartes que, como profesor de Matemáticas, desconocía la grandeza de la obra de Mary Somerville, por lo que agradezco a María y Julia, o Julia y María, que me ilustraran al respecto desde su estupendo programa "Radio pi al cuadrado", que recomiendo oir en su totalidad y percibir la emoción que transmiten.
Compartimos un nuevo multimedia correspondiente al proyecto "Matemáticas para todos con Descartes", desarrollado desde el Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija, durante el curso escolar 2016/2017 con un grupo de 4º ESO del área de Matemáticas Orientadas a las Enseñanzas Académicas, coordinado desde el aula virtual de Matemáticas, que tiene acceso para invitados, donde se fueron publicando, paulatinamente, las distintas fases con las correspondientes instrucciones para el alumnado. Así, con la pregunta ¿Qué tienes que hacer?, se decía que el reto a superar consiste en generar contenido audiovisual de Matemáticas. Concretamente, tienes que grabar un vídeo en el que se ejecute y explique la resolución de dos ejercicios sobre fracciones polinómicas.
La experiencia ha resultado sumamente satisfactoria y quiero felicitar desde el portal de RED Descartes al equipo Mary Somerville por la calidad técnica del producto final conseguido. Agradecimiento extensivo a su familia por autorizar la publicación y difusión de este vídeo en internet y las redes sociales, conscientes de lo beneficioso para la formación de sus hijos.
Gracias a nuestra integración en Cero en conducta y en la Tribu 2.0, tuvimos constancia de la existencia del curriculum para docentes sobre Alfabetización Mediática e Informacional, como parte de una estrategia integral para auspiciar que las sociedades sean alfabetizadas en medios e información y promover la cooperación internacional, constituyendo un gran aporte para la innovación y mejora en todas las etapas educativas.
A su vez, fuimos conscientes de la necesidad de formarnos en comunicación audiovisual y de iniciar un Plan de Alfabetización Audiovisual en las aulas para lograr una buena formación del futuro espectador. Para ello, creamos un grupo de trabajo en el CEP de Lebrija con la denominación "Elaboración y desarrollo del Plan de Alfabetización Audiovisual para el IES Bajo Guadalquivir, en el marco del proyecto Cine y Educación".
En consecuencia, son ya bastantes años de experiencia con satisfacciones por lo conseguido, aunque nos queda un camino por delante en el que hay que ir insistiendo en esta línea y mejorando paulatinamente. Dejamos aquí enlace a lo más significativo, por si puede servir de orientación y ayuda a los docentes que se inicien en este ámbito. Añadir que cada audiovisual generado por el alumnado es completamente diferente, cual película enfocada por distintos directores de cine, demostrando así su creatividad e imaginación y sacando parte de esas capacidades ocultas que poseen nuestros alumnos y alumnas.
| TRIGONOMETRÍA EN 1º BACHILLERATO |
- Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes
- Comunicación audiovisual con iCartesiLibri
- Resolución de problemas y comunicación audiovisual y multimedia con Descartes
- ¡Diviértete! aprendiendo con Descartes
- El ángulo de depresión y la comunicación audiovisual con Descartes
- Giros: una unidad PISA en comunicación audiovisual
- ¿La Trigonometría?, pero si es muy fácil con Descartes
- Alumnos explican el cálculo del ángulo de elevación con Descartes
| RESOLUCIÓN DE PROBLEMAS EN 4º ESO |
- Aprendemos a resolver problemas con Descartes y Wiris
- Resolvemos problemas con Descartes y Photomath y comunicamos y compartimos usando medios tecnológicos
- Aprendemos a resolver problemas con Descartes, a desarrollar nuestra comunicación audiovisual y a compartir usando medios tecnológicos
| FRACCIONES POLINÓMICAS EN 4º ESO |
- Matemáticas para todos con Descartes
- Comunicación audiovisual en Matemáticas con Descartes
La materia de Matemáticas Orientadas a las Enseñanzas Académicas se distribuye a lo largo de tercero y cuarto de Educación Secundaria Obligatoria en cinco bloques que no son independientes entre sí : Procesos, métodos y actitudes en Matemáticas, Números y Álgebra, Geometría, Funciones y, por último, Estadística y Probabilidad.
Entre los contenidos de este bloque se contempla la utilización de medios tecnológicos en el proceso de aprendizaje, entre otros para:
- la elaboración de informes y documentos sobre los procesos llevados a cabo y los resultados y conclusiones obtenidos.
- comunicar y compartir, en entornos apropiados, la información y las ideas matemáticas.
A su vez, en los criterios de evaluación para este bloque aparece emplear las herramientas tecnológicas adecuadas, de forma autónoma, realizando cálculos numéricos, algebraicos o estadísticos, haciendo representaciones gráficas, recreando situaciones matemáticas mediante simulaciones o analizando con sentido crítico situaciones diversas que ayuden a la comprensión de conceptos matemáticos o a la resolución de problemas. CMCT, CD, CAA.
También se dice utilizar las tecnologías de la información y la comunicación de modo habitual en el proceso de aprendizaje, buscando, analizando y seleccionando información relevante en Internet o en otras fuentes, elaborando documentos propios, haciendo exposiciones y argumentaciones de los mismos y compartiendo éstos en entornos apropiados para facilitar la interacción. CCL, CMCT, CD, CAA.
Más específicos aún son los estándares de aprendizaje evaluables, donde se recoge:
12.1. Elabora documentos digitales propios (texto, presentación, imagen, video, sonido,…), como resultado del proceso de búsqueda, análisis y selección de información relevante, con la herramienta tecnológica adecuada, y los comparte para su discusión o difusión.
12.2. Utiliza los recursos creados para apoyar la exposición oral de los contenidos trabajados en el aula.
12.3. Usa adecuadamente los medios tecnológicos para estructurar y mejorar su proceso de aprendizaje recogiendo la información de las actividades, analizando puntos fuertes y débiles de su proceso académico y estableciendo pautas de mejora.
| DESCRIPCIÓN DE LA EXPERIENCIA |
Esta iniciativa, desarrollada desde el Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija, durante el curso escolar 2016/2017 con un grupo de 4º ESO del área de Matemáticas Orientadas a las Enseñanzas Académicas, se ha coordinado desde el aula virtual de Matemáticas, que tiene acceso para invitados, donde se fueron publicando, paulatinamente, las distintas fases con las correspondientes instrucciones para el alumnado. Así, con la pregunta ¿Qué tienes que hacer?, se decía que el reto a superar consiste en generar contenido audiovisual de Matemáticas. Concretamente, tienes que grabar un vídeo en el que se ejecute y explique la resolución de dos ejercicios sobre fracciones polinómicas.
El primero deberá ser simplificar una fracción polinómica, y se extraerá de la página "Para practicar", seleccionando la opción simplificar fracciones. Tienes que escoger una fracción que tenga segundo grado tanto en el numerador como en el denominador.
El segundo tratará sobre operaciones con fracciones polinómicas, pudiendo elegir entre sumar, restar, multiplicar o dividir, y será extraído de la página "Fracciones algebraicas" del libro Descartes.
Para ello, estableceremos distintas etapas o fases.
| PRIMERA FASE |
La clase se organizará en equipos constituidos por dos personas, actuando una de ellas como coordinador o coordinadora del equipo que, además, deberá llevar el nombre de un personaje matemático, hombre o mujer.
Será el coordinador o coordinadora la persona encargada de entregar las tareas en las distintas fases y en los plazos establecidos.
| SEGUNDA FASE |
Comienza la fase de investigación y documentación, así que te propongo algunas sugerencias y te recomiendo espacios y recursos. Por ejemplo:
- Guía rápida para grabar en vídeo. ¡Muy bueno!
Necesitas un guion para tu película, con lo que vas a grabar y a decir, pudiendo alternar planos de lo que se visualiza en el ordenador, tableta o smartphone con planos de la ejecución técnica del ejercicio, es decir, el desarrollo con las fórmulas y operaciones. Puedes realizar los ejercicios en una pizarra, en un cuaderno o folio, con un software que lo permita, grabando en interior o en exterior y, por supuesto, todo lo que se te ocurra. Aquí es donde entra en juego tu creatividad e imaginación.
Recuerda que tú no eres el protagonista de la película, sino la resolución del ejercicio, por lo que no es necesario que aparezcas ni que se te vea.
En cualquier caso, se debe ver y oir cómo se elige el ejercicio desde el libro digital del Proyecto Descartes, comprobando después la solución en el mismo libro y usando, además, una de las dos herramientas que hemos aprendido en clase, es decir, Wiris Calc o Photomath, o incluso ambas.
Recuerda que publicaremos en internet el producto final, así que procura la mejor calidad de imagen y audio posibles.
El lenguaje matemático será primordial para las explicaciones, por eso, me enviaréis, desde el foro "Entrega del guion", el borrador del guion para que yo pueda revisarlo.
No puedes usar ni imágenes ni música con derechos de autor. Para estos casos, te recomiendo:
- Banco de imágenes y sonidos del INTEF.
- Imágenes con licencia Creative Commons, del mismo banco anterior o de Pixabay.
- Jamendo, descarga de música libre y gratis.
En cualquier caso, hay que citar en el vídeo el lugar de procedencia de las imágenes y audios usados.
Deberá aparecer en el vídeo, ya sea al final o al principio, el logotipo del IES Bajo Guadalquivir.
En cualquier caso, hay que dedicar una página de créditos para citar en el vídeo el lugar de procedencia de las imágenes y audios usados.
Si tienes alguna idea y no sabes cómo llevarla a efecto, puedes consultar en el foro del aula virtual denominado "Dudas sobre la segunda fase".
¡Es el momento de la CREATIVIDAD E IMAGINACIÓN!
| TERCERA FASE |
Para entregar el vídeo puedes usar un servicio gratuito para envío de archivos de gran tamaño. Si no conoces ninguno, te recomiendo WeTransfer.
Cuando la página te avise que se ha concluído la transferencia, me envías un mensaje por la plataforma para que me lo descargue. Así quedará constancia de haber entregado el vídeo en su plazo y me llegará un aviso a mi correo para que me descargue vuestra obra.
Para evaluar el producto final se tendrán en cuenta las siguientes variables:
La experiencia ha resultado sumamente satisfactoria y quiero felicitar desde el portal de RED Descartes al equipo Sophie Germain por la calidad del producto final conseguido.
Aprendemos a resolver problemas con Descartes es una iniciativa del Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija, realizada con alumnos y alumnas de 4º ESO durante el curso escolar 2015/2016, basada en la experiencia para el "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes" y llevaba a cabo anteriormente con el alumnado de 1º de Bachillerato de Ciencias e Ingeniería, con objeto de fomentar en nuestros alumnos y alumnas el aprendizaje de las técnicas necesarias del lenguaje cinematográfico y audiovisual, a la vez que proporcionarles una formación básica que les permita, de forma autónoma, generar y producir sus propios contenidos audiovisuales.
Con el lema “Resolvemos problemas con Descartes“, abrimos un foro de suscripción forzosa en el aula virtual de Matemáticas-4º para coordinar la experiencia, dar las indicaciones, organizar los equipos, elegir los problemas, prestar asesoramiento y fomentar el trabajo en colaboración, aunque también se generaba debate en el día a día del aula física.
Decir que, durante todo el curso, los alumnos y alumnas asistieron a clase con sus portátiles de la Escuela TIC 2.0 que les entregaron cuando se encontraban en 5º de Primaria, usando junto a la PDI el libro digital interactivo del Proyecto ED@D y los cuadernos de trabajo Descartes que incorpora cada unidad interactiva, estando en contacto permanente con el profesor desde el aula virtual y desde la red social Twitter.
| 1ª FASE: PROPUESTA DE PROBLEMAS Y DIFUSIÓN EN TWITTER |
Cada equipo tuvo que seleccionar dos problemas de la unidad interactiva "Ecuaciones y sistemas", concretamente uno de primer grado y otro de segundo, que se encuentran en el menú ejercicios y que se denominan "Sistemas de ecuaciones lineales" y "Sistemas de segundo grado", respectivamente, y comunicarlo en el foro del aula virtual para conocimiento del profesor y del resto de equipos. Posteriormente, y una vez acordado con el profesor los dos problemas seleccionados para su resolución en lo que sería su "ópera prima", al menos en Matemáticas, tuvieron que diseñar una imagen alusiva al contenido de los problemas, incorporar sus enunciados y darle difusión por la red social Twitter con el hashtag del curso #MATES4ABAJO.
| 2ª FASE : DOCUMENTACIÓN Y GUIÓN DE LA OBRA |
Comienza la fase de investigación y documentación, así que damos las indicaciones desde el aula virtual, aportamos sugerencias, consejos y recomendamos espacios y recursos. Por ejemplo:
- Guía rápida para grabar en vídeo. ¡Muy bueno!
- Necesitáis un guión de lo que váis a grabar y a decir, pudiendo alternar planos virtuales de lo que se visualiza en el ordenador, tableta o smartphone con planos reales de la ejecución técnica de los ejercicios, que podéis realizar en una pizarra, en un cuaderno o folio, con un software que lo permita, grabando en interior o en exterior y, por supuesto, todo lo que se os ocurra. Aquí es donde entra en juego vuestra creatividad e imaginación.
- Recordad que publicaremos en internet el producto final, así que procurad la mejor calidad de imagen y audio posibles.
- El lenguaje matemático será primordial para las explicaciones y la comunicación audiovisual, por eso me enviaréis el borrador del guión, a través de la tarea del aula virtual, para que yo pueda revisarlo.
- No podéis usar ni imágenes ni música con derechos de autor. Para estos casos, os recomiendo:
- Banco de imágenes y sonidos del INTEF.
- Imágenes con licencia Creative Commons, del mismo banco anterior o de Pixabay.
- Jamendo, descarga de música libre y gratis.
- En cualquier caso, es recomendable dedicar una página de créditos para citar en el vídeo la autoría y el lugar de procedencia de las imágenes y audios usados.
- Debería aparecer, al menos, el logotipo del IES Bajo Guadalquivir, nuestro instituto.
- Cuando tengáis todo preparado y ensayado, os aconsejo hacer algunas pruebas de grabación cortas para comprobar si obtenéis el resultado deseado y las calidades demandadas
Si tenéis alguna idea y no sabéis cómo llevarla a efecto, podéis consultar en este foro o por el servicio de mensajería de la Moodle.
¡Es el momento de la CREATIVIDAD E IMAGINACIÓN!
| 3ª FASE : EVALUACIÓN |
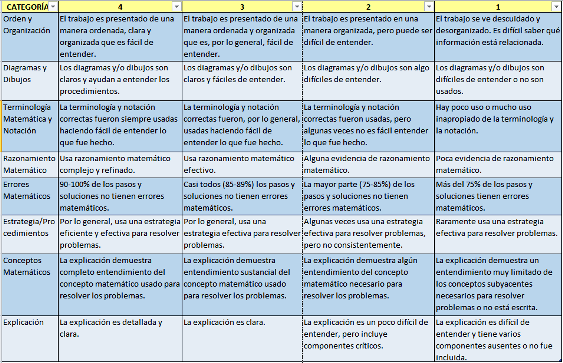
Para la evaluación relativa a los aspectos curriculares del producto final presentado por cada equipo, se ha utilizado la rúbrica que compartimos en este artículo, elaborada desde Rubistar, y que ya empleamos en la experiencia para el "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes". Con un clic sobre la imagen puede ampliarse para una correcta visualización.
Si visualizas y oyes el vídeo con detenimiento, sin duda, encontrarás leves errores de expresión escrita o verbal, tanto en el lenguaje ordinario como en el lenguaje matemático, lo que nos induce a dar una continuidad a la iniciativa y extrapolarla a otros cursos para ir consiguiendo nuestro objetivo paulatinamente. Además, la localización y análisis de errores es una de las mejores estrategias de aprendizaje. No obstante, quiero desde aquí felicitar a todos mis alumnos y alumnas de 4º A por sorprenderme con su creatividad e imaginación, por ser competentes para generar contenido multimedia con sus dispositivos móviles, sin que su profesor sepa ayudarles en este ámbito, por afrontar todos los retos que se han encontrado por el camino hasta conseguir el producto final y por permitirme descubrir y fomentar algunas de sus capacidades ocultas.
Muchas gracias también a sus familias por apoyar la iniciativa autorizando las grabaciones y su difusión por las redes sociales, lo que obviamente repercute en una mejora de la formación de sus hijos e hijas como ciudadanos y ciudadanas del s. XXI y en su preparación para la siguiente etapa educativa.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)











 CONTACTO
CONTACTO
