Mostrando artículos por etiqueta: rectángulo
En el número 106 de la revista Epsilon (ISSN: 2340-714X) de la Sociedad Andaluza de Educación Matemática Thales se ha publicado el artículo titulado "Congruencias en el triángulo de Pascal y el rectángulo de Newton" cuyo autor es nuestro socio José R. Galo Sánchez. Un trabajo de investigación, que como se refleja en la filiación de la autoría, ha sido desarrollado dentro de nuestra RED Descartes.
Este trabajo fue prepublicado en nuestro blog en tres artículos en los que el autor divulgaba la investigación realizada:
- El paralelogramo de Newton el 6 de marzo de 2020.
- El rectángulo de Newton como "simétrico" del triángulo de Pascal el 27 de marzo de 2020.
- Congruencias en el triángulo de Pascal el 24 de abril de 2020.
y, posterioriormente compiló el artículo que sometido a revisión por pares se ha publicado en la revista indicada.
En el resumen se indica :
"El rectángulo de Newton surge como extensión del actualmente denominado triángulo de Pascal partiendo de la versión escalonada de Stifel. Sin embargo, si se parte del esquema organizativo aportado por Pascal entonces el rectángulo de Newton se obtiene mediante una simple simetría signada. Así pues, basta estudiar las congruencias con cero de los números combinatorios y en su análisis aportamos que éstas se ubican en una sucesión de triángulos básicos que se distribuyen de manera periódica. En base a esa periodicidad se incluye un criterio que permite determinar directamente la congruencia de un número combinatorio."
El plantemiento conceptual que sigue, puede sintetizarse en:
- Presentación del conocido triángulo de Pascal en su representación actual como triángulo isósceles escalonado y como triángulo rectángulo que es la original de Pascal, y presentación del menos divulgado rectángulo de Newton.
- Reducción del rectángulo de Newton al de Pascal mediante una simetría signada.
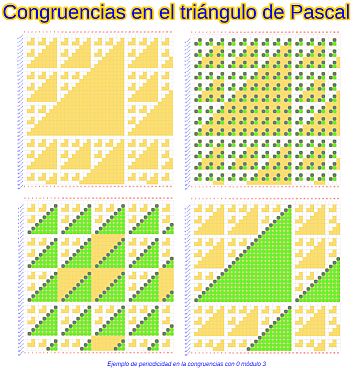
- Muestra de las congruencias con cero en el triángulo de Pascal y revisión de resultados previos de otros autores. Esos resultados se presentan normalmente de manera algebraica y, en general, son oscuros y difíciles de interpretar por profanos dada la abstracción que suele introducir el Álgebra, pero aquí son visualizados geométricamente quedando mostrados de manera diáfana tanto para legos como para ilustrados.
- Finalmente se enuncian algebraicamente los resultados obtenidos por el autor, los cuales muestran la periodicidad de las congruencias módulo p de los números combinatorios y la regla que permite su determinación directa a partir de la descomposición p-ádica del índice superior e inferior, y se visualiza el porqué de ese resultado.
Todo está aderezado por numerosas escenas interactivas que permiten al interesado reproducir la investigación y cómo, apoyándose en ellas, puede potenciarse la reflexión que permite alcanzar la meta lograda. ¡Acceda pulsando sobre la siguiente imagen!
 Pulsa sobre la imagen para abrir la escena
Pulsa sobre la imagen para abrir la escena
Os incluimos a continuación dicho artículo y os invitamos a su lectura, a que realicéis observaciones y comentarios al mismo y a que lo divulguéis a través de vuestras redes sociales y profesionales. También a que, usando los recursos interactivos ahí enlazados y disponibles en nuestra web, abordéis actividades en vuestra aulas en las que divulgar el Triángulo de Pascal, el rectángulo de Newton y las curiosas congruencias que acontecen en ellos y a la vez que podáis promover en vuestro alumnado la inquietud básica, la chispa a partir de la cual se cataliza la vocación investigadora.