Mostrando artículos por etiqueta: Euclides
En nuestro artículo "Euclides y el Teorema de Pitágoras", publicado en este blog de la RED Descartes, acudimos a "Los Elementos” de Euclides como fuente primigenia de la demostración académica del Teorema de Pitágoras con el objetivo de mostrar e introducir al lector interesado en la demostración matemática de una propiedad basándose en un sistema axiomático y deductivo y, a la vez, difundir la menos conocida generalización de esta propiedad. En concreto, acudimos a la primera versión en español de estos libros debida a Rodrigo Çamorano y seguimos en la guía lógica-deductiva aportada por David E. Joyce en su versión interactiva con applets de Java (actualmente estos applets presenta problemas de compatibilidad en algunos sistemas y cuando eso ocurre se suplen con imágenes).
En 1847, Oliver Byrne publicó su libro "The First six books of the Elements of Euclid whith coloured diagrams and symbols" en el que, como él indica, el uso de diagramas coloreados y símbolos en lugar de letras facilita el aprendizaje a los estudiantes. El libro de Byrne puede considerarse una revolucionaria propuesta innovadora en la enseñanza de las Matemáticas ya que sustituye el usual sistema literal e introduce atractivos elementos gráficos coloreados que le sirven de soporte y medio para abordar las demostraciones matemáticas de manera visual y por ende evitando la, muchas veces, farragosa expresión escrita que requiere una interpretación de lo leído, es decir, pone en práctica el conocido dicho: "más vale una imagen que mil palabras". De hecho, basta ver por primera vez una página de este precioso libro de Byrne para sentirse atraído con su diseño y verse sorprendido por el potencial comunicador y didáctico que encierra. El libro de Byrne podemos consultarlo en español en la versión elaborada por Nicholas Rougeux, y nosotros, con modestia introduciremos algo más de interactividad.
Fig. 1. Demostración del teorema de Pitágoras según Byrne
Pulse sobre la imagen para verlo en el libro de Byrne.
Si en el artículo antes citado buscábamos introducir al lector en el academicismo euclidiano, en éste buscamos mostrar cómo Euclides puede adentrarse en el aula de una manera didáctica, aproximándonos al aprendiz, pero respetando al gran maestro y referente. Para ello, hemos desarrollado dos escenas interactivas que abordan las demostraciones gráficas del Teorema de Pitágoras y de la generalización del mismo. Le invitamos a acceder a ellas y a interactuar con las mismas.
Byrne y su demostración gráfica del teorema de Pitágoras
Con esta primera escena se busca conseguir los siguientes objetivos:
- Conocer una versión de "Los elementos" de Euclides con una perspectiva .
- Percibir la plasticidad de la mente humana y cómo un mismo concepto tiene diversas formas de reflejarse.
- Tomar contacto con la didáctica matemática en el sistema axiomático euclidiano.
- Ver cómo Byrne realiza la demostración euclidiana del teorema de Pitágoras con una metodología deductiva basada en gráficos de colores.
- Comprender cómo se aborda un razonamiento deductivo apoyándose en axiomas y proposiciones.
- Sentar las bases para asimilar que la metodología empleada condiciona el aprendizaje.
Fig. 2. Acceso a la miscelánea "Byrne y su demostración gráfica del teorema de Pitágoras".
Pulse sobre la imagen para acceder.
La versión clásica euclidiana de este resultado puede consultarla en nuestra miscelánea "Demostración euclidiana del Teorema de Pitágoras".
Byrne y su demostración gráfica de la generalización del teorema de Pitágoras
Siguiendo la línea de trabajo abordada en la miscelánea anterior, a continuación, divulgamos el resultado menos conocido que es "La generalización del Teorema de Pitágoras" y aquí, de nuevo, lo haremos según la versión coloreada de Byrne, expuesta en la p. 259 de su libro "The First six books of the Elements of Euclid whith coloured diagrams and symbols".
Los objetivos a lograr son los mismos que en la miscelánea anterior, pero centrados en esta generalización.
Fig. 6. Acceso a la miscelánea "Byrne y su demostración gráfica de la generalización euclidiana del teorema de Pitágoras".
Pulse sobre la imagen para acceder.
La versión clásica euclidiana de esta generalización puede consultarla en nuestra miscelánea "Generalización euclidiana del Teorema de Pitágoras".
Reflexión
Comparando las versiones clásicas con las que aquí presentamos podrá experimentar la dureza que pueden encerrar algunos argumentos literarios matemáticos y el lenguaje matemático en sí —una posible causa de la desmotivación de nuestro alumnado— y cómo esta aspereza puede ser salvada con métodos didácticos innovadores. El academicismo euclidiano y, en general, de nos, los matemáticos, siendo en nuestra profesión necesario, esencial, imprescindible y loable, pensamos ha de saber reconducirse cuando lo que se desea es enseñar y divulgar el conocimiento. Byrne así lo entendió y nos marcó un esplendoroso camino del que aprender y tratar de adaptar, más en estos tiempos en los que las herramientas tecnológicas son una ayuda innegable e imprescindible que no se pueden obviar en nuestra labor docente.
El Teorema de Pitágoras es, posiblemente, el resultado matemático más "conocido" tanto por legos como expertos, al menos como sabedores de su existencia, aunque incluso no se sea capaz de dar un enunciado correcto y ni siquiera se sepa el porqué de su importancia ni su aplicación. Un resultado con más de dos mil años de antiguedad y que fue recogido y divulgado por Euclides en "Los Elementos”. Es una propiedad que está indisolublemente ligada a la perpendicularidad que condiciona nuestras vidas y nuestro entorno, dado que estamos sujetos a la fuerza gravitatoria y, de ahí, su máxima importancia en cualquier construcción o diseño ergonómico que permita satisfacer nuestras necesidades de movilidad y acomodación. ¿Quién no ha visto la representación geométrica de este Teorema?:
.png)
Fig. 1. Representación geométrica del Teorema de Pitágoras
o ¿quién no ha visto en algún momento su más críptica representación algebraica?:
a2 + b2 = c2
Fig. 2. Representación algebraica del Teorema de Pitágoras
Pero menos divulgado, aunque Euclides también lo incluye en el libro VI de los Elementos, es la "Generalización del Teorema de Pitágoras" donde se extiende el resultado a cualquier terna de figuras semejantes que se dibujen sobre los catetos y la hipotenusa de un triángulo rectángulo. Euclides en su demostración hace una representación gráfica con rectángulos, pero la demostración se realiza de manera general.
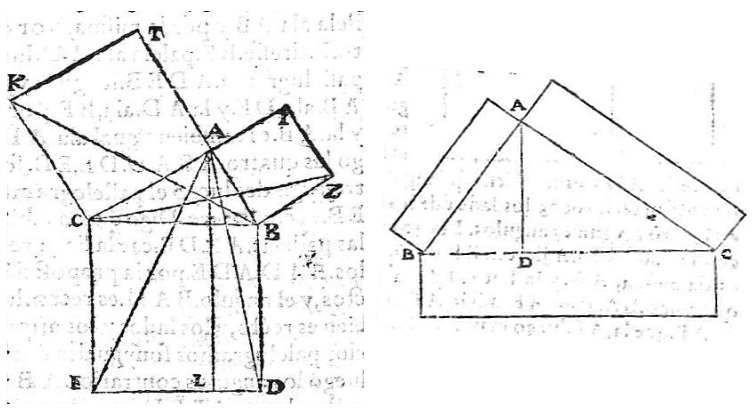
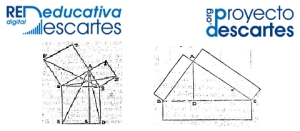
Fig. 3. Ilustraciones originales de los Elementos.
Izq. Teorema de Pitágoras. Dcha. Generalización del teorema de Pitágoras
El artista renacentista Alberto Durero mostró un profundo interés por la geometría, un conocimiento que se revitalizó en Europa gracias a la primera edición impresa de los Elementos de Euclides. Esta edición, publicada en 1482, se basó en la traducción y comentarios del matemático Campano de Novara. A su vez, el trabajo de Campano se fundamentó en versiones árabes, una de las cuales fue la influyente traducción que realizó en el siglo XII Adelard of Bath. Aunque Adelard de Bath tradujo la obra de un texto en árabe andalusí, la afirmación de que lo obtuvo por espionaje de la biblioteca de Madīnat al-Zahrā (Medina Azahara) en Córdoba es una leyenda sin fundamento histórico.
Durero, formador de artesanos a los que dedicó sus libros, conocidos colectivamente como los libros "De la Medida", fundamental para la construcción de formas y la perspectiva, también refleja la generalización del Teorema de Pitágoras y dibuja los casos particulares de triángulos y cuadrados en dicha construcción sobre un triángulo rectángulo.
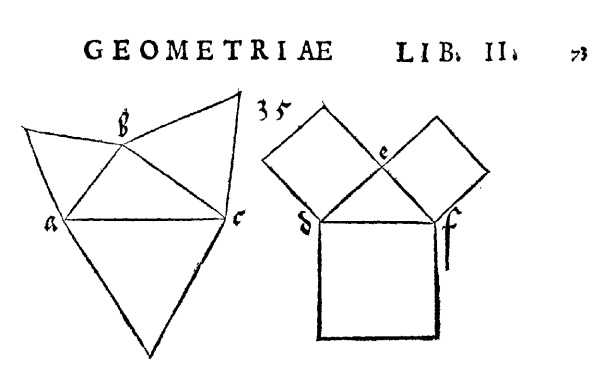
Fig. 4. Ilustraciones de Albert Durero en el libro II de la Medida.
Izq. Generalización del Teorema de Pitágoras con triángulos. Dcha. teorema de Pitágoras con cuadrados.
Y en la siguiente imagen podemos observar otras muestras de este resultado:
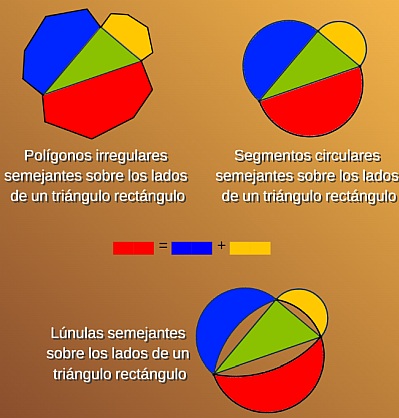
Fig. 5. Otros ejemplos de la generalización del Teorema de Pitágoras.
Para quienes estén interesados en profundizar sobre este tema hemos desarrollado dos misceláneas que se adentran en estos contenidos y los detallan. Les invitamos a acceder e interactuar con ellas.
Demostración euclidiana del teorema de Pitágoras
En las indicaciones de la miscelánea con este título, puede leer la motivación, los objetivos y las instrucciones e interactuando con ella podrá acceder a su contenido.
Fig. 6. Acceso a la miscelánea "Demostración euclidiana del teorema de Pitágoras".
Pulse sobre la imagen para acceder.
Generalización euclidiana del teorema de Pitágoras
De manera análoga también en las indicaciones de la miscelánea con este título, puede leer la motivación, los objetivos y las instrucciones e interactuando con ella podrá acceder a su contenido.
Fig. 6. Acceso a la miscelánea "generalización euclidiana del teorema de Pitágoras".
Pulse sobre la imagen para acceder.
Título: Algoritmo de Euclides
Sección: Prometeo
Bloque: Álgebra
Unidad: Números y operaciones
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Gustavo Magallanes Guijón
Diseño funcional: Julio Arnoldo Prado Saavedra / Victor Manuel Amezcua y Raz
Programación: Julio Arnoldo Prado Saavedra / Victor Manuel Amezcua y Raz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Prometeo en https://proyectodescartes.org/Prometeo/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional