Mostrando artículos por etiqueta: Descartes

En el número 102 de la revista Epsilon (ISSN: 2340-714X) de la Sociedad Andaluza de Educación Matemática Thales se ha publicado el artículo titulado "Partición prismática de paralelepípedos en seis pirámides triangulares equivalentes" cuyo autor es nuestro socio José R. Galo Sánchez. Un trabajo de investigación, que como se refleja en la filiación de la autoría, ha sido desarrollado dentro de nuestra RED Descartes.

Este trabajo generaliza el publicado en 2018 con el título "Partición prismática de un cubo en seis pirámides triangulares equivalentes" y en él, como se refleja en el resumen:

"Se analiza en detalle la descomposición de los diferentes tipos de paralelepípedos en pirámides cuadriláteras y en pirámides triangulares. Se obtienen de manera constructiva las particiones con cardinal mínimo y se profundiza en aquellas que, sin tener cardinal mínimo, están formadas por seis pirámides que forman dos prismas. Se cuantifican y detallan todas las particiones posibles y se proporcionan enlaces a recursos interactivos que permiten verlas digitalmente y, a su vez, también obtener los desarrollos planos con los que abordar su reproducción real o tangible y su manipulación. Para cualquier paralelepípedo que defina el interesado se obtiene un entretenido puzle, no siempre fácil de componer."

Por ejemplo, en la siguiente escena se han englobado todas las posibilidades al permitir al usuario seleccionar el tipo de paralelepípedo que quiera, indicar las dimensiones que desee, elegir una partición de todas las posibles y, procediendo a imprimir los desarrollos planos de las pirámides que la componen, pasar a construir, como un puzle, un modelo tangible del paralelepípedo considerado. Para ello, en la escena, se cuenta con un menú con las siguientes opciones:

• Selecciona el paralelepípedo (Cubo, Ortoedro, Romboedro con corte por la diagonal menor o la mayor y Romboiedro).
• Ver el desarrollo plano de las diferentes pirámides que pueden aparecer en la partición del paralelepípedo.
• Elegir la partición que se desee construir, reflejándose los desarrollos planos de las seis pirámides que intervienen en la misma, pudiendo proceder a la impresión de cada uno de ellos.

Pulsa sobre la imagen para abrir la escena

Os incluimos a continuación dicho artículo y os invitamos a su lectura, a que realicéis observaciones y comentarios al mismo y a que lo divulguéis a través de vuestras redes sociales y profesionales. También a que, usando los recursos interactivos ahí enlazados y disponibles en nuestra web, construyáis particiones de diferentes paralelepípedos y en el aula abordéis su reconstrucción y propiedades.

Finalmente destaquemos que el autor, en las conclusiones del estudio, nos señala que el germen de este análisis fue la observación de una escena desarrollada en el año 2001 por nuestra colega Ángela Núñez Castaín, entrañable y querida pionera del proyecto Descartes. En concreto, en esas conclusiones se refleja que el exhaustivo estudio realizado:

"Comprende una amplia casuística que surgió a raíz de la adaptación a DescartesJS de una escena en la que se observaba una partición prismática de un cubo (Núñez Castaín, A., 2001) y en cada uno de los prismas, en los que quedaba dividido, aparecían diferentes tipos de pirámides equivalentes entre sí. Al abordar el análisis de la situación se comprobó que las referencias a las particiones de un cubo en pirámides quedaban planteadas de manera deslavazada o inconexa, mostrando sólo aquellos casos particulares en los que se encuentra mayor regularidad, pero no desde un punto de vista global e integrador. Eso fue el objetivo primario de estudio realizado en un artículo anterior (Galo-Sánchez J.R., 2018) y el objetivo secundario su generalización a los paralepípedos que es lo que aquí ha quedado realizado. La extensión a hexaedros convexos de caras cuadriláteras {4,4,4,4,4,4}, como poliedro no regular que puede considerarse similar al cubo, también ha sido realizada por el autor e implica algunas particularidades adicionales interesantes que serán objeto de una publicación ulterior."  

Ese último análisis ha sido descrito por el autor en la página 104 y siguientes del artículo interactivo "Partición de hexaedros convexos de caras cuadriláteras en pirámides" que está publicado en nuestro servidor dentro del proyecto de libros interactivos iCartesiLibri.

A punto de comenzar el nuevo curso académico, desde la Red Educativa Digital Descartes se quiere presentar distintos Proyectos con recursos digitales para su utilización en la Universidad. Estos materiales facilitan la realización de actividades basadas en la exploración, visualización y adquisición y ampliación de conocimientos así como promover el trabajo individual y colaborativo.

Los Proyectos desarrollados por la RED Descartes para el profesorado y para la comunidad educativa universitaria son los siguientes:

•  Misceláneas. Escenas aisladas que puede utilizar el profesorado directamente para ilustrar conceptos o para construir actividades de trabajo en el aula o de forma autónoma por los estudiantes.

• Unidades didácticas Interactivas para la Universidad. Dentro del proyecto Un_100 se han publicado 101 unidades didácticas para nivel universitario desarrollado por docentes de México, España, Colombia y Chile. El desarrollo de las unidades se ha  organizado en los siguientes temas:
  • Álgebra lineal
  • Cálculo de una variable
  • Cálculo de varias variables
  • Combinatoria
  • Economía y finanzas
  • Física general
  • Fractales y caos
  • Geofísica
  • Geometria 1: básica
  • Geometría 2: analitica
  • Geometría 3: avanzada
  • Lógica, conjuntos y categorías
  • Matemáticas de la computación
  • Mecánica celeste
  • Mecánica: estática
  • Métodos numéricos
  • Estadística y probabilidad
  • Termodinámica
  • Variable compleja
• Libros digitales iCartesLibri. Recursos digitales en formato libro con contenidos variados y para distintos niveles.
• Ingeniería y tecnología. Repositorio de recursos digitales agrupados según el siguiente índice temático
  • Ciencias computacionales
  • Física: estática
  • Mecánica de materiales
  • Elementos de máquinas
  • Hormigón o concreto
  • Análisis estructural
  • Hidráulica
  • Topografía
  • Termodinámica
  • Ciencias administrativas y económicas
  • Ciencias básicas
• • • Cálculo de una variable
    • Cálculo de varias variables
    • Métodos numéricos
    • Álgebra lineal
    • Geometría
    • Estadística
    • Probabilidad
    • Física General
    • Química

En el siguiente video se muestra cómo acceder a estos recursos junto con algunos ejemplos de muestra.

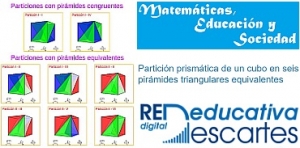
En el Vol. I, Núm. 2 del Open Journal "Matemáticas, Educación y Sociedad"  (ISSN: 2603-9982) se ha publicado el artículo titulado "Partición prismática de un cubo en seis pirámides triangulares equivalentes". Un detallado trabajo de investigación que, como se refleja en la autoría, ha sido desarrollado dentro de nuestra RED Descartes por nuestro socio José R. Galo Sánchez.

Os invitamos a su lectura, a que realicéis observaciones y comentarios al mismo y a que lo divulguéis a través de vuestras redes sociales y profesionales.

NOTA: En este pdf hay numerosos enlaces externos a recursos interactivos desarrollados con Descartes y que están publicados en nuestro servidor de contenidos. Os aconsejamos que la apertura de cada uno de estos enlaces la realicéis posicionando el ratón sobre el enlace y pulsando Ctrl+clic, de esta manera el recurso enlazado se abre en una nueva pestaña y permite realizar una lectura del pdf sin necesidad de tener que volver a posicionarse en el punto desde el que se produjo el salto. 

Este mes vamos a ver los movimientos en el plano, correspondientes a 3ºESO Académicas:

1.Vectores
   Concepto de vector. Coordenadas
   Vectores equipolentes
   Suma de vectores

2.Traslaciones
   Traslación según un vector
   Composición de traslaciones

3.Giros
   Giro de centro O y ángulo α
   Simetría central
   Figuras invariantes de orden n

4.Simetría axial
   Simetría de eje e
   Figuras con eje de simetría
   Composición de simetrías axiales

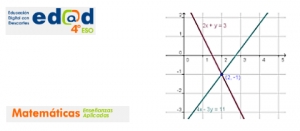
Este mes vamos a ver la unidad de "Sistemas de ecuaciones" de 4ºESO Aplicadas:

De forma muy breve hemos tratado los siguientes temas:

1.Sistemas de ecuaciones lineales
   Ecuación lineal con dos incógnitas
   Sistemas de ecuaciones lineales
   Clasificación de sistemas

2.Métodos de resolución
   Reducción
   Sustitución
   Igualación

3.Aplicaciones prácticas
   Resolución de problemas

4.Sistemas de inecuaciones con una
   incógnita
   Resolución 

Este mes vamos a ver el resumen de fracciones de 1ºESO:

Hemos tratado los siguientes puntos en nuestro vídeo:

1.Concepto de fracción.
   Las fracciones en nuestra vida.            
   Elementos de una fracción.       
   Cómo se lee una fracción.
   El valor de una fracción.
   Pasar una fracción a un decimal.  

2.Fracciones equivalentes.
   Fracciones equivalentes.
   Productos cruzados.    
   Simplificar una fracción.

3.Operaciones con fracciones.
   Paso a común denominador.
   Suma de fracciones.
   Suma y resta de fracciones.
   Multiplicación de fracciones.
   Fracción inversa de una fracción.
   División de fracciones.
   Operaciones combinadas

4.Aplicaciones
   Problemas con fracciones

Este mes vamos a ver una unidad de 1ºESO correspondiente a números decimales. Veamos al vídeo:

En este vídeo hemos visto los siguientes puntos:

1.Números decimales
   Numeración decimal
   Orden y aproximación
   Representación
   
2.Operaciones
   Suma y resta
   Multiplicación
   División
   
3.Sistema Métrico Decimal
   Longitud
   Capacidad
   Peso

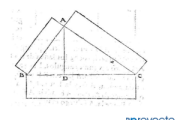
En el número 94 de la revista Epsilon de la Sociedad Andaluza de Educación Matemática Thales se ha publicado el artículo titulado "Sobre la forma y el crecimiento cordobés del Nautilus pompilius". Un detallado trabajo de investigación desarrollado dentro de nuestra RED Descartes, reflejándose así en la autoría, por los socios José R. Galo Sánchez, Ángel Cabezudo Bueno e Ildefonso Fernández Trujillo.

Os invitamos a su lectura, a que realicéis observaciones y comentarios al mismo y a que lo divulguéis a través de vuestras redes sociales y profesionales.

Desde los inicios del desarrollo de la herramienta Descartes, ésta, ha ido unida a un proyecto educativo de profesorado, que trabaja para el profesorado y para la comunidad educativa de la aldea global.

Las líneas de trabajo, de manera simplificada, se centran en:

1. Desarrollo de recursos educativos interactivos que:
   • promuevan el aprendizaje del alumnado de manera activa, convirtiéndolo en protagonista de su aprendizaje y actor principal del mismo.
   • permitan al profesorado una enseñanza innovadora en la que se contemplen nuevas prácticas educativas, motivadoras y metodológicamente situadas más en el aprendizaje que en la enseñanza en sí.
2. Promover la innovación en el aula entendiendo ésta no sólo como un espacio físico cerrado, sino como un contexto abierto, virtual, no sujeto a periodos temporales acotados, todo en base y gracias a las tecnologías de la información y la comunicación y a los recursos de Descartes.
3. Experimentar nuevos procedimientos y métodos para la consecución de una mejora educativa.

Desde la comunidad Descartes se pone a disposición de la comunidad educativa los resultados y avances mediante sus dominios: ProyectoDescartes.org, y REDDescartes.org y DescartesJS.org