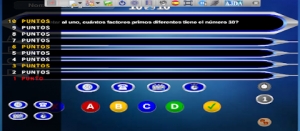
El nuevo juego 10x10 (I)
El primer juego didáctico que se realizó dentro del Proyecto AJDA fue una versión del programa de TV ¿Quién quiere ser millonario?, allá por el año 2007, llamada 10x10, ya que había que conseguir 10 puntos contestado a 10 preguntas, siguiendo la dinámica del popular concurso.
Este juego ha sido elegido como punta de lanza para realizar una ambiciosa potenciación de los juegos del Proyecto AJDA, mejorando su programación, funcionalidades y estilos. Por ello, el presente artículo va a ser el primero de una serie en la que se van a ir tratando y detallando los elementos y cambios introducidos. En esta primera publicación de la secuencia vamos a presentar de forma general las mejoras introducidas y en los siguientes las iremos desgranando. La relación de novedades es la siguiente:
- Nuevo menú superior desplegable.
- Nueva interfaz de introducción de parámetros de configuración de la partida.
- Rediseño de la pantalla para la introducción de ficheros de contenidos para juegos.
- Unificación en un sólo juego de todas las modalidades del mismo (modalidad con preguntas en ficheros, preguntas orales, sin preguntas...).
- Mejora integral de la presentación y estilos.
- Utilización de un diseño "Responsive".
- Perfeccionamiento del sistema de carga de los ficheros de preguntas.
- Potenciación de la interfaz traductora.
- Mejora en el código de programación y adaptación a la última versión de DescartesJS.
- Implementación de nuevas funcionalidades: guardado de configuración y partida, continuación de partidas, control de velocidad de animación, nuevos elementos de navegación y visualización, etc.
- Introducción de otros elementos y detalles.
Finalmente dejamos el enlace del nuevo juego 10x10 y emplazamos a seguir la serie de artículos que comenzamos.
Proyecto de investigación en AJDA (IV)
En este artículo cometamos las principales actuaciones que se están desarrollando dentro del Proyecto de Investigación que llevan conjuntamente el departamento de Ingeniería Telemática de la ETSI de la Universidad de Sevilla y el Proyecto AJDA durante el curso 2021-2022.
Los Trabajos Fin de Grado en que están actualmente en desarrollo son los siguientes:
- Módulo de administración general.
- Módulo de comunicación síncrona con juegos.
- Módulo de generación y administración de ficheros de preguntas.
- Módulo de LTI.
- Módulo de realización de estadísticas.
- Investigación sobre el estado del arte sobre gamificación on-line y propuesta de validación.
- Realización de documentación para el desarrollo de Proyectos.
- Generación de un cuerpo común de bibliografía.
- Actualización de la guía para desarrolladores.
- Mejora de la plataforma de gestión común para desarrolladores.
- Puesta a punto del entorno común para desarrolladores con todas las partes del Proyecto.
- Puesta a punto de un servidor en la nube con todas las partes del Proyecto.
- Unificación funcional de todos los módulos del Proyecto.
- Unificación de estilos/tecnologías del proyecto integrado y desarrollo de mejora de funcionalidades.
- Mejora en la interfaz del comunicación de los juegos seleccionados.
- Mejora en la interfaz del comunicación de los juegos seleccionados.
Juegos, estilos y Descartes
Gracias a la gran evolución de la aplicación Descartes, los juegos didácticos de ADJA se ha podido ir mejorando en funcionalidad, jugabilidad, integración y estética. En este artículo nos vamos a centrar en este último aspecto, ya que recientemente se ha realizado una revisión de los juegos de AJDA, siendo uno de sus principales objetivos la mejora en el estilo de los mismos.
A modo de ejemplo indicamos a continuación algunas de las mejoras más significativas introducidas en la interfaz de los juegos:
- Los controles, especialmente los de tipo botón, se muestran con bordes redondeados, resaltado al pasar el ratón por encima, sombra, distinción entre borde y relleno, posibilidad de mostrar o no degradados, introducción de imágenes, alineación de texto, etc. También otros controles han introducidos la posibilidad de introducir color, personalizar flechas, tamaño de letra, etc.
- La presentación de textos se ha mejorado sensiblemente: alineación, bordes sombreados, saltos de línea, posibilidad de introducir nuevas fuentes, etc., además de muchas funciones para trabajar con cadenas de numéricas y alfanuméricas.
- El manejo imágenes se ha enriquecido mucho: posibilidad de escalado, transparencia, rotación, recorte, introducción de imágenes en controles y fondos...
- Se han incluido funcionalidades interesantes para trabajar con los distintos espacios: transparencias, bordes, redondeado de esquinas, posibilidad de redimensionamiento, nuevos fondos, etc. Además de la interesantísima posibilidad de trabajar con espacios html.
- Unificación de estilos en el conjunto de juegos.
Difusión de ADJA y Descartes en la ETSI de la Universidad de Sevilla
 _
_La Escuela de Alquimia 2
Tras la magnífica acogida que la "Escuela de Alquimia" ha tenido entre el alumnado, hemos realizado ampliaciones en la "academia", de forma que se mantenga todo lo que hay y los objetivos del juego, pero aumentando el número de estancias y las opciones disponibles. Además introduce como parte de la mecánica del juego la realización de cuestionarios de preguntas. Comentamos a continuación las principales novedades.
En la sala de recaudación se pueden conseguir "tiradas mágicas" a través de cuestionarios de preguntas, además de la forma establecida en Alquimistas 1.
Desde la sala de alquimistas, los aspirantes además de pasar al laboratorio lo pueden hacer a las siguientes salas: cofres, conocimiento, retos, apuestas, ascensos y comercio. Mientras el participante tenga tiradas mágicas podrá ir pasando de una de estas salas a otra y decidir donde utilizarlas.
En la sala de cofres los aspirantes pueden utilizar sus tiradas mágicas para abrir cofres dentro de los cuales se encuentras premios muy similares a los del laboratorio. De igual forma podrán conseguir: ascensos, tiradas, gemas, X2 y cartas.
En la sala de conocimiento los participantes podrán gastar hasta 5 de sus tiradas mágicas para conseguir: oro, poción o conocimiento. Por cada tirada empleada el participante recibirá una pregunta. Según el número de respuestas correctas al final de la serie de preguntas se podrán canjear por los elementos conseguidos. Por un acierto 1 elemento, por dos aciertos 3, por tres aciertos 6, por cuatro aciertos 10 y por cinco respuestas correctas 15.
La sala de retos permite al jugador que está en su turno retar a otro participante. El duelo tendrá un máximo de 5 preguntas. Si ambos jugadores aciertan la cuestión planteada recibirán una tirada mágica, mientras que si ambos fallan la perderán. Si uno da la respuesta correcta y otro falla, el acertante ganará dos tiradas mágicas que perderá su oponente. Si alguno de los jugadores se queda sin tiradas mágicas el duelo finaliza.
En la sala de apuestas el participante que tiene el turno puede seleccionar hasta un máximo de 5 oponentes. A todos se les planteará hasta un máximo de 5 preguntas y para cada pregunta el retador decidirá el valor de la apuesta entre una y tres tiradas mágicas. Los que acierten ganarán el valor de la apuesta realizada y los que fallen la perderán. Los jugadores que se queden sin tiradas dejarán de participar. Si el retador se queda sin tiradas la ronda se termina.
La sala de ascensos es la estancia en la que pagando dos tiradas mágicas y respondiendo correctamente a cinco preguntas los aspirantes consiguen un ascenso. Tienen un comodín que les permite cometer un fallo. Si no superan la prueba descienden una posición en su rango.
La última sala nueva es la sala de comercio. En ella el aspirante que tiene el turno podrá pagar una tirada mágica para que, durante su turno, se establezca por sorteo una nueva tabla de precios. Además podrá comprar oro, poción o conocimiento al precio en tiradas mágicas que esté establecido.
Otra consideración es que se eleva a 10 el número máximo de oro, poción y conocimiento que cada aspirante puede acumular en su marcador.
El objetivo sigue siendo alcanzar el máximo rango dentro de la jerarquía alquimista del juego y superar al resto de los aspirantes.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)







 CONTACTO
CONTACTO
