Mostrando artículos por etiqueta: cónicas
Título: Ecuación general de las cónicas. Enfoque vectorial
Sección: Prometeo
Bloque: Álgebra
Unidad: Álgebra lineal
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Ana Belém Zavaleta Ramos
Diseño funcional: Ana Belém Zavaleta Ramos
Programación: Ana Belém Zavaleta Ramos
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Prometeo en https://proyectodescartes.org/Prometeo/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Lugares geométricos y las cónicas
Sección: Unidades didácticas
Bloque: Geometría
Unidad: Cónicas
Nivel/Edad: 1º Bachillerato CCNN (16 años)
Idioma: Castellano
Autoría: Antonio Caro Merchante
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de las Unidades Didácticas en
https://proyectodescartes.org/uudd/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
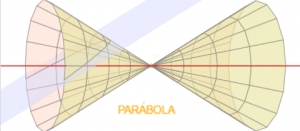
Las cónicas como lugares geométricos: La Parábola.
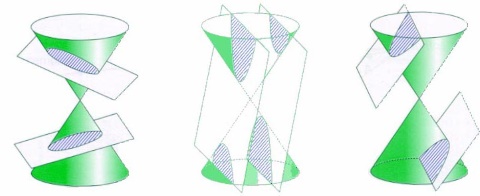
Dentro del estudio de los lugares geométricos tienen un especial interés los relativos a las cónicas por motivos muy diversos, fundamentalmente geométricos, físicos y filosóficos. Esta es la razón por la que en esta entrada vamos a continuar la aproximación a su conocimiento genérico analizando algunos aspectos de la Parábola considerada como lugar geométrico. Aprovechamos la oportunidad para señalar el aspecto popular, lúdico y funcional que la Geometría clásica ha tenido en las poblaciones cultas: el cucurucho con sus múltiples aplicaciones, los niños y niñas jugando con el aro, la peonza, el yoyo...
Consideramos, por tanto, que el estudio se centra en los ll.gg. generados por puntos que se mueven en el plano de forma que la razón (excentricidad) entre sus distancias a un punto fijo (foco) y a una recta (directriz) se mantiene constante.
Dentro del amplio grupo de trabajos relacionados con el tema destacamos, además de los que se muestran en la bibliografía, los que se enlazan a continuación.
- La Parábola como lugar geométrico.
- Generación de la Parábola como lugar geométrico.
Trabajo muy detallado de la creación del l.g. Ignacio Larrosa Cañestro (Grupo XeoDin)
Tomando como base, fundamentalmente, la documentación anterior hemos elaborado, con DescartesJS, las escenas que se exponen a continuación. Queremos notar que en dichos trabajos se hace uso de gran parte de los conceptos elementales de Geometría del Curriculum para ESO y Bachillerato.
Ambos trabajos dejan, para quien tenga interés en el tema, una buena cantidad de opciones de ampliación y mejora.
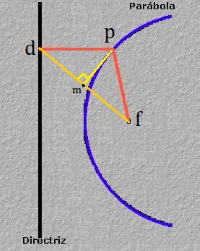
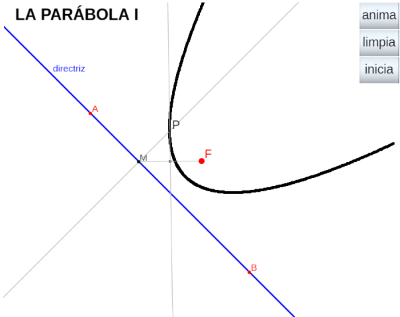
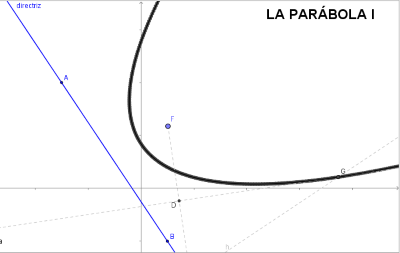
- Estudio de la PARÁBOLA I. La parábola como l.g. generado por el método, basado en la definición, del triángulo isósceles.
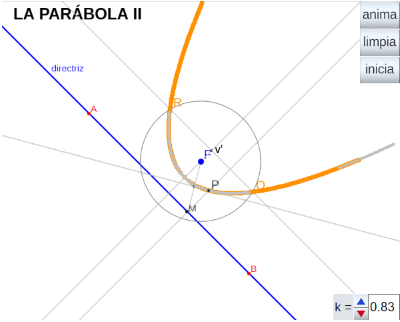
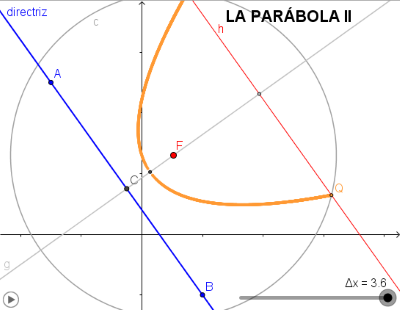
A partir de una recta d (directriz) y de un punto F (foco) consideramos que un punto del plano, P, pertenece a la parábola (F,d) si la distancia de P a M (ver imagen) es igual a la distancia de P a F. Esto es, el triángulo PMF es isósceles y por lo tanto la altura de dicho triángulo trazada desde P corta al lado FM en su punto medio. O bien que la intersección de la perpendicular a la directriz por un punto M de la misma con la perpendicular por el punto medio de FM es un punto de la parábola. Haciendo que M recorra la directriz obtendremos la parábola (F,d). - Estudio de la PARÁBOLA II. En esta ocasión se considera la parábola como el l.g. generado por los puntos, Q y R, intersección de la circunferencia c(F,r) con la paralela a la directriz por el vértice cuando el vértice, como punto virtual v', se desplaza por el eje focal desde su posición original hasta el infinito alejandose de la directriz (ver la animación completa), el radio de la circunferencia, r es igual a la distancia del vértice virtual v' a la directriz.
Es trivial comprobar que los puntos Q y R siempre son puntos de la parábola.
Se ha construido el l.g. por este segundo método sobre la construcción anterior por motivos didácticos.
En la primera escena el botón anima y en la segunda el pulsador k y el botón anima, generan el l.g. (parábola).
Continuamos animando a conocer el editor DescartesJS. Volvemos a exponer la adaptación a DescartesJS de la Unidad realizada por el profesor Antonio Caro Merchante debido a su relación con los conceptos en estudio.
Como en anteriores ocasiones notamos que las utilidades mostradas son fácilmente adaptables y admiten las modificaciones y/o ampliaciones que se consideren convenientes para los propósitos particulares de uso.
Las siguientes imágenes enlazan con pequeñas herramientas realizadas con el programa GeoGebra en las que se recrean los procesos de generación de la Parábola, primero por el método del triángulo isósceles y a continuación por el método clásico de la intersección de recta y circunferencia.
La Parábola. Método I.
hoja de trabajo de la parábola (I)
La siguiente imagen es el vínculo a la utilidad que muestra la generación del l.g. por el segundo método, intersección de paralela a la directriz con la circunferencia de centro el foco y radio variable..
La Parábola. Método II.
Proponemos el análisis de las utilidades anteriores, su modificación y mejora con objeto de lograr un profundo conocimiento de ambas plataformas y así potenciar la inclusión del cálculo simbólico en escenas DescartesJS de forma eficaz.
Esta vez en la sección de vídeo hemos elegido uno que muestra la deducción, paso a paso, de la ecuación del lugar geométrico que define a una curva cónica.
Las Cónicas como lugares geométricos
Continuando con la creación de la miscelánea "Las Espirales sugerimos completar su elaboración extrayendo el contenido relacionado con los lugares geométricos estudiados para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
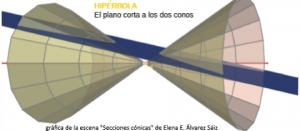
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
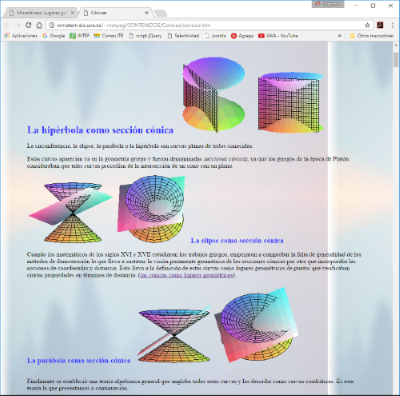
Lugares geométricos: La Hipérbola.
Dentro del estudio de los lugares geométricos tienen un especial interés los relativos a las cónicas por motivos muy diversos y no únicamente cronológicos; si no que también filosóficos, mercantilísticos y geométricos y en esta entrada vamos a continuar la aproximación a su conocimiento genérico analizando algunos aspectos de la Hipérbola considerada como lugar geométrico. Aprovechamos la oportunidad para señalar el aspecto popular, lúdico y funcional que la Geometría clásica ha ejercido sobre las poblaciones cultas: el cono como cucurucho para envolver desde tiempos ancestrales, los niños y niñas jugando con el aro y el yoyo...
Consideramos, por tanto, que el estudio se centra en los ll.gg. generados por puntos que se mueven en el plano de forma que la razón (excentricidad) entre sus distancias a un punto fijo (foco) y a una recta (directriz) se mantiene constante.
Dentro del amplio grupo de trabajos relacionados con el tema destacamos, además de los que se muestran en la bibliografía, los que se enlazan a continuación.
- La Hipérbola como lugar geométrico. MB (M. Banasik)
- Construcción de la hipérbola como lugar geométrico, a partir de un circulo y un punto exterior al círculo. La hipérbola que se genera tiene como focos el centro del círculo y el punto exterior al círculo. DORIS ÁLVAREZ QUINTERO
Tomando como base, fundamentalmente, la documentación anterior hemos elaborado, con DescartesJS, las escenas que se exponen a continuación. Queremos notar que en dichos trabajos se hace uso de gran parte de los conceptos elementales de Geometría del Curriculum para ESO y Bachillerato.
Ambos trabajos dejan, para quien tenga interés en el tema, una buena cantidad de opciones de ampliación y mejora.
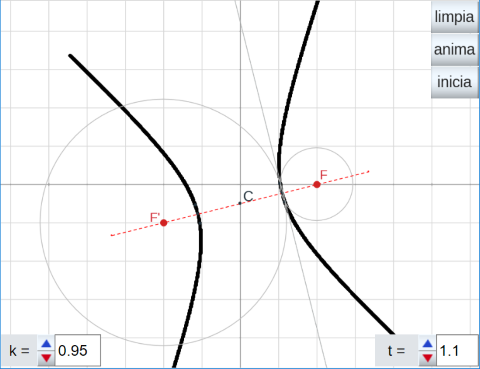
- Estudio de la HIPÉRBOLA I. La hipérbola como l.g. generado, la mitad del mismo, por los puntos de intersección de dos circunferencias: una con centro en el foco F y radio k y otra de centro el foco F' y radio r dependiente del pulsador k, de forma que cuando un radio aumenta el otro también. La otra mitad de la hipérbola se genera intercambiando los radios.
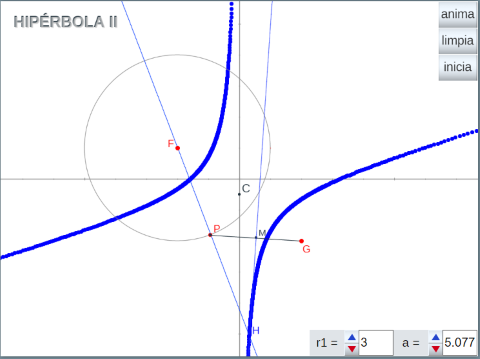
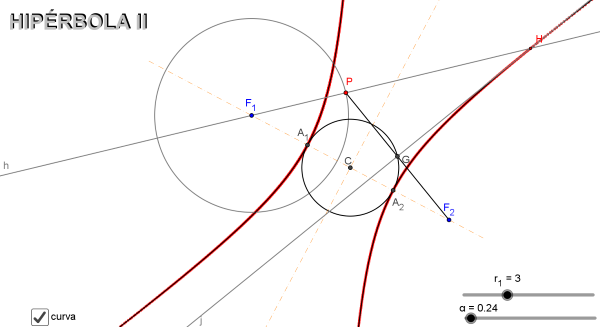
- Estudio de la HIPÉRBOLA II. En esta ocasión se considera la hipérbola como el l.g. generado por un punto, H cuando un punto P gira alrededor de la circunferencia de centro uno de los focos y radio cualquiera r1. El punto H se obtiene de la siguiente forma:
- Los puntos F y G son dos puntos libres que van a ser los focos de la hipérbola.
- Se traza la recta que une el centro de la circunferencia, punto F (uno de los focos), con el punto P.
- Se une el punto P con el otro foco, punto G.
- Se halla el punto medio del segmento PG, punto M y por él se traza la perpendicular al segmento.
- La intersección de las dos rectas trazadas es el punto H.
En ambas escenas los pulsadores k y a o el botón anima, generan el l.g. (hipérbola).
Continuamos animando a conocer el editor DescartesJS. Exponemos, en esta ocasión, la adaptación a DescartesJS de una Unidad realizada por el profesor Antonio Caro Merchante
Como en anteriores ocasiones notamos que las utilidades mostradas son fácilmente adaptables y admiten las modificaciones y/o ampliaciones que se consideren convenientes para los propósitos particulares de uso.
Las siguientes imágenes enlazan con pequeñas herramientas realizadas con el programa GeoGebra en las que se recrean los procesos de generación de la Hipérbola, primero como el l.g. creado por los dos puntos intersección de las circunferencias con centro en los focos y radios variables y en segundo lugar el l.g. generado por un punto cuando otro se desplaza por una circunferencia.
La Hipérbola. Método I.
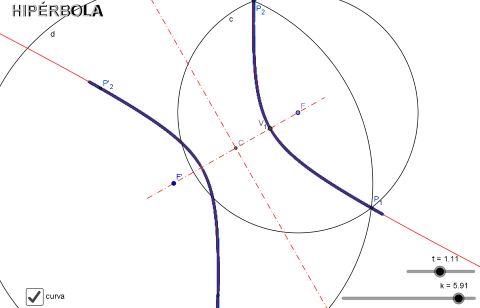
hoja de trabajo de la hipérbola (I)
La siguiente imagen es el vínculo a la utilidad que muestra la generación del l.g. por el segundo método.
La Hipérbola. Método II.
Proponemos el análisis de las utilidades anteriores, su modificación y mejora con objeto de lograr un profundo conocimiento de ambas plataformas y así potenciar la inclusión del cálculo simbólico en escenas DescartesJS de forma eficaz.
Esta vez en la sección de vídeo hemos elegido uno que muestra la creación, paso a paso, del lugar geométrico que define a la hipérbola.
Las Cónicas como lugares geométricos
Continuando con la creación de la miscelánea "Las Espirales sugerimos completar su elaboración extrayendo el contenido relacionado con los lugares geométricos estudiados para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
Título: Cónicas. Tangencias I
Sección: Miscelánea
Bloque: Geometría
Unidad: Cónicas
Nivel/Edad: 1º Bachillerato CCNN (16 años)
Idioma: Castellano
Autoría: Antonio Caro Merchante
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Cónicas. Tangencias II
Sección: Miscelánea
Bloque: Geometría
Unidad: Cónicas
Nivel/Edad: 1º Bachillerato CCNN (16 años)
Idioma: Castellano
Autoría: Antonio Caro Merchante
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: La elipse
Sección: Miscelánea
Bloque: Geometría
Unidad: Cónicas
Nivel/Edad: Taller 3º ESO (14 años)
Idioma: Castellano
Autoría: Antonio Caro Merchante
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: La elipse: Definición II
Sección: Miscelánea
Bloque: Geometría
Unidad: Cónicas
Nivel/Edad: 1º Bachillerato CCNN (16 años)
Idioma: Castellano
Autoría: Ildefonso Fernández Trujillo
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: La elipse: Definición I
Sección: Miscelánea
Bloque: Geometría
Unidad: Cónicas
Nivel/Edad: 1º Bachillerato CCNN (16 años)
Idioma: Castellano
Autoría: Ildefonso Fernández Trujillo
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Lugares geométricos: Las Cónicas.
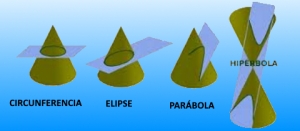
Continuamos con el estudio de los lugares geométricos y en esta entrada vamos a desarrollar una aproximación al conocimiento genérico de las curvas Cónicas no degenaradas, esto es: de la circunferencia, la Elipse, la Parábola y la Hipérbola consideradas como lugares geométricos. Curvas estas resultantes del trabajo de observación y posterior interpretación geométrica de la relación entre el ser humano y la naturaleza, por parte de los sabios griegos clásicos. En esta ocasión estudiaron la incidencia, en el cono de la visión ocular, de las ondas visibles, con objeto de establecer los principios teóricos del conocimiento de las formas y los colores.
Es de interés recordar que estas curvas están entre las primeras que fueron estudiadas y descritas.
Consideramos, por tanto, que el estudio se centra en los ll.gg. generados por puntos que se mueven en el plano de forma que la razón (excentricidad) entre sus distancias a un punto fijo (foco) y a una recta (directriz) se mantiene constante.
Dentro del amplio grupo de trabajos relacionados con el tema destacamos los que se enlazan a continuación.
- Estudio de las CÓNICAS. Trabajo realizado por M. Teresa Pérez y Oscar Arratia. Universidad de Valladolid.
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas.
- CÓNICAS, del profesor Antonio Caro Merchante. Tanto la unidad didáctica como la miscelánea que sobre este tema creó en su día el profesor Caro Merchante están en fase de adaptación al nuevo editor DescartesJS; no obstante avanzamos algunos resultados, aún provisionales, por el interés didáctico y posibilidad de uso del material en clase para consolidar conceptos y sobre todo como ayuda a la realización de ejercicios sobre cónicas: ecuaciones, tangencias, clasificación,.....
Tomando como base, fundamentalmente, la documentación anterior hemos elaborado o adaptado, con DescartesJS, las misceláneas que se exponen a continuación. Queremos notar la intención didáctica de dichos trabajos en los que se condensan una buena cantidad de los conceptos elementales de Geometría del Curriculum.
- Los trabajos dejan, para quien tenga interés en el tema o desee trabajar la precisión en clase, el ajuste fino de algunas variables controladas con pulsadores.
- Las siguientes posibles mejoras de la utilidad:
- convertir los pulsadores en animaciones.
- mostrar la ecuación de la elipse en algunas de sus formas
- ampliar la generación del l.g. al caso en el que el eje mayor de la elipse sea el vertical
- .................
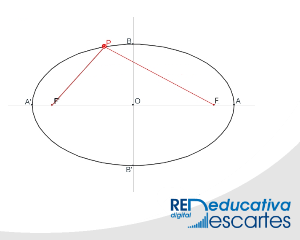
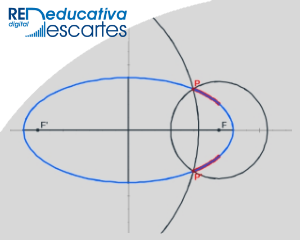
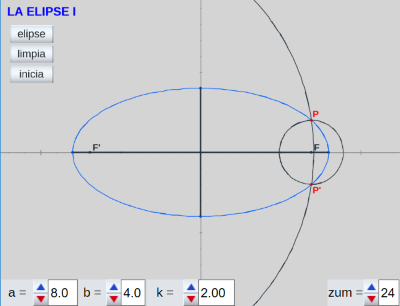
- Estudio de la ELIPSE I. La elipse como l.g. generado por los puntos, P y P', de intersección de dos circunferencias una con centro en el foco F y otra en el F' ambas con radios dependientes del pulsador k de forma que cuando un radio aumenta el otro disminuye.
Tanto en esta como en la siguiente miscelánea el pulsador k controla la generación del l.g.
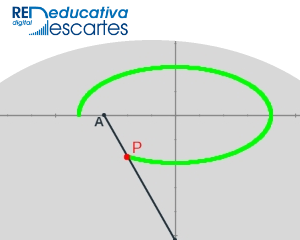
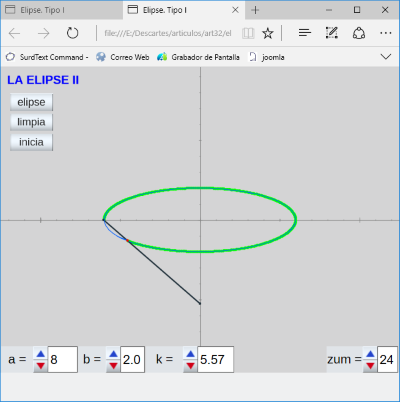
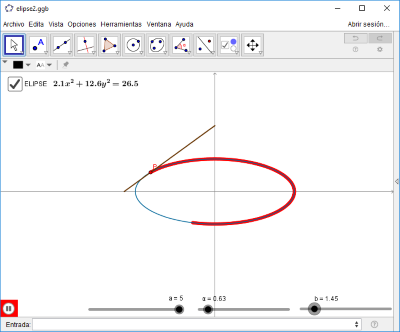
- Estudio de la ELIPSE II. En esta ocasión se considera la elipse como el l.g. generado por un punto de un segmento, distinto de los extremos, cuando dicho segmento desliza sin separarse por dos rectas perpendiculares tal como se muestra a continuación.
-
A continuación exponemos la adaptación a DescartesJS de la miscelánea realizada por el profesor Antonio Caro Merchante como ilustración de la contundencia didáctica del uso interactivo de una utilidad simple, que muestra de forma palpable un único concepto, como la enlazada a continuación.
propiedad de los puntos de la elipseLas miceláneas siguientes, que abordan algunas situaciones de tangencia, son también consecuencia directa del trabajo del profesor Caro Merchante.
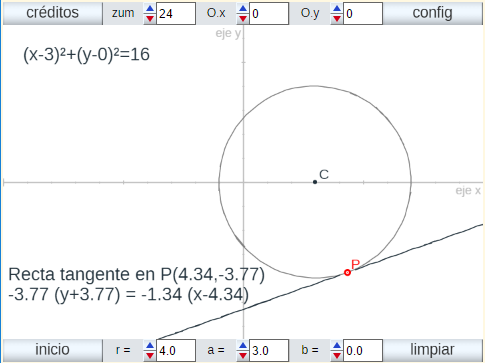
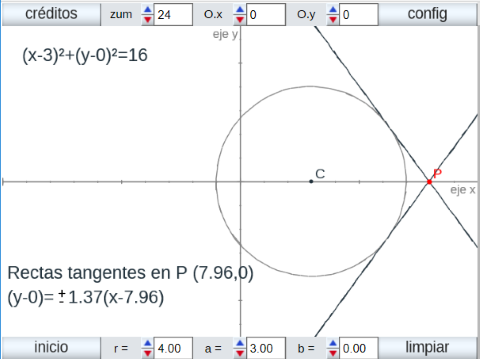
- Estudio de la ecuación de la tangente a una circunferencia por uno de sus puntos.
- Estudio de las ecuaciones de las tangentes a una circunferencia desde un punto exterior.
Como en anteriores ocasiones notamos que las utilidades mostradas son fácilmente adaptables y admiten las modificaciones y/o ampliaciones que se consideren convenientes para los propósitos particulares de uso.
Las siguientes imágenes enlazan con pequeñas herramientas realizadas con el programa GeoGebra en las que se recrean los procesos de generación de la Elipse, primero como el l.g. creado por los dos puntos intersección de las circunferencias con centro en los focos y radios variables y en segundo lugar el l.g. generado por un punto de un segmento cuando dicho segmento se desliza por dos rectas perpendiculares.
La Elipse. Método I.
hoja de trabajo de la Elipse (I)
La siguiente imagen es el vínculo a la utilidad que muestra la generación del l.g. por el segundo método.
La elipse. Método II.
Proponemos el análisis de las utilidades anteriores, su modificación y mejora con objeto de lograr un profundo conocimiento de ambas plataformas y así potenciar la inclusión del cálculo simbólico en escenas DescartesJS de forma eficaz.
Esta vez en la sección de vídeo hemos elegido uno que muestra la deducción, paso a paso, de la ecuación del lugar geométrico que define a una curva cónica.
Las Cónicas como lugares geométricos
Continuando con la creación de la miscelánea "Las Espirales" sugerimos completar su elaboración extrayendo el contenido relacionado con los lugares geométricos estudiados para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- "Secciones cónicas" de la profesora: Elena E. Álvarez Sáiz.
- " Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- " Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017