Mostrando artículos por etiqueta: universidad
Título: Métodos de punto fijo
Sección: Un_100
Bloque: Análisis
Unidad: Métodos numéricos
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: José R. Galo Sánchez
Diseño funcional: José R. Galo Sánchez
Programación: José R. Galo Sánchez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Mínimos cuadrados
Sección: Un_100
Bloque: Análisis
Unidad: Métodos numéricos
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Elena E. Álvarez Sáiz
Diseño funcional: Elena E. Álvarez Sáiz
Programación: Elena E. Álvarez Sáiz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Integración Numérica
Sección: Un_100
Bloque: Análisis
Unidad: Métodos numéricos
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Elena E. Álvarez Sáiz
Diseño funcional: Elena E. Álvarez Sáiz
Programación: Elena E. Álvarez Sáiz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Derivación Numérica
Sección: Un_100
Bloque: Análisis
Unidad: Métodos numéricos
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Elena E. Álvarez Sáiz
Diseño funcional: Elena E. Álvarez Sáiz
Programación: Elena E. Álvarez Sáiz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Fuerzas internas
Sección: Un_100
Bloque: Fuerzas y presiones
Unidad: Estática
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Juan Guillermo Rivera Berío
Diseño funcional: Juan Guillermo Rivera Berío
Programación: Juan Guillermo Rivera Berío
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Equilibrio de un cuerpo rígido
Sección: Un_100
Bloque: Fuerzas y presiones
Unidad: Estática
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Juan Guillermo Rivera Berío
Diseño funcional: Juan Guillermo Rivera Berío
Programación: Juan Guillermo Rivera Berío
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Fuerzas distribuidas
Sección: Un_100
Bloque: Fuerzas y presiones
Unidad: Estática
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Juan Guillermo Rivera Berío
Diseño funcional: Juan Guillermo Rivera Berío
Programación: Juan Guillermo Rivera Berío
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Estática de una partícula
Sección: Un_100
Bloque: Fuerzas y presiones
Unidad: Estática
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Juan Guillermo Rivera Berío
Diseño funcional: Juan Guillermo Rivera Berío
Programación: Juan Guillermo Rivera Berío
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Momento de una fuerza respecto a un punto
Sección: Un_100
Bloque: Fuerzas y presiones
Unidad: Estática
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Juan Guillermo Rivera Berío
Diseño funcional: Juan Guillermo Rivera Berío
Programación: Juan Guillermo Rivera Berío
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
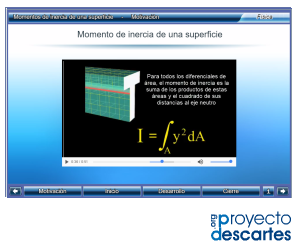
Título: Momentos de Inercia de una superficie
Sección: Un_100
Bloque: Fuerzas y presiones
Unidad: Estática
Nivel/Edad: Universidad (18 años en adelante)
Idioma: Castellano
Diseño del contenido: Juan Guillermo Rivera Berío
Diseño funcional: Juan Guillermo Rivera Berío
Programación: Juan Guillermo Rivera Berío
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Un_100 en https://proyectodescartes.org/Un_100/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional