Mostrando artículos por etiqueta: bachillerato
El cese de la actividad lectiva debido a las medidas excepcionales por la evolución del COVID-19 durante este tercer trimestre, nos ha obligado a replantear algunos aspectos relacionados con la docencia en las diferentes etapas educativas.
La etapa final de bachillerato merece especial atención ante la inminente realización de la Evaluación de Bachillerato para el acceso a la Universidad, que se llevará a cabo, previsiblemente, antes del verano. Muchos de los proyectos de la RED contienen materiales interactivos para 2º de bachillerato, que permiten al alumnado seguir el curso desde su casa y con la ayuda del profesorado, prepararse para las pruebas de selectividad.
En el siguiente vídeo presentamos la unidad Matrices, Determinantes y Sistemas de Ecuaciones del proyecto iCartesiLibri de la RED para el estudio del álgebra matricial y sus aplicaciones en la resolución de sistemas de ecuaciones. Su diseño, en forma de libro dinámico interactivo, proporciona una forma ágil y sencilla de navegación entre las diferentes páginas.
El contenido se ha elaborado siguiendo las pautas que marca el currículo de Matemáticas II de 2º de bachillerato y contiene, además de la parte teórica, muchos ejemplos y ejercicios para practicar.
Al final de la unidad se presenta una escena con los problemas de Álgebra propuestos en la Evaluación de Bachillerato para el acceso a la Universidad del año 2018, en cada distrito universitario de España.
Título: EVALUACIÓN de BACHILLERATO para el Acceso a la Universidad
Sección: Miscelánea
Bloque: Álgebra, Geometría y Análisis matemático
Unidad: Álgebra lineal, Geometría tridimensional, Funciones
Nivel/Edad: Bachillerato y Universidad (17 años o más)
Idioma: Castellano
Autoría: María José García Cebrian
Haz clic en la imagen para abrir el recurso
Descargar recurso Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Congruencias en el triángulo de Pascal
Sección: Miscelánea
Bloque: Álgebra
Unidad: Números y operaciones
Nivel/Edad: Bachillerato y Universidad (17 años o más)
Idioma: Castellano
Autoría: José R. Galo Sánchez
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Título: Muestrario de congruencias en el triángulo de Pascal
Sección: Miscelánea
Bloque: Álgebra
Unidad: Números y operaciones
Nivel/Edad: Bachillerato y Universidad (17 años o más)
Idioma: Castellano
Autoría: José R. Galo Sánchez
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Título: Estimación. Intervalos de confianza para la proporción y media poblacional. Test ciego.
Sección: Plantillas
Bloque: Aplicaciones
Unidad: Matemáticas - Estimación. Intervalos de confianza.
Nivel/Edad: 2º Bachillerato y universidad (17 o más años)
Idioma: Castellano
Autoría: Juan Jesús Cañas Escamilla
Haz clic en la imagen para abrir una muestra de este recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todas las plantillas en
https://proyectodescartes.org/plantillas/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
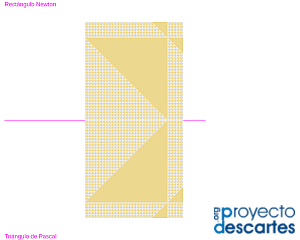
En el artículo "El rectángulo de Newton como «simétrico» del triángulo de Pascal" llegamos a la conclusión de que si conocemos las congruencias con cero de los coeficientes en el Triángulo de Pascal, según la orientación dada por Pascal a su triángulo, entonces, por simetría, tenemos las correspondientes al rectángulo de Newton. Eso es lo que se refleja en la siguiente imagen.
Imagen de las congruencias con cero módulo dos de los coeficientes binomiales en el rectángulo de Newton.
Simetría respecto a esas congruencias en el Triángulo de Pascal
En este artículo vamos a centrarnos en analizar cuándo un coeficiente binomial es divisible por un determinado número primo, un problema sobre el que podemos encontrar bastantes resultados con fundamento aritmético y algebraico. Aquí, nos centraremos en aquellos resultados que nos permitan determinar y visualizar gráficamente esas congruencias, es decir, poder obtener el gráfico de la imagen anterior, u otros análogos, sin necesidad de calcular el coeficiente binomial y determinar su congruencia u obtener ésta mediante una recurrencia.
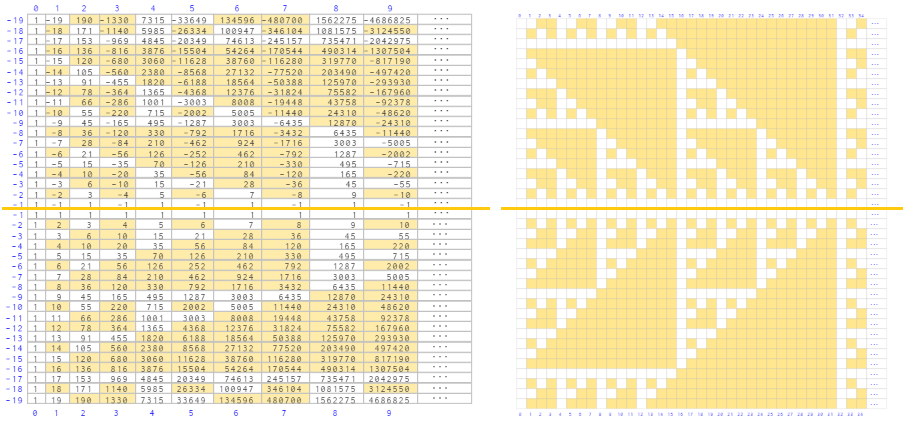
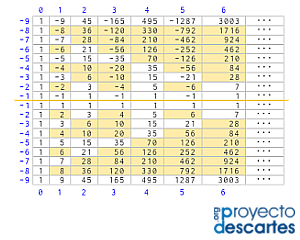
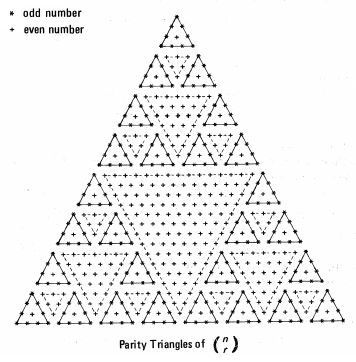
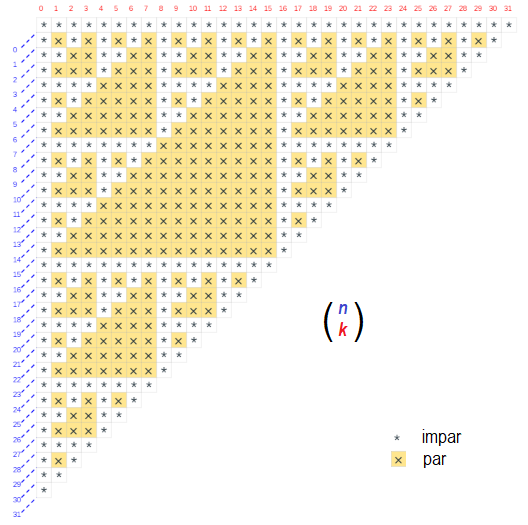
La primera representación gráfica de estas congruencias puede situarse en un brevísimo artículo de Kung (1976). Esa gráfica se muestra en la siguiente imagen, la situada a la izquierda, y en la de la derecha se refleja la gráfica análoga, pero mostrándola según la orientación original de Pascal y coloreando en naranja los números combinatorios pares (en ella cada número se determina observando el correspondiente índice superior en color azul y en rojo el inferior):
 |
 |
|
Triángulos de paridad en el Triángulo de Pascal. Kung, S. H. L. (1976). |
Triángulos de paridad en el Triángulo de Pascal en su orientación original |
Kung adicionalmente afirma, sin incluir la demostración, que para i entero no negativo:
- Si n = 2i y 1 ≤ k ≤ n-1, entonces
es par. - Si n = 2i-1 y 0 ≤ k ≤ n, entonces es impar.
Y ello se observa en las imagenes anteriores ya que para n = 0, 3, 7, 15, 31, todos los símbolos en esas filas o diagonales, respectivamente, son asteriscos (números impares). Y para n = 2, 4, 8, 16, 32, son todos cruces (números pares), salvo el primero y el último.
Ese es un breve artículo, pero que marca unas pautas que son extrapolables a la obtención de patrones en las congruencias con cero módulo otros números primos. De hecho, ese resultado es un caso particular de los dos que fueron enunciados en 1947 por N. J. Fine en su artículo "Binomial coefficients modulo prime", si bien el primero de ellos (según Joris et al. en un artículo de 1985) ya lo formuló Ram en 1909 (B. RAM, Common factors of n!/m!(n-m)!, (m= 1, 2 ,..., n- l), J. Indian Marh. Club (Madras) 1 (1909), 39-43):
- La condición necesaria y suficiente para que todos los coeficientes binomiales con 0 < k < n, sea divisible por un primo p es que n sea una potencia de p.
- La condición necesaria y suficiente para que ningún coeficiente binomial de índice superior n, con n = n0 + n1 p + n2 p2 + ⋅⋅⋅ + nm pm, siendo 0 ≤ nr < p y nr > 0, sea divisible por p es que nr = p - 1 para r < m.
Veamos cómo se reflejan estos resultados de una manera gráfica en las dos imágenes siguientes:
- En la imagen izquierda, se refleja gráficamente el primer resultado cuando p = 3, mostrándose todas las líneas en las que todos los números combinatorios son divisibles por 3, salvo el primero y el último. Esas líneas se corresponden con con 0 < k < n y n = 30, 31, 32, 33,... Gráficamente vienen a ser las "hipotenusas" de los triángulos rectángulos que particionan al triángulo de Pascal y que lo muestran a diferentes escala y posteriormente utilizaremos esta analogía y terminología coloquial para ubicar y describir otros resultados.
- En la de la derecha se reflejan aquellas líneas en las que ningún número combinatorio es divisible por 3. En la parte superior de esa imagen se reflejan las separaciones entre esas filas (por falta de espacio tipográfico no se refleja el caso 30) y a la derecha se muestra la descomposición p-ádica del índice n correspondiente a los números combinatorios de cada una de esas líneas (expanda la imagen pulsando sobre ella para verlo). Por ejemplo, para 53 = 2 30 + 2 31 + 2 32 + 1 33 y eso nos muestra el camino de "saltos" de amplitud potencias de tres que se han de dar para, partiendo de 0, llegar a 53 (dos de amplitud 30, dos de 31, dos de 32 y uno de 33). Es decir, logramos mostrar visualmente, geométricamente, lo que queda escondido en un abstracto resultado algebraico, el cual puede ser chocante a cualquiera que accede a él por primera vez. Emulando a nuestro alumnado a la pregunta: ¿a quién se le ocurre que la descomposición p-adica da respuesta a este problema? le mostramos que el resultado algebraico, posiblemente, fue consecuencia de su visualización y la "pureza" matemática procedió a esconderlo.
 |
 |
|
Números combinatorios |
Números combinatorios |
En la miscelánea del final de este artículo podemos reproducir las situaciones descritas para cualquier primo hasta el 31 y en este enlace se tiene un muestrario rápido de las mismas.
Y justamente, en base a la observación de esos patrones geométricos, podemos visualizar y deducir la propiedad que nos permite detectar todas las hipotenusas de todos los triángulos rectángulos isósceles que muestran esas congruencias. Podemos ver cómo hay triángulos de diferente tamaño, siendo pa-1 el tamaño de las hipotenusas respectivas, y cada uno de ellos tienen una distribución periódica en horizontal y vertical con un periodo pa. Por ejemplo, en la siguiente imagen se reflejan en color naranja los números combinatorios congruentes con cero módulo 5 y se observan tres tipos de triángulos según su tamaño: los de hipotenusa 4 = 51-1, los de 24 = 52-1 y parcialmente (en la esquina inferior derecha) el de 124 = 53-1. La hipotenusa del primero se ha reflejado en color verde y el triángulo se repite periódicamente en horizontal y vertical con un periodo 5, según se ve en dicha imagen. La del segundo está reflejada en color violeta y se repite también periódicamente con periodo 52, y así sería de manera análoga y sucesiva.
Periodicidad en las hipotenusas de los triángulos congruentes
Lo anterior, ahora le invito a que mire con ojos algebraicos, queda englobado en el resultado que enuncio a continuación:
p es divisor de todos los números combinatorios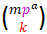 
con m, a, k ∈ ℕ, 0 < k < mpa y k no divisible por pa (1)
Este resultado personal puede relacionarse o considerarse como una reinterpretación —que se centra, enfoca y destaca el aspecto de periodicidad— del aportado por Ram (1909) —del que puede verse la demostración realizada por Albree (1972)— que afirma:
Para cualquier entero positivo n , pr = mcd { con 0 < k < n, y mcd (k, p)=1 } donde p es primo, r es un entero positivo y pr divide a n.
Y ¿por qué les remarco que es de gran interés determinar esas hipotenusas? La respuesta también puede visualizarse en la imagen anterior y lo detallamos a continuación ya que conocida una hipotenusa de números congruentes con 0 módulo p, con r < k < s, por la propiedad de los números combinatorios que relaciona los de índice superior n+1 con los de índice n,
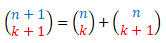
se deduce que los números combinatorios que componen el triángulo rectángulo T(n; r, s)
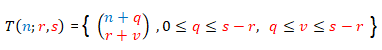(2)
—ver imagen siguiente— son también congruentes con 0 módulo p. La justificación es simple, dado que la suma de dos números divisibles por p es un número divisible por p.
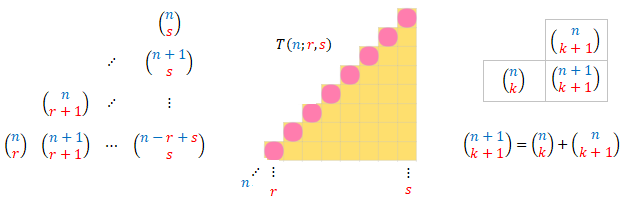Transmisión de la congruencia en las hipotenusas a los triángulos rectángulos
Joris et al. (1985) abordan un estudio más profundo al que necesitamos aquí de las propiedades de estos triángulos y a él dirigimos a quienes estén interesados en incrementar su conocimiento en este tema.
Combinando (1) y (2), concluyo que los números combinatorios congruentes con 0 módulo p siguen un patrón de triángulos "rectángulos" T(pa; 1, pa-1) cuyas hipotenusas están constituidas por los números combinatorios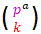 
con a, k ∈ ℕ, 0 < k < pa.
Patrón de triángulos T(pa; 1, pa-1) con p=3 y a = 1,2, y 3
distribuyéndose de forma periódica según el esquema:
T(m pa; 1+k pa, (1+k)pa-1) con 0 ≤ k < m y a, m ∈ ℕ
Eso es lo que se observa en el siguiente mosaico de imágenes donde se refleja:
-
- imagen superior izquierda: números combinatorios congruente con 0 módulo 3 en color naranja.
- imagen superior derecha: triángulos congruentes con T(31; 1, 31-1) en color verde claro y las hipotenusas en verde oscuro, y desplazamiento periódico en horizontal y vertical con periodo 3.
- imagen inferior derecha: triángulos congruentes con T(32; 1, 32-1) en color verde claro y las hipotenusas en verde oscuro, y desplazamiento periódico en horizontal y vertical con periodo 32.
- imagen inferior derecha: triángulos congruentes con T(33; 1, 33-1) en color verde claro y las hipotenusas en verde oscuro, y desplazamiento periódico en horizontal y vertical con periodo 33.
Esquema de periodicidad de los triángulos T(pa; 1, pa-1) con p=3 y a = 1, 2, y 3
Así pues la reproducción de todas las congruencias con 0 es una mera reiteración gráfica, periodicidad, de esos triángulos básicos citados.
Pero dado un número combinatorio ¿podemos saber si es o no congruente con 0 módulo p sin necesidad de calcularlo, de una manera sencilla, rápida y sin aplicar recursividad, o lo que es equivalente, sin basarse en diagonales, es decir, en números combinatorios con índice superior menor que n? ¡Veamos que sí! y para ello nos vamos a basar en la posición relativa (fila y columna) que ocupa cada número combinatorio en el triángulo de Pascal original. Observemos que el número ocupa la fila n-k y la columna k, que todos los números combinatorios de índice n cumplen que la suma de la fila y la columna que ocupan es n, y que los números combinatorios del triángulo rectángulo T(n; r, s) cumplen que la suma de la fila y la columna de todos ellos es mayor o igual que n. Con este dato y en base a la periodicidad podemos afirmar lo siguiente:
Dado el número combinatorio , consideremos la descomposición p-ádica de n-k y de k
n-k = a0 + a1 p + a2 p2+ ⋅ + am pm
k = b0 + b1 p + b2 p2+ ⋅ + bm pm
con m = max (ent(logp(n-k)), ent(logp(k)) ), 0 ≤ aj, bj < p, se verifica que:
es divisible por p si y solo si aj + bj ≥ p al menos para algún j, 0 ≤ j ≤ m.
Además, para los valores de j en los que aj + bj ≥ p, entonces está en un triángulo T(pj+1; 1, pj+1-1) de números congruentes con 0 módulo p.
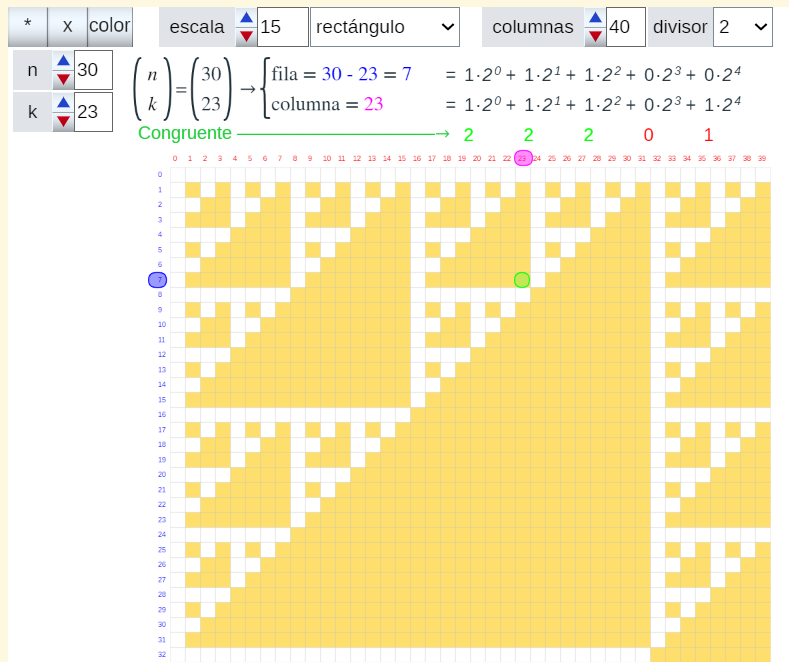
En la siguiente escena se puede reproducir visualmente todos los resultados indicados anteriormente y profundizar en el conocimiento de las interioridades del Triángulo de Pascal.
Pulsa sobre la imagen para abrir la escena
En la imagen anterior se observa como el número combinatorio 30 sobre 23 es congruente con cero módulo 2 y forma parte de un triángulo rectángulo básico de hipotenusa 1 , otro de hipotenusa 3 y otro de hipotenusa 7 (para éste último es evidente, para los dos anteriores haga traslaciones de los triángulos básicos, según el periodo antes indicado, y verá que ese número combinatorio está incluido en ellos). Todo se obtiene sin más que observar la relación de los coeficientes en la descomposición 2-ádica de la fila y columna que ocupa, ya que en este caso, para las tres primeras potencias de 2 la suma de los coeficientes es mayor o igual que el valor del módulo (en este caso 2).
Llegados a esta meta, estando aún confinados por la pandemia del COVID-19, cabe preguntarse si este artículo, y los dos anteriores publicados en este blog sobre este tema, tendrá o no continuidad... el tiempo lo dirá o quizás la necesidad de cambiar de temática para relajar la mente en otros ámbitos lo interrumpa. Tenga o no alguna nueva adenda, gracias a todos los que habéis dedicado parte de vuestro tiempo en leer lo descrito y los nuevos resultados hallados y expuestos en esta trilogía.
Título: Muestrario de simetrías en las congruencias en el paralelogramo de Newton y el triángulo de Pascal
Sección: Miscelánea
Bloque: Álgebra
Unidad: Números y operaciones
Nivel/Edad: Bachillerato y Universidad (17 años o más)
Idioma: Castellano
Autoría: José R. Galo Sánchez
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Título: El rectángulo de Newton como "simétrico" del triángulo de Pascal (congruencias)
Sección: Miscelánea
Bloque: Álgebra
Unidad: Números y operaciones
Nivel/Edad: Bachillerato y Universidad (17 años o más)
Idioma: Castellano
Autoría: José R. Galo Sánchez
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Título: El rectángulo de Newton como "simétrico" del triángulo de Pascal
Sección: Miscelánea
Bloque: Álgebra
Unidad: Números y operaciones
Nivel/Edad: Bachillerato y Universidad (17 años o más)
Idioma: Castellano
Autoría: José R. Galo Sánchez
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Con motivo de la gravísima situación que estamos sufriendo, las autoridades educativas instan a los centros a adoptar las medidas que consideren más adecuadas para garantizar la continuidad de los procesos de enseñanza-aprendizaje a través de tareas y actividades que puedan ser desarrolladas por el alumnado en sus domicilios, utilizando los medios de comunicación electrónicos establecidos o acordados entre el alumnado y el profesorado, como pueden ser entornos virtuales de aprendizaje. Ahora bien, como manifiesta Fernando Trujillo en Twitter, cuya opinión comparto, no debemos empezar buscando la herramienta de comunicación, sino qué información daremos a nuestro alumnado, qué deben desarrollar con ella, cómo deben hacerlo y cómo los evaluaremos, en su caso. Particularmente, y es lo que haré en estos días, recomiendo usar las herramientas de intercomunicación que venimos empleando durante el curso, indicando a nuestro alumnado, día a día, todos los aspectos que menciona Fernando.
Superadas estas decisiones iniciales, obviamente necesitaremos recursos especialmente diseñados para la enseñanza a distancia y, con todos mis respetos a otras alternativas, los que mejor reúnen estas características son los libros interactivos del Proyecto ED@D, que fueron diseñados por el CIDEAD, Centro para la Innovación y Desarrollo de la Educación A Distancia, organismo dependiente del Ministerio de Educación, con el objetivo de atender "a los ciudadanos españoles en el exterior y a aquellas personas que, aun residiendo en territorio nacional, se ven imposibilitadas para recibir enseñanza a través del régimen ordinario", a pesar de encontrarse en edad de escolarización obligatoria.
Por diseño, se trata de un material interactivo autosuficiente, proporcionando tanto las convenientes explicaciones teóricas como un número suficiente de actividades y ejercicios en los que la introducción de semillas aleatorias aportan diferentes instancias de los mismos, permitiendo practicar a la medida de las necesidades de cada cual, ya que van acompañadas de correcciones automáticas. Consecuentemente se promueve el objetivo de “aprender a aprender”, se refuerza la autonomía personal y el adecuado desarrollo competencial.
En base a estos supuestos, cada unidad consta de seis secciones, cuyos detalles pueden consultarse en la página del proyecto, bajo los epígrafes: Antes de empezar, Contenidos y resumen, Ejercicios para practicar, Autoevaluación, Para enviar al tutor y Para saber más, disponiendo de versiones para las distintas materias de Matemáticas en la ESO en castellano, catalán y gallego.
En caso de necesidad, ofrecemos tutoriales con los detalles concretos de cada unidad y el procedimiento para insertar estos y otros recursos en un aula Moodle.
La Organización No Gubernamental RED Descartes viene ofreciendo, desde hace casi siete años, recursos educativos abiertos para todas las etapas educativas durante 24 horas al día y los 365 días del año, de forma completamente altruista, queriendo aportar nuestro granito de arena en estos tiempos tan difíciles. Por ello, elaboramos y difundimos este especial artículo con resumen y acceso a todos los recursos disponibles.
