Mostrando artículos por etiqueta: universidad
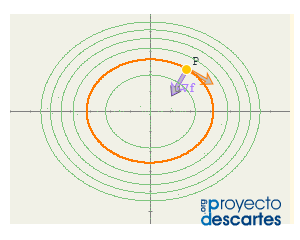 Título: Gradiente y curvas de nivel
Título: Gradiente y curvas de nivel
Sección: Miscelánea
Bloque: Análisis
Unidad: Derivación de funciones
Nivel/Edad: Universidad (18 o más años)
Idioma: Castellano
Autoría: Elena E. Álvarez Sáiz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.
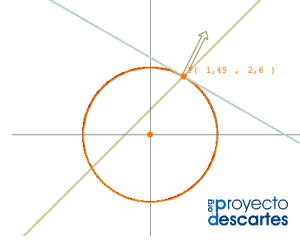 Título: Derivación de curvas paramétricas
Título: Derivación de curvas paramétricas
Sección: Miscelánea
Bloque: Análisis
Unidad: Derivación de funciones
Nivel/Edad: Universidad (18 o más años)
Idioma: Castellano
Autoría: Elena E. Álvarez Sáiz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.
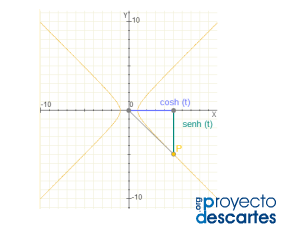 Título: Funciones trigonométricas e hiperbólicas
Título: Funciones trigonométricas e hiperbólicas
Sección: Miscelánea
Bloque: Análisis
Unidad: Representación gráfica de funciones
Nivel/Edad: Universidad (18 o más años)
Idioma: Castellano
Autoría: Elena E. Álvarez Sáiz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm
Este material está publicado bajo una licencia:

Creative Commons Atribución-NoComercial- CompartirIgual 3.0.
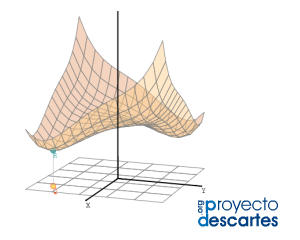 Título: Extremos de funciones de dos variables: Método del hessiano
Título: Extremos de funciones de dos variables: Método del hessiano
Sección: Miscelánea
Bloque: Análisis
Unidad: Derivación de funciones
Nivel/Edad: Universidad (18 o más años)
Idioma: Castellano
Autoría: Elena E. Álvarez Sáiz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm
Este material está publicado bajo una licencia:

Creative Commons Atribución-NoComercial- CompartirIgual 3.0.
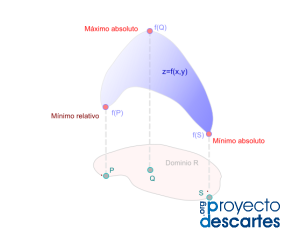 Título: Extremos absolutos de una región cerrada y acotada
Título: Extremos absolutos de una región cerrada y acotada
Sección: Miscelánea
Bloque: Análisis
Unidad: Derivación de funciones
Nivel/Edad: Universidad (18 o más años)
Idioma: Castellano
Autoría: Elena E. Álvarez Sáiz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm
Este material está publicado bajo una licencia:

Creative Commons Atribución-NoComercial- CompartirIgual 3.0.
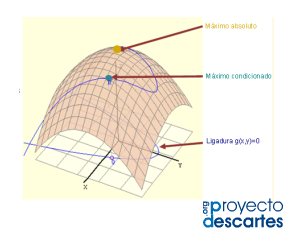 Título: Extremos: Multiplicadores de Lagrange
Título: Extremos: Multiplicadores de Lagrange
Sección: Miscelánea
Bloque: Análisis
Unidad: Derivación de funciones
Nivel/Edad: Universidad (18 o más años)
Idioma: Castellano
Autoría: Elena E. Álvarez Sáiz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm
Este material está publicado bajo una licencia:

Creative Commons Atribución-NoComercial- CompartirIgual 3.0.
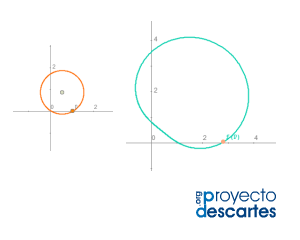 Título: Transformaciones complejas elementales
Título: Transformaciones complejas elementales
Sección: Miscelánea
Bloque: Análisis
Unidad: Representación gráfica de funciones
Nivel/Edad: Universidad (18 o más años)
Idioma: Castellano
Autoría: Elena E. Álvarez Sáiz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm
Este material está publicado bajo una licencia:

Creative Commons Atribución-NoComercial- CompartirIgual 3.0.
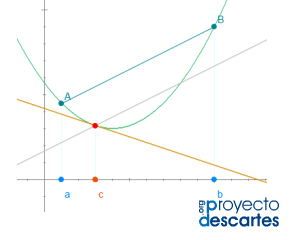 Título: Teorema del valor medio
Título: Teorema del valor medio
Sección: Miscelánea
Bloque: Análisis
Unidad: Límites y continuidad de funciones
Nivel/Edad: Universidad (18 o más años)
Idioma: Castellano
Autoría: Elena E. Álvarez Sáiz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm
Este material está publicado bajo una licencia:

Creative Commons Atribución-NoComercial- CompartirIgual 3.0.
 Título: Series: Suma parcial enésima
Título: Series: Suma parcial enésima
Sección: Miscelánea
Bloque: Análisis
Unidad: Sucesiones y progresiones
Nivel/Edad: Universidad (18 o más años)
Idioma: Castellano
Autoría: Elena E. Álvarez Sáiz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm
Este material está publicado bajo una licencia:

Creative Commons Atribución-NoComercial- CompartirIgual 3.0.
 Título: Series de potencias. Series de Taylor
Título: Series de potencias. Series de Taylor
Sección: Miscelánea
Bloque: Análisis
Unidad: Límites y continuidad de funciones
Nivel/Edad: Universidad (18 o más años)
Idioma: Castellano
Autoría: Elena E. Álvarez Sáiz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm
Este material está publicado bajo una licencia:

Creative Commons Atribución-NoComercial- CompartirIgual 3.0.







