Mostrando artículos por etiqueta: función afín
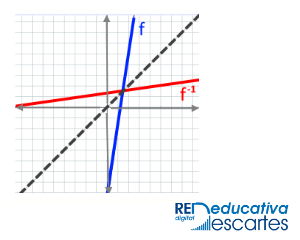
Título: Ejercicios de cálculo de la función inversa
Sección: Miscelánea
Bloque: Análisis
Unidad: Operaciones con funciones
Nivel/Edad: 4º ESO (14 o más años)
Idioma: Castellano
Autoría: Rita Jiménez Igea
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Este mes vamos a ver la unidad de funciones linales de 3º eso:
En el video hemos seguido el siguiente esquema:
1.Función de proporcionalidad directa
Definición
Representación gráfica
2.Función afín
Definición
Representación gráfica
3.Ecuación de la recta
Forma punto-pendiente
Recta que pasa por dos puntos
Forma general
4.Posición relativa de dos rectas
Análisis en forma explícita
Análisis en forma general
5.Aplicaciones
Problemas simples
Problemas combinados
6.Funciones cuadráticas
La parábola y=ax²
Traslaciones de una parábola
Aplicaciones
Este mes vamos a ver la unidad correspondiente de funciones:
En este vídeo hemos tocado los siguientes puntos:
1. Funciones polinómicas
Función de proporcionalidad directa
Funciones afines
Funciones cuadráticas
2. Otras funciones
Función de proporcionalidad inversa
Función exponencial
Funciones definidas a trozos
Función valor absoluto
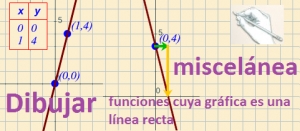
El objeto dibujar funciones cuya gráfica es una línea recta que presentamos hoy pertenece al proyecto miscelánea de la RED y tiene como objetivo aprender a dibujar funciones reales de variable real cuya representación gráfica es una línea recta.
Los coeficientes de las funciones lineales se modifican aleatoriamente y para su representación se puede elegir dados dos puntos o dado un punto y la pendiente. Una vez seleccionada la función y los datos, se inicia una animación que muestra los pasos a seguir. Al finalizar la animación se puede seleccionar un nuevo ejercicio que se puede resolver en el cuaderno y después activar la animación para comprobar si se ha realizado correctamente.
En este vídeo se muestra también cómo embeber un objeto digital en un espacio web, en este caso un curso Moodle, utilizando el código para embeber:
<iframe style="width: 810px; height: 585px;" src="/descartescms/ https://proyectodescartes.org/miscelanea/materiales_didacticos/dibujar_funciones_con_grafica_una_recta-JS/index.html"></iframe>
Título: Opúsculo sobre la función lineal y afín, la recta en el plano
Sección: iCartesiLibri
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: Secundaria, bachillerato y Universidad (15 años o más)
Idioma: Castellano
Autoría: Varios autores
Editora: Manuela Benítez Martinengo
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)



 CONTACTO
CONTACTO
