Mostrando artículos por etiqueta: escenas
Desde RED Descartes Colombia y desde la Institución Universitaria Pascual Bravo os deseamos una Feliz Navidad para todos los cartesianos y pascualinos.
El editor de escenas se puede descargar para distintos sistemas en el siguiente enlace. Además desde el propio editor se pueden cargar las actualizaciones y mejoras que se van incorporando. Cuando el editor detecta una nueva actualización indica mediante un mensaje la posibilidad de proceder a realizarla.
Desde RED Descartes Colombia y desde la Institución Universitaria Pascual Bravo os deseamos una Feliz Navidad para todos los cartesianos y pascualinos.
Escenas con voz y sonido. Secuenciación temporal.

Introducción
El programa Descartes nos permite elaborar escenas incluyendo voces y sonidos. Podemos hacer que aparezcan en determinadas circunstancias según la actuación del alumno y pueden servir como explicación, como mensajes de ayuda o como felicitación cuando se ha resuelto bien una actividad.
También podemos hacer que sea el alumno quien ponga en marcha esos sonidos mediante controles, pero no trataremos con detalle en este artículo este tipo de controles de audio sino los eventos que darán origen a la reproducción de audio cuando se cumple cierta condición en el programa.
Hay que tener en cuenta que muchos ordenadores tienen deshabilitado el audio, por ello es conveniente que la actividad que se pide al alumno en la escena no dependa exclusivamente de los mensajes de voz que en ella se den.
Un programa interesante de uso libre que permite grabar voz y editar sonido para incorporar en las escenas de Descartes es Audacity. Puede exportarse el audio producido en diferentes formatos. Lo usual es el formato mp3 aunque en principio se puede utilizar cualquier formato compatible con HTML y el navegador Web utilizado.
Conviene tener en cuenta que el actual Editor de Escenas de Descartes no reproduce sonidos, aunque se puedan programar. Para comprobar que el sonido programado con Descartes funciona correctamente debemos guardar la escena en un archivo HTML y abrirla en un navegador Web – consultar este enlace sobre compatibilidad-.
Como se programan los sonidos en la escena
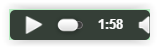
Podemos hacer que un sonido se escuche a través de un control de tipo audio.
 |
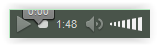 |
| Aspecto con Google Chrome | Aspecto con Mozilla Firefox |
Figuras 1a-b
Por ser de sobra conocido por todos no es necesario describir el funcionamiento de reproducción, pausa y parada proporcionado por este elemento multimedia.
La siguiente imagen muestra el panel Controles y los parámetros que se han establecido para el control de audio que se ha añadido en una escena. El control ha quedado identificado en este ejemplo por el nombre “sonido”.
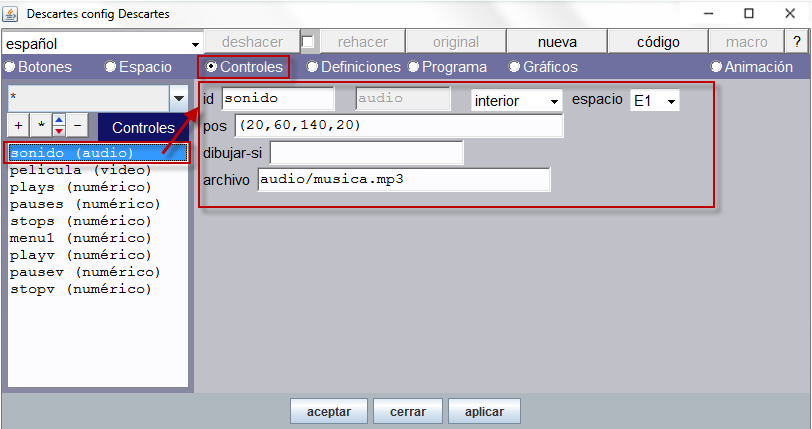
Figura 2
Los parámetros de este control son los referidos a la posición, el espacio, la condición dibujar-si y la trayectoria donde se encuentra el archivo de sonido p.e. "audio/musica.mp3" -ver documentación http://reddescartes.org/documentacion/audio-video/ -
Por lo general suele interesar que el sonido se escuche en situaciones especiales y por tanto se programa como auxiliar evento. En el artículo anterior, Escenas con DescartesJS: Técnicas y trucos (M05) - Adaptación de escenas. Librería de proyecto. Espacios HTMLIframe, se producía un sonido característico cuando un puzle quedaba armado correctamente. Este sonido se había programado como evento.
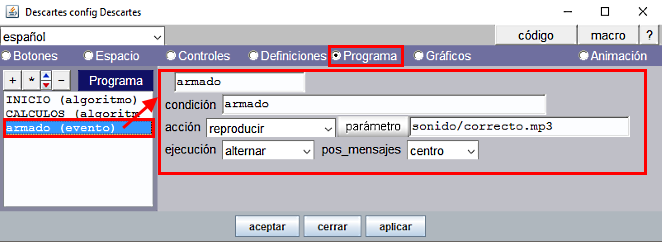
Figura 3
Verificar dicho sonido, desde este enlace, después de armar el puzle.
En la condición ponemos una expresión lógica que cuando es verdadera se reproduce el sonido. La acción que hay que seleccionar es "reproducir". El parámetro que se declara es la trayectoria donde se encuentra el archivo de audio, "sonido/correcto.mp3". En el apartado ejecución elegimos de entre las opciones "una-sola-vez", "alternar" o "siempre" que determina el modo de ejecución de la acción del evento, esto es:
- Una-sola-vez, sólo se ejecuta la primera vez que se cumple la condición.
- Alternar, se ejecuta la primera vez que la condición se cumple, pero si la condición deja de ser válida y vuelve a serlo luego, entonces vuelve a ejecutarse la acción.
- Siempre, se ejecuta siempre que se cumpla la condición.
El valor por defecto es "alternar".
Ejercicio práctico
Como práctica de la inclusión de sonidos te proponemos que selecciones una de tus escenas o bajes una de las cuatro escenas que ya han sido publicadas en esta sección del blog e incluyas en ella voz y sonido.
Los temas que hemos tratado son:
- Escenas con DescartesJS: Técnicas y trucos (B01) – Situar puntos en el plano cartesiano
- Escenas con DescartesJS: Técnicas y trucos (B02) – Identificar nombres en una imagen
- Escenas con DescartesJS: Técnicas y trucos (B03) – Distribución de nombres en un mapa
- Escenas con DescartesJS: Técnicas y trucos (M04) – Puzle de arrastre con efecto imán
Puedes grabar tu voz o buscar voz y sonido ya publicado, grabarlo y editarlo. También te aportamos los sonidos “correcto.mp3” y “Error.mp3” que se utilizan en las unidades “La suma 1” y “La resta 1” y que puedes descargar desde el enlace al final de este artículo.
- Primeramente, coloca la carpeta "audio", que contiene los sonidos, junto al archivo de la página HTML en la que está la escena donde vas a incluirlos.
- Vamos a poner un sonido para indicar que se ha resuelto bien la actividad de la escena.
- Abre el Editor de escenas y con él la página con la escena que vas a modificar.
- En el Panel programa haz clic sobre el signo + para añadir un auxiliar evento. En condición observa y pon lo mismo que hay en el mensaje de felicitación en el apartado dibujar-si.
- Puesto que con el Editor de escenas no se reproducen los sonidos, guarda los cambios y comprueba su funcionamiento abriendo la página con el navegador Web.
Sonido secuenciado
Cuando se incluyen varios sonidos que se deben de reproducir de forma sucesiva, si no queremos que se solapen uno con otro, tenemos que producir una secuenciación de los mismos y separarlos en el tiempo mediante una animación, asignando a cada uno de ellos el momento en el que debe comenzar a reproducirse.
Vamos a utilizar un ejemplo muy sencillo de secuenciación programado para esta ocasión. El diseño está inspirado en la escena Sumando con los dedos de la unidad didáctica de Eduardo Barbero Corral titulada “La suma 1” para 2º curso de Primaria, que como se podrá observar atiende aspectos didácticos más amplios. Se utilizan los mismos sonidos de voz para contar (1a.mp3, 2a.mp3, 3a.mp3, …, 10a.mp3) y las imágenes de las manos han sido coloreadas. También puede consultarse, del mismo autor, la escena similar Restando con los dedos de la unidad didáctica “La resta 1”.
En la escena del ejemplo una animación ha hecho posible la secuenciación temporal de los distintos sonidos y también de la representación gráfica de los números 1 al 10.
Figura 4 (Abre la escena)
En el Editor de Descartes disponemos de un panel para configurar la animación. Una animación en Descartes es un algoritmo especial que refresca la escena cada vez que realiza un ciclo. Como todo algoritmo tiene la estructura inicio – hacer – mientras que se corresponde con la estructura de bucle “do… while” de los lenguajes C y Java y “repeat… while” de Pascal.
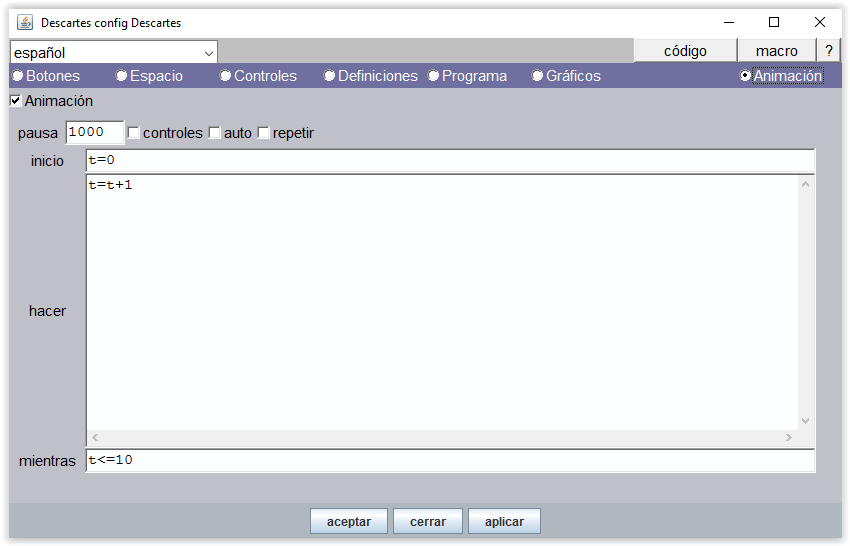
Figura 5
Interesa ver la documentación referida a Animaciones
Animación
La animación funciona como los algoritmos de Descartes, pero tiene sus propias singularidades. Se pone en marcha cuando se activa la acción de animar, ejecuta al principio las operaciones reflejadas en la casilla inicio, separadas por “;”, transforma sus valores según lo que se le indica en hacer y se detiene cuando deja de cumplirse la condición que se pone en mientras. Pero eso lo realiza no de forma instantánea, sino ralentizada por lo indicado en pausa. La pausa indica los milisegundos que espera el programa entre dos pasos sucesivos de la animación que por defecto vale 60.
La figura anterior es el panel animación de la escena de “contar hasta 10”.
Hay que seleccionar la casilla Animación para que esta esté activada y se puedan editar sus parámetros. Si esta casilla no se selecciona no se puede editar los campos del panel ni se puede activar la animación en el programa, aunque esté editada.
El bucle se inicia poniendo el contador a cero, t=0 y en cada ciclo o paso se incrementa en una unidad t=t+1. Cuando el contador supera el valor 10 la animación finaliza.
Es importante entender que una animación se puede poner en marcha de dos formas:
- De forma automática al iniciarse la escena. Para ello tiene que haberse seleccionado la casilla “auto”.
- Cuando se ejecuta la acción animar. Esta acción es una posible opción que tienen los controles numéricos en el panel Controles y también los eventos en el panel Programa.
En la siguiente imagen se muestra cómo se consigue poner en marcha la animación de la escena “contar hasta 10”
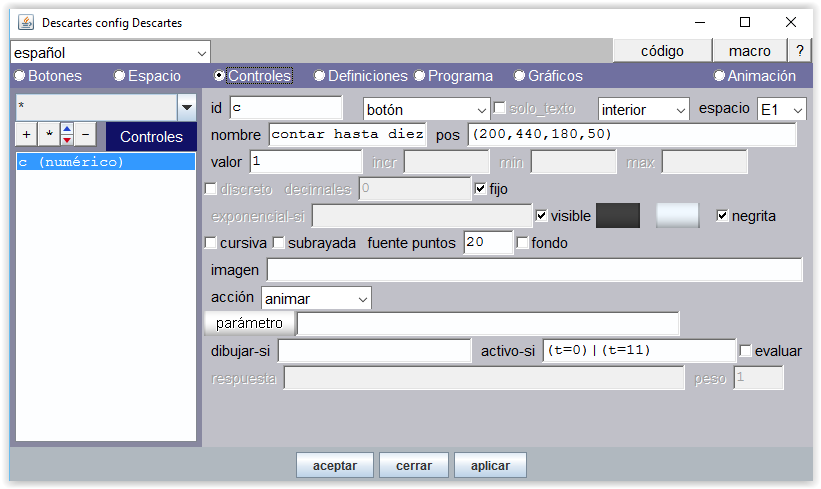
Figura 6
Se ha añadido a la escena un control numérico de tipo botón identificado por la variable c, rotulada con el nombre “contar hasta diez” y lleva la acción “animar” cuando se pulsa, en cuyo caso toma el valor 1 (este valor puede utilizarse para averiguar, p.e, si el control de botón ha sido pulsado).
En la ventana de activo-si se ha escrito la condición "(t=0)|(t=11)"; esto supone que el botón se puede pulsar y activar la animación cuanto t=0 ó t=11. En consecuencia, el botón queda desactivado a lo largo de la animación. Por defecto activo-si está en blanco.
Sonidos y gráficos secuenciados
Sonidos
La animación lo que produce es que una variable t se incrementa cada cierto tiempo, indicado por el parámetro pausa. En nuestra escena del ejemplo, t es un contador que se incrementa cada 1000 ms (1 segundo). Este tiempo es suficiente para que se reproduzca de forma secuenciada (para cada valor de t) cada uno de los 10 archivos de voz independientes: “uno”, “dos”,…, “diez”. Cada sonido se reproduce para un valor determinado del contador. Un evento, en este contexto, consiste en reproducir un archivo de voz cuando el contador t toma cierto valor.
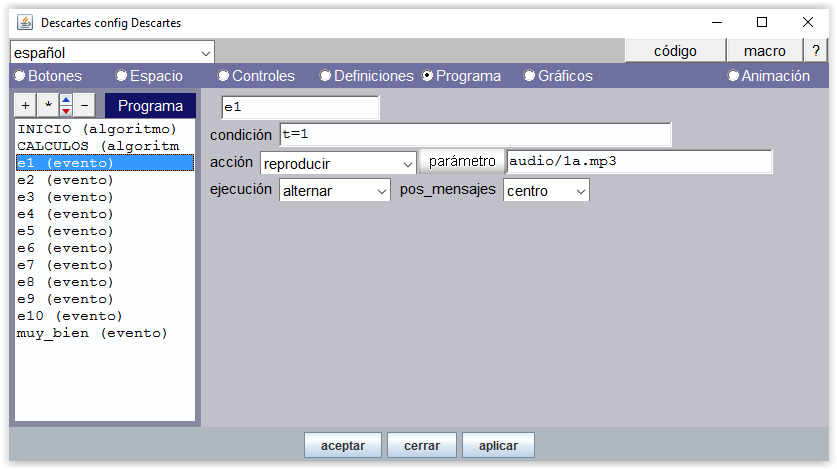
Figura 7
Un sonido de felicitación, "muy_bien.mp3" se reproduce cuando se termina de contar (condición t=11)
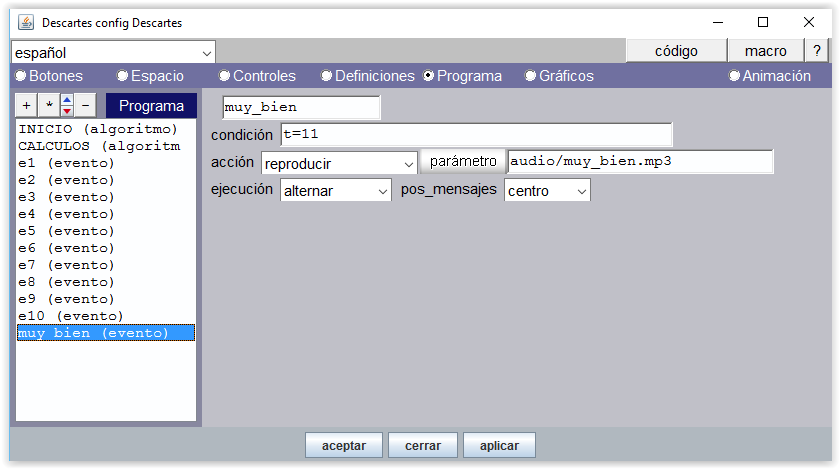
Figura 8
Gráficos
La misma animación que reproduce sonidos como eventos puede llevar aparejada la representación simultánea de gráficos de imágenes, textos, etc., que se vinculan con el valor del contador t.
En la escena de “contar hasta 10”, para cada valor de t, se representa la composición de las dos manos (derecha e izquierda) mostrando el número de dedos que señalan cada cantidad contada.
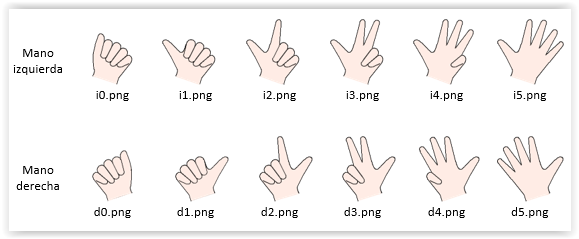
Figura 9
Así, para contar del 1 al 5, la mano izquierda tiene que estar cerrada, representada por "i0.png".
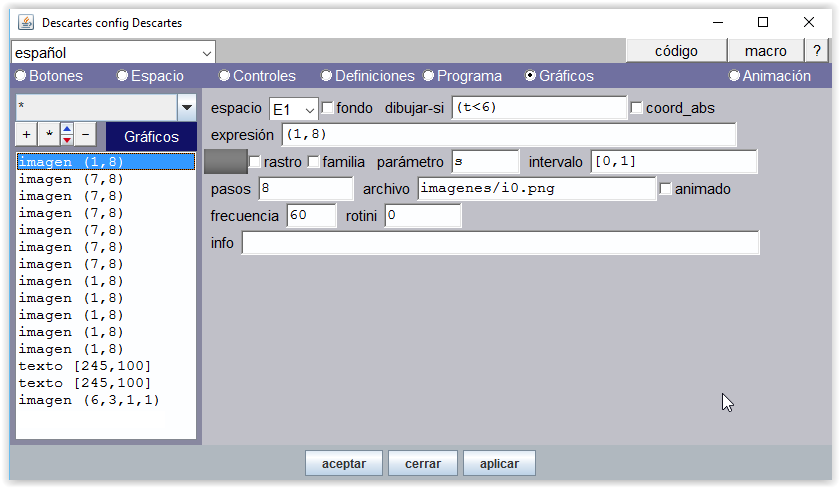
Figura 10
Antes de empezar a contar, t=0, la mano derecha está cerrada y queda representada por "d0.png".
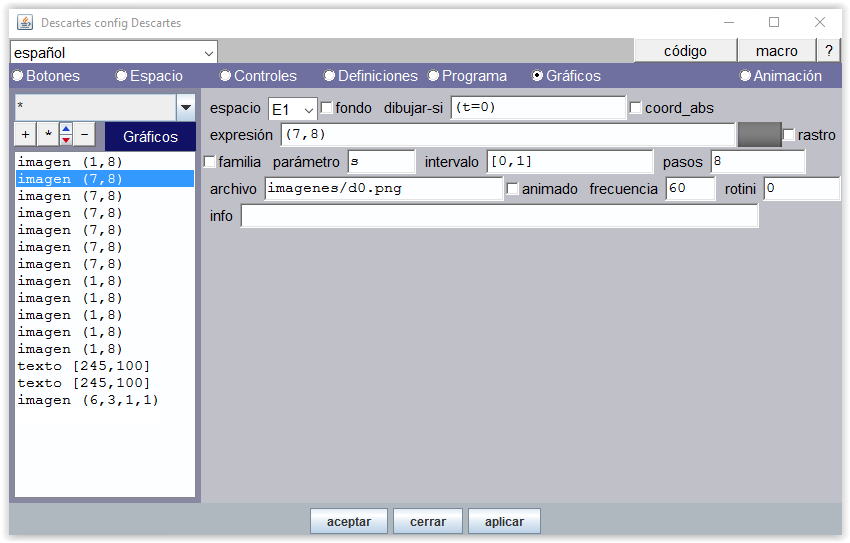
Figura 11
De t=1 a t=5 la mano derecha va mostrando sucesivamente el mismo número de dedos: d1.png,... , d5.png.
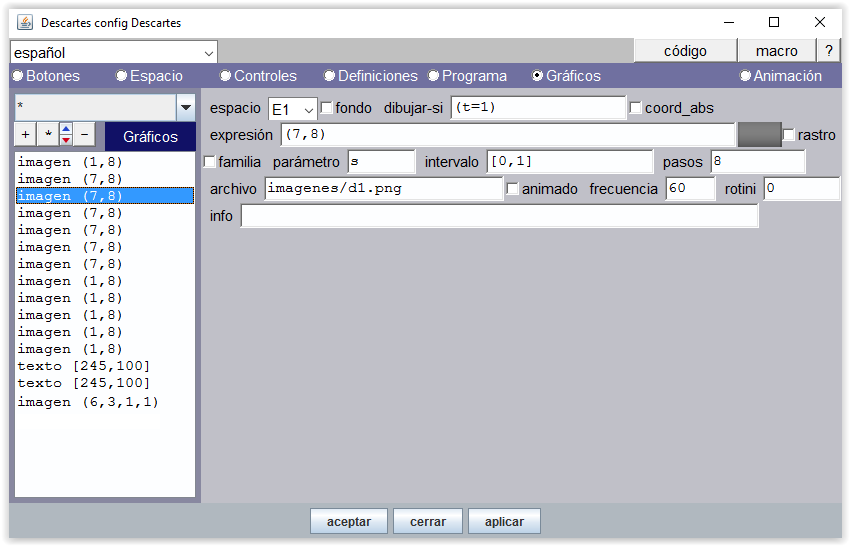
Figura 12
A partir de 5, la mano derecha tiene que mostrar los 5 dedos.
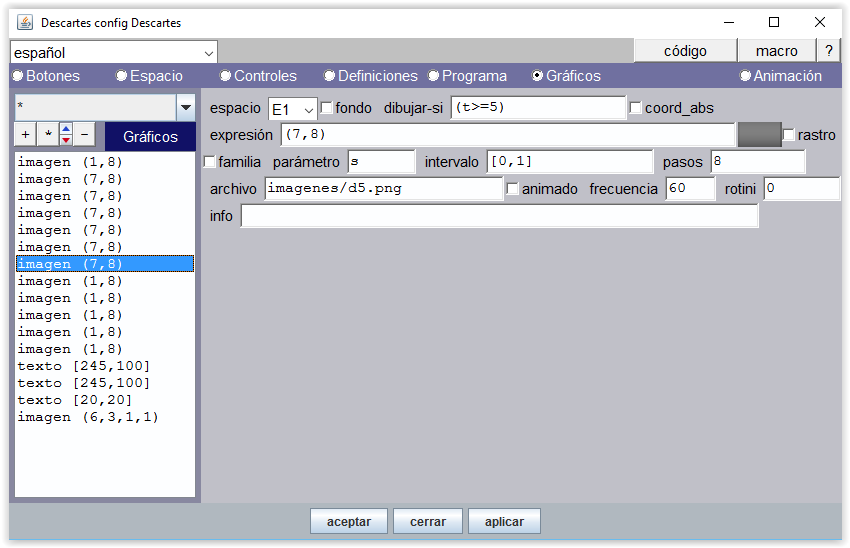
Figura 13
De t=6 a t=10, la mano izquierda va mostrando sucesivamente i1.png,... , i5.png.
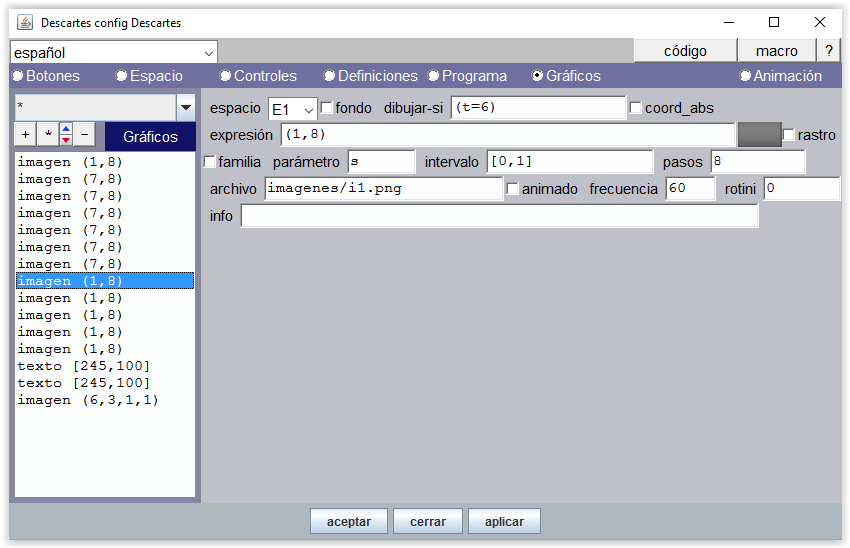
Figura 14
A partir de 10 la mano izquierda mostrará 5 dedos.
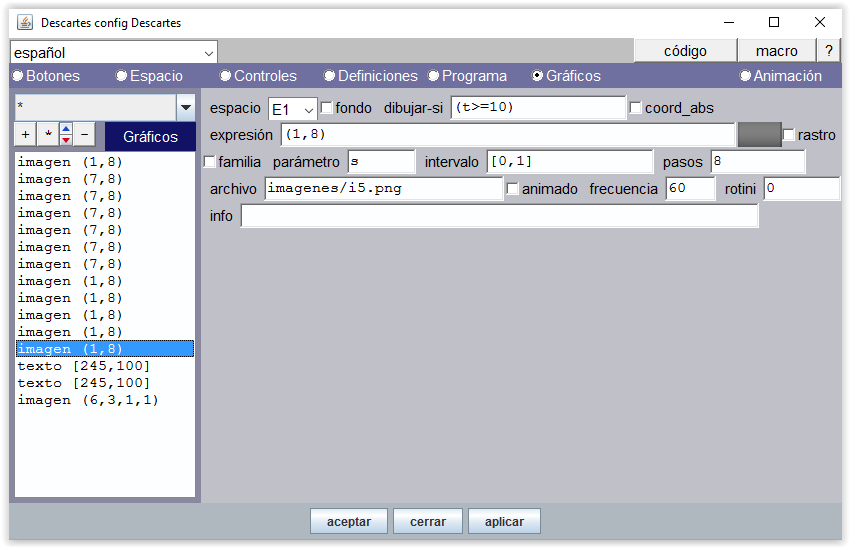
Figura 15
Un gráfico tipo texto reproduce el valor de la variable t en cada momento.
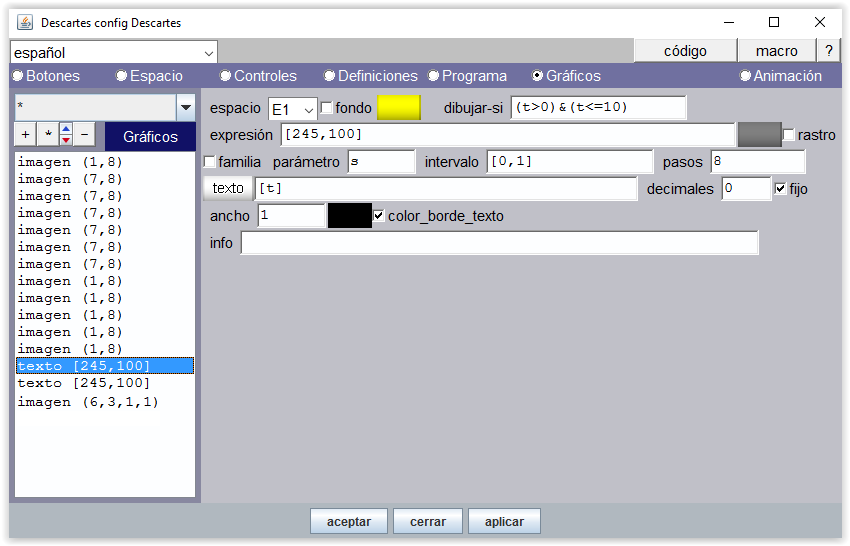
Figura 16
Cuando se termina de contar, t=11, por lo que hay que reproducir el valor de t-1 para mantener el valor 10 del texto.
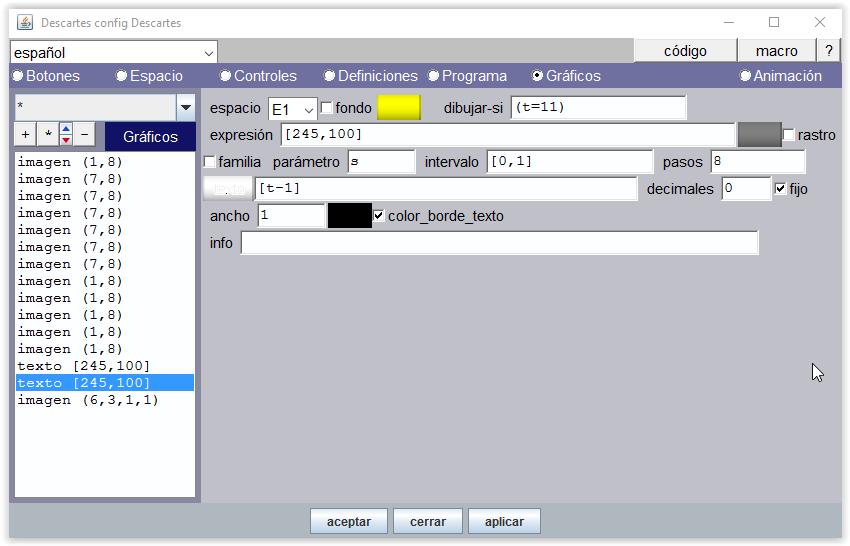
Figura 17
Una imagen acompaña al sonido de felicitación cuando se termina de contar (condición t=11).

Figura 18
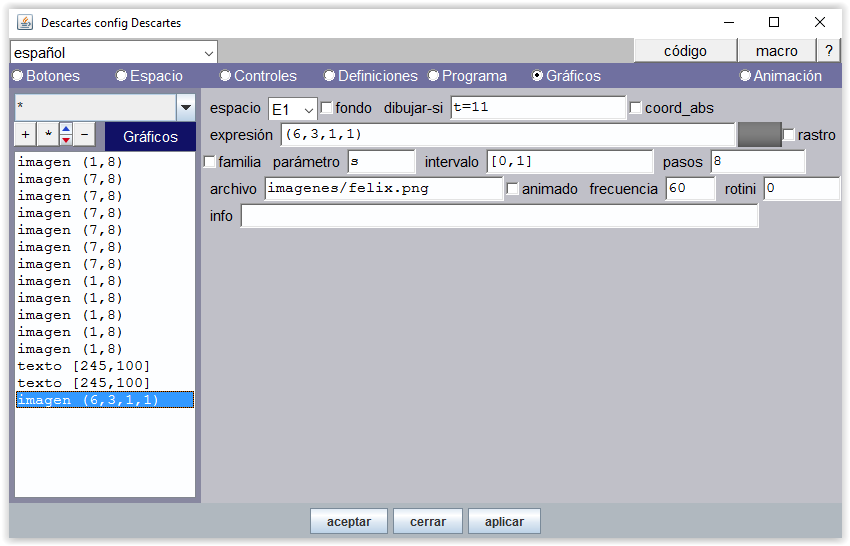
Figura 19
Proyecto
|
Escena_M06: Escenas con voz y sonido. Secuenciación temporal Como viene siendo habitual en esta serie de artículos vamos a proponer un proyecto relacionado con la secuenciación y el uso de la animación de Descartes para aquellos lectores que estén interesados en practicar y progresar un poco más en la programación con DescartesJS. Se trata de conseguir una escena lo más parecida a la siguiente. Figura 20 (Abre la escena) Como podrá observase está inspirada en la escena Sumando con los dedos de la unidad didáctica “La suma 1”. Pero se ha simplificado para quedarnos solo con los elementos de la programación relacionados con la secuenciación temporal de eventos producida por una animación, motivo de este artículo. He pretendido conseguir los mismos efectos de la escena original pero sin poner empeño alguno en que coincidieran sus respectivos códigos de programación. Se trata de practicar la suma de dos cantidades n1 y n2 que toman valores espectivos de 1 a 9. Para ello la escena tiene que contar con los dedos desde la composición con ambas manos para representar n1 hasta n1+n2: “Contar desde n1 otros n2 más”. Los sumandos n1 y n2 se generan aleatoriamente cada vez que se pulsa el control numérico de botón que lleva la acción de inicio (rotulado con el nombre “otra cuenta”). La expresión de DescartesJS que genera un número natural entre 1 y 9 es ent(rnd*9+1)
Figura 21-a Es decir, calcula la parte entera de rnd*9+1, siendo rnd una variable reservada en DescartesJS que cuando se invoca obtiene un valor real alatorio en el intervalo [0, 1). El control numérico de botón etiquetado con el nombre “contar” ejecuta la acción animar cuando se pulsa. La animación realiza un contador t=t+1 mientras t<n2+1. Los sonidos de voz se corresponden con los valores n1+1, n1+2, …, n1+n2 y en la práctica se utilizan desde 2a.mp3 (cuando n1=1) hasta 18a.mp3 (cuando n1=n2=9).
Figura 21-b Incluimos la posibilidad de contar sin reproducir la voz. Para ello se utiliza un control numérico de botón id="sonido", sin etiquetado de nombre “_._”, que lleva asociada la imagen de un altavoz "sonido-on.png". En la casilla pos de posición que ocupa el control se pone las dimensiones de la imagen 56x50 píxeles. Se muestra con la condición (dibujar-si) "sonido=1". Al pulsarlo toma el valor 0, acción calcular "sonido=0".
Figura 21-c Al pulsar el control id="sonido" se muestra en su lugar el control id="sinsonido", que lleva la imagen de un altavoz tachado "sonido-off.png". Este control al ser pulsado calcula "sonido=1", con lo que se activa la voz y se dibuja el control id="sonido".
Figura 22 El siguiente tríptico indica tres detalles que se deben de conseguir al programar la escena:
Figura 23-a
Para asignar posiciones de los controles y los elementos gráficos (imágenes, puntos, textos,…) en la escena hay que configurar en primer lugar el tamaño que tendrá la escena, asignar un valor de escala y determinar dónde tiene que aparecer el origen de coordenadas cartesianas. Cada punto amarillo, cuya posición es la de su centro, debe ir por encima de la punta del dedo correspondiente y el punto asociado de tamaño 0 cuya misión es la de poner texto [n1+t] sobre aquel, se posiciona teniendo en cuenta que este texto se muestra a cierta distancia del centro del punto correspondiente.
Figura 23-b
Figura 23-c En la solución que damos a este proyecto, se puede comprobar que la escena tiene dimensión 600x500 píxeles. La imagen siguiente muestra el panel Espacio del Editor de Descartes de dicha escena.
Figura 24 Las marcas red, ejes y números muestran un espacio con cuadrícula y ejes cartesianos numerados. Una vez situados los controles y gráficos se pueden desactivar. Este es el aspecto que presenta el espacio después de programado.
Figura 25 El espacio debe quedar fijo. El origen de coordenadas se ha desplazado hacia abajo 245 px y hacia la izquierda -298 px La unidad cartesiana (escala) es de 48 px. Recuérdese que las posiciones de los controles y los gráficos tipo texto se hace en píxeles tomando como origen [0, 0] el vértice superior izquierdo de la escena mientras que los gráficos tipo punto y tipo imagen se posicionan en coordenadas cartesianas con origen en (O.x, O.y). Como el tamaño de las imágenes de las manos es de 199x199 px y el posicionamiento de las mismas en el espacio es el del vértice superior izquierdo de la imagen podemos verificar en la figura anterior que la mano izquierda está posicionada en (1, 8) y la derecha en (7,8). |
Animamos a que con esta descripción y las herramientas de DescartesJS facilitadas en la serie de artículos publicados hasta este momento, el lector interesado sea capaz de programar la escena de este proyecto.
Facilitamos en los enlaces siguientes las descargas de las carpetas de contenidos de los materiales para que se pueda hacer uso de los archivos de sonido e imágenes y servir de ayuda al comprobar la estructura de carpetas y revisar o estudiar el código de las escenas con el Editor de Descartes.
|
Autoría:
Eduardo Barbero Corral
- Propuesta del proyecto.
- Técnicas de programación contenidas en las unidades didácticas inspiradoras “La suma 1” y “La resta 1” para 2º de Primaria
Ángel Cabezudo Bueno
- Interpretación, ilustraciones y redacción.
- Programación y edición de las escenas contenidas en la carpeta del proyecto “escena_M06”
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional

Una cualidad muy importante de la herramienta Descartes es que nos permite elaborar nuevas escenas, modificando otra que ya es funcional, con el objeto de conseguir diferentes resultados: cambiando, añadiendo o eliminando el correspondiente código mediante los paneles de configuración del Editor de Escenas. No se descarta la intervención directa sobre el código HTML en el archivo que contiene la escena, con un editor de texto externo tipo Bloc de notas o Notepad++. Otras veces el cambio de la escena es producido sin alterar el código, simplemente al cambiar los archivos de contenido multimedia que acompañan. Esta es la forma habitual de proceder de los desarrolladores de escenas de Descartes. En este artículo tratamos precisamente como llevar a cabo todo esto.
Contenidos que se abordan
- Basándonos en la escena M04 del puzle 2x2 de arrastre con efecto imán, que desarrollamos en el artículo precedente vamos a elaborar nuevos puzles de tamaño 3x3.
- Después produciremos un determinado número de puzles 3x3 obtenidos a partir del primero utilizado de modelo: todos ellos tienen en común el mismo código de la escena, pero difieren en el conjunto de piezas para montar un puzle particular.
Proyecto para visualizar de forma selectiva una colección de puzles ![]()
- Reuniremos todos los puzles en un mismo proyecto que será gestionado desde otra escena que llamaremos principal. Esta escena principal facilita que podamos seleccionar a voluntad desde un determinado espacio R2 los diferentes puzles que hemos producido para tal fin. Tendremos ocasión de conocer la opción Librería de proyecto del Gestor de Escenas y el espacio HTMLIframe, que es común, donde se visualizan los puzles.
Autoría
- La adaptación de un puzle 2x2 a puzle 3x3 es una propuesta de Eduardo Barbero Corral. Aparte de hacer los cambios propios para redimensionar el puzle y tener en cuenta ahora las 9 piezas en vez de 4, se dan nuevas instrucciones para la detección de piezas montadas (superpuestas) y para controlar las acciones cuando el puzle ha sido armado correctamente.
- La idea de utilizar un espacio HTMLIframe donde presentar las diferentes escenas de los puzles procede de un documento instructivo redactado por nuestro maestro cartesiano Juan Guillermo Rivera Berrío
- La interpretación de estas fuentes, la selección de las imágenes para cada uno de los puzles, la elaboración de las piezas, la edición de las escenas y finalmente la redacción de este artículo es de Ángel Cabezudo Bueno.
Enlaces a los artículos precedentes de esta serie
Dejamos los enlaces a los artículos anteriores por si alguien necesita repasar algún detalle de procedimiento que en este obviamos:
- Escenas con DescartesJS: Técnicas y trucos (B01) – Situar puntos en el plano cartesiano
- Escenas con DescartesJS: Técnicas y trucos (B02) – Identificar nombres en una imagen
- Escenas con DescartesJS: Técnicas y trucos (B03) – Distribución de nombres en un mapa
- Escenas con DescartesJS: Técnicas y trucos (M04) – Puzle de arrastre con efecto imán
Idea del proyecto
|
Escena_M05: Adaptación de escenas. Librería de proyecto. Espacios HTMLIframe Se trata de modificar esta escena, motivo del artículo anterior (la Figura 1 lleva un enlace) Figura 1 Por esta otra (la Figura 2 lleva enlace a la nueva escena) Figura 2 Cuando se superponen dos piezas y también cuando el puzle ha quedado armado debe de indicarse mediante sendos mensajes de texto. También, este segundo caso tendrá que ir acompañado de una señal acústica.
La nueva estructura de carpetas es la que se muestra en la figura 5
Figura 5 La carpeta piezas contiene 9 archivos: 1.jpg, 2.jpg,.. , 9.jpg.
|
|
La figura muestra el caso para el listado del panel Controles que es similar al de los demás.
Figura 6
Figura 7
Figura 8 En esta ventana es posible seleccionar un bloque de elementos, por ejemplo desde g1 a g4 inclusive, copiarlos con ctrl+C, abrir una línea después de g4 y pegarlos con ctrl+V; a continuación se puede modificar uno a uno los elementos de la copia. |
||||||||||
Transformaciones que producen la adaptación del puzle 2x2 al puzle 3x3
Es fundamental repasar las explicaciones que se dieron para elaborar la escena 2x2 del artículo anterior y entender bien el significado de los auxiliares que se utilizaron:
- c1, c2, c3, c4: toman el valor 1 cuando la correspondiente pieza está casi colocada en una casilla, no necesariamente la correcta. Así p.e., c1=(g1.x<0)*(abs(g1.x-ent(g1.x)-0.5)<0.05)*(abs(g1.y-ent(g1.y)-0.5)<0.05)
- s12, s13, s14, s23, s24, s34: toman valor 1 cuando están montadas la pareja de piezas que indican los subíndices. P.e en
s12=c1*c2*(ent(g1.x)=ent(g2.x))*(ent(g1.y)=ent(g2.y)) las piezas 1 y 2 está encajadas en una casilla c1=c2=1 y además sus posiciones coinciden.
- montadas = s12+s13+s14+s23+s24+s34 vale 0 si ninguna pieza está montada. Si al menos un sumando vale 1 hay piezas montadas.
- armado, vale 1 si todas las piezas están encajadas en su corresopondiente casilla. Así p.e. la pieza 1 debe de encajarse en la casilla cuyo vértice superior izquierda es (-2,1) y en consecuencia (ent(g1.x)=-2)*(ent(g1.y)=1) tiene que vale 1. Cada pieza bien encajada se evalúa a través de una expesión similar a la anterior y armado se define como el producto de las cuatro expresiones.
En la adaptación al puzle 3x3 se ha cambiado la lógica y no se utilizan las expresiones s12, s13, ... En su lugar, Eduardo Barbero Corral, propone una definición de los auxiliares p1, p2, p3,.., p9, de tal manera que cada casilla queda identificada por un número diferente y las expresiones para montadas y armado vienen dadas como veremos más adelante en función de estos nuevos auxiliares.
La escena ya adaptada se puede descargar desde aquí y verificar las trasformaciones que se explican a continuación.
| 1. |
Creación de la carpeta escena_M04-adaptada Simplemente se copia la carpeta escena_M04 que puede descargarse desde aquí y se renombra. |
||
| 2. |
Creación de las subcarpetas img y sonido Se incorporan a las mismas los archivos correspondientes. |
||
| 3. |
Sustitición de las imagenes en la carpeta piezas Las nuevas imagenes se denominan segun el lugar (fila, columna) que ocupan en la cuadrícula, 1.jpg para la casilla (1,1), 2.jpg para la (1,2),... , 9.jpg para la (3,3). Se obtienen troceando una imagen de 450x450 píxeles con alguna herramienta específica. En el artículo anterior explicábamos como se hace con PhotoScape 3.7. Las piezas o trozos obtenidos tienen el tamaño 150x150px. Para la elaboración de este artículo hemos elegido el tema de animales y en particular la adaptación del puzle 2x2 a 3x3 que estamos explicando se basa en la imagen de una ardilla. |
||
| 4. |
Actuaciones en el Gestor de Escenas Configuración: Cambiar las dimensiones a 800x510 Espacio: Escala 150 (no cambia), O.x=80, O.y=225, Imagen de fondo img/fondo.jpg, despl_imagen='expand.' Se expande dado que la imagen tiene menor tamaño que el espacio que debe ocupar. Controles: Eliminar el control de Inicio. La adaptación de esta escena está orientada a poder formar parte de una colección de puzles dentro del mismo proyecto. Cada puzle podrá ser seleccionado y por tanto iniciado de otra forma. Añadir g5,…, g9, g5.x, g5.y,… , g9.x, g9.y y mantener separada cada agrupación de controles. Modificar los valores min y máx de los controles numéricos para acomodarlos al nuevo tamaño del espacio. Desplazar finalmente los controles añadidos a la posición correcta en el listado segun el grupo al que pertenezca (Ver figura 9) 'g1.x' expresión='(0,0,0,0)' valor='rnd+0.6' min='-3.3' max='2.3' antes era min=’ -2.3’ y max=’2.3’
Figura 9 Gráficos Imágenes: Añadir las piezas 5.jpg a 9.jpg (para reducir esfuerzos se puede utilizar las herramientas de gestión del listado similar a Controles, copiando una imagen ya existente y modificando nombres). Cambio de las dimensiones del tablero:
Imagen: dibujar-si='armado', expresión='(1.1, 2, 0.5, 0.5)', archivo='img/feliz.png’
Programa
Figura 11
p1=c1*(ent(g1.x)+10*ent(g1.y)) Si cada pieza ocupa su posición correcta se obtiene un valor diferente para cada expresión: p1=17, p2=18, p3=19, p4=7, p5=8, p6=9, p7=-3, p8=-2, p9=-1 montadas=c1*((p1=p2)+(p1=p3)+(p1=p4)+(p1=p5)+(p1=p6)+(p1=p7)+(p1=p8)+(p1=p9))+c2*((p2=p3)+(p2=p4)+(p2=p5)+(p2=p6)+(p2=p7)+(p2=p8)+(p2=p9))+c3*((p3=p4)+(p3=p5)+(p3=p6)+(p3=p7)+(p3=p8)+(p3=p9))+c4*((p4=p5)+(p4=p6)+(p4=p7)+(p4=p8)+(p4=p9))+c5*((p5=p6)+(p5=p7)+(p5=p8)+(p5=p9))+c6*((p6=p7)+(p6=p8)+(p6=p9))+c7*((p7=p8)+(p7=p9))+c8*(p8=p9) armado=(p1=17)*(p2=18)*(p3=19)*(p4=7)*(p5=8)*(p6=9)*(p7=-3)*(p8=-2)*(p9=-1)
evento='sí', condición='armado', acción='reproducir', parámetro='sonido/correcto.mp3', ejecución='alternar'
|
|
Proyecto para visualizar de forma selectiva una colección de puzles Nuestro objetivo ahora es reunir una colección de puzles similares al adaptado en escena_M04-adaptada y utilizar un espacio HTMLIframe de DescartesJS donde poderlos visualizar de una forma selectiva y controlada. Puede resultar interesante para algún propósito educativo reunir una colección de puzles que trate un mismo tema, por ejemplo “animales”. Una vez elaborado un puzle con la imagen de cierto animal, como la ardilla, es muy sencillo transformarlo en otro puzle con diferente imagen, ya que bastaría tomar una imagen del mismo tamaño 450x450 píxeles y trocearla en 9 cuadrados de 150x150px con la misma numeración 1.jpg, 2.jpg,.. 9.jpg que reemplazarían las correspondientes de la ardilla. Los distintos puzles así obtenidos los guardaríamos en carpetas con nombres diferenciados: puzle1, puzle2, puzle3,… Como cada puzle va a ser consultado desde una misma escena, es conveniente que el mismo interprete descartes-min.js se comparta con lo que se ahorra espacio. Tiene sentido hablar de Librería de proyecto y que otorguemos esta categoría a dicho intérprete. Basta sacarlo de cada carpeta en los diferentes puzles, eliminando la carpeta lib y situando esta al mismo nivel que las carpetas de aquellos. La estructura de carpetas del proyecto sería como la mostrada en la figura 15
Actuaciones sobre los archivos puzle.html Tenemos que cambiar la referencia al lugar que ahora ocupa el intérprete descartes-min.js: Donde dice: <script type='text/javascript' src='lib/descartes-min.js'></script> hay que escribir <script type='text/javascript' src='../lib/descartes-min.js'></script> Ya que la carpera lib está situada ahora fuera de la carpeta que contiene el puzle, un nivel por encima. Esto se puede hacer modificando directamente cada archivo con un editor de texto plano o bien abriéndolo a través del Gestor de Escenas de Descartes, seleccionando la opción Librería de proyecto > solo para JS y guardando, sin más que hacer.
La Figura 18 lleva un enlace al proyecto resultante Figura 18 Interaccionar con la escena y observar los resultados facilita la comprensión del objetivo del proyecto. |
Actuaciones en el Gestor de Escenas
Accedemos al Gestor de Escenas, Descartes.jar. Por defecto obtenemos una escena dimensión 970x550 píxeles con la opción Librería Portable solo para JS. Esta opción es la que nos interesa ahora para la escena que debe contener el archivo index.html según la estructura mostrada en la Figura 15. Abramos el Editor de Escenas para proceder a configurarla.
- Redimensionado de la escena
En primer lugar, abrimos la ventana del código, pulsando el botón código desde cualquiera de los paneles de configuración (por defecto al abrir el Editor de escenas está activo el panel de Espacio).
La dimensión de la escena debe de llevar los valores width=970 y height=610
- Panel Botones
Desmarcar los cuatro botones créditos, config, inicio y limpiar
- Panel Espacio
El espacio por defecto E1 (2-D) lo ocupa todo y lleva por fondo la imagen imagenes/fondo2.jpg que debe expandirse pues el tamaño de esta es menor que el del espacio.
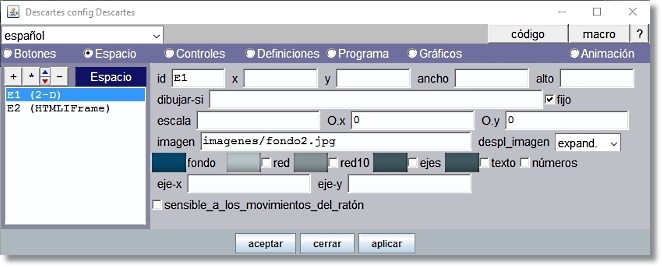
Figura 19
Desmarcar la red, los ejes, el texto y los números.
Se añade el espacio E2 (HTMLIframe) y queda superpuesto a E1.
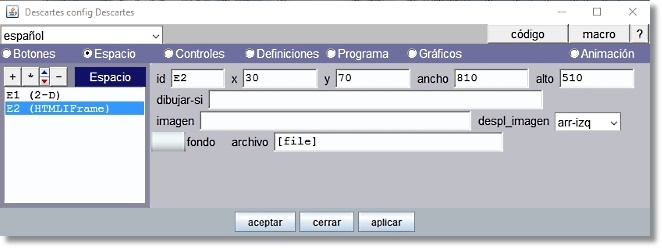
Figura 20
 |
Los espacios HTMLIframe permiten la visualización de todo el contenido incluido en un fichero html. Los parámetros en este tipo de espacio pueden consultarse con más detalle en la documentación técnica sobre Espacios HTMLIframe |
Observar que el ancho 810 píxeles y alto 510 píxeles coincide con la dimensión de la escena de cada puzle que tiene que ser representada en este espacio.
Situamos el comienzo de la representación en x=30 píxeles (distancia al borde izquierdo de E1) y en y=70 píxeles (distancia al borde superior de E1). Es decir hemos dejado un margen lateral de 30 píxeles y un margen en la cabecera donde situar en otro momento el título de la escena “PUZLES DE ANIMALES”
Obsérvese que nos queda a la derecha un margen de representación para E1 de 970 – (810 +30) = 130 píxeles con suficiente holgura para situar los controles de botón rotulados como Puzle1, Puzle2, Puzle3,…
El margen al pie de E1 es 610-(70+510) = 30 píxeles donde se escribirá el nombre del animal cuya imagen representa el puzle seleccionado. (ver Figura 18)
El parámetro archivo lleva la expresión [file], file es una variable que en todo momento contiene la trayectoria al archivo puzle.html que ha sido seleccionado. [file] explicita el contenido actual de la variable file.
La figura 21 muestra la escena tal como se ve en el Editor de escenas hasta este momento de la configuración
Figura 21
- Panel Controles
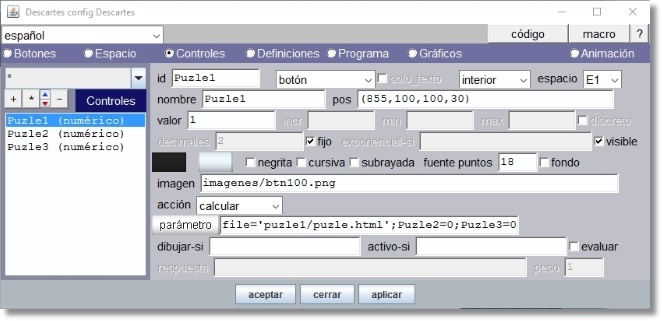
Figura 22
Este panel lleva los controles de botón identificados respectivamente como Puzle1, Puzle2, Puzle3,… tantos como puzles tengamos en la colección, en este caso son tres.
Consultar documentación Imágenes en controles numéricos tipo botón.
El nombre o rótulo que lleva el botón se ha hecho coincidir con el identificador.
La expresión de posición pos=’(855,100,100,30)’ para Puzle1 se ajusta al formato (x,y,w,h) donde x= distancia (píxeles) al borde lateral izquierdo de E1, y= distancia al borde superior de E1, w= ancho del botón, h=alto del botón.
Para Puzle2, y=150 y para Puzle3, y=200. Vamos desplazando 50 píxeles hacia abajo los sucesivos botones.
Valor = 1 es el valor que toma la variable identificada por Puzle1, Puzle2, Puzle3,… cuando se pulsa el botón correspondiente.
El texto del rótulo lleva formato: se escribe con color de relleno y borde y se selecciona un valor (18 puntos) para la fuente.
El archivo imágenes/btn100.png se utiliza en lugar del botón y coincide en tamaño. En la misma carpeta imagenes hay otras dos con el mismo nombre seguido de “_over” y “_down” , en este caso estás imágenes aparecerán en vez de btn100.png cuando el cursor del ratón se encuentra sobre el botón o cuando se pulsa respectivamente.
La acción “calcular” se realiza cuando el botón es pulsado y el parámetro contiene las tres asignaciones separadas por ; que se ejecutan: file='puzle1/puzle.html'; Puzle2=0; Puzle3=0. Las asignaciones para el botón Puzle2 son file='puzle2/puzle.html'; Puzle1=0; Puzle3=0 y para Puzle3, file='puzle3/puzle.html'; Puzle1=0; Puzle2=0.
- Panel Programa
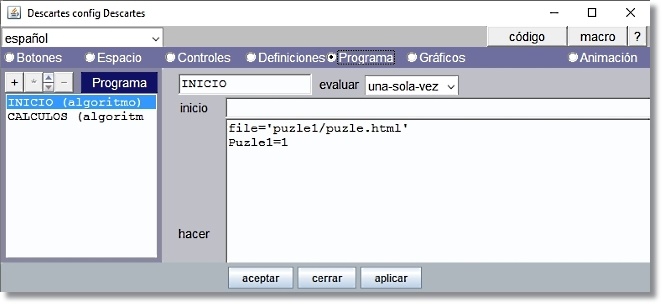
Figura 23
El algoritmo INICIO establece los valores cuando se inicia la escena. Establece que puzle debe de visualizarse al inicio asignando file='puzle1/puzle.html' y Puzle1=1.
El algoritmo CALCULOS (añadido por defecto a Programa) no se utiliza y puede eliminarse.
- Panel Gráficos
Añadimos cuatro elementos gráficos tipo texto. El primero para poner título a la escena “PUZLES DE ANIMALES” en el espacio de cabecera
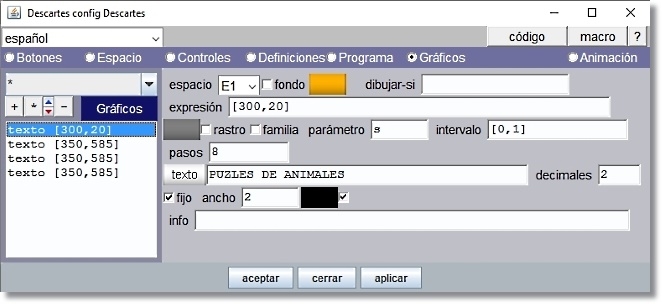
Figura 24
El color de relleno del texto (fondo) es ‘ffa800’ sin trasparencia. Lleva formato Texto simple, tipo de letra SansSerif, negrita, 28 ptos y borde negro.
Los restantes tres textos sirven para informar en el pie de la escena el puzle que se ha seleccionado y el nombre del animal representado en la imagen.
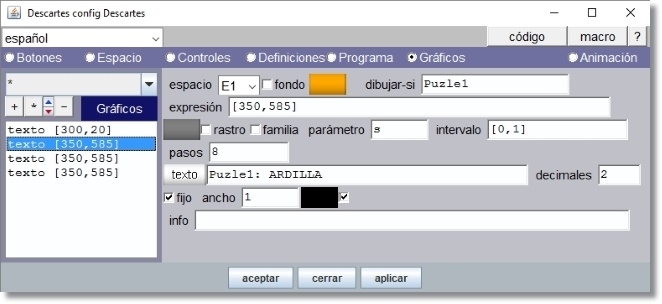
Figura 25
El color de relleno del texto (fondo) es ‘ffa800’ sin trasparencia. Lleva formato Texto simple, tipo de letra SansSerif, negrita, 18 ptos y borde negro.
La diferencia entre estos tres textos está en el identificador que lleva dibujar-si y en el texto que se escribe.
Autoría:
Eduardo Barbero Corral (Programación de la adaptación al puzle 3x3)
Ángel Cabezudo Bueno (Interpretación, elaboración de las escenas, ilustraciones y redacción)
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
 Los puzles son un excelente material de motivación y está probado que son facilitadores del aprendizaje.
Los puzles son un excelente material de motivación y está probado que son facilitadores del aprendizaje.
La elaboración de un puzle con DescartesJS es una tarea interesante y ahora nos va a permitir seguir avanzando en la presentación de los distintos recursos que se pueden extraer de esta herramienta de programación.
La propuesta que se hace aquí procede, como ya hemos hecho en las escenas precedentes, de una aportación de técnicas con las que nuestro compañero cartesiano Eduardo Barbero Corral realiza sus propios puzles.
Hago repaso de su esquema de trabajo y aporto conceptos complementarios que pueden ayudar a comprender mejor al lector menos experimentado con DescartesJS.
Hemos clasificado este trabajo como de nivel medio debido a que algunas propuestas que se incluyen requieren tener cierta soltura y conocimiento de la herramienta, pero quien esté trabajando a un nivel básico todavía, bien que podrá superar sin dificultad y con estudio una gran parte del contenido.
Un puzle de arrastre parte de una imagen que está troceada en piezas de igual tamaño, generalmente de forma cuadrada y la actividad consiste en armar o componer la imagen original a partir de dichas piezas.
La programación de un puzle, aunque este sea elemental, p.e de cuatro piezas, va a requerir que se aborden estas cuestiones:
- Trocear una imagen en piezas cuadradas utilizando alguna aplicación como PhotoScape o TileMage-Image Splitter ambas gratuitas.
- Diseñar y realizar un tablero virtual donde hay que situar una cuadrícula – que habrá que dibujar con Descartes y las piezas (imágenes).
- Desplazar las imágenes apoyadas en su correspondiente control gráfico.
- Restringir el movimiento de los controles gráficos para que las piezas no puedan desaparecer de la escena cuando se arrastren.
- Procurar un efecto imán para que la imagen sea atraída y encajada en un cuadro cualquiera cuando aquella se sitúe a una distancia muy próxima del mismo.
- Verificar si hay piezas montadas en el mismo cuadro y comunicarlo mediante un mensaje de texto.
- Verificar si todas las piezas están correctamente encajadas en su cuadro correspondiente y comunicarlo mediante un mensaje de texto.
Dejamos los enlaces a los artículos anteriores por si alguien necesita repasar algún detalle de procedimiento que en este obviamos:
Idea del proyecto
|
Escena_M04: Puzle de arrastre con efecto imán La escena va a ser sencilla. Disponemos a un lado, de una cuadrícula de 2x2 (2 filas y dos columnas) y tendremos al otro lado las cuatro piezas mezcladas, situadas de forma aleatoria cada vez que se inicia la escena. Una vez realizado este trabajo se podrá seguir una pauta similar para programar puzles nxn de mayor dimensión: 3x3, 4x4, 5x5, etc. o más general de forma rectangular nxm. La Figura 1 te lleva al puzle ya elaborado para que puedas practicar y entender mejor los resultados que se pretende conseguir en este proyecto. Figura 1La escena debe permitir interaccionar con las piezas, poderlas arrastrar hacia la cuadrícula y situarlas correctamente en su cuadro. Decimos entonces que el puzle ha quedado armado. En dos momentos se requiere que el usuario reciba información a través de sendos mensajes de texto:
En este proyecto se abordarán los siete puntos de la Introducción. Proponemos la siguiente organización para las carpetas y archivos que se van a utilizar en el proyecto. La siguiente Figura 4, indica una estructura similar utilizada para desarrollar las escenas de los anteriores proyectos
La carpeta lib contiene el intérprete descartes-min.js y se puede generar automáticamente sin más que guardar en la carpeta escena_M04, con la opción Librería portable > sólo para JS, el archivo puzle.html que incluye el código de la escena. La carpeta piezas contiene las 4 piezas que se deberán denominar 1.jpg, 2.jpg, 3.jpg y 4.jpg Para realizar este proyecto debes de conseguir una imagen que sea cuadrada para trocear. Si no lo fuera debes recortarla con un programa de edición de imagen y si fuera el caso redimensionarla. Para este artículo se ha seleccionado una imagen cuadrada de 300x300 px. Cada una de las cuatro piezas del troceado resulta ser una imagen cuadrada de 150x150px. |
Troceado de la imagen
|
Existen diferentes programas que permiten trocear una imagen. Si no dispones de ninguno puedes descargarte PhotoScape que es gratuito e incluye una opción de troceado dentro de una interesante gama de posibilidades de edición. Figura 5 |
 |
Paso 1: Añadir la imagen. Seleccionar 2 columnas y 2 filas. Trocear
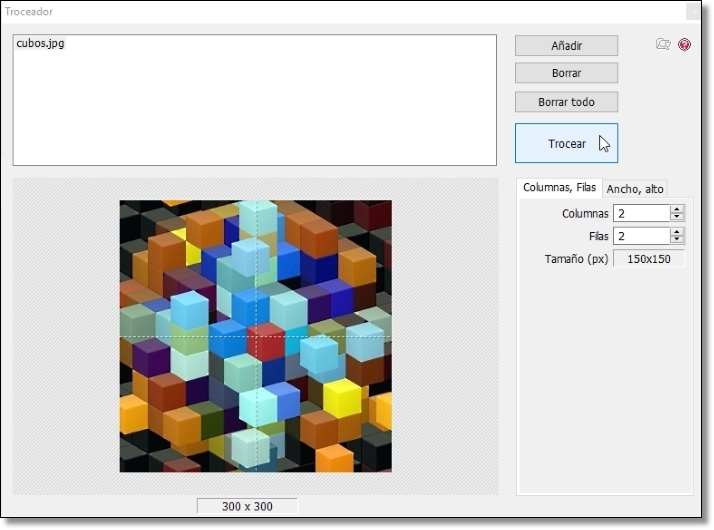
Figura 6
Paso 2: Trocear. Seleccionar carpeta de destino. Trocear.
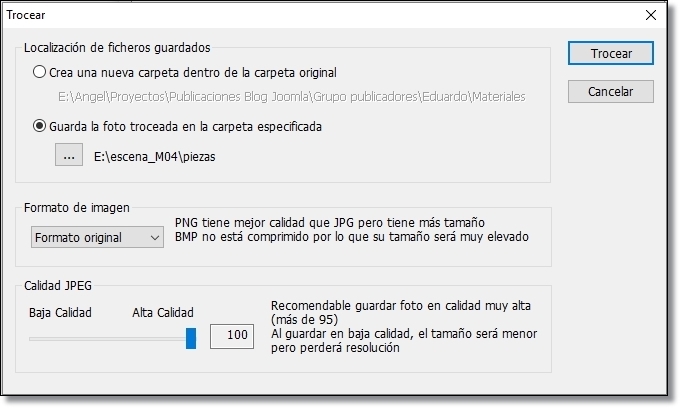
Figura 7
Paso 3: Acceder a la carpeta de destino. Renombrar las imágenes.
PhotoScape nombra cada imagen troceada añadiendo al nombre de la imagen original un número de orden contando de arriba a abajo y de izquierda a derecha es decir sigue un orden por filas y luego por columnas: la pieza 1 es la que corresponde a la casilla (1, 1), la pieza 2 la correspondiente a la casilla (1, 2), la pieza 3 la correspondiente a la casilla (2,1) y la pieza 4 la correspondiente a la casilla (2, 2).
Editor de escenas de Descartes
Abrir el Gestor de escenas y editar la escena, modificando en primer lugar su tamaño a 700x400px.
Escena adecuada para situar una cuadrícula de 300x300px y un espacio separado para situar inicialmente las cuatro imágenes.
Actuaciones en el panel Botones
Desmarcar los cuatro botones.
Actuaciones en el panel Espacio
Ponerlo fijo, para que no se pueda desplazar por arrastre. La escala será de 150 y debe coincidir con la longitud del lado de la pieza para simplificar los cálculos de situación.
Cuida que el tablero esté colocado adecuadamente, debe de estar a la izquierda y verse entero, para ello modificas los valores O.x, O.y según convenga.
 La posición por defecto del origen de coordenadas (O.x, O.y) es el centro de la escena a 350px del borde izquierdo y a 200px del borde superior. La posición por defecto del origen de coordenadas (O.x, O.y) es el centro de la escena a 350px del borde izquierdo y a 200px del borde superior.
La Figura 8, muestra la red, los ejes y los números en el espacio. Esto nos permite ver mejor cómo organizar los elementos que van a aparecer en la escena. Después hay que quitarlos y poner un color de fondo para la escena al gusto del programador (ver Figura 1)
Para dibujar más adelante la cuadrícula 2x2 en el lado izquierdo de la escena, debemos posicionar el origen de coordenadas de tal manera que las coordenadas de los vértices del marco sean valores enteros sencillos. Hemos preferido que estos vértices sean (0,0), (0,2), (-2,2), (-2,0) así que para que la cuadrícula 2x2 quede dentro de la escena hay que situar O.y 150 píxeles más abajo, tal como se aprecia en la Figura 9.
|
Actuaciones en el panel Controles
Las piezas, que son gráficos de imagen, se mueven con controles gráficos que hay que definir previamente.
Agrega el primer control gráfico g1. Ponle un tamaño en número de píxeles que sea la mitad del de la escala, eso significa los pixeles que tiene de radio, para que coincida con el tamaño de una pieza de puzle. Posición (rnd+0.6, rnd*2) para que inicialmente aparezca a la derecha en lugar aleatorio.
Después pon dibujar-si=0 para que sea invisible el disco del control gráfico y no tape la pieza.
Los restantes controles g2, g3 y g4 se definen idénticamente como g1. Para añadir más rápidamente estos controles se pueden copiar g1 tres veces con la herramienta * situada en la ventana de agregar.
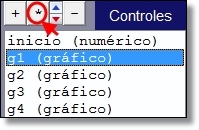 Figura 10
Figura 10
|
La Figura 11 nos muestra cómo se va a apoyar la pieza del puzle 1.jpg al control gráfico g1. El número de cada celda que aparece en la figura indica el lugar de destino para la correspondiente pieza, ¡no debe de verse en el puzle! La posición de destino correcta de la imagen 1.jpg es (-2, 2) ya que si se da únicamente la expresión de las coordenadas de una imagen, estas se refieren a la posición del vértice superior izquierdo.
Al definir el control g1 con la condición dibujar-si = 0, el control no se verá en la escena y dejará completamente descubierta la imagen que va apoyada. |
Actuaciones en el panel Gráficos
Lo primero es dibujar la cuadrícula 2x2. Esto se consigue, para este caso tan simple, dibujando un polígono de vértices (0,0)(0,2)(-2,2)(-2,0)(0,0) y ancho 6 (ancho en píxeles de la línea) para resolver el borde y dos segmentos perpendiculares para hacer la división en cuatro cuadrados: (-1,0)(-1,2) y (-2,1)(2,1), ancho 1. Poner el mismo color a las líneas (p.e. blanco) y color de relleno al polígono (Ver Figura 10).
Luego se van agregando una a una las imágenes de las piezas.
Para la pieza 1, el archivo es piezas/1.jpg, pones de coordenadas la expresión (g1.x-0.5, g1.y+0.5) para que se pueda mover con el control gráfico y esté centrada. Observar la expresión que ponemos para que la imagen encaje correctamente con el control sobre el que va apoyado, según la Figura 11. Por lo que explicaremos seguidamente escribimos la condición dibujar-si = (c1=0).
 |
dibujar-si es un campo de texto donde puede escribirse una expresión booleana u otra expresión que se interpreta como tal dependiendo del valor que tenga. |
La particularidad de este puzle es el efecto imán. Es decir, que cuando una pieza está muy cerca de ser colocada en una casilla parece como si una fuerza obliga a adaptarse perfectamente en ella. Para conseguir este efecto imán, para cada pieza incluiremos dos entradas de la misma imagen, una se dibuja cuando c1=0 y otra se dibuja cuando c1=1.
Veamos la circunstancia que se da para cada uno de estos valores posibles de la variable auxiliar c1.
Después de leer las actuaciones en el panel Programa para el caso c1=1 hay que añadir una nueva entrada en el panel Gráficos para dibujar la pieza 1.jpg en la posición (ent(g1.x), 1+ent(g1.y)) y dibujar-si = (c1=1).
En resumen, en el panel Gráficos tenemos para cada pieza 1.jpg, 2.jpg, 3.jpg y 4.jpg dos definiciones, una con la condición dibujar-si = (c1=1) y otra con la condición dibujar-si = (c1=0) y en este mismo orden para que las piezas cuando sean arrastradas sobre el tablero lo hagan por encima de las que ya están encajadas.
Es conveniente añadir también un control numérico de botón con la acción de iniciar la escena.
Actuaciones en el panel Programa
En el algoritmo Cálculos y evaluar siempre, en relación con la variable auxiliar c1 asociada a la imagen 1.jpg, escribimos la entrada
c1=(g1.x<0)*(abs(g1.x-ent(g1.x)-0.5)<0.05)*(abs(g1.y-ent(g1.y)-0.5)<0.05)
abs y ent son las funciones valor absoluto y la parte entera respectivamente con la definición matemática habitual.
La parte (g1.x<0) de la expresión es para que el efecto imán solo se produzca cuando la imagen está en el lado izquierdo de la escena, donde está el tablero para situar las piezas.
Observar que c1 tendrá valor 1 cuando la pieza esté colocada a una distancia muy próxima para encajar en una casilla. Esta distancia se ha fijado en menos de 0.05 tanto para la abscisa como para la ordenada de la pieza (0.05 unidades cartesianas de 150 píxeles equivale aproximadamente a 8 píxeles.).
Cuando c1 tome el valor 1, entonces la imagen en las coordenadas (g1.x, g1.y) se sustituye por la misma imagen en las coordenadas (ent(g1.x), 1+ent(g1.y)), es decir en las coordenadas del vértice superior izquierdo de la casilla que tiene tan cerca.
Añadimos después las restantes auxiliares c2, c3 y c4 asociadas a las imágenes respectivas 2.jpg, 3.jpg y 4.jpg.
Para que el proceso sea menos tedioso podemos obtener estas auxiliares copiando cada vez c1 y cambiando las referencias al subíndice 1 por 2, 3 y 4 en su correspondiente caso.
Propuesta final
Son tres las cuestiones que hasta este momento han quedado sin resolver y aunque el puzle, con lo dicho, es funcional conviene no desatenderlas:
- Notificar mediante un mensaje de texto cuando el puzle ha quedado armado. P.e: ¡Enhorabuena!.
Dependiendo del tema tratado en la imagen original, no siempre resulta fácil saber si la imagen ha sido bien recompuesta. - Notificar mediante un mensaje de texto cuando dos piezas se han superpuesto en la misma casilla.
P.e: “Hay piezas montadas! o, mejor, “Hay piezas superpuestas”. - Restringir el movimiento de los controles gráficos para que no puedan desaparecer de la escena cuando se arrastren, pues se corre el riesgo de hacer desaparecer alguna pieza si se arrastra más allá de los bordes del tablero.
El programador de DescartesJS con más recursos podrá resolver estas cuestiones cuando el número de piezas del puzle supere con mucho a cuatro. Pero queremos que también participen de esta actividad cualquier lector con nivel básico y teniendo en cuenta que manejamos pocas piezas, damos las siguientes pautas para ello.
Notificar mediante un mensaje de texto cuando el puzle ha quedado armado
Para verificar que la pieza 1 ha quedado encajada en la casilla 1 basta preguntar si la expresión c1*(ent(g1.x)=-2)*(ent(g1.y)=1) toma el valor 1.
Análogamente haremos para verificar si las restantes piezas 2, 3 y 4 están encajadas en sus respectivas casillas.
La condición para que las cuatro piezas estén encajadas en sus respectivas casillas y el puzle, por tanto, haya quedado armado es que el producto de las cuatro expresiones correspondientes valga 1.
Recomiendo crear un auxiliar, p.e. llamado armado, en el algoritmo CALCULOS del panel Programa y asignarle el valor del producto anterior.
Luego en el panel Gráficos poner la condición dibujar-si = armado, al Texto "¡Enhorabuena!" (ver Figura 3).
Notificar mediante un mensaje de texto cuando dos piezas estén superpuestas en la misma casilla
Supongamos que dos piezas, la 1 y la 2, están superpuestas y encajadas en cierta casilla, no necesariamente la casilla 1 o la casilla 2. Es obvio que se verifica c1*c2=1 pero también ent(g1.x)=ent(g2.x) y ent(g1.y)=ent(g2.y). En consecuencia c1*c2*(ent(g1.x)=ent(g2.x))*(ent(g1.y)=ent(g2.y)) tomará el valor 1.
Análogamente podemos suponer para las parejas de piezas 1 y 3, 1 y 4, 2 y 3, 2 y 4, 3 y 4. ¡En total hay 6 combinaciones posibles!.
Asignemos cada expresión a su correspondiente auxiliar, por ejemplo, s12, s13, s14, s23, s24, s34 y añadámoslos como entradas en el algoritmo CALCULOS.
Añadamos una entrada más, definiendo p.e el auxiliar montadas = s12+s13+s14+s23+s24+s34
Es obvio que montadas tomará el valor 1 cuando alguna pareja de piezas está superpuesta en una determinada casilla. Para notificar al usuario del puzle de esta circunstancia, bastará añadir, en el panel Gráficos, una entrada con el texto “Hay piezas montadas” y dibujar-si=montadas (ver Figura 2).
Restringir el movimiento de los controles gráficos
Es importante limitar el desplazamiento de los controles gráficos y en consecuencia la correspondiente pieza que va apoyada. Con esto evitaremos que por descuido al arrastrar el control más allá de los bordes del tablero la pieza pueda desaparecer y no podamos terminar de montar el puzle.
Sabemos que (g1.x, g1.y) son las coordenadas del control gráfico g1. Estas coordenadas se pueden definir convenientemente como controles numéricos y podemos conseguir esa limitación de movimientos.
En estas condiciones definimos el control gráfico g1 en la posición por defecto (0, 0) y definimos g1.x y g1.y según se indica en las figuras
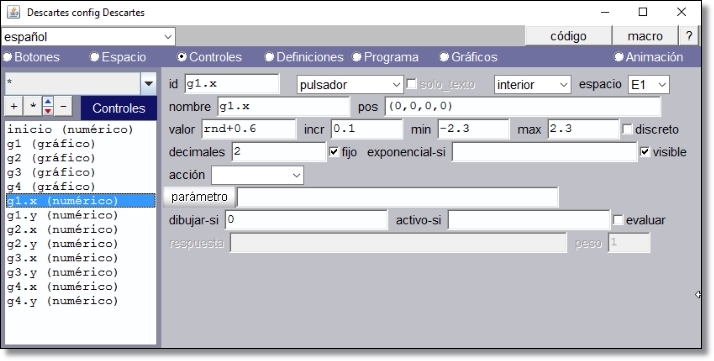
Figura 12
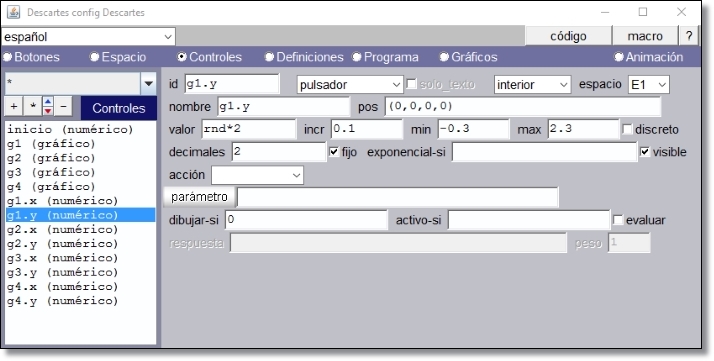
Figura 13
Estos controles quedan ocultos en la escena con la condición dibujar-si=0. El valor se g1.x y g1.y cambia al arrastrar el control gráfico g1 pero el desplazamiento queda restringido al espacio entre los valores mínimo y máximo.
Completamos copiando las mismas definiciones de g1.x y g1.y para g2.x y g2.y, g3.x yg3.y, g4.x yg4.y
Tablero con cuadrícula o sin cuadrícula
El programador del puzle podrá optar por facilitar un tablero con cuadrícula para situar las piezas o prescindir de la misma. El puzle que hemos instrumentado en este artículo podría seguir siendo funcional si prescindimos de los dos segmentos perpendiculares que acompañan al polígono de 4 vértices que delimitan el tablero.
Ahora bien si nos interesa dejar la cuadrícula y pensamos en puzles de mayor dimensión, por ejemplo de 4x5 es más práctico dibujarla utilizando dos familias de segmentos. Solo con el fin de diferenciar aquí las dos familias utilizamos en el ejemplo siguiente un color diferente para dibujar cada una, en el puzle todos los segmentos tendrán el mismo color.

Figura 14
Configuración de la familia de 5 segmentos horizontales:
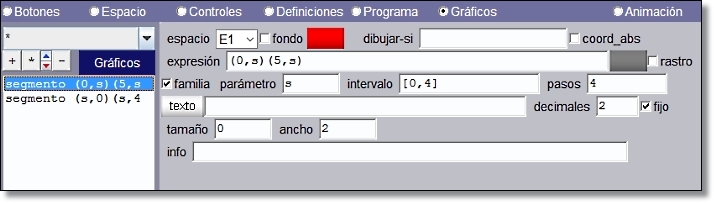
Figura 15
 |
|
Configuración de la familia de 6 segmentos verticales:
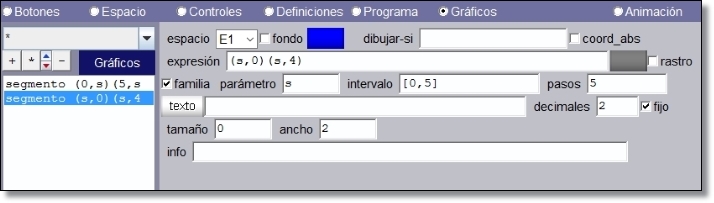
Figura 16
Esperamos haber facilitado con esta nueva edición de Técnicas y Trucos el aprendizaje a los que siguen el nivel básico y estimulado a todos los demás cartesianos para enfocar, con su propia técnica, la solución de los problemas abordados aquí.
Autoría:
Eduardo Barbero Corral (Proyecto y técnicas de programación)
Ángel Cabezudo Bueno (Interpretación, edición de la escena, ilustraciones y redacción)
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional

En el presente artículo se explica una técnica empleada por nuestro compañero Eduardo Barbero Corral que permite validar cuando se han distribuido correctamente una serie de nombres sobre un espacio bidimensional.
Creemos que ya no es necesario detallar, de la misma forma como lo hicimos en los dos proyectos precedentes, las herramientas de edición necesarias, como conseguirlas y como invocarlas a lo largo del proceso de elaboración. Basta remitirse a los primeros pasos indicados en “Escenas con DescartesJS: Técnicas y trucos” y en “Escenas con DescartesJS: Técnicas y trucos (B02)”.
-
Suponemos que el lector sabe acceder al editor de escenas de DescartesJS, desplazarse por los distintos paneles de configuración, agregar elementos a la lista en cada panel, rellenar ventanas y casillas correspondientes a cada elemento.
-
Recordamos que la escena tiene que ser generada con la opción Librería portable-solo para JS y que habrá que modificar las dimensiones de la escena por defecto, 970x550 píxeles, abriendo la ventana de código desde cualquier panel de configuración.
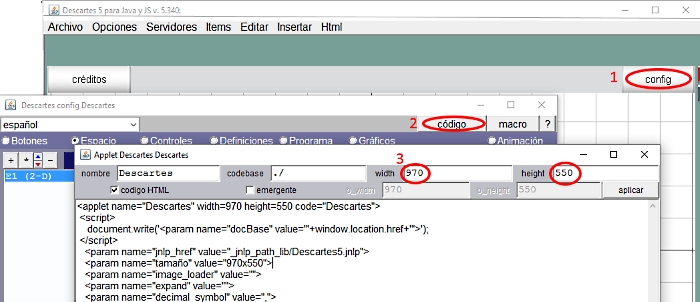
Figura 1
Idea del proyecto
| Escena_B03: Distribución de nombres en un mapa.
Se trata de una escena en la que aparece, como fondo, la imagen del mapa político de la Comunidad Autónoma de Castilla y León (España), a un lado, en columna, los nombres de sus nueve provincias. El alumno debe moverlos, arrastrando el puntero, hasta colocarlos en el lugar correspondiente. Comenzamos por conseguir la imagen del mapa. Debe ser una imagen limpia y de buena calidad, de un tamaño adecuado a lo que pretendemos y la situaremos en la carpeta raíz del proyecto escena_B03 El archivo que contiene la imagen del mapa se denomina mapacylmudo.jpg y como su nombre indica es un mapa mudo. Esta figura lleva un enlace a la escena ya elaborada, donde se puede practicar y en consecuencia comprender lo que se pretende hacer en este proyecto. La siguiente Figura 3 muestra la estructura de carpetas que contiene los materiales del proyecto.
Figura 3 La carpeta lib debe de contener el archivo descartes-min.js necesario para que la escena que porta el archivo index.html pueda ser interpretada. El tamaño de la escena por defecto tiene que modificarse para que coincida con el de la imagen, 605x410 píxeles y debe de ser la imagen de fondo en la escena (Ver la Figura 1) Solo en el caso de que los nombres de las provincias estén bien situados deberá aparecer el mensaje “muy bien” indicando esta circunstancia y desaparecer el texto titular “Coloca cada nombre en el centro de la provincia”, como nuestra la Figura 4 |
Actuaciones en el panel Botones
En esta ocasión hay que desmarcar las casillas de los cuatro botones Créditos, Config, Inicio y Limpiar que por defecto ocuparían las cuatro esquinas de la escena. Aunque deben de quedar ocultos, en cualquier momento se pueden ver en una ventana emergente al hacer clic derecho sobre la escena.
Actuaciones en el panel Espacio
En el panel Espacio se escribe el nombre de la imagen, mapacylmudo.jpg, indicando la trayectoria dentro de la carpeta del proyecto, que se verá como fondo de la escena y en posición centrada.
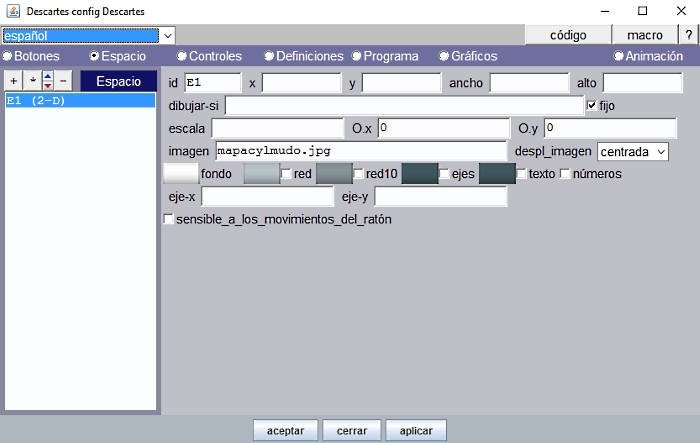
Figura 5
Obsérvese que están desmarcadas las casillas que dibujan la red, los ejes, texto y números. Así es como se desea que quede el espacio finalmente, pero es conveniente que se activen a lo largo del proceso de elaboración de la escena pues facilita las coordenadas de posición que deben ocupar los diferentes textos.
La escala (píxeles de la unidad coordenada) por defecto es 48, por lo que no es necesario explicitar este valor.
Marcaremos la casilla de fijo para que el espacio no se desplace al arrastrar el puntero.
Actuaciones en el panel Controles
Insertamos tantos controles gráficos como número de provincias g1, g2, g3, ..., g9.
Estos controles quedarán alineados en columna, a la izquierda. (-4.5, 3.2), (-4.5, 2.4), (-4.5, 1.6), (-4.5, 0.8), (-4.5, 0), (-4.5, -0.8), (-4.5, -1.6), (-4.5, -2.4), (-4.5, -3.2)
Tienen un tamaño de 20 píxeles, adecuado según la escala para poderlos seleccionar fácilmente y ser arrastrados a la posición correspondiente sobre el mapa.
El control existe, pero no se tiene que ver en la escena pues la idea es que sirva exclusivamente de soporte al nombre de la provincia que le va a acompañar; esto se consigue poniendo valor 0 en la ventana de condición dibujar-si.
Veremos con más detalle en el panel Gráficos la relación que debe de existir entre las coordenadas de esos controles y las de los textos de las provincias.
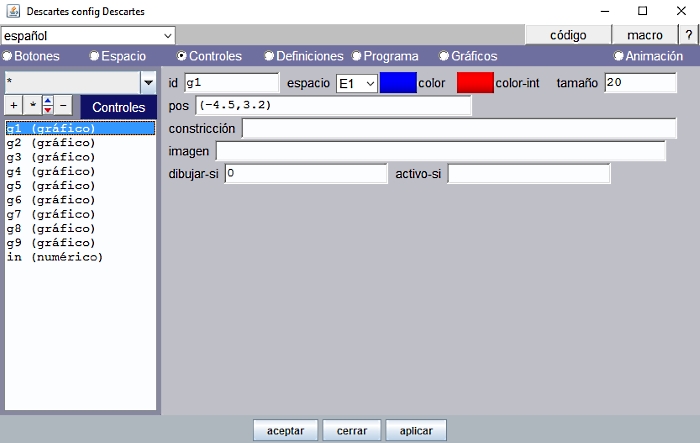
Figura 6
También ponemos un control numérico, tipo botón, para ejecutar la acción de inicio, que quedará en el ángulo inferior izquierdo, interior, de la escena. Este botón permite reiniciar la escena y practicar de nuevo desde un principio.
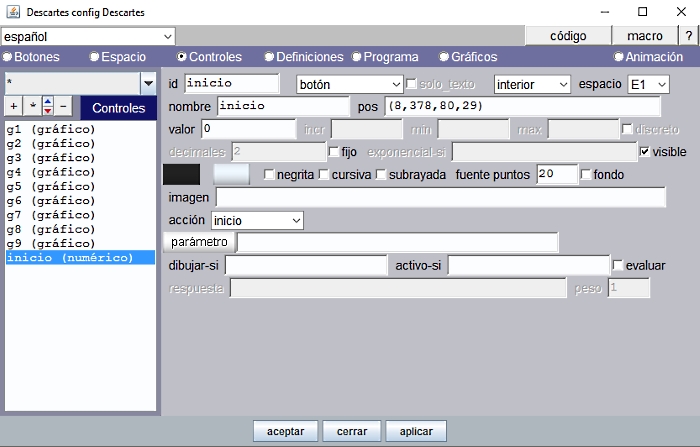
Figura 7
Actuaciones en el panel Programa
En esta sección determinamos la forma de averiguar si el control gráfico se ha arrastrado al sitio adecuado en el mapa.
Empezamos por anotar las coordenadas de un punto centrado en la región del mapa correspondiente a cada provincia. Podemos utilizar por ejemplo una hoja de cálculo o un simple editor de texto. Para ver las coordenadas de estos puntos marcamos la casilla texto en el panel Espacio a fin de que se visualicen las coordenadas del punto cuando se hace clic izquierdo sobre el mapa. Una vez registradas las coordenadas de estos puntos se debe desmarcar la casilla texto en el panel Espacio.
Así por ejemplo un punto centrado en la región del mapa correspondiente a la provincia de Ávila tiene las coordenadas (-0.3, -2.56)
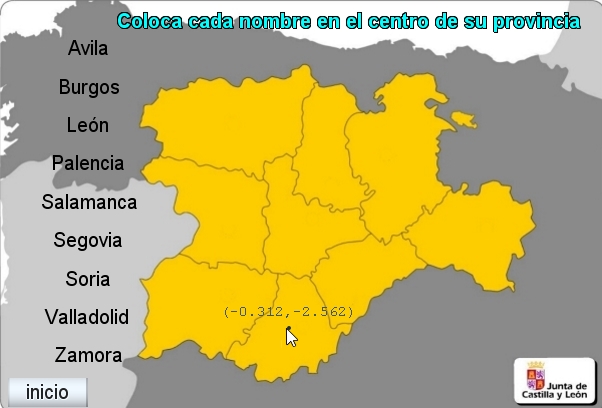
Figura 8
Necesitamos una variable auxiliar para cada provincia cuyo valor refleje si el control gráfico se ha aproximado lo suficiente a ese punto centrado en la región del mapa y así poder validar la posición. Basta que este auxiliar tome en cada momento el valor 0 o el valor 1. Estableceremos un margen de aproximación de las coordenadas: Para Ávila, la diferencia de abcisas, en valor absoluto, menor que 0.5 y la diferencia de ordenadas, en valor absoluto, menor que 0.7
avb=(abs(g1.x+0.3)<0.5)*(abs(g1.y+2.56)<0.7)
Si el control gráfico g1 está dentro de esa zona la respuesta es correcta y el auxiliar avb toma el valor 1.
Los márgenes son diferentes para cada provincia dado que la forma y el tamaño de cada región en el mapa es irregular.
Los auxiliares y su correspondiente expresión algebraica para las distintas provincias se pueden observar en la Figura 9.
Han sido escritas en el algoritmo CALCULOS y se evalúan siempre.
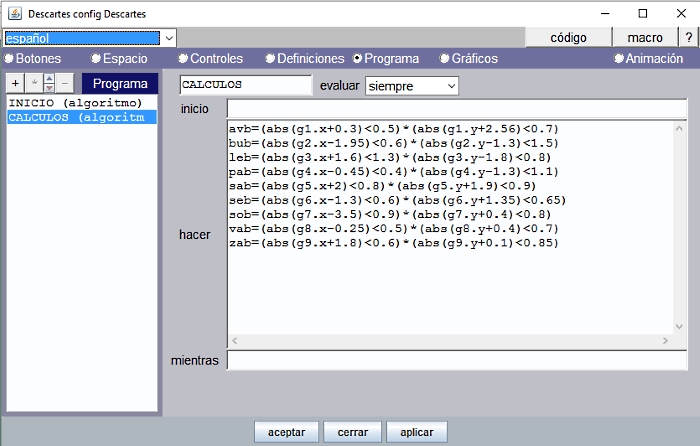
Figura 9
Actuaciones en el panel Gráficos
Situar el texto titular
Al inicio, encabezando la escena vemos el texto “Coloca cada nombre en el centro de su provincia”
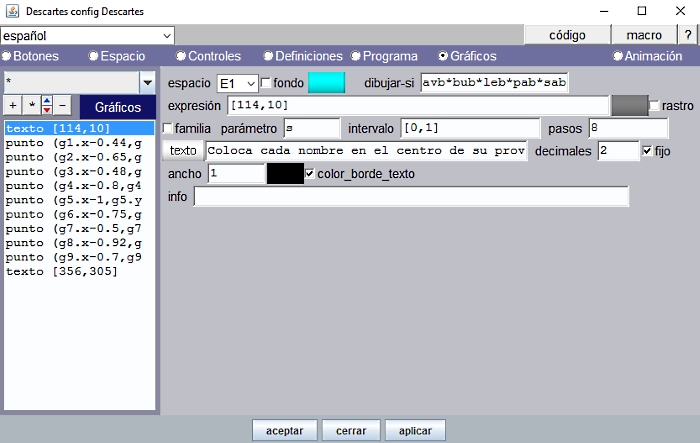
Figura 10
Utilizamos un gráfico tipo texto para escribirlo y la opción Texto simple para dar formato: SansSerif, Negrita y tamaño 20. El color es turquesa (rojo=00, verde=ff, azul=ff) y lleva borde de color negro.
La posición en escena de un gráfico tipo texto se expresa en píxeles, como ya hemos advertido en las ediciones anteriores. Aquí este texto va situado en [114,10] es decir a 114 píxeles hacia la derecha y 10 píxeles hacia abajo del vértice superior izquierdo de la escena que se toma como origen [0,0].
Para determinar esta posición se visualiza, solo con esta finalidad, la red, ejes coordenados y números del espacio y se tiene en cuenta que la unidad coordenada es de 48 píxeles (escala por defecto).
Podemos hacer un cálculo muy simple para determinar la posición del texto:
114 píxeles=48 píxeles*2.38 (unidades coordenadas hacia la derecha)
10 píxeles=48 píxeles*0.21 (unidades coordenadas hacia abajo)
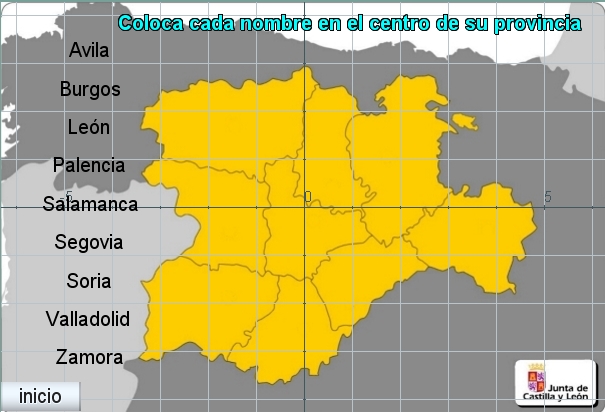
Figura 11
El texto tiene que verse únicamente cuando los nombres de las provincias no están aún bien situadas en su región en el mapa, así pues, debemos de poner la condición
dibujar-si: avb*bub*leb*pab*sab*seb*sob*vab*zab=0
es decir, mientras algún nombre de provincia no esté bien situado.
Situar los nombres de las provincias .
Insertamos tantos puntos como nombres de provincias haya que distribuir en el mapa. Observemos que un punto puede llevar asociado un texto que se visualiza próximo a modo de etiqueta. Cada texto será el nombre de una provincia y va a estar apoyado en un control gráfico (g1.x, g1.y), (g2.x, g2.y),… (g9.x, gy.9). De esta manera conseguimos que el nombre asociado al punto se desplace al arrastrar el control gráfico.
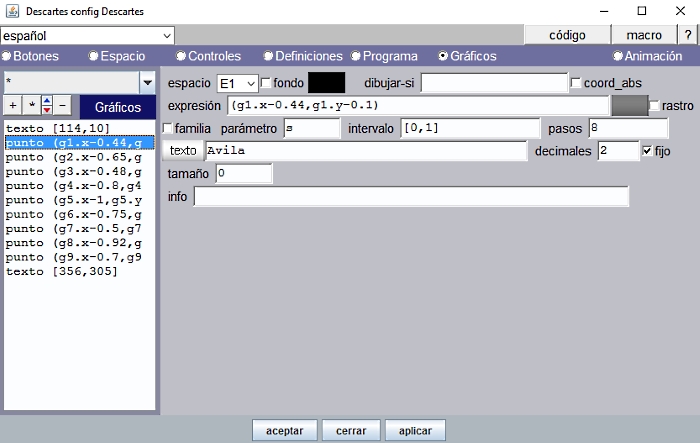
Figura 12
Modificamos algo la colocación del punto gráfico para que el centro de cada control gráfico coincida con el centro de cada nombre:
(g1.x-0.44, g1.y-0.1), (g2.x-0.65, g2.y-0.1), (g3.x-0.48, g3.y-0.1), (g4.x-0.8, g4.y-0.1), (g5.x-1, g5.y-0.1), (g6.x-0.75, g6.y-0.1), (g7.x-0.5, g7.y-0.1), (g8.x-0.92, g8.y-0.1), (g9.x-0.7, g9.y-0.1)
Al arrastrar el control gráfico que, aunque oculto, queda situado en el centro del nombre de la provincia, arrastramos también el nombre de la provincia cuyas coordenadas están vinculadas a las de aquel.
El formato del texto se consigue con la opción Texto simple, pulsando el botón texto que precede a la ventana donde se escribe el nombre de la provincia: Tipo de letra SansSerif y tamaño 20.
Situar el texto "muy bien"
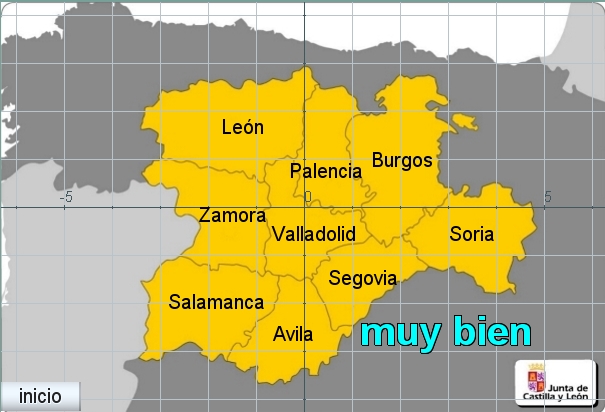
Figura 13
Se verá solamente cuando todos los nombres estén correctamente colocados, para ello se pone la condición
dibujar-si: avb*bub*leb*pab*sab*seb*sob*vab*zab=1
es decir, si todos los auxiliares de provincias tiene el valor 1 y por lo tanto los controles gráficos correspondientes están bien situados dentro del margen establecido.
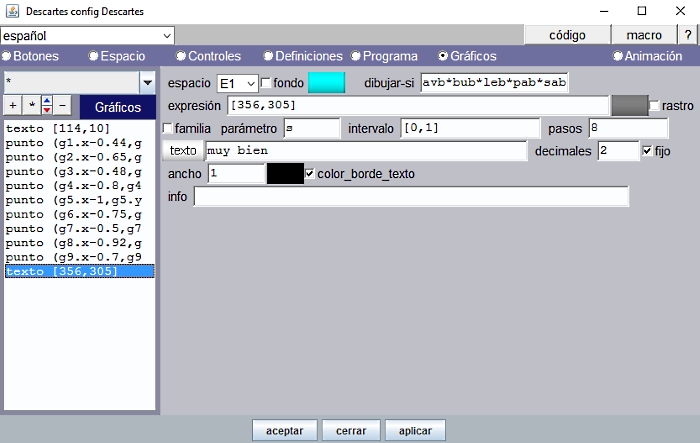
Figura 14
El formato del texto es SansSerif, Negrita y tamaño 40 y se obtiene con la opción Texto simple. El color es turquesa, como el texto de encabezado y se bordea, también, con color negro.
Propuesta final
Animamos a la realización de escenas que sigan el mismo principio técnico de elaboración que hemos presentado en este artículo, por ejemplo:
- Posicionar adecuadamente los nombres de los elementos de un polígono regular (radio, apotema, lado, diagonal).
El docente sabrá encontrar enseguida otras aplicaciones relacionadas con la actividad que esté desarrollando con sus alumnos. Se debe entender que el fondo de la escena puede ser una imagen de naturaleza cualquiera, no necesariamente la de un mapa geográfico y los nombres tendrían que ver con el contexto donde deban de ir situados.
Autoría:
Eduardo Barbero Corral (Idea del proyecto y técnicas de programación DescartesJS)
Ángel Cabezudo Bueno (Interpretación, edición de la escena, ilustraciones y redacción)
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
 Muchas gracias por la atención que ha recibido nuestro primer artículo de nivel básico de “Escenas con DescartesJS: Técnicas y trucos”. Esperamos seguir manteniendo vuestro interés por la ayuda que os podamos prestar desde aquí.
Muchas gracias por la atención que ha recibido nuestro primer artículo de nivel básico de “Escenas con DescartesJS: Técnicas y trucos”. Esperamos seguir manteniendo vuestro interés por la ayuda que os podamos prestar desde aquí.
Cuando Eduardo Barbero Corral me proporcionó una lista de títulos de entre su colección de recursos de cosecha propia, enseguida me fijé en este que hoy os presentamos para dar continuidad a la serie: no me cabe duda que os va a gustar. La redacción de este artículo mantiene el mismo método de trabajo con el anterior; he utilizado las ideas de Eduardo, la descripción que él me hace de este recurso según su técnica de programación y las anotaciones en cada etapa para el proceso de elaboración de la escena: Botones, Espacio, Controles, Auxiliares, Cálculos y Gráficos.
La mejor forma de entender su proceso y darlo a conocer a través de este artículo es seguir sus pautas de una forma práctica: me pongo manos a la obra, genero la escena, voy anotando mis propias observaciones en aquellas partes que requieren alguna explicación más amplia, saco imágenes sobre los materiales, la escena y los paneles de configuración del Editor de Escenas para que sirvan de ayuda al lector interesado… Después de un intercambio de opiniones con su autor para la mejora didáctica procedo a la redacción del artículo.
Este trabajo trata los controles numéricos tipo campo de texto para escribir sobre ellos palabras (contenido alfanumérico).
Veremos cómo podemos programar escenas en las que el alumno debe contestar escribiendo una palabra en un control numérico tipo campo de texto.
Los controles numéricos se emplean en muchas escenas; en un principio en ellos solamente se podían escribir números, pero actualmente, la herramienta Descartes también permite que se utilice un control numérico para que el alumno escriba en él una expresión alfanumérica y que se pueda interpretar como texto. Esto nos posibilita crear escenas tipo test.
¡No confundir un control numérico tipo campo de texto con un control texto al manipular el panel Controles o si se consulta la Documentación técnica!
Cuando tratemos más adelante el panel de Controles para programar la escena si el lector lo considera necesario puede consultar el artículo sobre Controles numéricos en la Documentación técnica.
Idea del proyecto
|
Escena_B02: En esta escena el alumno debe de escribir los nombres de las partes de una montaña con letras minúsculas. Se ha buscado la imagen de una montaña donde se pueden observar estas partes, se trata del archivo monte.jpg
Figura 1 El tamaño de la escena por defecto tiene que modificarse para que coincida con el de la imagen, 530x296 píxeles, que debe de verse como fondo de la escena. En la escena el alumno dispone de sendos campos de texto junto a las partes de la montaña y debe de escribir en ellos la respuesta. Se considera respuesta correcta para la parte más alta "cima", "cumbre" o "pico", para la parte intermedia "falda" o "ladera" y solo se aceptará "pie" para la parte más baja. El programa debe de responder según estos dos casos posibles:
|
La siguiente Figura 2 lleva un enlace a la escena ya elaborada a partir de la idea expuesta. Interaccionad con ella para comprender la funcionalidad y después explicaremos los recursos de DescartesJS que se emplean utilizando el Editor de Escenas.
Figura 2

Figura 3
Primeros pasos, herramientas y recomendaciones
Ya dijimos en el artículo anterior cuales son los primeros pasos que hay que dar antes de empezar a programar la escena, las herramientas que se necesitan y algunas recomendaciones para quienes se inician con DescartesJS.
Remitimos a estos preliminares, explicados con detalle y ahora solo hacemos un recordatorio esquemático:
- El Gestor de escenas de Descartes, denominado Descartes.jar, debe de haberse descargado y disponer de un acceso directo (recomendable) en el escritorio de Windows. Además, es conveniente un editor de texto como Notepad++ que dispone de un modo particular para presentar las líneas de código y facilitar la lectura y edición de los archivos HTML.
- Crear la carpeta de contenidos. En este trabajo la hemos denominado escena_B02
- Incluir la subcarpeta lib que contiene el archivo intérprete descartes-min.js.
- El archivo index.html incluye el código de la escena encerrado entre etiquetas <ajs> </ajs> y la referencia al interprete, <script type='text/javascript' src='lib/descartes-min.js'></script>, delante de la etiqueta de cierre </head>.
- Los pasos 2 a 4 se pueden realizar desde el mismo Gestor de Escenas.
El procedimiento preliminar consiste:
- Abrir el Gestor de Escenas
- Seleccionar en el menú Opciones > Librería portable > Sólo para JS (verificando esta elección en la línea de estado, línea inferior en la ventana del Gestor)
 Figura 4
Figura 4 - Seleccionar en el menú Archivo > Guardar como, especificando la carpeta destino (creándola en ese momento si no existe) y el nombre que damos al archivo portador de la escena index.html
Figura 5
De esta manera disponemos ya del archivo index.html que contiene el código necesario para poder ver una escena básica que por defecto ha creado el Gestor. La Figura 6 muestra el código del archivo así creado visto desde el editor Notepad++
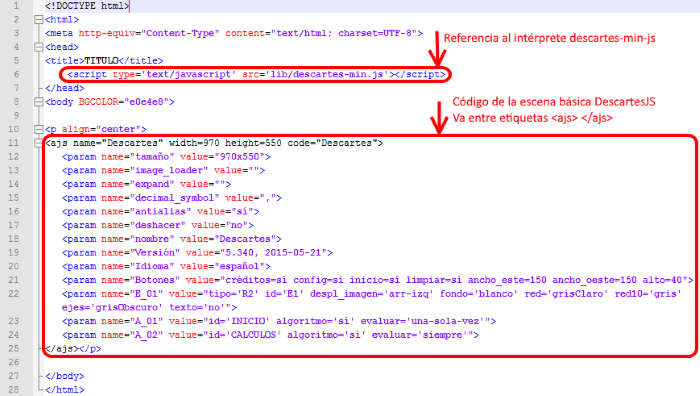 Figura 6
Figura 6
Para continuar, no olvidar incluir en la carpeta de contenidos escena_B02 el archivo monte.jpg.
Iremos describiendo paso a paso la trasformación de esta escena básica, utilizando el Editor de Escenas del Gestor Descartes.jar hasta culminar el proyecto.
Es importante que las explicaciones que aquí damos se acompañen, si fueran insuficientes, con la consulta puntual del concepto que se esté aportando en la "documentación técnica", sin pretender conocerlo todo desde un principio y solo para entender la aplicación en esta escena en concreto.
Apertura del Editor de Escenas y cambio de las dimensiones de la escena
La escena por defecto tiene un botón básico en cada esquina: créditos (arriba-izq), config (arriba-dcha), inicio (abajo-izq), limpiar (abajo, dcha).
Con la escena básica en la ventana del Gestor, accedemos a configurarla con el Editor de Escenas, de dos formas alternativas:
- Pulsando el botón E (editar) al lado derecho, fuera de la ventana.
- Pulsando el botón config (configurar) en la esquina superior derecha de la escena.
Figura 7
Estos botones pueden desactivarse posteriormente (todos o solo alguno), si creemos que no son necesarios que se muestren en la escena, pero podemos en cualquier momento acceder a ellos haciendo clic derecho sobre cualquier parte de la escena como se muestra en la Figura 8
Figura 8
La figura siguiente muestra el panel Botones del Editor con todos ellos desactivados. Así es como vamos a configurarlo en este proyecto.
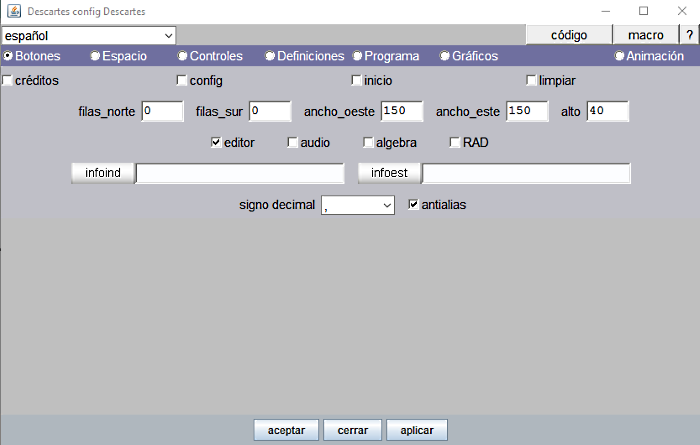
Figura 9
Para cambiar el tamaño de la escena, que por defecto es 970x550 píxeles, recordemos que hay que hacerlo desde el código de la escena. Al pulsar el botón código (arriba a la derecha) accedemos al código fuente de la escena y escribimos el ancho (530px) y el alto (296px) especificado para este proyecto
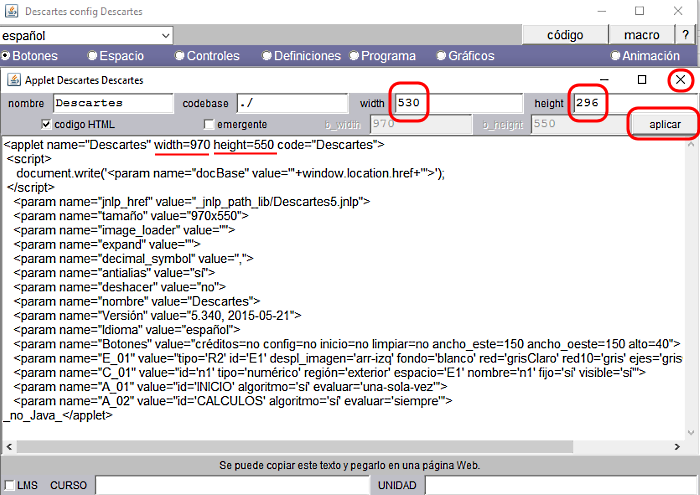
Figura 10
Para proceder con este cambio habrá que aplicar y cerrar (X) la ventana de código para regresar al panel de configuración del Editor de Escenas.
Cambios en el panel Espacio
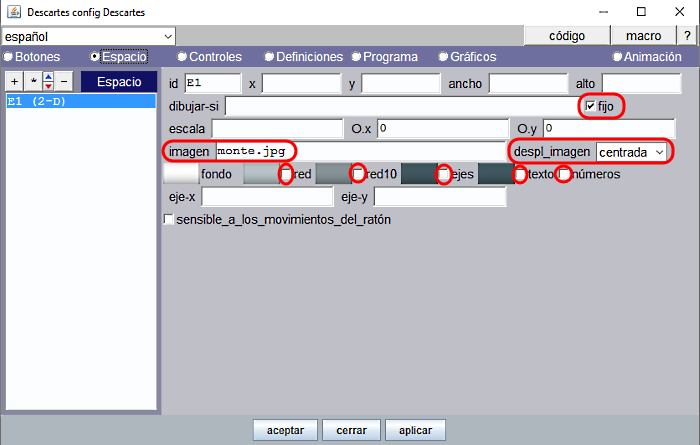
Figura 11
- En el campo “imagen”, escribimos el nombre del archivo, monte.jpg, incluyendo su trayectoria respecto del archivo index.html, que lleva el código de la escena.
- Elegimos la opción centrada en el campo “despl_imagen” (desplazamiento de la imagen).
- La red, los ejes y los números están desactivados.
- La escala cuando no lleva valor es por defecto 48 píxeles.
Cambios en el panel Controles
Iremos añadiendo (+) sucesivamente los controles numéricos identificados internamente (id) como n1, n2 y n3, seleccionando el tipo “campo de texto” y que utilizamos respectivamente para dar respuesta a cada una de las tres partes de la montaña: cima, cumbre o pico, ladera o falda y pie. Estos controles hay que definirlos como “interiores” y así podremos situarlos donde mejor convenga dentro de la escena. El control tiene forma rectangular.
Las posiciones respectivas sobre la escena serán las siguientes:
- Para la respuesta n1, la posición junto a la cima es (244,10, 70,30)
- Para la respuesta n2, la posición junto a la ladera es (386,100,70,30)
- Para la respuesta n3, la posición junto al pie es (310,210,70,30)
Los cuatro números, leídos ordenadamente y encerrados entre paréntesis, (x, y, w, h), significan:
- x: Distancia horizontal en píxeles del vértice superior izquierdo del control al lado izquierdo de la escena
- y: Distancia vertical en píxeles del vértice superior izquierdo del control al lado superior de la escena.
- w: ancho del control
- h: alto del control
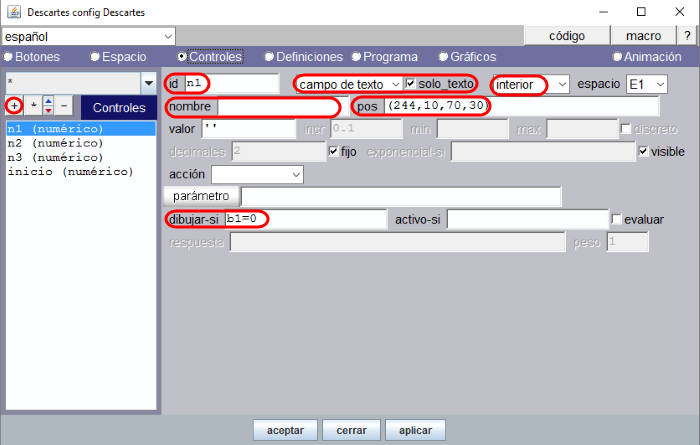
Figura 12
En la Figura 12 se muestra los parámetros del control n1. No mostramos las figuras correspondientes a n2 y n3 dado que son similares a n1 diferenciándose en el campo “pos” y en el auxiliar para la condición “dibujar-si” (b2=0 en el control n2 y b3=0 en el control n3).
El campo “nombre” es el nombre externo que tiene el control, a modo de etiqueta, a la izquierda del control. Si no ponemos nombre la etiqueta en un control numérico de campo de texto, la etiqueta no va a aparecer y solo se muestra el área rectangular del control para recibir el texto como respuesta.
También es posible indicar que el “nombre” es vacío con las expresiones _._, _nada_ o _void_. Estas fórmulas son en cambio necesarias en los controles numéricos tipo pulsador (que trataremos en otros proyectos) pero no en los de tipo campo de texto.
Es importante marcar la opción “solo texto” para que se interprete la entrada como un dato no numérico y escribir el “valor” inicial como cadena vacía, abriendo y cerrando apóstrofos '' (acentos simples) o abriendo y cerrando barras verticales ||. Si no iniciamos el control con cadena vacía, aparecerá el valor 0 por defecto, antes de que podamos escribir un texto: cuando pedimos al alumno que escriba una palabra preferimos que el rectángulo esté totalmente en blanco.
Queremos que los controles desaparezcan cuando el alumno ha contestado bien, por eso en el control n1 se ha puesto la condición dibujar-si='b1=0'. Es decir, desaparecerá cuando el auxiliar b1 toma valor distinto de 0. De esa manera el alumno puede corregir hasta dar una respuesta correcta. Cuando la respuesta es correcta el control desaparece, pero en su lugar debemos hacer que aparezca la palabra que ha escrito el alumno. Para ello, más adelante en el panel de Gráficos añadimos un gráfico tipo texto con el contenido de n1 que se dibuja cuando la respuesta es correcta, ahora con la condición dibujar-si=’b1’
Hemos añadido un cuarto control para que la escena se reinicie y se pueda practicar con ella cuantas veces se quiera desde el principio. En este caso en vez de utilizar el botón básico, seleccionado desde el panel Botones, hemos incluido un control numérico tipo botón interior para configurar a nuestro gusto su posición y tamaño en la escena x=0, x=266, w=80, h=30. El tamaño de la fuente con que se escribe el nombre externo del control, que funciona como etiqueta, es de 20 puntos.
Obsérvese que se ha vinculado la “acción=inicio”, fundamental para nuestro propósito, cuando se pulsa el control tipo botón.
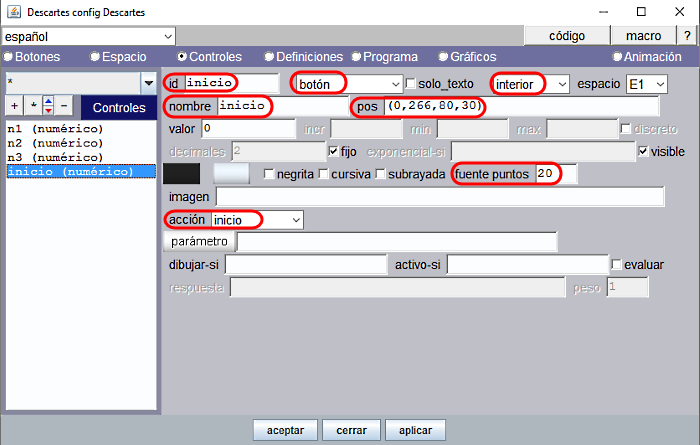
Figura 13
Cambios en el panel Programa
Debemos de definir los valores de las respuestas que vamos a considerar acertadas. Para ello disponemos del panel Programa.
La respuesta que se proporcione a través del control tiene que ser perfectamente coincidente con la palabra que hemos programado, pero a veces nos interesa permitir que también se considere válido si contesta con una palabra sinónima o si esa palabra tiene tilde y el alumno no lo ha puesto.
En la parte más alta de una montaña es válido poner “cima”, “cumbre” o “pico”. Para la parte intermedia, generalmente inclinada, es válido “falda” o “ladera”. Solo aceptaremos “pie” como respuesta correcta de la parte más baja.
Los cálculos deben de evaluarse siempre que se realicen cambios al escribir las respuestas. La figura 14 muestra estos cálculos que se explican en los siguientes dos puntos:
- Auxiliares de respuestas correctas. Una respuesta está bien cuando coincide con cualquiera de las respuestas válidas.
Utilizamos las variables b1, b2 y b3 para registrar cada una de las tres respuestas, para que sean correctas. El valor resultante de cada variable podrá ser 1 o 0. Así pues, b1 valdrá 1 si n1=’cima’ O n1=’cumbre’ O n1=’pico’ y b1 se expresa como una suma de las tres expresiones. Dicho esto, es fácil entender las definiciones que escritas en este panel para b1, b2 y b3. Observar que toda expresión de la forma (A) = (B) tiene un valor booleano {0,1}. - Auxiliares de respuestas incorrectas. Una respuesta está mal cuando la respuesta es diferente de todas las posibles respuestas válidas y también es diferente de no haber puesto nada.
Utilizaremos las variables m1, m2 y m3 para registrar la respuesta de cada parte de la montaña cuando es incorrecta o falsa. La variable m1 tomará el valor 1 si ninguna de las respuestas que se den para la parte más alta de la montaña es la convenida: n1#'cima', n1#'cumbre' y n1#'pico'. Es condición necesaria para que se registre una respuesta como incorrecta si además se contesta escribiendo algo, luego también ha de cumplirse que n1#''. Por tanto, m1 se expresa como producto de las cuatro expresiones anteriores. Procedemos análogamente para definir los cálculos de m2 y m3.
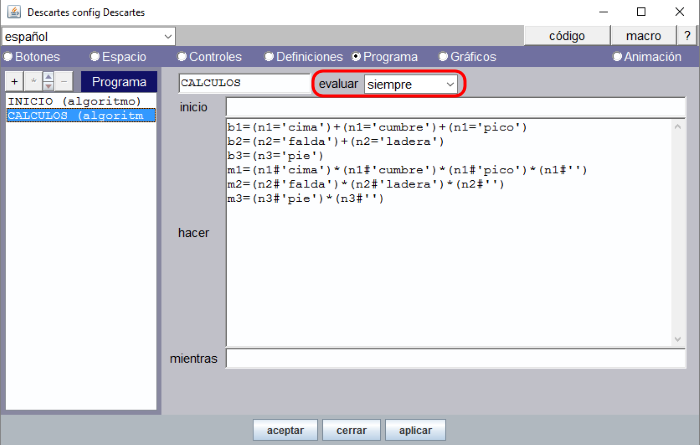
Figura 14
Observación:
Para indicar que dos expresiones (A) y (B) toman distinto valor lo expresaremos con el operador binario desigualdad que puede escribirse como # o bien !=. Ver operadores en la Documentación técnica. Por tanto (A) # (B) o (A) != (B) tienen un valor booleano {0, 1}.
Cambios en el panel Gráficos
En las figuras 2 y 3 donde se presenta la idea del proyecto, vemos que hay tres clases de gráficos de tipo texto:
- El texto para el título de la escena: “Partes de una montaña”
- Los tres textos [n1], [n2] y [n3] que contienen las respuestas correctas que reemplazarán a sus respectivos controles n1, n2 y n3
- Los textos con los que el programa responde: “¡Muy bien!” cuando las tres respuestas son correctas y “nombre incorrecto” cuando al menos una de las respuestas es incorrecta.
El texto para el título de la escena (Figura 15)
Escribimos el título de la escena “Partes de una montaña” en el lado izquierdo y más o menos centrado verticalmente, expresión= [10,110].
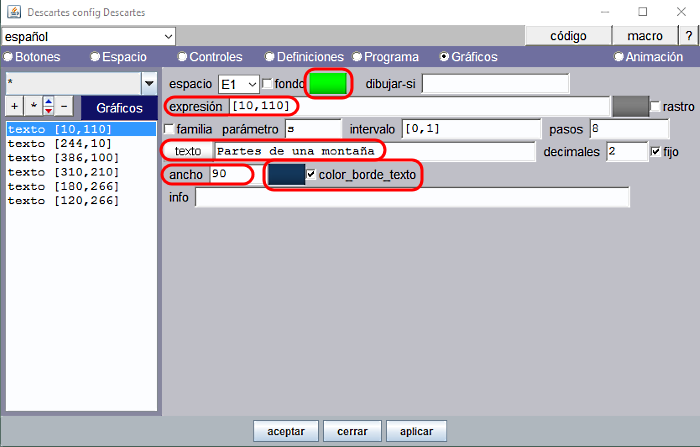
Figura 15
Observemos en la Figura 2 que el texto está dividido en tres líneas: como consecuencia de haber especificado ancho=90 puntos el texto se tiene que acomodar a este ancho y se ve obligado a saltar 2 veces de línea. Para que esto funcione así hay que escribir el texto con la opción texto simple. El formato elegido es SansSerif, Negrita y 20.
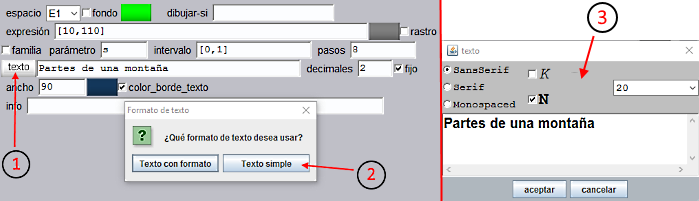
Figura 16
El color del texto es verde estándar (R=00, V=ff, A=00) y se adorna con un borde obscuro de color aditivo Rojo=14, Verde=38, Azul=5C. Este color se ha obtenido mediante una herramienta Cuentagotas seleccionando la zona de sombra producida en los huecos de la ladera de la montaña.
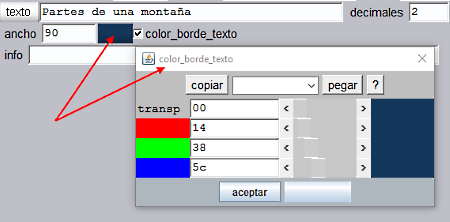
Figura 17
Queremos que los controles desaparezcan cuando el alumno ha contestado bien (Figura 18), por eso en el control n1 se ha puesto la condición dibujar-si='b1=0' Es decir, desaparecerá cuando el auxiliar b1 toma valor 1. De esa manera el alumno puede corregir sobre el control hasta dar una respuesta correcta.
Cuando la respuesta es correcta el control desaparece, pero en su lugar debemos hacer que aparezca la palabra que ha escrito el alumno en la misma posición, expresión= [244,10].
Observar que hay que escribir con la opción texto simple el contenido de la variable [n1] y no el nombre de la variable n1. El formato del texto es SanSerif, 20 y en color blanco (R=ff, V=ff, A=ff).
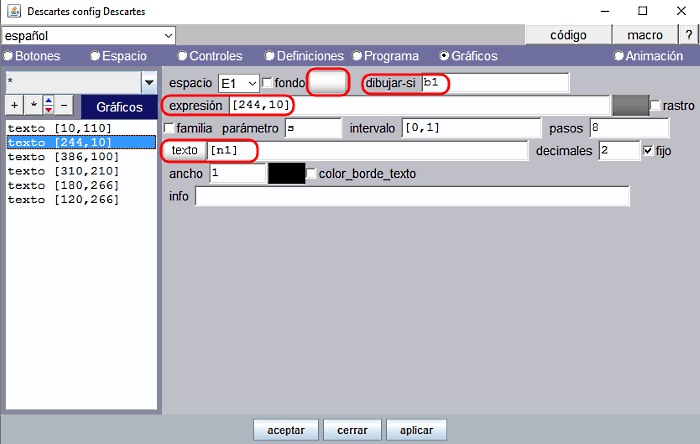
Figura 18
Análogamente escribiremos con el mismo formato y color que [n1] las respuestas correctas [n2] en la posición expresión= [386,100] con la condición dibujar-si ='b2' y [n3] en la posición expresión= [310,210] con la condición dibujar-si = 'b3'
Texto de respuesta del programa cuando se contesta bien (Figura 19)
El texto “¡Muy bien!” se dibuja cuando se cumple la condición b1*b2*b3=1 >0 por lo que basta escribir dibujar-si=b1*b2*b3 es decir cuando b1=1, b2=1 y b3=1.
Este texto se dibuja en la posición [180,266], con la opción Texto simple y el formato siguiente: SansSerif, Negrita, 28. Color amarillo estándar (R=ff, V=ff, A=00) y borde negro (R=00, V=00, A=00).
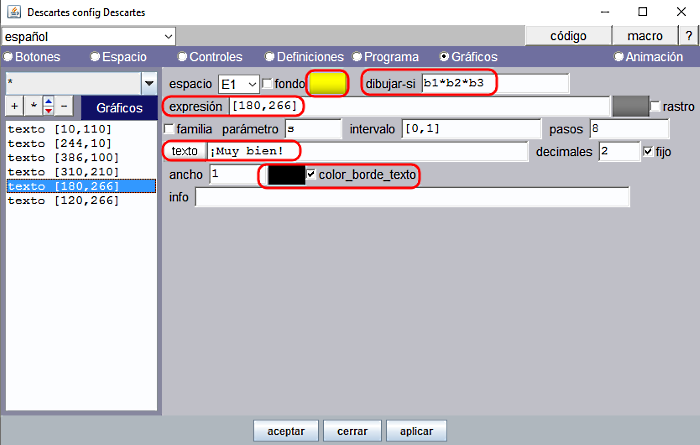
Figura 19
Texto de respuesta del programa cuando se contesta incorrectamente (Figura 20)
El texto “nombre incorrecto” se dibuja cuando se cumple la condición m1+m2+m3>0 por lo que basta escribir dibujar-si= m1+m2+m3 es decir cuando m1=1 o m2=1 o m3=1 (alguno de los nombres es incorrecto).
Este texto se dibuja en la posición [180,266], Texto simple con el formato siguiente: SansSerif, Negrita, 28. Color rosa estándar (R=ff, V=af, A=af) y borde negro (R=00, V=00, A=00).
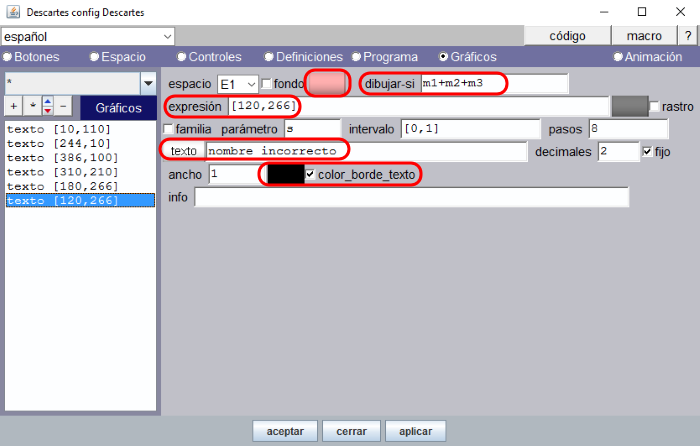 Figura 20
Figura 20
La condición dibujar-si y propuesta alternativa para dibujar texto con el gráfico tipo punto
La condición dibujar-si
Tanto para dibujar los controles como para dibujar los textos que aparecen en la escena de este proyecto hemos utilizado la condición expresada en el campo dibujar-si. Es oportuno explicar cómo funciona este campo dependiendo de los valores que puede tomar.
- Si el campo se deja vacío (valor por defecto) siempre se dibuja
- Si el campo tiene valor 0 o es negativo no se dibuja.
- Si el campo es mayor que 0 se dibuja.
- Si el campo lleva la condición A = B, se dibujará si A = B es una expresión verdadera y tiene valor lógico 1 (punto 3), en caso contrario es una expresión falsa, tiene un valor lógico 0 y no se dibuja (punto 2).
Escribir texto con el tipo gráfico punto vs tipo gráfico texto
En el primer artículo correspondiente al proyecto Escena_B01 utilizamos el gráfico tipo punto para dibujar texto.
En este artículo hemos utilizado el tipo gráfico texto, cuya expresión para el posicionamiento en la escena es (x, y), donde x=distancia en píxeles al borde izquierdo de la escena e y=distancia en píxeles al borde superior de la escena.
Recordemos que el punto como elemento gráfico tiene la posibilidad de asociar un texto que se escribe próximo. El recurso para escribir solo el texto consiste en dar un tamaño 0 al punto, con lo cual éste no se dibuja.
La posición del punto como elemento gráfico se expresa en coordenadas cartesianas (x, y), no en píxeles y la longitud de la unidad cartesiana es el valor que asignemos a la escala que por defecto es 48 píxeles.
La siguiente imagen es utilizada de fondo del espacio en la escala de nuestro actual proyecto Escena_B02. Se dibujan ahora los ejes, la red y los números para facilitar la localización del punto de tamaño 0 que deberíamos dibujar asociando los textos de contenido [n1], [n2] y [n3]
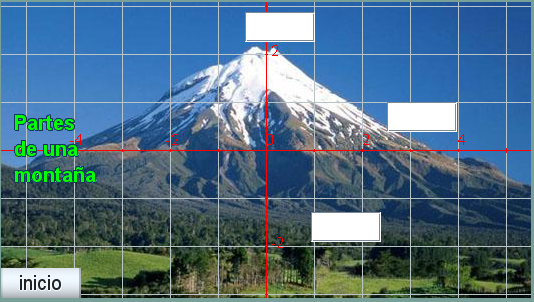
Figura 21
Proponemos al lector verificar que la posición de los tres puntos para dibujar los textos [n1], [n2] y [n3] asociados podrían ser respectivamente (-0.5, 2.5), (2.5, 0.5) y (1, -1.8) y si está interesado en ver los resultados que elabore una segunda escena donde las respuestas se dibujen como textos de gráficos tipo punto en vez de gráficos tipo texto.
Determinación del espacio:
- Ancho= 530 píxeles, alto=296 píxeles, Escala=48 píxeles.
- Unidades representadas en el eje OX=530/48=11.04, unidades representadas en el eje OY=296/48=6.17
Autoría:
Eduardo Barbero Corral (Idea del proyecto y técnicas de programación DescartesJS)
Ángel Cabezudo Bueno (Interpretación, edición de la escena, ilustraciones y redacción)
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Proporcionalidad. Las Espirales V
Entre las innovaciones producidas en el ámbito de la Red Educativa Digital Descartes y gracias al convenio trilateral entre la Facultad de Ciencia y Tecnología de la Universidad Autónoma de Entre Ríos (FCyT-UADER) en la provincia de Entre Ríos en Argentina, la Red Educativa Digital Descartes Colombia (colDescartes) y la Red Educativa Digital Descartes (RED Descartes), están: el libro Opúsculo sobre la función lineal y afín, la recta en el plano creado por las profesoras Irma Manuela Benitez - Alicia Elena Carbonell y María Alicia Gemignani, la siguiente imagen enlaza con dicho libro
y la integración de los mapas de Google en una escena DescartesJS realizada por Diego Feria Gómez, que abre un amplio abanico de posibilidades al proyecto GEOGráfica según muestra la escena que enlazamos a continuación.
También cabe destacar la aportación de la profesora Montserrat Gelis Bosch que ha adaptado al catalán el material sobre planos de simetría en 3D creado por el profesor José R. Galo Sánchez que puede consultarse en los siguientes vínculos,
y el Opúsculo sobre los complejos de María José García Cebrian que se enlaza a continuación y que, encarecidamente, aconsejamos visitar y utilizar en el tema de Complejos por su completitud y potencial didáctico.
De la espléndida colección de libros dinámicos, interactivos y multimedia del subproyecto iCartesiLibri que los profesores: Juan Jesús Cañas Escamilla, José R. Galo Sánchez, Juan Guillermo Rivera Berrío, Irma Manuela Benitez, Alicia Elena Carbonell y María Alicia Gemignani han creado sobre algunos temas de Estadística y Análisis enlazamos, por su indudable interés, el libro de estadística.
La extraordinaria acogida a los materiales del proyecto @prende, recientemente elaborado por: José Luis Abreu León (Instituto de Matemáticas), Joel Espinosa Longi (Instituto de Matemáticas), Deyanira Monroy Zariñán (LITE) y equipo para Primaria, comentada ampliamente en los foros hace que no sea necesario reiterar los elogios a tan meritotia creación, en la imagen siguiente enlazamos el recurso dedicado a las áreas.
Seguimos insistiendo en la necesidad de estar al día de las posibilidades operativas y de uso de los materiales y escenas de la Red Educativa Digital Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS, en especial a estos, que llevan a la información sobre las animaciones y la construcción, paso a paso, de algunas escenas ejemplo, elaborada por el profesor Juan Guillermo Rivera Berrío.
Antes de comenzar con el análisis de como hemos incluido en la miscelánea que estamos creando las escenas de la espiral de Teodoro y las espirales de tres a veinte centros, vamos a mostrar un vídeo de la presencia de la espiral en el organismo con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa.
Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales.
En el artículo anterior terminamos de estudiar el proyecto de miscelánea, tal y como estaba hasta aquella fecha, indicando que íbamos a integrar en el mismo el contenido de la escena de la espiral de Teodoro.
También hemos añadido al proyecto el contenido de la siguiente escena sobre como dibujar las espirales de 3, 4, 5 ... 20 centros
La escena de la espiral de n centros, que vemos a continuación
está formada por:
- dos controles tipo pulsador
- un control gráfico de color rojo que es la referencia para la construcción de la gráfica.
- un texto.
- dos familias de puntos (los vértices y sus trasladados)
- dos familias de segmentos (los lados y sus prolongaciones).
- una familia de arcos.
Los pulsadores controlan, respectivamente, la cantidad de centros de la espiral y la longitud del lado del polígono regular sobre cuyos vértices se encuentran dichos centros. Inicialmente es visibles la espiral de tres centros.
Con objeto de que puedan verse todas las espirales, la escala del espacio donde se representan tiene un valor de 16 en lugar de 48 que es el valor por defecto. Aunque para ver bien las espirales de más de 9 centros es conveniente poner la longitud del lado a 1. Esto se ha hecho así para que se practique con el cambio de escala. Puede conseguirse el mismo efecto poniendo un control en la escena que modifique la escala; o reduciendo - aumentando el tamaño del lado del polígono base.
Para poder dibujar la colección de centros y los segmentos de los lados y sus prolongaciones, hemos definido:
- Cuatro vectores de tamaño dinámico para albergar las coordenadas de los vértices y sus trasladados que harán posible la gráfica de los segmentos de la escena.
- Un algoritmo que calcula las coordenadas de los vértices y sus trasladados.
Desde este enlace puede descargarse el proyecto de miscelánea con la espiral de Teodoro y las espirales de n centros incluidas, se puede observar que el nombre del archivo ha cambiado respecto al original, es así para que se puedan comparar los códigos y ver los cambios realizados. Aconsejamos, a quienes comienzan a crear escenas fundamentalmente, y a cualquiera que visite el Blog, leer detenidamente el extraordinario artículo creado por el profesor Ángel Cabezudo Bueno sobre las Escenas con DescartesJS: Técnicas y trucos, donde se detalla con rigor el significado y uso de los componentes que pueden intervenir en una escena aportando una buena colección de atajos y utilidades que agilizan la creación y dotan a las escenas de funcionalidades extraordinarias.
La escena del proyecto puede verse a continuación:
Como aplicación de la proporción Humana hemos elaborado la siguiente escena.
También, en la misma dirección, hemos creado, con el programa GeoGebra, una breve aplicación que muestra como teselar un triángulo cordobés con triángulos cordobeses.
Acceso al recurso en GeoGebraTube
En próximas entradas continuaremos con el paso a paso de la escena incluyendo la espiral Cordobesa, la de Durero, la de Fibonacci y otras más entre sus funcionalidades, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo

Abrimos esta nueva sección del Blog que hemos titulado genéricamente "Escenas con DescartesJS: Técnicas y trucos" con una escena propuesta por nuestro compañero cartesiano Eduardo Barbero Corral y contamos con él para que nos siga mostrando sus técnicas y trucos en sucesivas ediciones de esta sección del blog. Una muestra de sus habilidades para el desarrollo de escenas de Descartes puede ser consultada en el siguiente enlace al artículo "Recomendaciones, indicaciones y elementos prefabricados" que está publicado en la "Documentación técnica y de usuario de Descartes 5" (en lo sucesivo "Documentación técnica").
Las "técnicas y trucos" que se irán explicando en sucesivos artículos tendrán dos niveles, uno básico y otro avanzado. Con el nivel básico pretendemos acercar la herramienta DescartesJS a quien le pueda interesar iniciarse en la programación de escenas. El nivel avanzado estará orientado a quien ya tiene cierto dominio de la herramienta y facilitará la interpretación de las instrucciones que se incluyen en los diferentes paneles del Editor de Escenas y que nadie ignora, a veces resultan difíciles de comprender sin la correspondiente documentación del programa.
otro avanzado. Con el nivel básico pretendemos acercar la herramienta DescartesJS a quien le pueda interesar iniciarse en la programación de escenas. El nivel avanzado estará orientado a quien ya tiene cierto dominio de la herramienta y facilitará la interpretación de las instrucciones que se incluyen en los diferentes paneles del Editor de Escenas y que nadie ignora, a veces resultan difíciles de comprender sin la correspondiente documentación del programa.
Pretendemos que esta sección esté abierta a cualquier "cartesiano" que quiera comunicar alguna "técnica o truco" para resolver escenas con DescartesJS. Siempre estamos dispuestos a aprender y a recibir el estímulo de los demás.
En este supuesto poneros en contacto conmigo y acordaremos las condiciones para su publicación en este blog.
Un primer contacto con DescartesJS: Programación de una escena paso a paso
Eduardo me entregó la idea de esta escena y el proceso que él sigue en su realización que seguidamente vamos a documentar. También puso unas notas sobre lo que considera necesario preparar de antemano y los retoques y mejoras que cabe hacer con la escena.
Con todo esto, mi trabajo como redactor de este artículo ha consistido en elaborar la escena siguiendo sus pautas e interpretar sus propuestas de mejora. He ido observando todo lo que sería conveniente añadir, explicaciones e imágenes tomadas directamente de la escena o de las herramientas de trabajo, para facilitar la comprensión a quien se anime a emularlo y aprender a programar.
Quizá a alguien le pueda resultar excesivo el detalle en algunas ocasiones pero hay que pensar que se trata de la primera escena para el nivel básico y pretende que el neófito o el que ha experimentado muy poco con DescartesJS tenga la orientación suficiente para dar los primeros pasos, no se despiste demasiado y le estimule a seguir practicando. Espero haber acertado en mi pretensión.
Es importante que las explicaciones que aquí damos se acompañen, si fueran insuficientes, con la consulta puntual del concepto que se esté aportando en la "documentación técnica", sin pretender conocerlo todo desde un principio y solamente para entender la aplicación en esta escena en concreto.
Una nueva escena elaborada desde cero
Solamente comenzaremos desde cero si pretendemos elaborar una escena totalmente nueva y diferente de las que tenemos. Cuando elaboramos escenas parecidas a otras es más fácil actuar sobre la escena antigua, quitando y poniendo lo que interese, nos ahorraremos mucho trabajo.
En este caso vamos a hacer una escena totalmente nueva.
Las herramientas que se necesitan
| 1. | Un editor de texto plano (uno recomendable es Notepad++). Importante para poder consultar y si fuera el caso editar el código HTML del archivo que lleva la escena de DescartesJS. La escena se reconoce porque va entre etiquetas <ajs> y </ajs>. |
| 2. |
El Gestor de Escenas de Descartes (Descartes.jar) y la carpeta lib conteniendo el archivo intérprete descartes-min.js. |
El Gestor de Escenas está desarrollado en la "Documentación técnica" y puede descargarse desde http://arquimedes.matem.unam.mx/Descartes5/distribucion/
Crea una carpeta y nómbrala p.e. "Descartes5" para guardar esta descarga. Para abrir el Gestor de Escenas basta hacer doble clic en el nombre del archivo Descartes.jar. Es práctico tener un acceso directo a este archivo desde el Escritorio de Windows, cada vez que se quiera trabajar con él. Este es el aspecto que tiene la ventana del Gestor de Escenas cuando se abre en pantalla, mostrando por defecto una escena básica nueva.
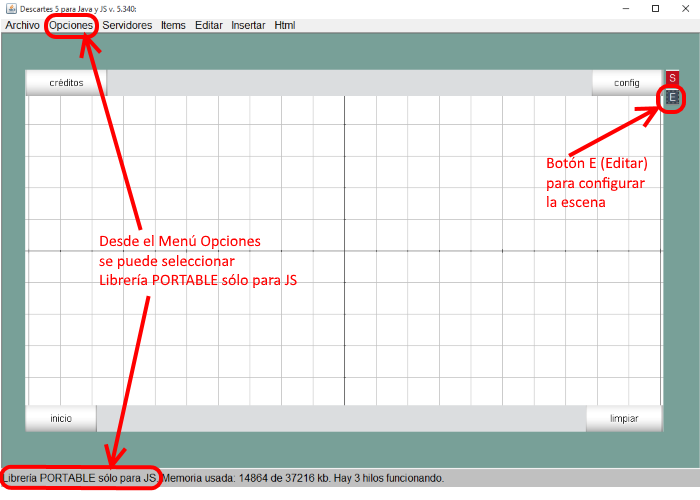
Figura 1
Una de las herramientas que nos interesa por ahora del Gestor de Escenas es el Editor de Escenas que facilita la escritura del código de la escena a través de un determinado número de paneles de configuración: Botones, Espacio, Controles, Definiciones, Programa, Gráficos y Animación.
Las escenas que vamos a explicar en esta serie de artículos son escenas de DescartesJS. El sufijo JS viene a señalar que el intérprete está escrito en JavaScript. Una escena escrita en DescartesJS necesita la referencia a un archivo llamado descartes-min.js para que pueda ser interpretada cuando se abra el archivo HTML que la contiene y se visualice en un navegador Web como Google Chrome, Mozilla Firefox o Safari de Apple. Este archivo puede ser descargado desde
http://arquimedes.matem.unam.mx/Descartes5/lib.
La imagen siguiente muestra la estructura de carpetas que va a tener nuestro proyecto.
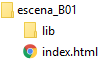
Figura 2
Para el caso de la escena que vamos a desarrollar en este artículo el archivo descartes-min.js debe de estar en la carpeta llamada lib. Esto se consigue simplemente seleccionando desde el Menú Opciones, Librería portable y solo para JS. Puede observarse que este modo está seleccionado si aparece escrito en la línea de estado de la ventana del Gestor de Escenas (Figura 1)
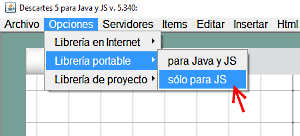
Figura 3
El archivo index.html lleva el código de la escena y la referencia al intérprete descartes-min.js (ver más adelante el apartado Preparar lo Necesario)
Idea del proyecto
|
Escena_B01: Se trata de una escena para que el alumno aprenda a situar puntos sobre el plano cartesiano. Será una escena de tipo actividad, es decir que el alumno debe contestar actuando sobre la escena y el ordenador le indicará si lo hace bien o mal. Es conveniente que primero dibujemos en un papel nuestro proyecto. En la escena solamente aparecerán los ejes de coordenadas y la frase "Coloca este punto en su sitio:" Continuando la frase aparecerá el punto y entre paréntesis sus coordenadas cartesianas, empleando números enteros. Esos valores de las coordenadas serán números aleatorios para que cada vez que se inicia la escena sean diferentes. El alumno deberá mover ese punto con el puntero hasta colocarlo adecuadamente en su lugar. Cuando ese punto esté en su sitio aparecerá el mensaje "MUY BIEN ". |
La siguiente imagen lleva un enlace a la escena ya elaborada a partir de la idea expuesta. Interaccionar con ella para comprender su funcionalidad y después veremos cómo se crea el programa en DescartesJS utilizando el Editor de Escenas.
Figura 4
Preparar lo necesario
Crear una carpeta, p.e. escena_B01, que contendrá archivo HTML que se va a elaborar, p.e. index.html. En ella también debe estar la subcarpeta lib con el archivo intérprete descartes-min.js.
Esta operación puede realizarse completamente desde el Gestor de Escenas tal como indicamos seguidamente.
Una vez abierto el Gestor y seleccionada la opción Librería portable > solo para JS, se guarda desde el menú Archivo seleccionando Guardar como, que permite seleccionar la carpeta escena_B01 si ya existe o crearla en su caso y poner nombre al archivo que portará la escena p.e index.html.
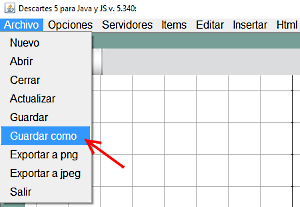
Figura 5
Dentro del archivo index.html que contiene la escena por defecto entre etiquetas <ajs> y </ajs>, el Gestor de Escenas ha colocado la línea de código <script type='text/javascript' src='lib/descartes-min.js'></script> delante de la etiqueta de cierre </head>
Para familiarizarse con estos conceptos conviene consultar el código HTML del archivo index.html para la escena básica abriéndolo con un editor de texto plano como Notepad++.
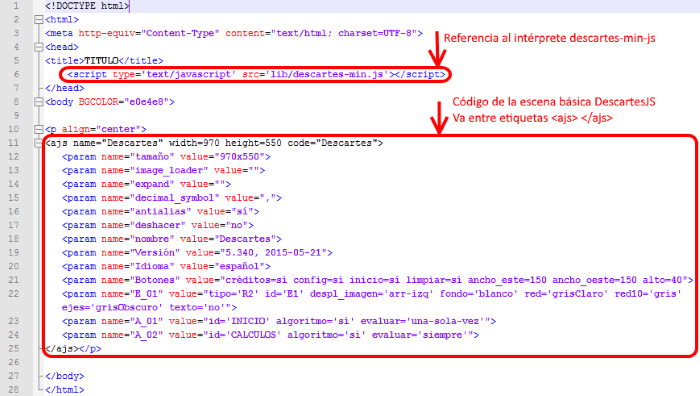
Figura 6
La escena ocupará un espacio rectangular de 800x510 píxeles. Con una unidad coordenada de 32 píxeles van a poderse ver con cierta holgura puntos (x,y), x entre -10 y 10 e y entre -5 y 5.
Al abrir el Gestor nos muestra una escena por defecto (escena básica) de dimensiones 970x550 píxeles (Figura 1). Éstas se cambian pulsando el botón E (edición) o Config y después, en el Editor de Escenas, el botón código (Figura 7) modificando los valores width (ancho) y height (alto) (Figura 8)
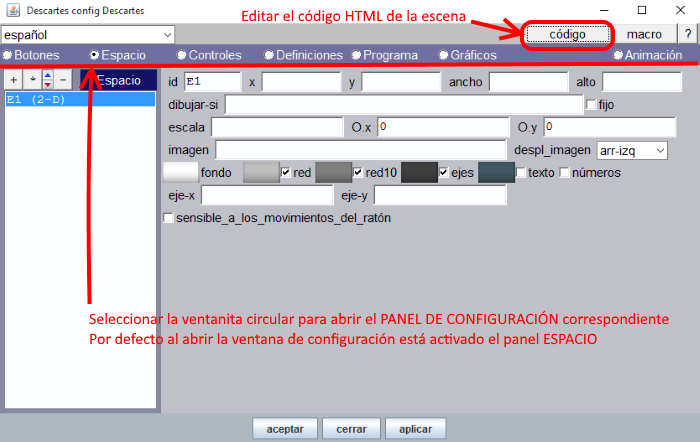
Figura 7
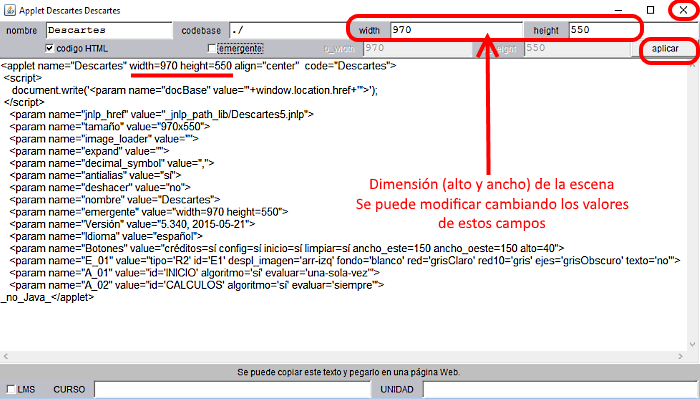
Figura 8
Para fijar el cambio se pulsa aplicar y se cierra (X) la ventana de código. Pueden verse estos cambios si pulsamos aplicar/aceptar en la ventana Descartes Config (Figura 7)
Proceso a seguir en el Editor de Escenas
| 1. |
Desde el Gestor de Escenas se accede al Editor de Escenas. Se selecciona el panel Botones y se desmarcan las casillas de créditos, config y limpiar, dejando solamente marcada la de inicio. Para que surta los efectos de este cambio hay que pulsar aplicar y aceptar para salir del editor aceptando los cambios. El botón Inicio aparecerá en el ángulo inferior izquierdo de la escena (Figura 4) y cuando se pulse repondrá la escena en condiciones iniciales del programa. |
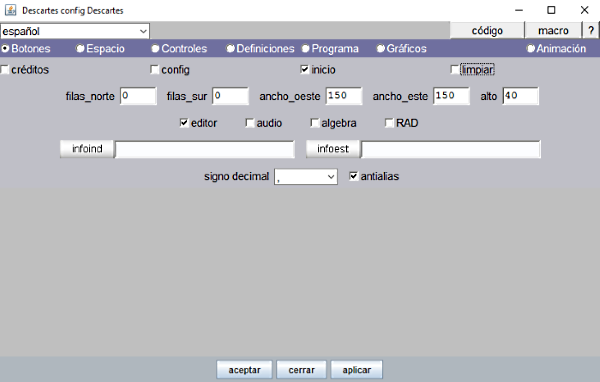
Figura 9
| 2. | En el panel Espacio, se fija una escala a 32 y se marcan únicamente las casillas para que se vea red, ejes y números. La escala es el número de píxeles que contiene la unidad coordenada. La casilla fijo, si está marcada, consigue que el espacio quede fijo y no se podrá desplazar cuando se arrastra el puntero sobre el mismo |
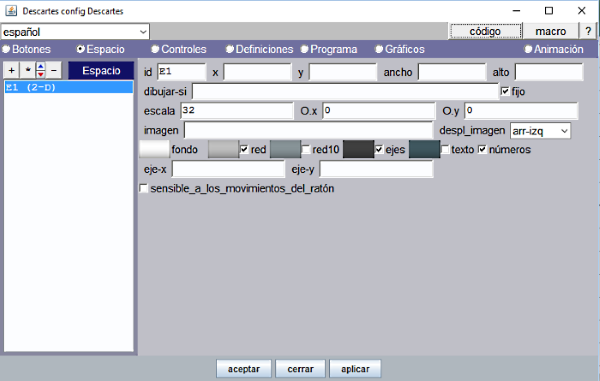
Figura 10
| 3. |
Para situar en escena la frase "Coloca este punto en su lugar" se selecciona el panel Gráficos y se añade un gráfico tipo punto de tamaño 0 y en la ventana texto se escribe esa frase. Se cambian sus coordenadas (0, 0) en la ventana expresión por (-7, 6.5) o hasta que la frase quede en el lugar que interese. Se pulsa aplicar y se comprueba que aparece en la escena. La Figura 11 siguiente, muestra el panel Gráficos con el primer punto añadido. Para añadir un gráfico en la escena hay que pulsar el botón (+) y seleccionarlo de una lista ofrecida con los diferentes tipos. Si queremos que solo aparezca este texto basta indicar que el tamaño del punto sea 0. El gráfico tipo texto en cambio situaría el texto según una expresión encerrada entre corchetes [x,y] donde x e y vienen dados en píxeles siendo el origen [0,0] el vértice superior izquierdo de la escena. |
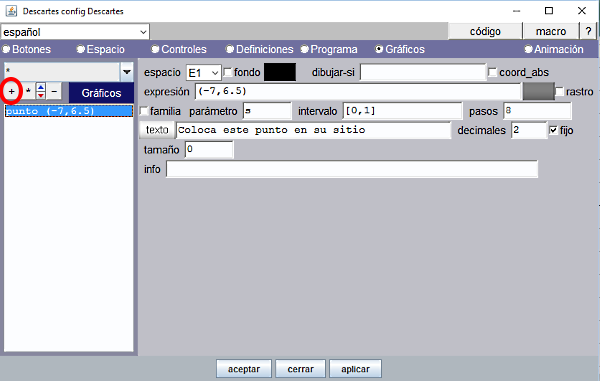
Figura 11
| 4. |
Ahora es necesario crear un control gráfico para poder referenciar sobre él un punto que podamos mover arrastrándolo con el puntero. |
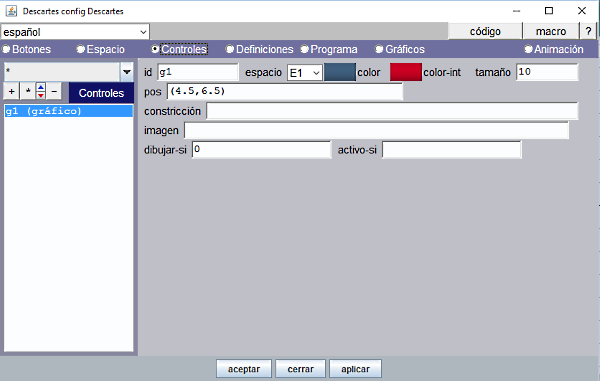
Figura 12
|
Pero el disco del control no tiene que verse, por eso debe de figurar dibujar-si=0. Esta es una condición lógica que debe de verificarse para que se dibuje el control. Al asignar el valor 0 o FALSO no se dibujará. Las coordenadas x e y del control gráfico como el g1 se pueden referenciar en cualquier parte del programa escribiendo g1.x y g1.y como vemos en el siguiente paso. |
| 5. |
En el panel Gráficos se añade un nuevo gráfico tipo punto. |
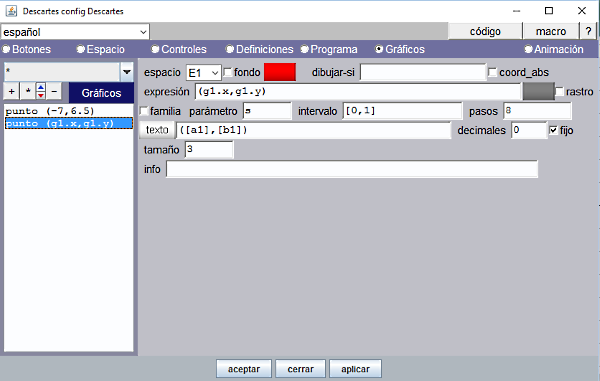
Figura 13
|
Observar que para que se escriban los valores de las variables a1 y b1 y no estos nombres hay que encerrarlos entre corchetes [a1] y [b1]. Para que no se escriban estos valores con coma decimal hay que poner 0 en la ventana de decimales. |
| 6. |
Estos valores auxiliares a1 y b1 se definen en el panel Programa. Puede hacerse en el algoritmo INICIO que se calcula solo una vez, escribiendo en el campo hacer, a1=ent(rnd*21)-10 En a1 se obtiene un valor aleatorio entero comprendido entre -10 y +10. Observar que rnd es una función interna de Descartes que genera un valor dentro del intervalo [0, 1). |
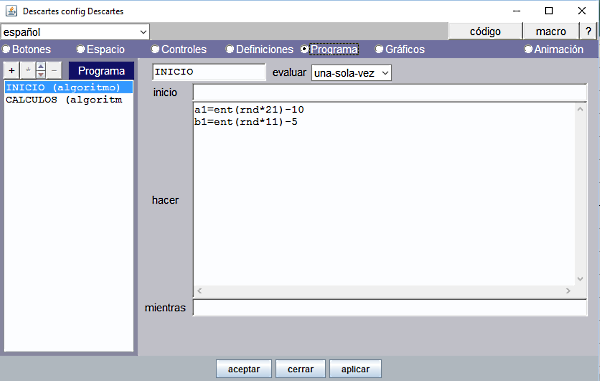
Figura 14
|
Es conveniente Guardar desde el menú Archivo cada vez que hemos completado un proceso, para que no se pierda nuestro trabajo en caso de que surja algún problema con el ordenador. |
| 7. |
Queremos que el programa compruebe que el alumno, cuando interacciona con la escena, coloca el punto en su sitio y que entonces aparezca un mensaje indicando que está bien. Para ello debemos definir un auxiliar en el panel Programa, en el algoritmo CÁLCULOS y que se evalúe siempre: bien1= (abs(a1-g1.x)<0.1)*(abs(b1-g1.y)<0.1) bien1 es el resultado de multiplicar 2 expresiones que únicamente pueden valer 0 ó 1. Es necesario darle un pequeño margen 0.1 porque sino sería muy difícil acertar. Esta fórmula comprueba que las coordenadas en que se coloca el punto son las mismas que las del control gráfico, (g1.x, g1.y). Si el punto está en el lugar adecuado, entonces bien1 valdrá 1. |
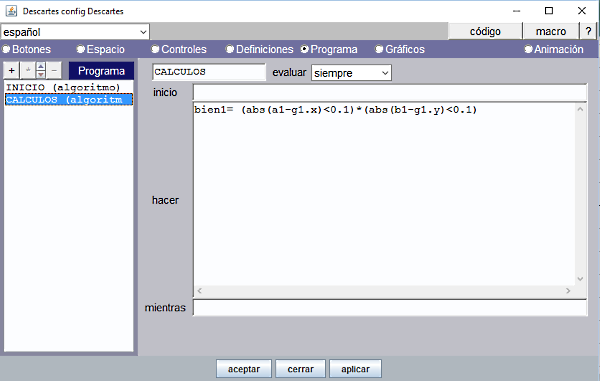
Figura 15
| 8. |
Falta añadir en el panel Gráficos un tercer punto, de tamaño 0, con el texto "MUY BIEN"; poniendo la condición dibujar-si=bien1. Es decir el texto se escribe cuando bien1 toma el valor 1 o VERDADERO. |
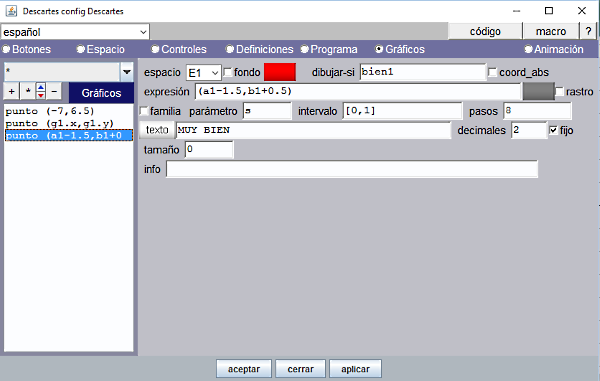
Figura 16
|
Conforme se ha ido elaborando la escena se comprueba que todo funciona y aparece lo que se quiere. |
| 9. |
Finalmente, hay que Guardar y Cerrar desde el menú Archivo del Gestor de Escenas. |
Retoques y mejoras
Todas excepto la última de las que se indican se han tenido en cuenta al describir el proceso anterior.
| 1. | El tamaño de la escena por defecto es muy grande. Para modificar el tamaño de la escena, se hace desde el código fuente, cambiando los números que aparecen inicialmente y que indican el ancho y el alto de la escena. |
| 2. |
Modificaciones en el panel espacio. Conviene que la escala sea la deseada y que no se pueda arrastrar el espacio con el puntero, por ello en el panel espacio se marca la casilla fijo. No deben de verse las coordenadas del puntero al hacer clic izquierdo, para ello se deja desmarcada la casilla texto. |
| 3. | Es conveniente que el color, el tipo y el tamaño de la letra sea lo adecuado. En este trabajo se da formato a los textos utilizando la opción Texto simple
, al pulsar el botón texto,
que permite cambiar algunos atributos básicos, tales como el tipo de letra, tamaño, negrita y cursiva. La otra opción Texto con formato dispone de un repertorio más amplio y se podrá ver en sucesivos trabajos. |
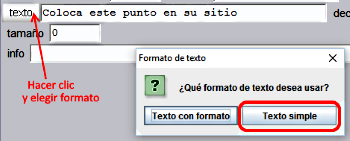 Figura 17 Figura 17
|
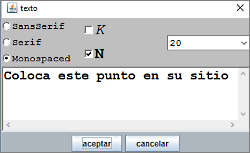 Figura 18 Figura 18
|
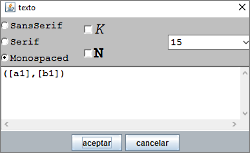 Figura 19 Figura 19
|
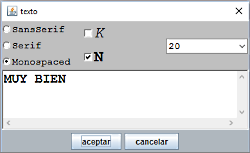 Figura 20 Figura 20
|
| Se habrá podido observar como el color del punto que debe ser movido y el texto "MUY BIEN" llevan color rojo. Hemos visto que la opción Texto simple no dispone del atributo color; en este caso el color del texto puede modificarse utilizando el botón de color (1) que figura en el panel Gráficos. Al pulsar el botón de color (1) se abre una ventana que facilita le selección del color, bien a través de un listado de colores estándar (2), o mediante una combinación cualquiera de valores hexadecimales desde 00 a FF para cada uno de los tres colores básicos rojo verde y azul. |
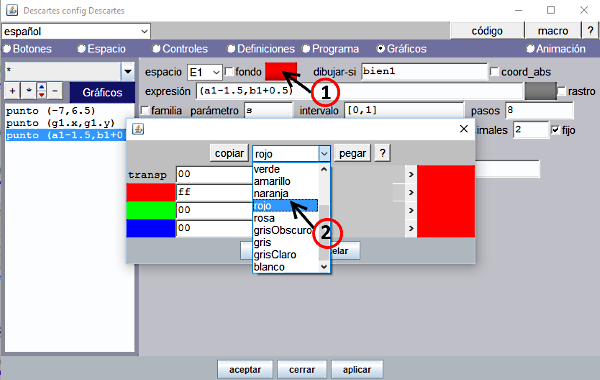
Figura 21
| 4. | En la frase del principio "Coloca este punto en su sitio" y en "MUY BIEN " no interesa que se vea el punto del texto, por eso ponemos tamaño=0. |
| 5. | Una posible mejora se consigue poniendo en la escena varios puntos para situar correctamente en el plano cartesiano en vez de uno solo y también los auxiliares necesarios para ello. No obstante, es mejor que la escena no quede recargada y que todo ello tenga un aspecto simple. |
Autoría:
Eduardo Barbero Corral (Idea del proyecto y técnicas de programación DescartesJS)
Ángel Cabezudo Bueno (Interpretación, edición de la escena, ilustraciones y redacción)
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)



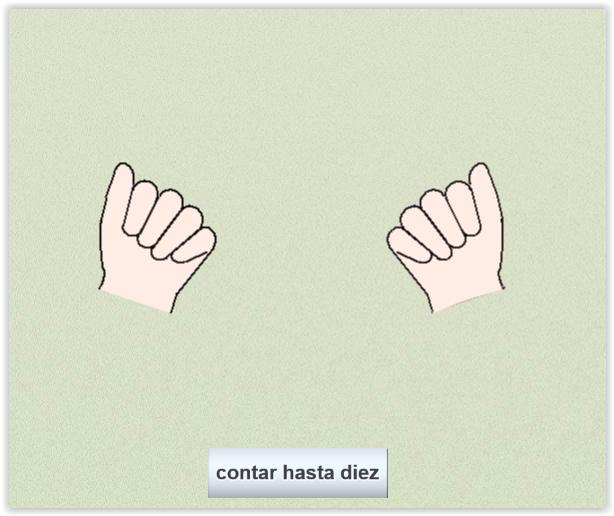

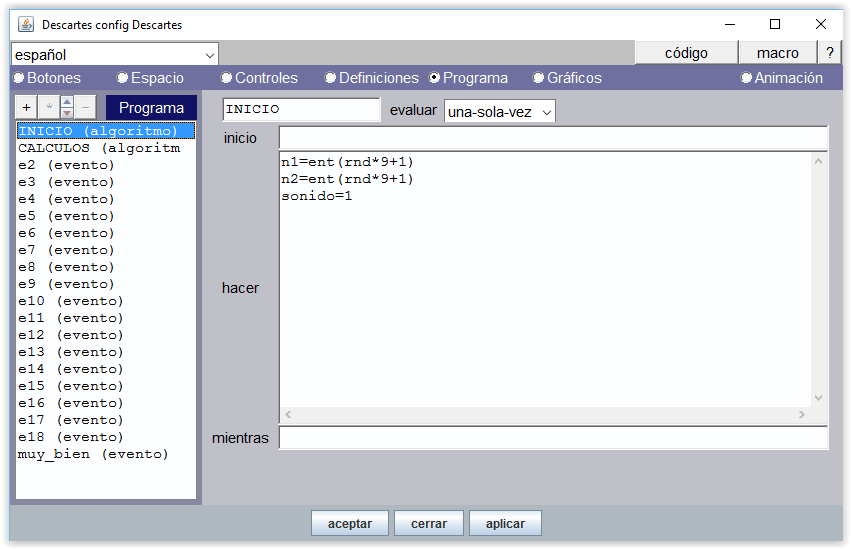
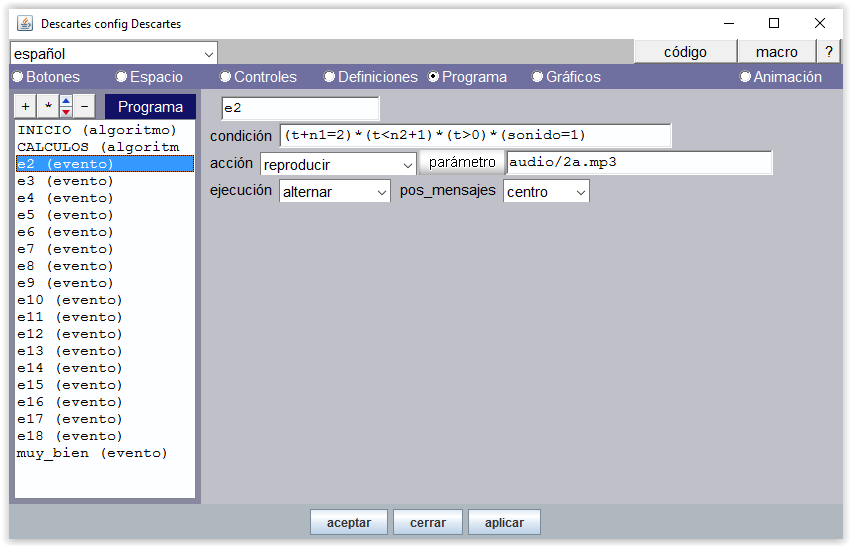
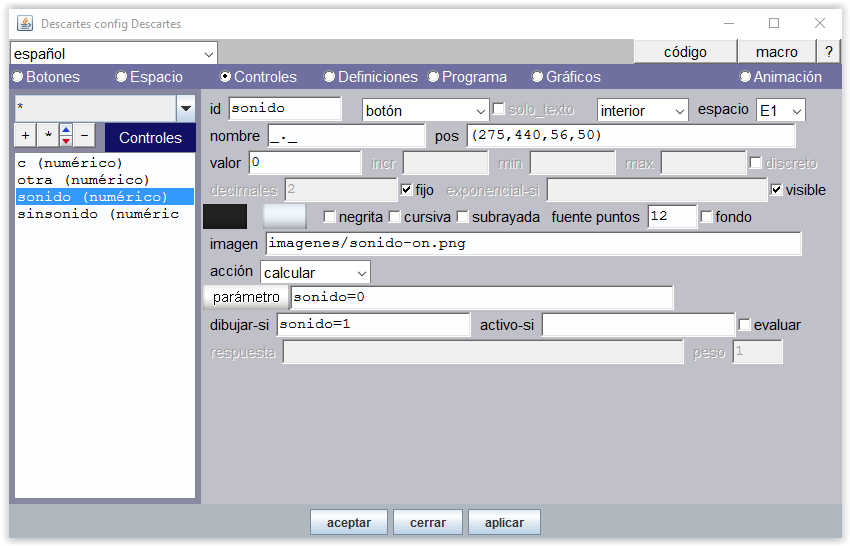
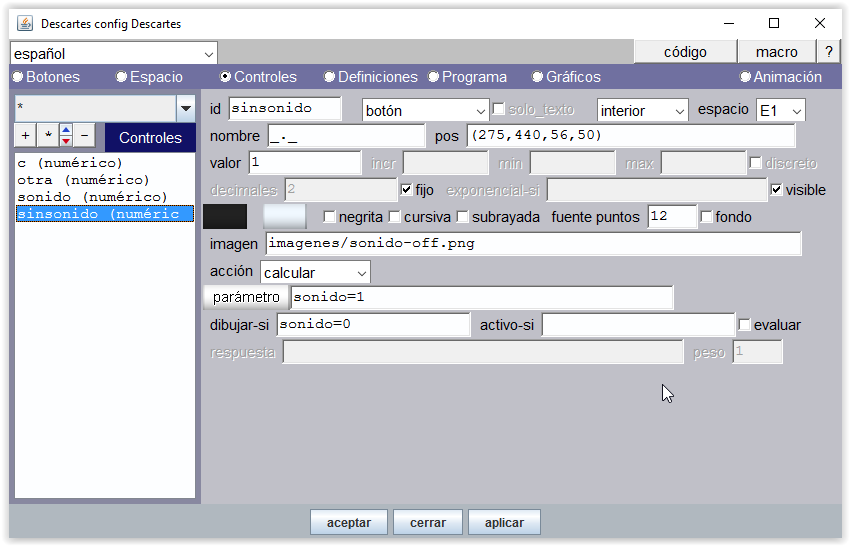

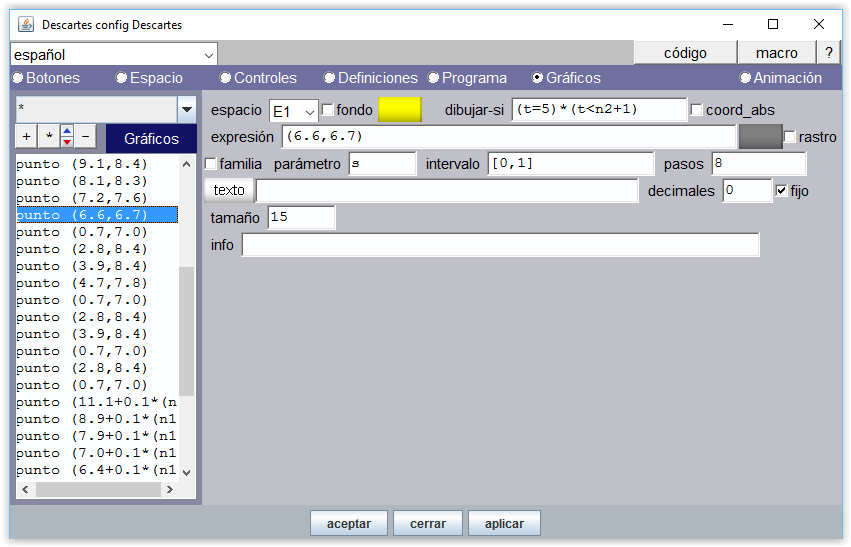
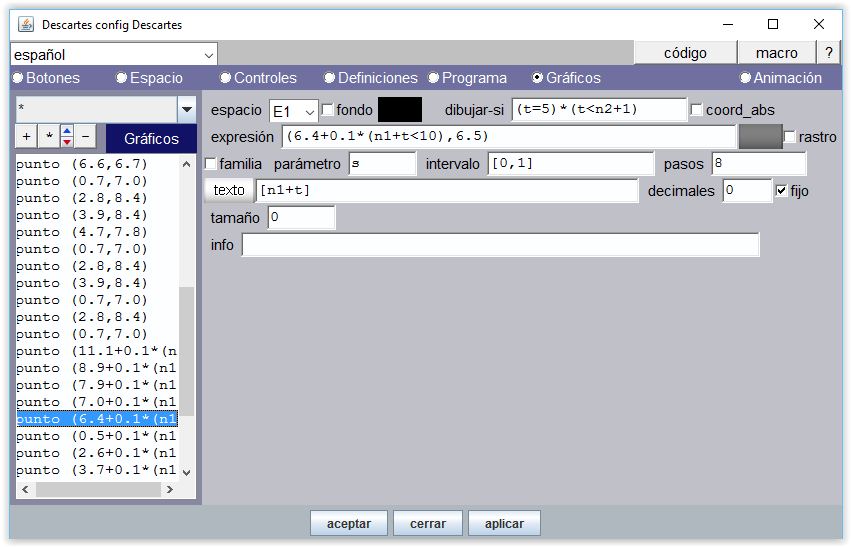
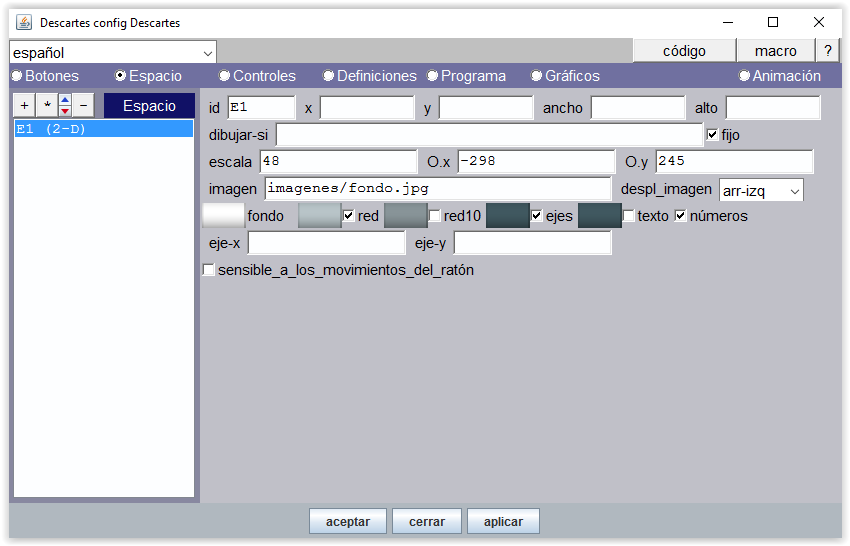






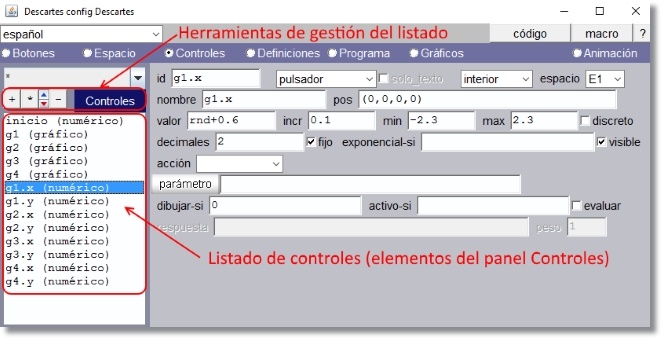




 a ventana con la lista de controles hasta ese momento añadidos con sus definiciones que pueden ser editadas como en un editor de texto (ver Figura 7)
a ventana con la lista de controles hasta ese momento añadidos con sus definiciones que pueden ser editadas como en un editor de texto (ver Figura 7)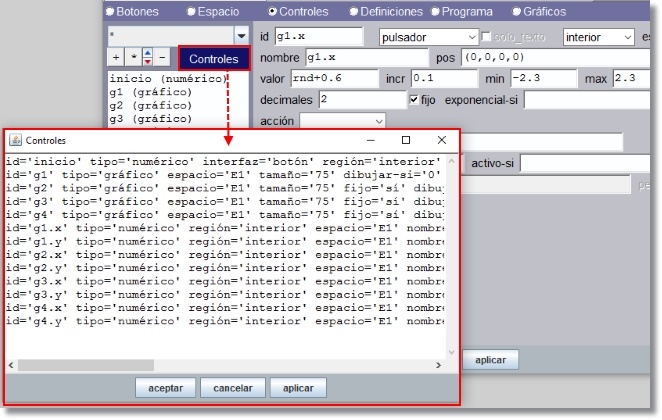
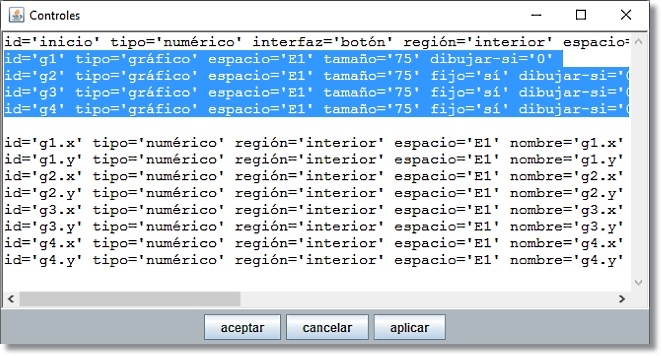
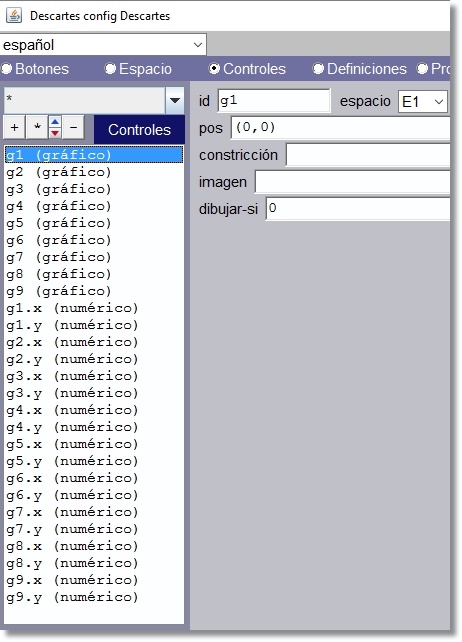

 Figura 10
Figura 10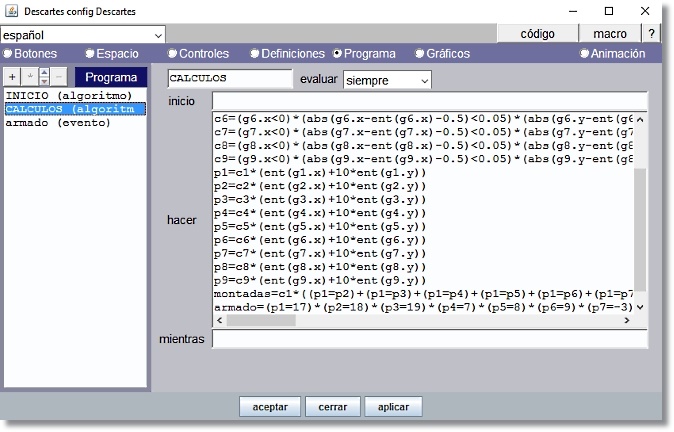
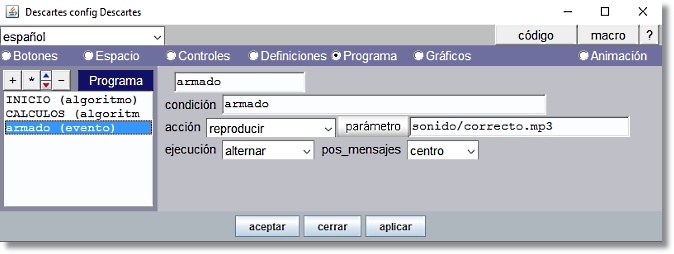
 El archivo index.html lleva la escena que controla la visualización de cada uno de los puzles en un único espacio HTMLIfame que enseguida pasaremos a explicar.
El archivo index.html lleva la escena que controla la visualización de cada uno de los puzles en un único espacio HTMLIfame que enseguida pasaremos a explicar.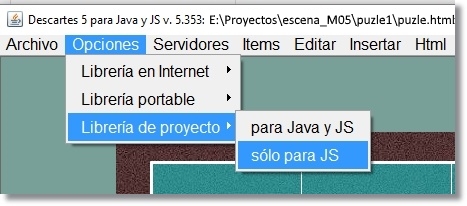



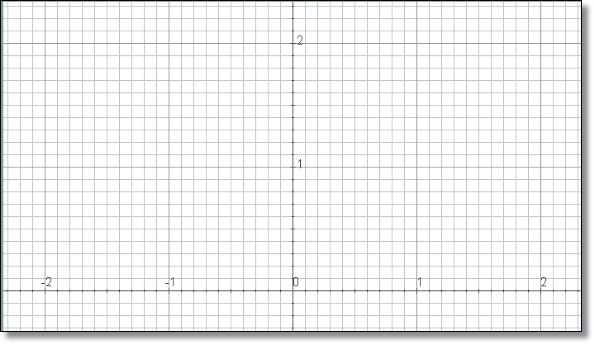
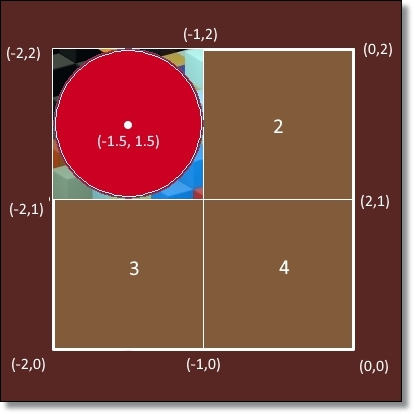

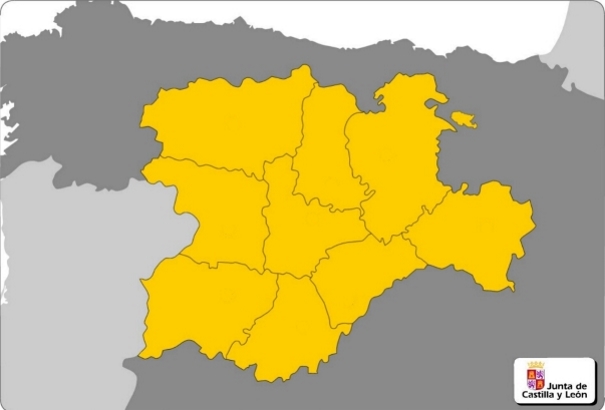
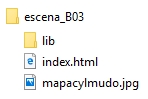
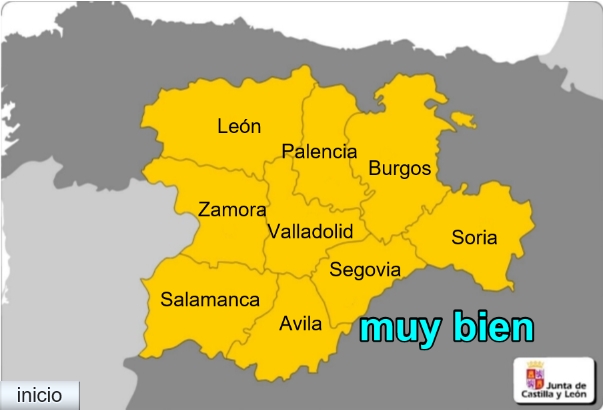






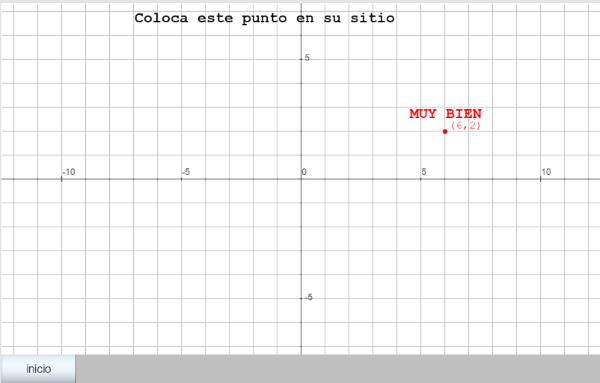

 CONTACTO
CONTACTO
