Juan Guillermo Rivera Berrío
Red Educativa Digital Descartes
Córdoba (España)
2023
Título de la obra:
Resistencia de materiales
Libro interactivo para ingenieros
Autor:
Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Foto portada: El Partenón, foto de nonbirinonko, en Pixabay.
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-77-6

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual
Puente metálico (Till Voigt , Pixabay).
La resistencia de materiales es una disciplina que estudia cómo reaccionan los diferentes tipos de materiales ante las distintas condiciones ambientales y cargas aplicadas, se ocupa del estudio del comportamiento de los sólidos deformables cuando se someten a cargas externas. La comprensión de este comportamiento es fundamental para el diseño de estructuras y máquinas seguras y eficientes.
Este libro tiene como objetivo proporcionar una comprensión de los principios fundamentales de la resistencia de materiales. Comenzando con los conceptos básicos de la tensión y la deformación, se examinan las diferentes propiedades mecánicas de los materiales y cómo se relacionan con su capacidad para resistir cargas. Se exploran los diferentes tipos de cargas que pueden actuar sobre una estructura, y se presentan los diferentes tipos de esfuerzos que se generan en respuesta a estas cargas.
Además, se estudia la teoría de la flexión y los diferentes tipos de vigas y sus características. También se aborda la teoría de la torsión y los diferentes tipos de secciones transversales y sus propiedades.
El libro se ha diseñado para el programa de Ingeniería Civil de la Corporación Universitaria Remington.
Para ilustrar mejor la información suministrada en este libro, hemos incluido, entre otros elementos multimedia, los siguientes:

Imagen de portada: Rascacielos de Singapur (Jason Goh, en Pixabay).
Imagen de esta página: Puente atirantado, foto de Engin Akyurt, en Pixabay.
Los esfuerzos en un elemento estructural son las fuerzas internas que experimenta el elemento cuando está sometido a cargas externas. Estas fuerzas internas pueden ser de diferentes tipos, como esfuerzos de tracción, compresión o flexión, y tienden a deformar o fracturar el elemento estructural. El diseño de elementos estructurales implica determinar la resistencia y rigidez del material estructural para soportar estos esfuerzos.
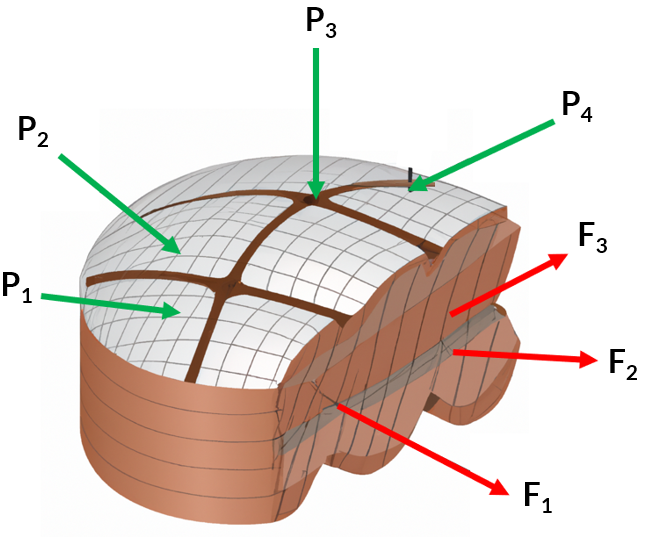
Nuestro objetivo, entonces, es identificar y cuantificar las fuerzas internas en un cuerpo sólido, las cuales son las fuerzas que se ejercen mutuamente entre las distintas partes o elementos del cuerpo sólido. Estas fuerzas son el resultado de las cargas externas que actúan sobre el cuerpo sólido ($P_i$ en la figura 1.1), y se distribuyen a través de los diferentes elementos de la misma; por ejemplo, en una estructura: en las vigas, columnas, tirantes, etc.
Las fuerzas internas ($F_i$ en la figura 1.1) incluyen la fuerza normal, que es la fuerza perpendicular a la sección transversal de un elemento, la fuerza cortante, que es la fuerza tangencial, y el momento, que es la fuerza resultante de un momento de torsión aplicado. El análisis de las fuerzas internas es fundamental para el diseño y la construcción de las mismas, pues permite saber si la estructura es lo suficientemente fuerte y resistente como para soportar las cargas externas a las que estará expuesta.
El esfuerzo axial es un tipo de fuerza interna en una estructura que se produce cuando una carga actúa a lo largo del eje longitudinal de un miembro estructural. También se puede definir como el esfuerzo resultante de las tensiones perpendiculares (normales) a la sección transversal de un miembro estructural. El esfuerzo axial se representa comúnmente por la letra griega $\sigma$ y se calcula dividiendo la fuerza aplicada por el área transversal de la sección del miembro.
$$\sigma = \frac{P}{A}\tag{1.1}$$En un elemento prismático (una viga o columna, por ejemplo), el
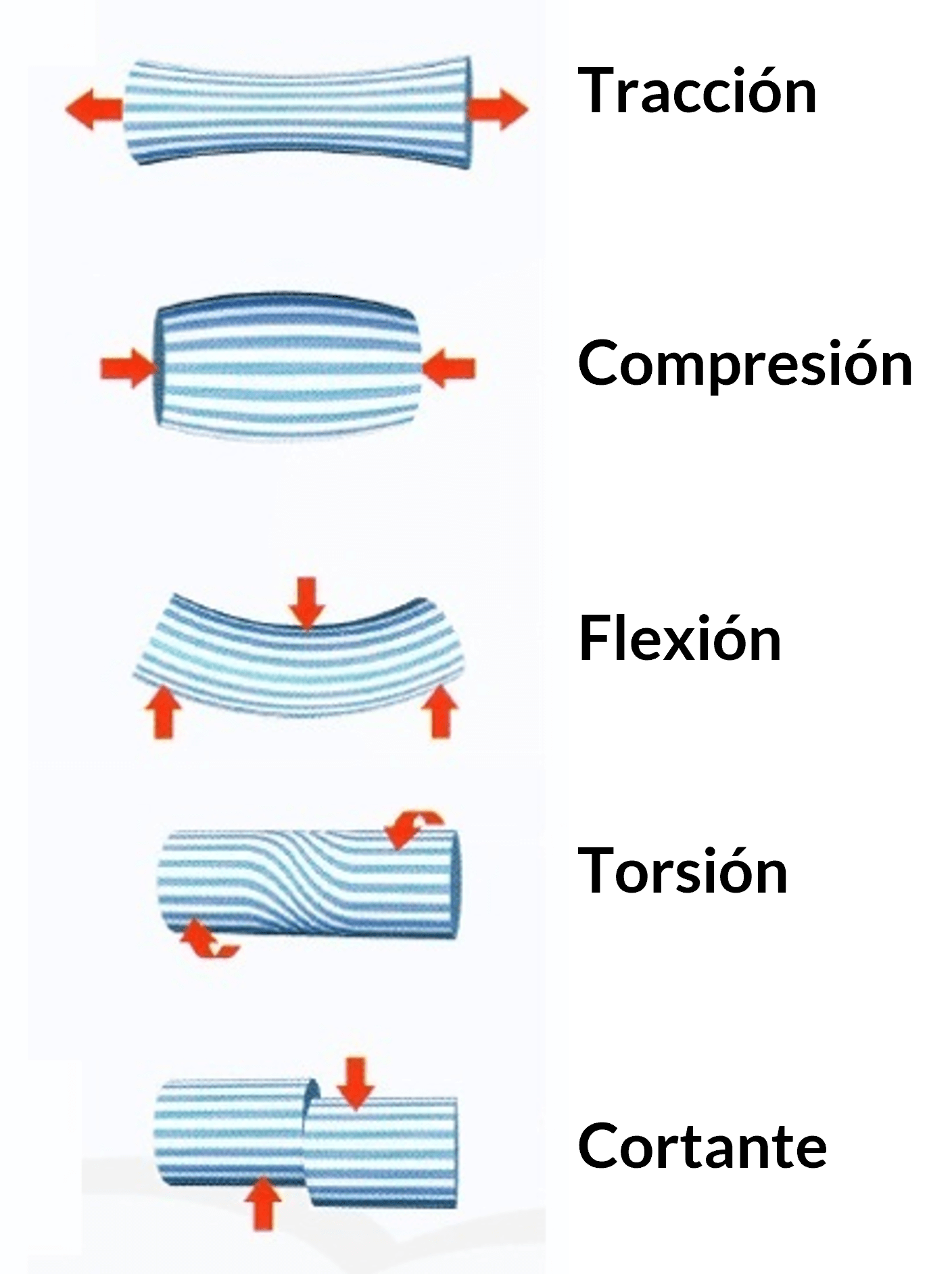
esfuerzo axial puede comprimir (esfuerzo de compresión) o estirar (esfuerzo de tracción) el elemento, tal como lo muestra la figura 1.2.
El esfuerzo cortante, también conocido como esfuerzo de corte o de cizalladura, es otro tipo de fuerza interna en una estructura que ocurre cuando hay una carga que actúa perpendicularmente al eje longitudinal de un miembro estructural. En el caso del esfuerzo cortante, las tensiones que resultan son paralelas a la sección transversal y cortan a través del miembro estructural. El esfuerzo cortante se representa comúnmente por la letra griega $\tau$ y se puede calcular dividiendo la fuerza cortante por el área transversal del miembro.
$$\tau = \frac {V}{A} \tag{1.2}$$
El estado general de esfuerzo actuando sobre un elemento infinitesimal se reduce a estos dos tipos de esfuerzos (normal y cortante); por ello, en este capítulo nos dedicaremos a su análisis y discusión, suponiendo que los elementos de la estructura están constituidos de materiales homogéneos e isotrópicosUn material homogéneo tiene las mismas propiedades físicas y mecánicas en todo su volumen, y un material isotrópico tiene estas mismas propiedades en todas las direcciones.
En general, las fuerzas internas actúan sobre elementos infinitesimales con magnitudes y direcciones variables, tal como se muestra en la siguiente figura 1.3.
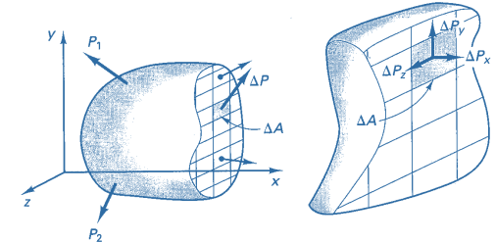
De la figura anterior, definimos:
$$\tau_{xx} = \lim_{\Delta A \to 0}\frac{\Delta P_x}{\Delta_A}\;\;\;\tau_{xy} = \lim_{\Delta A \to 0}\frac{\Delta P_y}{\Delta_A}\;\;\;\tau_{xz} = \lim_{\Delta A \to 0}\frac{\Delta P_z}{\Delta_A}$$El primer subíndice del esfuerzo cortante ($\tau$) indica la dirección perpendicular al plano considerado, que para el caso es $x$, y el segundo subíndice indica la dirección del esfuerzo.
En un elemento infinitesimal, como en el mostrado en el interactivo 1.1, en cada cara tendríamos tres componentes de esfuerzo, dos de ellos cortantes y uno axial. Los esfuezos axiales serían $\tau_{xx},\;\tau_{yy},\; \tau_{zz}$, los cuales se suelen representar por la letra $\sigma$, así: $\sigma_x,\; \sigma_y$, y $\sigma_z$
Dado que el esfuerzo representa la intensidad de una fuerza sobre un
área, las unidades comunes en el SI son $N/m^2$ o $Pa$ y en el inglés $lib/pulg^2$, abreviado como $psi$.
Continuando con nuestro tensor, vamos a recurrir al teorema de Cauchy sobre los esfuerzos en un cuerpo, en el que una de sus propiedades indica que este tensor está dado sobre las coordenadas especificadas por una matriz simétrica, así:
$$\begin{bmatrix} \tau_{xx} & \tau_{xy} & \tau_{xz}\\ \tau_{yx} & \tau_{yy} & \tau_{yz}\\ \tau_{zx} & \tau_{zy} & \tau_{zz} \end{bmatrix} \equiv \begin{bmatrix} \sigma_x & \tau_{xy} & \tau_{xz}\\ \tau_{yx} & \sigma_y & \tau_{yz}\\ \tau_{zx} & \tau_{zy} & \sigma_zz \end{bmatrix}\tag{1.3}$$La propiedad de simetría de Cauchy significa que
$$\color{#0089cd}{\Large{\tau_{ij} = \tau_{ji}}}\tag{1.4}$$En la mayoría de los casos que estudiaremos, más de dos pares de esfuerzos cortantes rara vez actuarán sobre un elemento. Por consiguiente, los subíndices usados para identificar los planos y sentidos de los esfuerzos cortantes resultan superfluos. En tales casos, los esfuerzos cortantes serán designados por $\tau$ sin ningún subíndice
Considerando la ecuación 1.4, los esfuerzos en el plano, pueden escribirse como:
$$\begin{bmatrix} \sigma_x & \tau & 0\\ \tau & \sigma_y & 0\\ 0 & 0 & 0 \end{bmatrix} \tag{1.5}$$Dichos esfuerzos los hemos representado en el siguiente objeto interactivo. Puedes rotar la representación 3D con clic izquierdo sostenido.
En el objeto interactivo de la derecha, vemos una fuerza externa $P$ aplicada en el extre- mo de una barra prismática y, en color amarillo, las fuerzas internas en el elemento que reaccionan a la fuerza externa para mantener el equilibrio. Bajo el supuesto que el material es homogéneo e isotrópico, la sección transversal de la barra está sometida a una distri- bución del esfuerzo normal constante (fuezas internas de color amarillo).
Por lo tanto, cada área infinitesimal $\Delta A$, en la sección transversal, estaría sometida a una fuerza $\Delta F = \sigma \Delta A$. La sumatoria de estas fuerzas (color amarillo), que actúan sobre toda el área de la sección transversal, debe ser equivalente a la fuerza externa $P$ aplicada en esa sección. Si hacemos que $\Delta A \to dA$ y $\Delta F \to dF$, entonces como $\sigma$ es constante, se obtiene
Los esfuerzos normales o axiales ($\sigma$) pueden ser de compresión o de tracción, tal como se ilustra en el siguiente video:
Para este libro, asumiremos un signo positivo para los esfuerzos de tracción (también conocidos como esfuerzos de tensión), y un signo negativo para los esfuerzos compresivos o de compresión.
En la caja de herramientas de este libro, hemos puesto una tabla de conversión de unidades, en la cual puedes deducir que 1 psi es aproximadamente igual a 7 kPa, y que 1 ksi se aproxima a 7 MPa, unidades de esfuerzo comunes en ingeniería. Veamos un ejemplo, a continuación.
Dos barras cilíndricas sólidas AB (diámetro $d_1$) y BC (diámetro $d_2$) están soldadas en B y cargadas como se muestra en las imagen de abajo. Si se sabe que $d_1 = 40\; mm$ y $d_2 = 50 \; mm$, halla el esfuerzo normal promedio en la sección central de a) la barra AB, b) la barra B
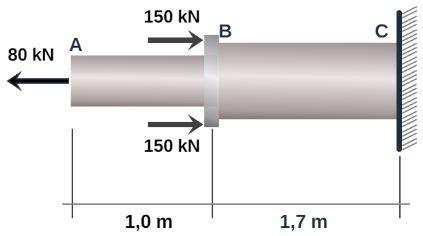
Solución
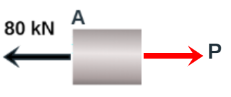
Haciendo un corte en la barra AB, encontramos que $P = 80\;kN$ a tracción; por lo tanto:
$$\sigma = \frac{80\;kN}{\pi(20\;mm)^2} = 0.0637\; kN/mm^2$$
Resultado que podemos expresar así:
$$\frac{0.0637\;\cancel{kN}}{\cancel{mm^2}}\times \frac{10^3\;N}{1\;\cancel{kN}}\times\frac{10^6\; \cancel{mm^2}}{m^2} = 63.7 Mpa$$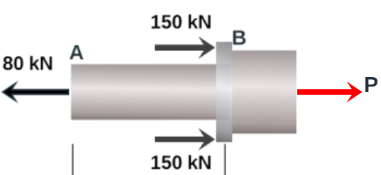
Haciendo un corte en la barra BC, encontramos que $P = -220\;kN$ a compresión; por lo tanto:
$$\sigma = \frac{-220\;kN}{\pi(25\;mm)^2} = -0.1120\; kN/mm^2$$
Resultado que podemos expresar así:
$$\frac{-0.1120\;\cancel{kN}}{\cancel{mm^2}}\times \frac{10^3\;N}{1\;\cancel{kN}}\times\frac{10^6\; \cancel{mm^2}}{m^2} = -112 Mpa$$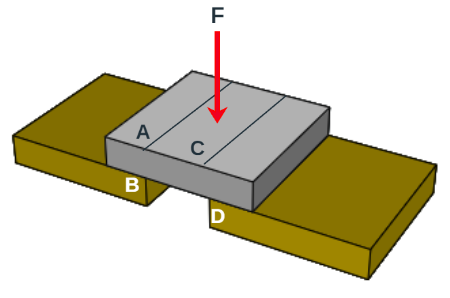
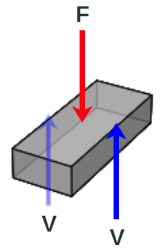
El esfuerzo cortante actúa en el plano del área seccionada, tal como lo vimos en el tensor de esfuerzos y denominados con $\tau_ij$. En la figura de la derecha se está aplicando una fuerza $F$, la cual tiene como efecto que el material de la barra se deforme y falle a lo largo de los planos AB y CD.
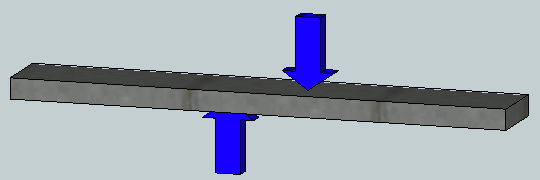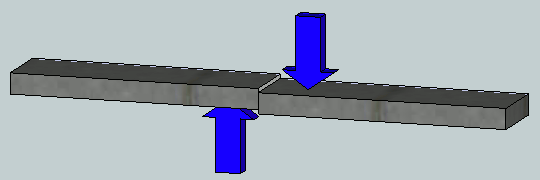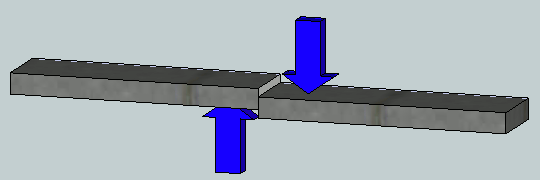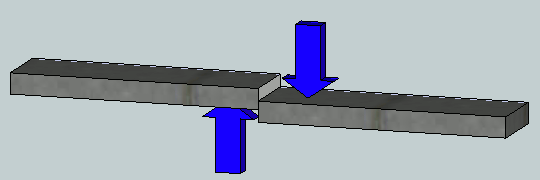
Los esfuerzos cortantes se encuentran comúnmente en pernos, pasadores y remaches utilizados para conectar diversos elementos estructurales y componentes de máquinas
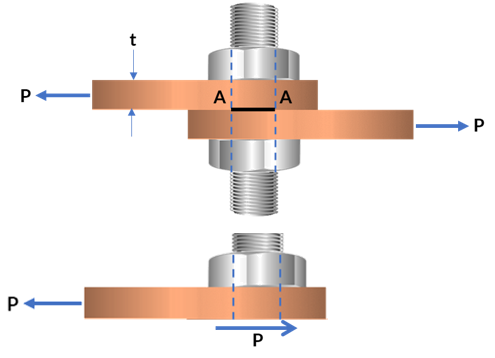
Otra situación se muestra en la Figura 1.6, en la que el perno está somtido a dos fuerzas cortantes. Una de ellas se muestra aplicada en la placa central, cuyo esfuerzo sería:
$\displaystyle\tau = \frac{P/2}{A} = \frac{P}{2A}$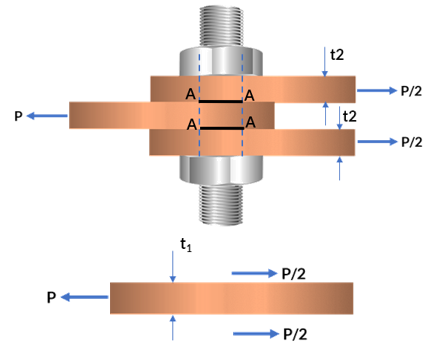
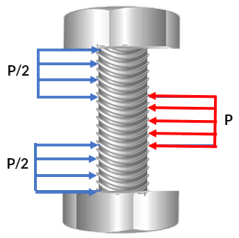
El análisis de interés son los esfuerzos cortantes sobre el perno, que se ilustan en la imagen de la derecha, indicando un esfuerzo máximo producido por la placa central $\displaystyle\tau = \frac{P}{A}$, donde $A$ es el área proyectada de la sección del tornillo ($d\cdot t_1$). Se ha asumido un esfuerzo cortante uniforme que, en realidad, no es correcto, como veremos más adelante en este libro pero, por ahora, usaremos suposición de un esfuerzo cortante promedio.
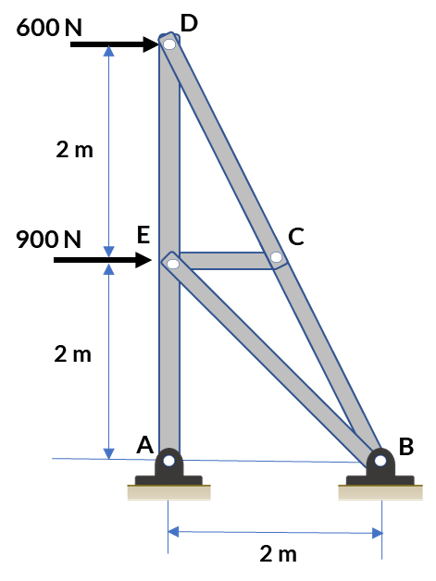
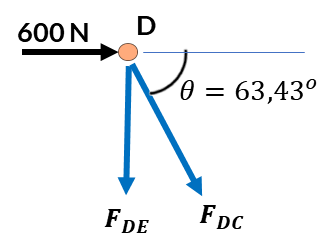
Usando el método de los nodos, hemos aislado el nodo D (figura derecha). El valor del ángulo $\theta$ es fácil de hallar con las dimensiones de la armadura. Aplicando las ecuaciones de equilibrio, obtenemos:
$$\sum F_x = 0 \;(\rarr +)$$Por otra parte,
$$\sum F_y = 0 \;(\uarr +)$$ $$-F_{DE} +1.34\;sen\theta = 0\\ F_{DE} = 1.20\; kN\; \text{ a tracción}$$El esfuerzo cortante medio, lo calculamos con $F_{DC}$, que es la mayor fuerza cortante en el pasador D:
$$\tau = \frac{F_{DC}}{2A} = \frac{1.34\;kN}{2\pi \cdot (0.3\;m)^2}$$ $$\tau = 2.37 \;kPa$$Las fuerzas axiales causan esfuerzos tanto normales como cortantes en planos que no son perpendiculares al eje del elemento. De manera similar, las fuerzas transversales ejercidas sobre un perno o pasador producen esfuerzos tanto normales como cortantes en planos que no son perpendiculares al eje del perno o pasador
En el siguiente objeto interactivo se oberva una sección inclinada que corta el bloque formando un ángulo con la sección normal. Iteractúa con el objeto y analiza los esfuerzos normales y cortantes sobre el plano inclinado. El objeto te permite realizar ejercicios.
Haz clic en el botón continuar para que observes los esfuerzos sobre el plano inclinado, que se muestran cuando actúan en sus direcciones positivas; es decir, el esfuerzo normal es positivo a tracción y el cortante es positivo cuando tiende a producir un giro del bloque en sentido contrario al de las manecillas del reloj. Igualmente, puedes
observar la expresiones para los esfuerzos normales y cortantes, que se distribuyen uniformemente sobre la sección inclinada.
En ingeniería estructural, el esfuerzo admisible es el máximo esfuerzo permitido para que un material soporte cargas sin sufrir daños permanentes. Esta admisibilidad está asociada a un factor de seguridad, que es un número que se utiliza para tener en cuenta la incertidumbre en las propiedades del material y las cargas a las que estará sujeta la estructura. Los esfuerzos admisibles para una estructura están determinados por el tipo de material utilizado, las condiciones de carga y el factor de seguridad deseado. Los esfuerzos permisibles se utilizan para diseñar la estructura de modo que no supere su resistencia y permanezca segura durante su vida útil prevista.
Carga última o carga de falla. Los materiales usados en ingeniería, se suelen someter a pruebas en laboratorio (observa el video 3.2 del profe yus), con el objetivo de determinar la carga que produce la falla en el material, dicha carga es conocida como carga última $P_u$. Si dividimos esta carga última entre el área transversal original, obtenemos el esfuerzo último o resistencia última del material.
Factor de seguridad. Para el diseño de estructuras o máquinas en ingeniería, no sería responsable usar la resistencia última, pues los elementos colapsarían; por ello, se usa un Factor de Seguridad (FS), que reduce el valor del esfuerzo último a un valor de diseño mas pequeño, el cual se conoce como esfuerzo admisible y siempre se debe cumplir que $\text{el esfuerzo admisible }\lt \text{el esfuerzo último}$. El Factor de Seguridad, entonces, sería:
$$FS = \frac{\text{esfuerzo último}}{\text{esfuerzo admisible}}$$La selección del factor de seguridad que debe usarse es una de las tareas más importantes de los ingenieros. Si el factor de seguridad se elige demasiado pequeño, la posibilidad de falla se torna inaceptablemente grande. Por otra parte, si un factor de seguridad es demasiado grande, el resultado es un diseño caro o no funcional
Para el diseño de elementos sometidos a carga axial, se usaría la siguiente expresión:
$$A = \frac{P}{\sigma_{\text{admisible}}}\tag{1.6}$$Si la sección transversal está sometida a una fuerza cortante promedio, entonces el área requerida para el diseño sería:
$$A = \frac{V}{\tau_{\text{admisible}}}\tag{1.7}$$Veamos un ejemplo:
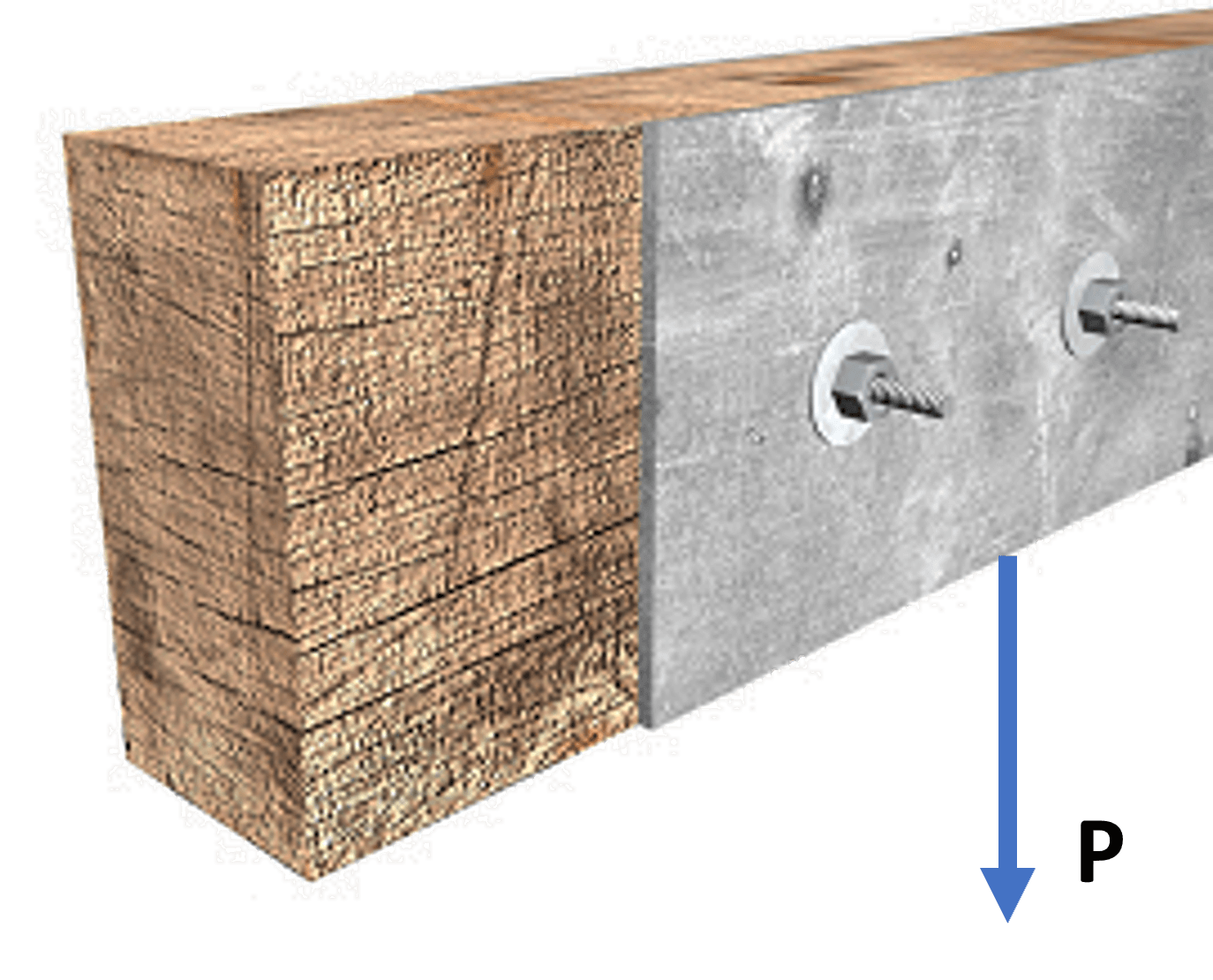
Solución
La carga para cada perno sería $P_p = 12 \;kips$ con un área de:
$$A = \pi \bigg(\frac{3}{8}\bigg)^2 pulg^2 = 0.442 \;pulg^2$$El esfuerzo cortante admisible, sería:
$$\tau_{adm} = \frac{P_p}{A} = \frac{12\;kips}{0.442 \;pulg^2} = 27.16\;ksi$$El Factor de Seguridad:
$$FS = \frac{\tau_u}{\tau_{adm}} =\frac{52\;ksi}{27.16\;ksi} = 1.91$$Foto en Cleveland (USA) de (Lance Anderson, en Unsplash).
Imagen de portada: Túnel con metal retorcido (Amy, en Pixabay).
Imagen de esta página: Palacio de eltham, Sur de londres, foto de Ron Porter, en Pixabay.
Las deformaciones en estructuras son cambios en la forma o tamaño de un objeto debido a la aplicación de fuerzas. En ingeniería, se utilizan diferentes términos para describir estos cambios, como desplazamientos y deflexiones. La deformación puede ser temporal o permanente, dependiendo de si desaparece después de la eliminación de las fuerzas aplicadas. La mecánica estructural es una teoría que se aplica a las estructuras y estudia los cuerpos deformables [1]. Las cargas que actúan sobre un elemento estructural pueden causar deformaciones en magnitud y sentido, que dependen de la fuerza que las origina [2]. Las estructuras metálicas, en particular, pueden admitir deformaciones mayores que las estructuras de hormigón [3]. En general, el estudio de las deformaciones en estructuras es importante para garantizar la seguridad y estabilidad de las mismas.
Hay diferentes tipos de deformaciones que pueden ocurrir en una estructura, incluyendo: deformación elástica, deformación plástica, deflexión, desplazamiento, defor- mación por corte y deformación torsional:
[1] https://ocw.uc3m.es/
[2] https://core.ac.uk/
[3] https://riunet.upv.es/
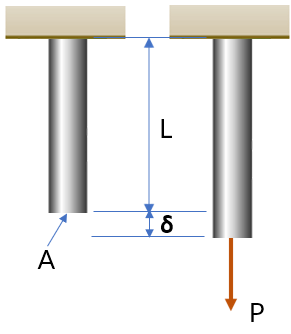
Uno de los ensayos más comunes en resistencia de materiales, es el ensayo de cargar axial, tanto a compresión como a tracción. En la figura, una barra empotrada en la parte superior de longitud inicial $L$ y área de sección transversal $A$, es sometida a una carga axial de tracción o tensión, produciendo un aumento en su longitud $\delta$.
El alargamiento o contracción por unidad de longitud inicial se conoce como deformación unitaria normal o axial ($\epsilon$), la cual se puede calcular con la siguiente expresión:
Dado que la fracción en 2.1 está compuesta de unidades de longitud que se cancelan, la deformación unitaria es adimensional; sin embargo, se suele escribir con expresiones como $mm/mm$, $pulg/pulg$, $\mu m/\mu m$, etc.
La deformación $\delta$, en los ejemplos que presentamos a continuación, se obtiene restando la longitud final del elemento después de aplicar la carga, de la longitud inicial: $\delta = L_f - Li$, por lo tanto:
$$\epsilon = \frac{L_f - L_i}{L_i}$$
En el siguiente objeto interactivo, presentamos un primer ejemplo de cálculo de la deformación unitaria $\epsilon$.
En los ensayos de carga axial, se registra una serie de datos con los esfuerzos aplicados ($\sigma = P/A$) y las deformaciones unitarias obtenidas, que al graficarlos, con $\sigma$ en el eje $y$ y $\epsilon$ en el ejex $x$, se obtiene una curva de esfuerzo deformación, tal como se observa en el siguiente video:
La máquina universal, semejante a una prensa, es la más usada en ingeniería para someter materiales a ensayos de tracción y compresión y medir sus propiedades. Usando la aplicación de Vinayak Mukherjee en la escena interactiva de la página siguiente, puedes ver al detalle la máquina universal HOYTOM.
En la escena interactiva, haz clic en el botón de la esquina superior derecha y usa el scroll vertical para ver la imagen en su tamaño real. Podrás observar la pantalla táctil integrada a esta máquina, la cual permite que obtengamos los datos de carga y deformación y, posteriormente, dibujar el diagrama de esfuerzo deformación.
Inicialmente, puedes observar la máquina de ensayo a tracción en la parte inferior y compresión en la parte superior.
El diagrama de esfuerzo-deformación es muy útil, pues proporciona información sobre algunas propiedades mecánicas del material que ha sido sometido a carga axial.
Observa un diagrama esfuerzo-deformación en la figura 2.1, a partir del cual vamos a explicar el comportamiento del material en las zonas elástica y plástica.
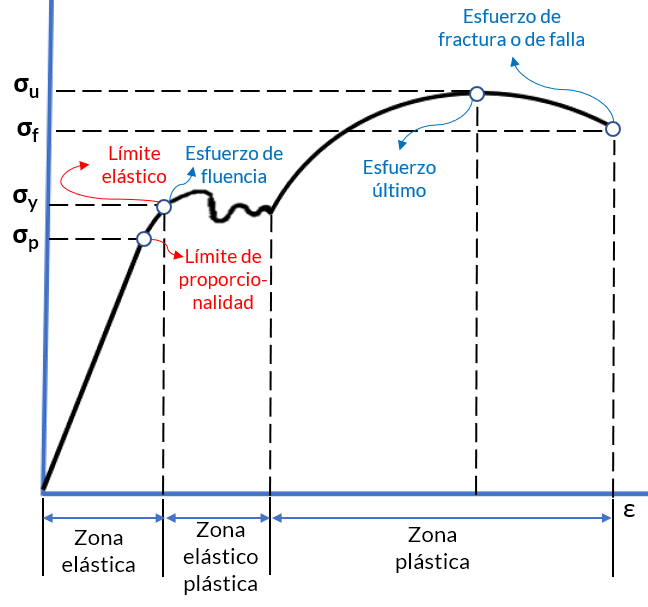
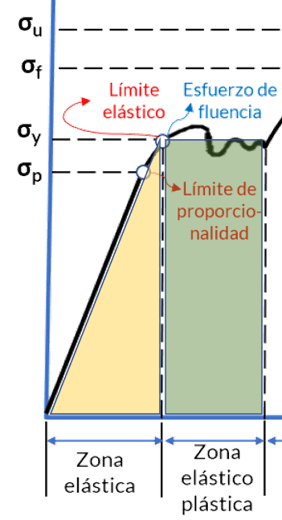
Comportamiento en la zona elástica. En la figura 2.2 hemos resaltado la zona elástica con el triángulo de color amarillo. Observa que es lineal en la mayoría de la zona, lo que significa que el esfuerzo es proporcional a la deformación, aquí el material en esta región es elástico lineal, con un límite superior del esfuerzo para esta relación lineal que se denomina límite de proporcionalidad. A partir de este límite, la curva tiende a aplanarse hasta llegar al límite de la zona, conocido como límite elástico. En este límite, al retirarse la carga, el material recuperará su forma original. El esfuerzo en el límite elástico, se conoce como esfuerzo de fluencia o de cedencia ($\sigma_y$).
Comportamiento en la zona elástico plástica. Un ligero aumento de carga por encima del límite elástico genera una deformación permanente (región rectangular de color verde en la figura 2.2). Esta zona es común en materiales dúctilesLos materiales que no presentan cedencia, o que es muy pequeña, se conocen como materiales frágiles, como el hormigón; por ello, es necesario reforzarlo con acero (hormigón armado), para soportar cargar a tracción. como el acero estructural, observa que se genera una gran deformación con un incremento relativamente pequeño de la carga aplicada.
Comportamiento en la zona plástica. Una vez terminada la cedencia en la zona elasto plástica, el material empieza a soportar aumentos de carga, evidenciado en una curva ascendente hasta llegar a un
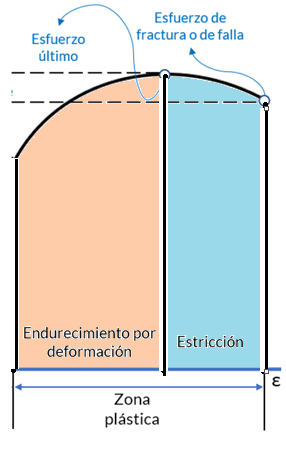
esfuerzo máximo llamado esfuerzo último ($\sigma_u$). Este incremento en la curva se llama endurecimiento por deforma- ción, como se muestra en la figura 2.3 en color naranja.
Durante el endurecimiento por deformación, el área de la sección transversal se reduce. Posterior al esfuerzo último, el área de la sección transversal sufre una reducción bastante notoria hasta la falla del material, esta zona se conoce como estricción (área de color azul en la figura 2.3). En esta última parte el diagrama esfuerzo-deformación se curva hacia abajo hasta llegar al esfuerzo de falla o fractura ($\sigma_f$).
Diagrama esfuerzo-deformación verdadero. Generalmente, usamos el área de la sección transversal y la longitud originales para calcular el esfuerzo y la deformación; sin embargo, es más preciso calcular el área de la sección transversal y la longitud en el momento en que se mide la carga, valores que se denominan esfuerzo verdadero y deformación verdadera, y sus gráfica "diagrama de esfuerzo-deformación verdadero". Se tendrían, entonces, $n$ mediciones con $n$ valores sucesivos de deformación, por lo que la deformación real es:
$$\epsilon_R = \sum_{i=1}^n \frac{\Delta L_i}{L_i}$$Las estructuras de ingeniería se diseñan de tal forma que las deformaciones sean muy pequeñas; es decir, que los esfuerzos ($\sigma$) estén en la parte recta del diagrama de esfuerzo-deformación, en la cual es directamente proporcional a la deformación ($\epsilon$):
$$\sigma = E\epsilon\tag{2.2}$$La ecuación 2.2 fue formulada por primera vez por Robert Hooke en 1660 y desde entonces ha sido ampliamente utilizada en física e ingeniería. $E$ es la constante de proporcionalidad, también llamada módulo de elasticidad o módulo de Young, en honor a Thomas Young quien publicó un estudio sobre él en 1807.
Un ejemplo sencillo es el siguiente. Si tenemos en el diagrama de esfuerzo-deformación un par de datos de la zona elástica; por ejemplo: $\sigma_p = 35 \;ksi$ y $\epsilon_p = 0.0012 \;pulg/pulg$, entonces $E = \sigma_p / \epsilon_p = 29\times 10^3 \;ksi$.
Descripciones de los colegas Aubrey y Waller. Se muestra con un resorte, un reloj de bolsillo, un fósil y un mapa de la ciudad de Londres después del Gran Incendio de 1666. Óleo sobre tabla de 2004 (Rita Greer, Wikimedia, Free Art License).
Como se observa en el diagrama esfuerzo-deformación, la Ley de Hooke es aplicable hasta el límite de proporcionalidad, lo cual ocurre en materiales que tiene un comportamiento elástico lineal.
A continuación, presentamos dos ejemplos de aplicación de la Ley de Hooke, que hemos desarrollado y capturado a través del siguiente video:
En el siguiente video, presentamos dos ejemplos tomados de los ejercicios propuestos en el libro "Mecánica de materiales" de Hibbeler.
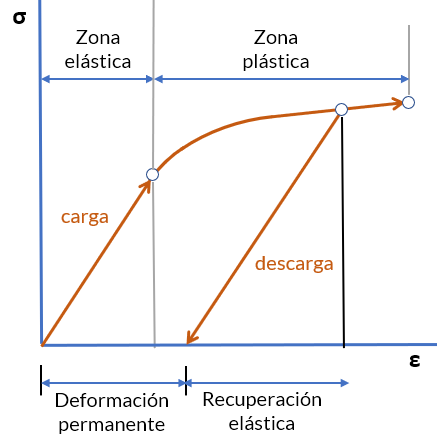
En un material dúctil como el acero cuando se carga en la región plástica y después se descarga, la deformación elástica se recupera, pero la deformación plástica permanece, generando una deformación permanente como se muestra en la figura 2.4.
Está deformación ocurre cuando se supera el esfuerzo de fluencia $(\sigma_y)$. Al aplicar una nueva carga el módulo de elasticidad ($E$) es el mismo; sin embargo, el material ha perdido ductilidad, de tal forma que $\sigma_y$ es mayor.
La aplicación repetida de la carga genera, finalmente, la fatiga del material.
En la deformación se genera una energía de deformación que, por unidad de volumen del material, podemos definirla como:
$$u = \frac{\Delta U}{\Delta V} = \frac12 \sigma\epsilon\tag{2.3}$$Aplicando la Ley de Hooke ($\sigma = E\epsilon$):
$$u = \frac12\frac{\sigma^2}{E}\tag{2.4}$$Si el esfuerzo alcanza el límite de proporcionalidad, se obtiene el denominado módulo de resilienciaLa resiliencia de un material representa su capacidad de absorber la energía sin experimentar ningún tipo de daño permanente
Pero, si usamos la ecuación 2.3, el módulo de resiliencia sería el área del triángulo:
$$u_r = \frac{\sigma_p\epsilon_p}{2}\tag{2.6}$$Al reemplazar la ecuación 2.2 en la ecuación 2.1, obtenemos:
$$\begin{aligned} \delta &= \epsilon L\\ &= \frac{\sigma}{E} L\\ \end{aligned}$$Por lo tanto,
$$\delta = \frac{PL}{AE}\tag{2.7}$$Esta ecuación se usa solo si el material es homogéneo ($E$ constante) y tiene una sección transversal uniforme con área $A$.
La IA Bard nos da la siguiente explicación:
Las deformaciones laterales (en las direcciones $y, z$), pueden medirse con instrumentación, observándose que $\epsilon_y = \epsilon_z$. De hecho, cualquier segmento orientado perpendicularmente al eje $x$ experimenta la misma deformación relativa que el orientado según esas direcciones $y$ o $z$
Retrato de Siméon Denis Poisson (1781-1840), matemático, geómetra y médico francés (François-Séraphin Delpech , Wikimedia, Dominio público).
La relación de Poisson, llamada así en honor del matemático francés Siméon Denis Poisson, se puede calcular con la siguiente expresión:
$$\nu = -\frac{\epsilon_y}{\epsilon_x} = -\frac{\epsilon_z}{\epsilon_x} \tag{2.8}$$El signo negativo en la ecuación significa que si en la dirección $x$ existe alargamiento, en las perpendiculares existe un acortamiento (o viceversa).
La mayoría de los materiales tienen valores de la relación de Poisson que oscilan entre 0.0 y 0.5.
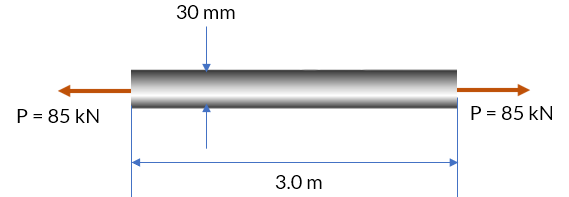
Solución
Calculemos el esfuezo axial:
$$\sigma = \frac{P}{A} = \frac{85\;kN}{\pi(0.03\;m)^2/4} = 120.2\times 10^3\;kPa = \color{brown}120 \;MPa$$Aplicando la Ley de Hooke:
$$\epsilon = \frac{\sigma}{E} = \frac{120\;MPa}{70\times 10^3\;MPa} = \color{brown}0.00171$$Podemos dar respuesta a la primera pregunta... el alargamiento:
$$\delta = \epsilon L_o = (0.00171)(3.0\;m) = 0.00514\; m = \color{brown}5.14\; mm$$La deformación lateral la podemos hallar con la relación de Poisson:
$$\epsilon_L = -\nu\epsilon = -\frac13 (0.00171) = -0.00057$$Finalmente, hallamos la reeducción del diámetro ($\Delta d$):
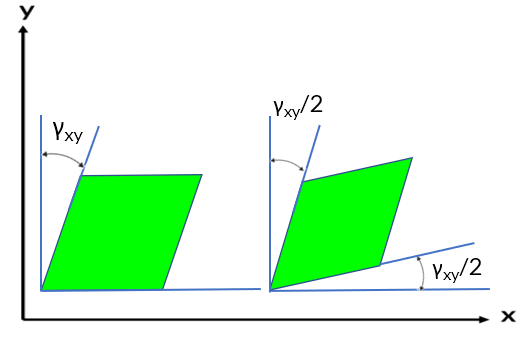
$$\Delta d = \epsilon_L d = -0.00057(30\;mm) = \color{brown}-0.0171\;mm$$Si el material es homogéneo e isotrópico, el esfuerzo cortante distorsiona uniformemente el material. La deformación por cortante $\gamma_{xy}$ mide la distorsión angular relativa a los lados que en un principio se encontraban a lo largo de los ejes $x$ y $y$.
Si el material tiene un comportamiento elástico lineal, por la Ley de Hooke, para el esfuerzo cortante podemos usar la siguiente expresión:
$$\tau _{xy} = G\gamma_{xy}\tag{2.9}$$Donde $G$ es el módulo de rigidez.
Recordemos, de la definición dada por la IA Bard, que:
$$G = \frac{E} {2(1+\nu)} \tag{2.10}$$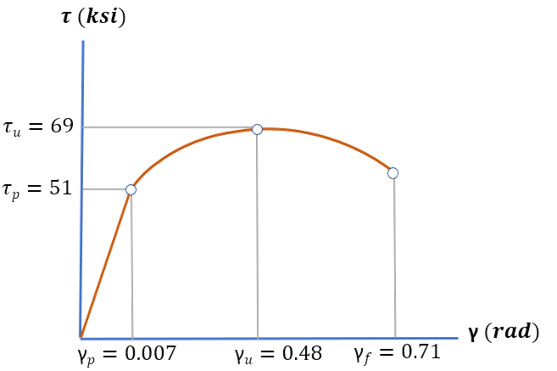
Solución
Calculemos el módulo de Rigidez en el límite de proporcionalidad:
$$G = \frac{\tau_p} {\gamma_p} = \frac{51\;ksi}{0.007} = 7286\;ksi$$
El límite de proporcionalidad y el esfuerzo último están indicados en la figura: $\tau_p = 51\;ksi$ y $\tau_u = 69\;ksi$
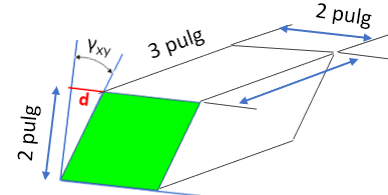
Ahora, calculemos $d$ sabiendo que la deformación cortante elástica máxima es de $0.007 \;rad$ que es un ángulo muy pequeño, por lo que $tan\;\gamma_{xy} = \gamma_{xy}$:
$$tan\;\gamma_{xy} = 0.007 = \frac{d}{2\;pulg}$$ $$d = 0.014\;pulg$$El esfuerzo cortante promedio es $\tau_p = 51 \;ksi$. La fuerza cortante $V$ necesaria que genera el desplazamiento es:
$$\tau_p = \frac{V}{A}$$ $$51\;ksi = \frac{V}{(3\;pulg)(2\;pulg)}$$ $$V = 306\;ksi$$Hasta el momento, hemos supuesto que la distribución de esfuerzos en un elemento es uniforme, tal como lo muestra la figura; por ello, hemos usado la expresión "esfuerzo promedio".
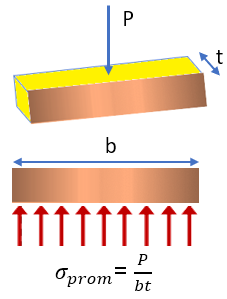
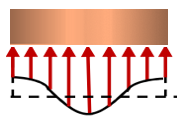
Sin embargo, al tener una carga concentrada, como en la figura 2.6, los elementos en la cercanía inmediata de los puntos de aplicación de la carga se encuentran sometidos a esfuerzos muy grandes, mientras que otros elementos cerca de los extremos del miembro están poco o nada afectados por la carga, tal como la muestra la figura 2.7. Se generan, entonces, grandes deformaciones y esfuerzos cerca de los puntos de aplicación de la carga y reducidas en las esquinas
El principio de Saint-Venant es un concepto importante en la mecánica de materiales que se refiere a la distribución de esfuerzos en una sección transversal de una barra o viga, cuando se aplica una carga. En el caso de esfuerzos axiales, el principio de Saint-Venant establece que la distribución de los esfuerzos no es uniforme a lo largo de la sección transversal de la barra o viga. En particular, cerca de los extremos de la sección transversal, la distribución de los esfuerzos tiende a ser no uniforme, pero hacia el centro de la sección transversal, los esfuerzos tienden a ser iguales a los que se habrían obtenido si la carga se hubiera aplicado en el centro de la sección transversal. Este concepto puede ser de gran utilidad al analizar estructuras como columnas y vigas que estén sometidas a cargas axiales.
Por otra parte, el esfuerzo se distribuirá de manera más uniforme en toda el área de la sección transversal cuando ésta esté más lejos del punto donde se aplica la carga $P$, tal como se muestra en la figura 2.8.
Excepto en la cercanía inmediata de los puntos de aplicación de las cargas, la distribución de esfuerzos puede suponerse independiente del modo de aplicación de la carga. Este enunciado, que se aplica no solo a cargas axiales sino prácticamente a cualquier tipo de carga, se conoce como el principio de Saint-Venant, en honor del matemático e ingeniero francés Adhémar Barré de Saint-Venant (1797-1886)
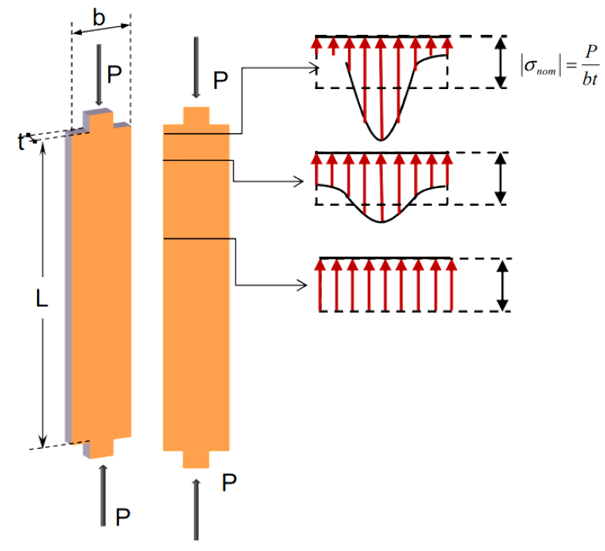
Si un elemento presenta una discontinuidad, como un agujero o un cambio en la geometría de su sección transversal, se presentan grandes esfuerzos en estas secciones críticas, tal como lo ilustra la figura 2.9, en la que se muestra una barra plana con un agujero circular y la distribución de esfuerzos a través del centro del agujero.
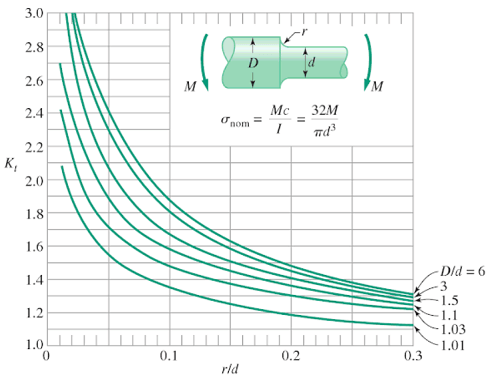
Para evitar cálculos complejos, se suele usar un factor de concentración del esfuerzo $K$, determinados experimentalmente o por análisis avanzados de la "Teoría de la Elasticidad". Para nuestros
propósitos, usaremos $K$ como una relación entre el esfuerzo máximo $\sigma_{máx}$ y el esfuerzo normal promedio $\sigma_{prom}$ (esfuerzo normal $\sigma_{n}$), así:
$$K = \frac{\sigma_{máx}}{\sigma_{prom}}\tag{2.11}$$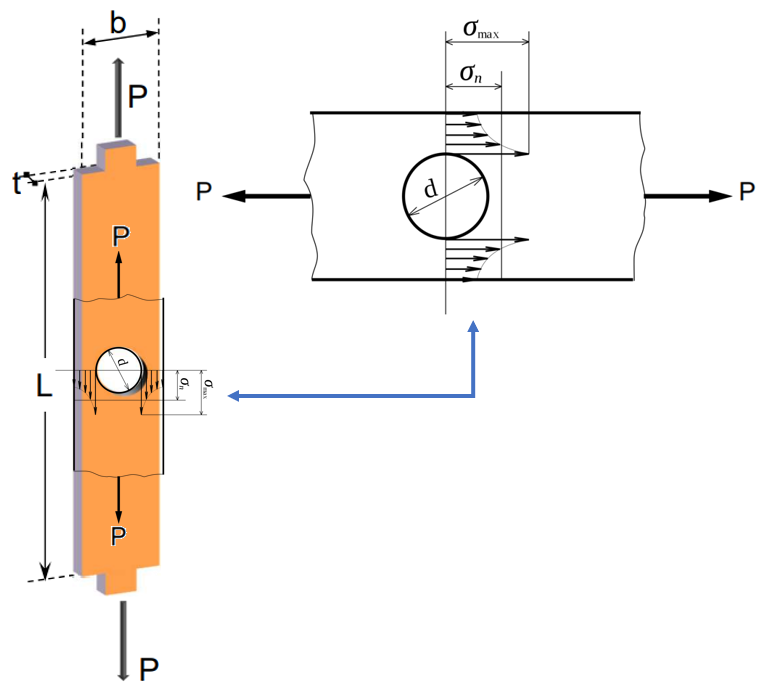
El valor de $K$ nos sirve para calcular el esfuerzo máximo $\sigma_{máx}$ en la discontinuidad de un elemento sometido a una carga axial $P$; para ello, calculamos el esfuerzo promedio $\sigma_{prom} = P/A$ en la discontinuidad, y multiplicar el resultado por el factor de concentración de esfuerzos $K$.
A continuación, presentamos algunas gráficas para hallar $K$:
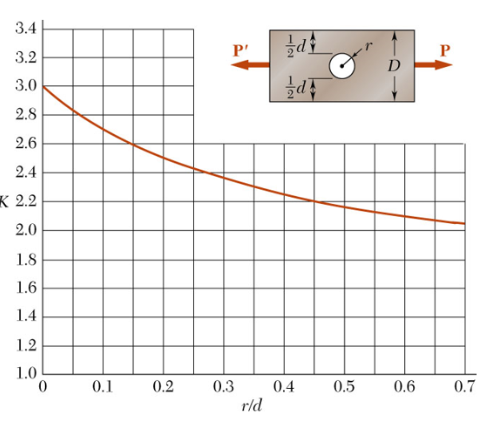
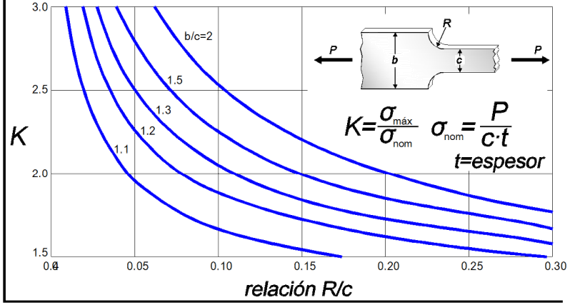
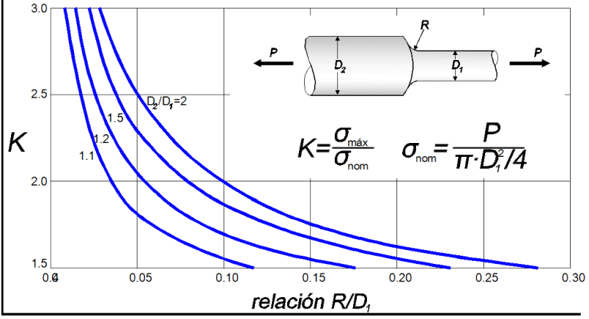
Un análisis, bastante amplio, de los factores de concentración de esfuerzos, lo puedes consultar el libro de Pilkey

Solución
Usamos la figura 2.11, para la cual $R = 4\;mm$, $c = (40\;mm - 8\;mm) = 32\;mm$ y $b = 40\;mm$, encontrando los siguientes datos para buscar $K$ en la gráfica:
$$\frac{R}{c} = \frac{4\;mm}{32\;mm} = \color{brown}0.125$$ $$\frac{b}{c} = \frac{40\;mm}{32\;mm} = \color{brown}1.25$$El valor aproximado de $K$ lo hallamos como lo muestra la figura 2.13.
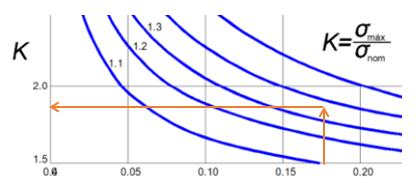
Ahora, usamos la ecuación 2.11, teniendo en cuenta que la carga máxima, sin cedencia en el acero, ocurre cuando $\sigma_{máx} = \sigma_y$ y el esfuerzo promedio es $\sigma_{prom} = P/A$:
$$K = \frac{\sigma_{máx}}{\sigma_{prom}}$$ $$1.75 = \frac{\sigma_y}{\sigma_{prom}}$$ $$1.75 = \frac{250\times 10^6\;Pa}{\sigma_{prom}}$$Despejando:
$$\sigma_{prom} = \frac{(250\times 10^6\;Pa)}{1.75}$$ $$\frac{P_{máx}}{A} = \frac{(250\times 10^6\;Pa)(0.002\;)(0.032\; m)}{1.75}\\$$ $$\color{brown}P_{máx} = 9.14\;kN$$Imagen generada por la IA Lexica.art con el prompt "casa de varios pisos construida en forma de media luna vertical al estilo ciberpunk por la noche" (Lexica).
Imagen de portada: Museo Cite du Vin en Burdeos (Oli Lynch, en Wikimedia, Dominio público).
Imagen de esta página: El Turning Torso, Malmö, Suecia, foto de Mirko Junge, en Wikimedia, CC BY-SA 2.0.
La torsión se refiere a la deformación de un objeto debido a un momento torsor aplicado a lo largo de su eje longitudinal. Un momento torsor es una medida de la fuerza de torsión aplicada a un objeto y se mide en unidades de fuerza multiplicadas por distancia. Cuando un objeto está sometido a un momento torsor, experimenta tensiones y giros que pueden calcularse utilizando las ecuaciones de la resistencia de materiales.
En el caso de perfiles circulares, las ecuaciones para calcular las tensiones y giros resultantes son relativamente simples. Sin embargo, para perfiles no circulares, el cálculo puede ser más complejo. También se puede calcular la energía de deformación acumulada en el objeto debido al momento torsor aplicado.
En algunos casos, el objeto puede estar sometido a más de un momento torsor o puede tener restricciones en sus desplazamientos o giros. Estos casos se conocen como problemas hiperestáticos en torsión y requieren métodos más avanzados para resolverlos.

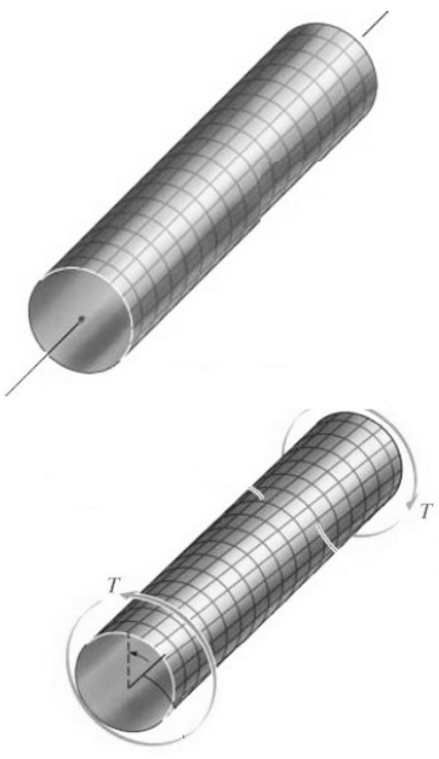
El momento torsor o, también denominado, par de torsión es un momento que genera una deformación como la mostrada en la figura 3.1. Observa, en la animación, que el momento trata de torcer el lingote sobre su eje longitudinal.
Hay dos formas de representar el momento torsor en un espacio 3D. La primera es usando la flecha curva similar al momento flector ($\large\curvearrowleft$), pero con su plano perpendicular al eje longitudinal del elemento, como lo muestra el objeto interactivo 3.1 en la ventana izquierda; la segunda, es usando una flecha de doble punta ($\Large\twoheadrightarrow$), en la dirección del eje longitudinal del elemento (ver el interactivo).
En el análisis de elementos sometidos a torsión, se usa el método de las secciones, separando el elemento por secciones perpendiculares al eje longitudinal. En el caso del objeto interactivo 3.1, el primer paso es hallar la reacción en el punto fijo, que para este caso coincide con el momento torsor $T$, luego se hace el análisis en tres secciones, pues el elemento la barra circular tiene tres diámetros diferentes.
Solución
En primer lugar, hallamos la reacción en $A$ (mostrada en color rojo en el objeto interac- tivo de la derecha), la cual debe equilibrar los pares de torsión; es decir, $T_A = -30\;klb\cdot pulg$ (asumimos positivos los momentos torsores que, según la regla de la mano derecha, van dirigidos hacia afuera del elemento).
Hemos hecho el corte en el tramo $Ax$ que se muestra en el objeto interactivo. Aplicando la condición de equilibrio, $T_x + 12 = 30$; por lo tanto: $T_x = 18\;klb\cdot pulg$.
En perfiles o ejes circulares, tendremos en cuenta las siguientes hipótesis:
En la figura 3.3 el ángulo $\gamma$ puede relacionarse con la longitud $dx$ y con el ángulo $d\phi$, así:
$$\gamma = \rho\frac{d\phi}{dx}\tag{3.1}$$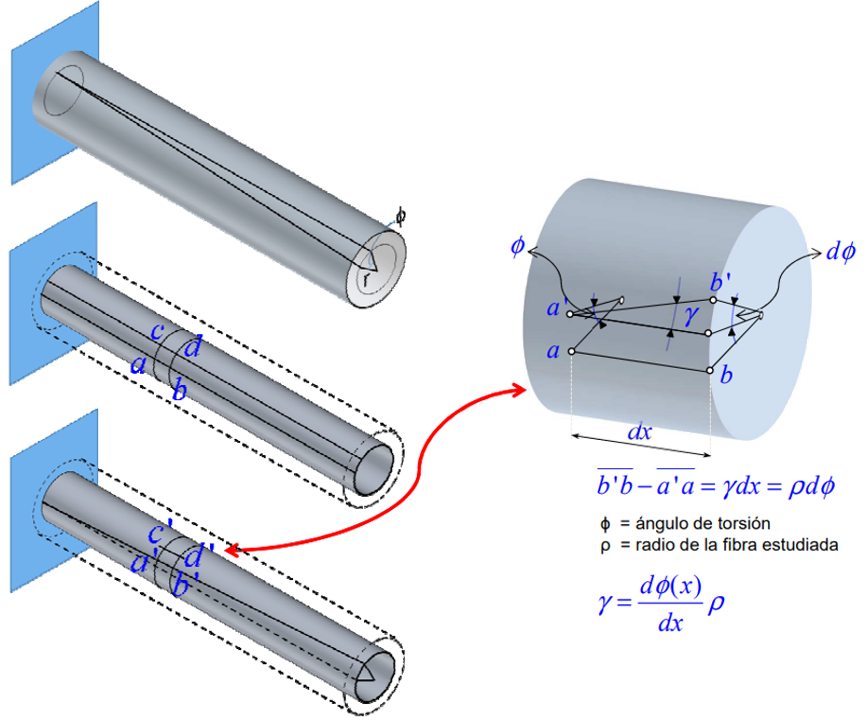
$dx$ y $d\phi$ son iguales en todos los puntos sobre la sección transversal en $x$, luego $d\phi/dx$ es constante en toda la sección transversal, entonces
$$\gamma = \Big(\frac{\rho}{c}\Big)\gamma_{máx}\tag{3.2}$$Interactúa con el siguiente objeto interactivo:
Solución
De la ecuación 3.1, podemos deducir:
$$\begin{aligned} \gamma &= \rho\frac{d\phi}{dx}\\ &= \int_0^L \rho\frac{d\phi}{dx}\\ &= \frac{\rho\phi}{L}\tag{3.3}\\ \end{aligned}$$Sabemos que la deformación cortante máxima se encuentra en la superficie de la varilla ($\rho = c$), por lo tanto:
$$\gamma_{máx} = \frac{c\phi}{L}\tag{3.4}$$La cual podemos escribir en función del diámetro:
$$\gamma_{máx} = \frac{d\phi}{2L}\tag{3.5}$$Ahora, despejamos el diámetro y reemplazamos los datos, teniendo en cuenta que $\phi = 3\degree \cdot \pi/180\degree = 0.05236\;rad$
Aplicando nuestra tercera hipótesis, sobre la ley de Hooke, y la ecuación 3.2, tenemos:
$$\tau = G\gamma = \Big(\frac{\rho}{c}\Big)G\gamma_{máx}$$ $$\tau = \Big(\frac{\rho}{c}\Big)\tau_{máx}\tag{3.6}$$Tal como se ilustra en la figura 3.4.
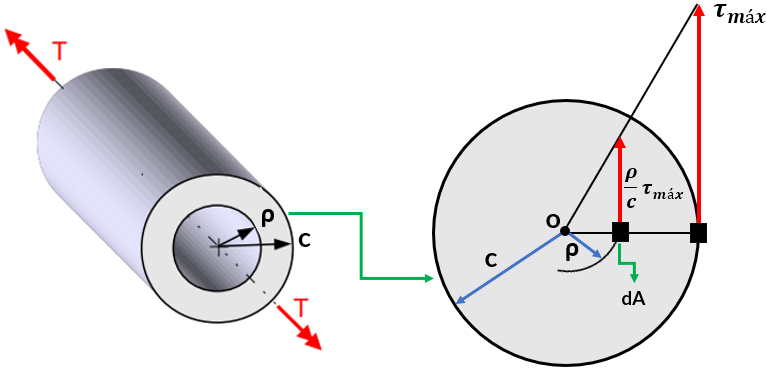
Ahora, sabemos que la fuerza cortante aplicada sobre $dA$ es $\tau dA$, por lo que el momento torsor sobre el eje longitudinal que pasa por el punto $o$ es la suma de todos los pares torsores, es decir:
$$T = \int \rho \tau dA\tag{3.7}$$Sustituyendo la ecuación 3.6:
$$T = \int \rho \Big(\frac{\rho}{c}\Big)\tau_{máx} dA = \frac{\tau_{máx}}{c}\int \rho^2 dA$$La última integral se conoce como momento polar de inerciaRecordemos, del curso de estática, que $J = \frac12 \pi c^4$ para un círculo, y $J = \frac12 \pi(c_2^4 - c_1^4)$ en una corona circular, donde $c_1$ y $c_2$ son los radios interior y exterior, respectivamente. y de la sección transversal con respecto a al punto $o$, que representaremos por la letra $J$. Así las cosas, tenemos:
$$T = \frac{\tau_{máx} J}{c}\tag{3.8}$$Despejando el esfuerzo cortante máximo, tenemos:
$$\tau_{máx} = \frac{Tc}{J}\tag{3.9}$$Para un radio menor que $c$:
$$\tau = \frac{T\rho}{J}\tag{3.10}$$Veamos un ejemplo de aplicación:

Solución
Inicialmente, calculemos el momento polar de inercia:
$$\begin{aligned} J &= \frac12 \pi(c_2^4 - c_1^4)\\ &= \frac12 \pi (0.015^4 - 0.01^4)\;m^4\\ &= 6.4\times 10^{-8}\;m^4 \end{aligned}$$Ahora, hallamos el par de torsión máximo para $\tau_{máx} = 100\;MPa$ y $c = c_2 = 0.015\;m$:
$$\begin{aligned} T &= \frac{\tau_{máx} J}{c}\\ &= \frac{(100\times 10^6\;Pa)(6.4\times 10^{-8}\;m^4)}{0.015\;m}\\ &= 426.7\;N\cdot m\\ &= 0.427\;kN\cdot m \end{aligned}$$Recordemos la ecuación 3.4:
$$\gamma_{máx} = \frac{c\phi}{L}$$En el rango elástico, como dijimos antes, se aplica la ley de Hooke:
$$\gamma_{máx} = \frac{\tau_{máx}}{G}$$Reemplazando por la ecuación 3.4 y 3.9, tenemos:
$$\frac{c\phi}{L} = \frac{\tau_{máx}}{G} = \frac{Tc}{JG}$$Encontrando, finalmente, la siguiente expresión para el ángulo de giro:
$$\phi = \frac{TL}{JG}\tag{3.11}$$
En el ejemplo 3.4, observa cómo cambia el ángulo de giro para diferentes diámetros. En algunos casos es bastante exagerado ¿qué puedes concluir? En el ejemplo, sólo hemos puesto los resultados; pero, veamos como se calcularon los esfuerzos cortantes máximos y el ángulo de giro, para el primer ejemplo en el tramo $AB$:
Si hacemos un corte en este tramo, el par de torsión es igual a la suma de los tres pares dados; es decir, $T = (12 + 9 + 9)\;klb\cdot pulg = 30\;klb\cdot pulg$. Para ese tramo
$$J_{AB} = \pi (c_{AB})^4/2 = \pi(1.5\;pulg)^4/2 = \color{brown}{7.95\;pulg^4}$$El esfuerzo cortante máximo, sería:
$$\begin{aligned} \tau_{AB} &= \frac{Tc_{AB}}{J_{AB}}\\ &= \frac{(30000\;lb\cdot pulg)(1.5\;pulg)}{7.95\;pulg^4}\\ &=\color{brown}{5660.3\;psi} \end{aligned}$$Seguramente, ya has advertido que el resultado en el objeto interactivo es un poco diferente ($\tau_{AB} = 5658.8\;psi)$. Esto ocurre por la simplificación que hicimos para $J$, prueba con $J_{AB} = 7.952149\;pulg^4$.
Ahora, hallemos el ángulo de giro:
$$\begin{aligned} \phi_{AB} &= \frac{TL}{JG}\\ &= \frac{(30\;klb\cdot pulg)(24\; pulg)}{(7.952149\;pulg^4)(11.6\times 10^3 klb/pulg^2)}\\ &= \color{brown}{0.0078\;rad} \end{aligned}$$Tal como lo dijimos en la sesión 2.7.2, si un elemento presenta una discontinuidad ,como un cambio abrupto en el diámetro de su sección transversal, se presentan concentraciones de esfuerzos cerca de esta discontinuidad. Para evitar cálculos complejos, se suele usar un factor de concentración del esfuerzo $K$, determinados experimentalmente o por análisis avanzados de la "Teoría de la Elasticidad".
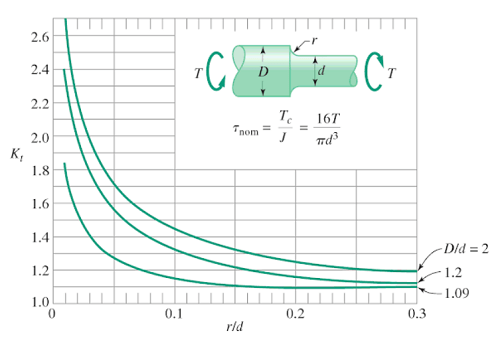
El esfuerzo cortante máximo, se calcularía así:
$$\tau_{máx} = K\frac{Tc}{J}\tag{3.12}$$Cheminée en tire bouchon, foto de Aquilafm, en Wikimedia, CC BY-SA 4.0.
Imagen de portada: Puente de madera (Peter H, en Pixabay).
Imagen de esta página: Puente en Praga, República Checa, foto de cs:ŠJů, en Wikimedia, CC BY-SA 3.0.
La flexión pura es un concepto de resistencia de materiales que se refiere a la flexión de un elemento bajo la acción de un momento flexionante constante. En la flexión pura, los esfuerzos cortantes sobre el elemento son cero. La flexión pura analiza los esfuerzos y deformaciones en elementos prismáticos sujetos a flexión. La flexión pura es un caso idealizado que se utiliza en el análisis estructural para simplificar los cálculos y comprender el comportamiento de las vigas bajo cargas de flexión.
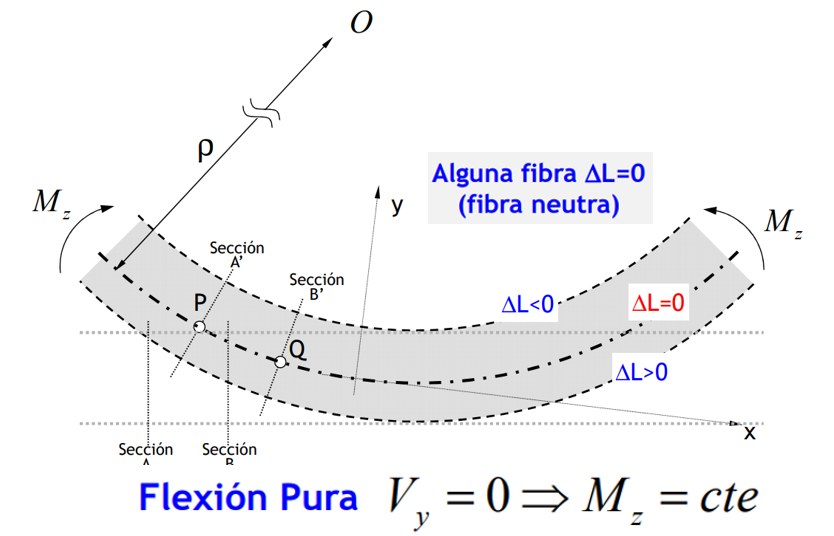
Una viga es un elemento estructural que se somete a cargas que actúan transversalmente al eje longitudinal, originando deformaciones y esfuerzos internos. Es importante, para el diseño de estos elementos, comprender el concepto de flexión, la curva elástica generada y cómo se determinan las deformaciones y esfuerzos internos. Este apartado puede ayudar a comprender el concepto de flexión en una viga sometida a cargas externas y a calcular los esfuerzos por flexión.
En el siguiente video, puedes observar cómo se deforma un elemento de goma sometidos a flexión.
En el siguiente video puedes observar qué ocurre con una viga de hormigón reforzado, sometida a flexión. En el tercer video, se someten a flexión un polímero y una viga de madera.
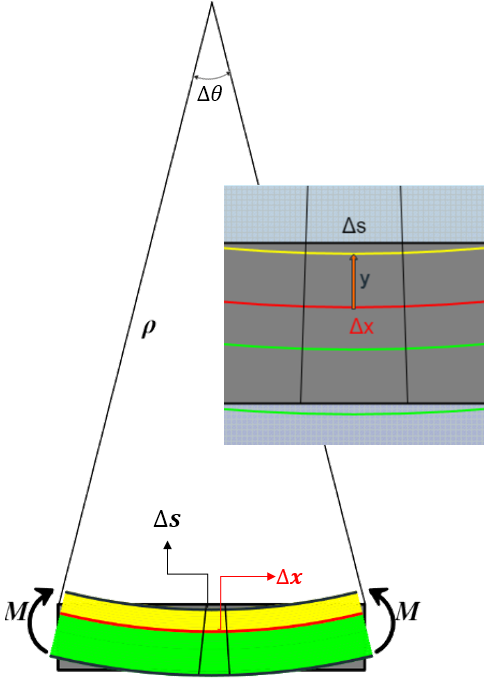
Observamos, en la página anterior, que el momento flexionante hace que las fibras inferiores del material se estiren y las de la parte superior se compriman. Entre estos dos grupos de fibras debe haber una superficie en la que las fibras longitudinales del material no sufrirán ningún cambio de longitud, esta superficie se conoce como superficie neutra y el eje longitudinal como eje neutro.
Partiendo de la hipótesis de Bernoulli que dice que "todas las secciones transversales de la viga permanecen planas y perpendi- culares al eje longitudinal durante la deformación", hemos aislado un pequeño segmento de la viga en el que cualquier segmento de recta $\Delta x$ (ver figura de la derecha), situado en la superficie neutra no cambia su longitud, mientras que cualquier segmento de recta $\Delta s$, ubicado a una distancia y por encima de la superficie neutra se comprime, por lo que:
$$\epsilon = \lim\limits_{\Delta x \to 0}\frac{\Delta s - \Delta x}{\Delta x}$$$\Delta x$ tiene un radio de curvatura $\rho$. De la figura se concluye que $\Delta x =\rho\ \Delta \theta$ y $\Delta s = (\rho - y)\Delta\theta$, luego:
$$\epsilon = - \frac{y}{\rho}\tag{4.1}$$En el siguiente objeto interactivo, presentamos una animación de la flexión pura y la deformación del elemento.
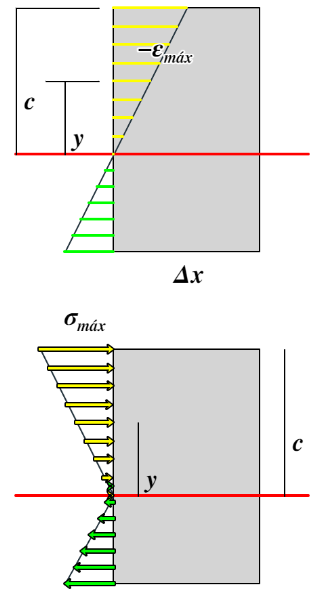
Una viga sometida a una carga se flexiona. Hemos observado que los planos superiores de la viga se comprimen (deformación que asumimos negativa), y que los planos inferiores se estiran o traccionan (deformación que asumimos positiva). En la gráfica de la derecha, observamos el diagrama de deformaciones, en amarillo las negativas (contracción) y en verde las positivas (tracción). Por la relación de triángulos y la expresión deducida para la deformación unitaria, concluimos:
$$\epsilon = -\Big(\frac{y}{c}\Big) \epsilon_{máx}$$Con el equilibrio de momentos, podemos demostrar:
$\displaystyle\sum M = 0\\ \to M = \int_A ydF = \int_A y(\sigma dA) = \int_A y \Big(\frac{y}{c}\sigma_{máx}\Big) dA\\ M = \frac{\sigma_{máx}}{c} \int_A y^2dA $La integral es el momento de inercia de la sección:
$$\displaystyle \sigma_{máx} = \frac{Mc}{I}\tag{4.2}$$A una altura $\bold{y}$ del eje neutro:
$$\sigma_x = -\frac{My}{I}\tag{4.3}$$El esfuerzo por flexión se determina con la expresión $\displaystyle\color{#0089cd}{\sigma_x = -\frac{My}{I}}$ en compresión y $\displaystyle\color{#0089cd}{\sigma_x = \frac{My}{I}}$ en tracción, que pueden representarse de varias formas (ver figura 4.2).
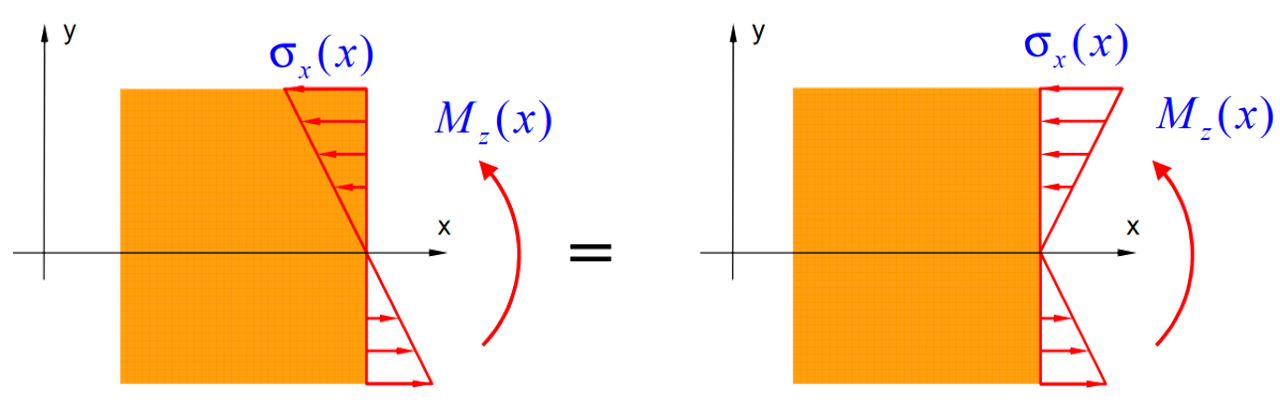
En secciones rectangulares, el valor de $\color{#0089cd}{y}$ a tracción es $\color{#0089cd}{-\frac h2}$, entonces $\displaystyle\color{#0089cd}{\sigma_x = \frac{6M}{bh^2}}$. En este tipo de secciones, se suele trabajar con el módulo sección elástico, dado por la expresión:
$$\color{red}{s= \frac{bh^2}{6}}\tag{4.4}$$Para estos casos:
$$\color{#0089cd}{\sigma_x = \frac{M}{s}\tag {4.5}}$$Una aplicación sencilla es el cálculo de esfuerzos en nervios o viguetas, tal como se observa en el siguiente objeto interactivo (puedes rotar la losa, para una mejor apreciación de las disposición de las vigas):
Las vigas de sesión compuesta son aquellas que están hechas de dos o más materiales con diferentes módulos de elasticidad, que se usan en la ingeniería estructural para resistir, especialmente, esfuerzos de tracción; por ejemplo, vigas de hormigón reforzado, en las cuales el acero es más resistente a la tracción que el hormigón, otro ejemplo son las vigas de madera reforzadas con platinas de acero.

Sabemos por la ecuación 4.1 que $\displaystyle\epsilon = - \frac{y}{\rho}$. Al existir dos materiales, se presentan dos módulos de elasticidad ($E_1$ y $E_2$) y, en consecuencia, dos esfuerzos:
El uso de un segundo material en la zona de tracción, significa que el primero no trabaja en dicha sección; por ello, se acostumbra usar una sección transformada equivalente como la de la figura 4.4, en la cual el segundo material (acero para el ejemplo) es un área equivalente del primero; para ello, se multiplica por un factor $n$.
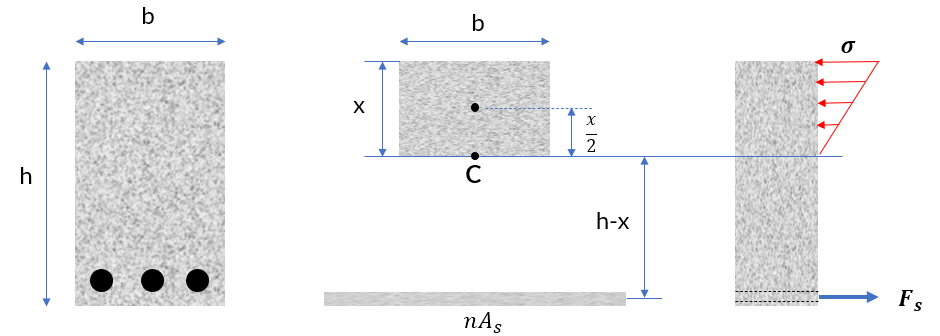
Este factor $n$, para un $dA$, se deduce de las condiciones de equilibrio $\sum F_x = 0$ y $\sum M = 0$, así:
$$F_c = \sigma dA = E_1\epsilon dA$$ $$F_s = \sigma ndA = E_2\epsilon \;ndA$$Igualando las fuerzas y simplificando:
$$n = \frac{E_1}{E_2} \tag{4.7}$$En el caso del hormigón reforzado (figura 4.4), la posición del eje neutro, se puede calcular con el primer momento de área:
$$bx(\frac{x}{2}) -nA_s(h-x)=0$$ $$\frac12 bx^2 + nA_sx - nA_sh = 0\tag{4.8}$$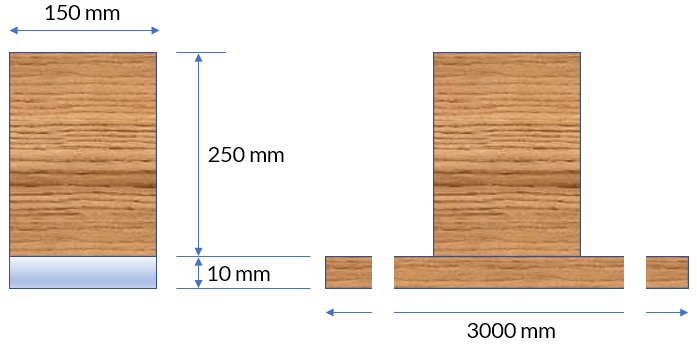
Solución
Transformamos la sección a madera, entonces:
Por lo tanto, el acero se transforma a una área de madera equivalente a $3000\;mm\times 10\;mm$ (ver figura). Ahora, hallamos la posición del eje neutro para un área compuesta, medida desde la parte superior:
$$\={y} = \frac{(150)(250)(125) + (3000)(10)(255)}{(150)(250) + (3000)(10)} = 183\;mm$$Por el teorema de los ejes paralelos, hallamos el momento de inercia:
$$\begin{aligned} I &= \frac{150\times 250^3}{12} + 150\times 250(125-183)^2\\ &\;\;\;\;\;\;+\frac{3000\times 10^3}{12} + 3000\times 10(255-183)^2\\ &= 478\times 10^6\; mm^4 \end{aligned}$$Calculamos el esfuerzo máximo en la madera:
$$\sigma_{w\; máx} = \frac{Mc}{I} = \frac{0.03\times 10^9 \times 183}{478\times 10^6} = 11.5\; MPa$$Ahora, el esfuerzo máximo en el acero:
$$\sigma_{s\; máx} = n\sigma_{w\; máx} = 20\times \frac{0.03\times 10^9 \times 77}{478\times 10^6} = 96.7\; MPa$$Por lo tanto,
$$\bold{\sigma_{admisible} = 11.5\; MPa}$$El siguiente ejemplo es similar al anterior, pero transformaremos la sección de madera en acero equivalente.
Solución
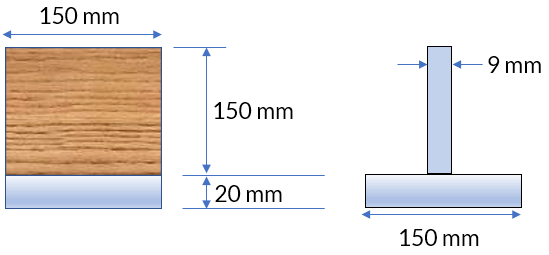
Transformamos la sección a acero, entonces:
$$n = \frac{E_w}{E_s} = 0.06$$Por lo tanto, la sección de madera se transforma a una área de acero equivalente a $9\;mm\times 150\;mm$ (ver figura). Ahora, hallamos
la posición del eje neutro para un área compuesta, medida desde la parte inferior:
$$\={y} = \frac{(9)(150)(95) + (150)(20)(10)}{(9)(150) + (150)(20)} = 36.38\;mm = 0.03638\;m$$Por el teorema de los ejes paralelos, hallamos el momento de inercia:
$$\begin{aligned} I &= \frac{9\times 150^3}{12} + 9\times 150\times(95-36.38)^2\\ &\;\;\;\;\;\;+\frac{150\times 20^3}{12} + 150\times 20\times(36.38-10)^2\\ &= 9.358\times 10^6\; mm^4\\ &= 9.358\times 10^{-6}\; m^4 \end{aligned}$$Calculamos el esfuerzo máximo en el acero:
$$\sigma_{s\; máx} = \frac{Mc}{I} = \frac{0.002\times 10^9 \times 36.38}{9.358\times 10^6} = 7.78\; MPa$$Ahora, el esfuerzo máximo en la madera:
$$\sigma_{w\; máx} = n\sigma_{s\; máx} = 0.06\times \frac{0.002\times 10^9 \times 133.62}{9.358\times 10^6} = 1.71\; MPa$$Por lo tanto,
$$\bold{\sigma_{admisible} = 1.71\; MPa}$$Observa que son problemas prácticamente iguales, que se resolvieron usando alternativas diferentes, tales como el material seleccionado para transformar y desde dónde se mide la posición del eje neutro.
Con la obtención de la sección transformada, podemos revisar las propiedades geométricas y mecánicas de una sección de hormigón reforzado a tracción; es decir, podemos obtener la localización del eje neutro, el momento de inercia, el módulo de la sección, los esfuerzos y, especialmente, el momento resistente.
En la siguiente escena, puedes practicar con la revisión de varias secciones rectangulares con refuerzo a tracción, situación que trabajarás más adelante en las asignaturas relacionadas con el hormigón.
Tal como lo dijimos en la sesión 2.7.2, si un elemento presenta una discontinuidad, como un cambio abrupto en el diámetro de su sección transversal, se presentan concentraciones de esfuerzos cerca de esta discontinuidad. Para evitar cálculos complejos, se suele usar un factor de concentración del esfuerzo $K$, determinado experimentalmente o por análisis avanzados de la "Teoría de la Elasticidad".
El esfuerzo a flexión máximo, se calcularía así:
$$\sigma_{máx} = K\frac{Mc}{I}\tag{4.8}$$Armadura de acero para una viga de hormigón reforzado, foto de Lionel Allorge, en Wikimedia, CC BY-SA 3.0.
Imagen de portada: Estructura de acero con elementos prefabricados (Syibeehive, en Wikimedia, CC BY-SA 4.0).
Imagen de esta página: El 'Gherkin' (pepino) de Norman Foster (Londres, 2004) se eleva por encima de la iglesia del siglo XIII de St Helen's Bishopsgate, foto de Barney Jenkins, en Wikimedia, CC BY-SA 3.0.
Todo elemento estructural sometido a fuerzas externas reacciona con otras fuerzas internas, las cuales permiten conocer si el elemento está en capacidad de resistir dichas fuerzas. El diseño de un elemento estructural depende de las propiedades del material y de la determinación de las fuerzas internas del elemento. Así las cosas, en este capítulo, tendremos como objetivos: Determinar las fuerzas internas que actúan en un punto cualquiera de un elemento estructural, y elaborar los diagramas de fuerza cortante y de momento flector.
Los diagramas de fuerza cortante y momento flector son herramientas fundamentales en el análisis estructural de vigas. Estos diagramas proporcionan una representación visual de las fuerzas internas que actúan a lo largo de la longitud de una viga, lo cual es crucial para comprender su comportamiento y determinar su capacidad de carga.
El diagrama de fuerza cortante muestra la variación de la fuerza cortante a lo largo de la viga. La fuerza cortante es la fuerza que actúa perpendicularmente a la longitud de la viga y tiende a cortar o separar la viga en dos partes.
El diagrama de fuerza cortante indica los puntos donde la fuerza cortante alcanza valores máximos y mínimos, y muestra cómo varía esta fuerza a medida que se mueve a lo largo de la viga.
Por otro lado, el diagrama de momento flector muestra la variación del momento flector a lo largo de la viga. El momento flector es una medida de la tendencia de una fuerza para hacer girar o flexionar la viga. El diagrama de momento flector indica los puntos donde el momento flector alcanza valores máximos y mínimos, y muestra cómo varía este momento a medida que se recorre la longitud de la viga.
Estos diagramas son importantes para comprender cómo se distribuyen las fuerzas internas a lo largo de la viga y para identificar las secciones críticas donde las cargas pueden generar tensiones o deformaciones significativas. Al analizar los diagramas de fuerza cortante y momento flector, los ingenieros pueden determinar el diseño y las dimensiones adecuadas de la viga, así como evaluar su resistencia y estabilidad estructural.
Como vimos en Estática, el método de las secciones nos permite calcular las fuerzas internas en armaduras. Algo similar haremos para vigas con cortes mucho más sencillos cuando son en voladizo. En las vigas, las fuerzas internas son de compresión, flexión, cortante y torsión, que se contraponen a las fuerzas externas, logrando el equilibrio.
En el siguiente video se evidencia la importancia de la fuerza cortante y del momento flector en el análisis y diseño de vigas:
El tipo de carga externa que se aplica a una viga determinará las fuerzas y tensiones internas que se desarrollan en la viga. Estas fuerzas y tensiones internas deben analizarse cuidadosamente para garantizar que la viga pueda soportar de manera segura la carga aplicada y evitar grandes deformaciones, como las que se muestran en el siguiente video:
En la página siguiente, presentamos ejemplos del uso de vigas en diferentes estructuras. La primera foto de la estructura de piedra "Stonehenge", corresponde a una viga simplemente apoyada. Otros ejemplos mostrados son de puentes y estructuras aporticadas.
Los siguientes objetos interactivos, son tomados de la Unidad Didáctica Interactiva "Fuerzas internas" del Proyecto Un_100, publicado en la Red Educativa Digital Descartes y en el portal Prometeo de la UNAM de México.
Una viga soportada por apoyos simples se le denomina “viga simplemente apoyada”. En la foto se observa una viga simple a la que le llegan cargas concentradas o puntuales.

En la siguiente escena interactiva, presentamos una viga simple con carga puntual, en la cual puedes cambiar la longitud de la viga, la posición de la carga y su valor.
Los apoyos de una viga pueden ser, a su vez, otras vigas (observa la foto de abajo). Las reacciones de las vigas que están en el plano superior se convierten en cargas puntuales para las vigas de apoyo.

En la siguiente escena interactiva, se presenta una viga con dos cargas de igual valor, situadas así: la primera a una distancia $a$ del apoyo izquierdo, y la segunda a una distancia $b$ del apoyo derecho. Hemos omitido el cálculo de las reacciones, que debes verificar.
Las vigas siempre tendrán, al menos, una carga distribuida que es su propio peso. Sin embargo, se hace necesario calcular otras cargas que se distribuyen continuamente a lo largo de la viga. Un ejemplo es la losa que se observa en la escena interactiva de abajo, el peso de esta losa se distribuye en cada uno de los nervios o viguetas que la soportan.
A continuación, podrás practicar con este tipo de vigas en otra escena interactiva, en la que omitiremos el cálculo de las reacciones, que debes verificar.
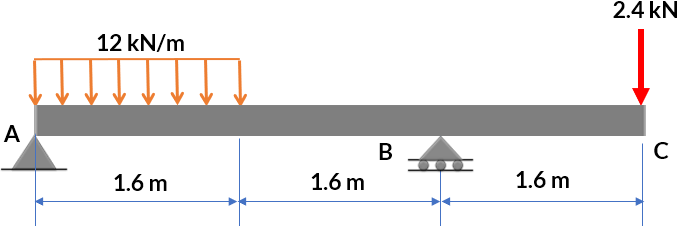
Vamos a hallar los diagramas de fuerza cortante y de momento para la viga que se muestra en la figura 5.4.
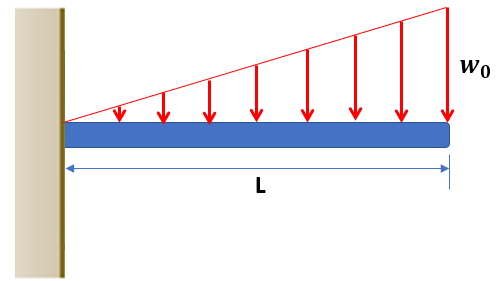
El cálculo de las reacciones es sencillo, tal como se muestra en al figuar 5.5:
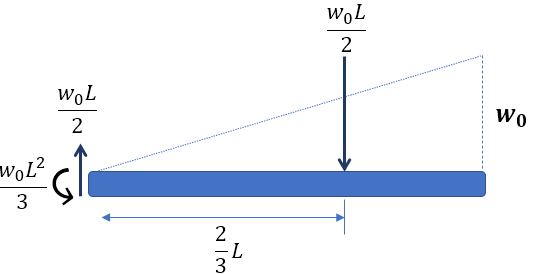
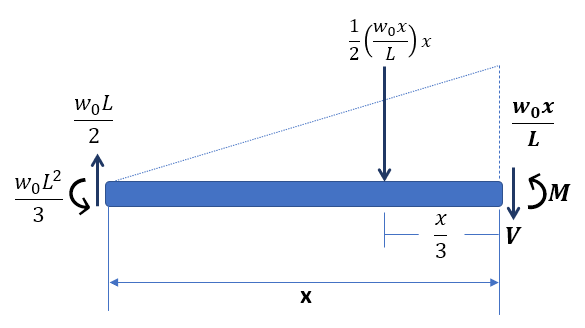
Ahora, hacemos un corte a una distancia $x$, tal como se muestra en la figura 5.6 (método de las secciones).
Ecuación del momento flector
$$+\curvearrowright \sum M_x = 0$$ $$\frac{w_0L^2}{3} - \frac{w_0L}{2}x + \frac12 \Big(\frac{w_0x}{L}\Big)x\Big(\frac13 x\Big) + M =0$$ $$\color{#0089cd}M = \frac{w_0}{6L}\big(-2L^3 + 3L^2x - x^3\big)$$Ecuación de la fuerza cortante
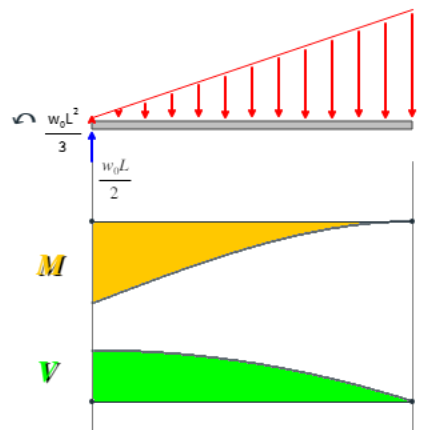
$$+\uparrow \sum F_y = 0$$ $$\frac{w_0L}{2} - \frac12\Big(\frac{w_0x}{L}\Big)x - V = 0$$ $$\color{#0089cd} V = \frac{w_0}{2L}\big(L^2 - x^2\big)$$Con estas dos ecuaciones, podemos dibujar los diagramas de momento y cortante, tal como se muestra en la figura 5.7.
En las vigas anteriores, observamos que el método de las secciones y las condiciones de equilibrio son suficientes para hallar las ecuaciones y los diagramas de momento y cortante; sin embargo, para la fuerza cortante usamos una ecuación diferencial en las tres primeras vigas. En el siguiente apartado, explicamos estas ecuaciones.
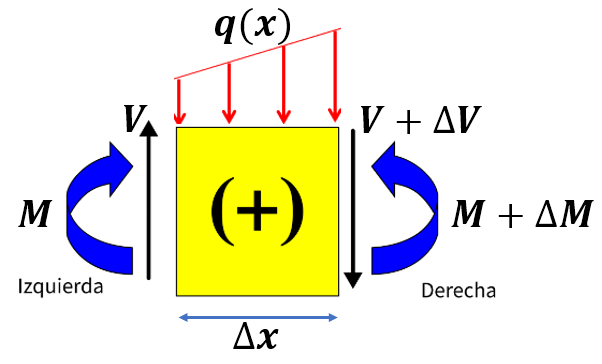
En la figura 6.8, hemos aislado un elemento diferencial de la viga con longitud $\Delta x$ y todas las fuerzas internas de acuerdo a la convención de signos positivos. Iniciemos con una primera condición de equilibrio.
$$+\uparrow \sum F_y = 0$$ $$V + q\Delta x - (V + \Delta V) = 0$$ $$\frac{\Delta V}{\Delta x} = q$$Cuando $\Delta x \to 0$
$$\frac{dV}{dx} = q\tag{5.1}$$Ahora, usemos equilibrio de momentos, teniendo en cuenta que, por ser un elemento diferencial, la resultante de la fuerza externa $(q)$, se aplica en $\Delta x/2$.
$$+\curvearrowright \sum M_x = 0$$ $$(M + \Delta M) - M - V\Delta x -(q\Delta x)(\Delta x/2) = 0$$ $$\frac{\Delta M}{\Delta x} = V + \frac{q\Delta x}{2}$$Cuando $\Delta x \to 0$
$$\frac{dM}{dx} = V\tag{5.2}$$Verifiquemos la ecuación 5.2 el caso de la última viga analizada en el apartado 5.5.4, en la que:
$$M = \frac{w_0}{6L}\big(-2L^3 + 3L^2x - x^3\big)$$Por lo tanto,
$$V = \frac{dM}{dx}$$ $$V = \frac{w_0}{6L}\big(3L^2 - 3x^2\big)$$ $$\color{#0089cd} V = \frac{w_0}{2L}\big(L^2 - x^2\big)$$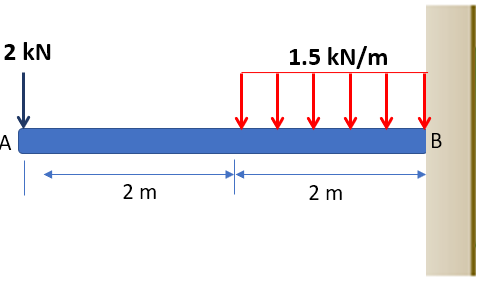
Solución
En primer lugar, dibujamos el diagrama de cuerpo libre y calculamos las reacciones, encontrando (verifica):
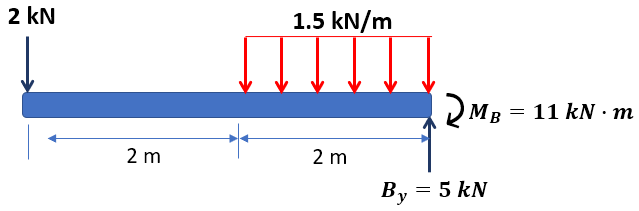
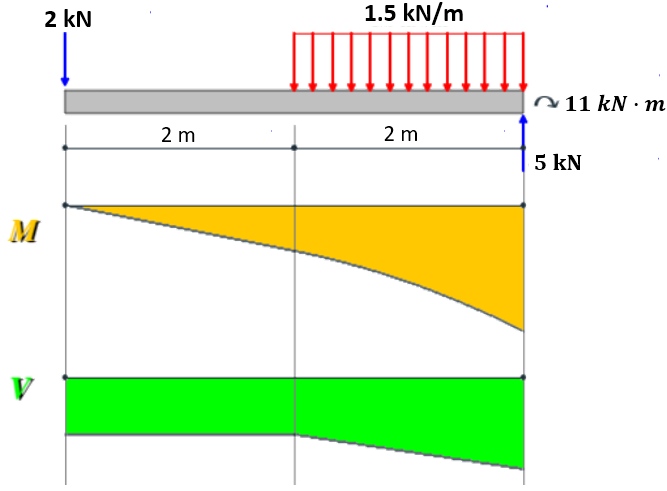
Ahora, hallemos las ecuaciones para fuerza cortante:
En el intervalo $[0, 2]$:
$$V = - 2$$En el intervalo $[2, 4]$: $\displaystyle V = - 2 - 1.5x$
La ecuación de momentos la podemos hallar integrando la ecuación 5.2, así $M = \displaystyle\int Vdx$:
En el intervalo $[0, 2]$: $\displaystyle M = \int -2dx = -2x$
En el intervalo $[2, 4]$:
$$M = \int[- 2 - 1.5(x-2)]dx = -2x - 0.75(x-2)^2$$Finalmente, dibujamos los diagramas:
Solución
El cálculo de las reacciones, es muy sencillo:
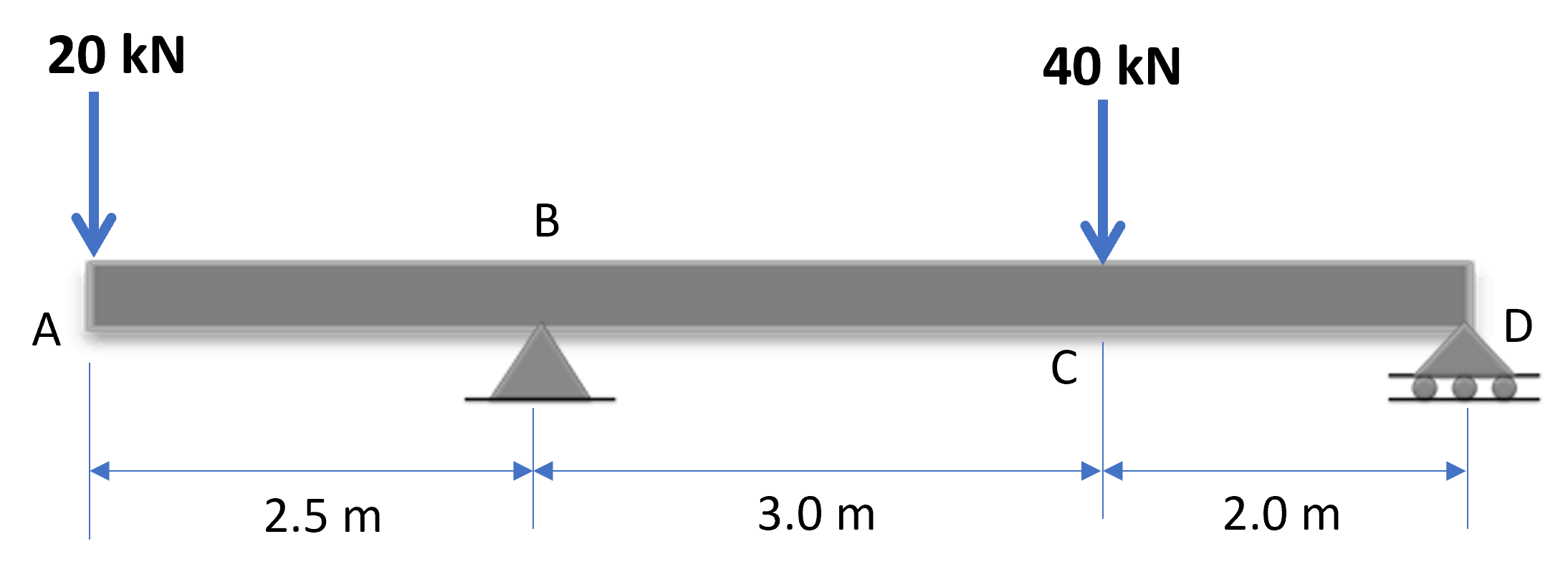
$$+\curvearrowright \sum M_B = 0$$ $$-2.5(20) + 3(40) - 5D_y = 0 \to D_y = 14\; kN$$$B_y$ equilibra las fuerzas verticales con $46\;kN$:
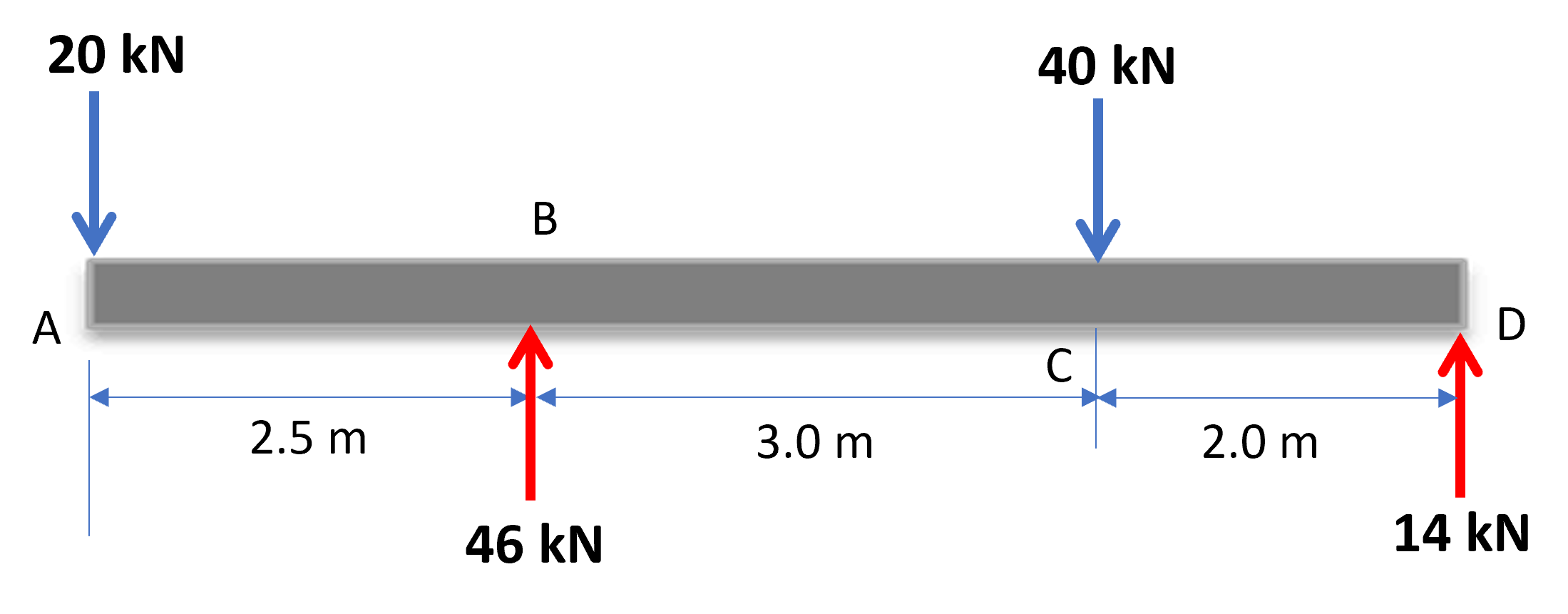
Ahora, hacemos cortes en tres tramos, así:
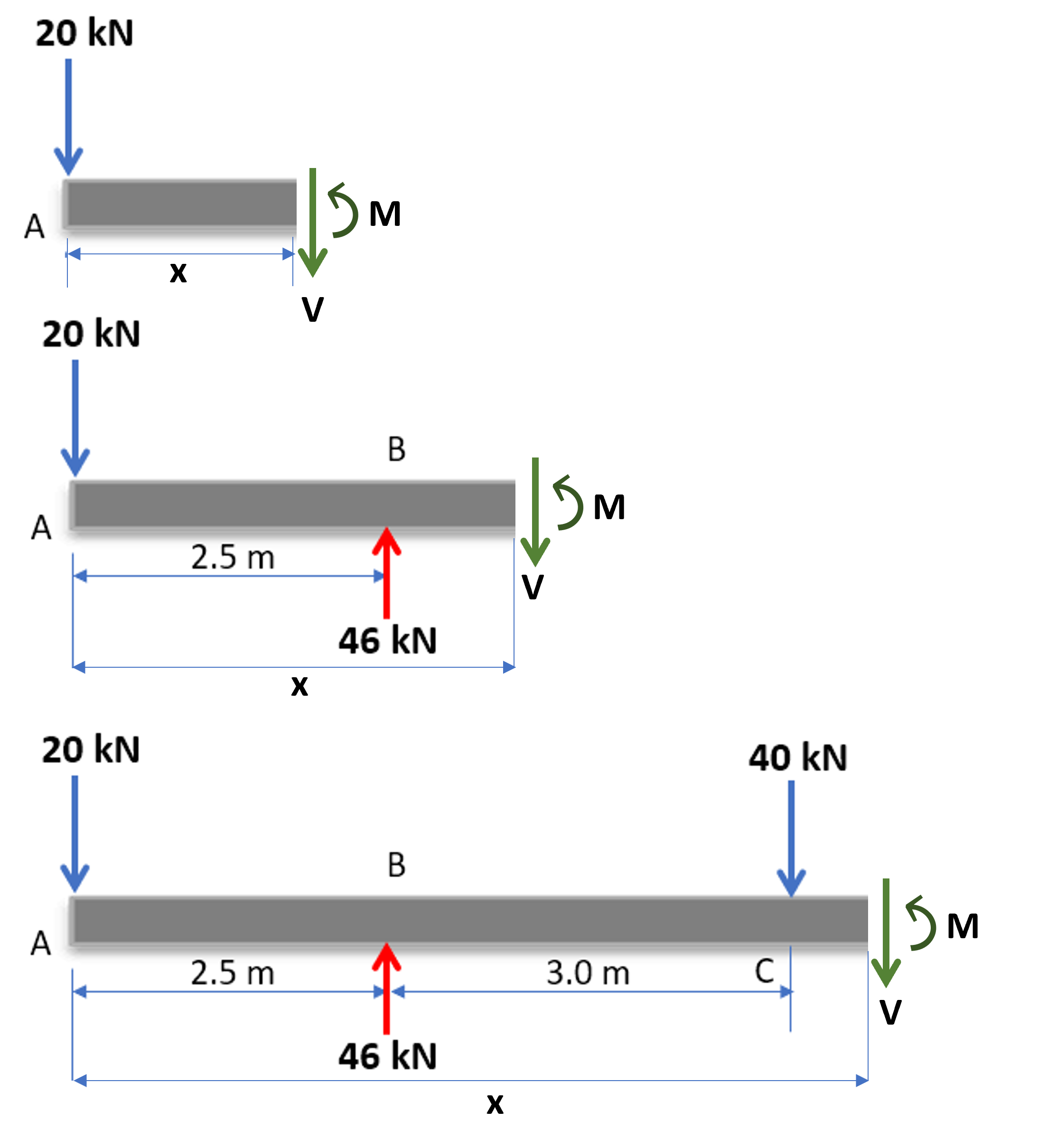
Por cada tramo, encontramos las siguientes ecuaciones para la fuerza cortante:
Para el tramo: $0 \le x \le 2.5$:
$$+\downarrow \sum F_y = 0$$ $$V + 20 = 0$$ $$V = -20\;kN$$Para el tramo: $2.5 \le x \le 5.5$:
$$+\downarrow \sum F_y = 0$$ $$V + 20 - 46 = 0$$ $$V = 26\;kN$$Para el tramo: $5.5 \le x \le 7.5$:
$$+\downarrow \sum F_y = 0$$ $$V + 20 + 40 - 46 = 0$$ $$V = -14\;kN$$En cada uno de los tres tramos, se presentan funciones constantes, que facilita considerablemente el dibujo de los diagramas para la fuerza cortante.
Ahora, hallamos las ecuaciones para los momentos que, para este caso, es más simple usar la ecuación de equilibrio para momentos. Una alternativa hubiese sido hallar las cortantes con las derivadas de los momentos.
Para el tramo: $0 \le x \le 2.5$:
$$+\curvearrowright \sum M_x = 0$$ $$M + 20x = 0$$ $$M = -20x$$Para el tramo: $2.5 \le x \le 5.5$:
$$+\curvearrowright \sum M_x = 0$$ $$M + 20x - 46(x - 2.5) = 0$$ $$M = 26x - 115$$Para el tramo: $5.5 \le x \le 7.5$:
$$+\curvearrowright \sum M_x = 0$$ $$M + 20x - 46(x - 2.5) + 40(x - 5.5) = 0$$ $$M = -14x + 105$$Finalmente, dibujamos los diagramas de momentos y fuerza cortante, teniendo en cuenta los tres intervalos analizados y, además, poniendo la parte positiva sobre el eje $x$.
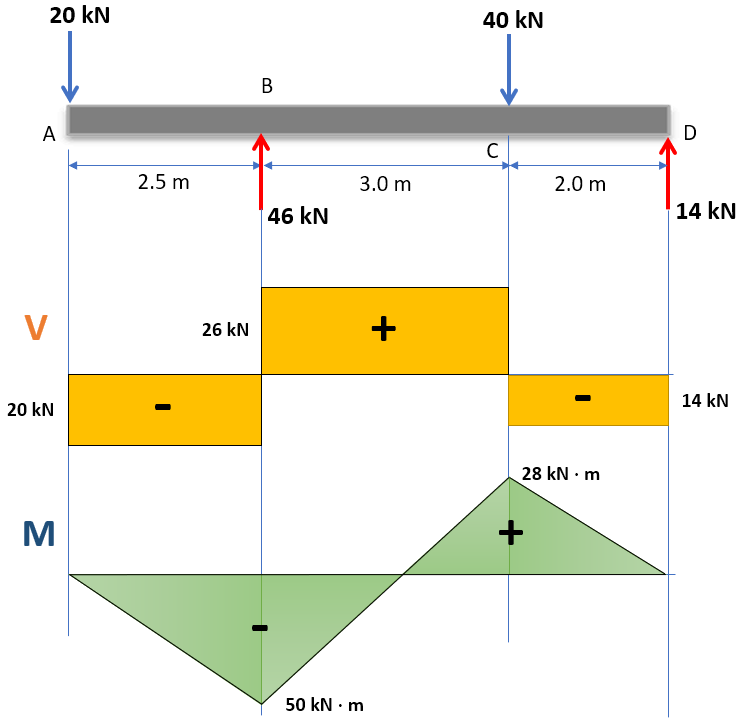
Terminamos este capítulo con el siguiente objeto interactivo, el cual incluye carga parcialmente distribuida y carga puntual. Puedes modificar las siguientes longitudes:
$L_1$: distancia entre los apoyos
$L_2$: longitud del voladizo
$a$: longitud de la carga distribuida
$c$: posición de la carga $P$
En el siguiente ejemplo explicamos cómo se obtienen las reacciones y las ecuaciones para momento flector y fuerza cortante.
Finalmente, realiza los ejercicios propuestos; no obstante, te recomendamos consultar la bibliografía para realizar otros ejercicios adicionales.
Solución
Puente de Mostar en Bosnia Herzegovina (Ramírez, en Wikimedia, CC BY-SA 4.0).
Imagen de esta página: Puente Nany en Iquitos, foto de ArticleAmazon, en Wikimedia, CC BY-SA 4.0.
Los esfuerzos cortantes pueden ser críticos en el diseño de vigas, ya que influyen en la resistencia y estabilidad de la estructura. Si los esfuerzos cortantes superan la capacidad de resistencia del material de la viga, puede producirse una falla por cortante, lo que puede provocar daños o colapso de la estructura.
Para garantizar la seguridad y estabilidad de las vigas, es necesario calcular y evaluar los esfuerzos cortantes utilizando métodos de análisis estructural, como la teoría de vigas o el método de elementos finitos. Esto permite dimensionar adecuadamente la viga y seleccionar los materiales adecuados para resistir los esfuerzos cortantes esperados.
Las fuerzas axiales ($\sigma_x dA$) y cortantes ($\tau_{xy} dA$ y $\tau_{xz} dA$) aplicadas en una sección transversal de una viga son equivalentes al momento flector $M$ y a la fuerza cortante $V$, que se muestran en la figura 6.2. Estas fuerzas son
$$\tau_{xy} dA = -V$$ $$M = \int Vdx$$ Sin embargo, nos interesa determinar el esfuerzo cortante en una sección longitudinal de la viga, muy útil para vigas de sección compuesta como las que tratamos en el apartado 4.4.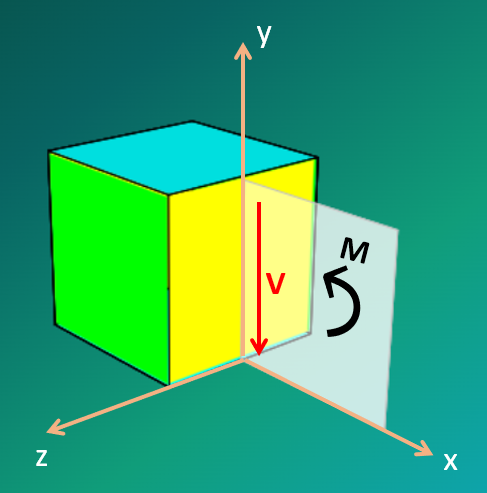
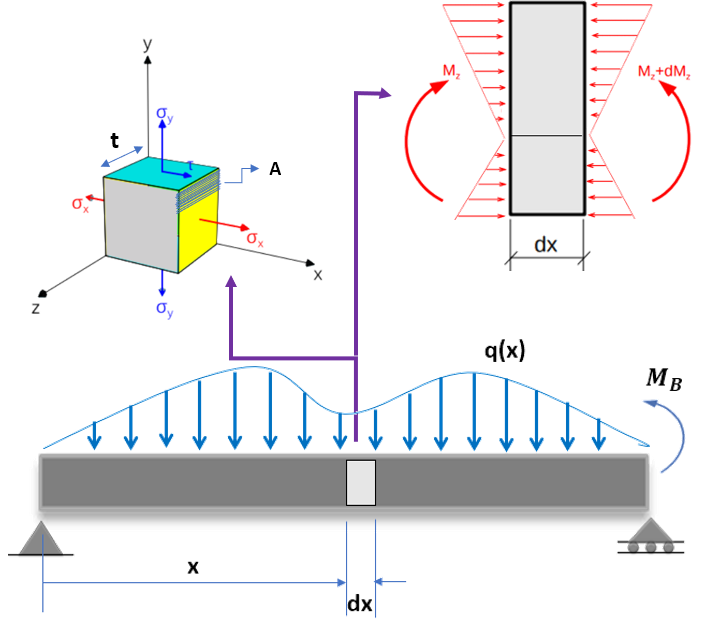
Una estrategia para determinar el esfuerzo cortante en la sección logitudinal de una viga es utilizando la ecuación de equilibrio de fuerzas horizontales; para ello, observa la figura 6.3 que, para $dx$, econtramos:
$$+ \to \sum F_x = 0$$ $$\int_A d\sigma_x dA - \int_A \sigma_x dA - \tau (tdx) = 0$$ $$\int_A \Big(\frac{M + dM}{I}\Big) ydA - \int_A \Big(\frac{M}{I}\Big) ydA - \tau (tdx) = 0$$ $$\Big(\frac{dM}{I}\Big) \int_A ydA = \tau (tdx)$$Despejando $\tau$:
$$\tau = \frac{1}{It}\Big(\frac{dM}{dx}\Big) \int_A ydA$$Recordemos que $\frac{dM}{dx} = V$ y, además, que la integral es el momento de área con respecto al eje neutro, que denotaremos por $Q$. Entonces:
$$\tau = \frac{VQ}{It}\tag{6.1}$$El cortante horizontal por unidad de longitud, que denotamos con la letra $q$, se obtiene para $t=1$:
Para esta última expresión, veamos un ejemplo que propone Popov
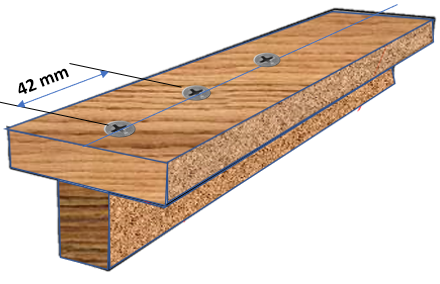
Solución
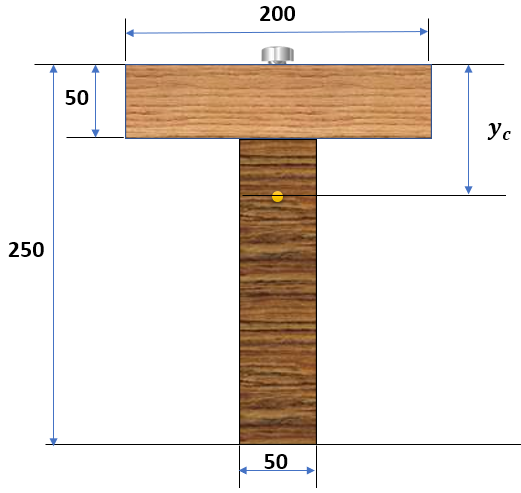
El plano de contacto entre los dos tablones tiende a deslizarse longitudinalmente. Apliquemos, entonces, la ecuación 6.2, hallando, inicialmente, la posición del eje neutro para una sección compuesta.
$$y_c = \frac{50\cdot 200\cdot 25 + 50\cdot 200\cdot 150}{50\cdot 200 + 50\cdot 200} = 87.5\;mm$$Ahora, hallamos el primero momento del área del tablón superior:
$$\begin{aligned} Q &= A\overline{y}\\ &= 50\cdot 200(87.5-25)\\ &= 625\times10^3\;mm^3 \end{aligned}$$El flujo de cortante, sería:
$$q = \frac{VQ}{I} = \frac{3000\times 625 \times 10^3}{113.54\times 10^6} = 16.5\;N/mm$$Así las cosas, los clavos que resisten una fuerza de $700\;N$, deben espaciarse, a lo largo de la viga, $700/16.5 = 42\;mm$.
En el objeto interactivo de la página siguiente, hemos representado un estado de esfuerzos plano con $\sigma_z = \tau_{zx} = \tau_{zy} = 0$ y las componentes de esfuerzo $\sigma_x, \sigma_y $ y $\tau_{xy}$ asociadas con un elemento infinitesimal; por otra parte, se muestran las componentes de esfuerzo $\sigma_x', \sigma_y' $ y $\tau_{x'y'}$ luego de girar el plano $xy$ un ángulo $\theta$ con respecto al eje $z$ (elemento inferior del objeto interactivo).
Supongamos que $\Delta A$ corresponde al área de la cara oblicua, por lo tanto las áreas de las caras vertical y horizontal son iguales a $\Delta A cos \theta$ y $\Delta A sen \theta$, respectivamente (figura 6.4).
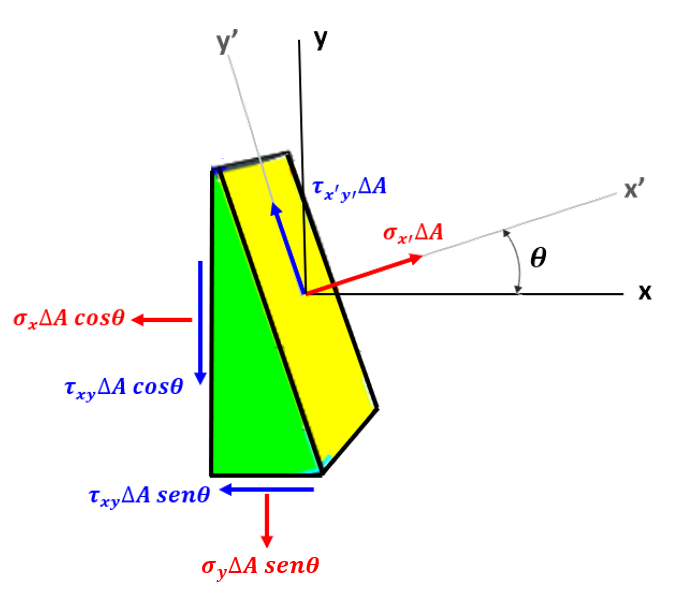
Usemos, ahora, las ecuaciones de equilibrio sobre los ejes $x'$ y $y'$:
$$\sum F_{x'} = 0$$ $$\sigma_{x'} \Delta A - \sigma_x(\Delta A cos \theta)cos \theta - \tau_{xy}(\Delta A cos\theta) sen\theta\\ -\sigma_y(\Delta A sen\theta)sen\theta - \tau_{xy}(\Delta A sen\theta)cos \theta = 0$$ $$\sum F_{y'} = 0$$ $$\tau_{x'y'}\Delta A + \sigma_x(\Delta A cos\theta)sen\theta - \tau_{xy}(\Delta A cos\theta)cos\theta\\ -\sigma_y(\Delta A sen\theta)cos\theta + \tau_{xy}(\Delta A sen\theta)sen\theta = 0$$Resolviendo para los esfuerzos en la cara inclinada, obtenemos:
$$\bold{\color{#000000}{\sigma_{x'} = \sigma_x cos^2\theta + \sigma_y sen^2\theta + 2 \tau_{xy} sen\theta cos\theta}}$$ $$\bold{\color{#000000}{\tau_{x'y'} = -(\sigma_x - \sigma_y)sen\theta cos\theta + \tau_{xy}(cos^2 \theta - sen^2 \theta)}}$$Usando las relaciones trigonométricas para ángulo doble, se logra obtener:
$$\bold{\color{#0090d8}{\sigma_{x'} = \frac{\sigma_x + \sigma_y}{2} + \frac{\sigma_x - \sigma_y}{2}cos\;2\theta + \tau_{xy} sen\;2\theta\tag{6.3}}}$$ $$\bold{\color{#0090d8}{\tau_{x'y'} = - \frac{\sigma_x - \sigma_y}{2} sen\;2\theta + \tau_{xy} cos\;2\theta\tag{6.4}}}$$Si en la ecuación 6.3 reemplazamos el ángulo $\theta$ por $\theta + 90\degree$, obtenemos $\sigma_{y'}$:
$$\bold{\color{#0090d8}{\sigma_{y'} = \frac{\sigma_x + \sigma_y}{2} - \frac{\sigma_x - \sigma_y}{2}cos\;2\theta - \tau_{xy} sen\;2\theta\tag{6.5}}}$$Si sumamos las ecuaciones 6.3 y 6.5, se verifica que:
$$\bold{\color{#0090d8}{\sigma_{x'} + \sigma_{y'} = \sigma_{x} + \sigma_{y}\tag{6.6}}}$$Para hallar el plano del esfuerzo normal máximo o mínimo, derivamos la ecuación 6.3 con respecto a $\theta$:
$$\frac{d\sigma_{x'}}{d\theta} = - \frac{\sigma_x - \sigma_y}{2}2sen\;2\theta + 2\tau_{xy}cos\;2\theta = 0$$Por lo tanto:
$$\bold{\color{#0090d8}{tan\;2\theta_p = \frac{2\tau_{xy}}{\sigma_x - \sigma_y}\tag{6.7}}}$$La ecuación 6.7 define dos valores para $2\theta_{p}$ separados a $180\degree$ y dos valores $\theta_{p}$ separados $90\degree$. Los planos que contienen las caras del elemento orientado en cualquiera de estos ángulos, se denominan planos principales de esfuerzo, y los valores correspondientes para $\sigma_{máx}$ y $\sigma_{mín}$ ejercidos sobre estos planos los llamamos esfuerzos principales . Por lo tanto:
$$\bold{\color{#0090d8}{\sigma_{máx, mín} = \frac{\sigma_x + \sigma_y}{2} \pm\sqrt{\Big(\frac{\sigma_x - \sigma_y}{2} \Big)^2 + \tau^2_{xy}}}}\tag{6.8}$$Ahora, derivando la ecuación 6.4 con respecto a $\theta$, obtenemos:
$$\bold{\color{#0090d8}{tan\;2\theta_s = -\frac{\sigma_x - \sigma_y}{2\tau_{xy}}\tag{6.9}}}$$Con un procedimiento similar al usado para la ecuación 6.8, tenemos:
En el objeto interactivo:
$$\bold{\color{#0090d8}{\sigma = \sigma_{prom} = \frac{\sigma_x + \sigma_y}{2}\tag{6.11}}}$$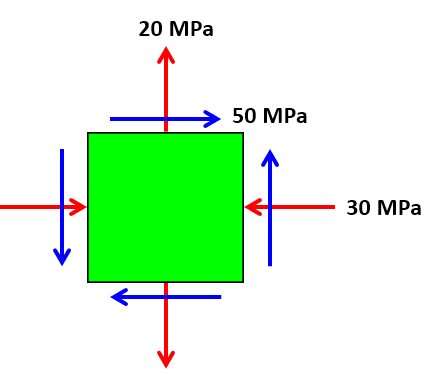
Solución
Planos principales
Se tienen la siguiente información:
$$\sigma_x = -30\;MPa\;\;\;\; \sigma_y = 20\;MPa\;\;\;\; \tau_{xy} = 50\;MPa\;\;\;\;$$Reemplazamos en la Ecuación 6.7:
$$\tan\;2\theta_p = \frac{2\tau_{xy}}{\sigma_x - \sigma_y} = \frac{2(50)}{-30-20} = -2$$ $$\theta_p = 58.3\degree\;\;\;\;\text{y}\;\;\;\;238.3\degree$$Esfuerzos principales
Reemplazando en la ecuación 6.8:
$$\begin{aligned} \sigma_{máx, mín} &= \frac{\sigma_x + \sigma_y}{2} \pm\sqrt{\Big(\frac{\sigma_x - \sigma_y}{2} \Big)^2 + \tau^2_{xy}}\\ &= \frac{-30 + 20}{2} \pm\sqrt{\Big(\frac{-30 - 20}{2}\Big)^2 + (50)^2}\\ &= -5 \pm 55.9 \end{aligned}$$ $$\sigma_{máx} = -60.9\;MPa\text{ a compresión}$$ $$\sigma_{mín} = 50.9\;MPa\text{ a tracción}$$Es importante anotar que para estos esfuerzos normales, $\tau_{x'y'} = 0$.
Esfuerzo cortante máximo
De la ecuación 6.10, obtenemos:
$$\tau_{máx} = \sqrt{\Big(\frac{\sigma_x - \sigma_y}{2}\Big)^2 + \tau^2_{xy}} = \sqrt{(-25)^2 + 50^2} = 55.9\;MPa$$Verifica con la ecuación 6.9 que $\theta_s = 13.3\degree$.
Siguiendo el análisis de Popov
Luego de elevarlas al cuadrado, sumarlas y simplificando, obtenemos:
$$\Big(\sigma_{x'} - \frac{\sigma_x + \sigma_y}{2} \Big)^2 + \tau^2_{x'y'} = \Big(\frac{\sigma_x - \sigma_y}{2}\Big)^2 + \tau^2_{xy}\tag{6.14}$$En situaciones prácticas de transformación de esfuerzos, $\sigma_x$, $\sigma_y$ y $\tau_{xy}$ son datos conocidos, por lo que serían constantes en la ecuación 6.14 y las variables serían $\sigma_x'$ y $\tau_{x'y'}$. Así las cosas, la ecuación 6.14 la podemos escribir así:
$$\big(\sigma_x' - a\big)^2 + \tau^2_{x'y'} = b^2\tag{6.15}$$Siendo $a = (\sigma_x + \sigma_y)/2$ y $b^2 = [(\sigma_x - \sigma_y)/2]^2 + \tau^2_{xy}$.
Ahora, tenemos la ecuación canónica de una circunferencia; no obstante, para que sea un círculo, hemos coloreado el interior de la circunferencia en la figura 6.5. En este círculo, tenemos:
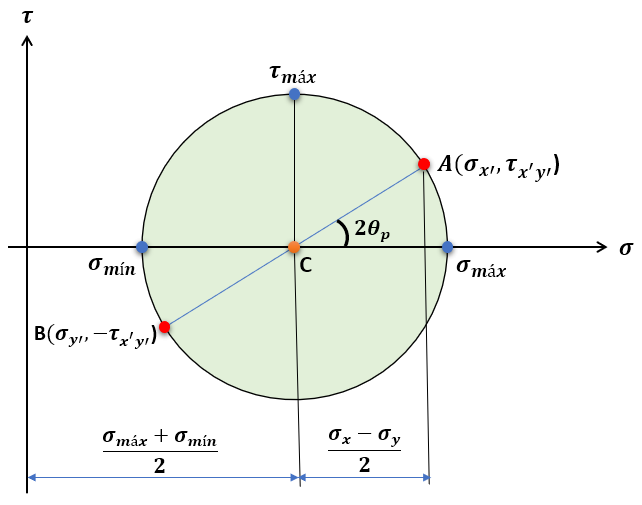
En la figura 6.5, el punto $A$ corresponde a los esfuerzos sobre la cara derecha del elemento, para $\theta = 0\degree$, punto en el cual $\sigma_x = \sigma_x'$ y $\tau_{xy} = \tau_{x'y'}$, situación que permite identificar $\theta_p$ para los planos principales, en tanto que:
$$tan\;2\theta_p = \frac{2\tau_{xy}}{\sigma_x - \sigma_y}$$Observa que el radio del círculo es igual a $\tau_{máx}$
Con la información anterior, resulta sencillo dibujar el círculo de Mohr; para ello, sigue los siguientes pasos:
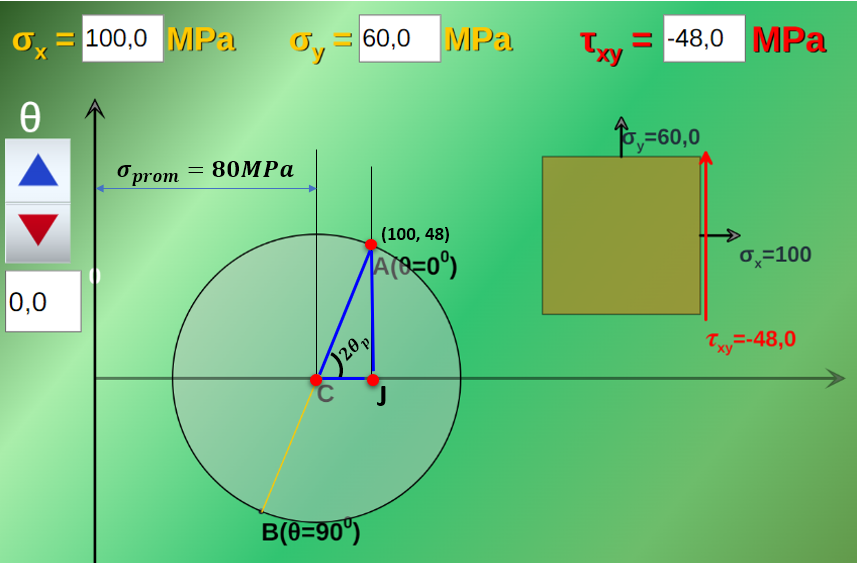
En la siguiente página, presentamos el Círculo de Mohr, el cual lo hemos diseñado con el editor DescartesJS. Haz la siguiente práctica (con clic izquierdo sostenido, puedes desplazar el círculo):
Recuerda que puedes ampliar el objeto interactivo, con clic en el botón superior derecho.
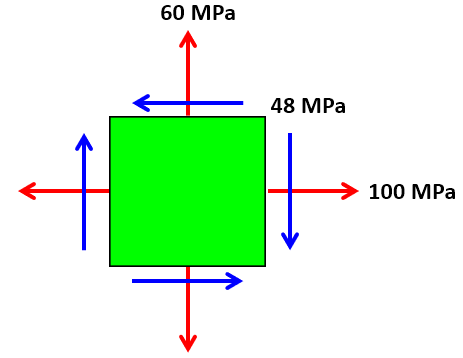
Solución
Tenemos tres alternativas para hallar los esfuerzos principales. La primera de ellas es usar las ecuaciones 6.7 y 6.8; por ejemplo, para $\theta_p$:
$$tan\;2\theta_p = \frac{2\tau_{xy}}{\sigma_x - \sigma_y} = \frac{2(-48)}{100-60} = -2.4\;\;\;\to\;\;\; \theta_p = -33.7\degree$$La segunda alternativa es dibujar el Círculo de Mohr (figura 6.7), en el cual se observa que:
$$tan\;2\theta_p = \frac{48}{100 - 60} = 2.4 \;\;\;\to\;\;\; \theta_p = 33.7\degree$$$\theta_p$ en esta alternativa debe ser negativo, pues va en el sentido de las manecillas del reloj.
En la figura 6.7 se observa que $R = \sqrt{20^2 + 48^2} = 52$, por lo tanto:
$$\sigma_{máx} = 80 + 52 = 132\;Mpa$$ $$\sigma_{mín} = 80 - 52 = 28\;Mpa$$Que puedes comprobar con la ecuación 6.8.
La tercera alternativa es usar el Círculo de Mohr Interactivo, tal como se muestra en esta animación: "haz clic aquí".
Finalmente, realiza los siguientes ejercicios propuestos, cuyos resultados puedes verificar con cualquiera de las tres alternativas.