3. $L_o = 15 \;pulg\\ L= \pi(5\;pulg)\\ \epsilon = \frac{L-L_o}{L_o} = \frac{5\pi-15}{15} = 0.0472\;pulg/pulg$
5. $\epsilon = \frac{\delta}{L} = \frac{L_f - Lo}{Lo} = \frac{1.011L_o - L_o}{L_o} = 0.011$
$\epsilon = \frac{P}{AE} = \frac{4P}{\pi d^2 E} \rarr d = \sqrt{\frac{4P}{\epsilon \pi E}}$
Reemplazando: d = 0.546 mm y $\sigma =\frac{P}{A} = \frac{4P}{\pi d^2}$ = 36.3 MPa.
7.
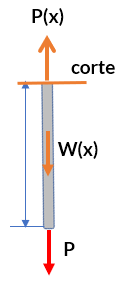
En el corte, indicado en la figura: $\gamma = \frac{W}{V} = \frac{W}{Ax} \rarr W = \gamma Ax$
Por sumatoria de fuerzas en $y$: $P(x) = P + \gamma Ax$
Por lo tanto:
$$\delta = \int_0^L \frac{(P + \gamma Ax)}{AE}dx = \frac{PL}{AE} + \frac{\gamma L^2}{2E}$$
9. Usando la expresión $\delta = \frac{P}{E}\bigg(\frac{L_1}{A_1} + \frac{L_2}{A_2} \bigg)$, se puede hallar $d$, cuyo resultado sería $d = 0.868\;pulg$
11. a) 0.0358 mm, b) -0.00258, c) -0.000344 mm, d) -0.00825 $mm^2$
13. $\sigma_{máx}$ = 190 MPa
15. P = 1.21 kip