CÁLCULO DIFERENCIAL E INTEGRAL
Modulo II
INTERACTIVO

Carlos Alberto Rojas Hincapié
Red Educativa Digital Descartes, Colombia
1ª edición – 2022
Medellín
Colombia
Título de la obra:
CÁLCULO DIFERENCIAL E INTEGRAL
Módulo II
Autor:
Carlos Alberto Rojas Hincapié.
1ª edición – 2022
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Red Educativa Digital Descartes
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN Obra completa: 978-84-18834-30-1
ISBN Módulo II: 978-84-18834-33-2
LICENCIA
Tabla de contenido
Prefacio
Este libro digital interactivo se ha diseñado con fundamento en la filosofía del Proyecto DescartesJS: "Trabajando altruistamente por la comunidad educativa de la aldea global", que sólo busca desarrollar contenidos educativos para el provecho de la comunidad académica, esperando únicamente como retribución el uso y difusión de estos contenidos. El contenido del libro, al igual que los objetos interactivos se han diseñado de tal forma que se puedan leer en ordenadores y dispositivos móviles sin necesidad de instalar ningún programa o plugin. El libro se puede descargar para su uso en local sin dependencia con la red, a excepción de algunos vídeos incluidos en el texto. Todos los objetos interactivos se han diseñado con el Editor DescartesJS.
Véase https://proyectodescartes.org/iCartesiLibri/descripcion.htm.
El libro se ha elaborado con fundamento en el currículo de la asignatura "Cálculo Integral" de la Institución Universitaria, pero ampliándolo con algunas secciones y bloques adicionales con objeto de poder cubrir las necesidades de cualquier otra Institución que incluya en su desarrollo curricular esta materia.
Antiderivada
Concepto de antiderivada
La antiderivada es la función que resulta del proceso inverso de la derivación, es decir, consiste en encontrar una función que, al ser derivada produce la función dada.
Una función $F$ recibe el nombre de antiderivada de $f$ sobre un intervalo $[a, b]$, para todo $x$ que pertenece a un intervalo $[a, b]$.
$$F'(x)=f(x) \space para \space todo \space x \space en \space I$$
Así, decimos que $F(x)$ es una primitiva de la función $f(x)$ si su derivada es precisamente la función $f(x)$.
Cualquier antiderivada de $f$ debe ser de la forma $G(x)= F(x) + C$, es decir, dos antiderivadas de la misma función pueden diferir a lo más en una constante. Por tanto, $F(x) + C$ es la antiderivada más general de $f(x)$.
Integral indefinida
Notación de la integral indefinida, por conveniencia, se introducirá la notación para una antiderivada de una función. Si $F(x)=f(x)$,la antiderivada más general de $f$ se representa por: $$\int f(x)\, dx = F(x) + C$$
El símbolo $\int$ fue introducido por Leibniz y se denomina signo integral. La notación $\int f(x)\, dx$ se denomina integral indefinida de $f(x)$ respecto a $x$. La función $f(x)$ se denomina integrando.
El proceso de encontrar una antiderivada se denomina antidiferenciación o integración. El número $C$ se denomina constante de integración.
La notación $F(x) + C$ representa una familia de funciones; cada miembro tiene una derivada igual a $f(x)$.
por ejemplo, la antiderivada más general de $f(x)=2x$ es la familia $F(x)=x^2 + C$, la gráfica de la antiderivada
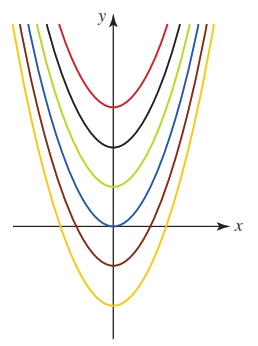
Siempre que se obtiene la derivada de una función, al mismo tiempo se obtiene una fórmula de integración. Por ejemplo,
| (1). $\displaystyle\frac{d}{dx} x=1$ | $\displaystyle\int \, dx = x + C$ |
| (2). $\displaystyle\frac{d}{dx} \frac{x^{n+1}}{n+1} = x^n$ | $\displaystyle \int x^n\, dx = \frac{x^{n+1}}{n+1} + C$ |
| (3). $\displaystyle\frac{d}{dx} Ln(x) = \frac{1}{x}$ | $\displaystyle\int \frac{1}{x}\, dx = Ln(x) + C$ |
Propiedades de la integral indefinida
- $\int kf(x)\, dx = kF(x) + C$, donde $k$ es cualquier constante.
- $\int [f(x)\pm g(x)] \, dx = \int f(x) \, dx \pm \int g(x) \, dx$,
donde las constantes $C_1 \pm C_2$ se sustituye por una simple $C$.
 Ejercicio. Integral Indefinida.
Ejercicio. Integral Indefinida.
Utiliza las formulas y propiedades para calcular la integral indefinida propuesta en el interactivo.
Escena de Juan Guillermo Rivera Berrío, grupo de investigación Gnomon.
Realiza primero los cálculos y verifica el resultado obtenido oprimiendo el botón solución. Por ultimo, oprime el botón otro ejercicio y repite los pasos anteriores.
 Ejercicio. Integral Indefinida.
Ejercicio. Integral Indefinida.
Utiliza las formulas y propiedades para calcular las integrales.
Escena de Juan Guillermo Rivera Berrío y Consolación Ruiz Gil.
Realiza primero los cálculos y verifica el resultado obtenido oprimiendo el botón solución. Por ultimo, oprime el botón otro ejercicio y repite los pasos anteriores.
Observar las gráficas de una función y sus integrales, ademas, de las gráficas de su familia de primitivas.
 Descarga:
Tabla de Integrales.
Descarga:
Tabla de Integrales.
Tomado de: Cálculo Transcendentes Tempranas. D. Zill 4ed.
Introducción a la Integral definida
El problema de área
Así como la derivada es motivada por el problema geométrico de construir una tangente a una curva, el problema histórico que conduce a la definición de integral definida es el problema de encontrar un área.
Históricamente, el cálculo integral surgió de la necesidad de resolver el problema de la obtención de áreas de figuras planas. Los griegos lo abordaron, llegando a fórmulas para el área de polígonos, círculos, segmentos de parábolas, etc.
El método que emplearon consistía en aproximar exhaustivamente la figura cuya área se deseaba calcular mediante polígonos de áreas conocidas.
Mueve el control N y observa:
Aproximación del área por medio de N polígonos. Adaptación de una escena de José Luis Abreu con licencia CC by-nc-sa
Veamos algo análogo, pero utilizando rectángulos que es como actualmente se plantea a nivel teórico, Mueve los controles N, desplaza y zum, y la observa escena:
Aproximación del área por medio de N rectángulos. Adaptación de una escena de José Luis Abreu con licencia CC by-nc-sa
Este procedimiento original de Eudoxo (406 a.C. - 355 a.C.) fue utilizado esporádicamente por Euclides (hacia 300 a.C.) y de forma sistemática por Arquímedes (286 a.C. - 212 a.C.) Hacia el siglo XVI de nuestra era, este método pasó a llamarse método de exhaución o método exhaustivo.

Basándose en ese método, los matemáticos del siglo XVII (Newton, Leibniz, etc.) introdujeron el concepto más general de integral definida de una función, $f$, en un intervalo. Este concepto fue posteriormente mejorado por Cauchy (1789-1857) y por Riemann (1826 - 1866).

A continuación y mediante un ejemplo mostraremos en qué consiste el método de exhaución. Aplicando la misma idea introduciremos de forma intuitiva el concepto de integral definida de una función.
El objetivo inicial será calcular el área del recinto plano limitado por el eje de abscisas, la gráfica de la función $f(x)$ y las rectas $x = a$ y $x = b$, siendo $a$ y $b$ números reales cualquiera. Queremos hallar el área de la región coloreada en la figura de la izquierda.
Arquímedes en su método de exhaución hacía lo siguiente: Para cada número natural n dividía el segmento $[a,b]$ en n partes iguales de longitud $\frac{b-a}{n}$. Sobre cada una de esas partes construía un rectángulo con la altura de la ordenada máxima (rectángulo superior o circunscrito).
 Ejercicio. Introducción a la integral definida. Escena de Juan Guillermo Rivera Berrío y Consolación Ruiz Gil.
Ejercicio. Introducción a la integral definida. Escena de Juan Guillermo Rivera Berrío y Consolación Ruiz Gil.
Calcular el área de la región sombreada en la figura.
Para iniciar, primero oprime el botón continuar.
Haz clic en el botón rectángulos superiores y realiza las actividades propuestas.
Puedes mover la gráfica con clic izquierdo o, si lo deseas, puedes ampliarla o reducirla con clic derecho sostenido.
Cambia la función y realiza de nuevo las actividades propuestas con sus respectivos análisis.
Antes de continuar con la solución del problema de área es necesario hacer una breve digresión para analizar una notación útil para una suma de números como: $$1 + 2 + 3+ 4 + 5 + 6 + ... + n$$
Notación sigma
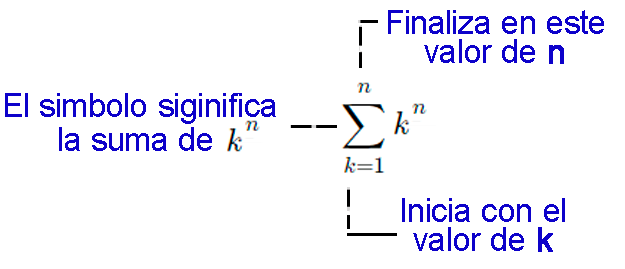
A menudo se usa la notación sigma para escribir de manera más compacta las sumas de muchos términos. Por ejemplo, $$\sum_{k=1}^n k^2 = 1^2 + 2^2 + 3^2 + 4^2 + ... + n^2$$
Fórmulas de sumas especiales, particularmente sumas que implican potencias de enteros positivos del índice de la suma. Para $n$ un entero positivo y $c$ cualquier constante,
| i). $\displaystyle \sum_{k=1}^n c = n\cdot c$ | ii). $\displaystyle \sum_{k=1}^n k = \frac{n(n+1)}{2}$ |
| iii). $\displaystyle \sum_{k=1}^n k^2 = \frac{n(n+1)(2n+1)}{6} \qquad$ | iv). $\displaystyle \sum_{k=1}^n k^3 = \frac{n^2(n+1)^2}{4}$ |
 Ejercicio. Sumatorias.
Ejercicio. Sumatorias.
Calcular el valor numérico de cada sumatoria. Escena de Juan Guillermo Rivera Berrío.
Realiza primero los cálculos y escribe el resultado obtenido, para verificar pulsa la tecla "enter <┘".
Por ultimo, oprime el botón Otro ejercicio y repite los pasos anteriores.
La notación sigma y las fórmulas de sumas anteriores se usarán de inmediato en el siguiente análisis.
Suma de Riemann
¿Qué son las sumas de Riemann?
Una suma de Riemann es una aproximación del área bajo la curva, al dividirla en varias formas simples (tales como rectángulos o trapecios).
Mueve el control N y observa la aproximación del área por medio de N rectángulos. Adaptación de una escena de José Luis Abreu con licencia CC by-nc-sa
Sea $y = f(x)$ una función definida sobre un intervalo cerrado $[a,b]$, donde:
- Se divide el intervalo $[a,b]$ en $n$ subintervalos $[x_{k-1}, x_k]$ de anchos $\triangle x_k = x_k - x_{k-1}$ donde: $$ a = x_0 < x_1 < x_2 < ... < x_{n-1} < x_k = b$$
- Se escoje un número $x_i$ en cada subintervalo $[x_{k-1}, x_k]$ que se denominan puntos muestra, estos $n$ números.
A menudo se usa la notación sigma para escribir de manera más compacta las sumas de muchos términos, por tanto, de lo anterior se forma la suma: $$\sum_{k=1}^n f(x_i). \triangle x_k$$
Sumas que corresponden a varias particiones de $[a, b ]$ que se denominan sumas de Riemann en honor del famoso matemático alemán Georg Friedrich Bernhard Riemann.
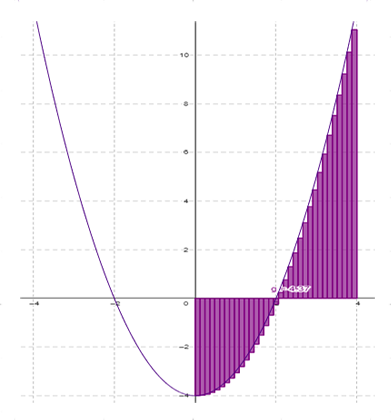 La suma representa el área total de los rectángulos y el resultado de esta suma se aproxima numéricamente al área bajo la curva $f$.
La suma representa el área total de los rectángulos y el resultado de esta suma se aproxima numéricamente al área bajo la curva $f$.
Desde luego, la aproximación al área bajo la curva mejora muchísimo en la medida que el número $n$ de particiones sea mayor. De esta manera la suma converge al área bajo la curva, cuando el número $n$ de particiones tiende a infinito.
la gráfica nos muestra la aproximación del área bajo la curva $f$, entre las abscisas $x=-2$ y $x=4$.
 Refuerza lo aprendido.
Refuerza lo aprendido.
Aplicación de la suma de Riemman.
Analiza los siguientes ejercicios resueltos y practica.
 Ejercicio. Sumatorias.
Ejercicio. Sumatorias.
Calcular el valor numérico de cada sumatoria según el gráfico dado. Escena de Juan Guillermo Rivera Berrío.
Primero, observa que el área buscada es la de un trapecio. Según los datos dados ¿Cuál es valor del ancho de cada rectángulo ($\triangle x_k$)?
Escribe el valor y pulsa la tecla "enter <┘".
Oprime el botón otro ejercicio para practicar con otras funciones, donde podrás modificar el valor de n y de a.
Puedes mover la gráfica con clic izquierdo o, si lo deseas, puedes ampliarla o reducirla con clic derecho sostenido.
De tal manera la siguiente definición indica que la integral definida de una función integrable puede aproximarse dentro de cualquier grado de exactitud mediante la suma de Riemann.
Definición.Definición tomada de: Cálculo de una variable. Conceptos y contextos. J. Stewart 4Ed.
Si $f$ es una función continua definida para $a \le x \le b$, dividimos el intervalo $[a, b]$ en $n$ subintervalos, con $\triangle x$ igual ancho
Sean $a=x_0, x_1, x_2, . . . , x_n=b$ los puntos extremos de estos subintervalos y sean $x^*_1, x^*_2, . . . , x^*_n$ los puntos muestra en estos subintervalos, de modo que $x^*_i$
se encuentre en el i-ésimo subintervalo $[x_{i-1}, x_i]$, Entonces la integral definida de $f$, desde $a$ hasta $b$, es
$$ \int_{a}^{b} f(x)\, dx = \lim_{n \to{}\infty}{\sum_{i=1}^n f(x_i). \triangle x}$$
donde, $\displaystyle\qquad \triangle x = \frac{b-a}{n}\qquad$ y $\displaystyle\qquad x_i = a + i.\triangle x $
El área como integral definida
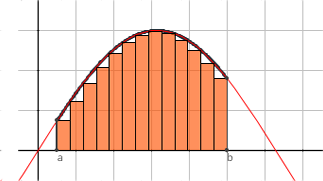 Aplicación de la integral definida, el área bajo una curva acotada por rectas verticales y el eje de abscisas.
Aplicación de la integral definida, el área bajo una curva acotada por rectas verticales y el eje de abscisas.
Aproximación del área bajo la curva $f$, entre las abscisas $x=a$ y $x=b$.
 Exploración. Aproximaciones del área. Escena de Juan Guillermo Rivera Berrío.
Exploración. Aproximaciones del área. Escena de Juan Guillermo Rivera Berrío.
Aproximación del área de la región, observa el gráfico, haz clic en el botón rectangulos interiores y en los botones de conclusión.
¿Que conclusiones podemos obtener?
Teorema.
Si $f$ es una función continua sobre el intervalo cerrado $[a, b ]$ y $f(x) \ge 0$ para toda $x$ en el intervalo, entonces el área A bajo la gráfica sobre $[a, b ]$ es
$$ A = \int_{a}^{b} f(x)\, dx $$
Aproximemos el área de la región de una fígura dada. Escena de Juan Guillermo Rivera Berrío.
¿Que conclusiones podemos obtener? Identifica la gráfica de la función y observa la integral del área bajo la curva, ingresa una nueva función y pulsa la tecla "enter <┘".
Teorema fundamental del cálculo.
Si $f$ es una función continua sobre el intervalo $[a, b ]$ y $F$ es una antiderivada de $f$ sobre el intervalo, entonces
$$ \int_{a}^{b} f(x)\, dx = F(b) - F(a)$$
Definición.Definición tomada de: Cálculo: Transcendentes tempranas. D. Zill. 4Ed.
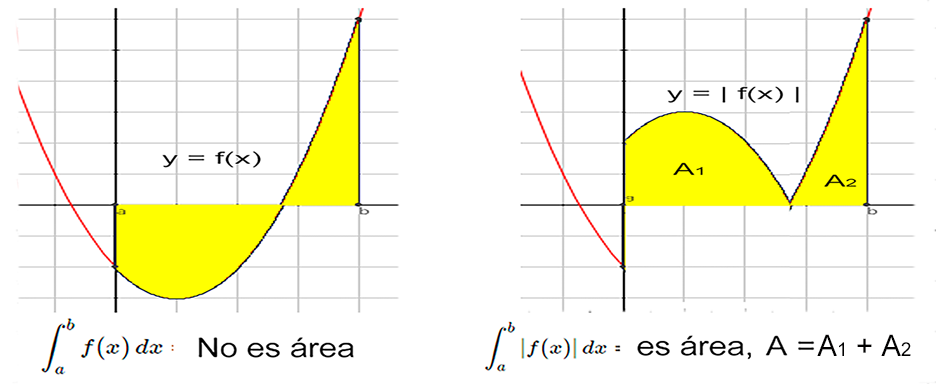
Si $y = f(x)$ es continua sobre $[a, b]$, entonces el área total A acotada por su gráfica y el eje $x$ sobre el intervalo está dada por
$$ \int_{a}^{b} |f(x)|\, dx $$
La definición anterior se puede proceder así, usando la propiedad aditiva del intervalo de la integral definida:
$$\begin{aligned} \int_{a}^{b} |f(x)|\, dx &= \int_{a}^{c} |f(x)|\, dx + \int_{c}^{b} |f(x)|\, dx \\ &= A_1 + A_2 \end{aligned}$$
Si $f$ es una función que asume valores tanto positivos como negativos sobre $[a, b]$, entonces la integral definida $ \int_{a}^{b} f(x)\, dx$ no representa el área bajo la gráfica
de $f$ sobre el intervalo.
 Ejercicio. Aplicación de la integral definida.
Ejercicio. Aplicación de la integral definida.
Cálcula el área de la región dada utilizando la integral definida. Escena de Juan Guillermo Rivera Berrío.
Ingresa el valor obtenido, oprime el botón solución y verificar tu respuesta. Si tu respuesta es correcta, oprime el botón otro ejercicio y repite los pasos anteriores.
 GeoGebra. Utiliza el software para graficar y verificar.
GeoGebra. Utiliza el software para graficar y verificar.
Clic Aqui.
Grafique otras funciones.
Para utilizar el software de GeoGebra, escriba la expresión a graficar en la barra de entrada, por ejemplo $\quad y=x^2 + 4$ se escribe:
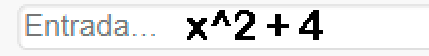
 Ejercicio. Área bajo la curva.
Ejercicio. Área bajo la curva.
Calcular el área bajo la gráfica de la función dada. Escena diseñada por Juan Guillermo Rivera Berrío. CC by-nc-sa
Ingresa el resultado obtenido y pulsa la tecla "enter <┘" para verificar la respuesta.
 ¡Recuerda!
¡Recuerda!
Utilizar propiedad aditiva en las integrales para valores negativos de $f(x)$.
La integral definida $\displaystyle \int_{a}^{b} f(x)\, dx$ no siempre representa el área bajo la gráfica de $f$ sobre el intervalo $[a, b]$. Comprueba aqui
El área de una región entre curvas
Identifica las funciones $f$ y $g$, observa como encontrar las intersecciones entre las curvas y verifica los resultados dados haciendo clic en el botón verificar. Escena diseñada por Juan Guillermo Rivera Berrío. CC by-nc-sa
Continua con la explicación, oprime el botón continuar hasta encontrar la expresión que calcula el área entre las curvas, por ultimo, observa el resultado. Ten presente la indicación dada oprimiendo el botón ¡Alerta!
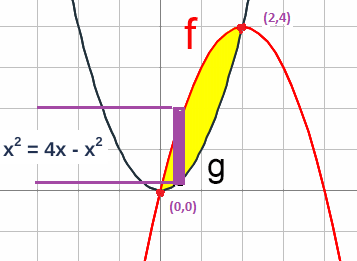
En lo visto hasta ahora, definimos y calculamos áreas de regiones que están bajo las gráficas de funciones, ahora usaremos integrales para calcular las áreas de regiones que quedan entre las gráficas de
dos funciones $f$ y $g$.
Definición.Definición tomada de: Cálculo: Transcendentes tempranas. D. Zill. 4Ed.
Si $f$ y $g$ son funciones continuas sobre un intervalo $[a, b]$, entonces el área A de la región acotada por sus gráficas sobre el intervalo está dada por
$$ A = \int_{a}^{b} ( f(x) - g(x) ) \, dx $$
 Exploración. Área entre curvas.
Exploración. Área entre curvas.
Observa la región comprendida entre las dos curvas.
Escena diseñada por Juan Guillermo Rivera Berrío. CC by-nc-sa
Mueve los controles a y b para Modificar la región comprendida entre las dos curvas. Oprime el botón otro ejemplo para ver más ejemplos.
En ocasiones es difícil, o hasta imposible, determinar los puntos donde se cortan exactamente las dos curvas.
 GeoGebra. Utiliza el software para graficar y verificar.
GeoGebra. Utiliza el software para graficar y verificar.
Clic Aqui.
Grafique otras funciones.
Como se muestra en los ejemplos anteriores, con la ayuda de una calculadora para graficar o de una computadora, podemos encontrar valores aproximados de los puntos de intersección, y luego proceder como antes.
En ocasiones la necesidad de hallar el área se facilita utilizando la construcción de utilizar rectangulos horizontales.
Algunas regiones se manejan mejor si se considera a $x$ como una función de $y$. Si una región está acotada con curvas de ecuaciones $x = f (y)$, $x =g(y)$, $y = c$ y $y = d$, donde $f$ y
$g$ son continuas y $f ( y) \ge g(y)$ para $c \le y \le d$, entonces su área es
$$ A = \int_{c}^{d} ( f(y) - g(y) ) \, dy $$

Área del elemento horizontal: $$\quad A = [gráfica \space derecha - gráfica \space izquierda] \cdot ancho $$
Ejemplos.
Cálculo de área encerrada por dos funciones. Escena de Consolación Gil Ruiz, adaptada por el autor.
Analiza la solución del área comprendida por las funciones $f(x)$ y $g(x)$ y delimitadas por las rectas $x=a$ y $x=b$
Para ver direfentes funciones, oprime el botón otros valores y observa la gráfica que forman las funciones y las rectas que delimitan, oprime el botón ver gráfica.
 Ejercicio 1. Área entre curvas.
Ejercicio 1. Área entre curvas.
Aplicación de la integral definida. Escena diseñada por Juan Guillermo Rivera Berrío. CC by-nc-sa
Cálcula el área de la región dada utilizando la integral definida.
Ingresa el valor obtenido del área de la región sombreada, pulsa la tecla "enter <┘"y verificar tu respuesta. Si tu respuesta es correcta, oprime el botón otro ejercicio.
 ¡Recuerda!
¡Recuerda!
El área acotada por las curvas esta dada por:
 Ejercicio 2. Área entre curvas.
Ejercicio 2. Área entre curvas.
Hallar el área encerrada por dos funciones. Escena de Consolación Gil Ruiz, adaptada por el autor.
Observa la región sombreada formada por las dos funciones, determina los límites de integración para encontar el área de la región.
Resuelve el ejercicio propuesto y luego verificar tus resultados, oprimiendo el botón solución.
Para realizar otro ejercicio, oprime el botón ejercicio.
 Practica lo aprendido.
Practica lo aprendido.
Ejercicio 1. Seleccione falso o verdadero. Escena de Consolación Gil Ruiz. CC by-nc-sa
Lee el enunciado y despliege el control de selección e indique si el enunciado es falso o verdadero y oprime el botón verificar al finalizar.
Ejercicio 2. Selección múltiple con única respuesta..
Responda las preguntas a continuación, seleccione la respuesta correcta, con ayuda del interactivo, ingresa la función dada, sus límites de integración y observe la región generada.
Volumen de un cuerpo de revolución
Cuando tratamos de calcular el volumen de un sólido, enfrentamos el mismo tipo de problema que al determinar áreas. Intuitivamente sabemos lo que significa un volumen, pero es necesario precisar la idea usando el cálculo, a fin de dar una definición exacta de volumen.
Rotamos las siguientes figuras, o lo que es lo mismo, rotar una función $f(x)$ en un intervalo y giramos su gráfica alrededor del eje de abscisas, generándose una superficie de revolución. Escenas (pag. 40,41) de Juan Guillermo Rivera Berrío.
Superficie de revolución
Las superficies de revolución son figuras que se forman al girar 360° una línea recta o una curva contenida en un plano, llamada generatriz, alrededor de un eje de rotación, contenido también en el mismo plano.
Sólidos de revolución o cuerpos de revolución
Los sólidos de revolución son figuras que se forman al girar 360° una región de un plano alrededor de una recta, o eje de rotación, contenido también en el mismo plano.
Volumen de revolución de un cuerpo sólido
 Exploración. Solidos de revolución.
Exploración. Solidos de revolución.
Volumen de revolución de un cuerpo sólido. Escena de Juan Guillermo Rivera Berrío.
¡Usa los controles para observar cómo se genera el volumen!
Un volumen de revolución se genera cuando una sección rota alrededor de un eje, para este caso la región de color amarillo la rotaremos alrededor del eje x.
El la siguiente escena interactiva, sigue los pasos y observa la región formada por el solido de revolución.
 Exploración. Solidos de revolución.
Exploración. Solidos de revolución.
Región formada por el solido de revolución. Escena de Juan Guillermo Rivera Berrío.
Observa la región formada por el solido de revolución.
Oprime el botón Paso 1 y sigue las indicaciones dadas en cada paso.
Puedes girar la gráfica con clic izquierdo o, si lo deseas, puedes ampliarla o reducirla con clic derecho sostenido.
Si una región $R$ en el plano $xy$ se hace girar alrededor de un eje $L$, se genera un sólido denominado sólido de revolución.
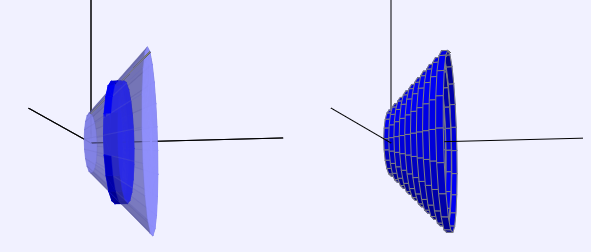
El volumen de este solido es $A (xi) \triangle x$, de modo que una aproximación a la concepción intuitiva del volumen de la i-ésima rebanada $S_i$ es: $$V(S_i) \approx A(xi) \triangle x$$
Al sumar los volúmenes de estas rebanadas, obtenemos un valor aproximado del volumen total (es decir, a lo que pensamos intuitivamente que es un volumen). Esta aproximación parece ser cada vez mejor cuando $n \to \infty $.
Definición.Definición tomada de: Cálculo de una variable. Conceptos y contextos. J. Stewart 4Ed.
Sea $S$ un sólido que está entre $x= a$ y $x= b$. Si el área de la sección transversal de $S$ en el plano $P_x$, a través de $x$ y perpendicular al eje $x$, es $A(x)$,
donde $A$ es una función continua, entonces el volumen de $S$ es
$$ V= \int_{a}^{b} A(x)\, dx = \lim_{n \to{}\infty}{\sum_{i=1}^n A(x_i). \triangle x}$$
Método del disco
Como se acaba de analizarse, el volumen $V$ de un sólido puede encontrarse por medio de una integral definida siempre que se conoce una función $A(x)$
que proporciona el área de una sección transversal formada al hacer pasar un plano por el sólido de forma perpendicular a un eje. En el caso de encontrar el volumen de un sólido de revolución,
siempre es posible encontrar A(x); el eje en cuestión es el eje de revolución $L$.
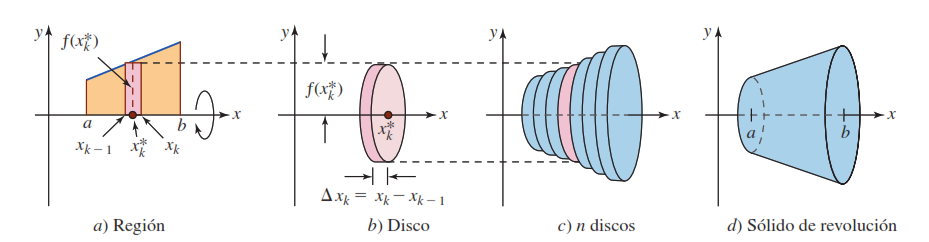
Cuando el elemento rectangular rojo en $a)$ gira alrededor del eje $x$ se genera el disco circular rojo en $b)$, donde es área de es disco circular es: $$ A(x) = \pi f(x)^2$$ por tanto, $$ V= \int_{a}^{b} A(x)\, dx = \int_{a}^{b} \pi f(x)^2\, dx = \pi \int_{a}^{b} f(x)^2\, dx$$
 Ejercicio 1. Área bajo la curva.
Ejercicio 1. Área bajo la curva.
Integral definida - Cálculo del área bajo la curva. Cálculo Integral, Proyecto Pi. Edición grupo de Investigación Gnomon. Instituto Tecnologico Metropolitano (ITM), Colombia, Medellín.
Cálcula el área bajo la curva.
Ingrese la función y pulsa la tecla "enter <┘"y observa los resultados.
 Ejercicio 2. Volumen de un solido de revolución.
Ejercicio 2. Volumen de un solido de revolución.
Integral definida - Cálculo del volúmen de un sólido. Cálculo Integral, Proyecto Pi. Edición grupo de Investigación Gnomon. Instituto Tecnologico Metropolitano (ITM), Colombia, Medellín.
Cálcula el volúmen del solido de revolución. Ingrese la función y pulsa la tecla "enter <┘"y observa los resultados.
Aplicaciones de la integral definida. Practica con varias funciones para calcular el área bajo la curva y el volumen de revolución.
Volumen de revolución de sección hueca
 Exploración. Sólido de revolución. Escena de Juan Guillermo Rivera Berrío.
Exploración. Sólido de revolución. Escena de Juan Guillermo Rivera Berrío.
Un volumen de revolución se genera cuando una sección rota alrededor de un eje, para este caso la región de color amarillo la rotaremos alrededor del eje x.
¡Usa los controles para observar cómo se genera el volumen!
Para rotar el solido formado, oprime en el mouse clic izquierdo sostentido y arrastra, o para cambiar la escala, oprime en el mouse clic derecho sostentido y arrastra, sobre el sólido.
 Exploración. Sólido de revolución.
Exploración. Sólido de revolución.
Observa la región formada por el solido de revolución.
Escena de Juan Guillermo Rivera Berrío.
Oprime el botón Paso 1 y sigue las indicaciones dadas en cada paso.
Puedes girar la gráfica con clic izquierdo o, si lo deseas, puedes ampliarla o reducirla con clic derecho sostenido.
Para rotar el solido formado, oprime en el mouse clic izquierdo sostentido y arrastra, o para cambiar la escala, oprime en el mouse clic derecho sostentido y arrastra, sobre el sólido.
Método de la arandela
Sea $R$ la región acotada por las gráficas de las funciones continuas $y = f (x)$, $y = g(x)$ y las rectas $x = a$ y $x = b$, que se hace girar alrededor del eje $x$.
Entonces una rebanada perpendicular al eje $x$ del sólido de revolución en $x_i$ es una circular o anillo anular. Cuando el elemento rectangular de ancho $\triangle x$
gira alrededor del eje $x$, genera una arandela. El área del anillo es
$$A (x_i) = área \space del \space círculo \space - \space área \space del \space orificio$$
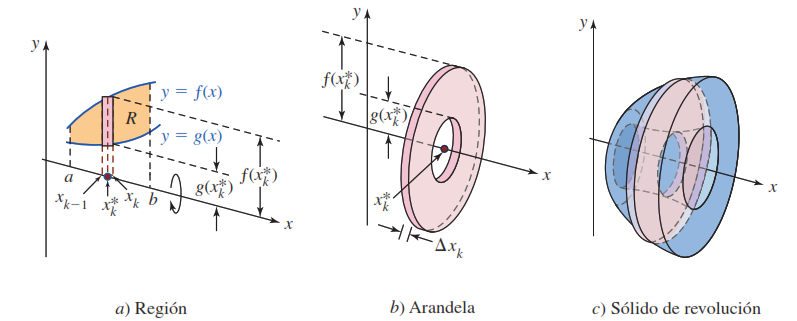
Cuando el elemento rectangular rojo $a)$ gira alrededor del eje $x$ se genera la arandela circular roja $b)$, entonces el volumen del sólido es $$ V= \int_{a}^{b} (A_1(x)-A_2(x))\, dx = \int_{a}^{b} \pi (f(x)^2 - g(x)^2) \, dx $$
 Ejercicio. Integral definida.
Ejercicio. Integral definida.
Cálculo del volúmen de un sólido formado por dos funciones. Escena de Juan Guillermo Rivera Berrío.
Ingresa el valor obtenido, pulsa la tecla "enter <┘"y verificar tu respuesta, si tu respuesta es correcta, oprime el botón otro ejercicio.
 Refuerza lo aprendido.
Refuerza lo aprendido.
Aplicación del área bajo la curva y el volumen de un solido de revolución. Analiza los siguientes ejercicios resueltos y practica.
Técnicas de Integración
Integración directa
Se utiliza haciendo uso de recursos algebraicos, propiedades y de las formulas que se encuentran el la tabla de integrales de formas básicas y que fueron trabajadas a principio del texto.

![]() En la parte superior derecha de este texto encontramos una TablaTomada de: Cálculo: Transcendentes Tempranas. D. Zill. 4Ed. más ampliada de fórmulas de integración.
En la parte superior derecha de este texto encontramos una TablaTomada de: Cálculo: Transcendentes Tempranas. D. Zill. 4Ed. más ampliada de fórmulas de integración.
Ejemplo. Evaluar $\displaystyle \int \frac{x-2}{\sqrt[3]{x}}\, dx$ $$\begin{aligned} \int (x-2)x^{-1/3}\, dx &= \int x^{2/3} \, dx - 2 \int x^{-1/3}\, dx \\ &= \frac {x^{\frac {5}{3}}}{\frac {5}{3}} - 2 \thinspace \frac {x^{\frac {2}{3}}}{\frac {2}{3}} + C \\ &= \frac {3 \thinspace \sqrt[3]{x^5}}{5} - 3 \thinspace \sqrt[3]{x^2} + C \end{aligned}$$
 Ejercicio. Integral indefinida - Directas.
Ejercicio. Integral indefinida - Directas.
Resuelve integrales de forma directa y observa su solución.
Escena de Consolación Gil Ruiz. CC by-nc-sa
 ¡Recuerda!
¡Recuerda!
La antiderivada o integral indefinida se representa por:
Integración por sustitución.
Integración por sustitución o cambio de variable.
Cuando se presentan funciones compuestas, en las que ya no es posible una integración directa, puede ser que con un cambio de variable se transformen en integrales inmediatas.
A menudo se encuentra una integral que no puede clasificarse en una forma conocida como la de la tabla de integrales o integrales que pueden llamarse inmediatas.
Por ejemplo, no es posible evaluar mediante la aplicación inmediata de cualquiera de las fórmulas de la tabla anterior la integral $$ \int x^5 (x^6 -3)^8 \, dx$$
No obstante, al aplicar una técnica de integración algunas veces es posible reducir una integral como ésta a una forma conocida.
En muchas ocasiones, cuando la integración directa no es tan obvia, es posible resolver la integral simplemente con hacer un cambio de variable adecuado. Este procedimiento se conoce como integración por sustitución.
En este caso las formulas de integrales se las puede observar no solo se utilizan en terminos $x$ sino para otra variable.
Regla de sustitución. Si $u=g(x)$ es una función derivable cuyo rango es un intervalo $I$ y $f$ es continua sobre $I$, entonces $$ \int f(g(x)).g'(x) \, dx = \int f(u) \, du$$
Procedimiento sugerido.
- Seleccione una sustitución $u = g(x)$.
- Hallar $du = g' (x) dx$ por tanto, $\quad du= 6x^5 dx$
- Reescribir la integral en términos de la variable $u$, entonces la integral será $\quad \displaystyle \frac16\int (u)^8 \, du$
- Evaluar la integral resultante en términos de $u$, por tanto, $$\frac16\int (u)^8 \, du = \frac{1}{54} (u)^9 + C$$ por ultimo, regresamos a la variable original $x$.
Por ejemplo, de $\displaystyle \int x^5 (x^6 -3)^8 \, dx$, tomaremos $\quad u=x^6 -3$
 ¡Recuerda!
¡Recuerda!
El método de integración por sustitución o cambio de variable tiene como origen la regla de la cadena de la derivada.
 Ejercicio 1. Integral indefinida - Sustitución
Ejercicio 1. Integral indefinida - Sustitución
Cálcula las siguientes integrales.
Escena de Consolación Ruiz Gil, Carlos Mario Restrepo Restrepo, Miguel Ángel Cabezón Ochoa y Juan Guillermo Rivera Berrío.
Resuelve el ejercicio propuesto y verificar tu respuesta, oprime el botón solución. Realiza otros ejercicios oprime el botón ejercicio.
La regla de sustitución para la integración aplica la regla de la cadena para la derivación. Por tanto, observe que, si $u =g(x)$, entonces $du =g'(x)dx$.
 Ejercicio 2. Integral indefinida - Sustitución
Ejercicio 2. Integral indefinida - Sustitución
Cálcula las siguientes integrales.
Escena de Consolación Ruiz Gil, Carlos Mario Restrepo Restrepo, Miguel Ángel Cabezón Ochoa y Juan Guillermo Rivera Berrío.
Para iniciar oprime el botón ejercicio.
Resuelve el ejercicio propuesto y verificar tu respuesta, oprime el botón solución. Realiza otros ejercicios oprime el botón ejercicio.
Se debe tener presente al utilizar el método, que la dificultad se puede presentar sino se escoge un cambio útil, ya que, en caso contrario, la integral resultante puede ser de mayor dificultad que la integral inicial.
 Ejercicio 3. Integral indefinida - Sustitución
Ejercicio 3. Integral indefinida - Sustitución
Cálcula las siguientes integrales.
Escena de Consolación Ruiz Gil, Carlos Mario Restrepo Restrepo, Miguel Ángel Cabezón Ochoa y Juan Guillermo Rivera Berrío.
Para iniciar oprime el botón ejercicio.
Resuelve el ejercicio propuesto y verificar tu respuesta, oprime el botón solución. Realiza otros ejercicios oprime el botón ejercicio.
¿Que sucede con las integrales definidas?
El método de cambio de variable es un poco más complicado cuando se aplica en integrales definidas porque al cambiar la variable, deben actualizarse los extremos de integración. Una forma de evitar este problema es resolver primero la integral indefinida.
Cuando se evalúa una integral definida por sustitución, pueden solucionarse de dos formas:
- Una forma, es evaluar primero la integral indefinida y, enseguida, aplicar el teorema fundamental, por ejemplo: $$ \int_{0}^{4} \sqrt {2x+1}\, dx = \frac{1}{2}\int_{}^{} u^{\frac{1}{2}}\, du = \frac{1}{3}(2x+1)^{\frac{2}{3}} = $$ $$\frac{1}{3}(2(4)+1)^{\frac{2}{3}}-\frac{1}{3}(2(0)+1)^{\frac{2}{3}}= \frac{1}{3}(9)^{\frac{2}{3}}-\frac{1}{3}(1)^{\frac{2}{3}}=\frac{26}{3}$$
- Otra forma que suele ser preferible, es cambiar los límites de integración cuando se cambia la variable, por ejemplo: $$u=2x+1 \space donde \space u=2(0)+1=1, \space u=2(4)+1=9$$ $$\begin{aligned} \int_{0}^{4} \sqrt {2x+1}\, dx = \frac{1}{2}\int_{1}^{9} u^{\frac{1}{2}}\, du &= \frac{1}{3}(u)^{\frac{2}{3}} \Big]_{1}^{9} \\ &= \frac{1}{3}(9)^{\frac{2}{3}}-\frac{1}{3}(1)^{\frac{2}{3}} \\ &= \frac{26}{3} \end{aligned}$$
Regla de sustitución. Si $g'$ es continua en $[a,b]$ y $f$ es continua en el intervalo de $u=g(x)$, entonces $$ \int_{a}^{b} f(g(x)).g'(x) \, dx = \int_{g(a)}^{g(b)} f(u) \, du$$
Integración por partes
Toda regla de derivación tiene una correspondiente regla de integración. Por ejemplo, la Regla de sustitución para integración corresponde a la Regla de la cadena para derivación.
La regla que corresponde a la Regla del producto para derivación se denomina regla para integración por partes.
Pasos para utilizar la integración por partes:
- Se realiza la elección de $u$ y $dv$ en la integral dada, donde $u$ es igual a una de las expresiones de la integral de tal forma que su derivada sea una expresión más simple y la función $dv$ suele ser el factor más complicado en el producto que puede integrarse.
- Luego se diferencia el factor $u$ y se integra la función $dv$. $$ u=f(x)\xrightarrow[]{Derivar} du=f'(x) \\ dv = g'(x)dx \xrightarrow[Integrar]{} v=\int g'(x) \, dx $$
- Luego expresamos los datos obtenidos en la expresión:

 Ejercicio 1. Integral indefinida - Por partes.
Escena de Consolación Gil Ruiz. CC by-nc-sa
Ejercicio 1. Integral indefinida - Por partes.
Escena de Consolación Gil Ruiz. CC by-nc-sa
Resuelve el ejercicio propuesto y verificar tu respuesta, oprime el botón solución. Realiza otros ejercicios oprime el botón ejercicio.
Consideremos otra regla nemotécnica que nos va a guiar en la elección, a priori, más adecuada para selecionar la función $u$, es la palabra LIATE, que se un acrónimo de:
L ogaritmicas.
I nversas.
A lgebraicas.
T rigonométricas.
E xponenciales.
Formula de integración por partes:
 Ejercicio 2. Integral indefinida - Por partes.
Ejercicio 2. Integral indefinida - Por partes.
Cálcula las siguientes integrales.
Escena de Consolación Gil Ruiz. CC by-nc-sa
Oprime el botón clic para iniciar, resuelve el ejercicio propuesto y completa la respuesta. Oprime el botón ver la solución y verifica, realiza más ejercicios oprime el botón otro ejercicio.
Potencias de funciones trigonométricas
Cómo integrar potencias superiores de $sen x$ y $cos x$, productos de potencias de $sen x$ y $cos x$, se usan identidades trigonométricas para integrar ciertas combinaciones de funciones trigonométricas.
Esta técnica es utilizada para integrales de la forma $$ \int Sen^m(x).Cos^n(x) \, dx$$ Para evaluar integrales de este tipo se tienen dos casos:
Caso I: Si $m$ o $n$ es entero positivo impar.
Se utliza una de las siguientes identidades:
- $Sen^2(x) = 1- Cos^2(x)$
- $Cos^2(x) = 1- Sen^2(x)$
Caso II: Si $m$ y $n$ son enteros positivos pares.
Se utliza una de las siguientes identidades de angulo dobles (ambas si se requieren):
- $Sen^2(x) = \frac{1}{2} (1- Cos(2x))$
- $Cos^2(x) = \frac{1}{2}(1+ Cos(2x))$
Para cada caso, una vez transformada la integral mediante la identidad trigonométrica apropiada, ésta se resuelve de manera directa o usando la técnica de sustitución.
Supongamos $Cos^m(x)$, donde $m$ es impar, o sea $m= 2k+1$, entonces:
$\ce{Cos^{2k+1}(x)=Cos^{2k}(x).Cos(x) -> Se \space descompone}$
$\ce{(Cos^2(x))^k.Cos(x) -> Se \space reorganiza} $
$\ce{(1-Sen^2(x))^k(x).Cos(x) -> Se \space Utiliza \space identidad \space Cos^2(x)}$
$$ \int (1-Sen^2(x))^k(x).Cos(x) \, dx = \int (1-u^2)^k du$$ donde, $u=Sen(x)$ y $du= Cos(x)dx$.
 Ejercicio 1. Potencias de funciones trigonométricas.
Ejercicio 1. Potencias de funciones trigonométricas.
Cálcula las siguientes integrales.
Escena de Héctor Javier Herrera Mejia y Juan Guillermo Rivera Berrío.
Sea $Sen^m(x)$, donde $m$ es impar, o sea $m= 2k+1$, entonces:
$\ce{Sen^{2k+1}(x)=Sen^{2k}(x).Sen(x) -> Se \space descompone}$
$\ce{(Sen^2(x))^k.Sen(x) -> Se \space reorganiza} $
$\ce{(1-Cos^2(x))^k.Sen(x) -> Se \space Utiliza \space identidad \space Sen^2(x)}$
$$ \int (1-Cos^2(x))^k(x).Sen(x) \, dx = -\int (1-u^2)^k du$$ donde, $u=Cos(x)$ y $du= -Sen(x)dx$.
 Ejercicio 2. Potencias de funciones trigonométricas.
Ejercicio 2. Potencias de funciones trigonométricas.
Cálcula las siguientes integrales.
Escena de Héctor Javier Herrera Mejia y Juan Guillermo Rivera Berrío.
 Ejercicio 3. Potencias de funciones trigonométricas.
Ejercicio 3. Potencias de funciones trigonométricas.
Cálcula las siguientes integrales.
Escena de Héctor Javier Herrera Mejia y Juan Guillermo Rivera Berrío.
Ejercicio 3 y 4, del tipo $Sen^m(x)Cos^n(x)$, con $m$ o $n$ impar.
Ejemplo. Evaluar $\displaystyle \int Sen^3(x) Cos^6(x)\, dx$ $$\begin{aligned} \int Sen^3(x) Cos^6(x)\,dx &= \int Sen(x)Sen^2(x)Cos^6(x)\,dx \\&= \int Sen(x)(1 - Cos^2(x))Cos^6(x) \,dx \end{aligned}$$
Sea $\quad u = Cos(x)$,$\quad$ entonces $\quad du = -Sen(x)dx$
Por tanto, la integral con cambio de variable es: $$\begin{aligned} \int Sen(x)(1 - Cos^2(x))Cos^6(x) \,dx &= - \int (1 - u^2)u^6 du \\&= -\int (u^6 - u^8)du \\&= -\frac {u^7}{7} + \frac {u^8}{8}+C \end{aligned}$$ $$\int Sen^3(x) Cos^6(x)\, dx = -\frac {Cos^7(x)}{7} + \frac {Cos^8(x)}{8}+C$$
 Ejercicio 4. Potencias de funciones trigonométricas.
Ejercicio 4. Potencias de funciones trigonométricas.
Cálcula las siguientes integrales.
Escena de Héctor Javier Herrera Mejia y Juan Guillermo Rivera Berrío.
Cómo integrar productos de potencias de $Tan (x)$ y $Sec(x)$, se usan identidades trigonométricas para integrar ciertas combinaciones de funciones trigonométricas.
Esta técnica es utilizada para integrales de la forma $$ \int Tan^m(x)Sec^n(x) \, dx$$
Para este tipo de integrales se usan las identidades:
- $m$ par y $n \in R$, se utiliza
$1 + Tan^2(x)=Sec^2(x)$ y sustituir $u=Tan(x)$ - $n$ impar y $m \in R$, se utiliza
$Tan^2(x)=Sec^2(x)-1$ y sustituir $u=Sec(x)$ - $m$ impar y $n=0$, utilizar integración por partes, donde
$u=Sec^{m-2}(x)$ y $dv=Sec^2(x)dx$ - $m$ impar y $n$ par, se utiliza
$Tan^2(x)=Sec^2(x)-1$, y emplear integración por partes. - $m=0$ y $n \in Z^+$, se utiliza
$1 + Tan^2(x)=Sec^2(x)$ y sustituir $u=Tan(x)$
Observaciones.
- Para los dos primeros casos, una vez transformada la integral median te la identidad trigonometrica apropiada, ésta se resuelve usando la técnica de sustitución.
- Para el cuarto caso, al usar la identidad indicada, la integral se reduce al tercer caso.
 Ejercicio 3. Potencias de funciones trigonométricas.
Ejercicio 3. Potencias de funciones trigonométricas.
Cálcula las siguientes integrales.
Escena de Miguel Ángel Cabezon Ochoa, Héctor Javier Herrera Mejia y Juan Guillermo Rivera Berrío.
Resuelve el ejercicio propuesto y verificar tu respuesta, oprime el botón solución. Realiza otros ejercicios oprime el botón ejercicio.
Para resolver integrales que incluyen combinaciones entre cotangentes y cosecantes se procede de manera idéntica a la planteada en la tabla usando las identidades de la cotangente y cosecante.
Veamos ahora productos de funciones trigonométricas escritos como sumas y restas, donde aplicamos otras identidades trigonométricas, observa los siguientes ejemplos, oprime el botón de la identidad deseada:
 Ejercicio. Potencias de funciones trigonométricas.
Ejercicio. Potencias de funciones trigonométricas.
Cálcula las siguientes integrales.
escenas de Miguel Ángel Cabezon Ochoa, adapatadas por el autor.
Caso I. $\quad r^2=a^2-x^2$
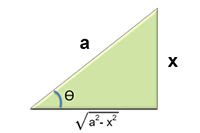 En integrales que contienen expresiones del tipo $\sqrt{a^2 - x^2}$.
En integrales que contienen expresiones del tipo $\sqrt{a^2 - x^2}$.
Donde, $\displaystyle Sen \theta = \frac{x}{a}$, entonces suponemos $\color{blue}x=a.sen \theta$
En el triangulo se observa que:
$ \sqrt{a^2 - x^2} = a.cos \theta \quad$ con $\displaystyle \quad -\frac{\pi}{2} \le \theta \le \frac{\pi}{2}$
Caso II. $\quad r^2=a^2+x^2$
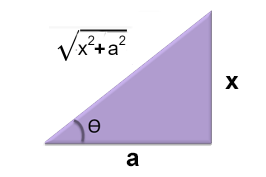 En integrales que contienen expresiones del tipo $\sqrt{a^2 + x^2}$.
En integrales que contienen expresiones del tipo $\sqrt{a^2 + x^2}$.
Donde, $\displaystyle Tan \theta = \frac{x}{a}$, entonces suponemos $\color{blue}x=a.tan \theta$
En el triangulo se observa que:
$\sqrt{a^2 + x^2} = a.sec \theta \quad$ con $\displaystyle \quad -\frac{\pi}{2} \le \theta \le \frac{\pi}{2}$
Caso III. $\quad a^2=r^2-x^2$
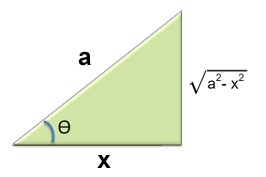 En integrales que contienen expresiones del tipo $\sqrt{a^2 - x^2}$
En integrales que contienen expresiones del tipo $\sqrt{a^2 - x^2}$
Donde, $Sec \theta = \frac{x}{a}$, entonces suponemos $\color{blue}x=a.sec \theta$
En el triangulo se observa que:
$\sqrt{a^2 - x^2} = \pm a.tan \theta \quad$ con $\quad 0 \le \theta \le \frac{\pi}{2} \quad $ o $\quad \frac{\pi}{2} \le \theta \le \pi $
Observa los siguientes ejemplos.
INTEGRALES que contienen expresiones del tipo $\sqrt{a^2 - x^2}$
 Ejercicio. Sustitución trigonométrica.
Ejercicio. Sustitución trigonométrica.
Cálcula las siguientes integrales.
Escena de Juan Guillermo Rivera Berrío.
Cálcula las siguientes integrales, utilizando la regla $$\displaystyle \int\displaystyle \frac{1}{\displaystyle \sqrt{a^{2}-x^{2}}}\space dx=\sin^{-1} \big(\displaystyle \frac{x}{a} \big)+C$$
Resuelve el ejercicio de emparejamiento, encuentra las parejas, arrastrando las flechas de la integral de la columna izquierda a la solución de la columna derecha.
Verificar y realiza otro ejercicio, oprime el botón otro ejercicio.
Integración en fracciones parciales
En la integración por descomposición en fracciones parciales, integramos funciones racionales (razones entre polinomios) al expresarlas como sumas de fracciones más sencillas.
Cuando una función racional $\displaystyle \frac{p(x)}{q(x)}$ es una fracción propia, o sea que el grado del numerador es menor que el grado del denominador, se recomienda usar el metodo de fracciones parciales.
Fracciones parciales:
Si una fracción propia puede escribirse como la suma de fracciones cuyos numeradores son de grado menor que el grado del denominador de la fracción dada, cada una de esas fracciones sumadas se llaman fracción parcial de la fracción originalmente dada.
Procedimiento:
- Analizar la Fracción Parcial, verificar que el polinomio del numerador sea de menor grado que el denominador. En caso contario, se transforma la fracción a una forma mixta, usando el Teorema de la División (Prueba de la división).
- Factorizar el denominador si no lo está. Siempre es conveniente tener el denominador en factores.
- Determinar las constantes, dependiendo del sistema de ecuaciones que se obtenga se procede a resolverlo para determinar el valor de las constantes del sistema.
- Reemplazar las constantes, se sustituyen los valores de las constantes determinadas para la expresión.
Se presentan varios casos, segun los factores presentes en el denominador:
Caso I. Factor lineal
Es un factor de la forma $ax+b$. En este caso la fracción parcial correspondiente es de la forma:
$$\frac{A}{ax+b}$$
Caso II. Factor lineal repetido.
En este caso se deben asignar $n$ fracciones parciales y tiene la forma:
- Para el caso $x^n$, las $n$ fracciones son: $$\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x^3}+ ... +\frac{N}{x^n}$$
- Para el caso $(ax+b)^n$, las $n$ fracciones son: $$\frac{A}{ax+b}+\frac{B}{(ax+b)^2}+\frac{C}{(ax+b)^3}+ ... +\frac{N}{(ax+b)^n}$$
Caso III. Factores cuadráticos.
En este caso la fracción parcial correspondiente es de la forma:
- Factor cuadrático no factorizable. Es todo factor de la forma $(ax^2 + bx + c)$ con $b^2 4ac <0$. $$\frac{Ax+B}{ax^2+bx+c}$$
- Factor cuadrático no factorizable repetido. Es todo factor de la forma $(ax^2 + bx + c)^n$ con $b^2 4ac <0$, las $n$ fracciones parciales son: $$\frac{Ax+B}{ax^2+bx+c}+\frac{Cx+D}{(ax^2+bx+c)^2}+ ... +\frac{Mx+N}{(ax^2+bx+c)^n}$$
En todos los casos $A, B, C, D, ..., M$ y $N$ son constantes a determinar por medio de un sistema de ecuaciones.
 Ejercicio. Fracciones parciales. Escena de Miguel Ángel cabezón Ochoa con licencia CC by-nc-sa
Ejercicio. Fracciones parciales. Escena de Miguel Ángel cabezón Ochoa con licencia CC by-nc-sa
Resuelve el ejercicio propuesto y verificar tu respuesta, oprime el botón solución. Realiza otros ejercicios oprime el botón ejercicio.
Para esta actividad encontaremos integrales de funciones como: $$ \int \frac{4x+3}{x^3-5x^2-40x+34} \, dx$$
Esto te obligará a practicar, a su vez, factorización de polinomios, aqui encontraras algunas escenas de factorización.
 Ejercicio. Fracciones parciales.
Ejercicio. Fracciones parciales.
Cálcula las siguientes integrales. Escena de Miguel Ángel cabezón Ochoa con licencia CC by-nc-sa
Resuelve el ejercicio propuesto y verificar tu respuesta, oprime el botón solución. Realiza otros ejercicios oprime el botón ejercicio.
Caso. Grado del numerador igual o mayor al denominador
Si el grado del numerador es igual o mayor al del denominador, la fracción debe reducirse a una expresión mixta dividiendo el numerador para el denominador. Para ello se aplica el "Teorema de la División" (Prueba de la división): $$\frac{P(x)}{divisor(x)}= Resultado(x) + \frac{Residuo(x)}{divisor(x)}$$
Ejemplo. Evaluar $\displaystyle \int \frac{x^3+4}{x^2+4} \, dx $
Como el grado del numerador es mayor que el del denominador, utilizamos Teorema de la División, expresando la fracción en mixta: $$\begin{aligned} &\quad \cancel{x^3}+4 \qquad \underline{| \space x^2+4} \\ &\underline{-\cancel{x^3}-4x} \qquad x \\ &\qquad \quad 4-4x \end{aligned}$$ donde: $\quad x^3-4x=(4-4x)+x(x^2+4)$ dividiendo por $x^2+4$ toda la expresión, se tiene que: $$\frac{x^3-4x}{x^2+4}=\frac{4-4x}{x^2+4}+\frac{x(x^2+4)}{x^2+4}$$ $$\frac{x^3-4x}{x^2+4}=\frac{4-4x}{x^2+4}+x$$
La nueva integral queda igua a: $$\int \frac{x^3+4}{x^2+4} \, dx =\int \frac{4-4x}{x^2+4} \, dx + \int x \, dx$$
Se presentan dos integrales, donde la $\int x \, dx$ es de solución directa: $$\int x \, dx= \frac{x^2}{2}+c_1$$
La otra integral, $\displaystyle \int \frac{-4x+4}{x^2+4} \, dx$ presenta un factor cuadrático irreductible $x^2+4$. En consecuencia, la descomposición en fracciones parciales es de la forma: $$\frac{-4x+4}{x^2+4}=\frac{Ax+B}{x^2+4}$$
Entonces, al igualar los cieficientes, se obtiene que: $$-4x+4=Ax-B \\ A=-4 \quad y \quad B=4 $$
En consecuencia, la integral se convierte en: $$\int \frac{Ax+B}{x^2+4} \, dx=\int \frac{-4x+4}{x^2+4} \, dx=\int \frac{-4x}{x^2+4} \, dx + \int \frac{4}{x^2+4} \, dx$$ $$=-4\int \frac{x}{x^2+4} \, dx + 4\int \frac{1}{x^2+4} \, dx$$
¡Recuerda! Utilizando la formula de integración: $$\int \frac{1}{x^2+a^2} \, dx = \frac{1}{a}.Tan^{-1}(\frac{x}{a}) + C$$
$$= - 2.Ln|x^2+4| + 2.Tan^{-1}(\frac{x}{2}) +c_2$$En consecuencia, la solución de la integral esta dada por:
$$\int \frac{x^3+4}{x^2+4} \, dx = \frac{x^2}{2} - 2.Ln|x^2+4| + 2.Tan^{-1}(\frac{x}{2})+C $$
Resumen. Casos de fracciones parciales
Factor $x^n$ | Forma del factor | Forma de la Fracción parcial |
|---|---|---|
$n=0$ | A = constante | No existe |
$n=1$ | $ax+b$ | $\frac{A}{ax+b}$ |
$n=1$ | $(ax+b)^n$ | $\frac{A}{ax+b}+\frac{B}{(ax+b)^2}+\frac{c}{(ax+b)^3}+...$ |
$n=2$ | $ax^2+bx+c$ | $\frac{Ax+B}{ax^2+bx+c}$ |
$n=2$ | $(ax^2+bx+c)^n$ | $ \frac{Ax+B}{ax^2+bx+c}+\frac{Cx+D}{(ax^2+bx+c)^2}+...$ |
| En todos los casos $A, B, C, D, ...,$ son constantes a determinar por medio de un sistema de ecuaciones. |
Integrales impropias
Se ha estudia la integral de una función $f$ acotada y definida en un intervalo $[a,b]$, donde $a$,$b$ reales.
Ahora intentaremos generalizar este concepto de integral para funciones que no verifican que:
- Los límites de integración eran números finitos, y que
- La función $f$ era continua sobre $[a, b]$ o, en caso de ser discontinua, que estaba acotada sobre el intervalo.

Exploración. Escena de Juan Guillermo Rivera Berrío.
¿Se puede utilizar directamente el teorema fundamental del cálculo?
Ahora puedes utilizar el teorema fundamental del cálculo y luego la teoría de límites para solucionar la integral. Esto se puede ver, por ejemplo en:
- La integral de una función no acotada, definida en un intervalo acotado, por ejemplo: $$\quad f(x)=\frac{1}{x} \space en \space (0,a]$$
- La integral de una función acotada, definida en un intervalo no acotado, por ejemplo: $$\quad f(x)=\frac{1}{x} \space en \space [1,+\infty]$$
- La integral de una función acotada, definida en un intervalo no acotado, por ejemplo: $$\quad f(x)=\frac{1}{x} \space en \space (0,+\infty]$$
 ¡Estudiaremos!
¡Estudiaremos!
El concepto de una integral definida en el caso donde el intervalo es infinito y también en el caso donde $f$ tiene una discontinuidad infinita en $[a, b]$.
En uno u otro de estos dos casos la integral se denomina integral impropia. A continuación, veamos los casos que se pueden presentar para solucionar este tipo de integrales.
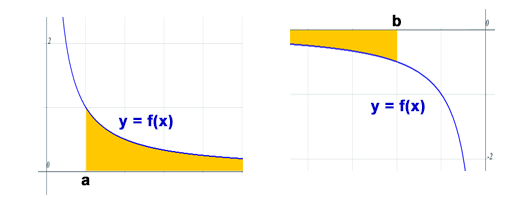
Tipo I. Intervalos infinitos (no acotado).
Si el integrando $f$ está definido sobre un intervalo no acotado, hay tres integrales impropias posibles con límites de integración infinitos:
- Si $f$ es continua sobre $[a, +\infty)$, entonces $$ \int_{a}^{+\infty} f(x)\, dx = \lim_{b \to{+}\infty}{\int_{a}^{b} f(x)\, dx } $$
- Si $f$ es continua sobre $(-\infty, b]$, entonces $$ \int_{-\infty}^{b} f(x)\, dx = \lim_{a \to{-}\infty}{\int_{a}^{b} f(x)\, dx } $$
- Si $f$ es continua sobre $(-\infty, +\infty)$, entonces $$ \int_{-\infty}^{+\infty} f(x)\, dx=\int_{-\infty}^{c} f(x)\, dx + \int_{c}^{+\infty} f(x)\, dx $$
Las integrales impropias $ \int_{a}^{+\infty} f(x)\, dx$ y $\int_{-\infty}^{b} f(x)\, dx$ se denominan convergentes si existe el límite correspondiente y divergentes si el límite no existe.
Para la definición (3), la integral $\int_{-\infty}^{+\infty} f(x)\, dx$ es convergentes si las dos integrales convergen, de lo contrario, es divergente.
El área sombreada en la figura representa el valor de la integral impropia:
Observa en la siguiente escena Escenas de Juan Guillermo Rivera Berrío. algunas integrales de este tipo. ¿Determina si convergen o divergen?
 ¡Recordemos!
¡Recordemos!
El área sombreada en la figura representa el valor de la integral, expresada como: $$ A = \int_{a}^{b} f(x)\, dx $$
 Exploración. Integrales impropias.
Exploración. Integrales impropias.
Integrandos infinitos.
Observa el área de la región comprendida por la curva $f(x)$, oprime el botón Ampliar gráfica
Oprime el botón Otro ejemplo para ver otra función $f(x)$.
 ¡Recordemos!
¡Recordemos!
La regla para calcular límites que tienden a $\pm \infty$, donde $n$ es un entero positivo, entonces:$$\lim_{x \to \infty} \frac{1}{x^n} = 0$$
Ejemplo - Evaluar la integral, ¿Converge o diverge? $$\int_{2}^{\infty} \frac{1}{x^3} \, dx$$
$$\int_{2}^{\infty} \frac{1}{x^3} \, dx = \lim_{b \to{+}\infty}{\int_{2}^{b} \frac{1}{x^3} \, dx } = \lim_{b \to{+}\infty}{\int_{2}^{b} x^{-3} \, dx }$$
Resolviendo y evaluando la integral, se tiene: $$\lim_{b \to{+}\infty}\Big[{-\frac{1}{2x^2}} \space \Big]_{2}^{b}= \lim_{b \to{+}\infty}{\Big[-\frac{1}{2(b)^2}+\frac{1}{2(2)^2}\Big]}=$$
Evaluando el límite: $$-\frac{1}{2} \lim_{b \to{+}\infty}{\frac{1}{(b)^2}+ \frac{1}{2}\lim_{b \to{+}\infty}\frac{1}{4}}= -\frac{1}{2}(0) + \frac{1}{2}.\frac{1}{4}=\frac{1}{8}$$
Por tanto, $$\int_{2}^{\infty} \frac{1}{x^3} \, dx=\frac{1}{8}$$
Esto significa que la integral Converge.
Tipo II. Integrados discontinuos.
Discontinuidades infinitas
Se dice que es impropia si $f$ no está acotada sobre $[a, b]$, es decir, si $f$ tiene una discontinuidad infinita en algún número en el intervalo de integración, sus definiciones se resumen como:
- Si $f$ es continua sobre $[a,b)$ y discontinua en $b^-$, entonces $$ \int_{a}^{b}f(x)\, dx = \lim_{t \to{b^-}}{\int_{a}^{t} f(x)\, dx } $$
- Si $f$ es continua sobre $(a,b]$ y discontinua en $a^+$, entonces $$ \int_{a}^{b} f(x)\, dx = \lim_{t \to{a^+}}{\int_{t}^{b} f(x)\, dx } $$
- Si se tiene una discontinuidad en $c$, para un $c$ en $(a,b)$ y $f$ es continua en los demás números en $[a,b]$ , entonces $$ \int_{a}^{b} f(x)\, dx=\int_{a}^{c} f(x)\, dx + \int_{c}^{b} f(x)\, dx $$
Las integrales impropias $ \int_{a}^{b} f(x)\, dx$ se denomina convergentes si existe el límite correspondiente y divergentes si el límite no existe.
Para la definición (3), la integral $\int_{a}^{b} f(x)\, dx$ con $c$ una discontinuidad entre $[a,b]$ son convergentes si las dos integrales convergen, de lo contrario, es divergente.
 Exploración. Integrales impropias.
Exploración. Integrales impropias.
Integrandos discontinuos.
Escena de Juan Guillermo Rivera Berrío.
Observa la función $f(x)$ y oprime el botón Cálcula Límite y observa el análisis de la solución correspondiente.
Oprime el botón Otro ejemplo para ver otra función.
 Ejercicio. Integrales impropias.
Ejercicio. Integrales impropias.
Integrandos discontinuos. Escena de Juan Guillermo Rivera Berrío.
Ingresa el valor obtenido, pulsa la tecla "enter <┘"y verificar tu respuesta, si tu respuesta es correcta, oprime el botón otro ejercicio, para ver otra integral.
Observa el planteamiento del cálculo de la integral impropia: $$\int_{0}^{33} \frac{1}{{(x-1)}^{\frac{1}{5}}} \, dx = \int_{0}^{1} \frac{1}{{(x-1)}^{\frac{1}{5}}} \, dx +\int_{1}^{33} \frac{1}{{(x-1)}^{\frac{1}{5}}} \, dx $$ $$= \lim_{t \to 1^-}\int_{0}^{t} \frac{1}{{(x-1)}^{\frac{1}{5}}} \, dx + \lim_{t \to 1^+}\int_{t}^{33} \frac{1}{{(x-1)}^{\frac{1}{5}}} \, dx $$
Completa el proceso y concluye, ¿diverge o converge?
Evalua lo aprendido, resuelve el siguiente test respondiendo a las cinco preguntas propuesta.
 Preguntas. Selección la respuesta correcta.
Preguntas. Selección la respuesta correcta.
Haz click sobre la respuesta correcta.
Coordenadas Polares
Introducción
Hasta ahora se a utilizado el sistema de coordenadas rectangular o cartesiano para especificar un punto $P$ o describir una curva $C$ en el plano. Podemos considerar este sistema como una retícula de líneas horizontales y verticales. Las coordenadas $(a, b)$ de un punto $P$ están determinadas por la intersección de dos rectas: una recta $x = a$ es perpendicular a la recta de referencia horizontal llamada el eje $x$, y la otra $y = b$ es perpendicular a la recta de referencia vertical llamada el eje $y$.
Otro sistema son las coordenadas polares, que ofrecen un modo alternativo de localizar puntos en un plano. Son útiles porque, para ciertos tipos de regiones y curvas, las coordenadas polares dan descripciones y ecuaciones muy sencillas. Las principales aplicaciones de esta idea se presentan en cálculo de varias variables: la evaluación de integrales dobles y la derivación de las leyes de Kepler del movimiento planetario.
Para establecer un sistema de coordenadas polares empleamos un sistema de círculos centrados en un punto $O$, denominado polo, y líneas rectas o rayos que emanen de $O$. Tomamos como eje de referencia una media línea horizontal dirigida hacia la derecha del polo, a la cual se le nombra eje polar.
Para especificar una distancia $r$ dirigida (con signo) desde $O$ y un ángulo $θ$ cuyo lado inicial es el eje polar y cuyo lado final es el rayo $OP$, se identifica el punto $P$ mediante $(r, θ)$.
Se dice que el par ordenado $(r, θ)$ son las coordenadas polares de $P$.
Usamos la convención de que un ángulo es positivo si se mide en dirección contraria al giro de las manecillas de un reloj desde el eje polar, y negativo si se mide en dirección de las manecillas de un reloj.
Si $P=O$, entonces $r=0$ y convenimos que $(r, θ)$ representa el polo para cualquier valor de $θ$.
- Los ángulos $θ>0$ se miden en el sentido contrario al de las manecillas del reloj a partir del eje polar, en tanto que los ángulos $θ<0$ se miden en el sentido de las manecillas del reloj.
- Para graficar un punto $(-r, θ)$, donde $-r<0$ se miden $|r|$ unidades a lo largo del rayo $θ + \pi$.
- Las coordenadas del polo $O$ son $(r, θ)$, donde $θ$ es cualquier ángulo.
Nótese que $(-r, θ)$ representa el mismo punto que $(r, θ+ \pi)$.
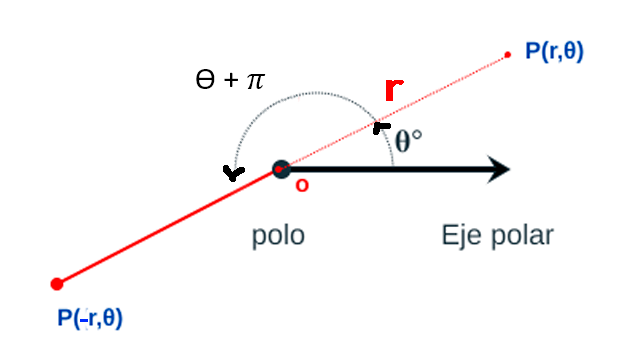
Gráfica de puntos polares
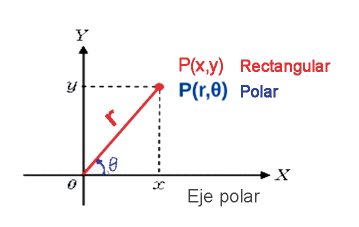
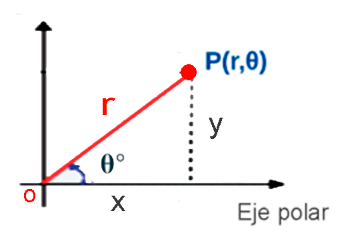
La representación polar de un punto $P$ en el plano también tiene una interpretación visual, donde $r$ es la distancia a la que se encuentra el punto $P$ desde el origen, y $θ$ mide el ángulo que forma el segmento desde el origen hasta el eje x positivo, ver gráfica:
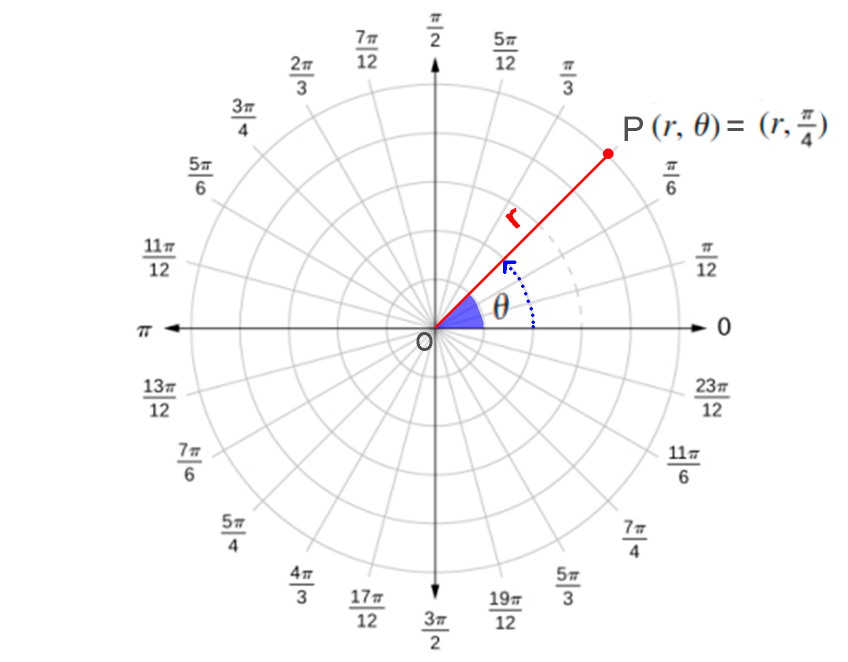
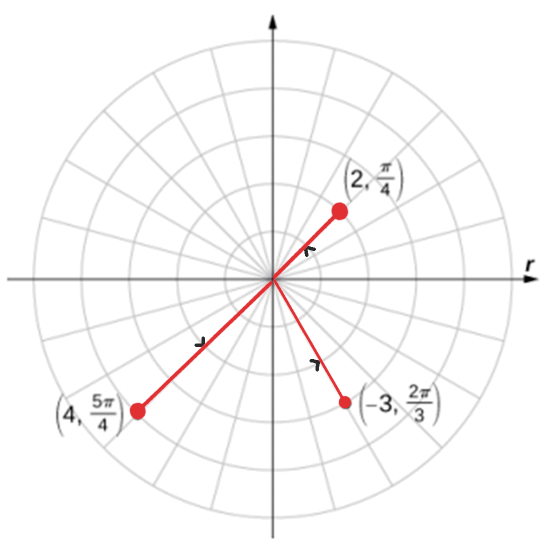
Observemos la gráfica de los siguientes puntos:
- Gráfica del punto $P(2,\frac\pi4)$
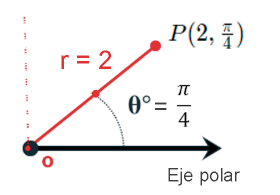
Su unidad de medida es $2$ unidades a lo largo del segmento $\frac\pi4$ con el eje polar
como se muestra en la figura.
- Gráfica del punto $P(-3,\frac{2\pi}{3})$
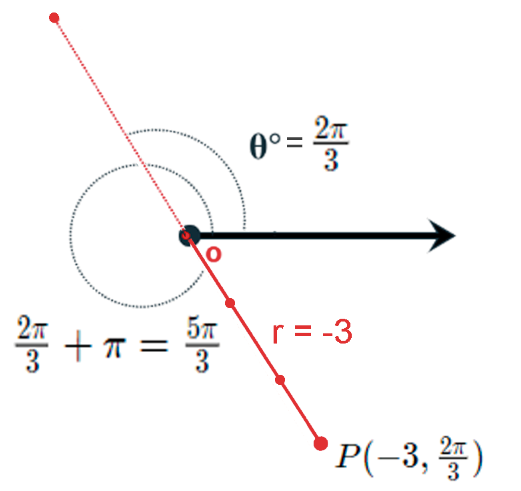
Su medida es $|-3|=3$ unidades a lo largo del
segmento $\frac{2\pi}{3}+\pi=\frac{5\pi}{3}$ con el eje polar. De manera equivalente, pueden medirse $3$ unidades a lo largo del segmento extendidas hacia atrás a través del polo.
Se observa en la figura que el punto no está en el mismo cuadrante que el lado final del ángulo.
- Gráfica del punto $P(4,\frac{5\pi}{4})$
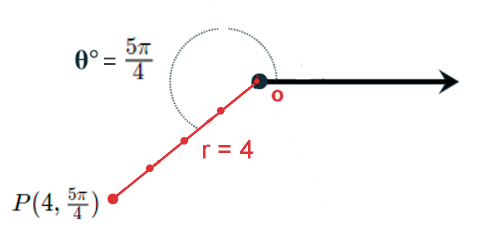
Su unidad de medida es $4$ unidades a lo largo del segmento $\frac{5\pi}{4}$ con el eje polar,
como se muestra en la figura.
Representación de los tres puntos en el sistema de coordenadas.
 Exploración.
Exploración.
Coordenadas polares.
 Gráfica de un punto $P$ en el sistema de coordenadas polares.Red Educativa Digital Descartes. Proyecto Un_100 Unidades didácticas Interactivas Autor: Elena E. Álvarez Sáiz, Universidad de Cantabria, España.
Gráfica de un punto $P$ en el sistema de coordenadas polares.Red Educativa Digital Descartes. Proyecto Un_100 Unidades didácticas Interactivas Autor: Elena E. Álvarez Sáiz, Universidad de Cantabria, España.
Mueva los controles, observa el punto $P$ en Coordenadas polares, encuentra su equivalente en Coordenadas rectangulares
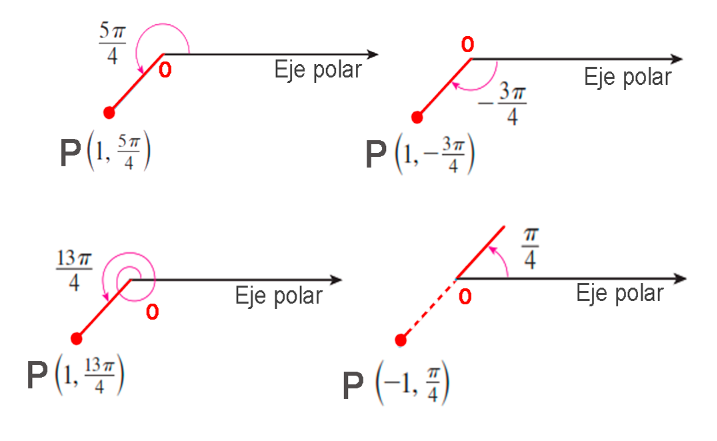
En el sistema de coordenadas cartesianas todo punto tiene sólo una representación, pero en el sistema de coordenadas polares cada punto tiene numerosas representaciones, por ejemplo:
$$P(1,\frac{5\pi}{4})=P(1,-\frac{3\pi}{4}) = P(1, \frac{13\pi}{4})=P(-1,\frac{\pi}{4})$$
 ¡Recordemos!
¡Recordemos!
Una rotación completa en sentido contrario al giro de las manecillas de un reloj está dada por un ángulo de $2 \pi$.
El punto $P$ representado por coordenadas polares $P(r, θ)$, con $n$ cualquier entero, también está representado por:
$$P(r, θ)=P(r, θ+2n\pi)=P(-r, θ+(2n+1)\pi)$$
Conversión de coordenadas
La relación entre coordenadas polares y cartesianas:
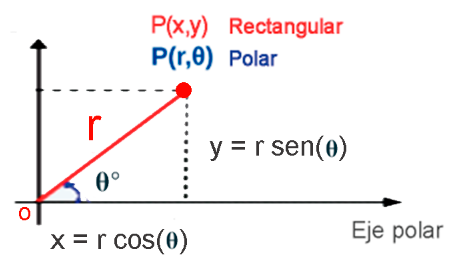
Donde, el polo corresponde al origen $O$ y el eje polar es el eje positivo de las $x$, entonces el punto $P$ tiene coordenadas cartesianas $P(x, y)$ y coordenadas polares $P(r, θ)$.
Cuando sobreponemos un sistema de coordenadas rectangulares sobre un sistema de coordenadas polares o visceversa, se puede hallar, conocidas $x$ y $y$, o conocidos $r$ y $θ$ podemos expresar un punto $P$ en
cualquiera de los dos sistemas de coordenadas, para esto, utilizamos la trigonometría del triángulo rectángulo.
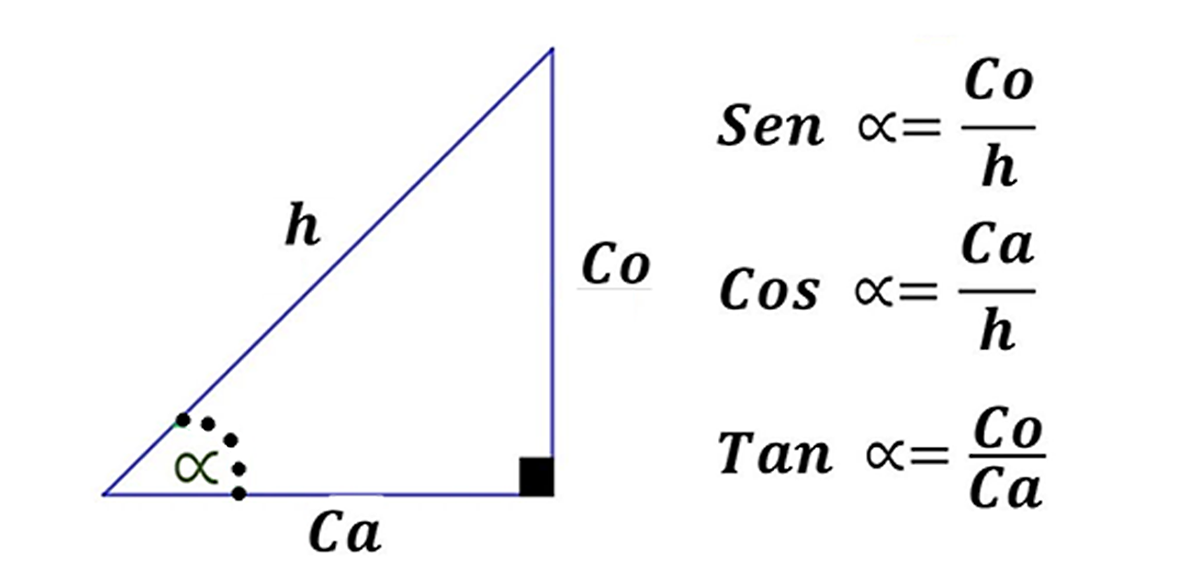
Coordenadas rectangulares en polares
Para expresar un punto $P$ de coordenadas cartesianas $(x, y)$ a coordenadas polares $(r, θ)$, las siguientes ecuaciones son verdaderas para el punto $P$:
 Para hallar $r$ y $θ$ cuando $x$ y $y$ se conocen, usamos las ecuaciones:
$$r^2=x^2+y^2 \tag{$1$}$$
$$Tan(θ)= \frac xy \tag{$2$}$$
Para hallar $r$ y $θ$ cuando $x$ y $y$ se conocen, usamos las ecuaciones:
$$r^2=x^2+y^2 \tag{$1$}$$
$$Tan(θ)= \frac xy \tag{$2$}$$
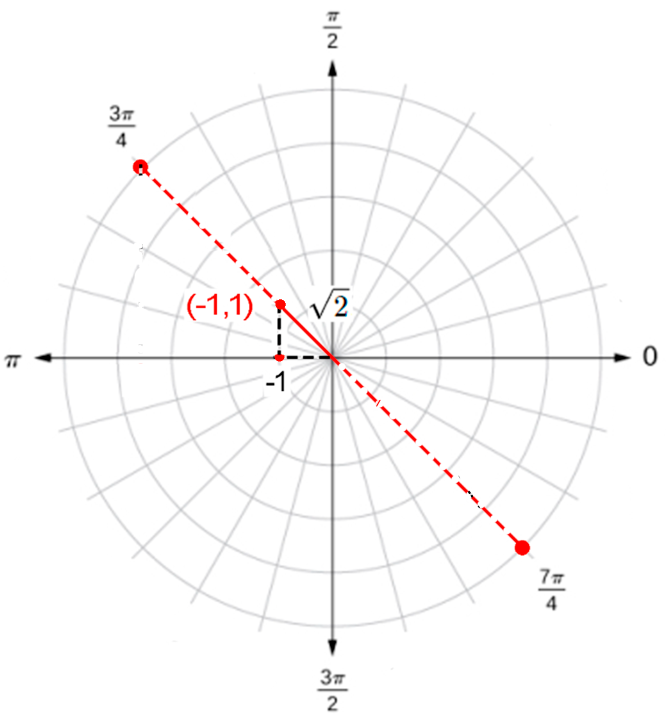
Ejemplo - Convierta las coordenadas rectangulares $(1,-1)$ en coordenadas polares.
Con $x=-1$ y $y=1$ y remplazando en la ecuación $(1)$, se tiene: $$\begin{aligned} r^2=x^2+y^2 \qquad &\to \quad r^2=(-1)^2+(1)^2 \\ &\to \quad r^2= 2 \\ &\to \quad r= \pm \sqrt{2} \end{aligned}$$
Ahora, utilizando la ecuación $(2)$, se tiene: $$Tan(θ)= \frac xy =\frac{-1}{1}=-1$$ $$Tan(θ)=-1$$ $$θ=Tan^{-1}(-1)$$
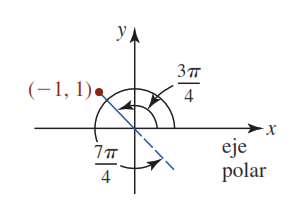
Con $r= \pm \sqrt{2}$ y $Tan(θ)=-1$ y tomando dos de los muchos ángulos que satisfacen $Tan(θ)=-1$, como son:
$$\frac{3\pi}{4}\quad y \quad \frac{7\pi}{4}$$
como se ve en la gráfica, por tanto, dos posibles representaciones en coordenadas polares de $(1,-1)$ son:
$$P_1(\sqrt{2},\frac{3\pi}{4}) \quad y \quad P_2(-\sqrt{2},\frac{7\pi}{4})$$
Coordenadas polares en rectangulares
Para expresar un punto $P$ de coordenadas polares $(r, θ)$ a coordenadas cartesianas $(x, y)$, a partir de las relaciones trigonométricas: $$Cos(θ)=\frac xr \quad y \quad Sen(θ)=\frac yr$$
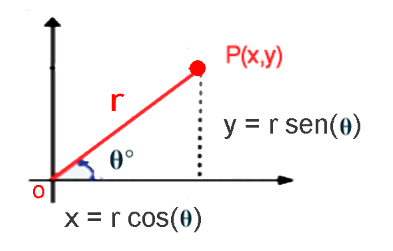
Para hallar $x$ y $y$ cuando $r$ y $θ$ se conocen, usamos las ecuaciones:
$$x = r.cos(θ) \tag{$1$}$$
$$y = r.sen(θ) \tag{$2$}$$
Ejemplo
Convertir coordenadas polares en coordenadas rectangulares.
 ¡Recordemos!
¡Recordemos!
Cada punto en el plano tiene un número infinito de representaciones en coordenadas polares. Sin embargo, cada punto en el plano tiene solo una representación en el sistema de coordenadas rectangular.
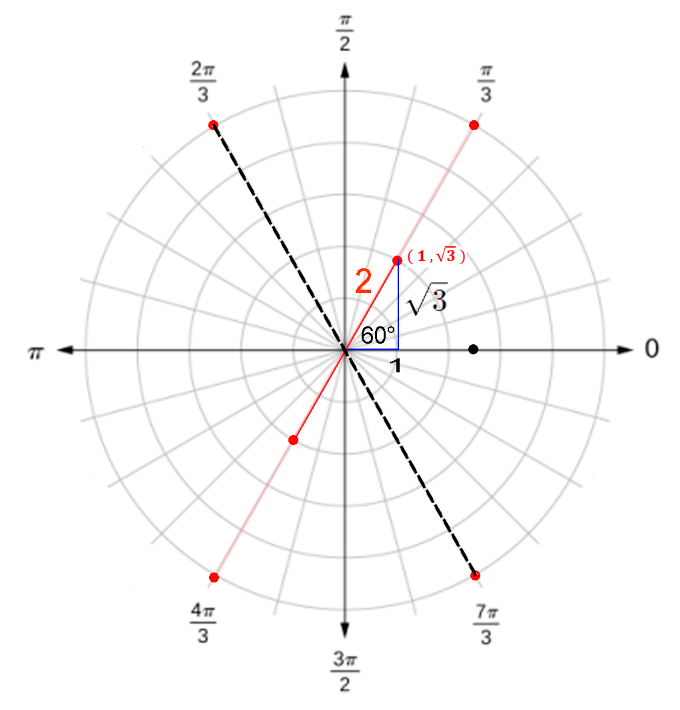
Las coordenadas polares $(2, \fracπ3)$ y $(2,\frac{7π}{3})$ representan el punto $(1,\sqrt{3})$ en el sistema rectangular. Además, el valor de $r$ puede ser negativo.
Por lo tanto, el punto con coordenadas polares $(−2,\frac{4π}{3})$ también representa el punto $(1,\sqrt{3})$ en el sistema rectangular, verifiquemos usando las ecuaciones $(1)$ y $(2)$
$$\begin{aligned}
x &= r . cos (θ)\\
&=-2.cos(\frac{π}{3})\\
&=-2(-\frac12)=1
\end{aligned}$$
$$\begin{aligned}
y &= r . sen (θ)\\
&= -2.sen(\frac{4π}{3})\\
&= -2(-\frac{\sqrt{3}}{2})=\sqrt{3}
\end{aligned}$$
 Exploración.
Exploración.
Punto $P$ en el sistema de coordenadas polares y rectangulares.
Ejemplo.Red Educativa Digital Descartes. Proyecto Un_100 Unidades didácticas Interactivas Autor: Elena E. Álvarez Sáiz, Universidad de Cantabria, España.
Para iniciar, oprime el botón Ejemplos y observa la conversión entre los sistemas de coordenadas polares y rectangulares (o cartesianas) de un punto $P$, haciendo clic en los botones ver ejemplos, visualiza la gráfica del punto $P$ en los dos sistemas.
Gráfica de una ecuación polar
La gráfica de una ecuación polar expresada como $r$ en función de $\theta$ es: $$r= f(\theta)$$ O más generalmente $F(r,\theta)=0$, consiste de todos puntos $P$ que tienen al menos una representación polar $(r,\theta)$ cuyas coordenadas satisfacen la ecuación.
Representación gráfica de la ecuación $r=a$ en un círculo con centro $o$ y radio $| a |$, donde, $\theta$ no se especifica, entonces, un punto $(a, \theta)$ yace sobre la gráfica
de $r = a$ para cualquier valor de $\theta$ y $a$
El punto $(a, \theta)$ se encuentra a $a$ unidades del origen, ver gráfica.
Simetría en curvas polares y ecuaciones
Consideremos la curva generada por la función $r = f(θ)$:
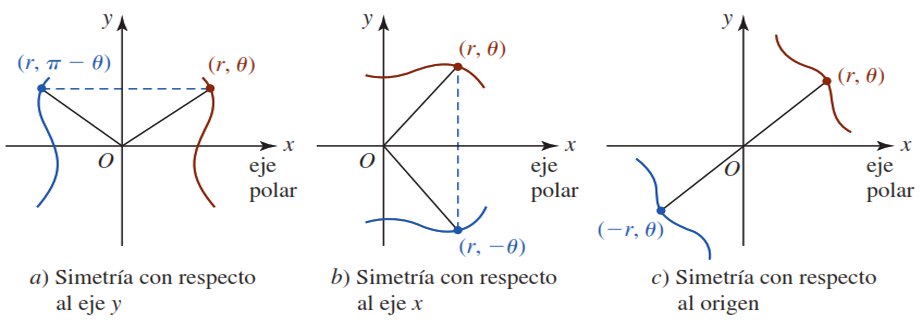
- (Eje y). La curva es simétrica respecto a la recta vertical $θ = \frac{π}{2}$ si para cada punto $(r, θ)$ en el gráfico, el punto $(r, π − θ)$ también está en el gráfico. De manera similar, la ecuación $r = f(θ)$ no cambia cuando $θ$ se reemplaza por $π − θ$.
- (Eje x). La curva es simétrica sobre el eje polar si para cada punto $(r, θ)$ en el gráfico, el punto $(r, −θ)$ también está en el gráfico. De manera similar, la ecuación $r = f(θ)$ no cambia al reemplazar $θ$ por $−θ$.
- (Origen $o$). La curva es simétrica sobre el polo si para cada punto $(r, θ)$ en el gráfico, el punto $(r, π + θ)$ también está en el gráfico. De manera similar, la ecuación $r = f(θ)$ no cambia cuando se reemplaza $r$ con $−r$, o $θ$ con $π + θ$.
Construcción de gráficas en coordenadas polares
En un curso de cálculo de funciones, se aprendió que un posible procedimiento para construir la gráfica de una función $y=f(x)$ es utilizar una tabla, como se ilustra en la siguiente gráfica:

En el caso de las coordenadas polares, la construcción de la gráfica de $r = f(θ)$ auxiliándose de una tabla de valores, como en el caso de coordenadas cartesianas.
Por ejemplo, construyamos la gráfica de $r = 1+2cos(\theta)$ en un sistema de coordenadas polares con ayuda de una tabla de valores.
Una manera de graficar esta ecuación es incorporar unos cuantos puntos bien escogidos correspondientes a $0 \le \theta \le 2 \pi$, como se ve en la siguiente tabla,
Tabla de valores de $\qquad r = 1+2cos(\theta)$.
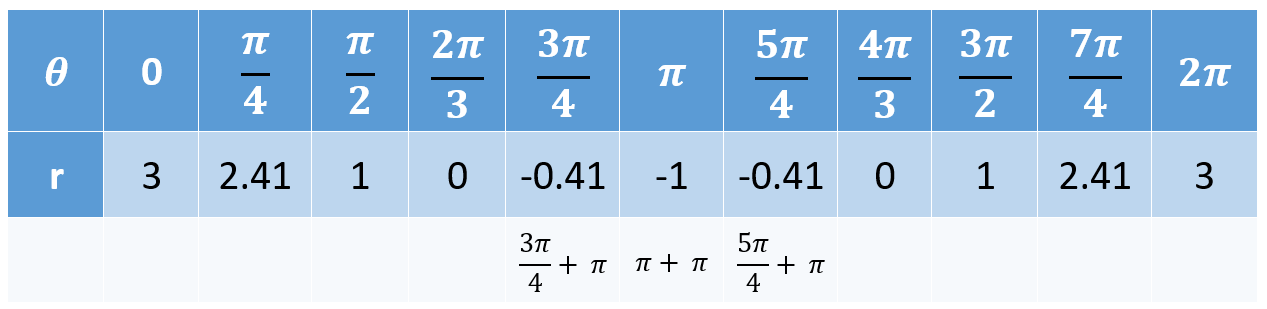
 ¡Recordemos!
¡Recordemos!
Cuando $r<0$, el punto debe dibujarse a un ángulo $(\theta + \pi)$.
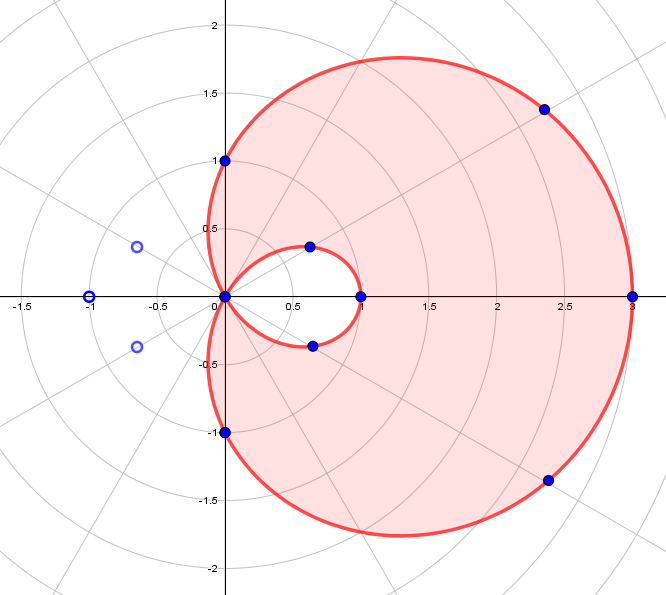
 Exploración.
Exploración.
Ver gráficas con la calculadora gráficadora de GeoGebra.
 Para ver la animación oprime el botón
Para ver la animación oprime el botón  . Observa como se forma la gráfica de la función $(r, θ)$ en coordenada polares.
. Observa como se forma la gráfica de la función $(r, θ)$ en coordenada polares.
Utiliza la escena para verificar las gráficas de las funciones en coordenadas polares $(r, θ)$.
Gráficas de funciones polares, Características de las gráficas.
 Descarga:
Descarga:
Resumen. Gráficas de las curvas polares.
Plano en coordenadas polares
Utiliza la escena para graficar curvas $(r,\theta)$, para ingresar el simbolo $\theta$ combina las teclas Alt + t.
 GeoGebra. Utiliza el software para graficar en coordenadas cartesianas y comparar las funciones en los dos planos.
GeoGebra. Utiliza el software para graficar en coordenadas cartesianas y comparar las funciones en los dos planos.
Clic Aqui.
Área en coordenadas polares
El problema de determinar el área de una región acotada por gráficas polares no es tan directo como lo fue en el desarrollo de encontrar e área apartir de aproximaciones con rectangulos, ahora, en lugar de un rectángulo usamos un sector de un círculo, el área A de un sector circular es proporcional al ángulo central $\theta$, medido en radianes, y ya que el área del círculo completo es $\pi r^2$, entonces se tiene: $$\frac{a}{\pi r^2}=\frac{\theta}{2 \pi} \qquad o \qquad A=\frac{1}{2} r^2\theta$$
Teoremas.Definición tomada de: Cálculo: Transcendentes tempranas. D. Zill. 4Ed.
Área en coordenadas polares.
Si $r=f(\theta)$ es una función continua no negativa sobre $[\alpha, \beta]$, entonces el área acotada por su gráfica y los rayos $\theta =\alpha$ y $\theta =\beta$ estan dados por: $$\int_{\alpha}^{\beta} \frac12 [f(\theta)]^2 \, d\theta = \frac12 \int_{\alpha}^{\beta} r^2 \, d\theta$$
Área acotada para dos gráficas
Si las funciones $f$ y $g$ son continuas sobre $[\alpha, \beta]$ y $f(\theta) \geqslant g(\theta)$ sobre el intervalo, entonces el área acotada por las gráficas de $r=f(\theta)$, $r=g(\theta)$, $\theta =\alpha$ y $\theta =\beta$ es: $$\frac12 \int_{\alpha}^{\beta} ([f(\theta)]^2 - [g(\theta)]^2) \, d\theta$$
 Ejemplo.
Ejemplo.
Calcular el área de la región de color azul comprendida:
Dentro de $r = 3 sen(\theta)$ y fuera de $r = 2 - sen(\theta)$
Solución - Gráfica formada por las dos curvas, donde el problema plantea calcular el área de la región sombreada:
Encontramos los puntos de intersección entre las dos curvas: $$\begin{aligned} 3sen(\theta)&=2 -sen(\theta) \\ 3sen(\theta)+sen(\theta)&=2 \\ 4sen(\theta)&=2 \\ sen(\theta)&=\frac12 \end{aligned}$$ $$\theta= sen^{-1}\big(\frac12 \big)$$
Por lo tanto, se tienen que los intersectos son: $\quad\theta=\frac{\pi}{6}$ y $\theta=\frac{5\pi}{6}$
Como el área acotada por las gráficas es simétrica respecto a $\frac{\pi}{2}$, entonces se calculará desde $\frac{\pi}{6}$ a $\frac{\pi}{2}$ y se multiplica por $2$, se expresa: $$\begin{aligned}A &=\frac12 \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} ([3sen(\theta)]^2 - [2 -sen(\theta)]^2) \, d\theta \\ &=\frac12 \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} (9sen^2(\theta) - 4 + 4sen(\theta)-sen^2(\theta)) \, d\theta \\ &=\frac12 \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} (8sen^2(\theta) + 4sen(\theta)- 4) \, d\theta \end{aligned}$$
Ahora, utilizamos la identidad $sen^2(\theta)=\frac{1-cos(2\theta)}{2}$, y remplazando, tenemos: $$\begin{aligned} A&=\frac12 \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} (\frac82(1-cos(2\theta)) + 4sen(\theta)- 4) \, d\theta \\ &=\frac12 \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} (4sen(\theta)-4cos(2\theta)) \, d\theta \\ &=\frac12[-4cos(\theta)-2sen(2\theta)] \bigg|_{\frac{\pi}{6}}^{\frac{\pi}{2}}\\ &= \frac12[4cos(\frac{\pi}{6})+2sen2(\frac{\pi}{6})]= 2\big(\frac{\sqrt[]{3}}{2}\big)+\big(\frac{\sqrt[]{3}}{2}\big) =\frac32\space\sqrt[]{3} \end{aligned}$$ Por lo tanto, el área de la región acotada por las curvas es $2A$, entonces $$A=3\space\sqrt[]{3} \quad u^2$$
 Ejercicio. Área encerrada por una curva.
Ejercicio. Área encerrada por una curva.
Área encerrada por una curva o curvas
Encuentre el área encerrada por la curva propuesta, oprima el botón solución para verificar la respuesta. Realice la gráfica de la curva para encontrar los límites de integración, oprima el botón ver gráfica. Oprima el botón otro ejercicio para ver otra curva..
Sucesiones y series
Sucesiones
¿Que es una sucesión?
Es un conjunto ordenado de elementos que pueden ser números, letras o figuras o una combinación de las anteriores. Estos elementos se caracterizan por seguir una determinada regla de formación. Se puede denotar por: $$a_1,a_3,a_3,a_4,...,a_n$$
El entero $n$ recibe el nombre de índice de $a_n$. Los términos de la sucesión se forman cuando el índice $n$ toma valores de $1, 2, 3, . . . $.
El número $a_1$ es el primer termino, $a_2$ el segundo termino y asi hasta llegar a $a_n$, termino n-énesimo o termino general de la sucesión.
Una sucesión es una función cuyo dominio es el conjunto de enteros positivos.
Nótese que para todo entero positivo $n$ hay un correspondiente número $a_n$ entonces una sucesión se puede definir como una función cuyo dominio es el conjunto de enteros positivos.
Notación y términos:
Una función sucesión se denota como $\displaystyle \{a_n\}$, donde el dominio es el conjunto $\{1,2,3,4...n\}$
Los valores $a_1,a_2.a_3,a_4,...a_n$ se llaman términos de la sucesión.
El número $a_n$ se denomina el término n-ésimo, $\displaystyle \{a_n\}$ es equivalente a: $$a_1, \space a_2, \space a_3, \space a_4,...a_n \quad ⇒ \quad Rango$$ $$\hspace{-6.0cm}\color{green}\uparrow \hspace{-1.3cm}\uparrow $$ $$1\quad 2\quad 3\quad 4\quad... n \quad ⇒ \quad Dominio$$
 Ejemplo.
Ejemplo.
Sea la sucesión $f(n)=\displaystyle \bigg\{ \frac{n+1}{2n-1}\bigg\}$, donde los terminos de la sucesión son:
$$f(1)=2,\space f(2)=1,\space f(3)=\frac{4}{5},\space f(4)=\frac{5}{7},\space f(5)=\frac{2}{3}\space...$$
Los pares ordenados son: $$(1,2),\space (2, 2),\space (3, \frac{4}{5}),\space (4,\frac{5}{7}),\space (5,\frac{2}{3})\space...$$
por lo tanto, los elemento de la sucesión pueden escribirse como: $$2,\space 1,\space \frac{4}{5},\space \frac{5}{7},\space \frac{2}{3},\space ...,\space \frac{n+1}{2n-1}$$
 ¡Ten presente!
¡Ten presente!
En algunas circunstancias es conveniente tomar el primer término de una sucesión como $a_0$ y la sucesión es entonces $a_0,a_1,a_2.a_3,a_4,...a_n$
Una sucesión se puede describir por medio de una formula que representa el termino n-esimo.
 Ejemplos.
Ejemplos.
Observa la formula de la sucesión y los primeros terminos para $n=1,2,3,4,...$
(a). $\displaystyle \bigg\{ \frac{n}{n+1}\bigg\}_{n=1} \quad ⇒ \quad a_n= \frac{n}{n+1}$ $\space ⇒ \space$ $\bigg\{\frac{1}{2},\space \frac{2}{3},\space \frac{3}{4},\space \frac{4}{5},\space ... \frac{n}{n+1}\bigg\}$
(b). $\displaystyle \bigg\{ \frac{e^n}{n^2}\bigg\}_{n=1} \quad ⇒ \quad a_n= \frac{e^n}{n^2}$ $\quad ⇒ \quad$ $\bigg\{\frac{e}{2},\space \frac{e^2}{4},\space \frac{e^3}{8},\space \frac{e^4}{16},\space ...\frac{e^n}{n^2}\bigg\}$
(c). $\displaystyle \bigg\{ \frac{5^n}{2^n}\bigg\}_{n=1} \quad ⇒ \quad a_n= \bigg(\frac{5}{2}\bigg) ^n$ $\quad ⇒ \quad$ $\bigg\{\frac{5}{2},\space \frac{5^2}{2^2},\space \frac{5^3}{2^3},\space \frac{5^4}{2^4},\space ...\frac{5^n}{2^n}\bigg\}$
(d). $\displaystyle \bigg\{ \frac{(-1)^n n}{3^n}\bigg\}⇒a_n= \frac{(-1)^n n}{3^n}$ ⇒
$\bigg\{-\frac{1}{3},\space \frac{2}{9}, -\frac{3}{27},\space \frac{4}{81},... \frac{(-1)^n n}{3^n}\bigg\}$
 ¡Ten presente!
¡Ten presente!
Cuando se presentan los términos con alternancia en los signos, positivo y negativo, se presenta una multiplicación por potencias de (-1):
- El factor $(-1)^n$ significa que la sucesión empieza con signo negativo.
- El factor $(-1)^{n-1}$ o $(-1)^{n+1}$ significa que la sucesión empieza con signo positivo.
Definición del límite de una sucesión.
Una sucesión $\displaystyle \{a_n\}$, tiene el límite L y se escribe $$\lim_{x \to \infty}\{a_n\}=L \qquad o \qquad {\{a_n\} \to L} \space cuando \space {n \to \infty}$$ Si $n$ toma valores suficientemente grandes, entonces, si $\displaystyle \lim_{x \to \infty}\{a_n\}$ existe, decimos que la sucesión converge ( o es convergente), de lo contrario, se dice que la sucesión diverge ( o es divergente).
Las leyes de los límites tambien se cumplen para los límites de sucesiones:
Determine si la sucesión $\displaystyle \bigg\{ \frac{n}{2n+1}\bigg\}$ es convergente o divergente.
Al sustituir $\displaystyle \{a_n\} =\bigg\{ \frac{n}{2n+1}\bigg\}\quad$ por $\quad \displaystyle \lim_{x \to \infty} \{a_n\},\quad $ se tiene: $$ \lim_{x \to \infty} \frac{x}{2x+1}=\lim_{x \to \infty} \frac{\frac{d}{dy}(x)}{\frac{d}{dy}(2x+1)}=\lim_{x \to \infty} \frac{1}{2}=\frac{1}{2}$$ $$\hspace{-1.0cm}\color{blue}\uparrow L'Hopital$$
Por lo tanto, se concluye que la función converge y que converge a $\frac{1}{2}$.
Determine si la sucesión $\displaystyle \bigg\{ \frac{e^n}{n^2}\bigg\}$ es convergente o divergente.
Al sustituir $\displaystyle \{a_n\} =\bigg\{\frac{e^n}{n^2}\bigg\}\quad$ por $\quad \displaystyle \lim_{x \to \infty} \{a_n\},\quad $ se tiene: $$ \lim_{x \to \infty} \frac{e^x}{x^2}=\lim_{x \to \infty} \frac{\frac{d}{dy}(e^x)}{\frac{d}{dy}(x^2)}=\lim_{x \to \infty} \frac{\frac{d}{dy}(e^x)}{\frac{d}{dy}(x^2)}=\lim_{x \to \infty} \frac{e^x}{2}=\frac{1}{2}e^{\infty}=\infty$$ $$\hspace{-6.5cm}\color{blue}\uparrow \hspace{-2.0cm}\uparrow L'Hopital $$
Por lo tanto, se concluye que la función diverge.
- Una sucesión $\{a_n\}$ se denomina creciente si $a_n < a_{n+1}$ para toda $n \geq 1$, es decir, si $a_1 < a_2 < a_3< ...$.
- Una sucesión $\{a_n\}$ se denomina decreciente si $a_n>a_{n+1}$ para toda $n \geq 1$, es decir, si $a_1>a_2>a_3>...$.
Una sucesión es monótona si esta es creciente o decreciente.
Verificar si la sucesión $\displaystyle \bigg\{ \frac{n}{n+1}\bigg\}$ es creciente.
Se debe demostrar que $a_n < a_{n+1}$, por lo tanto, se tiene la equivalencia: $$\frac{n}{n+1} < \frac{n+1}{n+2}$$ Esta desigualdad es equivalente a la que obtenemos al multiplicar cruzadamente: $$n(n+2) < (n+1)(n+1) \\ \cancel {n^2+2n} < \cancel {n^2+2n}+1$$ $$0<1$$ Por lo tanto, la desigualdad es verdadera, entonces la sucesión es creciente.
Qué es una sucesión recurrente
Las sucesiones recurrentes son aquellas cuyos términos se obtienen operando con los términos anteriores.
Por ejemplo, en la sucesión: $$\bigg\{0, 1, 1, 2, 3, 5, 8, 13, 21,...\bigg\}$$
En este caso, a partir del tercer término, cada término se obtiene como la suma de los dos términos anteriores. El siguiente término de esta sucesión sería 34, ya que es la suma de los dos anteriores, es decir, $13+21$.
 Ejercicio. Sucesiones.
Ejercicio. Sucesiones.
Analicemos la convergencia o divergencia de uan sucesión.
Encuentre los términos de ${a_n}$ y determine si la sucesión converge o diverge, si es creciente o decreciente, oprima el botón solución para verificar la respuesta.

 ¡Recordemos!
¡Recordemos!
Si $n$ es un entero positivo, el símbolo $n!$, que se lee “$n$ factorial”, es el producto de los primeros $n$ enteros positivos:
$n!=1$ x $2$ x $3$ x $4$ x...x $n$.
Por ejemplo, $\quad 6!=1$ x $2$ x $3$ x $4$ x $5$ x $4 = 720$
Una propiedad importante del factorial está dada por:
$\quad n!=(n-1)!$ x $n$
Enunciada de una manera diferente, es equivalente a:
$\quad (n+1)!=n!(n+1)$
 Preguntas. Selección la respuesta correcta.
Preguntas. Selección la respuesta correcta.
Haz click sobre la respuesta correcta.
Series
El concepto de una serie se relaciona estrechamente con el concepto de sucesión, una serie es la suma infinta de los términos de una sucesión.
Se llama serie infinita, o simplemente una serie a la expresión: $$a_1+a_2+a_3+.....+a_n+...$$ donde, se denota con el simbolo: $$\sum_{n=1}^\infty a_n$$ Por ejemplo, $$\sum_{n=1}^\infty \frac{1}{2^n} = \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+...+\frac{1}{2^n}+...$$
Sucesión de sumas parciales.
Asociada con toda serie finita $\sum_{k=1}^\infty a_k$, existe una sucesión de sumas parciales $\{S_n\}$ cuyos términos están definidos por: $$ \begin{aligned} &S_1=a_1 \\ &S_2=a_1+a_2 \\ &S_3=a_1+a_2+s_3 \\.\\ &S_n=a_1+a_2+a_3+a_4+...+a_n =\sum_{k=1}^\infty a_k \end{aligned}$$
La sucesión de sumas parciales $\{S_n\}$ , para la serie $\displaystyle\sum_{k=1}^\infty \frac{1}{2^k}$ es: $$\begin{aligned} &S_1=\frac{1}{2}\\ &S_2=\frac{1}{2}+\frac{1}{4}\\ &S_3=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}\\ &S_4=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16} \\.\\.\\ &S_n=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+...+\frac{1}{2^k} \end{aligned}$$
Sea $\{a_n\}$ una sucesión y $s_n=\sum_{k=1}^n a_k =a_1+a_2+a_3+...+a_k$ la n-ésima suma parcial de la sucesión.
- Si la serie $\sum_{n=1}^\infty a_n$ es convergente si la sucesión de sumas parciales $S_n$ es convergente; esto es,
$$\displaystyle \lim_{n \to \infty} \{S_n\}=\lim_{n \to \infty} \sum_{k=1}^n a_k =S$$
Si $\displaystyle \lim_{n \to \infty} \{S_n\}$ no existe, entonces se dice que la serie es divergente.
Serie Geométrica
Este tipo de serie puede probarse como convergente o divergente a partir directamente de su sucesión de sumas parciales que tiene la forma:
$$\sum_{n=1}^{\infty} a (r)^{n-1}=a+ar+ar^2+ar^3+...+a r^{n-1}+...$$
Donde,
- $a:\space$ Primer término de la serie.
- $r:\space$ Se denomina la razón común y, su magnitud determina si una serie geométrica converge o diverge.
La razón(r) de una serie geométrica se calcula dividiendo términos consecutivos: $$ r=\frac{a_{n+1}}{a_n}$$
Si $|r| < 1$, entonces una serie geométrica converge y su suma es $$\sum_{n=1}^{\infty} a r^{n-1}=\frac{a}{1-r}$$
Si $|r| \geq 1$, entonces una serie geométrica diverge.
 Exploración. Serie geométrica.
Exploración. Serie geométrica.
Situación problema.
Observa la siguiente situación problema, oprime el botón solución A o solución B para verificar las respuestas.

Verificar si la serie $\displaystyle \sum_{n=1}^{\infty} (2^{2n})(3^{1-n})$ es convergente o divergente.
Expresemos la serie dada en una serie geométrica, utilizamos propiedades de la potenciación: $$(2^{2n})(3^{1-n}) = 4^n\frac{3}{3^n}=3\frac{4^n}{3^n}=3 \bigg(\frac{4}{3}\bigg)^n$$ Multiplicamos la expresión por $\frac{4}{4}$, se tiene, $$\bigg(\frac{4}{4}\bigg) 3 \bigg(\frac{4}{3}\bigg)^n=4\bigg(\frac{3}{4}\bigg) \bigg(\frac{4}{3}\bigg)^n=4\bigg(\frac{4}{3}\bigg)^{-1} \bigg(\frac{4}{3}\bigg)^n=4\bigg(\frac{4}{3}\bigg)^{n-1}$$ Por lo tanto, se tiene la serie geométrica: $$\sum_{n=1}^{\infty} (2^{2n})(3^{1-n})=\sum_{n=1}^{\infty} 4\bigg(\frac{4}{3}\bigg)^{n-1}$$ donde, $\displaystyle \quad r=\frac{4}{3} > 1\quad$ entonces, la serie diverge.
Todo decimal repetido es una serie geométrica convergente.
$$1,931313131...= 1,9 + \frac{31}{10^3}+\frac{31}{10^5}+\frac{31}{10^7}+...$$
- Condición necesaria para convergencia.
Si la serie $\displaystyle \sum_{n=1}^{\infty} a_k$ converge, entonces $\displaystyle \lim_{n \to \infty} a_n=0$ - Prueba del término n-ésimo para divergencia.
Si $\displaystyle \lim_{n \to \infty} a_n =\not 0$ entonces la serie $\displaystyle \sum_{n=1}^{\infty} a_k$ diverge - Múltiplo constante de una serie.
Si $c$ es cualquier constante distinta de cero, entonces las series $\displaystyle \sum_{n=1}^{\infty} a_k$ y $\displaystyle \sum_{n=1}^{\infty} ca_k$ convergen ambas o divergen ambas.
- Suma de dos series convergentes.
Si $\displaystyle \sum_{n=1}^{\infty} a_k$ y $\displaystyle \sum_{n=1}^{\infty} b_k$ convergen a $S_1$ y $S_2$, respectivamente, entonces $\displaystyle \sum_{n=1}^{\infty} (a_k \pm b_k)$ convergen a $S_1 \pm S_2$.
- Suma de una serie convergente y una divergente.
Si $\displaystyle \sum_{n=1}^{\infty} a_k$ converge y $\displaystyle \sum_{n=1}^{\infty} b_k$ diverge, entonces $\displaystyle \sum_{n=1}^{\infty} (a_k + b_k)$ diverge.
Serie Armónica
La serie armónica es la suma de los recíprocos de los enteros positivos: $$\sum_{n=1}^{\infty} \frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{n}+...$$
Nicole Oresme demostró que la serie armónica es divergente, esto es, su suma crece sin parar, no tiene límite.
Esta divergencia de la serie armónica pese a que $\frac{1}{n}$ tiende a cero a medida que $n$ aumenta da lugar a resultados curiosos.
 Ejemplo. Demostración de que la serie armónica diverge.
Ejemplo. Demostración de que la serie armónica diverge.
Serie Telescópica
Una serie es telescópica cuando viene dada por la forma: $$\sum_{n=1}^{\infty} a_k-a_{k+1}$$ Observe que la suma parcial n-ésima es: $$S_n=\sum_{k=1}^{\infty} a_k-a_{k+1}= (a_1-a_2)+(a_2-a_3)+(a_3-a_4)+...$$ Los paréntesis se han colocado solamente para mostrar cómo aparece cada sumando.
Quitándo los paréntesis se hace evidente que se eliminan casi todos los terminos excepto el primero y el último. En definitiva la n-ésima suma parcial nos queda $$S_n=\sum_{n=1}^{\infty} a_k-a_{k+1}$$
Se tiene que una serie telescópica converge si y sólo si $a_k$ tiende a un número finito cuando ${n \to \infty}$.
La serie $\displaystyle S_n=\sum_{n=1}^{\infty} \frac{1}{n^2+n}$ ¿convege o diverge?
(Utilizando fracciones parciales), se tiene que:
$$S_n=\sum_{n=1}^{\infty} \frac{1}{n^2+n}=\sum_{n=1}^{\infty} \bigg(\frac{1}{n}-\frac{1}{n+1}\bigg)$$
La suma parcial n-ésima es:
$$S_n= \bigg(1-\cancel{\frac{1}{2}}\bigg)+\bigg(\cancel{\frac{1}{2}}-\cancel{\frac{1}{3}}\bigg)+\bigg(\cancel{\frac{1}{3}}-\cancel{\frac{1}{4}}\bigg)+...\bigg(\cancel{\frac{1}{n}}-\frac{1}{n+1}\bigg)$$
$$S_n= \bigg(1-\frac{1}{n+1}\bigg)$$
Entonces, su suma está dada por:
$$\lim_{x \to \infty} S_n=1-\lim_{x \to \infty} \bigg(\frac{1}{n+1}\bigg)=1-0=1$$
por tanto, la serie es convergente.
Determinemos si la serie $\displaystyle \sum_{n=1}^{\infty} \frac{n}{5n + 1}$ es convergente o divergente. Si es convergente, encuentremos su suma.
Una condición para que la serie $\displaystyle \sum_{n=1}^{\infty} a_k$ sea convergente, es que $\displaystyle \lim_{n \to \infty} a_n=0$, es decir, $$ \lim_{x \to \infty} \frac{x}{5x+1}=\lim_{x \to \infty} \frac{\frac{d}{dy}(x)}{\frac{d}{dy}(5x+1)}=\lim_{x \to \infty} \frac{1}{5}=\frac{1}{5}=\not 0$$ $$\hspace{-1.0cm}\color{blue}\uparrow L'Hopital$$
Por lo tanto, se concluye que la serie diverge
La serie $\displaystyle S_n=\sum_{n=1}^{\infty} \bigg(\frac{1}{n^2+n}+4\bigg(\frac{3}{4}\bigg)^{n-1}\bigg)$ ¿convege o diverge?
En consecuencia, la suma de la serie es $$ S=\sum_{n=1}^{\infty} \bigg(\frac{1}{n^2+n}+4\bigg(\frac{3}{4}\bigg)^{n-1}\bigg)= 1 + 16 =17$$
Prueba de la Integral
Esta técnica es importante porque se utiliza para demostrar la divergencia o convergencia de muchas otras series. Esta prueba, llamada prueba de la integral, compara una suma infinita con una integral impropia. Es importante tener en cuenta que esta prueba solo se puede aplicar cuando consideramos una serie cuyos términos son todos positivos.
Suponga que $\displaystyle \sum_{n=1}^{\infty} a_k$ es una serie de términos positivos y $f$ es una función continua que es no negativa y decreciente sobre $[1,\infty)$ tal que $f(k)=a_k$ para $k \geq 1$.
- $\quad$ Si $ \int_{1}^{+\infty} f(x)\, dx \quad$ converge, entonces $\displaystyle \sum_{n=1}^{\infty} a_k$ converge.
- $\quad$ Si $ \int_{1}^{+\infty} f(x)\, dx \quad$ diverge, entonces $\displaystyle \sum_{n=1}^{\infty} a_k$ diverge.
Para ver cómo funciona la prueba de la integral, usaremos la serie armónica $$\sum_{n=1}^{\infty} \frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{n}+...$$ como ejemplo, para demostrar que diverge.
Sea $\displaystyle f(x)=\frac{1}{x} \quad$ con $x \in [1,\infty)$, $f$ es una función continua, positiva y decreciente $\displaystyle \bigg(\frac{1}{n}>\frac{1}{n+1}\bigg)$
Evaluemos $\displaystyle \int_{1}^{+\infty} f(x)\, dx$, entonces, se tiene: $$\int_{1}^{+\infty} f(x)\, dx=\int_{1}^{+\infty} \frac{1}{x}\, dx=\lim_{b \to \infty} \int_{1}^{b} \frac{1}{x}\, dx$$ $$\begin{aligned}\lim_{b \to \infty} \int_{1}^{b} \frac{1}{x}\, dx&=\lim_{b \to \infty} [Ln(x)\Big]_1^b \\ &=\lim_{b \to \infty} [Ln(b)-Ln(1)] \\ &=\lim_{b \to \infty} [Ln(b)]=+\infty \end{aligned}$$
Por lo tanto, la integral $\displaystyle \int_{1}^{+\infty} \frac{1}{x}\, dx \quad $ diverge. Por la prueba de la integral, se deduce que la serie $\displaystyle \sum_{n=1}^{\infty} \frac{1}{n}\quad $ diverge.
La p-serie
La prueba de la integral es particularmente útil en cualquier serie de la forma
$$\sum_{n=1}^{\infty} \frac{1}{n^p}=1+\frac{1}{2^p}+\frac{1}{3^p}+\frac{1}{4^p}+...+\frac{1}{n^p}+...$$
La serie anterior se denomina p-serie.
- La p-serie es convergente si $\quad p>1$
- La p-serie es divergente si $\quad p \le 1$.
Por ejemplo,
- La serie $\displaystyle \sum_{n=1}^{\infty} \frac{1}{\sqrt[5]{n}}$ es equivalente a $\displaystyle \sum_{n=1}^{\infty} \frac{1}{n^{1/5}}$ y es divergente, ya que es una p-serie,
donde $\displaystyle p=\frac{1}{5}<1$
- La serie $\displaystyle \sum_{n=1}^{\infty} \frac{1}{n^4}$ es convergente, ya que es una p-serie, donde $\displaystyle p=4>1$
Prueba de comparación
Sabemos exactamente cuándo convergen o cuándo divergen las series geométricas, armónicas, p-series. Vamos a ver cómo usar la convergencia o divergencia de estas series para probar la convergencia o divergencia de otras series, utilizando un método llamado prueba de comparación.
Suponga que $\displaystyle \sum_{n=1}^{\infty} a_k$ y $\displaystyle \sum_{n=1}^{\infty} b_k$ son series de términos positivos.
- $\quad$ Si $\displaystyle \sum_{n=1}^{\infty} b_k$ es convergente y $a_n \le b_n$, entonces $\displaystyle \sum_{n=1}^{\infty} a_k$ tambien es convergente.
- $\quad$ Si $\displaystyle \sum_{n=1}^{\infty} b_k$ es divergente y $a_n \ge b_n$, entonces $\displaystyle \sum_{n=1}^{\infty} a_k$ tambien es divergente.
La idea de la prueba de comparación es tomar una serie convergente o divergente conocida y se multiplica cada uno de sus términos por algún número, luego la nueva serie también converge o diverge. No importa si el multiplicador es grande o pequeño, ya que cualquier número de la suma finita de la serie original es también un número finito. Una serie es como un múltiplo de otra serie.
Determinemos si la serie $\displaystyle \sum_{n=1}^{\infty} \frac{1}{2n^4 + 1}$ es convergente o divergente.
Tomemos la serie $$\displaystyle \sum_{n=1}^{\infty} \frac{1}{n^4}$$ que es una p-serie, donde $p=4>1$ entonces es convergente.
Ahora comparando con la serie original, se tiene que $$\quad \displaystyle \frac{1}{2n^4 + 1}<\frac{1}{n^4}$$ para cada entero positivo n.
Por lo tanto, podemos concluir que la serie dada $\displaystyle \sum_{n=1}^{\infty} \frac{1}{2n^4 + 1}$ es convergente.
Prueba de comparación del límite
Otro tipo de prueba de comparación implica tomar el límite del cociente entre el término general de la serie $\displaystyle \sum_{n=1}^{\infty} a_k$ y el término general de la serie de
prueba $\displaystyle \sum_{n=1}^{\infty} b_k$ que se sabe que es convergente o divergente.
Suponga que $\displaystyle \sum_{n=1}^{\infty} a_k$ y $\displaystyle \sum_{n=1}^{\infty} b_k$ son series de términos positivos. Si $$\lim_{n \to \infty} \frac{a_n}{b_n}=L$$ donde $L$ es finita y $L>0$ entonces las dos series son ya sea ambas convergentes o ambas divergentes.
Retomando el ejemplo anterior, tomamos como:
$\displaystyle a_n=\frac{1}{2n^4 + 1}\quad$ y $\quad\displaystyle b_n=\frac{1}{n^4}$
Se tiene que: $$\lim_{n \to \infty} \frac{\frac{1}{2n^4 + 1}}{\frac{1}{n^4}}=\lim_{n \to \infty} \frac{n^4}{2n^4 + 1}=\frac{1}{2}$$Por tanto, se compueba que son convergentes las series.
La siguiente tabla resume la prueba de comparación directa.
Sea $\displaystyle \sum_{n=1}^{\infty} a_k$
una serie de términos positivos y $\displaystyle \sum_{n=1}^{\infty} b_k$ una serie que se sabe que converge o diverge (una serie de pruebas).
Comparación de términos | Serie de prueba $$\displaystyle \sum_{n=1}^{\infty} b_k$$ | Conclusión sobre $$\displaystyle \sum_{n=1}^{\infty} a_k$$ |
|---|---|---|
$a_n \le b_n$ | Converge | Converge |
$a_n \le b_n$ | Diverge | Ninguna |
$a_n \ge b_n$ | Diverge | Diverge |
$a_n \ge b_n$ | Converge | Ninguna |
La prueba de comparación funciona muy bien si podemos encontrar una serie comparable que satisfaga la hipótesis de la prueba. Sin embargo, a veces encontrar una serie apropiada puede ser difícil. . |
Prueba de la razón y la raíz
Está prueba es muy útil para determinar si una serie dada es absolutamente convergente.
Suponga que $\displaystyle \sum_{n=1}^{\infty} a_k$ es una serie de términos positivos donde $$\lim_{n \to \infty} \frac{a_{n+1}}{a_n}=L$$
- $\quad$ Si $L<1$, la serie es convergente.
- $\quad$ Si $L>1$ o $L=\infty$, la serie es divergente.
- $\quad$ Si $L=1$, la prueba no proporciona ninguna información.
Por ejemplo, sea la serie $\displaystyle \sum_{n=1}^{\infty} \frac{3^n}{n!}$ determinemos si la serie converge o diverge, tenemos $$L=\lim_{n \to \infty} \frac{a_{n+1}}{a_n}=\lim_{n \to \infty} \frac{\frac{3^{n+1}}{(n+1)!}}{\frac{3^n}{n!}}=\lim_{n \to \infty} \frac{3^{n+1}n!}{3^n(n+1)!}$$ Se tiene que $(n + 1)! = n!(n + 1)$, $\quad$ entonces $$L=\lim_{n \to \infty} \frac{3^{n+1}}{3^n(n+1)}=\lim_{n \to \infty} \frac{3}{n+1}=0$$ como $L<1$, la serie es convergente.
Prueba de la raíz
La prueba, implica tomar la raíz n-ésima del término n-ésimo.
Suponga que $\displaystyle \sum_{n=1}^{\infty} a_k$ es una serie de términos positivos donde $$\displaystyle\lim_{n \to \infty} \sqrt[n]{a_n}=\lim_{n \to \infty} =(a_n)^{1/n}=L$$
- $\quad$ Si $L<1$, la serie es convergente.
- $\quad$ Si $L>1$ o $L=\infty$, la serie es divergente.
- $\quad$ Si $L=1$, la prueba no proporciona ninguna información.
Por ejemplo, sea la serie $\displaystyle \sum_{n=1}^{\infty} \frac{3^n}{n^n}$ determinemos si la serie converge o diverge, tenemos $$L=\lim_{n \to \infty} =(a_n)^{1/n}=\lim_{n \to \infty} \bigg( \bigg(\frac{3}{n}\bigg)^n\bigg)^{1/n} $$ Entonces, se tiene que $$L=\lim_{n \to \infty} \frac{3}{n}=0$$ como $L<1$, la serie es convergente.
Series alternantes
Cualquier serie cuyos términos alternan entre valores positivos y negativos se denomina serie alternante.
Se puede escribir una serie alternante, donde $a_n \ge 0$ para todos los enteros positivos $n$ como $$\sum_{n=1}^{\infty} (-1)^na_n=-a_1+a_2-a_3+a_4-...$$ $$\sum_{n=1}^{\infty} (-1)^{n+1}a_n=a_1-a_2+a_3-a_4+...$$
Se observa que el n-ésimo término de una serie alternante es de la forma
$\displaystyle b_n=(-1)^na_n \quad$ o $\quad \displaystyle b_n=(-1)^{n+1}a_n$
donde $b_n$ es un número positivo
Por ejemplo,
La serie $\displaystyle \sum_{n=1}^{\infty} \bigg(-\frac{1}{3}\bigg)^{n}=-\frac{1}{3}+\frac{1}{9}-\frac{1}{27}+\frac{1}{81}+... $ es una serie geométrica convergente, ya que $\quad \displaystyle r=|-\frac{1}{3}|<1$
Prueba de la serie alternante
Las pruebas de convergencia que hemos visto hasta aquí aplican sólo a series con términos positivos. En esta sección se trabajará con series cuyos términos no son necesariamente positivos.
Si la serie alternante $\sum_{n=1}^{\infty} (-1)^{n+1}a_n=a_1-a_2+a_3-a_4+...$ satisfase que
- $\quad$ Si $a_{n+1}\le a_n$, $\quad$ para toda $n$
- $\quad \displaystyle\lim_{n \to \infty} a_n=0$
La serie es convergente.
Para la serie $\displaystyle 1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+...=\sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n}$ Conocida como Serie armónica alternante. Se observa que mientras la serie armónica diverge, la serie armónica alternante converge.
Entonces, se tiene que se satisfase que:
- $\quad$ $a_{n+1}< a_n$, $\quad$ donde $\quad$ $\displaystyle \frac{1}{n+1}<\frac{1}{n}$ $\quad$ y que
- $\quad \displaystyle \lim_{n \to \infty} a_n=\lim_{n \to \infty} \frac{1}{n}= 0$
Por lo tanto, la serie serie armónica alternante es convergente, por la prueba de la serie alternante.
 Ejercicio.Series.
Ejercicio.Series.
Convergentes o divergentes
Determine si la serie converge o diverge, oprima el botón solución para verificar la respuesta.


