Imprimir

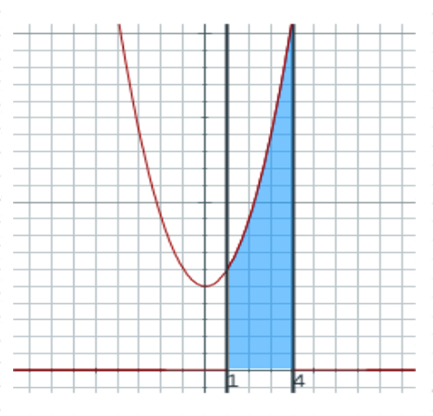
Ejercicio 1.
Calcular el área de una región acotada por la curva $f(x)=x^2+5$ y las rectas
$x=1, \space x=4$

Solución. $A=\int_{a}^{b} f(x)\, dx =\int_{1}^{4} (x^2+5)\, dx$

$\begin{aligned} A=\int_{1}^{4} (x^2+5)\, dx &= \frac{x^3}{3}+5x \space\space \bigg|_{1}^{4} \\ &= \frac{4^3}{3}+5(4) -\bigg( \frac{1^3}{3}+5(1) \bigg)\\ &= \frac{63}{3}+15=36\\ \end{aligned}$

por tanto, $\displaystyle\qquad A= \int_{1}^{4} (x^2+5)\, dx =36 u^2$

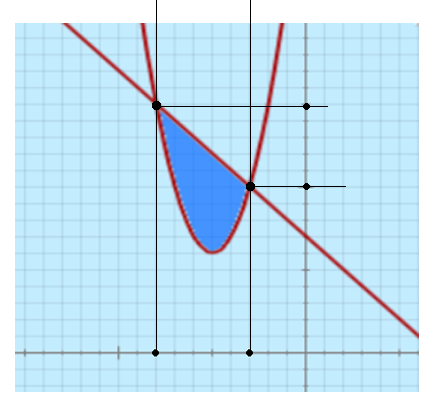
Ejercicio 2.
Calcular el área encerrada por las funciones $g(x)=7-x$ $f(x)=x^2+10x+31$

Solución.

Se debe hallar los puntos de corte entre las funciones, para esto, se igualan las funciones y se hallan los valores de $x$: $7-x=x^2+10x+31$ $x^2+11x+24=0$ $(x+8)(x+3)=0$ por lo tanto, $x=-8, x=-3$ $A=\int_{a}^{b} (f(x)-g(x))\, dx$ $A=\int_{-3}^{-8} (7-x-(x^2+10x+31))\, dx$ $\begin{aligned} A=\int_{-3}^{-8} (-x^2-11x-24)\, dx &= -\frac{x^3}{3}-\frac{11}{2}x^2-24x \space\space \bigg|_{-3}^{8} \\ &= \frac{63}{2}-\frac{32}{3}=\frac{125}{6}\\ \end{aligned}$

por tanto, $\displaystyle\qquad A= \int_{-3}^{-8} (-x^2-11x-24)\, dx =\frac{125}{6} u^2$

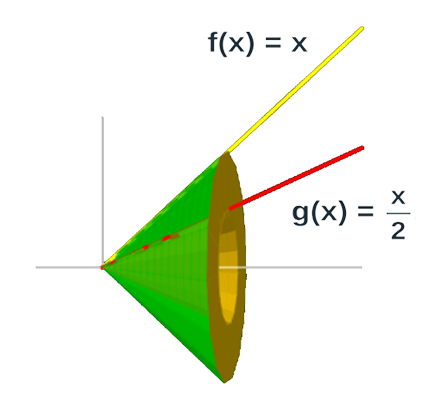
Ejercicio 3.
Cálcular del volúmen de un sólido formado entre el intervalo $[0, 3]$ y las funciones
$f(x)=x$ y $\displaystyle g(x)= \frac{x}{2}$,
al rotar en el eje $x$.

Solución.

Sólido de sección hueca, para esto utilizamos la expresión: $V=\pi \int_{a}^{b} (f(x)^2 - g(x)^2) \, dx=\pi \int_{0}^{3} (x^2 - (\frac{x}{2})^2) \, dx$ $\begin{aligned} V &= \pi \int_{0}^{3} (x^2 - (\frac{x}{2})^2) \, dx \\ &= \pi \int_{0}^{3} (x^2 - \frac{x^2}{4}) \, dx \\ &= \pi \int_{0}^{3} \frac{3}{4}x^2 \, dx \\ &= \pi \Big[{\frac{3}{4}x^2} \space \Big]_{0}^{3} \\ &= \pi \Big[{\frac{3}{4}(3)^2}-{\frac{3}{4}(0)^2}\Big] \\ &= \frac{27}{4}\pi \end{aligned}$ Por lo tanto, $V = \pi \int_{0}^{3} (x^2 - (\frac{x}{2})^2) \, dx = \frac{27}{4}\pi \space u^3$


Imprimir