Mostrando artículos por etiqueta: puzles
Si te gustan los puzles ¡estás de enhorabuena! ya que hemos publicado una unidad didáctica que te permite elaborarlos de una forma sencilla y cómoda, y contando con diferentes tipos y versiones.
En la unidad didáctica de Juan Guillermo Rivera Berrío, de la Red Educativa Digital Descartes Colombia, titulada "Puzles Descartes" se muestra y detalla, paso a paso, cómo elaborar puzles análogos a los que se presentan como ejemplo.
Estos atractivos puzles son actividades y test de memoria, de arrastre, de asociación y de intercambio, y se generan sin más que realizar simples y usuales tareas de edición de imágenes y de ficheros de texto. Se aprovecha el potencial educativo y la interactividad intrínseca de Descartes sin necesidad de desarrollar escenas de Descartes. Para ello se usan escenas, previamente desarrolladas, como cajas negras que recibiendo como entrada un conjunto de datos preparados por el profesor o profesora generan una actividad interactiva que pueden utilizarse e incorporarse en el proceso de enseñanza-aprendizaje. El profesorado no necesita conocer cómo elaborar la escena de Descartes sino que la utiliza como soporte para la consecución de su objetivo educativo, su tarea se centra en el diseño y elaboración de los datos e imágenes auxiliares que se usan como entrada o parámetros del puzle.
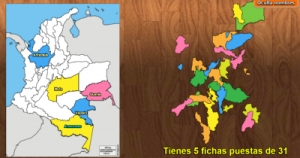
Los materiales que pueden elaborarse tienen encuadre en cualquier nivel educativo y materia, ya que es el contenido en sí el que marca su ubicación. Por ejemplo, un test de asociación puede establecerse entre poliedros regulares y sus denominaciones o bien entre imágenes de animales y sus nombres en castellano o en otro idioma; o en un test de memoria es posible identificar figuras geométricas con igual o análoga forma o bien animales de la misma especie, o palabras sinónimas. En definitiva la creatividad docente es la que mueve la herramienta en la consecución de logros educativos.
Las actividades que son necesarias realizar para el desarrollo de estos materiales se encuadran en tres tipos de acciones:
- Manipulación y transformación de imágenes.
- Edición de textos sin formato, tipo txt.
- Preparación de los datos necesarios para el recurso.
Sencillas tareas que utilizan herramientas auxiliares que se explicitan y describen en dicha unidad. Pero la tarea esencial y principal, la que hay que tener siempre presente y la que marca el éxito educativo, se centra en la focalización del objetivo docente, la planificación del mismo y la elección de la estrategia a seguir para su consecución, es decir, abordar el diseño conceptual a partir del cual podremos concretar el diseño material, que a su vez se plasmará en una temática y un tipo de actividad a desarrollar.
Os animamos a elaborar vuestos puzles y a que nos lo enviéis a Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo. para publicarlos en nuestro, vuestro, servidor.
La semana pasada en Radio Descartes, en el espacio “¿Quién es el personaje misterioso?” entrevistamos a una genial matemática nacida en Londres en 1815. Fue una adelantada a su tiempo en más de 100 años al ser capaz de describir con acierto las posibilidades de la máquina analítica que diseñara en aquel tiempo Charles Babbage y para la cual desarrolló un sistema simbólico de representación de instrucciones y concibió un “plan” o secuencia de instrucciones, basadas en tarjetas perforadas, para calcular la serie de números de Bernoulli utilizando los conceptos de bucle y subrutina.
Si a Charles Babbage se le considera el padre del hardware de un ordenador que podría funcionar de forma muy similar a como lo hacen los actuales, nuestra matemática, colaboradora en el proyecto de Babbage, se convirtió en la primera programadora de la historia y por tanto considerada madre de la programación de ordenadores.
Muestra genial matemática, cuya identidad se puede desvelar al montar el puzle realizado con DescartesJS que se acompaña a este artículo, en 1843 pudo asegurar que la máquina analítica no sólo podría servir para hacer cálculos matemáticos sino otras operaciones con informaciones de cualquier naturaleza como música o imágenes.
La imagen del puzle tipo jigsaw (piezas irregulares), es una composición donde aparece la elegante figura de nuestro personaje femenino y de fondo diferentes alusiones a la máquina analítica y a su “plan” de instrucciones.
Las 16 piezas barajadas, obtenidas al cortar la imagen, se sitúan amontonadas a la derecha de la escena. Para descubrir a nuestro personaje misterioso hay que montar estas piezas sobre una cuadrícula 4x4 a la izquierda de la escena arrastrándolas con clic mantenido y soltarlas sobre el cuadro donde quedan encajadas. Si la pieza se sitúa correctamente ya no es posible arrancarla de su cuadro. Si se montan dos piezas sobre un mismo cuadro, éste, quedará resaltado con color rojo advirtiendo de esta situación.
Inicialmente, a modo de ayuda, se puede ver detrás de la cuadrícula la composición en escala de grises. Un control de tipo botón permite ocultarla y así se sugiere para que el montaje del puzle suponga un mayor reto.
Cuando el puzle se completa aparece el nombre del personaje, una caricatura y se puede visionar un vídeo: se trata de un cuento audio descrito extraído del libro "La Liga de las Mujeres Extraordinarias" y que por su formato y contenido puede resultar interesante y muy motivador para los alumnos de Primaria y Educación Secundaria Obligatoria aunque a mí que ya peino canas también me ha gustado mucho.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana cuyo tamaño se adapta automáticamente al dispositivo de visualización y se acomoda manualmente al gusto personal pues emplea un Diseño Web Adaptativo (RWD).
El autor de este artículo, la edición de las imágenes y la programación del puzle es de Ángel Cabezudo Bueno y tiene licencia CC BY-NC-SA 4.0
El puzle de arrastre básico, tipo jigsaw, tiene su origen en una documentación aportada por Juan Guillermo Rivera Berrío.
Gracias por la atención que ha recibido la entrevista de este noveno personaje matemático y quedáis invitados para la siguiente.
Por Ángel Cabezudo Bueno – 13 de abril de 2015
La semana pasada en Radio Descartes, en el espacio “¿Quién es el personaje misterioso?” entrevistamos uno de los más grandes científicos de la antigüedad y de la historia: físico, ingeniero, inventor, astrónomo y matemático griego. Nació en Siracusa, Sicilia, en el 287 a.C.
Entre sus avances en física se encuentra sus fundamentos sobre estática, hidrostática y explicación de la palanca.
Estuvo muy interesado por las matemáticas a las que dio un gran impulso al estudiar las áreas y los volúmenes de cuerpos limitados por curvas. Era muy habilidoso y trataba de forma diferente la geometría al hacer demostraciones apoyándose en la mecánica. Dedicó su libro “El Método” a Eratóstenes al que conoció en su paso por la biblioteca de Alejandría.
Desvelamos en el presente artículo la identidad de este matemático mediante el montaje de una imagen dividida en 16 piezas de un puzle tipo jigsaw (piezas irregulares). Se trata de un grabado en colores sepia de nuestro personaje y representa el momento en que es sorprendido por un soldado romano en el asedio de Siracusa. Dibujaba figuras geométricas en la arena y le recriminó al ser molestado. Airado, el soldado le dio muerte con su espada.
Cuando el puzle se completa aparece el nombre del personaje… y algún detalle más.
También se puede visionar un interesante vídeo titulado “La sorprendente historia de…”, cuyo autor es Felipe Bonilla Aguilar ; el coordinador general de este proyecto es José Luis Abreu León.
La siguiente imagen lleva un enlace al puzle que utiliza Diseño Web Adaptativo (RWD Responsive Web Desing).
La edición de las imágenes y la programación del puzle son de Ángel Cabezudo Bueno y tiene licencia CC BY-NC-SA 4.0
El puzle de arrastre básico tiene su origen en una documentación aportada por Juan Guillermo Rivera Berrío.
Con este personaje, que hace el número doce de la serie, cerramos este ciclo dedicado a los matemáticos célebres en la historia donde hemos pretendido también dar a conocer su faceta humana y no sólo científica. Esperamos haber acertado en el intento y damos las gracias por la atención recibida.
Por Ángel Cabezudo Bueno – 9 de febrero de 2015
La semana pasada en Radio Descartes, en el espacio “¿Quién es el personaje misterioso?” entrevistamos al autor del texto más influyente de la ciencia moderna: “Philosophiae naturalis principia mathematica” – en castellano, “Principios matemáticos de la filosofía natural” donde presenta los fundamentos de la física y de la astronomía formulados en el lenguaje de la geometría pura. Se trata de una obra deductiva donde, a partir de unas proposiciones muy generales, se pueden demostrar propiedades mecánicas a modo de teoremas. La primera edición en latín de 1687, marcó un punto de inflexión en la historia de la ciencia y es considerada, por muchos, como la obra científica más importante jamás publicada.
Muestro genial científico, cuya identidad se puede desvelar al montar el puzle realizado con DescartesJS que se acompaña a este artículo, creía en la universalidad del pensamiento y nos dijo que buscó la verdad en todas las áreas del conocimiento incluyendo las Sagradas Escrituras y la alquimia.
Recibió en vida los mayores honores y reconocimientos. En el momento de su muerte, acaecida en Londres en 1727, fue tratado como un héroe y sepultado con la élite en la Abadía de Westminster.
La imagen del puzle tipo jigsaw (piezas irregulares), es un grabado a color de nuestro personaje, de joven, observando la descomposición de la luz solar cuando atraviesa un prisma de cristal. Las 16 piezas barajadas, obtenidas al cortar la imagen, se sitúan amontonadas a la derecha de la escena. Para descubrir a nuestro personaje misterioso hay que montar estas piezas sobre una cuadrícula 4x4 a la izquierda de la escena arrastrándolas con clic mantenido y soltándolas sobre el cuadro donde quedan encajadas. Si la pieza se sitúa correctamente ya no es posible arrancarla de su cuadro. Si se montan dos piezas sobre un mismo cuadro, éste, quedará resaltado con color rojo advirtiendo de esta situación.
Inicialmente, a modo de ayuda, se puede ver detrás de la cuadrícula la composición en escala de grises. Un control de tipo botón permite ocultarla y así se sugiere para que el montaje del puzle suponga un mayor reto.
Cuando el puzle se completa aparece el nombre del personaje, una caricatura y se puede visionar un vídeo: El número 7 de la serie “Universo Matemático” emitido por La 2 de TVE, titulada “A hombros de gigantes…” de la que es guionista y presentador Antonio Pérez Sanz.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana cuyo tamaño se adapta automáticamente al dispositivo de visualización pues emplea un Diseño Web Adaptativo (RWD Responsive Web Desing).
La edición de las imágenes y la programación del puzle es de Ángel Cabezudo Bueno y tiene licencia CC BY-NC-SA 4.0.
El puzle de arrastre básico, tipo jigsaw, tiene su origen en una documentación aportada por Juan Guillermo Rivera Berrío.
Gracias por la atención que ha recibido este décimo personaje matemático y no os perdáis el siguiente.
Esta entrada participa en la edición 5.X: Sofia Kovalévskaya del Carnaval de Matemáticas, cuyo blog anfitrión es ::ZTFNews.
El Carnaval de Matemáticas es una iniciativa que tiene por objeto acercar las Matemáticas al público, en general, e intentar mostrar que son más accesibles de lo que aparentan. Para ello, durante una semana al mes, se publican artículos de divulgación matemática en la blogosfera de habla hispana, consiguiendo una mayor densidad de producciones sobre "La reina de las ciencias", como la denominó Carl Friedrich Gauss.
Desde RED Descartes hemos decidido contribuir a esta edición con nuestro pequeño homenaje a la protagonista de este Carnaval, así que os dejamos una entrevista en Radio Descartes, publicada como VI Personaje Misterioso, y un puzle realizado con DescartesJS para tablet, smartphone y cualquier ordenador, que se publicó en su momento como Descubrimos al VI Personaje Misterioso.
¿Se te ocurre mejor forma de conocer a la protagonista de este Carnaval que dialogar con ella?
Esperamos que sea de vuestro agrado.
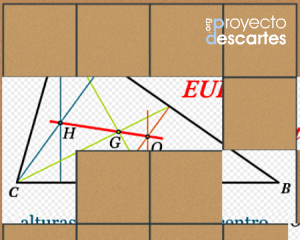Título: Puzles de puntos notables del triángulo
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: 3º ESO(14-15 años)
Idioma: Castellano
Autoría: Ángel Cabezudo Bueno
Haz clic en la imagen para abrir el recurso
Descargar recurso Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm
Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.
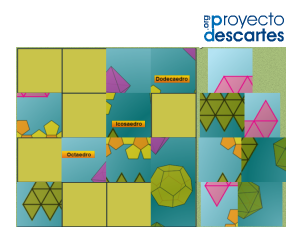Título: Rompecabezas de geometría
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana y tridimensional
Nivel/Edad: 6º Primaria (11 años)
Idioma: Castellano
Autoría: Ángel Cabezudo Bueno
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm
Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.
La semana pasada en Radio Descartes, en el espacio “¿Quién es el personaje misterioso?” entrevistamos al que se considera; primer algebrista de Europa (cronológicamente hablando) y como el introductor del sistema numérico árabe.
Resumiendo lo que nos dijo en su entrevista:
- Estudió una ciudad del norte de África, donde trabajaba su padre, bajo la dirección de un maestro árabe. Tuvo ocasión de conocer el sistema de numeración indo-árabe, del cual se convirtió en un acérrimo defensor.
- Aunque su parte favorita fue la aritmética, aprendió también geometría y álgebra.
- Nos dio pruebas de la “magia” del número Phi o Número Áureo.
- Una vez que regresó a su patria, en Italia, trató de enseñar las ventajas del cálculo con el sistema de numeración arábigo frente al que se enseñaba con el ábaco y escribió un libro donde recogió todo este saber.
- Poco a poco se fueron enseñando los nuevos signos para representar números y sus operaciones a artesanos, comerciantes y mercaderes.
Hoy, trascurrida una semana, corresponde desvelar su identidad, como sigue siendo habitual, a través un puzle realizado con DescartseJS. La imagen del puzle tipo jigsaw (piezas irregulares), es una composición donde aparece la efigie de nuestro personaje y de fondo diferentes manifestaciones del número Phi y de su famosa sucesión asociada.
Las 16 piezas barajadas, obtenidas al cortar la imagen, se sitúan amontonadas a la derecha de la escena. Para descubrir a nuestro personaje misterioso hay que montar estas piezas sobre una cuadrícula 4x4 a la izquierda de la escena arrastrándolas con clic mantenido y soltándolas sobre el cuadro donde quedan encajadas. Si la pieza se sitúa correctamente ya no es posible arrancarla de su cuadro. Si se montan dos piezas sobre un mismo cuadro, éste, quedará resaltado con color rojo advirtiendo de esta situación.
Inicialmente, a modo de ayuda, se puede ver detrás de la cuadrícula la composición poco contratada y con tonalidades grises. Un control de tipo botón permite ocultarla y así se sugiere para que el montaje del puzle suponga un mayor reto.
Cuando el puzle se completa aparece a la derecha el nombre del personaje, su caricatura en color, se escucha un brevísimo fragmento de una pieza musical italiana de la Edad Media y se puede ver un estupendo vídeo relacionado que se emitió, hace algún tiempo, en el programa de televisión Más por Menos.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana.
El autor de este artículo, la edición de las imágenes y la programación del puzle es Ángel Cabezudo Bueno y tiene licencia CC BY-NC-SA 4.0
El puzle de arrastre básico, tipo jigsaw, tiene su origen en una documentación aportada por Juan Guillermo Rivera Berrío.
Gracias por la atención que ha recibido este octavo personaje matemático y no os perdáis el siguiente.
La semana pasada en Radio Descartes, en el espacio “¿Quién es el personaje misterioso?” entrevistamos a una excepcional matemática y algebrista, expresión con la que ella misma se declaraba, conocida en los círculos científicos como “la madre del álgebra moderna”.
Resumiendo lo que nos dijo en su entrevista:
- Nació en Erlangen, Alemania en 1882 y falleció en Bryn Mawr, Pensilvania (EEUU) en 1935.
- El álgebra de su tiempo y gracias a su especial contribución, sufrió una profunda revolución. Trabajó en el campo del álgebra abstracta y una clase de sus estructuras fundamentales, los anillos, llevan su nombre.
- En 1915, en medio del conflicto bélico que supuso la Gran Guerra, se incorporó al Instituto de Matemáticas de Göttingen y colaboró con Hilbert y Klein investigando problemas sobre ecuaciones de la teoría de relatividad especial de Einstein.
- Las discusiones sobre matemáticas con sus alumnos avivaron aún más su interés en la investigación y la compensaron de sus penurias económicas por cobrar del instituto un humilde sueldo como ayudante honoraria.
- Desde 1928 a 1932 las cosas mejoraron para ella. Fue profesora visitante en Moscú y Frankfurt. Conferenciante en los Congresos Internacionales Matemáticos de Bolonia y Zurich. Recibió el premio memorial Alfred Ackermann-Teubner, junto a Emil Artin, por el “Avance del conocimiento matemático”.
- Por su condición de judía, emigró en 1933 a Estados Unidos expulsada de la universidad alemana por el gobierno del régimen nazi y fue contratada en Bryn Mawr College, una universidad para mujeres en Pensilvania. Muere aquí dos años más tarde víctima de un tumor.
Hoy, trascurrida una semana, corresponde desvelar su identidad, como sigue siendo habitual, a través un puzle realizado con DescartseJS.
La imagen del puzle tipo jigsaw (piezas irregulares), representa una fotografía de esta genial matemática apoyada en la barandilla de la cubierta de un barco, de espaldas al mar que se ve de fondo, quizá en su viaje de exilio hacia los EEUU de América.
Las 16 piezas barajadas, obtenidas al cortar la fotografía, se sitúan amontonadas a la derecha de la escena. Para descubrir a nuestro personaje misterioso hay que montar estas piezas sobre una cuadrícula de 4x4 cuadros, a la izquierda de la escena, arrastrándolas con clic mantenido y soltándolas sobre el cuadro correspondiente donde quedan encajadas. Si la pieza se sitúa correctamente ya no es posible arrancarla de su cuadro. Si se montan dos piezas sobre un mismo cuadro, éste, quedará resaltado con color rojo advirtiendo de esta situación.
Inicialmente, a modo de ayuda, se puede ver detrás de la cuadrícula la foto poco contrastada y tonalidades muy suaves. Un control de tipo botón permite ocultarla y así se sugiere para que el montaje del puzle suponga un mayor reto.
Cuando el puzle se completa aparece a la derecha de la foto el nombre del personaje, su caricatura en color y se escucha su saludo sacado de la entrevista.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana.
El autor de este artículo, la edición de las imágenes y la programación del puzle es Ángel Cabezudo Bueno y tiene licencia CC BY-NC-SA 4.0
El puzle de arrastre básico, tipo jigsaw, tiene su origen en una documentación aportada por Juan Guillermo Rivera Berrío.
Gracias por la atención que ha recibido este séptimo personaje matemático y no os perdáis la nueva entrevista en este blog de difusión.
La semana pasada en Radio Descartes, en el espacio “¿Quién es el personaje misterioso?”, entrevistamos a una matemática excepcional que vivió desde 1850 a 1891. Considerada como la más grande anterior al siglo XX, destacó por dos ideas fundamentalmente, como nos dijo la profesora de la universidad de Estrasburgo Michèle Audin (nacida en 1954): Su famoso teorema, asociado al nombre de Cauchy, que asombró a su maestro Weierstrass, prueba que no siempre una ecuación en derivadas parciales con coeficientes analíticos y condiciones iniciales analíticas tiene solución analítica y el estudio dificilísimo del movimiento de rotación de un cuerpo sólido alrededor de un punto fijo, cuya modelización matemática conduce a un sistema de ecuaciones diferenciales y por el que le concedieron en 1888 el Premio Bordin de la Academia de las Ciencias de París.
Hoy, trascurrida una semana, corresponde desvelar su identidad, como sigue siendo habitual, a través de una escena de DescartesJS que presenta tres imágenes que se pueden ir seleccionando sucesivamente a través de un control de botón. Cada imagen ha sido recortada en 24 cuadrados que pueden girar 90 grados alrededor de su centro cada vez que se hace clic con el ratón sobre cada uno de ellos hasta completar una vuelta completa. Esto es lo que conocemos como puzle giratorio. Un contador indica el número de piezas que están correctamente rotadas con lo que se puede saber si el puzle ha sido armado y en su caso cuantas piezas nos faltan por obtener la imagen definitiva.
La primera imagen representa el DOODLE que GOOGLE-RUSSIA dedicó el día 15 de enero de 2014 a nuestra matemática rusa en el 164 aniversario de su nacimiento.
La segunda imagen es una composición de una fotografía de nuestra matemática muy joven, quizá recién casada, poco antes de salir de su Rusia natal en 1869 para estudiar en Heidelberg y un retrato de su maestro Carl Weierstrass con quien estudió posteriormente en Berlín.
La tercera imagen representa las portadas de tres libros que tratan de nuestra matemática. Uno de ellos se menciona al final de la entrevista que la hicimos, el titulado “Demasiada felicidad” de Alice Munro, Premio Nobel de Literatura en 2013. Los otros libros son “Recordando a…” de Michèle Audin, a la que ya hemos mencionado anteriormente y “Love and Mathematics” de Pelageya Polubarinova-Kochina (1899-1999), jefa del departamento de mecánica teórica de la Universidad de Novosibirsk.
El autor de este artículo, la edición de las imágenes y la programación del puzle es Ángel Cabezudo Bueno y tiene licencia CC BY-NC-SA 3.0.
El puzle giratorio básico tiene su origen en una documentación aportada por Juan Guillermo Rivera Berrío.
Gracias por la atención que ha recibido este sexto personaje matemático y no os perdáis el septimo podcast que emitiremos el próximo día 3 de noviembre en este blog de difusión.
