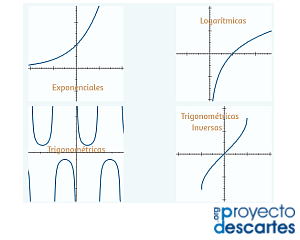
Funciones trascendentes
Título: Funciones trascendentes
Sección: Miscelánea
Bloque: Cálculo
Unidad: Funciones elementales
Nivel/Edad: Bachillerato y Universidad (17 años o más)
Idioma: Castellano
Autor: José R. Galo Sánchez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Análisis matemático para Bachillerato
Título: Análisis Matemático para Bachillerato
Sección: iCartesiLibri
Bloque: Análisis Matemático
Unidad: Funciones, límites, derivación e integración
Nivel/Edad: 2º Bachillerato y Universidad (17 años o más)
Idioma: Castellano
Autores:
José R. Galo Sánchez y María José García Cebrian
ISBN: 978-958-52963-7-4
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Curso de libros interactivos
Título: Curso de libros interactivos
Sección: iCartesiLibri
Bloque: Formación
Unidad: Formación en Descartes JS
Nivel/Edad: Bachillerato y Universidad (16 años o más)
Idioma: Castellano
Autores: Juan Guillermo Rivera Berrío y Joel Espinosa Longi
ISBN: 978-958-52963-8-1
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los libros interactivos de iCartesiLibri en
https://proyectodescartes.org/iCartesiLibri/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Volumen VI de la publicación periódica "Recursos educativos interactivos de RED Descartes"
Nuestra organización no gubernamental "Red Educativa Digital Descartes" (RED Descartes) ha publicado el sexto volumen de su publicación periódica anual
Recursos educativos interactivos de RED Descartes
ISSN: 2444-9180 Dep. Legal: CO-2079-2015
Este volumen consta de tres números y recogen todos los materiales que se han desarrollado a lo largo del año 2020 y aquellos que han sido modificados durante dicho periodo. Los contenidos de cada número son los siguientes:
- Vol. VI-Núm. 1:.
- Competencias.
- iCartesiLibri.
- Ingeniería.
- Plantillas.
- Prometeo.
- Vol. VI-Núm. 2:
- ED@D.
- Misceláneas.
- Vol. VI-Núm. 3:
- Aplicaciones de juegos didácticos en el aula.
Estos DVD se pueden descargar desde la zona de descargas de nuestro espacio web.
Enhorabuena a todas y todos los socios de RED Descartes por la publicación de este nuevo volumen, el cual ayudará a la difusión del trabajo altruista que realizan en pro de la Educación en la aldea global, gracias a las TIC.
Vol. VI
Materiales publicados en DVD.
ISSN: 2444-9180 Dep. Legal: CO-2079-2015
| Vol. VI, enero de 2021 | ||
 |
 |
|
| Vol. VI - Núm. 1 (3,1 GB) | Vol. VI - Núm. 2 (2,4 GB) | |
|
Incluye todos los nuevos materiales desarrollados y sólo aquellos que se han actualizado durante 2020 correspondientes a los subproyectos: Competencias, iCartesiLibri, Ingeniería, Plantillas y Prometeo. |
Incluye todos los nuevos materiales desarrollados y sólo aquellos que se han actualizado durante 2020 correspondientes a los subproyectos: ED@D y Misceláneas. |
|
 |
||
| Vol. VI - Núm. 3 (3,2 GB) | ||
|
|
Incluye los materiales actualizados del subproyecto "Aplicaciones de juegos didácticos en el aula". |
| Portadas, contraportada y galletas de los DVD |
Nota: La imagen que ha servido de base para la portada y galleta de los DVDs ha sido tomada desde pixabay.com