Las coordenadas geográficas
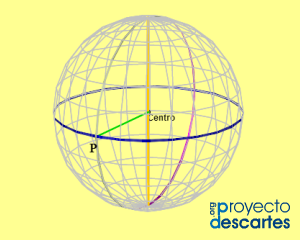 Título: Las coordenadas geográficas
Título: Las coordenadas geográficas
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría tridimensional
Nivel/Edad: 3º ESO (12-14 años)
Idioma: Castellano
Autoría: Josep Mª Navarro Canut
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm
Este material está publicado bajo una licencia:

Creative Commons Atribución-NoComercial- CompartirIgual 3.0.
Dos progresiones aritméticas sobre elementos geométricos
 Título: Dos progresiones aritméticas sobre elementos geométricos
Título: Dos progresiones aritméticas sobre elementos geométricos
Sección: Miscelánea
Bloque: Álgebra
Unidad: Números y operaciones
Nivel/Edad: 3º ESO (12-14 años)
Idioma: Castellano
Autoría: Josep Mª Navarro Canut
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm
Este material está publicado bajo una licencia:
Baricentro de un triángulo
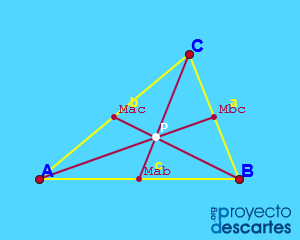 Título: Baricentro de un triángulo
Título: Baricentro de un triángulo
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: 1º ESO (12-14 años)
Idioma: Castellano
Autoría: Josep Mª Navarro Canut
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm
Este material está publicado bajo una licencia:

Creative Commons Atribución-NoComercial- CompartirIgual 3.0.
Cálculo de divisores
Sección: Miscelánea
Bloque: Álgebra
Unidad: Números y operaciones
Nivel/Edad: 1º ESO (12-14 años)
Idioma: Castellano
Autoría: Juan Madrigal Muga
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm
Este material está publicado bajo una licencia:
Diagonales de polígonos regulares
 Título: Diagonales de polígonos regulares
Título: Diagonales de polígonos regulares
Sección: Miscelánea
Bloque: Geometría
Unidad: Geometría plana
Nivel/Edad: 1º ESO (12-14 años)
Idioma: Castellano
Autoría: Josep Mª Navarro Canut
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de Miscelánea en https://proyectodescartes.org/miscelanea/index.htm
Este material está publicado bajo una licencia:








